Transformations and representations supporting spatial perspective taking

Abstract

Spatial perspective taking is the ability to reason about spatial relations relative to another’s viewpoint. Here, we propose a mechanistic hypothesis that relates mental representations of one’s viewpoint to the transformations used for spatial perspective taking. We test this hypothesis using a novel behavioral paradigm that assays patterns of response time and variation in those patterns across people. The results support the hypothesis that people maintain a schematic representation of the space around their body, update that representation to take another’s perspective, and thereby to reason about the space around their body. This is a powerful computational mechanism that can support imitation, coordination of behavior, and observational learning.

Spatial perspective taking is the ability to understand spatial relations relative to a viewpoint different than one’s own. This ability is important for communication and as a means to explore hypothetical situations. For example, one way to give driving directions is to imagine driving the route while calling out the left and right turns relative to the imaginary viewpoint. Spatial perspective taking is described by conventional metaphors such as “Seeing things from someone else's point of view,” and “standing in someone else's shoes.” Spatial perspective taking is important for navigation and for interacting with objects and people in everyday task performance (David et al., 2006; Wolbers & Hegarty, 2010). Previous studies of spatial perspective taking have focused either on the mental representations that people construct during perspective taking or on the mental transformations that people perform in order to take a spatial perspective. Here, we combined chronometric measures of representational format and of transformational computation to test a new mechanistic account of how spatial perspective taking works.

Representations

Spatial perspective taking depends on specialized representations, particularly spatial reference frames and spatial frameworks. Spatial reference frames are representations that locate things in space. Psychologically relevant reference frames can be divided into three categories: egocentric, object-centered, and environment-centered (McCloskey, 2001). Egocentric reference frames locate things with respect to one’s body, for example “on my left” or “in front of me.” Object-centered reference frames locate things with respect to the intrinsic structure of an object, for example “the front of the plane” or “the bottom of the cup.” Environment-centered reference frames locate things with respect to the environment they are situated in, for example “the end of the hallway” or “the top of the mountain.”

A spatial framework is a type of mental model that represents the space near one’s body in an egocentric reference frame. Spatial frameworks were proposed to account for how people access information about objects in their nearby environment (Franklin & Tversky, 1990). According to spatial framework theory, the speed of locating an object relative to the egocentric reference frame is influenced by schematic knowledge about ecological regularities and by one’s current posture. Most important, the ease of locating an object with respect to the head-feet, front-back, and left-right axes is proposed to vary predictably. For an upright observer, the head-feet axis is predicted to be the most accessible of all three axes. This is because the head-feet axis is aligned with two powerful asymmetries: the direction of gravity and the direction from head to foot in the body. Gravity is unique in that it provides a constant directional signal independent of which direction the upright observer is facing, and the head-to-foot direction is important because objects near the head afford very different interactions (e.g., grasping) than objects near the foot (e.g., kicking). The front-back axis is predicted to be the second most accessible for an upright observer because it is aligned with the front-back asymmetry of the body, which like the head-to-foot asymmetry determines which actions are afforded: Objects in front of the body are graspable, whereas those behind the body. This also entails an asymmetry in this axis, such that objects in front are more accessible than objects behind. Finally, the left-right axis is predicted to be the least accessible because it is aligned with no stable external asymmetry such as gravity and because the human body is roughly left-right symmetric. According to spatial framework theory, this pattern of accessibility should change if the person were to lie down. Now, the front-back axis would be aligned with gravity; as a result, its accessibility should increase and the accessibility of the head-feet axis should decrease.

Franklin and Tversky (1990) originally demonstrated spatial framework use in participants who read narratives describing scenes with objects around a second-person protagonist (e.g. “Directly behind you, at your eye level, is an ornate lamp attached to the balcony wall”). A subsequent study (Bryant, Tversky, & Franklin, 1992) found similar results using narratives written from a third person perspective, and even using narratives in which the central character was an inanimate object such as a tool box or a chair. Spatial framework patterns also have been observed in judgments relative to one's own body in a real-life scene (Bryant, Tversky, & Lanca, 2001), a model scene featuring a doll (Bryant, Lanca, & Tversky, 1995), and in 2-dimensional diagrams with depth represented along a diagonal line (Bryant & Tversky, 1999). These results suggest that when people are asked to imagine a scene from another viewpoint, they may form a spatial framework that represents the locations of objects relative to an imagined egocentric reference frame. The formation of that spatial framework would then constitute perspective taking. For example, suppose you were standing with a colleague, noticed that they had a piece of tape stuck to their clothing, and were planning an action or utterance to assist them. Spatial framework theory predicts that you might form a spatial framework corresponding to your colleague’s body position. You should then be able rapidly to verify whether the tape was near their head or feet, more slowly to verify whether the tape was in front of them or behind them, and slowest to verify whether the tape was on their left or right side.

However, people may solve such tasks using alternative strategies. For example, Bryant and Tversky identified a potential alternative strategy that does not involve forming a representation in an egocentric reference frame, which they dubbed an intrinsic computation strategy (Bryant & Tversky, 1999; Bryant et al., 2001). In this strategy, rather than constructing a spatial framework from the point of view of the other person, the viewer maintains an outside perspective and relies on the object-centered reference frame of the person. This strategy does not involve any perspective taking; rather, all the computations are carried out from one’s actual perspective. For upright human bodies, the two strategies make very similar response time predictions, for somewhat different reasons. When using an intrinsic computation strategy, one quickly identifies the person’s top-bottom (head-feet) axis because it is elongated and because the head is functionally salient. Then the observer identifies the front-back axis, and finally can derive the left-right axis from the previous two axes. The relative location of an object can then be determined relative to this constructed representation.

One difference between the spatial framework and intrinsic computation strategies is their predictions for figures in non-upright postures. The intrinsic computation strategy predicts the same relative pattern of response times to the three axes when the figure is not upright, because axes are identified and accessed in the same relative order regardless of the figure’s orientation. The spatial framework strategy predicts that access to the head-feet axis is no longer the fastest when non-upright because it is no longer aligned with the environmental upright. Therefore, only when people use a spatial framework strategy should posture influence the accessibility of the head-feet and front-back axes. An additional difference between the two strategies is that the spatial framework strategy strongly entails that objects in front are more accessible than objects behind. The intrinsic computation makes no such prediction. This prediction is mostly supported by the available data (Bryant, Tversky & Frankly, 1992; Bryant et al., 2001; but see Bryant & Tversky, 1999). Table 1 specifies response time predictions for spatial frameworks and intrinsic computation.

Table 1.

Predicted patterns of response times for each of the three representational strategies, based on body position.

	Posture
Representational strategy	Upright	Reclining
Spatial framework	Head/Feet < Front/Back < Left/Right	Front/Back < Head/Feet < Left/Right
	Front < Back	Front < Back
Intrinsic computation	Head/Feet < Front/Back < Left/Right	Head/Feet < Front/Back < Left/Right
	Front = Back	Front = Back

In sum, one way of describing spatial perspective taking is in terms of the representations people establish to reason about another person. Spatial frameworks provide a theoretically coherent account of these representations. Using a spatial frameworks analysis, perspective taking can be distinguished from alternative reasoning strategies that do not involve perspective taking, such as the intrinsic computation strategy.

Transformations

Spatial framework theory gives an account of the representations underlying spatial perspective taking, but is mute regarding the transformations (or computations) that operate on those representations. Other theories specify the transformations but are vague in characterizing the representations on which they operate. One computational account of perspective transformations comes from the multiple systems framework (Zacks & Michelon, 2005; Zacks & Tversky, 2005), which builds on proposals by Piaget and Inhelder (1956, 1971), Parsons (1987), and others to distinguish different sorts of computations that underlie different forms of spatial reasoning. The multiple systems framework proposes that one way of performing spatial perspective taking is by a transformation that continuously updates the viewer’s egocentric reference frame until it corresponds with the egocentric reference frame that is to be imagined. This is called a perspective transformation (Zacks, Vettel, & Michelon, 2003; Zacks & Tversky, 2005). In terms of the three reference frames described previously, a perspective transformation involves updating an egocentric reference frame relative to fixed object-centered and environment-centered reference frames. Consider again the example of encountering a colleague afflicted with tape stuck to their clothing. You might imagine your egocentric perspective translating and rotating as it would if you walked and turned so as to stand next to your colleague. Researchers interested in spatial transformations often study perspective taking using tasks that require the participant to locate something relative to another person’s egocentric reference frame (e.g., “Is the student raising their right hand?”). In such tasks, participants often report imagining themselves in the alternative perspective (Yu & Zacks, 2010; Zacks & Tversky, 2005). In several experiments, the orientation relationship between the observer’s perspective and the participant’s perspective (also known as orientation disparity) has been manipulated across trials. In such tasks, the time to make location judgments depends non-monotonically on both the orientation disparity and on the plane of rotation. Parsons (1987) found the same patterns when participants were explicitly instructed to perform a perspective transformation, and argued from this that his participants were using perspective transformations to perform the perspective-taking task.

However, people may sometimes use mechanisms other than perspective transformations to perform perspective-taking tasks. One alternative strategy is to transform an object-centered reference frame, an object-based transformation (Zacks & Tversky, 2005). For example, the lecturer in our previous example could simulate rotating the student’s body so that they both face the same direction, rather than updating her own perspective. In the present experiments, we used a task setup that was designed to encourage perspective transformations and discourage object-based transformations, based on previous studies (Presson, 1982; Wraga, 2000). These studies showed that when participants are asked to perform an object-based rotation of an array of objects, they tend to perform a piece-wise translation of the object being probed rather than holistically rotate the array. If an additional object is probed or if the object to be probed is not known before the transformation is performed, performance breaks down. To discourage the use of object-based transformations in the present studies, we used arrays multiple objects and probed items unpredictably.

Participants may also adopt a strategy that does not involve a spatial transformation at all. For example, when asked whether an object is visible from another perspective, people may respond by tracing a line of sight from the imagined viewer to the object and checking whether the line intersects any obstacles (Michelon & Zacks, 2006). In child development, Flavell and colleagues dubbed this “level 1” perspective-taking, and distinguished it from “level 2” perspective-taking, which corresponds to performing a perspective transformation (Flavel, Everett, Croft, and Flavel, 1981). Crucially, if one takes a non-transformation strategy then response times should not depend on the orientation of the to-be-adopted perspective. (Instead, as Michelon & Zacks showed, response times depend on the length of the line of sight from the imagined perspective to the imagined object.)

In sum, a second way of describing perspective taking is in terms of the transformations or computations that underlie it. Often, the transformation underlying performance on a perspective taking task may be a perspective transformation; however, other strategies may be used in some cases.

A hypothesis regarding the relations between representations and transformations in perspective taking

Of course, a complete account of perspective taking needs to offer a unified account of both its representation-oriented and transformation-oriented aspects. Surprisingly, very little is known about how spatial transformation use and spatial representation use correspond. Here, we propose a computationally explicit hypothesis that brings together representation-oriented and transformation-oriented accounts of perspective taking: When people use a perspective transformation to perform a perspective-taking task, the result is a spatial framework. And, conversely, when people rely on a spatial framework to perform such tasks, they do so by performing a perspective transformation.

A spatial framework is a mental model constructed within a real or imagined egocentric reference frame. A perspective transformation updates one’s imagined egocentric reference frame. The research reviewed here associates both the use of spatial frameworks and the performance of perspective transformations with perspective-taking tasks. The representation-oriented view provided by studies of spatial frameworks fits nicely with the transformation-oriented view provided by studies of perspective transformations to converge on the hypothesis just stated. If it is true, then situations that encourage participants to use perspective transformations should also encourage them to use spatial frameworks, and individuals who show signs of using spatial frameworks also should show signs of performing perspective transformations. That is, measures spatial framework use and perspective transformation performance should vary similarly across experimental conditions and across individuals. If the hypothesis is false, then there should be no relationship between the behavioral indices even when there is evidence for each process in isolation. We tested this hypothesis using a novel paradigm that allowed us to measure indices of participants’ spatial representation use and spatial transformation performance simultaneously in a common task.

Experiment 1

The first experiment was designed to test the hypothesis that the result of using a perspective transformation to reason about the space around another person is a spatial framework aligned to that person’s reference frame. We started from a procedure developed by Bryant, Tversky, and Lanca (2001), in which participants learned the locations of an array of objects from a picture, and then were asked to assume an imagined perspective indicated by a picture of a man (the avatar) and to locate objects relative to that imagined perspective. In many previous spatial framework studies, the orientation of the figure was fixed over a larger number of probes and then manipulated in a systematic fashion by rotating it 90° around its vertical axis in a clockwise or counter-clockwise fashion (Bryant & Tversky, 1999; Franklin et al., 1992; but see Franklin, Tversky, & Coon, 1992). Unlike those previous studies, in Experiment 1 we manipulated the orientation of the avatar more frequently and in a pseudo-random fashion so that the avatar’s orientation on any given trial was unpredictable. This allowed us to test the hypothesis that participants use perspective transformations to reason about misaligned avatars, by measuring the time taken to prepare for each new orientation. Based on previous studies, we chose rotation directions such that use of perspective transformations should result in increasing response time with increasing orientation disparity (Parsons, 1987), allowing us to test whether they were performing a perspective transformation. In the same task, we could test whether participants used spatial frameworks by measuring how long it took them to respond to location probes as a function of target location. As described previously, when people use spatial frameworks they show a characteristic pattern of location probe times (Franklin & Tversky, 1990).

We expected individual participants to vary in the degree to which they used perspective transformations and spatial frameworks. To the extent to which they performed a perspective transformation, the time it should take to adopt a new perspective should increase with increasing orientation disparity; to the extent that they adopted a non-transformation strategy, this should not be the case. To the extent to which they utilized spatial frameworks, their response times when asked to locate objects from the imagined perspective should vary as indicated in the top row of Table 1; to the extent that they used an intrinsic computation strategy, their responses times should vary as indicated in the bottom row. Importantly, if performing a perspective transformation results in a spatial framework, then people who show chronometric evidence of performing perspective transformations should also show chronometric evidence of using a spatial framework, and those who fail to show evidence of performing perspective transformations should not.

In this paradigm, we expected that participants would adopt a consistent strategy across trials. To preview an important surprising result, we found evidence that viewers may adopt different strategies depend on whether the imagined perspective is upright or lying down (supine or prone).

Method

Participants

Fifty-four participants (36 female, age 18-22) were recruited using the Washington University Psychology Department subject pool.

Task

The task was designed to measure two components of the perspective-taking process: adopting the perspective of an avatar, and then locating a particular object relative to that perspective. Participants first memorized an array of objects from a picture, memorizing the locations of the objects from their own perspective (Figure 1, top). They then completed a series of trials, each consisting of two phases (Figure 1, bottom): 1) a preparation phase in which participants studied a picture depicting the avatar in an upright, supine, or prone pose at an orientation disparity between 0° and 180° (Figure 2), and 2) a probe phase where an object name probe was presented auditorily and participants were asked to locate the named object relative to the avatar’s egocentric perspective, by moving a Nintendo Wii remote (Kyoto, Japan) in the appropriate direction using their dominant hand. Two probes were presented in each trial.

Figure 1.

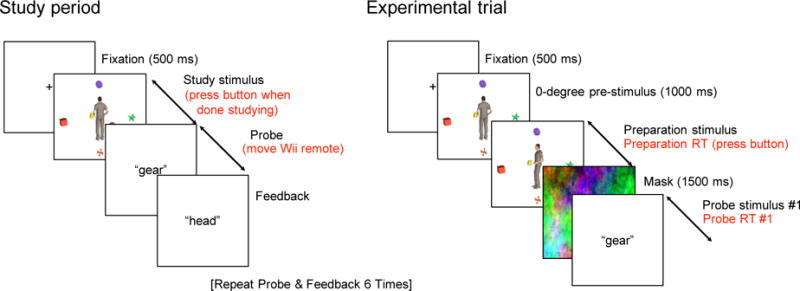
Sequence of events study period (left) and in a single experimental trial (right) in Experiment 1. Participant inputs are labeled with red text. Probes and feedback in quotation marks were presented as synthesized speech.

Figure 2.

Examples of each of the orientations and postures in Experiment 1.

Trials were grouped into blocks consisting of a study period followed by 48 trials. During the study period, participants viewed a scene consisting of six objects and an avatar facing away from the participant. The instructions asked the participant to adopt the perspective of the avatar, and to try to remember the locations of objects relative to the avatar’s perspective. Participants were instructed to study the scene for as long as they wished, and to press a button on the button box when they believed that they were familiar with the locations of the items in the scene. After doing so, they responded to six consecutive object name probes by moving the Wii remote at least 15 cm in the appropriate direction. If all six probes were answered correctly by an appropriate movement in the correct direction, the experimenter ended the study period and started the test period before leaving the room. If at least one probe was answered incorrectly, the study period was restarted so that the participant had a chance to study the scene again. To discourage verbal coding, participants were asked not to repetitively rehearse the objects’ names. The experimenter pointed at the objects located at the avatar’s head, feet, front, back, left, and then right locations in an example figure while giving this instruction.

The participant then completed 48 experimental trials, each consisting of a preparation phase and two probe responses, as illustrated in Figure 1. At the start of each trial in the test period, participants viewed a brief reminder of the study scene for 1000 ms. The reminder was exactly the same image as the one depicting the avatar at 0° orientation disparity. After the reminder image, participants saw a blank white screen for 500 ms, which was immediately followed by the test scene depicting a reoriented avatar. This scene was exactly the same image as the study scene reminder in the case of 0° disparity trials. Participants were instructed to adopt the perspective of the avatar and to try to remember the locations of the objects relative to that position. The test scene remained on the screen until the participant pressed a button on the button box to indicate their readiness to proceed. This latency of this response relative to the onset of the test scene was considered to be the preparation RT. A multi-colored mask was presented for 1500 ms after the test scene to prevent participants from responding to probes on the basis of a sensory trace of the scene. After the mask, the first object-name probe was presented auditorily, and participants were given 3250 ms to make their response by moving the Wii remote. We defined the probe RT as the movement onset latency relative to the onset of the object name probe. At the end of each response period, even when participants failed to initiate a response, the correct answer was presented auditorily as a single direction term (“head”, “feet”, “front”, “back”, “left”, or “right”). A second object name probe was then presented in the same fashion as the first and then followed by the correct answer. Participants were instructed to move the Wii remote back to the starting position after making their first response, which allowed them to respond to the first and second probes from the same starting position.

Design

Each participant’s session consisted of at least three blocks of 48 experimental trials; only data from the first three blocks were analyzed. Across the 48 experimental trials per block, three variables were manipulated: the orientation disparity of the avatar (0°, 90°, or 180°), the location of the cued object (head, feet, front, back, left, right), and the posture of the avatar (upright, prone, or supine). Our primary focus was on upright trials, because the response time predictions for the effects of orientation disparity on perspective transformations are strongest for upright figures (Parsons, 1987). Supine and prone trials were included primarily to test the prediction from the spatial framework analysis that the head-foot axis would be most accessible for upright avatars whereas the front-back axis would be most accessible for supine and prone avatars. Orientation disparity on the upright trials was fully counterbalanced within each block and presented in pseudorandom order. Orientation disparity on non-upright trials was partially counterbalanced within each block, where each unique orientation was associated with either the prone or supine posture in a given block. Assignments were reversed for the next block, ensuring complete sampling with each set of two blocks. Location was partially counterbalanced within each trial (containing two probe responses) according to the following scheme. Participants were asked to identify the location of one of the six objects in the scene as the first probe response. For the second probe response, they were asked to identify the location of one of the four possible objects located on a different axis than the first object.

Stimulus rendering

The task utilized computer-rendered scenes depicting a lifelike male avatar surrounded by six objects, rendered in Poser 8 (Smith Micro, Aliso Viejo, CA). Each block used a single scene with a unique object configuration. Each scene was rendered stereoscopically for every possible orientation disparity value (0°, 90°, 180°, and 270°) for each of the three posture conditions (upright, prone, and supine). The virtual cameras were placed so that they were above and slightly to the left of the avatar at 0° orientation disparity to avoid occlusion of any objects by the avatar’s body. Example stimuli and additional details are provided in Appendix A of the online supplement.

Apparatus

Stimuli were presented on a 20” Apple iMac computer running PsyScope X (http://psy.ck.sissa.it). The computer’s display was situated approximately 80 cm from the participant’s eyes. A stereoscopic viewing device was used to present images with depth cues to the participant. The device contained a set of adjustable mirrors to present only half of the display to each eye, making the effective field of view approximately 15° in each eye. A dark shroud was placed around the viewing device and the computer to block out ambient light and to heighten the illusion of depth by occluding the edges of the computer display. Participants responded using a button box with their non-dominant hand and a Nintendo Wii remote held in their dominant hand. The viewing and response devices were placed at the right edge of the table for right-handed participants and the left edge for left-handed participants, allowing participants to move their dominant hand freely in any direction without hitting the table. Triggers associated with stimulus events and button presses were sent by PsyScope X through a cable and registered as button presses on the Wii remote. These triggers were recorded along with movement data from the Wii remote using OSCulator (http://www.osculator.net). This allowed probe RTs, derived from the movement data, to be measured relative to the onset of the object name probe.

Procedure

At the start of the experiment, a practice version of the procedure was administered, consisting of a study period and a test period with four to six experimental trials. This was followed by the main experimental blocks of study and experimental trials. After participants had finished 3 blocks or 110 minutes of participation, the experimenter stopped the computer procedure and the participant completed a strategy questionnaire with a free-response question asking them to describe their strategy for performing the task. Upon finishing, participants were asked whether they had followed the experimenter’s instruction to avoid using a verbal reciting strategy, and if not, to indicate when they had used such a strategy.

Results

A total of 54 participants were run. Thirteen were excluded for failing to complete three blocks of the experiment within 110 minutes. Early in testing, some participants who completed the three blocks in under 110 minutes were allowed to complete additional testing blocks (which were not analyzed). Six participants were excluded for having error rates greater than 40% in any posture condition. Data from the remaining 35 participants (22 female, 4 left-handed, age 18-22) were trimmed by excluding trials with errors in the object probe response (17.7% of all trials), those with preparation RTs less than 200 ms or exceeding the participant’s condition mean plus two standard deviations (2.5% of all trials), and finally those with irregularities in the Wii remote data, defined as trials where there was either unreadable data or a sample-to-sample interval greater than 75 ms (3.9% of all trials). A total of 22.9% of all trials were excluded with this procedure. Three participants reported that they failed to follow the experimenter’s instructions on a subset of trials. Their responses to the question about when they used a verbal reciting strategy were: “sometimes”, “the first few blocks”, and “for the first few trials in block 2”. These participants were examined separately in the key analyses but their data did not differ substantially from other participants and were therefore retained in the analysis.

Perspective transformation analysis

Preparation RTs were analyzed for evidence of perspective transformations (Figure 3). Per-participant means were obtained for each unique combination of orientation (0°, 90°, and 180°) and posture (upright, supine, and prone), and submitted to a repeated measures ANOVA. Response times increased with increasing orientation, leading to a significant main effect of orientation, F(2, 68) = 5.7, p = .005, ${\mathrm{\eta }}_p^2$ = .144. Responses to upright figures were fastest and responses to prone figures were slowest, resulting in a significant main effect of posture, F(2, 68) = 51.2, p < .001, ${\mathrm{\eta }}_p^2$ = .601. The interaction between orientation and posture was also significant, F(4, 136) = 6.5, p < .001, ${\mathrm{\eta }}_p^2$ = .161; orientation had the largest effect in the upright condition and the smallest effect in the prone condition.

Figure 3.

Preparation RT (as z scores) over orientation in both experiments. Error bars in this figure and subsequent figures depict the standard error of the mean across participants.

As can be seen in the upper left panel of Figure 3, the relationship between orientation and response time for upright figures was not strictly linear as predicted (Parsons, 1987, but see Wraga, Creem & Proffitt, 2000). At the individual level, a substantial number of participants showed an increase in response time from 0° to 90° but did not show further slowing at 180° (18 of 35 participants). We will return to this finding in the Discussion.

To summarize perspective transformation use by each participant, an orientation dependence measure was calculated using the Pearson product-moment correlation coefficient between the orientation disparity value on each trial and the associated preparation response RT. We used only the upright condition because it is the only condition for which the predicted influence of orientation disparity is straightforward and linear (Parsons, 1987). To ensure stable variance across the range of the r statistic, we converted all orientation dependence values using Fisher’s z-transformation before submitting them to two-tailed t tests. At the individual level, 30 out of 35 participants exhibited orientation dependence scores greater than zero. At the group level, preparation RTs were significantly orientation dependent [mean r = .183, t(34) = 6.9, p < .001, d = 1.16].

Probe response and spatial framework analysis

The motion data for each probe response were processed off-line after the experiment. Appendix B of the online supplement describes the complete procedure for calculating probe response time and accuracy. We defined probe RT z score residuals (subsequently referred to as “probe RT”) as the z scores of movement initiation times after controlling for the linear effects of orientation disparity and block number and on a per-participant basis. Probe RTs for each probe direction are depicted in Figure 4. In the upright avatar condition, the fastest responses were to head-feet locations, which were faster than responses to front-back locations (t(34) = 4.6, p < .001, d = .77) and left-right locations (t(34) = 6.3, p < .001, d = 1.07). Responses to front-back locations were faster than to left-right locations (t(34) = 3.1, p = .004, d = 0.52). There was a strong asymmetry in front-back probe RTs, where “front” responses were much faster than “back” responses (t(34) = 7.9, p < .001, d = 1.44). Other axes did not have significantly asymmetric probe RTs. We first used the head/feet < front/back < left/right criterion to determine whether participants used spatial frameworks. When considering only the upright trials using this method, 16 out of 35 participants conformed to the expected spatial framework pattern of axis dependence. We also looked for front/back < head/feet < left/right responses from non-upright trials in order to distinguish a spatial framework strategy from an intrinsic computation strategy. Taking this relatively strict approach, only 5 out of 35 participants were classified as using spatial frameworks. A number of participants exhibited the pattern predicted by an intrinsic computation strategy (head-feet < front-back < left-right even in non-upright conditions): 12 in the supine condition, and 8 in the prone condition.

Figure 4.

Probe RT z-score residuals across all canonically-located probe directions in both experiments.

To summarize spatial framework use in individuals, we calculated two summary scores. The first was an axis dependence score, computed by taking the correlation between probe RT z scores and the predicted pattern of RTs. For upright trials, we used predicted values of -1, 0, and 1 for the head-feet, front-back, and left-right axes, respectively. For non-upright trials, values of -1, 0, and 1 were used. Values greater than zero are consistent with spatial framework use, while values near zero or less than zero are inconsistent with spatial framework use. Fisher’s z-transformed axis dependence scores were tested for difference from zero by t tests. For upright trials, mean axis dependence was greater than zero (mean = .178, t(34) = 6.6, p < .001, d = 1.12) and 30 out of 35 participants exhibited axis dependence values greater than zero. Contrary to the expected spatial framework pattern (and to the pattern expected from an intrinsic computation strategy), axis dependence did not differ from zero for either prone trials (mean = −.024, t(34) = 0.68, p = .500, d = 0.12) or supine trials (mean = −.011, t(34) = -0.37, p = .710, d = 0.06).

The second index of spatial framework use was the back minus front difference, defined as the difference between probe RTs to “back” and “front” objects. Positive values indicate faster responses in the front direction relative to the back direction, as expected for participants using spatial frameworks but not for those using an intrinsic computation strategy. This score was significantly greater than zero across all postures (upright: t(34) = 8.5, p < .001, d = 1.44; supine: t(34) = 4.1, p < .001, d = 0.70; prone: t(34) = 4.8, p < .001, d = 0.81), which argues against the possibility that particicipants were frequently using an intrinsic computation strategy.

Together, axis dependence and the back minus front difference indicate the degree to which a participant’s responses conform to the two main predictions of spatial framework theory. Axis dependence scores were weakly correlated with the back minus front difference (r = .168). Table 2 shows the number of participants with positive scores on both spatial framework measures. In total, 30 out of 35 participants in the upright avatar condition exhibited both patterns consistent with the use of spatial frameworks. Only 15 and 11 participants exhibited such patterns for the supine and prone conditions, respectively. In sum, the axis dependence and back minus front difference gave somewhat conflicting estimates of the overall rate of spatial framework use, and the axis dependence score gave evidence that some participants may have used an intrinsic computation strategy at least some of the time. One possibility consistent with these results is that participants were more likely to adopt an intrinsic computation strategy when reasoning about supine or prone avatars.

Table 2.

Number of participants conforming to expected spatial framework patterns of response times

	Axis dependence > 0	Back minus front > 0	Both measures > 0
Experiment 1
Upright	30 (85.7%)	33 (94.2%)	30 (85.7%)
Supine	20 (57.1%)	25 (71.4%)	15 (42.9%)
Prone	14 (40%)	28 (80%)	11 (31.4%)
Experiment 2
Upright	30 (85.7%)	25 (71.4%)	21 (60%)
Supine	16/29 (55.2%)	18/29 (62.1%)	10/29 (34.5%)
Prone	12/33 (36.4%)	12/33 (36.4%)	2/33 (6.1%)

Note: Denominator is 35 unless otherwise specified.

Relations between measures of perspective transformations and measures of spatial frameworks

To test our primary hypothesis, that measures of perspective transformations would be correlated across individuals with measures of spatial framework use, we examined whether orientation dependence of the preparation RTs predicted the patterns of probe RTs for upright figures (axis dependence and the back minus front difference). Again, we used only the upright condition because it is the only condition for which the predicted influence of orientation disparity is straightforward and linear. As hypothesized, axis dependences were positively correlated with orientation dependence (r = .365, p = .03). Contrary to our predictions the correlation between the back minus front difference and orientation dependence was not significant (r = -.149, p = .41). Both relationships are plotted in Figure 5.

Figure 5.

Relationship between spatial framework measures and orientation dependence for upright avatar trials in Experiment 1. Orange best-fit line denotes significant correlation (uncorrected p < .05) while dashed blue line indicates non-significant correlation.

Discussion

Overall, participants showed evidence of using both perspective transformations and spatial frameworks for reasoning about the space around another person’s body. There was evidence for the hypothesized relationship: Participants who showed evidence of using perspective transformations in the pattern of their preparation RTs also showed evidence of using spatial frameworks as measured by axis dependence in their probe RTs. Contrary to the hypothesis, the back minus front measure was not positively correlated with orientation dependence.

Evidence for perspective transformations, and caveats

Participants exhibited orientation dependence in their preparation responses, as evidenced by the positive correlations between orientation and preparation RT. One aspect of that orientation dependence merits further comment: Approximately half of the participants showed increases from 0° to 90° but not from 90° to 180°. One potential explanation for the discontinuity at 90° is that some participants may have used a different strategy on trials featuring 180° orientations. For example, with a “reverse” strategy for avatars facing the participant, the participant responds with a leftward movement if the object was on the right side of the screen relative to their own perspective. This can be thought of as a verbally-mediated “trick,” in which the participant rehearses something like “see left, respond right.” Another possibility is that this pattern results from performing a “blink transformation,” which is a perspective transformation in which the new reference frame is not continuously transformed from the old reference frame, but is instead generated anew from a structural description of the scene (Wraga et al., 2000). A control experiment (Appendix D in the online supplement) verified that when participants were directly instructed to imagine themselves rotating around the upright axis, response times increased from 90° to 180°, supporting the first explanation. To the extent that either of these occurred, they would have worked against the hypothesized relationship between measures of perspective transformations and of spatial framework use.

Evidence for spatial frameworks, and caveats

Group level data gave strong evidence for the use of spatial frameworks for upright avatars. At the individual level, 16 out of 35 participants exhibited the strict spatial framework pattern of response times (head/feet < front/back < left/right, and front < back), and 30 of 35 met a more relaxed criterion, where both axis dependence and back minus front measures were greater than zero. Two important caveats are in order, however. First, probe responses showed evidence that participants’ strategies varied as a function of the avatar’s pose, with spatial frameworks being less likely for supine and prone poses. This ambiguity also makes the interpretation of the data for the upright figures, which are of primary interest, less certain. Second, the two measures of spatial framework use were not strongly correlated across observers, as they would be expected to be if they measure the use of the same underlying representation.

We were concerned that the variations we saw in movement times could be contaminated by variability in the musculoskeletal difficulty of moving the Wii remote in some directions compared to others. A control experiment (Appendix D) ruled out this possibility.

In sum, results from Experiment 1 suggest that participants generally performed perspective transformations, that they formed spatial framework representations, and that individual differences in the former were related to individual differences in the latter. However, the data suggested that participants sometimes employed alternative strategies, and that these may have varied with the pose of the figure. Experiment 2 was designed to do three things: first, to replicate the primary results of Experiment 1 using a more complex and naturalistic spatial array; second, to better characterize the possible variability in strategy use; third, to try to better characterize the lack of increase in preparation response times from 90° to 180° orientation disparity for upright avatars.

Experiment 2

In Experiment 1, we found that preparation response times for upright figures increased substantially when the orientation increased from 0° to 90°, but that changes from 90° to 180° were variable across participants. One possibility is that participants sometimes used a strategy in which they coded the 180° rotations using a verbally mediated “reverse” strategy, responding on the side opposite the target on the screen rather than performing a spatial transformation. In Experiment 2, we eliminated the 180° orientation disparity condition in order to discourage the use of non-transformation strategies such as using reversed-egocentric responses, and manipulated orientation disparity in 45° increments to allow us to better characterize the orientation-dependence of responses. We expected this to strengthen the orientation dependence of responses and thus our ability to detect perspective transformations.

Experiment 1 used a small number of fixed object locations, like most other spatial framework studies. The limited number of object locations in Experiment 1 raises the possibility that participants encoded location-object relationships propositionally, as a set of categorical relations between a locational concept (“right-ness”) and an object’s identity (“ball”). Researchers have posited a distinction between categorical and metric spatial representations (Kosslyn et al., 1989). In categorical representations, objects within a particular region of space can be represented using the same abstract code (e.g., “the tree is to the left of my body”). Metric (coordinate) representations explicitly represent the quantitative locations of objects and distances between them (e.g., “the tree is 5 meters to the left of my body”). The distinction between categorical and metric representations is often related to response modality: verbalized responses are considered to reflect representations that are more categorical in nature, whereas motor responses can reflect both categorical and metric representations (Creem & Proffitt, 1998). In Experiment 2, we asked whether spatial frameworks are preferentially used to represent space only when categorical representations are unambiguous, as has typically been the case where objects were placed in distinct locations along orthogonal axes projecting from the body. In real-world environments, objects typically are located at many locations other than those on the canonical axes. If spatial framework patterns can be observed even when objects are placed irregularly around the avatar, it would suggest that spatial frameworks reflect the relative accessibility of directions even when those directions are not easily labeled with a single word like “above” or “front”. Alternatively, it could be that people use spatial frameworks only the special cases when objects are arranged solely on canonical axes, or only for objects that happen to fall near a canonical axis.

In sum, two important changes were introduced in Experiment 2. First, orientation was manipulated at a finer grain. We hypothesized that this would increase the use of perspective transformations and also yield a stronger relationship between perspective transformations and spatial framework use. Second, objects were placed in locations other than on the canonical axes. This allowed us to test the generality of spatial framework use, asking whether it is limited to situations in which objects are arranged in a regular array, or to objects falling on a canonical axis.

Method

Participants

A total of 43 participants were run. Five were excluded for failing to complete the experiment within 110 minutes. Three were excluded for having error rates greater than 40% in the upright condition.

Design

The design of Experiment 2 was similar to that of Experiment 1, with the following changes: Only 4 objects were included per scene because pilot data indicated that error rates were excessive when more than 4 objects were used. In the preparation phase, the avatar was rotated by 0°, 45°, 90°, or 135° in either the clockwise or counterclockwise direction about the vertical axis. Orientation was fully counterbalanced within the upright condition and was partially counterbalanced in the prone and supine conditions providing a total of 21 preparation RT responses per block. The ratio of upright to non-upright trials was increased to 2:1 to provide better power to detect axis-dependence in the upright trials. In the probe phase, participants were asked to identify the location of one of the four objects in the scene as the first probe response. For the second probe response, they were asked to identify the location of one of the other three objects. This procedure was designed to yield a full set of 7 (orientation disparity) × 4 (probe object) = 28 probe RT responses across 14 upright trials. The seven remaining trials in the block were split between prone and supine avatar postures. The entire experiment consisted of 8 blocks of 21 trials, yielding 168 preparation responses and 336 probe responses.

Stimuli

Participants studied stimuli depicting an avatar surrounded by four objects. The avatar adopted one of three postures (upright, supine, and prone) and faced one of seven possible orientations by rotation along the vertical axis of the scene. There were 26 possible object locations, located on a sphere centered on the avatar’s abdomen, spaced at 45° increments (Figure 6). Six were the same canonical locations used in Experiment 1. Twelve locations were located at combinations of two of the canonical directions (head-front, feet-front, head-back, feet-back, head-left, head-right, feet-left, feet-right, front-left, front-right, back-left, back-right) and the remaining eight locations were combinations of three canonical directions (head-front-left, head-front-right, feet-front-left, feet-front-right, head-back-left, head-back-right, feet-back-left, feet-back-right). For each participant, 32 object-location pairs were assigned, consisting of 20 objects at non-canonical locations and 12 objects at canonical locations. We doubled the number of objects located at canonical locations to increase power for a direct comparison with Experiment 1, yielding an overall ratio of canonical to non-canonical probes of 3:5. Scenes were constructed by shuffling the 32 location assignments across eight blocks until each scene met a set of criteria that required the objects to be spread out, not occluding each other, and not clustered on the canonical axes (see Appendix A for details).

Figure 6.

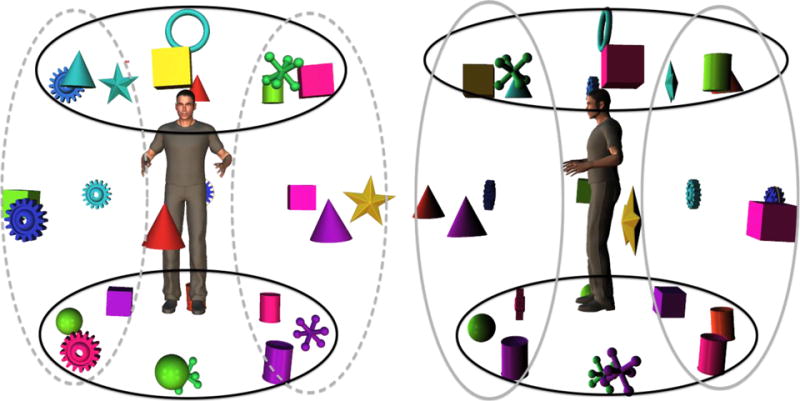
Hemisphere-based object locations. The dark solid, light solid, and light dashed ovals denote the set of object locations classified as belonging to the head-feet, front-back, and left-right hemispheres, respectively.

Apparatus

The apparatus was modified from the one used in Experiment 1 to allow participants to move the Wii remote in all 26 directions without hitting their own bodies. Participants were asked to either stand or lean against a 76 cm high bar stool while performing the task. The display, stereoscopic viewer, and response box were raised to maintain an equivalent position relative to the participant’s head across both experiments.

Procedure

At the start of the session, the experimenter explained the experimental procedure to participants, who then provided informed consent. A practice version of the experiment was administered, consisting of a study phase and a short test phase with at least four experimental trials. The example test phase was extended until the experimenter determined that the participant understood the requirements of the task.

The main experiment consisted of eight blocks. As in Experiment 1, each consisted of a study period and a test period. We made a slight adjustment to the study procedure to facilitate easier memorization: During the study period, participants first viewed a picture of a scene consisting of four objects and an avatar in the 0° orientation. The entire scene was then continuously rotated at 90° per second in the counter-clockwise direction until the participant indicated that they were ready to go on. At this point the movie was paused in the 0° orientation, and participants were allowed to study the scene further. Participants were given the opportunity to watch the movie again if they were unsure about the positions of objects. We found that this animation facilitated encoding of the objects’ positions. After study, participants responded to four consecutive object name probes, all presented from the 0° orientation. If all four probes were answered correctly, the experimenter ended the study period and started the test period before leaving the room. If one or more probes was answered incorrectly, the study period was repeated.

Test period trials were similar to those in Experiment 1, with the following modifications: The response deadline was increased to 4250 ms, and accuracy feedback was given after each response, in the form of an auditory tone with an onset approximately 750 ms after the response deadline. A high-pitched tone was played for unambiguously correct responses (angular disparity < 22.5° from the correct response) and a medium-pitched tone was played for almost correct responses that deviated between 22.5° and 45° from the correct response. Under this criterion, a “head-right” response would be considered almost correct for a probe requiring a “head-front-right” response. A low-pitched tone was played when the movement direction was incorrect (angular disparity >= 45°) or when the participant’s movement was not detected. A dissonant chord was played in rare cases when the classifier script failed due to irregularities in the data from the Wii remote. Approximately 750 ms after the feedback for the first probe, a second object name probe was presented in the same fashion, and feedback was again provided at the end of the movement.

After 110 minutes of participation or the completion of 8 blocks (whichever arrived sooner), the experimenter stopped the computer procedure and asked the participant to fill out a strategy questionnaire (see Appendix F of the online supplement for further details).

Results

Data from 35 participants were trimmed by excluding trials with errors in the object probe response (26.5% of all trials), those with preparation RTs less than 200 ms or exceeding the participant’s condition mean plus two standard deviations (2.8% of all trials), and finally those with irregularities in the Wii remote data (2.7% of all trials). A total of 28.7% of all trials were excluded with this procedure.

Perspective transformation analysis

Consistent with a transformation-based account, preparation RTs increased with increasing values of orientation disparity in the upright condition (Figure 3, bottom row). An ANOVA on preparation RT revealed main effects of both orientation (F(3, 102) = 19, p < .001, ${\mathrm{\eta }}_p^2$ = .36) and posture (F(2, 68) = 133, p < .001, ${\mathrm{\eta }}_p^2$ = .64). The interaction was also significant (F(6, 204) = 10.0, p < .001, ${\mathrm{\eta }}_p^2$ = .25). Fisher z transformed orientation dependence values showed that responses were orientation dependent (t(34) = 12, p < .001, d = 2.10), and in fact even more orientation dependent in Experiment 2 than Experiment 1 (t(68) = 2.6, p < .01, d = 0.63), suggesting that the finer-grained manipulation of orientation in Experiment 2 was successful in promoting perspective transformation use. Consistent with this finding, 32 of 35 participants showed an increase in RT from 90° to 135°. (Recall that in Experiment 1, 18 of 35 increased in RT from 90° to 180°.)

Spatial framework analysis

Probe RT data were analyzed using the same method as Experiment 1. To allow direct comparison with Experiment 1, the initial analysis only examined responses to objects at canonical locations (approximately 30% of all trials). The right column of Figure 4 depicts means of the probe RTs across the six canonical object locations while excluding the 20 non-canonical object locations. Of the 35 participants, 19 exhibited the strict pattern of response times consistent with the use of spatial frameworks for the upright avatar condition (head/feet < front/back < left/right), which was comparable to the 16 participants exhibiting a similar pattern in Experiment 1. As in Experiment 1, a number of participants exhibited the pattern predicted by an intrinsic computation strategy (head-feet < front-back < left-right even in non-upright conditions): 7 each in the supine and prone conditions. Axis dependence scores conformed to the expected spatial framework pattern in the upright condition (t(34) = 6.7, p < .001, d = 1.13), but not the prone condition (t(34) = 0.1, p = . 921, d = 0.02), and only marginally so in the supine condition (t(34) = 1.8, p = .085, d = 0.30). Back minus front difference scores were also greater than zero in the upright condition (t(34) = 3.2, p = . 003, d = 0.54), but not the prone (t(33) = -1.4, p = . 164, d = 0.24) or supine conditions (t(31) = .745, p = . 462, d = 0.13). By our modified criteria, 21 out of 35 participants exhibited the expected spatial framework pattern in the upright condition (see Table 2). Nine participants showed evidence for intrinsic computations. A small number of participants made enough errors in the non-upright conditions to lack a probe RT estimate for at least one axis, or the front or back locations, and were therefore excluded from the analysis of non-upright trials (6 and 2 in the supine and prone conditions, respectively). Only 7 out of 29 and 5 out of 32 participants exhibited the strict spatial framework pattern (front/back < head/feet < left/right) in the supine and prone conditions, respectively. Using our modified criteria, 10 out of 29 participants in the supine condition and 2 out of 33 in the prone condition showed evidence of using spatial frameworks. There was little evidence for widespread use of spatial frameworks in non-upright conditions, nor was there consistent evidence for any of the alternative strategies.

Expanded spatial framework analysis

Hemisphere-based probe RTs were obtained by taking the mean probe RT to all 18 locations in the hemisphere associated with each canonical axis (e.g. “head” and “feet”, along with all other locations referencing “head” and “feet” in their names) while excluding RTs to the eight locations that were situated at the midpoint of that axis (e.g. “back” and “front-right”). In this approach, RTs to objects at non-canonical locations contribute to multiple hemisphere means. For example, “front-right” RTs contribute to both “front” and “right” hemisphere means. This hemispheric averaging is depicted in Figure 6. This process yielded a new set of data incorporating responses to all 26 object locations instead of just the six canonical locations. The resulting hemisphere-based probe RTs are plotted in the rightmost panel of Figure 7. For comparison, they are plotted alongside analogous data from Experiment 1 and from responses to objects at only canonical locations in Experiment 2.

Figure 7.

Canonical and hemisphere-based probe RT residuals for upright avatar trials. The left panel depicts data from Experiment 1 and the central panel shows the analogous data from Experiment 2, using only the probe RTs to canonical locations. The rightmost panel shows the hemisphere-based data from Experiment 2.

Hemisphere-based probe RTs were tested for axis- and direction-dependence in the same fashion as the canonical location probe RTs. Head-feet responses were faster than front-back responses (t(34) = 3.9, p < .001, d = 0.65), which were in turn marginally faster than left-right responses (t(34) = 1.9, p = .060, d = 0.33). Head-feet responses were also faster than left-right responses (t(34) = 5.6, p < .001, d = 0.94). Finally, front responses were faster than back responses (t(34) = 5.5, p < .001, d = 0.93). This set of results provides strong evidence that participants used spatial frameworks in Experiment 2, even when objects were placed at irregular locations. The hemisphere-based probe RTs from Experiment 2 were compared to two references: the data from Experiment 1, and the analogous data from Experiment 2 using only canonically-located objects. These measures are depicted in the central and leftmost panels of Figure 7, respectively. Responses to objects at canonical locations exhibited a pattern very similar to the hemisphere-based approach, with faster responses to objects at head-feet locations (front-back minus head-feet: t(34) = 7.7, p < .001, d = 1.31; left-right minus head-feet: t(34) = 5.8, p < .001, d = 0.98). Interestingly, the canonical location analysis differed in that it failed to find a difference between responses to front-back and left-right locations (t(34) = 0.17 p = .869, d = 0.03). This suggests that a hemisphere-based approach has greater power to detect a response time difference between axes, potentially because it averages across more responses and therefore provides a more stable estimate of the probe RT for each axis. These data are most consistent with our categorical access hypothesis, which proposes that all objects associated with a location category (e.g., “objects in front of me”) conform to the spatial framework pattern regardless of whether they were located at canonical or non-canonical locations.

In sum, the spatial framework analyses again found converging evidence for spatial framework use in the upright condition, but not in the prone or supine conditions. Patterns of accessibility suggest that the object’s locations were coded with respect to the canonical axes.

Relations between measures of perspective transformations and measures of spatial frameworks

As in Experiment 1, we tested the hypothesis that there would be a positive correlation between the use of perspective transformations and spatial frameworks. The relationships for objects in canonical locations are plotted in the left column of Figure 8. The only significant relationship was the correlation between orientation-dependence and the back minus front difference (r = .348). This relationship was in the predicted direction, with a greater front to back difference in participants exhibiting higher orientation dependence. The correlation between orientation dependence and axis dependence was not significant (r = .008). (In Experiment 1, the correlation between orientation-dependence and axis dependence was significant, whereas the correlation between orientation-dependence and back-minus-front difference was not.)

Figure 8.

Relationship between spatial framework measures and orientation dependence for upright avatar trials in Experiment 2. The left column depicts spatial framework measures derived from canonically-located objects, while the right column depicts hemisphere-based spatial framework measures.

Next, we examined the relationship between orientation-dependence and hemisphere-based measures of spatial framework use. A hemisphere-based axis dependence value was computed by correlating the predicted axis pattern with the corresponding hemisphere-based probe RTs for each posture condition. As in the axis dependence values for canonical locations, these values were also significantly greater than zero for upright trials (t(34) = 7.8, p < .001, d = 1.33). However, the axis dependence values were not significantly different from zero in the prone and supine conditions (prone: t(34) = 1.2, p = .234, d = 0.20; supine: t(34) = 1.8, p = .074, d = 0.31), meaning that responses in the non-upright condition did not conform to the pattern expected from spatial framework use. This is similar to the pattern for canonical locations, where there was a marginally significant deviation from zero in the supine condition. Unlike the analyses of objects at canonical locations in Experiments 1 and 2, there was no evidence of a relationship between the use of perspective transformations and hemisphere-based spatial framework measures (Figure 8).

Discussion

The first goal of Experiment 2 was to examine spatial frameworks in a situation that included objects in more naturalistic arrays, including non-canonical locations. A hemisphere-based analysis of non-canonical object probes in Experiment 2 showed a trend similar to that for the canonical object probes in both Experiments. This result supports the proposal that spatial frameworks are a general representational mechanism used for representing complex scenes surrounding bodies, rather than ad hoc representations used to remember objects in artificial scenarios featuring one-to-one mappings between objects and canonical locations.

A second goal was to better characterize the apparent variability in strategy across different poses of the avatar. The results converged with those of Experiment 1, in that there was good converging evidence for spatial framework use in the upright trials but not in the prone or supine trials. Thus, this appears to be a robust feature of such tasks.

A final goal was to explore why preparation times did not increase beyond 90° in some participants. To discourage nonspatial strategies, we manipulated avatar orientation in 45° increments and increased the proportion of trials in which the avatar was upright. As predicted, this resulted in incerased orientation dependence and consistent increases in response time past 90°. Thus, a reasonable explanation for the lack of increase beyond 90° for some participants in Experiment 1 is the use of a nonpspatial “cheating” strategy on the 180° trials, verbally coding of the fact that left and right are reversed for these trials.

As in Experiment 1, we found that participants who exhibited evidence of using perspective transformations also tended to exhibit evidence of using spatial frameworks. However, this relationship was significant for axis dependence in Experiment 1 and the back minus front difference in Experiment 1 2.

Unlike the analysis using only canonical objects, individual differences in the hemisphere-based spatial framework measures did not correlate with the measure of perspective transformation use in Experiment 2. One possibility is that making judgments about non-canonical objects depended more heavily on orientation-dependent processes. During the preparation phase, participants could not predict whether the upcoming probe objects would be at canonical or non-canonical locations, but they may have selectively prioritized the representation of canonical objects during their perspective transformation. This would have left them inadequately prepared for probes of objects at non-canonical locations, requiring another perspective transformation at the time of the probe based on a surface representation of the scene.

General Discussion

In these two experiments, we tested a mechanistic hypothesis regarding how people sometimes perform perspective-taking tasks: that they perform perspective transformations, resulting in the construction of a spatial framework from an imagined perspective. In both experiments, during a perspective-taking phase response times were consistent with perspective transformations, and during an object-location phase response times were consistent with spatial frameworks. Moreover, participants who showed stronger evidence of performing perspective transformations when asked to imagine another viewpoint also showed stronger evidence of using a spatial framework to locate objects relative to that imagined viewpoint.

Thus, the results support a mechanism for spatial perspective taking that can be described in terms of a specific representation—a spatial framework—and a specific transformation—a perspective transformation. The overall pattern and the individual differences relations argue against other potential representational and transformational mechanisms as being dominant in these tasks. Specifically, based on these data it is unlikely that the participants primarily utilized an “intrinsic computation” strategy depending on locating objects with respect to the avatar’s object-centered reference frame, used alternate transformations such as object-based transformations or “blink” transformations, or avoided spatial transformations altogether by using a verbal reasoning strategy.

However, an important caveat is that these patterns held for judgments about upright figures but not for figures presented lying down. The data therefore also support the view that different people may adopt different strategies for such tasks, and even that a given person may adopt different strategies on different trials. Few participants showed extreme versions of the perspective transformation chronometric profile nor of the spatial frameworks profile, and some participants’ behavior was not at all consistent with those profiles.

Front-back asymmetries

We found a much larger front-back asymmetry in probe responses than previously reported, though front-back asymmetries have been consistently associated with axis asymmetries in spatial framework access (e.g. Bryant, Tversky, & Franklin, 1992, Exps. 2, 3, & 4; Bryant, Tversky, & Lanca, 2001, Exp. 2). Bryant, Tversky, and Franklin (1992) argued that the front-back axis of the human body is unique in that the front is more behaviorally relevant, and is more visible, than the back. The strong asymmetry within the front-back axis highlights the relevance of this measure for characterizing spatial frameworks, and the importance of separately examining front and back responses.

In Experiment 2, the magnitude of the front-back difference was the spatial framework measure that was significantly associated with signatures of perspective transformations, whereas in Experiment 1 it was the differences amongst the three canonical axes. It is not immediately evident why this difference across the experiments emerged. One possibility is that this simply reflects a pair of complementary false negative results; this is quite possible given the modest power of these experiments. Another possibility is that some feature of the stimulus design modulated the salience of the front-back asymmetry across the experiments for those participants who performed perspective transformations (Maki, Maki & Marsh, 1977). This issue merits further investigation.

Egocentric perspective as a source of interference

Perspective transformations involve a component of representational conflict: The egocentric perspective must be suppressed when reasoning about another person (May, 2004). If participants performed perspective transformations to establish spatial frameworks, we should see evidence of this representational conflict in their response. To test this, we examined the egocentricity of movement responses, defined as the degree to which participants’ movements were incorrectly pulled in an egocentrically-coded direction instead of the correct direction from the avatar’s point of view (Appendix C of the online supplement). Participants responded egocentrically not only when they produced incorrect responses, but also when they were almost correct. This supports theories proposing that multiple spatial reference frames are initially activated during language comprehension and scene perception (Carlson-Radvansky & Irwin, 1994; Wang, Johnson, Sun, & Zhang, 2005). Other groups have described how movement-based responses, such as mouse trajectories, can reveal the timecourse of conflict resolution in tasks with multiple response options (Duran, Dale, & McNamara, 2010; Tanenhaus, Spivey-Knowlton, Eberhard, & Sedivy, 1995). We extended these approaches to 3-dimensional arm-movement responses, revealing a persistent effect of egocentric coding of object locations even when adopting the perspective of an avatar. These findings of interference converge with the other analyses in supporting a tight relationship between perspective transformations and the establishment of spatial frameworks.

Alternative strategies

In constructing this task, we focused on distinguishing a perspective-transformation strategy from a the intrinsic computation strategy, which does not rely on spatial transformations. This strategy cannot have been used on most trials because it would have produced equally fast responses for front and back objects, whereas in fact objects in front of the avatar were consistently responded to more quickly than objects behind. Another alternative possibility is that perspective transformations are sometimes performed using a “blink” transformation in which the egocentric reference frame is constructed afresh from a new perspective rather than continuously transformed. This strategy cannot have been used on most trials because response times increased consistently with increasing orientation—especially when rotation was sampled in smaller increments in Experiment 2. However, it is quite possible that participants used one or both of these strategies on some trials.

A final alternative possibility is that participants performed some other spatial reference frame transformation that took increasing time with increasing orientation. For the geometry used here, performing an object-based transformation would have this effect. We think that this is unlikely given how we designed the task: The difficulty of object-based transformations increases with the complexity of the object being rotated (Bethell-Fox & Shepard, 1988), and people appear to have grave difficulty holistically rotating an array of objects as a unit (Presson, 198). A strong demonstration of this limitation comes from a study by Wraga, Creem and Profitt (2000), in which participants were directly instructed to imagine an array of objects rotating. If they were expecting to be probed for the location of one object after the array rotation but were then probed for an unexpected object, performance suggested that their mental preparation was completely ineffective. In the present experiments, we probed multiple items after each preparation phase, which should effectively rule out an object-based transformation of the array. Nonetheless, the possibility remains that some participants did successfully utilize object-based transformations. In future work it would be valuable to use planes of rotation such that perspective transformations and object-based transformations produce very different effects of rotation on response time (Parsons, 1987).

Limitations in diagnosing representations and transformations from chronometric data

Although the data presented here support the hypothesis that participants use perspective transformations and spatial frameworks and that the two are related—at least for upright figures—they point to an important limitation of chronometric analyses. Such analyses require an adequate sample of trials for each participant on which a consistent strategy is adopted. When strategies can vary ad hoc or as a function of the experimental manipulations, interpreting the data is a challenge. The field is in sore need of techniques that can diagnose features of representational format and transformations based on observations of single trials rather than collections of trials.

Sex differences

Because it is a matter of continuing interest in spatial reasoning (e.g., Halpern, 2013) we compared performance of males and females on all measures. The only significant difference observed was in response time to the location probes: females were faster than males. This difference was significantly larger in Experiment 2 than in Experiment 1. (See Appendix E of the online supplement.)

Embodied spatial reasoning

These results suggest that spatial perspective taking is embodied, at least for some people some of the time (see Kessler & Thomson, 2010, for converging evidence). Our participants performed a spatial perspective-taking task by constructing a representation, a spatial framework, that preserves knowledge about the way the body behaves in the world. The head-feet axis is strongly asymmetric with respect to gravity and the types of items found above and below the body are strongly constrained (Mandler & Parker, 1976). Information about whether an object is in front of one’s self (or in the case of perspective taking, one’s projected self) is accessed more quickly than information about whether it is behind or to the left or right (Avraamides & Carlson, 2003). This reflects the functional asymmetry of the front-back axis of the human body: it is much easier to perceive and manipulate objects in front of the body. Finally, the left-right distinction is the most difficult because of the vertical axis of symmetry of the human body (R. H. Maki et al., 1977). In these tasks, such asymmetric relations from one’s first-person real world experience were present when reasoning about the space surrounding another, depicted, person. Perspective transformations allow one to bring a representation of one’s body into registration with another body in a common egocentric reference frame, reducing but not completely eliminating sensorimotor interference from the egocentric perspective. This is a powerful computational mechanism for imitating or coordinating behavior with another person and for learning by observer another’s actions.