Overestimation of the classification accuracy of a biomarker for assessing heavy alcohol use

Reports of alcohol intake by subjects or other informants may be unreliable which limits the ability to identify individuals at risk for an alcohol use disorder or related health problems such as liver disease, heart disease and cancer. To improve the assessment of alcohol intake\consumption, Liu et al.¹ proposed a blood biomarker based on methylation information from 144 CpG sites. The 144 CpGs were identified by screening a set of ~440,000 CpGs in a discovery sample of 6,926 subjects. To evaluate the ability of these CpGs to identify heavy alcohol drinking, they calculated the area under the curve (AUC) in four replication cohorts of 920-2003 subjects. The 144 CpGs in combination with age, sex and body mass index (BMI) produced AUCs that ranged from 0.90–0.99 for heavy drinkers versus non-drinkers and 0.85–0.99 for heavy versus light drinkers. The AUC is a measure of discriminatory power with a random classifier having an AUC of 0.5 and a perfect classifier an AUC of 1. Thus, their results suggested excellent to almost perfect classification accuracy and the authors concluded that the 144 CpGs performed better than commonly used clinical variables and biomarkers in discriminating current heavy alcohol drinking.

We have a methodological concern related to the estimation of the AUC in the replication cohorts. Although these cohorts were not used to select the 144 CpGs, the authors did not use the coefficients from the discovery set to determine classification accuracy. Instead, they re-estimated these coefficients by fitting a logistic regression model in each replication cohort. This carries the risk of overestimating the AUC because these cohorts can no longer yield a truly independent assessment of the classification accuracy. This risk increases with the number of CpGs, as models with more variables are more likely to capitalize on idiosyncrasies of individual data sets thereby resulting in “overfitting”².

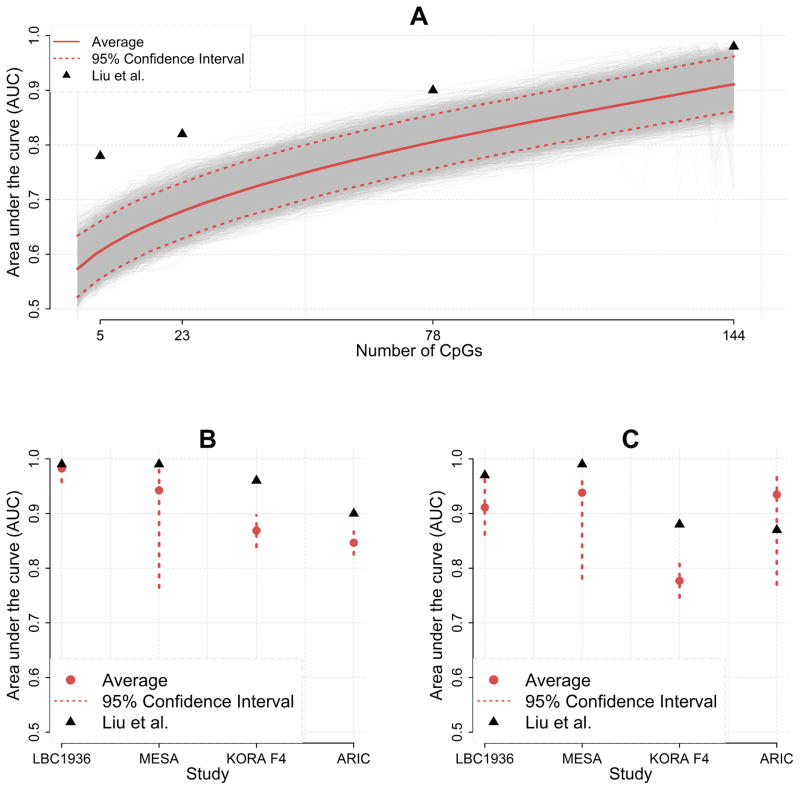
We performed simulation studies assuming CpGs were completely independent of alcohol intake. In panel A of the figure, we mimicked one of the replication cohorts (see legend for details) and displayed results along the lines of Figure 2 in Liu et al.¹. Results show that the AUC increases with the number of CpGs included in the classifier, which is a pattern very similar to what was observed by Liu et al. For 144 CpGs, the average AUC for the 10,000 simulated data sets was 0.909 with a 95% confidence interval of 0.859–0.961. Thus, although the CpGs were unrelated to alcohol use in our simulations, the AUC incorrectly suggested substantial classification accuracy. The simulations were repeated for all 4 replication cohorts and 2 outcomes (i.e., heavy drinkers versus nondrinkers and heavy drinkers versus light drinkers) studied by Liu et al. Results in panel B and C suggest severe overestimation of the AUC in all analyses.

Figure. Area under the curve for simulated methylation data without effects.

A) We simulated 10,000 data-sets with parameters mimicking the Lothian Birth Cohort 1936 (LBC1936) that has 574 individuals who are light drinkers and 61 heavy drinkers (Table 1 in Liu et al.). We first simulated age, sex, and BMI so that logistic regression produced an average AUC of 0.57, which is approximately the value of the “Null” model (right panel of Figure 2 in Liu et al.). Next, we added simulated CpG data to the model that was independent of the outcome. To illustrate the effect of the number of predictors\variables on the AUC, we increased the number of CpGs included from 0 to 144 in steps of 4 (i.e., 0, 4, 8,…,144). To maximize compatibility with Figure 2 in Liu et al., the x-axis displays only the sets of 5, 23, 78, and 144 CpGs. In the figure we plotted the average AUC (red solid curve) with the 95% confidence intervals (red dashed lines). The black triangles indicate the values reported by Liu at al. B) The above simulation was repeated for all other replication cohorts comparing non- vs Heavy drinkers. Sample sizes were: LBC 1936:181 vs. 61, MESA: 691 vs. 51, KORA F4: 534 vs. 230, ARIC: 1519 vs. 348. Only the results for the full model with 144 CpGs are reported. We did not include the FHS cohort because, as mentioned by Liu et al., this cohort was also used in the discovery stage to find the 144 CpGs. In the figure we plotted the average AUC (red solid point) with the 95% confidence intervals (red dashed lines). The black triangles indicate the values reported by Liu at al. C) We also performed simulations using the sample sizes for the analysis comparing light vs heavy drinkers are: LBC 1936: 574 vs. 61, MESA: 444 vs. 51, KORA F4: 751 vs. 230, ARIC: 67 vs. 348. See panel B for explanation of legend etc.

The replication cohorts differed from those used in the discovery stage on either ancestry or biosample type. The use of the (different) regression coefficients from the discovery cohorts may therefore underestimate the predictive power. In these scenarios, techniques such as k-fold cross-validation may provide an alternative for obtaining an unbiased estimate of the predictive power while accounting for differences between discovery and replication cohorts². This approach first randomly partitions each cohort into k equal sized subsamples. Next, k – 1 subsamples are used to estimate the regression coefficients for all CpGs and these coefficients are then used in the remaining samples to estimate the classification accuracy. Using this approach for the simulation scenario in panel A, we obtained an average AUC of 0.499 (95% confidence intervals 0.408 – 0.584) indicating that predictive power was no longer overestimated. We should note that in this specific case k-fold cross-validation may not necessarily be the best approach. For example, because the discovery set had a much larger sample size, it is possible that use of those coefficients would give better results as the smaller standard errors may potentially offset the fact that the coefficients are different in the replication cohorts.