Distribution of brain sodium long and short relaxation times and concentrations: a multi-echo ultra-high field ²³Na MRI study

Abstract

Sodium (²³Na) MRI proffers the possibility of novel information for neurological research but also particular challenges. Uncertainty can arise in in vivo ²³Na estimates from signal losses given the rapidity of T2* decay due to biexponential relaxation with both short (T₂*_short) and long (T₂*_long) components. We build on previous work by characterising the decay curve directly via multi-echo imaging at 7 T in 13 controls with the requisite number, distribution and range to assess the distribution of both in vivo T₂*_short and T₂*_long and in variation between grey and white matter, and subregions. By modelling the relationship between signal and reference concentration and applying it to in vivo ²³Na-MRI signal, ²³Na concentrations and apparent transverse relaxation times of different brain regions were measured for the first time. Relaxation components and concentrations differed substantially between regions of differing tissue composition, suggesting sensitivity of multi-echo ²³Na-MRI toward features of tissue composition. As such, these results raise the prospect of multi-echo ²³Na-MRI as an adjunct source of information on biochemical mechanisms in both physiological and pathophysiological states.

Introduction

In the physiological state, the maintenance of the transmembrane sodium (²³Na) concentration gradient (10–15 mM intracellular sodium concentration and ~140 mM extracellular sodium concentration) is a precondition for several critical cellular functions. These include the transport of ions, neurotransmitters and nutrients; regulation of osmotic and electrostatic forces on cells and macromolecules; as well as the transmission of action potentials^1–3. In the diseased state, multiple pathological pathways can lead to aberrations of these functions. Such alterations can lead to changes in intra- and extracellular concentrations due to a reduced ability to maintain resting conditions and due to conformational changes in cells themselves as well as the cellular environment in which they are embedded. Thus, ²³Na-MRI is a potential source of more direct and quantitative biochemical information than is generally possible with conventional proton (¹H) MRI⁴. As such, there is substantial interest in ²³Na-MRI regarding a range of neurological conditions despite the additional complications of acquiring ²³Na-MRI signal, including stroke⁵, epilepsy⁶, tumors⁷ and neurodegenerative diseases^8–12.

The quadrupolar ²³Na nucleus (spin = 3/2) is subject to the influence of fluctuations in neighbouring electric fields due to net positive and non-uniform distribution of charge^3,13–15. In the presence of a magnetic field, ²³Na nuclei exhibit four discrete energy states, with three possible (single quantum, SQ) transitions (−1/2, +1/2 “central transition”; −3/2, −1/2 and 1/2, 3/2 “satellite transitions”). In highly motile environments such as plasma or cerebrospinal fluid (CSF), the correlation time (τ_C) is much shorter than the Larmor period (ω₀⁻¹) (ω₀∙ τ_C ≪ 1), leading to monoexponential longitudinal (T₁) and transverse (T₂) relaxation. This is in contrast to tissue environments such as within cells and the interstitial spaces between cells where diffusion is restricted by interactions of the ²³Na cation with macromolecular anions. Such interactions modulate decay behaviour in a measurable way: the satellite transitions are subject to additional fast relaxation processes so that both T₁ and T₂ reflect biexponential decay. Literature T₂ estimates in brain parenchyma are in the range ~0.5–5 ms and ~15–30 ms for the short and long components of biexponential decay, respectively².

In the environments that give rise to biexponential behaviour, further transitions beyond SQ coherences (SQC) are possible. Such double and triple quantum coherences (D/TQC) can be selectively detected by appropriate multiple quantum filtering (MQF), and thus provide a source of information regarding short and long components of T₂* decay. However, there is a strong penalty in terms of signal-to-noise ratio (SNR) and resolution for a given acquisition length². Inversion recovery (IR) methods^16–18 can be used to suppress signal arising from unrestricted aqueous environments such as CSF spaces, though interstitial extracellular areas are not ‘unrestricted’ environments and therefore suppression is incomplete. Furthermore, measurement of concentration remains an unachieved goal for IR methods^3,15. Both MQF and IR imaging may be argued to provide an unspecified weighting toward intracellular signal beyond the weighted average obtained when measuring the total tissue sodium concentration (TSC). However, all ²³Na-MRI methods continue to receive contributions from intracellular and extracellular spaces^3,14,15.

Crucially, the rapid decay of the short component of T₂ (T₂*_short) has direct consequences for the accuracy and SNR of ²³Na-MRI¹⁹, leading to signal losses of up to 60%. As such, ²³Na-MRI acquisition schemes involving ultra-short echo times (UTE, ~0.2 ms) developed as a strategy that minimises uncertainty in T₂ signal loss due to biexponential relaxation^20,21. However, this does not address variation in T₂ that may be influenced by methodological or physiological factors. The latter in particular may be of interest in the interpretation of ²³Na-MRI signal as a measure of healthy and aberrant biochemical function. Accurate in vivo multi-echo relaxometry techniques may provide an adjunct source of information regarding the contribution and distribution of T₂*_short and T₂*_long. Previous attempts to characterise in vivo brain T₂ decay times have been conducted at lower field strengths with lower sampling rates in the temporal domain without separating multiple T₂* components^22–24, or at higher fields only provide estimates of T₂*_long^25,26 or did not consider variation between tissue types (white matter, WM; grey matter, GM)¹⁸ or between different regions^27,28.

Here, we designed a novel approach based on the density adapted radial sequence²⁹, at 7 T with multiple-echoes (n = 24) (Fig. 1) ensuring echo time (TE) sampling with the requisite number, distribution and range to robustly assess the distribution of both in vivo T₂*_short and T₂*_long through biexponential modelling. Modelling was applied to empirical estimates of sodium signal in healthy volunteers between WM and GM and, for the first time, among several subcortical regions. In addition the fraction of signal or magnetization (M0) at short TEs (M0_SF) and at long TEs (M0_LF) was converted to concentrations, by modelling the relationship between ²³Na signal (M0) and concentration (mM) in reference tubes. As such, in vivo ²³Na concentrations (Na_SF, Na_LF) corresponding to different signal fractions for the various tissues and regions were provided for the first time (Fig. 2).

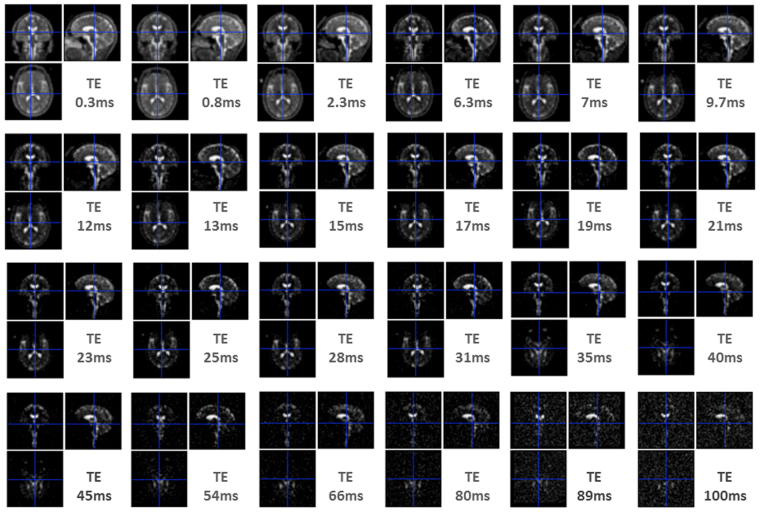
Figure 1.

Exemplar ²³Na-MRI images from a single subject across echo times. Note the decrease in signal as a function of the length of echo time (TE), and the change in the relative contributions from tissue and cerebrospinal fluid, with the latter providing most signal at long TEs.

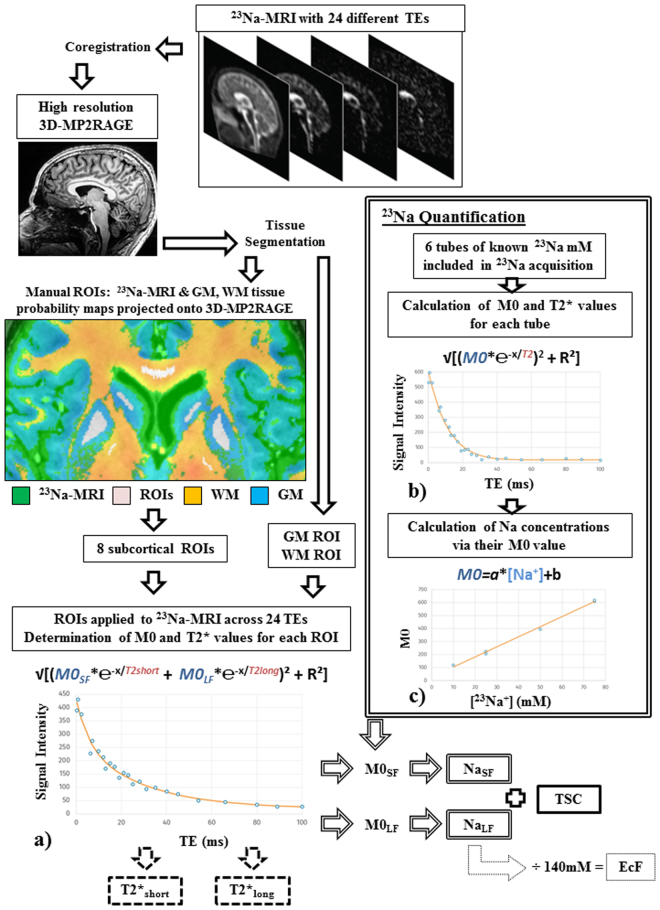
Figure 2.

Schematic workflow of processing procedure applied to data and the six measures obtained. After image post-processing, several fitting procedures were applied to ²³Na-MRI data derived from 10 ROIs (examples shown include the caudate, putamen, pallidum and corpus callosum). Fitting included: (a) a biexponential model to obtain estimates of the magnetization (M0_SF, M0_LF) apparent from the signal fractions associated with short and long T₂* components from in vivo ROIs; (b) a monoexponential model to obtain estimates of M0 for each reference tube and (c) a linear model of the relationship between M0 and known reference concentrations. The six output parameters and their derivation are marked: two T₂* components (dashed outline), a Na concentration for each component (double outline), TSC (solid outline) and EcF (dotted outline) See text for more details. Abbreviations: TE, echo time; mM, millimolar; ms, milliseconds; ROIs, regions of interest.

Results

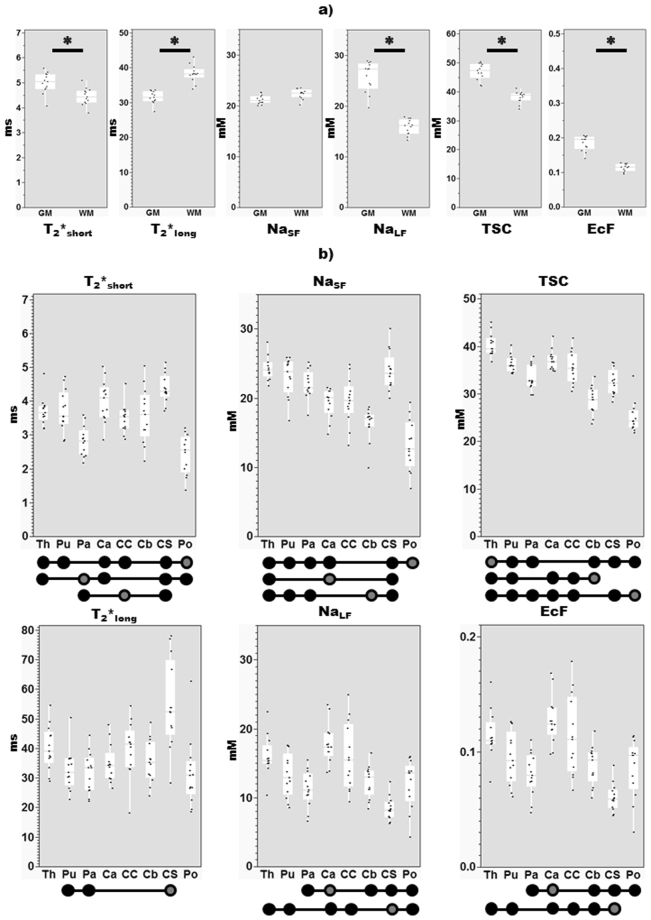
Figure 2 provides an overview of the workflow applied to data, including the extraction of decay time components (T₂*_short and T₂*_long), concentrations (Na_SF, Na_LF), total sodium concentration (TSC) and extracellular fraction (EcF). See Table 1 for mean estimates of each parameter for each tissue type and region.

Table 1.

Mean (Mn) and standard deviation (s.d) for each dependant variable for each tissue type and region. EcF, extracellular; GM, grey matter; TSC, total sodium concentration. WM, white matter.

		T2*short (ms)	T2*long (ms)	NaSF (mM)	NaLF (mM)	TSC (mM)	EcF
GM	Mn	4.99	31.51	21.16	25.75	46.92	0.18
	s.d	0.41	1.78	0.87	2.97	2.83	0.02
WM	Mn	4.44	38.25	22.28	15.87	38.15	0.11
	s.d	0.34	2.45	0.97	1.49	1.97	0.01
Thalamus	Mn	3.70	40.13	24.28	16.02	40.30	0.11
	s.d	0.41	7.50	1.66	2.85	2.33	0.02
Putamen	Mn	3.72	32.66	23.04	13.25	36.29	0.09
	s.d	0.61	7.00	2.82	3.19	1.76	0.02
Pallidum	Mn	2.82	31.62	21.99	11.25	33.24	0.08
	s.d	0.44	6.87	2.08	2.62	2.62	0.02
Caudate	Mn	4.00	34.79	19.26	17.80	37.06	0.13
	s.d	0.61	6.37	2.10	2.95	2.09	0.02
Corpus Callosum	Mn	3.48	39.82	19.57	15.96	35.52	0.11
	s.d	0.42	9.16	3.30	4.87	3.35	0.03
Cerebellar WM	Mn	3.57	35.51	16.29	12.31	28.60	0.09
	s.d	0.81	7.26	2.34	2.35	2.88	0.02
Centrum Semiovale	Mn	4.37	54.74	23.93	8.46	32.39	0.06
	s.d	0.43	14.98	2.83	1.68	2.74	0.01
Pons	Mn	2.43	31.52	13.19	11.99	25.18	0.09
	s.d	0.58	11.45	3.68	3.53	3.17	0.03

Goodness of fit indicated high performance of the biexponential decay model across the 10 ROIs including complete GM and WM segmentations and eight sub-cortical ROIs (mean r² = 0.97 ± 0.01(s.d.)). The mean proportion of the signal fraction (f) associated with the short T₂* component to total signal estimated by the biexponential model is 57.7% ± 0.07 (s.d.). There was also variation among ROIs (Fig. 3) with the overall highest value obtained for the centrum semiovale (70% ± 0.04 (s.d.)). The caudate nucleus (52% ± 0.06 (s.d.)) and pons (52% ± 0.1 (s.d.)) jointly provide the lowest estimates among subcortical regions, while the lowest mean estimate across all ROIs was for the entire GM segmentation (46% ± 0.03(s.d.)).

Figure 3.

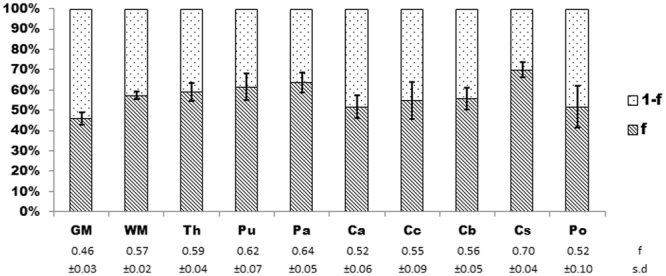
Estimated percentage signal contributions of short (f) and long (1-f) T₂* components. Mean and standard deviation (s.d) for f are provided at the bottom of the figure, and s.d. is represented as error bars on the stacked chart. Long component percentage contributions are necessarily the inverse (1-f). ROIs: Th, thalamus; Pu, putamen; Pa, pallidum; Ca, caudate; Cc, corpus callosum; Cb, cerebellum, Cs, centrum semiovale; Po, pons.

T₂*_short and T₂*_long differences between white and grey matter

Table 2a provides results for the whole model (ANOVA, corrected at P < 0.008) and main effects of Tissue Type (GM, WM) for each parameter. Effects of Age and Sex were not found to be significant for any parameter. Significant effects were observed for whole model for T₂*_long (P < 0.0001) and T₂*_short (P = 0.005) as well significant effects of tissue type for T₂*_long (P < 0.0001) and T₂*_short (P = 0.001).

Table 2.

Significant (P < 0.008) main effects (F). Results of ANOVAs applied to a) data from whole GM, WM masks and b) sub-regions. Numbers in brackets indicate degree of freedom. Non-significant main effects indicated by a dash (—). EcF; extracellular fraction; TSC, total sodium concentration.

		F-Values
	Dependant variable	Whole Model (3)	Tissue Type (1)	Sex (1)	Age (1)
a)	T2*short	5.75	14.39	—	—
	T2*long	26.07	72.95	—	—
	NaSF	—	—	—	—
	NaLF	36.7	109.63	—	—
	TSC	29.25	85.33	—	—
	EcF	36.7	109.31	—	—
	Dependant variable	Whole Model (9)	Region (7)	Sex (1)	Age (1)
b)	T2*short	12.44	15.97	—	—
	T2*long	7.23	9	—	—
	NaSF	24.41	30.02	—	—
	NaLF	9.5	12.13	—	—
	TSC	37.36	46.64	8.03	—
	EcF	9.5	12.13	—	—

Results of post-hoc Steel-Dwass tests are detailed in Table 3 and represented in Fig. 4. Significantly higher (z = −3.03, P < 0.003) values of T₂*_short were observed in GM (4.99 ms ± 0.41(s.d.)) versus WM (4.44 ms ± 0.34(s.d.). Conversely, higher T₂*_long estimates were observed in WM (38.25 ms ± 2.45 (s.d.)) versus GM (31.51 ms ± 1.78(s.d.)) (z = 4.31, P < 0.0001).

Table 3.

Significant differences between regions. Differences (z) are provided for each significant comparison (P < 0.008), with the corresponding P value provided in italics, and non-significant comparisons indicated by a dash (—). Diagonal elements with asterisks represent borders between the results of different tests, for example in the top row the bottom triangle represents results between regions for T₂*_short, while the upper triangle represents results between regions for T₂*_long.  Th, thalamus; Pu, putamen; Pa, pallidum; Ca, caudate; Cc, corpus callosum; Cb, cerebellar WM, Cs, centrum semiovale; Po, pons.

		Th	Pu	Pa	Ca	Cc	Cb	Cs	Po
T2*short	Th	********	—	—	—	—	—	—	—	Th	T2*long
	Pu	—	********	—	—	—	—	—3.59,0.008	—	Pu
	Pa	3.79,0.004	—	********	—	—	—	−3.79,0.004	—	Pa
	Ca	—	—	−3.74,0.005	********	—	—	—	—	Ca
	Cc	—	—	—	—	********	—	—	—	Cc
	Cb	—	—	—	—	—	********	—	—	Cb
	Cs	—	—	−4.31,0.0004	—	3.74,0.005	—	********	—	Cs
	Po	4.21,0.0007	3.9,0.003	—	−4.15,0.0009	−3.95,0.002	—	−4.31,0.0004	********	Po
		Th	Pu	Pa	Ca	Cc	Cb	Cs	Po
NaSF	Th	********	—	—	—	—	—	4.21,0.0007	—	Th	NaLF
	Pu	—	********	—	—	—	—	3.64,0.007	—	Pu
	Pa	—	—	********	—3.95,0.002	—	—	—	—	Pa
	Ca	4.31,0.0004	—	—	********	—	—3.79,0.004	—4.3,0.0004	—3.74,0.005	Ca
	Cc	—	—	—	—	********	—	—4,0.002	—	Cc
	Cb	4.31,0.0004	3.9,0.003	4.15,0.0009	—	—	********	—	—	Cb
	Cs	—	—	—	3.85,0.003	—	4.31,0.0004	********	—3.64,0.007	Cs
	Po	4.31,0.0004	4.15,0.0009	—4.21,0.0007	—3.69,0.006	—	—	−4.31,0.0004	********	Po
		Th	Pu	Pa	Ca	Cc	Cb	Cs	Po
TSC	Th	********	—	—	—	—	—	4.21,0.0007	—	Th	EcF
	Pu	3.74,0.005	********	—	—	—	—	3.64,0.007	—	Pu
	Pa	4.25,0.0005	—	********	−3.95,0.002	—	—	—	—	Pa
	Ca	—	—	—	********	—	−3.79,0.004	−4.3,0.0004	−3.74,0.005	Ca
	Cc	—	—	—	—	********	—	−4, 0.002	—	Cc
	Cb	4.31,0.0004	4.31,0.0004	—	−4.31,0.0004	3.9, 0.003	********	−3.64,0.007	—	Cb
	Cs	4.31,0.0004	—	—	—	—	—	********	—	Cs
	Po	4.31,0.0004	4.31,0.0004	−3.85,0.003	−4.31,0.0004	−4.1,0.001	—	−3.85,0.003	********	Po
		Th	Pu	Pa	Ca	Cc	Cb	Cs	Po

Figure 4.

Post-hoc differences (z, Steel-dwass). Note the y-axis scale differs between parameters. Results of tests applied to (a) data from whole GM, WM masks (Significant differences of P < 0.008 marked with a bar and asterisk), and (b) sub-regions. Due to the number of comparisons between subregions, significant differences at Bonferroni-corrected level between a region (circle with dark grey interior) with other regions (full black circles) are indicated below each graph. Abbreviations: EcF, extracellular fraction; GM, grey matter; mM, millimolar; ms, milliseconds; TSC, total sodium concentrations; WM, white matter; Th, thalamus; Pu, putamen; Pa, pallidum; Ca, caudate; Cc, corpus callosum; Cb, cerebellar WM, Cs, centrum semiovale; Po, pons.

T₂*_short and T₂*_long differences between sub-cortical regions

ANOVAs revealed significant (P < 0.0001) effects for both the whole model and the effect of Region (Table 2b) on both T₂*_short and T₂*_long. Overall, in terms of the post-hoc analysis (Table 3, Fig. 4b), we observed substantial variation for each parameter between subcortical regions. The shortest mean decay time components were observed in the pons for both T₂*_short (2.43 ms ± 0.58(s.d.)) and T₂*_long (31.52 ms ± 11.45(s.d.)), with the longest observed in the centrum semiovale (T₂*_short: 4.37 ms ± 0.43(s.d.); T₂*_long: 54.74 ms ± 14.98(s.d.)). The centrum semiovale also evidenced a wide distribution of T₂*_long estimates between subjects.

Concentration differences between white and grey matter

The whole model and the main effect of tissue type were significant (P < 0.0001) for Na_LF, TSC and EcF. Whole model and tissue type effects for Na_SF did not survive correction for multiple comparisons. Post-hoc Steel-Dwass tests revealed significantly higher values in GM versus WM for Na_LF (25.75 mM ± 2.97(s.d.), 15.87 mM ± 1.49(s.d.); z = −4.31, P < 0.0001), extracellular fraction (0.18 ± 0.02(s.d.), 0.11 ± 0.01(s.d.); z = −4.31, P < 0.0001) and TSC (46.92 mM ± 2.83(s.d.), 38.15 mM ± 1.97(s.d.); z = −4.31, P < 0.0001).

Concentration differences between sub-cortical regions

Both NaSF and NaLF, as well as TSC and EcF, demonstrated significant (P < 0.0001) effects for both the whole model and the effect of Region. A significant effect of Sex was also observed for TSC (P = 0.006). As above, concentrations and derived metrics showed a variety of variations between regions. The thalamus demonstrated the highest mean estimates of Na_SF (24.28 mM ± 1.66(s.d.)) and TSC (40.30 mM ± 2.33(s.d.)), with the lowest estimates observed in the pons (Na_SF: 13.19 mM ± 3.68(s.d.); TSC: 25.18 mM ± 3.17(s.d.)). The caudate (Na_LF: 17.80 mM ± 2.95(s.d.); EcF: 0.13 ± 0.02(s.d.)) and centrum semiovale (Na_LF: 8.46 mM ± 1.68(s.d.); EcF: 0.06 ± 0.01 (s.d.)), provided the highest and lowest estimates, respectively, for both Na_LF and EcF. Inter-subject variability was especially present for EcF and Na_LF in the corpus callosum.

Discussion

Data from a multi-echo ²³Na radial sequence acquired at ultra-high field (UHF) were analysed using a biexponential relaxation model to derive T₂*_short and T₂*_long relaxation times. In addition, ²³Na concentrations apparent at short and long TEs were quantified. As such, to our knowledge, we provide the first ²³Na-MRI data to address regional variation in T₂*_short at UHF, and to quantify the apparent ²³Na concentrations corresponding to short and long signal fractions associated with the respective components of T2* relaxation. Given the interest in ²³Na-MRI particularly for neurological research, quantification of these parameters and characterisation of their variation is necessary as an adjunct to even standard UTE ²³Na-MRI protocols.

The overall contribution of short and long T₂* components to the measured sodium signal is considered to be ~60% to 40%², respectively, consistent with our mean estimate of 57.7% ± 0.07% (s.d.) for the signal fraction associated with the short T₂* component (f) across all considered ROIs. In the biexponential relaxation model applied here contributions of different T₂* components were not fixed. The model revealed that while f was comparable to the general estimate in some regions (eg the entire WM), it varied in others (eg. the lowest signal contributions over the entire GM) (Fig. 3). Additionally, variation was observed across sub-cortical ROIs which are themselves likely to include diverse proportions of grey and white matter. Examples include regions that mainly contain white matter tracts but also grey matter nuclei (eg. Pons), as well as the inverse (eg. thalamus). Deviation from the theoretical ratio of 60:40 may reflect the contribution of additional compartments, for example an increased contribution of highly motile ions pool in CSF where signal decay is monoexponential (eg T₂* ~ 47 ms)²⁷. Higher estimates of f may reflect reduced contributions of this type, for example in the centrum semiovale which provided the highest signal fraction associated with the short T₂* component observed here.

T₂* relaxation refers to the dephasing of collections of nuclei due to reciprocal interactions of their local magnetic fields (T₂) in addition to magnetic field inhomogeneities (T₂’)³⁰. Attempts to characterize in vivo ²³Na relaxation times in human brain tissue have been made for several decades^22,24. Such applications show variation in terms of applied methods, following developments in sequence design and the availability of higher field strengths. These factors are especially important for ²³Na, given not only the relative rapidity of biexponential relaxation but also due to its lower concentration and intrinsic sensitivity compared to ¹H. This leads to a relatively lower SNR in ²³Na-MRI, which can be partly compensated for by higher fields^3,31. Consequently, among studies that attempt to quantify either long or short components of T₂* relaxation in brain tissues (for an overview see Table 4), progressively higher fields have been employed. At 4 T, values of T₂*_long were observed to vary little between cortical GM and WM ROIs, though with some evidence of variation in subcortical regions (thalamus) and higher values in some white matter structures like the corpus callosum (CC)²⁵. In line with theoretical expectations, and as observed in animal experiments³², longer relaxation times are observed at the higher field strengths in the current data (Table 1) and more generally at 7 T (Table 4). At 7 T, despite the lack of variation in T₂*_long values between general GM and WM ROIs, variation among other sub-regions comparable to the relative levels of T₂*_long seen in the current work was observed (thalamus > CC > cerebellar WM > putamen)²⁶. Due to insufficient data points to characterize the initial portion of the decay curve, given that the smallest TEs are > 3 ms, these studies did not attempt to quantify T₂*_short. Thus the possibility of an unknown bias in measurement, relative to studies that model both T₂* components remains. In a 7 T study in healthy controls of both T₂*_short and T₂*_long in white matter, estimates in excellent agreement with the current data were observed by Nagel et al.¹⁸. More recent data²⁷ in five subjects provide similarly concordant data for GM, though some disagreement for relative T₂*_short relaxation times between tissues should be noted. Recently, Blunck et al.²⁸ validated a multi-echo sequence with a large numbers of TEs, estimating decay components in 4 subjects, and observe T₂*_short relaxation times that are within the range of those seen here, as well as less variation between GM and WM for T₂*_long. The principal methodological differences between this study and the previous studies characterising both T₂*_short and T₂*_long in GM and WM at 7 T, beyond a slightly larger sample, is the distribution of early TEs during the first part of the decay curve thought to be dominated by the short T₂* component. For example the three shortest TEs correspond to 0.3–0.8–2.3 ms here, versus 0.4–4.5–8.5 ms for Blunck et al.²⁸ and 0.35–1–1.5 ms for Niesporek et al.²⁷. The echo time choices made here are dictated by the minimum inter-echo spacing of about 6 ms. With 3 separate acquisitions there is additional flexibility in the TE choices. The approach adopted was to use logarithmic spacing for the first echoes and equal spacing for later echoes. Logarithmic spacing on the early echoes provides good sensitivity to a range of T₂*_short values. The current data suggest that GM and WM give rise to significantly different time constants of decay, and do so differentially for short and long T₂* components. These considerations, in addition to the variation among subregions and between T₂* components for given regions, raise the possibility of the influence of tissue composition on observed relaxation (discussed below).

Table 4.

Examples of literature estimates for short and long component of T₂* derived using biexponential models, and CSF transverse relaxation rates using monoexponential models. Note that data is attributed to structures as described in the papers concerned, and the details of ROIs likely differ between reports. Brain parenchyma refers to estimates derived from (an) ROI(s) where no specific anatomic attribution was made. Values reproduced from Bartha and Menon²⁵, Fleysher et al.²⁶, Nagel et al.¹⁸, Blunck et al.²⁸ and Niesporek et al.²⁷. Abbreviations: Ref, reference; T, Tesla; TE, echo time; GM, grey matter; WM, white matter.

Structure	Ref	Field Strength (T)	TE n:range (ms)	T2*short (ms)		T2*long (ms)
				GM	WM	GM	WM
Brain Parenchyma	25	4	10: 3.8–68.7	—	—	21.1 ± 0.5
	26	7	2: 12–32	—	—	28 ± 2	29 ± 2
	18	7	56: 0.35–55	—	4.7 ± 0.2	—	40 ± 2
	28	7	38: 0.4–150	2.02 ± 1.67	1.99 ± 2.09	25.9 ± 8.3	22.4 ± 7.8
	27	7	32: 0.35–85	5.4 ± 0.2	3.5 ± 0.1	36.4 ± 3.1	23.3 ± 2.6
Frontal lobe	26	7	2: 12–32	—	—	27 ± 2	31 ± 1
Prefrontal	25	4	10: 3.8–68.7	—	—	21.2 ± 2.2	19.3 ± 2.9
Occipital Lobe	26	7	2: 12–32	—	—	29 ± 1	28 ± 1
	25	4	10: 3.8–68.7	—	—	22 ± 2.4	—
Parietal lobe	25	4	10: 3.8–68.7	—	—	—	18.2 ± 1.9
Insula	25	4	10: 3.8–68.7	—	—	21.6 ± 1.2	—
External capsule	25	4	10: 3.8–68.7	—	—	—	18.3 ± 2.9
Thalamus	26	7	2: 12–32	—	—	32 ± 2	—
	25	4	10: 3.8–68.7	—	—	16.9 ± 2.4	—
Putamen	26	7	2: 12–32	—	—	23 ± 2	—
Peri-ventricle WM	26	7	2: 12–32	—	—	—	34 ± 1
Cerebellum	26	7	2: 12–32	—	—	—	24 ± 1
Splenium of CC	26	7	2: 12–32	—	—	—	28 ± 2
CC	25	4	10: 3.8–68.7	—	—	—	22 ± 2.7
CSF	26	7	2: 12–32	54 ± 4
	25	4	10: 3.8–68.7	63.7 ± 4.7
	28	7	38: 0.4–150	57.2 ± 6.6
	18	7	56: 0.35–55	56 ± 4
	27	7	32: 0.35–85	46.9 ± 2.1

By modelling the relationship between signal (M0) and known reference concentrations, we obtained – from estimates of M0_SF and M0_LF derived from in vivo data – quantitative values for the apparent ²³Na (Na_SF, Na_LF) concentrations relating to short (f) and long (1-f) signal fractions (Fig. 2). Na_SF was observed to be comparable between GM (21.16 mM ± 0.87(s.d.)) and WM (22.28 mM ± 0.97(s.d.)). These values are higher than the reference intracellular sodium concentration (10–15 mM) commonly cited in the literature^1–3, possibly reflecting contributions from extracellular spaces. Various attempts have been made to weight measures of concentration toward the restricted sodium pool. For example, subtraction of only two SQ sodium images as a means of suppressing contributions from the long T₂* component obtains a concentration of 25.9 ± 1.2 mM for bound sodium in the ‘healthy’ GM of patients with brain tumours³³. This estimate is not dissimilar to our estimates of GM though most similar to the Na_LF concentration we observe in WM (Table 1). Recent studies – utilizing IR at 3T^4,34 and TQF at UHF^10,35 – find little difference in concentration estimates weighted toward the restricted pool between GM and WM in their healthy control comparison samples. This is consistent with the similarity between our estimates of Na_SF from whole tissue type segmentation maps for GM (21.16 mM ± 0.87(s.d.) and WM (22.28 mM ± 0.97(s.d.)) (Fig. 4a). Similarly, attempts to measure volume fractions associated with bound sodium (WM > GM)^10,35, are complementary with the current work’s estimate of sodium extracellular fraction (GM > WM) derived from Na_LF. Indeed, the sodium EcF estimates observed here (0.06–0.18) fall well within the expected overall volume fraction of the extracellular space in healthy adult brains (0.2) derived from a variety of methods³⁶. Furthermore, they specifically correspond to previous estimates of greater ²³Na extracellular volume fractions in grey versus white matter using ²³Na-MRI^4,34.

Most in vivo studies of brain ²³Na-MRI provide estimates in terms of total sodium concentration (TSC), thus we computed an equivalent metric to permit comparison. Estimates here (GM: 46.92 mM ± 2.83 (s.d.); WM: 38.15 mM ± 1.97 (s.d.)) fall well within the literature range for TSC in GM (30–70 mM) and WM (20–60 mM)^2,14. Specifically, in the majority of studies that report healthy control values in GM, TSC is observed to exhibit higher values compared to WM, including across field strengths and different acquisitions^{8,10,12,37–40}. Niesporek et al.⁴¹, employing a partial volume correction method adapted from PET accounting for both point spread function spreading and resolution issues in ²³Na-MRI, suggest corrected TSC values for GM (48 mM ± 1 (s.d.)) and WM (43 mM ± 3(s.d.)) notably similar to our estimates. Where available, regional TSC estimates in healthy controls are concordant with the current results in terms of finding higher values in the thalamus and caudate compared to putamen and pallidum as well as much lower values in the cerebellum¹¹, and specifically its white matter³⁷. The correspondence of our observed TSC values (the sum of Na_SF and Na_LF) and those in the literature are encouraging, suggesting that the current methods appropriately characterize the overall ²³Na signal with respect to the rest of the literature. This lends further credence to the signal fractions and concentrations associated with the short and long T₂* components as observed here. Crucially, the current methods achieve this without a high SNR penalty and permit quantification.

Relaxation is influenced by factors constraining molecular motion as well as the structure and content (tissue density) of the molecular environment experienced by nuclei³⁰. For example, one factor of tissue density is water/fluid content which can be explored via invasive electrophysiological measures of impedance⁴², in vivo MRI estimates of proton density⁴³ and post-mortem wet-to-dry mass ratios⁴⁴. Higher water/fluid content is observed in GM tissues versus WM, and particularly in the caudate among sub-cortical regions explored here. This may be reflected here by lower signal fractions associated with the short T₂* component observed in GM and the caudate in the current data (Fig. 3), and inversely higher values of Na_LF and the related metric EcF (Table 1, Fig. 4). Conversely, the white matter ROI in the centrum semiovale provides the highest short signal fraction (f) and the lowest estimates of Na_LF and EcF.

The extent and an-/isotropy of the mobility of nuclei also impacts relaxation, with the structure and cellular make-up and the constituents of intracellular and extracellular environments all potentially playing a role. The fluid environment in the interstitium between brain cells differs from the environment of CSF in the ventricles due to the presence of the negatively-charged long-chain molecules of the extracellular matrix^36,45. The extracellular matrix regulates the ionic environment necessary for cellular functions such as synaptic transmission and action potentials, interacts with diffusion through extracellular spaces via viscous drag and the interaction with positive charged ion species such as ²³Na, and varies in composition and density across brain structures^3,36,45. The properties of the extracellular space and matrix are in turn influenced by cellular populations of neurons and glia, in terms of the distribution of different subtypes and the manner in which they constrain the structure of their environment via the formation of sheets, extension of processes and size alterations influencing the volume of intra-/extracellular spaces³⁶.

Estimates from histology, DNA extraction and immunocytochemistry suggest that the human brain contains ~100 billion neurons and an equivalent number of non-neuronal cells including glia (oligodendrocytes > astrocytes > microglia)⁴⁶ and a small proportion of endothelial cells, leading to an approximate overall glia-to-neuron ratio (GNR) of 1:1⁴⁷. At the same time, GNRs vary widely between brain regions with extremes including the cerebellum (0.23) due to its small, densely packed neurons, while reaching 11.35 in other regions of the brain including brainstem, diencephalon and striatum (i.e. many of the subregions considered here)^47–50. These variations are thought not to reflect differences in glia density, which varies much less between structures, but rather with increasing neuronal density that is itself due to decreasing neuronal cell size (including soma and dendritic and axonal arborisations)^47,49. 500-fold variation in average neuronal cell masses are observed across structures and species versus 1.4-fold for glia⁴⁸. The above evidence suggests that while the WM represents a restrictive environment determined mainly by the anisotropy⁵¹ of axons and small-bodied⁴⁶ myelin-supporting oligodendrocytes, the GM represents a wider variety of cellular environments especially given the range of neuronal sizes. This is a possible explanation for the variation in relaxation times, associated signal fractions and derived metrics observed here. Similarly, these factors may contribute to the variation between regions (Fig. 4) to the extent that they reflect proportions of white and grey matter. It is notable that T₂*_short and T₂*_long, as well as Na_LF tend to be lowest in axon/myelin-rich structures. This is most evident across metrics in the pallidum and pons, but also to some extent in centrum semiovale, cerebellar white matter and the corpus callosum. It should be recognized that variability across metrics among these regions suggests additional factors at work as well.

Considering concordance of our results and the available relevant literature, in addition to recent insights into tissue composition, this raises the prospect of multi-echo ²³Na-MRI’s sensitivity to microstructural properties of imaged tissues. Future work, including additional measures of microstructure, such as via the measurement of the diffusion properties of ¹H or ²³Na itself^14,15,18,52, could confirm and expand the current results, and speak to limitations of the current approach. For example, despite the measures taken to avoid partial volume effects, as is the case for all ²³Na-MRI there is a remaining possibility of an unknown bias due to the influence of higher concentrations of ²³Na in extracellular and cerebrospinal fluid, and the possibility of differences between tissue types in terms of this bias. Further gains in spatial resolution could further ameliorate this issue³, as well as the application of partial volume correction methods originally applied in positron emission tomography and recently adapted to ²³Na-MRI^27,41. Given the duration of the scan required to characterise the decay curve, there is the possibility of artefacts arising from subject motion. Measures such as the use of foam supports to support subjects’ heads and constrain movement were employed; however optimisation of the sequence to shorten overall acquisition times should be pursued. In any case, this will be required for clinically feasible scan times.

In summary, we provide evidence that in the physiological state multi-echo ²³Na-MRI depicts variation in T₂* relaxation between major distinctions in tissue structure – GM and WM – as well as between diverse brain regions of differing composition and structure. This includes variations in decay times, including the T₂*_short component. Additionally, quantification of ²³Na concentrations apparent at short and long TEs was evaluated via a quantitative multi-echo approach for the first time. This provides a foundation for the examination of the alteration of these properties in pathophysiological populations, as a means of shedding light on both disease processes and the mechanisms underlying normal ionic homeostatic mechanisms as imaged by ²³Na-MRI.

Methods

Subjects

14 healthy subjects with no history of neurological or psychiatric illness provided informed consent and were enrolled in the protocol, as approved by the local Ethics Committee (Comité de Protection des Personnes sud Méditerranée 1). All methods were performed in accordance with the relevant guidelines and regulations. Due to excessive movement in one subject, the final sample consisted of n = 13 subjects (5 female) (mean age: 23.9 ± 3.6 (s.d.) years, range: 20–32).

MRI acquisition

Data were acquired on a whole-body 7 T Magnetom MR system (Siemens, Erlangen, Germany). ²³Na-MRI was acquired using a dual-tuned ²³Na/¹H QED birdcage coil and a multi-echo density adapted 3D projection reconstruction pulse sequence (TR = 120 ms, 10000 spokes, 384 radial samples per spoke, radial fraction p of 0.32, 500 us hard RF pulse, bandwidth 200 Hz/pixel, 3.5 mm nominal isotropic resolution, 8 echoes, acquisition time = 20 min). To ensure a sufficient number and distribution of TEs, especially for measuring T₂*_short, while taking into account the 5 ms readout of the sequence, we applied the sequence three times in one exam in order to obtain 24 TEs ranging from 0.3 ms to 100 ms (Run 1: 0.3–6.3–13–19–25–31–54–89 ms; Run 2: 0.8–7–12–17–23–35–45–80 ms; Run 3: 2.3–9.7–15–21–28–40–66–100 ms). The three first subjects underwent an exam of 23 TEs across the same range (Run 1: 0.3–6.3–13–19–25–31–50–100 ms; Run 2: 2–7–12–17–23–40–45–80 ms; Run 3: 3–9–15–22–28–34–70 ms). Six cylinder tubes filled with 2% agar gel doped with a range of sodium concentrations (10–75 mM) were arrayed in the field of view in front of the subject’s head as external references for quantitative assessment of brain sodium concentration. Foam cushions were used to immobilize and support the head as well as the external references.

¹H-MRI was performed during the same session as ²³Na-MRI after a short pause to permit the changing of head coils. A high-resolution proton MRI 3D-MP2RAGE (TR = 5000 ms/TE = 3 ms/TI1 = 900 ms/TI2 = 2750 ms, 256 slices, 0.6 mm isotropic resolution, acquisition time = 10 min) was obtained using a 32-element (32Rx/1Tx) ¹H head coil (Siemens).

Pre-processing

Sodium images were reconstructed offline in Matlab (Mathworks, Natick, MA) using a Kaiser-Bessel gridding method²⁹ leading to a full 3D data set for each individual, at each echo time (See Fig. 1 for an example). ²³Na images from all TEs were realigned to the shortest TE (0.3 ms) for each individual. 3D ²³Na images from the shortest TE were then realigned to high resolution 3D-MP2RAGE images obtained from the same individual and the resulting spatial transform was applied to the remaining ²³Na images (SPM12; Wellcome Institute, London, UK). Subsequent analyses using ROIs (see below) were applied to these coregistered ²³Na-MRI images in the native 3D-MP2RAGE space. Figure 2 provides an overview of the workflow applied to data.

Using SPM12, ¹H images were segmented into probability maps of GM, WM and CSF to create masks to be applied to sodium images. A conservative probability threshold of 0.9 for tissue type segmentation was applied to GM and WM prior to the creation of masks. FSL (version 6.0, FMRIB, Oxford, UK) was used to define 8 regional sub-cortical ROIs using ¹H images, thresholded GM and WM maps and ²³Na images of the earliest (high SNR) TE (0.3 ms). Sodium images and thresholded tissue probability maps were projected onto ¹H images to aid expert (S.G.) manual definition of ROIs for each individual. In addition to thresholding of tissue probability maps attempts to limit partial volume effects included the avoidance of tissue boundaries and evident areas of heightened signal due to the proximity of CSF spaces such as the ventricles during manual ROI definition (Fig. 2). In total, 10 ROIs were applied for each individual to derive mean ²³Na signal (MARSBAR toolbox, SPM12) for each ROI for each echo time. ROIs correspond to the entire (thresholded) GM and WM segmentations, in addition to eight sub-cortical manual bilateral ROIs: thalamus, pallidum, putamen, caudate nucleus, corpus callosum, centrum semiovale, cerebellar white matter and pons.

Biexponential model

Considering the design of the sodium sequence providing a maximum reduction of T1 weighting (TR = 120 ms, around four times longer than the T1 values⁷), determination of signal fractions and the time constants of short and long T2* components of signal decay in ²³Na images can be modelled by a bi-exponential fitting procedure. For each ROI, we analysed the mean signal intensity across each of the 24 TEs and apply a biexponential model to the obtained curve (Fig. 2a) using the equation:

$$Signal=\sqrt{\left[A^2{\left(f\cdot {\mathrm{e}}^{\frac{-TE}{T{2^{⁎}}_{short}}}+\left(1-f\right)\cdot {\mathrm{e}}^{\frac{-TE}{T{2^{⁎}}_{long}}}\right)}^2+Ri{c}^2\right]}$$

where A is an amplitude scaling term, f is the signal fraction associated with the short T₂* component and Ric refers to a Rician noise-related scaling parameter as described in Gudbjartsson et al.⁵³. The best-fit parameters were obtained from nonlinear least-squares (lsqnonlin) fitting. Model performance was measured by goodness of fit (r²). From the model we estimated a signal fraction for short (f) and long (1-f) T₂* components, as well as estimating the time constants (T2*_short and T2*_long). We calculated magnetization (M0) corresponding to the signal fraction estimated by the model in terms of the intercepts of the signal fraction components of the model, obtaining M0_SF = A·f and M0_LF = A·(1-f).

Quantification: Na_SF & Na_LF

As these signal fraction parameters are expressed in arbitrary units, we attempted to obtain quantitative values to access the same measurement scale across subject in order to explore variations in tissue types and regions, and permit literature comparisons. For each reference tube for each individual, we obtained the value of M0 and the time of transverse relaxation (T₂*) for a given tube across the 24 TEs, through monoexponential fitting via MATLAB (R2012a, MathWorks) (Fig. 2b). We then model a linear relationship between obtained M0 and known concentrations across all tubes (Fig. 2c), which can be applied to parameters estimated from the biexponential model of in vivo data (M0_SF and M0_LF, Fig. 2a). As such, the apparent concentrations equivalent to a given level of magnetization was obtained, yielding quantitative estimates (Na_SF and Na_LF) for each brain ROI. Note that given that we have dynamic information in the form of the curve of signal intensity across TEs, we can hypothesize that at the longest TEs, the major signal contributors will be the slowest relaxing/most motile pools. Accordingly, the magnetization estimated from the intercept of the signal fraction associated with the long T₂* component may be considered a good approximation of the sodium concentration of extracellular spaces. ‘Extracellular fraction’ (EcF) was obtained by the division of Na_LF by the commonly used value of 140 mM for extracellular Na concentration^7,15,54. We also calculated the parameter total sodium concentration (TSC) as the sum of Na_SF and Na_LF.

Statistical analyses

Six dependant variables of interest were investigated via analysis in JMP v.9 (SAS Institute Inc., Cary, NC). These included T₂*_short and T₂*_long (ms) derived from the biexponential fitting procedure, the quantitative estimates Na_SF and Na_LF,(mM), as well as TSC (mM) and EcF. An ANOVA was applied separately to the six dependant variables to investigate the factor of interest Tissue Type (2 levels: GM, WM), in addition to factors for Sex and Age. Additionally, an ANOVA was applied to the sub-cortical regional data, with the factor of interest Region (8 levels) as well as Sex and Age. Differences between the levels of factors of interest that were found to be significant were further investigated via non-parametric Steel-Dwass (p < 0.05, adjusted for multiple comparisons between levels) in a pairwise fashion. Based on the possibility of dependence between measures, Bonferroni correction was also applied across tests based on 6 dependant variables yielding a corrected α-level of P = 0.05/6 = 0.008.

Data Availability

Generated datasets are available on reasonable request from the corresponding author.

Author Contributions

B.R., M.B., J-P.R. and W.Z. designed the experiments. A.N. and M.B. implemented the multi-echo sequence in the Siemens scanner. B.R., M.B., S.B., P.V., J.V., J.-P.R. and W.Z. contributed to the acquisition, processing and analysis of data. B.R., A.N., M.B., A.M. J.-P.S., S.G., J.V., P.V., M.G., J.-P.R. and W.Z. interpreted the results and contributed to the final manuscript. All authors reviewed the manuscript.

Competing Interests

The authors declare no competing interests.