Abstract
Transcription factors (TFs) exert their regulatory influence through the binding of enhancers, resulting in coordination of gene expression programs. Active enhancers are often characterized by the presence of short, unstable transcripts termed enhancer RNAs (eRNAs). While their function remains unclear, we demonstrate that eRNAs are a powerful readout of TF activity. We infer sites of eRNA origination across hundreds of publicly available nascent transcription data sets and show that eRNAs initiate from sites of TF binding. By quantifying the colocalization of TF binding motif instances and eRNA origins, we derive a simple statistic capable of inferring TF activity. In doing so, we uncover dozens of previously unexplored links between diverse stimuli and the TFs they affect.
Transcription is orchestrated by the sequence-specific binding of transcription factors (TFs) to DNA, resulting in regulation of gene expression programs (Spitz and Furlong 2012). Hence, TFs function as major determinants of cell state (Takahashi and Yamanaka 2006; Rackham et al. 2016). Chromatin immunoprecipitation (ChIP) studies have identified binding sites for many of the approximately 1400 TFs encoded within the human genome (Vaquerizas et al. 2009), allowing estimation of a DNA-binding motif model for more than 600 factors (Kulakovskiy et al. 2013). However, studies comparing TF binding events to RNA expression levels have revealed that many TF binding sites have no apparent effect on nearby transcription (Li et al. 2008; Fisher et al. 2012; Read et al. 2016). Distinguishing such “silent” TF binding events from those with regulatory capacity is a fundamental challenge. Despite their critical importance for controlling cellular phenotypes, it is difficult to ascertain when a TF is active, e.g., contributes to nearby transcription.
One notable attempt to infer TF activity leveraged patterns of TF motif instances at annotated protein coding genes to explain changes in expression (The FANTOM Consortium and Riken Omics Science Center 2009; Balwierz et al. 2014). Yet, most TF binding occurs within regions of the genome distal to protein coding genes (Spitz and Furlong 2012). These binding events often correspond to enhancer regions known to be important for regulation of gene expression and cellular identity (Heintzman et al. 2009). Active enhancers are often characterized by the presence of short, unstable, bidirectional transcripts termed enhancer RNAs (eRNAs). When a specific TF is activated, eRNA transcription generally increases at the location of the TF binding event (Danko et al. 2013; Hah et al. 2013; Allen et al. 2014; Puc et al. 2015). While the functions of eRNAs are only beginning to be understood (Hah et al. 2013; Li et al. 2013; Sigova et al. 2015), their presence is nonetheless an indicator of enhancer activity (Andersson et al. 2014; Danko et al. 2015).
eRNA detection requires extremely sensitive methods, both in the laboratory as well as computationally. Because they are unstable, eRNAs are rarely observed via steady-state RNA assays such as RNA-seq. Nascent transcription assays capture transcription throughout the genome, including eRNA transcription (Core and Lis 2008; Core et al. 2014; Nojima et al. 2015). We recently described a model capable of estimating sites of bidirectional transcript initiation at single-base-pair resolution (Azofeifa and Dowell 2017). Transcription fit (Tfit) leverages the known behavior of RNA polymerase II (RNAP) to identify individual transcripts within nascent transcription data (Azofeifa and Dowell 2017). Although Tfit does not implicitly assume polymerase initiation will be bidirectional, we observed bidirectional transcription at both promoters and enhancers (Azofeifa and Dowell 2017). Whether bidirectional (two transcripts) or unidirectional (one transcript), our model precisely infers the point of RNA polymerase loading, i.e., the origin point of transcription.
Here, we leverage the Tfit model to ascertain TF activity. We show that, by calculating the frequency of TF binding motif instances relative to the location of eRNA initiation, the activity of the TF itself can be inferred from nascent transcription data alone. We apply our model to hundreds of publicly available human and mouse nascent transcription data sets to discover previously unknown links between TF activity and diverse biological phenomena.
Results
eRNA origins mark sites of regulatory TF binding
To utilize Tfit across a broad set of nascent transcription data sets, we modified the algorithm both to rapidly identify all sites of transcript initiation genome-wide and to account for the variable distances between forward and reverse strand transcripts observed across distinct nascent transcription data sets (see Methods). As a first application and validation of this revised algorithm, we identified 39,633 putative sites of bidirectional transcription in a K562 GRO-cap data set (Core et al. 2014), of which 30,324 were not associated with an annotated promoter (Supplemental Figs. S1, S2). As previously observed (Danko et al. 2015; Azofeifa and Dowell 2017), marks of active chromatin as well as TF binding events strongly associate with Tfit-predicted sites of bidirectional transcription (Supplemental Figs. S3–S5; Supplemental Table S1). Given their distal location relative to promoters, their overwhelming co-association with marks of active chromatin, and their association with TF binding complexes (Supplemental Fig. S6), we refer to non-promoter-associated Tfit polymerase loading positions as eRNA origins.
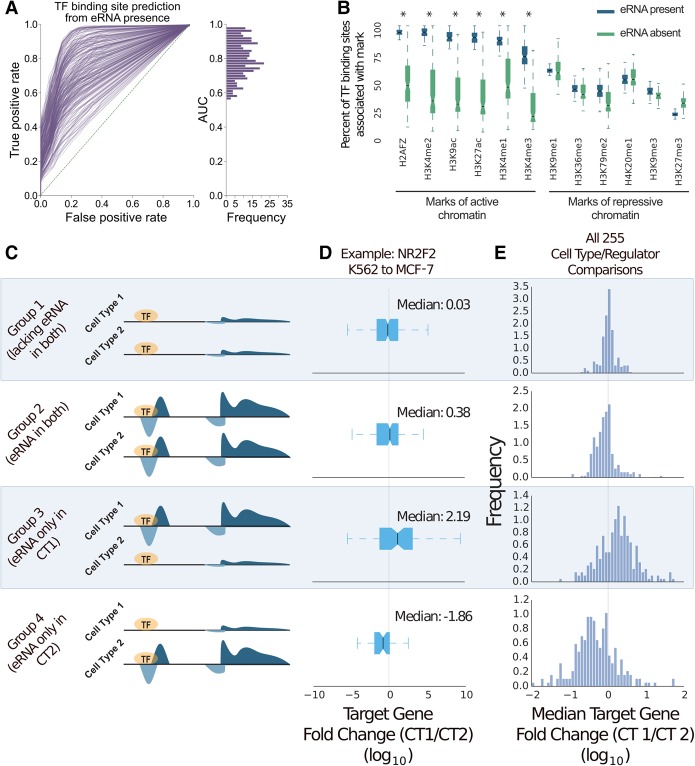
Although the vast majority of eRNA origins localize with TF binding, only a fraction of TF binding sites overlap eRNA origins (Supplemental Fig. S3A). Previous efforts to predict sites of TF binding using joint eRNA and TF-DNA motifs focused on only a small set of TFs (Danko et al. 2015). We extended this analysis to include 139 TF ChIP-seq experiments and observed a wide spectrum of association between TF binding sites and eRNA presence, suggesting that eRNA presence alone is not sufficient to fully explain TF binding (Fig. 1A). These data are consistent with the observation that only a fraction of TF binding sites result in a concomitant change in nearby gene expression (Cusanovich et al. 2014; Savic et al. 2015).
Figure 1.
Enhancer RNA (eRNA) presence marks the active subset of TF binding. (A) ROC analysis of TF binding site prediction via eRNA presence. False-positive and true-positive rates are varied by thresholding the penalized likelihood ratio statistic generated from Tfit. (B) TF binding peaks (Supplemental Table S1) were grouped according to eRNA association. A box-and-whiskers displays the median/variability in proportion of histone mark association between the groups across all TFs (Supplemental Table S1). Asterisks indicate a P-value <10−10 by z-test. All data in A and B are K562 cells. (C) Pairwise cell type–associated TF binding peaks were grouped according to eRNA presence from matched cell types (Supplemental Table S2). A gene was considered “neighboring” by a distance <10 kb. (D) Log base 10 FPKM fold change of “neighboring” genes related to eRNA-grouped NR2F2 binding peaks. (E) Histogram of Log base 10 FPKM fold change of “neighboring” genes for all possible eRNA-grouped TF ChIP-seq data sets (n = 255).
Given the strong relationship between active chromatin and eRNA transcription, we asked whether eRNAs discriminate “silent” from “active” TF binding. In support of this hypothesis, TF binding sites occurring at sites of eRNA origination display a significantly increased overlap with canonical marks of active chromatin relative to non-eRNA-associated TF binding (Fig. 1B). Moreover, no statistical difference is detected between these categories for repressive chromatin marks.
Although regulatory TF binding is often enriched for open and active chromatin, functional TF binding must ultimately lead to a change in gene expression. To this end, we considered TF binding events within enhancers conserved between two cell types but differing in terms of eRNA presence with the hypothesis that neighboring gene expression would be elevated in the eRNA-harboring cell type (Fig. 1C). There are 95 TFs profiled in at least two cell types for which cell-type–matched nascent transcription is available (Supplemental Table S2). For example, binding of the TF NR2F2 was profiled in both K562 and MCF-7 cell lines, yielding 30,618 and 16,678 binding peaks, respectively, with 3491 peaks shared between the two cell types (Fig. 1D). Of these cell-type–invariant peaks, 25% harbor an eRNA origin in both cell types, 7% only in K562, and 12% only in MCF-7, and 56% do not harbor an eRNA origin in either cell type. Measuring the transcription level of nearby target genes (TF binding site <10 kb of gene promoter) revealed that eRNA presence is significantly correlated with elevated local gene expression (P-value <10−6). After making a total of 262 possible pairwise cell type comparisons (95 TFs, four cell types), we noted that 73% of these comparisons display such dynamics (Fig. 1E; Supplemental Table S2). In the same vein, TF binding sites that overlap a region with strong enhancer activity—as measured by a CapStarr-seq enhancer assay (Vanhille et al. 2015)—are five times more likely to associate with eRNAs than regions considered inactive by the enhancer assay (P-value <10−19, hypergeometric). These results are consistent with a model where eRNA presence discriminates silent from functional TF binding.
eRNA origins colocalize with TF binding motif instances
Given that many TFs bind DNA in a sequence-specific manner, we next sought to determine the precise spatial relationship between instances of the TF-DNA motif model and eRNA transcription. To this end, we measured the distance between genomic instances of the TF motif model and eRNA origins in a K562 GRO-cap data set (Core et al. 2014). We observed a stark colocalization of the motif instance with the eRNA origin specifically in the TF-bound fraction of eRNAs (Supplemental Fig. S7A), suggesting that the motif sequence is present at the precise point of eRNA origination. This led to the speculation that the genome-wide patterns of motif sequence to eRNA co-occurrence could identify the set of active TFs directly regulating eRNA transcription, even when ChIP data are not available.
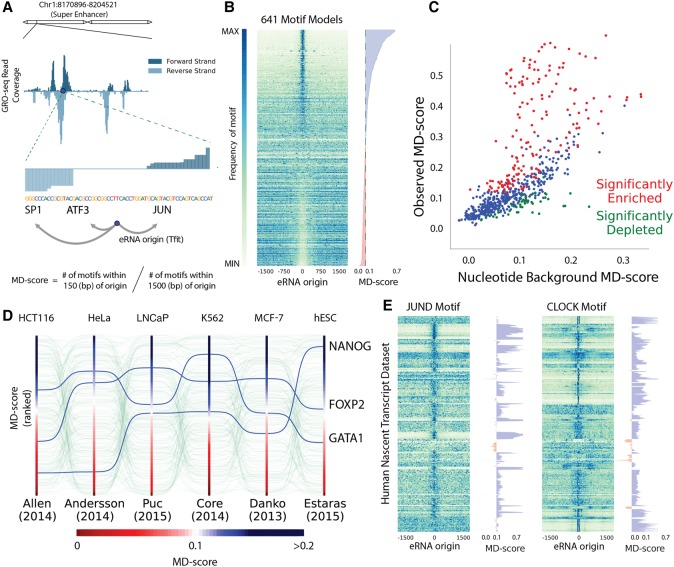
To investigate this hypothesis systematically requires a measurement of the colocalization of motif instances with eRNA origins. With this in mind, we devised a simple statistic—the motif displacement score (MD-score)—which computes the proportion of TF sequence motif instances within an h-radius of eRNA origins relative to a larger local H-radius (Fig. 2A). Similar to the average length of a nucleosome free region (Yadon et al. 2010), we set the h-radius based on the average estimated distance between the forward and reverse strand transcript peaks at eRNA origins (h = 150 bp; Supplemental Fig. S7B) and the H-radius as the average length of chromatin marks associated with active regulatory loci (H = 1500 bp; Supplemental Fig. S8). Consistent with the patterns observed in ChIP data, the MD-score is elevated in the bound set of eRNAs relative to the not bound set (Supplemental Fig. S7C).
Figure 2.
Motif colocalization with eRNA origins varies by cell type. (A) An example locus of GRO-seq, the inferred eRNA origin, and computation of “motif displacement” (MD) and the associated MD-score. (B) Each row is a TF motif model, and each column is a bin of a histogram (100) where heat is proportional to the frequency of a motif instance at that distance from an eRNA origin. (C) A comparison between the expected MD-score for a motif model (x-axis) and the observed MD-score in a K562 GRO-cap experiment (Core et al. 2014). Red and green dots indicate a P-value <10−6 above or below expectation hypothesis tests, respectively. (D) MD-scores were computed and ranked under six nascent transcription data sets. (E) Each row corresponds to a nascent data set, and each column relates to motif frequency. These MD distributions are shown for two demonstrative examples (JUND and CLOCK) and the associated MD-scores, sorted by publication.
In order to expand our approach to include TFs for which no ChIP-seq is available, we leveraged a hand-curated database of TF binding motif models (HOCOMOCO, 641 motif models) (Kulakovskiy et al. 2013) and measured the distribution of motif instances proximal to K562 eRNA origins (Fig. 2B). Under a uniform nucleotide background model, 32% of the motif models colocalized significantly with eRNAs (P-value <10−6). However, similar to gene promoters and TF binding motifs, enhancers exhibit heightened GC content (Fenouil et al. 2012; The ENCODE Project Consortium 2012), which may artificially induce GC-rich motif presence at eRNA origins (Supplemental Fig. S9A). To control for local sequence bias in our colocalization metric, we developed a simulation-based method to perform empirical hypothesis testing of the MD-score (Supplemental Fig. S9B). We observed that—even in light of a significant nucleotide bias—27% of motif models remain significantly colocalized with eRNA origins in the K562 GRO-cap data set (Fig. 2C).
Interestingly, a subset of TFs display significantly lowered MD-scores relative to expectation (green dots in Fig. 2C), suggesting that in these cases, the instances of the motif model are significantly depleted at eRNA origins. Consistent with this observation, a previously published knockout of the Rev-Erb family of transcriptional repressors (Nr1d1 and Nr1d2) resulted in the gain of eRNAs (Lam et al. 2013). Taken together, these results suggest that repressors suppress eRNA activity proximal to their DNA response element.
Significant enrichment or depletion of a motif model near eRNA origins likely indicates that the TF protein is present and functionally active, as either an activator or repressor, respectively. To validate that MD-scores reflect TF activity, we first examined the MD-scores of all motif models across a set of nascent transcription data sets from six distinct cell types. Our analysis revealed wide fluctuations in MD-scores of several motif models across experiments (Fig. 2D). Importantly, we observed that the MD-score associated with cell-type–specific TFs are elevated in their known lineage of activity. For example, NANOG is elevated in embryonic stem cells, consistent with its role in maintaining pluripotency (Mitsui et al. 2003; Estarás et al. 2015). Additionally, GATA1 is elevated in K562 cells, consistent with its role in leukemia (Shimamoto et al. 1995).
To further evaluate the MD-score, we predicted eRNA origins in a large collection of publicly available nascent transcription data sets (67 publications, 34 cell types and 205 treatments; Supplemental Table S3). Our compendia include a diverse collection of nascent transcription protocols, cell types, sequencing depths, and laboratory of origin. Across the compendium, the spatial relationship between eRNA transcription and motif sequence is exceedingly dynamic (Supplemental Fig. S10), as exemplified by the JUND and CLOCK motif models (Fig. 2E). Given that we observed a modest correlation between sequencing depth and eRNA-identification (Supplemental Fig. S11), we next sought to determine the extent to which the inferred MD-score simply reflected batch effects. To this end, we leveraged the fact that many TFs play a pivotal role in cell fate and identity (Mitsui et al. 2003). Indeed, dimensionality reduction of our MD-score compendium (491 human nascent transcription experiments) revealed statistical influences based predominantly on underlying cell type (Supplemental Figs. S12, S13). Notably, 78% of motif models in HOCOMOCO are significantly colocalized with eRNA origins in at least one data set. While the experimental details clearly influence the ability to infer specific eRNAs, the aggregation of genome-wide signal makes MD-scores relatively robust to experimental variability. Importantly, key cell-type–specific TFs show elevated MD-scores only in the relevant cell type (Fig. 2D), suggesting that MD-scores quantify activity for broad classes of TFs across cell types, despite differences in protocol, sequencing depth, and/or laboratory of origin. Overall, these results indicate that MD-scores fluctuate across cell types and conditions in a manner that suggests changes in TF activity.
As an alternative validation, we examined the transcription patterns of the gene encoding the TF. For many TFs, we observed higher transcription of the TF when the MD-score significantly differed from expectation (Supplemental Fig. S14A). Overall, 45% of TFs show a correlation across all samples between the eRNA inferred MD-score and the transcription level (FPKM) of the gene encoding the TF (Supplemental Fig. S14B), suggesting that some TFs are themselves regulated at transcription. However, the observed correlations were often weak and complex—typically neither linear or monotonic—consistent with the observation that expression levels of a gene are poorly correlated with protein levels (Vogel and Marcotte 2012). Many TFs, including TP53 (Supplemental Fig. S14C), are post-transcriptionally or post-translationally modified to regulate their activity, and therefore, FPKM and MD-scores are not expected to correlate (Oren 1999; Everett et al. 2010).
MD-scores quantify TF activity
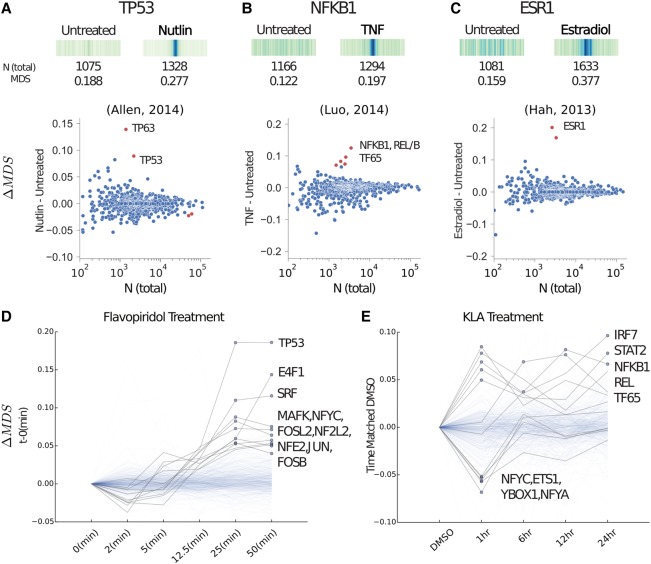
To better investigate whether MD-scores reflect TF activity, we turned to experiments where the activity of individual TFs is perturbed (Supplemental Table S4). We reasoned that alterations in TF activity should be detected as significant changes in the MD-score. In previous work, we utilized the drug Nutlin-3a to activate TP53 in HCT116 cells (Allen et al. 2014). Here we observe a significant increase in the colocalization of the TP53 motif sequence and eRNA origins following 1 h of Nutlin-3a exposure (ΔMD-score 0.17, P-value <10−33). In fact, of the 641 available TF-motif models, only TP53 and TP63, which have nearly identical motif models, displayed elevated MD-scores following Nutlin-3a treatment (P-value <10−6) (Fig. 3A). A number of other studies have specifically activated TFs, including tumor necrosis factor (TNF, also known as TNF-alpha) activation of the NF-κB complex (NFKB1/NFKB2/REL/RELA/RELB) (Luo et al. 2014) and estradiol activation of ESR1 (Hah et al. 2013). In both cases, we observed dramatic shifts in the MD-score for the TF(s) known to be activated by each stimulus (Fig. 3B,C). Despite the fact that treatments involving Nutlin-3a, TNF, and estradiol are known to modulate gene expression (Hah et al. 2013; Allen et al. 2014; Luo et al. 2014), we observed no detectable differences in MD-scores when considering only promoter-associated bidirectional transcript sites (Supplemental Fig. S15). In all three cases (Fig. 3A–C), TF activation resulted in the production of new eRNAs that are uniquely enriched for the relevant motif model, effectively elevating the TF's MD-score (Supplemental Fig. S16).
Figure 3.
MD-scores predict TF activity. (A, top) The MD distribution, MD-score, and the number of motifs within 1.5 kb of any eRNA origin before and after stimulation with Nutlin-3a (e.g., Nutlin) on TP53 (Allen et al. 2014), the TF known to be activated. (Bottom) For all motif models (each dot), the change in MD-score (ΔM DS) following perturbation (y-axis) relative to the number of motifs within 1.5 kb of any eRNA origin (x-axis). Red points indicate significantly increased and/or decreased MD-scores, respectively (P-value <10−6). Similar analysis for TNF activation of the NF-κB complex (B) (Luo et al. 2014) and estradiol activation of estrogen receptor (ESR1; C) (Hah et al. 2013). (D) A time series data set following treatment with flavopiridol (Jonkers et al. 2014). The y-axis indicates the MD-score change relative to time point zero. Blue dots indicate a MD-score difference <10−6. A darker shaded line indicates a time trajectory with at least one significant MD-score. (E) Time series data set following treatment with Kdo2-lipid A (KLA) where each time point is normalized to time-matched DMSO (Kaikkonen et al. 2014). Therefore, the y-axis indicates MD-score difference relative to the time point–matched DMSO sample. NCBI Sequence Read Archive (SRA) SRR numbers of these comparisons are outlined in Supplemental Table S4.
We next sought to evaluate the robustness of the ΔMD-score approach for inferring altered TF activity. First, differential MD-score analysis between biological replicates revealed no significant shifts in motif sequence to eRNA colocalization, indicating that our false-discovery rate is low (Supplemental Fig. S17). Second, we randomly subsampled reads from the Nutlin-3a experiment to generate data sets with considerably lower depth. With increasingly less depth, fewer eRNAs are detected and the inferred MD-score drops. However, the magnitude of the ΔMD-score remains relatively consistent, indicating that the metric is largely robust to sequencing depth (Supplemental Fig. S18). Finally, we varied the h-radius from 0 to 1500 (the full H-radius) to assess the impact of the h-radius on differential MD-score analysis. We found detectable differences in the MD-score across a broad range of h-radius values, indicating that detection of significant ΔMD-score is robust to the choice of h-radius (Supplemental Fig. S19). Collectively, these results indicate that differential MD-score analysis is a robust method of detecting changes in TF activity.
In each of the aforementioned perturbations, nascent transcription was assessed at a ≤1-h time point. Therefore, we next sought to determine whether MD-scores could capture TF activity across broader time frames. First, we observed that detectable changes in TF activity are exceedingly rapid, as exemplified by flavopiridol (a CDK9 inhibitor)-treated mouse embryonic cells (Laitem et al. 2015), which display a dramatic and monotonic increase in the MD-scores of TP53 and E4F1 (Fig. 3D). For a number of TFs, MD-scores trend upward at 12.5 min and show significant changes within 25 min of exposure. Interestingly, this result indicates that eRNA activity proximal to key TFs increases at short time points, even though flavopiridol is a general repressor of transcription. Mouse T cells treated for a longer time course with Kdo2-lipid A (a highly specific TLR4 agonist) (Kaikkonen et al. 2013) showed dynamic and time-ordered shifts in MD-scores for a number of key TFs (Fig. 3E), including interferon (IRF7) and STAT2. Furthermore, YBOX1 decreases in colocalization (reduced MD-score), consistent with its known role as a transcriptional repressor that increases in expression after KLA exposure (Liu et al. 2009). Collectively, these results indicate that profiles of eRNA transcription—when combined with motif models—identify shifts in TF activity in response to perturbation.
Discussion
We leveraged the observation that eRNAs mark the functional activity of TFs to develop a simple statistic that reflects a TF's functional activity. Importantly, we do not assign TFs to individual enhancers, because most eRNAs have numerous motif instances proximal to their origin. Our approach does not determine which of these possibilities is critical to the regulation of the eRNA. Instead, our statistic, the MD-score, measures the global colocalization of eRNAs with a TF motif model in order to capture changes in TF activity after diverse stimuli.
While the biological functions of eRNAs remain largely unknown, eRNAs clearly represent a powerful readout for TF functional activity. Previous work demonstrated that the presence of eRNAs correlates with active regulatory regions and, consequently, a subset of TF binding sites (Danko et al. 2015). Separately, it has been noted that some binding sites are apparently “silent” with respect to transcription (Cusanovich et al. 2014) or reflect artifacts of ChIP (Teytelman et al. 2013; Worsley Hunt and Wasserman 2014). Therefore, to determine whether eRNAs mark sites of TF activity, we leveraged binding events across cell lines that differed only in their eRNA activity. Our results indicate that TF binding sites that correspond to eRNA synthesis are more likely to positively affect nearby gene expression than those lacking eRNA transcription. Undoubtedly, assigning enhancers to the nearest gene is not optimal, as many enhancers are known to regulate target genes at great distances (Yao et al. 2015). However, incorrect enhancer to gene assignments would only increase noise within our comparison. Thus, given the instability and short half-lives of eRNAs (Li et al. 2016), their presence within a cell reflects ongoing TF activity.
Consequently, we directly assess TF activity from motif models and nascent transcription. We observe that many motif models show significantly enriched colocalization with eRNA origins beyond expectation, suggesting that these TFs are both present and functionally active in regulation. As the detection of eRNAs is dependent on sequencing depth, future TF-activity inference methods should consider both eRNA-motif colocalization as well as read depth. Even still, we show that TF activity is a strong predictor of cell type, even across distinct protocols, sequencing depths, and laboratory of origin. Hence, our approach has utility in identifying potentially diagnostic signatures of TF activity.
Most importantly, MD-scores can be used to identify when the activity of a TF differs between two data sets, due to either an experimental stimulus or differences in cell type. Our metric utilizes the genome-wide patterns of TF motif sequence colocalization with eRNA origins to identify changes in TF activity, regardless of whether the TF functions as an activator or repressor. Implicitly, changes in MD-score must thus reflect the gain and loss of eRNAs between two conditions, suggesting a direct relationship between functional TF binding and eRNA transcription initiation. However, we and others have observed changes in eRNA transcription levels after stimulus (Hah et al. 2013; Allen et al. 2014), suggesting that our metric could be improved by including changes in the transcription levels of pre-existing eRNAs.
Notably, our differential MD-score approach has some limitations. First, as described, our model considers the influence of each TF on transcription activity independently, yet TFs are often known to work cooperative or in combination (Spitz and Furlong 2012). If two (or more) TFs collaborate to induce eRNA activity and each motif model is enriched over expectation, both would be detected. However, if only the combination is enriched, we would not detect it in our current framework. Second, some families of TFs have similar recognition motifs, making distinguishing between them difficult. In a few cases, one or more family members is not transcribed. For example, upon stimulation with Nutlin-3a, both TP53 and TP63 show significant increases in MD-score (Fig. 3A), but in this cell type (HCT116), only TP53 is transcribed. Thus in this case, we can confidently assert that Nutlin-3a activates TP53. However, in most cases, we will not be able to distinguish family members apart. Finally, we focus here on colocalization of TF motif instances with eRNAs. However, a small set of TFs preferentially bind to promoters (The ENCODE Project Consortium 2012). For these factors, stronger signals may be obtained by computing MD-scores from all sites of polymerase initiation (promoters and enhancers).
In conclusion, we showed that addition of diverse chemical stimuli to cells resulted in activation or deactivation of specific TFs. It is compelling to think that had we not known the nature of each stimulus, we could have inferred their effects from the unique eRNA profile obtained immediately after addition of the compound. As methods for measuring eRNA production become simpler and cheaper, our approach could eventually serve as a screen capable of discriminating between the direct mechanistic impact of closely related compounds and, hence, serve as another layer of information about the effects of a drug. Such data could help to define previously poorly understood molecular mechanisms underlying a drug's activity.
Methods
Public data sets
We examine the relationship (association and/or overlap) between genomic features such as TF binding peaks, chromatin modifications, DNA sequence, TF binding motif models, and eRNA presence. Data for all features were obtained from publicly available sources and compared relative to a human and mouse genome versions hg19 and mm10, respectively. Human and mouse nascent transcription data were obtained from the NCBI Gene Expression Ombnibus (Supplemental Table S3). ENCODE peak data were obtained from https://www.encodeproject.org/matrix/?type=Experiment. Most data were provided relative to hg19, but when necessary, ENCODE files were converted to hg19 via the Python LiftOver package. Accession numbers for all ENCODE data utilized are provided in Supplemental Table S1. Motif models were obtained from the HOCOMOCO v. 10 (Kulakovskiy et al. 2013, 2016) database and scanned against the genome. For complete details on the processing and remapping of these data sets, refer to the Supplemental Methods.
Tfit modification and parameters
In prior work (Azofeifa and Dowell 2017), we leveraged the known behavior of RNAP to identify individual transcripts within nascent transcription data. Our model (Azofeifa and Dowell 2017), known as transcription fit (Tfit), infers the precise point of RNA polymerase loading, e.g., the origin point of transcription. Formally, this origin point (µ) represents the expected value of a Gaussian (normal) random variable, discussed in great detail in our previous publication (Azofeifa and Dowell 2017).
For analysis of numerous nascent data sets, here we modify our previous approach in two ways. First, to rapidly identify all sites of transcription initiation genome-wide, we compute a likelihood ratio statistic between a fully specified exponentially modified Gaussian (Equation 1, the loading/initiation/pausing phase of our earlier Tfit model) (Azofeifa and Dowell 2017) against a uniform distribution background model (Equation 2) at some genome interval [a, b]. We hereafter refer to this approach as template matching. Second, we amend our earlier estimate of the loading step of polymerase activity to permit variable distances between the forward and reverse strand transcripts, hereafter referred to as a polymerase footprint. For completeness, we now describe both modifications in full detail below. We then validated the modified Tfit by comparison of predictions to histone marks and TF binding data (for full description of validation, see Supplemental Methods).
Template matching
The loading/initiation/pausing portion of our earlier model, fully specified in Azofeifa (Azofeifa and Dowell 2017), describes the initial activity of RNAP and captures initiating transcription, which is often bidirectional, genome-wide. Briefly, our model assumes RNAP is first recruited and binds to some genomic coordinate X as a Gaussian-distributed random variable with parameters µ, σ2, where µ might represent the typical loading position (e.g., origin of any resulting transcript either TSS or enhancer locus) and σ2 the amount of error in recruitment to µ. Upon recruitment, RNAP selects and binds to either the forward or reverse strand, which we characterize as a Bernoulli random variable S with parameter π. Following loading and preinitiation, RNAP immediately escapes the promoter and transcribes a short distance, Y. We assume that the initiation distance is distributed as an exponential random variable with rate parameter λ. In this way, the final genomic position Z of RNAP is a sum of two independent random variables (X + SY), where the density function (resulting from the convolution/cross-correlation) is given in Equation 1. Note that, in keeping with traditional notation, we let uppercase, non-Greek alphabet letters represent random variables and the associated lowercase letters refer to instances or observations of the stochastic process.
| (1) |
Above, ϕ(.) refers to the standard normal density function and R(.) refers to the Mill's ratio.
In contrast, reads obtained outside of initiation regions are captured by a uniform distribution (Equation 2).
| (2) |
where refers to the maximum likelihood estimator for the strand bias (Equation 3).
| (3) |
where I(.) is an indicator function. Finally, the (log-)likelihood of the exponentially modified Gaussian (LLemg) and uniform (Lu) distribution computed at a genomic interval [a,b] using aligned read counts is given in Equation 4.
| (4) |
Here, refers to the center of the window. Based on our previous study (Azofeifa and Dowell 2017), we set .
The algorithm is a simple sliding window of LLR computations. Overlapping (1-bp) regions of interest (LLR > τ) are merged. In every study profiled for bidirectional transcription by Tfit, τ = 103. More information on running and using Tfit output is available at https://biof-git.colorado.edu/dowelllab/Tfit.
EM algorithm and bidirectional origin estimation
On its own, however, the template matching module of Tfit does not provide an exact estimate over Θ (the parameters associated with a single loading position). To perform optimization over Θ and specifically μ (the origin of bidirectional transcription), we derived the expectation maximization algorithm (outlined in detail in our previous publication) (Azofeifa and Dowell 2017) to optimize the likelihood function of Equation 4. In brief, we used the following EM-specific parameters at each loci: The number of random reinitializations per loci was set to 64, the threshold at which the EM was said to converge, |llt − llt+1|, was set to 10−5. Finally for computational tractability, the EM algorithm halted after maximum of 5000 iterations.
At each window predicted by the sliding window algorithm, we perform inference over μ, σ, λ, and π by the EM algorithm. Details of the derivation, model selection, and algorithm design can be found in our previous report (Azofeifa and Dowell 2017).
Footprint estimation
Importantly, our previous effort at parameter estimation of the finite mixture model assumed that RNAP behaved as a point source (Azofeifa and Dowell 2017). Consequently, we could not incorporate a systematic approach to estimate observed gaps between the forward and reverse strand peaks, which deviate more than could be explained by an exponentially modified Gaussian density function. Here, we amend our earlier model only slightly to estimate this behavior. We call the distance between the forward and reverse strand peaks, the footprint of RNAP or fp. In brief, fp amounts to adding or removing a constant to zi, the genomic position of RNAP after loading and initiation. Assuming that fp > 0 then the above equations remain valid by a simple transformation to zi:
As in our previous effort (Azofeifa and Dowell 2017), we insert this new parameter into the conditional expectation of the latent variables given the observed random variables and perform a gradient step. This allows us to optimize for fp (Equation 5):
| (5) |
The interested reader should refer to our previous paper (Azofeifa and Dowell 2017) where each parameter is explained fully; derivation of the EM algorithm and fitting of the Tfit model are discussed heavily. For complete clarity, the full expression of the expectation operators is given by Equation 6:
| (6) |
TF binding site prediction via eRNA presence
We compute the receiver operating characteristic (ROC) curve to quantify the ability of bidirectional transcription to predict TF ChIP binding. ENCODE-called peaks within a TF's ChIP-seq data are considered truth, and randomly selected regions that do not overlap any previously seen ChIP-seq peak are considered a gold standard for noise. For each peak (truth or noise), a bidirectional model is fit using the expectation maximization algorithm. A Bayesian information criteria (BIC) score was calculated between the exponentially modified Gaussian mixture model and a simple uniform distribution with support across the entire peak. We record a true positive if the BIC score exceeds a threshold τ and the peak was one of the ENCODE peak calls. We record a false positive if the BIC score exceeds the threshold (τ) and the peak is a random noise interval. We vary the threshold τ to obtain the ROC curve of Figure 1 and compute an area under the curve (AUC).
Computation of bimodality
To assess whether the distribution of ChIP peaks or TF binding motif sequences around an eRNA origin is bimodal, we developed and employed a pairwise distribution test. We define the ΔBIC score (in Equation 8) to be the difference in BIC scores between a single Laplace-uniform mixture centered at zero (unimodal) and a two component Laplace-uniform mixture with displacement away from 0, i.e., c (bimodal). The density function of a Laplace distribution with parameters (c,b) is provided in Equation 7, and we use the formulation for the uniform distribution of Equation 2.
| (7) |
Here D refers to the set of distances, di ∈ [ − 1500, 1500], either the center of the TF binding peaks obtained from MACS (Zhang et al. 2008) or the center of TF binding motif sequence from the PSSM scanner relative to eRNA origin. If ΔBIC ≫ 0, we assume bimodality in TF peak location relative to the eRNA origin:
| (8) |
Θ* is optimized again by the Expectation Maximization algorithm where the update rules are given in Equation 9:
| (9) |
We refer to a signal as bimodal (i.e., not unimodal) when ΔBIC > 500, estimated from the distribution in Supplemental Figure S5D.
MD-score hypothesis testing
The MD-score relates the proportion of significant motif instances within some window 2h divided by the total number of motif instances against some larger window 2H centered at all bidirectional origin events. It is calculated on a per PWM binding model basis.
Let Xj = {x1,x2,…} be the set of bidirectional origin locations genome-wide for some experiment j. Let Yi = {y1,y2,…} be the set of all significant motif instances for some TF-DNA binding motif model i genome-wide, which is static as it only depends on the genome build of interest. Furthermore, because recent human genome builds vary little at the sequence level, the metric is not expected to change significantly between hg19 versus GRCh38. Therefore, the set of all MD-scores is calculated by Equation 10:
| (10) |
Here, δ(.) is a simple indicator function that returns one if the condition (.) evaluates true and zero if false. The double sum, i.e., g(a), is naively O(|X||Y|); however, data structures like interval trees reduce time to O(|X|log |Y|).
To be clear, there exist 641 TF-DNA binding models in the HOCOMOCO database, and therefore, 641 MD-scores exist for some experiment j. Let mdi be the MD-score computed for some TF-DNA binding motif model. Therefore, let MDj = {md1, md2, …, md641} be the vector of all MD-scores for some data set j.
MD-score significance under stationary model
If yi and xi are uniformly distributed throughout the genome, i.e., following a homogeneous Poisson point process, then g(h) is distributed as a binomial distribution with parameters p,N (Equation 11):
| (11) |
In cases where g(H) ≫ 0, the binomial is well approximated by a Gaussian distribution, and hypothesis testing under some α level can proceed in the typical fashion. In brief, significantly increased MD-scores (by a binomial test) is diagnostic of heightened motif frequency surrounding eRNA origins.
MD-score significance under a nonstationary background model
Motif instances, however, are not distributed uniformly throughout the genome. Specifically, particular regions, such as gene promoters of the genome, are known to exhibit significance sequence bias. Indeed, the localized GC content is highly nonstationary at eRNAs (Supplemental Fig. S9A). Consequently, a binomial test, which assumes a homogeneous Poisson process of motif locations genome-wide, may be a too liberal null model (e.g., the wrong background assumption).
To control for this nonstationarity, we propose a simulation-based method to compute P-values for MD-scores under an empirical CDF, i.e., a localized background model. Let p be a 4x2H matrix where each column corresponds to a position from an origin and each row corresponds to a probability distribution over the DNA alphabet {A,C,G,T}. To be clear, p0,0 corresponds to the probability of an A at position − H from any bidirectional origin, similarly p2,1500 corresponds to the probability that a G occurs at exactly the point of the bidirectional origin.
Therefore, the simulation-based method of the background model is simple. Given an experiment of Xj bidirectional origin locations, we simulate |Xj| sequences following this nonstationary GC content bias. We then iterate over all PWM models and look for significant motif hits. We then compute summary statistics about the displacement of the motif sequence relative to the set of synthetic sequences, i.e., MD = {md1, md2, …, md641}. It should be noted that, in this data set, any motif model match is by complete chance alone. We iterate this process 10,000 times to compute a random distribution over mdi, i.e., , and thus we can assess the probability of our observed (i.e., from real data) mdi relative to our empirically simulated . Example simulations are shown in Supplemental Figure S9B.
Cell type and TF enrichment analysis
This section serves to outline the rational for determining if heightened MD-scores correlate with a specific cell type category. More traditional approaches such as a one-way ANOVA test (MD-scores computed from similar cell types are grouped and within group variance is assessed via a F-distribution) will not adequately account for MD-scores with little support (i.e., motif hits that overlap very few eRNAs). To overcome this, we propose a relatively straightforward method that relies on performing hypothesis testing on all pairwise experimental comparisons.
Let j and k be two nascent transcription data sets of interest, then mdsj,i and mdsk,i refer to MD-scores for some TF-motif model (i) for which we can perform hypothesis testing over as outlined in MD-Score Hypothesis Testing. If we let α be the threshold at which we consider mdsj,i − mdsk,i to significantly increase, then we expect on average α · N − 1 false positives when considering a single experiment against the rest of the corpus of size N.
Put another way, if we let the random variable Sj,i refer to the number of times we consider mdsj,i − mdsk,i to significantly increase in a data set comparison, then Sj,i is binomial distributed with parameters N − 1 and α (Equation 12), assuming that there is not a relationship between the motif model i and the experiment j:
| (12) |
In practice we set α to 10−6, and refers to an indicator function that returns one in the case where the statement evaluates to truth, otherwise zero.
Naively, we could now ask for all the data sets annotated as some cell type ct and then perform hypothesis testing on Sct (the sum of Sj,i’s where experiment j belongs to the ct cell type set). Importantly, we only consider data set pairs for which i and j belong to different cell type sets. Unfortunately, a single experiment within the cell type set might show strong association with a TF (i.e., 90% of the N − 1 comparisons significantly deviate from zero) where the rest of the cell types show small numbers of significant deviations. By a binomial test, this is unlikely—even when considering the expansion induced by the cell type set—but intuitively does not fit into our notion of cell type association.
To this end, we define a final random variable Act,i to be the number of times motif model i is significantly enriched for a data set j and that data set j belongs to some cell type (Equation 13):
| (13) |
where CT refers to the set of experiments that are annotated as cell type ct. From there, it is easy to assess A across cell types and motif models under a contingency model using Fisher's exact test.
Transcription of the TF gene when the MD-score is elevated or depleted
To evaluate whether significantly altered (elevated or depleted) MD-scores reflect TF activity, we first calculate the nascent transcription levels over the gene encoding the TF. To this end, all RefSeq genes were downloaded from hg19. Samples with fewer than 5000 Tfit bidirectional regions were removed from subsequent consideration. FPKM was calculated for each gene in each human nascent transcription sample (n = 491) over the body of the gene, defined here as 1 kb to the end of the gene. For all TFs in HOCOMOCO >1 kb and with a RefSeq name (n = 635 TFs), the maximum FPKM of all annotated isoforms was utilized. All TF MD-scores were compared to expectation and classified on a per sample basis. Significant deviations from expectation were determined as passing both the stationary and nonstationary test (P-value <10−6). TFs with significant deviation were subsequently labeled as elevated if they had a minimum MD-score of 0.1 and were above expectation or labeled as depleted if they had a maximum MD-score of 0.1 and below expectation. To identify samples in which the TF is at expectation, we labeled a third set as at-expectation if they pass the stationary and nonstationary test (P-value <10−2). For the box plots of Supplemental Figure S14A, we excluded samples with fewer than 10 significant (depleted or elevated) or at-expectation samples. Across all samples, to avoid zero FPKM the minimum nonzero FPKM was utilized.
We next calculated the Spearman's rank correlation coefficient and P-value across all samples (n = 491; scipy v0.17.1) between MD-scores and the FPKM of the gene encoding the TF (Supplemental Fig. S14B). When shuffling the FPKMs across samples, we expect an average of 8.4 TFs to show correlation (permutation testing 100 times, standard deviation 2.4 TFs). For all eRNAs (MD-score from nonpromoter associated bidirectionals), 286 of 635 TFs show a correlation (P-value <0.01). For all bidirectionals (includes promoters), the same P-value cutoff finds 441 of 635 TFs with correlation (expectation 16.5, standard deviation 3.8).
We next examined regions evaluated by a functional assay, namely, CapStarr-seq (Vanhille et al. 2015), for their co-occurance with eRNA origins. In CapStarr-seq, they utilized mouse 3T3 cells, selected TF-bound regions (by ChIP), and determined whether the bound regions functioned as an enhancer using a GFP expression assay. Identified regions were moved to mm10 coordinates using LiftOver (Hinrichs et al. 2006). For comparison to nascent transcription, Tfit-called bidirectionals (both eRNA and promoter origins) for mouse samples (SRR1233867, SRR1233868, SRR1233869, SRR1233870, SRR1233871, SRR1233872, SRR1233873, SRR1233874, SRR1233875, SRR1233876) from the 3T3 cell lines were combined (Step et al. 2014). While 35.5% of regions classified as a strong enhancer (n = 186) by CapStarr-seq contained a bidirectional origin, only 7.9% of regions classified inactive (n = 4406) had a bidirectional origin. Generally, bidirectionals within strong enhancers (by CapStarr-seq) were identified by Tfit in multiple nascent transcription replicates, while bidirectionals within inactive regions were only in one nascent transcription replicate. Overall, regions defined as strong enhancers were four times more likely to contain an eRNA origin than regions defined as inactive enhancers.
MD-score significance between experiments
The MD-score constitutes a proportion, and as long as h is upper-bounded by H, then mdj,i will always exist within the semi-open interval [0,1). An important question is whether mdj,i has significantly shifted between two experiments: j,k as a function of Xj and Xk. This analysis is straightforward under the two proportion z-test. Specifically, we are testing the null and alternative hypothesis tests in Equation 14:
| (14) |
We can then compute the pooled sample proportion (pi) and standard error (SE) as shown in Equation 15. Therefore, our test statistic z (Equation 16) is normally distributed with mean 0 and variance 1:
| (15) |
| (16) |
Computation of the P-value can be assessed in the normal fashion under some α level. In all comparisons, we utilize multiple hypothesis correction outlined by Storey et al. (2007).
Supplementary Material
Acknowledgments
This work was funded in part by a National Science Foundation (NSF) IGERT grant number 1144807 (J.G.A., R.D.D.), a National Institutes of Health (NIH) grant T32 GM008759 (J.D.R.), a Sie post-doctoral fellowship (M.A.A.), the Boettcher Foundation's Webb-Waring Biomedical Research program (R.D.D.), and an NSF ABI DBI-12624L0 (R.D.D.). We acknowledge the BioFrontiers Computing Core at the University of Colorado Boulder for providing high-performance computing resources (NIH 1S10OD012300) supported by BioFrontiers’ IT.
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.225755.117.
Freely available online through the Genome Research Open Access option.
References
- Allen MA, Mellert H, Dengler V, Andryzik Z, Guarnieri A, Freeman JA, Luo X, Kraus WL, Dowell RD, Espinosa JM. 2014. Global analysis of p53-regulated transcription identifies its direct targets and unexpected regulatory mechanisms. eLife 3: e02200 10.7554/eLife.02200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson R, Gebhard C, Miguel-Escalada I, Hoof I, Bornholdt J, Boyd M, Chen Y, Zhao X, Schmidl C, Suzuki T, et al. 2014. An atlas of active enhancers across human cell types and tissues. Nature 507: 455–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azofeifa JG, Dowell RD. 2017. A generative model for the behavior of RNA polymerase. Bioinformatics 33: 227–234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balwierz PJ, Pachkov M, Arnold P, Gruber AJ, Zavolan M, van Nimwegen E. 2014. ISMARA: automated modeling of genomic signals as a democracy of regulatory motifs. Genome Res 24: 869–884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Core L, Lis J. 2008. Transcription regulation through promoter-proximal pausing of RNA polymerase II. Science 319: 1791–1792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Core LJ, Martins AL, Danko CG, Waters CT, Siepel A, Lis JT. 2014. Analysis of nascent RNA identifies a unified architecture of initiation regions at mammalian promoters and enhancers. Nat Genet 46: 1311–1320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cusanovich DA, Pavlovic B, Pritchard JK, Gilad Y. 2014. The functional consequences of variation in transcription factor binding. PLoS Genet 10: e1004226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danko C, Hah N, Luo X, Martins A, Core L, Lis J, Siepel A, Kraus W. 2013. Signaling pathways differentially affect RNA polymerase II initiation, pausing, and elongation rate in cells. Mol Cell 50: 212–222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danko CG, Hyland SL, Core LJ, Martins AL, Waters CT, Lee HW, Cheung VG, Kraus WL, Lis JT, Siepel A. 2015. Identification of active transcriptional regulatory elements from GRO-seq data. Nat Methods 12: 433–438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The ENCODE Project Consortium. 2012. An integrated encyclopedia of DNA elements in the human genome. Nature 489: 57–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Estarás C, Benner C, Jones KA. 2015. SMADs and YAP compete to control elongation of β-catenin:LEF-1-recruited RNAPII during hESC differentiation. Mol Cell 58: 780–793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Everett L, Hansen M, Hannenhalli S. 2010. Regulating the regulators: modulators of transcription factor activity, pp. 297–312. Humana Press, Totowa, NJ. [DOI] [PubMed] [Google Scholar]
- The FANTOM Consortium and Riken Omics Science Center. 2009. The transcriptional network that controls growth arrest and differentiation in a human myeloid leukemia cell line. Nat Genet 41: 553–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fenouil R, Cauchy P, Koch F, Descostes N, Cabeza JZ, Innocenti C, Ferrier P, Spicuglia S, Gut M, Gut I, et al. 2012. CpG islands and GC content dictate nucleosome depletion in a transcription-independent manner at mammalian promoters. Genome Res 22: 2399–2408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher WW, Li JJ, Hammonds AS, Brown JB, Pfeiffer BD, Weiszmann R, MacArthur S, Thomas S, Stamatoyannopoulos JA, Eisen MB, et al. 2012. DNA regions bound at low occupancy by transcription factors do not drive patterned reporter gene expression in Drosophila. Proc Natl Acad Sci 109: 21330–21335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hah N, Murakami S, Nagari A, Danko CG, Kraus WL. 2013. Enhancer transcripts mark active estrogen receptor binding sites. Genome Res 23: 1210–1223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heintzman ND, Hon GC, Hawkins RD, Kheradpour P, Stark A, Harp LF, Ye Z, Lee LK, Stuart RK, Ching CW, et al. 2009. Histone modifications at human enhancers reflect global cell-type-specific gene expression. Nature 459: 108–112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinrichs AS, Karolchik D, Baertsch R, Barber GP, Bejerano G, Clawson H, Diekhans M, Furey TS, Harte RA, Hsu F, et al. 2006. The UCSC genome browser database: update 2006. Nucleic Acids Res 34: D590–D598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jonkers I, Kwak H, Lis JT. 2014. Genome-wide dynamics of Pol II elongation and its interplay with promoter proximal pausing, chromatin, and exons. eLife 3: e02407 10.7554/eLife.02407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaikkonen MU, Spann NJ, Heinz S, Romanoski CE, Allison KA, Stender JD, Chun HB, Tough DF, Prinjha RK, Benner C, et al. 2013. Remodeling of the enhancer landscape during macrophage activation is coupled to enhancer transcription. Mol Cell 51: 310–325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaikkonen MU, Niskanen H, Romanoski CE, Kansanen E, Kivelä AM, Laitalainen J, Heinz S, Benner C, Glass CK, Ylä-Herttuala S. 2014. Control of VEGF-A transcriptional programs by pausing and genomic compartmentalization. Nucleic Acids Res 42: 12570–12584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulakovskiy IV, Medvedeva YA, Schaefer U, Kasianov AS, Vorontsov IE, Bajic VB, Makeev VJ. 2013. HOCOMOCO: a comprehensive collection of human transcription factor binding sites models. Nucleic Acids Res 41: D195–D202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulakovskiy IV, Vorontsov IE, Yevshin IS, Soboleva AV, Kasianov AS, Ashoor H, Ba-Alawi W, Bajic VB, Medvedeva YA, Kolpakov FA, et al. 2016. HOCOMOCO: expansion and enhancement of the collection of transcription factor binding sites models. Nucleic Acids Res 44: D116–D125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laitem C, Zaborowska J, Isa NF, Kufs J, Dienstbier M, Murphy S. 2015. CDK9 inhibitors define elongation checkpoints at both ends of RNA polymerase II–transcribed genes. Nat Struct Mol Biol 22: 396–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lam MTY, Cho H, Lesch HP, Gosselin D, Heinz S, Tanaka-Oishi Y, Benner C, Kaikkonen MU, Kim AS, Kosaka M, et al. 2013. Rev-Erbs repress macrophage gene expression by inhibiting enhancer-directed transcription. Nature 498: 511–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Xy, MacArthur S, Bourgon R, Nix D, Pollard DA, Iyer VN, Hechmer A, Simirenko L, Stapleton M, Hendriks CLL, et al. 2008. Transcription factors bind thousands of active and inactive regions in the Drosophila blastoderm. PLoS Biol 6: e27 10.1371/journal.pbio.0060027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W, Notani D, Ma Q, Tanasa B, Nunez E, Chen AY, Merkurjev D, Zhang J, Ohgi K, Song X, et al. 2013. Functional roles of enhancer RNAs for oestrogen-dependent transcriptional activation. Nature 498: 516–520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W, Notani D, Rosenfeld MG. 2016. Enhancers as non-coding RNA transcription units: recent insights and future perspectives. Nat Rev Genet 17: 207–223. [DOI] [PubMed] [Google Scholar]
- Liu X, Kelm RJ, Strauch AR. 2009. Transforming growth factor β1-mediated activation of the smooth muscle α-actin gene in human pulmonary myofibroblasts is inhibited by tumor necrosis factor-α via mitogen-activated protein kinase kinase 1-dependent induction of the Egr-1 transcriptional repressor. Mol Biol Cell 20: 2174–2185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo X, Chae M, Krishnakumar R, Danko CG, Kraus WL. 2014. Dynamic reorganization of the AC16 cardiomyocyte transcriptome in response to TNFα signaling revealed by integrated genomic analyses. BMC Genomics 15: 155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitsui K, Tokuzawa Y, Itoh H, Segawa K, Murakami M, Takahashi K, Maruyama M, Maeda M, Yamanaka S. 2003. The homeoprotein Nanog is required for maintenance of pluripotency in mouse epiblast and ES cells. Cell 113: 631–642. [DOI] [PubMed] [Google Scholar]
- Nojima T, Gomes T, Grosso ARF, Kimura H, Dye MJ, Dhir S, Carmo-Fonseca M, Proudfoot NJ. 2015. Mammalian NET-Seq reveals genome-wide nascent transcription coupled to RNA processing. Cell 161: 526–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oren M. 1999. Regulation of the p53 tumor suppressor protein. J Biol Chem 274: 36031–36034. [DOI] [PubMed] [Google Scholar]
- Puc J, Kozbial P, Li W, Tan Y, Liu Z, Suter T, Ohgi KA, Zhang J, Aggarwal AK, Rosenfeld MG. 2015. Ligand-dependent enhancer activation regulated by topoisomerase-I activity. Cell 160: 367–380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rackham OJL, Firas J, Fang H, Oates ME, Holmes ML, Knaupp AS, FANTOM Consortium, Suzuki H, Nefzger CM, Daub CO, et al. 2016. A predictive computational framework for direct reprogramming between human cell types. Nat Genet 48: 331–335. [DOI] [PubMed] [Google Scholar]
- Read T, Richmond PA, Dowell RD. 2016. A trans-acting variant within the transcription factor RIM101 interacts with genetic background to determine its regulatory capacity. PLoS Genet 12: e1005746 10.1371/journal.pgen.1005746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savic D, Roberts BS, Carleton JB, Partridge EC, White MA, Cohen BA, Cooper GM, Gertz J, Myers RM. 2015. Promoter-distal RNA polymerase II binding discriminates active from inactive CCAAT/enhancer-binding protein beta binding sites. Genome Res 25: 1791–1800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimamoto T, Ohyashiki K, Ohyashiki J, Kawakubo K, Fujimura T, Iwama H, Nakazawa S, Toyama K. 1995. The expression pattern of erythrocyte/megakaryocyte-related transcription factors GATA-1 and the stem cell leukemia gene correlates with hematopoietic differentiation and is associated with outcome of acute myeloid leukemia. Blood 86: 3173–3180. [PubMed] [Google Scholar]
- Sigova AA, Abraham BJ, Ji X, Molinie B, Hannett NM, Guo YE, Jangi M, Giallourakis CC, Sharp PA, Young RA. 2015. Transcription factor trapping by RNA in gene regulatory elements. Science 350: 978–981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spitz F, Furlong EEM. 2012. Transcription factors: from enhancer binding to developmental control. Nat Rev Genet 13: 613–626. [DOI] [PubMed] [Google Scholar]
- Step SE, Lim HW, Marinis JM, Prokesch A, Steger DJ, You SH, Won KJ, Lazar MA. 2014. Anti-diabetic rosiglitazone remodels the adipocyte transcriptome by redistributing transcription to PPARγ-driven enhancers. Genes Dev 28: 1018–1028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storey JD, Madeoy J, Strout JL, Wurfel M, Ronald J, Akey JM. 2007. Gene-expression variation within and among human populations. Am J Hum Genet 80: 502–509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi K, Yamanaka S. 2006. Induction of pluripotent stem cells from mouse embryonic and adult fibroblast cultures by defined factors. Cell 126: 663–676. [DOI] [PubMed] [Google Scholar]
- Teytelman L, Thurtle DM, Rine J, van Oudenaarden A. 2013. Highly expressed loci are vulnerable to misleading ChIP localization of multiple unrelated proteins. Proc Natl Acad Sci 110: 18602–18607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanhille L, Griffon A, Maqbool MA, Zacarias-Cabeza J, Dao LT, Fernandez N, Ballester B, Andrau JC, Spicuglia S. 2015. High-throughput and quantitative assessment of enhancer activity in mammals by CapStarr-seq. Nat Commun 6: 6905 10.1038/ncomms7905. [DOI] [PubMed] [Google Scholar]
- Vaquerizas JM, Kummerfeld SK, Teichmann SA, Luscombe NM. 2009. A census of human transcription factors: function, expression and evolution. Nat Rev Genet 10: 252–263. [DOI] [PubMed] [Google Scholar]
- Vogel C, Marcotte EM. 2012. Insights into the regulation of protein abundance from proteomic and transcriptomic analyses. Nat Rev Genet 13: 227–232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worsley Hunt R, Wasserman WW. 2014. Non-targeted transcription factors motifs are a systemic component of ChIP-seq datasets. Genome Biol 15: 412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yadon AN, Van de Mark D, Basom R, Delrow J, Whitehouse I, Tsukiyama T. 2010. Chromatin remodeling around nucleosome-free regions leads to repression of noncoding RNA transcription. Mol Cell Biol 30: 5110–5122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao L, Berman BP, Farnham PJ. 2015. Demystifying the secret mission of enhancers: linking distal regulatory elements to target genes. Crit Rev Biochem Mol Biol 50: 550–573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Liu T, Meyer CA, Eeckhoute J, Johnson DS, Bernstein BE, Nusbaum C, Myers RM, Brown M, Li W, et al. 2008. Model-based Analysis of ChIP-Seq (MACS). Genome Biol 9: R137. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.