FIND: difFerential chromatin INteractions Detection using a spatial Poisson process

Abstract

Polymer-based simulations and experimental studies indicate the existence of a spatial dependency between the adjacent DNA fibers involved in the formation of chromatin loops. However, the existing strategies for detecting differential chromatin interactions assume that the interacting segments are spatially independent from the other segments nearby. To resolve this issue, we developed a new computational method, FIND, which considers the local spatial dependency between interacting loci. FIND uses a spatial Poisson process to detect differential chromatin interactions that show a significant difference in their interaction frequency and the interaction frequency of their neighbors. Simulation and biological data analysis show that FIND outperforms the widely used count-based methods and has a better signal-to-noise ratio.

Chromatin folding constitutes one of the key mechanisms by which cells control their transcriptional program and cellular identity (Schmitt et al. 2016). Hi-C is one of the most widely adopted biochemical techniques to probe the genome-wide spatial organization of chromatin (Rao et al. 2014; Schmitt et al. 2016; Dekker et al. 2017). Computationally, the analysis of Hi-C data is challenging, largely due to the various sources of biases introduced by the various experimental steps (Imakaev et al. 2012). Therefore, much of the existing computational effort is focused on developing more reliable data preprocessing techniques, such as filtering and normalization, to extract much of the signal from the data (Hu et al. 2012; Sauria et al. 2015; Servant et al. 2015; Forcato et al. 2017). However, with the increasing accumulation of Hi-C data (Rao et al. 2014; Du et al. 2017), there is interest in performing more comparative analyses to study the structural variability between the different tissues and cellular conditions.

Surveying the literature, we noticed that there has not been a globally adopted conventional method for the detection of differential chromatin interactions (DCIs). One of the simplest strategies is to use fold change as a norm for the detection of DCIs. This strategy was generally adopted in the early Hi-C analysis papers. For example, Wang et al. (2013) used a simple fold-change strategy to detect DCIs between MCF-7 Hi-C samples before and after estrogen treatment. In a more elaborate model, Dixon et al. (2015) used large fold-change chromatin interactions to train a random-forest model to detect the epigenetic signals that are more predictive of the chromatin structural changes.

Other strategies use the binomial model to compare two normalized Hi-C contact maps and detect the pairwise interactions that show a significant change in their frequency. This type of test is adopted by the HOMER software (Heinz et al. 2010). However, in many of the recently published studies (Paulsen et al. 2014; Lun and Smyth 2015; Taberlay et al. 2016; Ulianov et al. 2016), we noticed an increasing adoption of count-based methods such as edgeR (Robinson et al. 2010) to detect DCIs. By comparing edgeR to binomial-based methods, Lun and Smyth (2015) showed that edgeR could outperform HOMER's results.

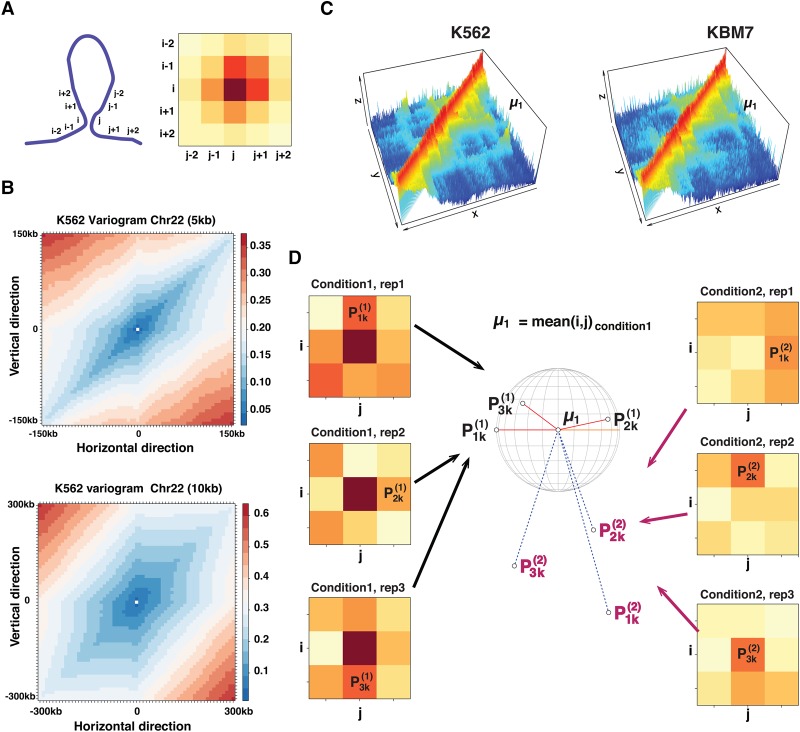
Since most of the methods for detecting DCIs were developed to analyze relatively low-resolution Hi-C contact maps (40 kb or more), the authors assumed independence among the different pairwise interactions. At low resolutions, this assumption is logical, as we only capture the spatial proximity between distant chromatin fibers. However, in the case of high-resolution contact maps (Rao et al. 2014), this assumption may break down. Due to the polymeric nature of the chromatin fiber, the establishment of a chromatin loop that brings two interacting loci (i, j) into spatial proximity will also influence the spatial distance between their adjacent loci (i − 1, i + 1 and j − 1, j + 1). In the Hi-C contact map, the distance change between the anchor points i and j should also be reflected in the interaction frequencies within the window centered around the pairwise interaction (i, j) (Fig. 1A). Clearly, in high-resolution Hi-C data, the detection of DCIs under the independence assumption can have a high error rate.

Figure 1.

Existence of the spatial dependency and the idea behind our model. (A) Illustration of the spatial dependency along neighboring loci in the Hi-C contact map. (B) Semivariogram showing the directional variability between interaction bins separated by a certain horizontal and vertical distance in the Hi-C contact map. (C) A differential interaction can be considered as a change of the intensity around the 3D coordinate (i, j, f_ij) of a reference point μ₁. (D) Principle of the k-nearest neighbor (KNN) intensity estimation in a 3×3 window around a pairwise interaction (i, j). Given an interaction (i, j) with a mean frequency ${\mu }_1=(i,j,\overline{f_{ij}})$ in the first condition (represented by the mountain tip in C), if there is no structural change, we expect the interaction frequencies from the second condition to have a similar density around the point μ₁ in the 3D space. Thus, for each condition and each replicate, we calculate the 3D distance between each bin in the surrounding window and μ₁ and order them according to their distance. We note $P_{nk}^{\left(c\right)}$ as the kth-nearest neighbor to the point μ₁ from the nth replicate of condition c ∈ {1, 2}. Then, we estimate the density of the KNNs around μ₁in the first condition $\left({\lambda }_k^{\left(1\right)}\right)$ and in the second condition $\left({\lambda }_k^{\left(2\right)}\right)$. The density of the KNNs around μ₁ is expected to be stable between the two conditions. To decide if the change of the KNN density around μ₁ $\left({\lambda }_k^{\left(2\right)}/{\lambda }_k^{\left(1\right)}\right)$ is significantly large or small, we use a Fisher distribution. The same principle applies if we use μ₂ (the mean in condition 2) as our reference point.

To resolve this issue, we developed a new computational method, FIND, that considers the local spatial dependency between interacting loci. FIND exploits a spatial Poisson process model to detect differential chromatin interactions that show both a significant change in their interaction frequency and the interaction frequency of their adjacent bins.

Results

High resolution Hi-C captures the spatial dependency between adjacent chromatin fibers

Improvement in the biochemistry of the Hi-C experiment, from the dilution Hi-C (Lieberman-Aiden et al. 2009) to the in situ Hi-C (Rao et al. 2014), helped reveal a more detailed snapshot of the chromatin folding and the spatial dependency among adjacent interacting loci. In the Hi-C contact map, the spatial dependency between nearby chromatin fibers can be illustrated by the schematic example in Figure 1A.

Given the polymeric nature of chromatin, a loop formation is characterized by the bending of the polymer chain and the establishment of a chromatin interaction between two physically proximal loci, i and j. When the spatial distance between i and j changes, the distance between their adjacent loci (such as i − 1, i + 1, j − 1 and j + 1) will also be influenced. In the Hi-C contact map, this phenomenon should be characterized by a change in the interaction frequencies of the bins within the 2D window centered at the pairwise interaction (i, j) (Fig. 1A). In this work, we call the pairwise interactions located in this window the “neighborhood interactions” of (i, j). To quantitatively measure the extent of the spatial dependency between adjacent loci in the Hi-C contact map, we calculated the directional variogram under different Hi-C resolutions (Fig. 1B; Supplemental Figs. S1, S2). The variogram is a measure widely used in geostatistics to describe the degree of spatial correlation of a given spatial process. It is based on calculating the mean variance between the values of all the pairs of points Z(x) and Z(x + h) separated by a given distance h in a given map (Pebesma 2004). If we consider the Hi-C contact map as a 2D surface and the interaction frequencies as values sampled from a spatial process Z(i, j), the variogram should give us an idea of the spatial dependency between adjacent bins. The distance-dependent contact probability plot generally used to describe Hi-C data informs us about the expected contact frequency along each diagonal within the Hi-C contact map. However, it does not inform us about the relationships between the interaction frequencies along the other directions in the 2D Hi-C contact map. These relationships can be captured through the variogram as it measures the mean interaction frequency variability between all the bins (i, j) and the bins separated by a distance h in the horizontal, vertical, and diagonal directions.

In Figure 1B, we show the directional variogram up to a separation distance of 30 bins calculated from 5- and 10-kb resolution-normalized Hi-C contact maps of Chromosome 22 in the cell line K562 (Rao et al. 2014). We notice that there is a small amount of variability among adjacently located pairwise interactions that are separated by short distances in all the directions of the 2D Hi-C contact map. We also notice that the interaction frequencies vary much more slowly along the diagonal than in the other directions. This indicates that the “zone of influence” of an interaction (i, j) is limited to its neighborhood and is independent from the distal interactions. The radius of the influence zone of (i, j) decreases with increasing resolution (Supplemental Figs. S1, S2), which confirms that in high-resolution analysis, the dependency between neighboring bins cannot be ignored.

Based on these observations, we built our differential chromatin interaction detection model to take into account the spatial dependences among neighboring loci.

Proposition of a spatial Poisson process to model differential chromatin interactions

If we consider the interaction frequencies of the Hi-C contact map in a three-dimensional parameter space in which the x-axis and y-axis represent the genomic coordinates and the z-axis represents the interaction frequencies, then the highly interacting regions would form mountain-like structures (Fig. 1C). In the case of a differential interaction, we would expect to see a significantly correlated change in the “mountain” shape (Fig. 1C). Conversely, if the difference is due to technical noise, we would expect a more random shape change in which the frequency change of a pairwise interaction will have no effect on its adjacent interactions.

Intuitively, to estimate this shape change between two conditions, we can take the three-dimensional location of the tip of the “mountain” in the first condition as a point of reference. Then, we calculate the change in the density of points around it between the first and second conditions (Fig. 1D).

Given an experimental design in which the Hi-C contact maps are generated in two biological conditions, each with n_c replicates (c ∈ {1, 2}). Let (i, j) be a pairwise interaction of interest for which we want to check the differential interaction state, and let W be the width of the window centered around it. For example, in the case of a window of width 3, the window will include all nine pairwise interactions with coordinates in the Cartesian product between the loci {i − 1, i, i + 1} and {j − 1, j, j + 1}. We also define μ₁ as the mean interaction frequency of the pairwise interaction (i, j) in experimental condition 1 and μ₂ as the mean interaction frequency in experimental condition 2.

In the case of no differential interaction, the interaction frequencies within the window centered at (i, j) are expected to be similarly distributed in the two conditions around μ₁. Hence, we expect the probability of observing the k-nearest neighbor (KNN) at a distance x ∈ ℝ³ from the reference point (i, j, μ₁) to be similar between the two biological conditions. Under the assumption that the neighboring interaction frequencies are sampled from a homogeneous spatial Poisson process, the probability of observing the KNN at a distance x depends only on the density of the KNNs around the reference point (i, j, μ₁) (Methods). Thus, in a window of width W, we consider the interaction (i, j) to be a DCI, if the majority of the KNNs show a significant change in their intensity.

More specifically, using the triplet (i, j, μ₁) as our reference and for each replicate in each condition, we can rank the W² interactions in the neighborhood of (i, j) according to their distance from the point (i, j, μ₁). Let $P_{nk}^{\left(c\right)}$ indicate the kth-nearest neighbor of (i, j, μ₁) in the nth replicate of condition c (Fig. 1D). For a fixed k (for example, the first nearest neighbor), we can use the point intensity estimator developed by Burguet (Burguet et al. 2009, 2011; Burguet and Andrey 2014) to estimate the intensity ${\lambda }_k^{\left(1\right)}\left({\mu }_1\right)$ of the KNNs $P_{nk}^{\left(1\right)}$ from the first condition and the intensity ${\lambda }_k^{\left(2\right)}\left({\mu }_1\right)$ of the KNNs $P_{nk}^{\left(2\right)}$ from the second condition around μ₁ (Methods). We consider the KNNs to show a change in their intensity at μ₁ if the ratio $R_k\left({\mu }_1\right)={\lambda }_k^2\left({\mu }_1\right)/{\lambda }_k^1\left({\mu }_1\right)$ is significantly different from unity. Under the null hypothesis that ${\lambda }_k^1\left(\mu \right)={\lambda }_k^2\left(\mu \right),$ the ratio R_k (μ₁) can be shown to follow a Fisher distribution with 2n₁ k and 2n₂ k degrees of freedom, respectively (Burguet et al. 2009; Methods).

Using the same window and the points (i, j, μ₁) and (i, j, μ₂) as references, we can calculate 2W² P-values for the pairwise interaction (i, j). These P-values will then be combined using the rth ordered P-value statistic (Song and Tseng 2014). The final false discovery rates will be estimated using the Benjamini-Hochberg method (Benjamini and Hochberg 1995; Methods).

Neighboring pairwise interactions have different sensitivity to the Hi-C contact frequency changes

To understand the behavior of our model and to check the contribution of each k-nearest neighbor to the final DCI decision, we simulated two Hi-C conditions, each with two replicates (Methods). Then, we used a major voting strategy in which a pairwise interaction (i, j) is considered a DCI if at least half of the KNNs in the window centered at (i, j) show a significant change in their density around μ₁ or μ₂.

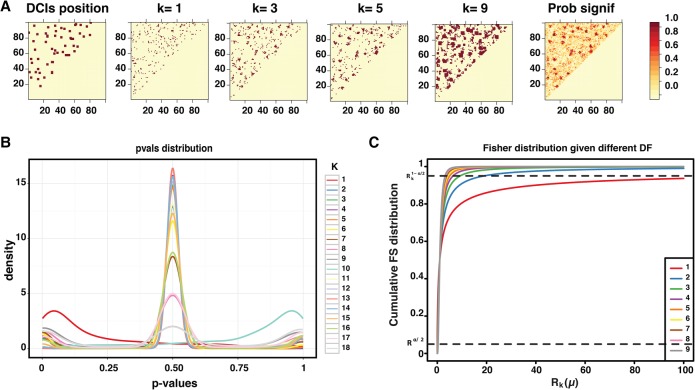
To assess the sensitivity of each KNN to the interaction frequency change, we used a window of width 3 and plotted the pairwise interactions that show a significant density change in their kth-nearest neighbor (k ∈ [1, 9], P-value <0.001) between the two conditions (Fig. 2A). We observe that the furthest neighbors are more sensitive to the variability in interaction frequency, because they tend to report more significant interaction changes, whereas the nearest neighbors are less sensitive. The analysis of the distribution of the P-values obtained from each KNN in Figure 2A indicated a similar conclusion (Fig. 2B), with distant neighbors having many of their P-values located at the extremities outside of the null hypothesis acceptance region

$$\left[R_k^{{\displaystyle \frac{\alpha }{2}}},R_k^{1-{\displaystyle \frac{\alpha }{2}}}\right],$$

and the nearest neighbors have more of their P-values more inside the acceptance region (Fig. 2B). In fact, this sensitivity is due to the speed of convergence of the Fisher-distribution cumulative density function (CDF), as illustrated in Figure 2C. We noticed that the smaller the degree of freedoms is, the slower is the convergence of the CDF to 1. Thus, for smaller k values, in order for the ratio R_k(μ) to be significant, it needs to be either very small $({\hat{\lambda }}_k^1(\mu )\ll {\hat{\lambda }}_k^2(\mu ))$ or very large $({\hat{\lambda }}_k^1(\mu )\gg {\hat{\lambda }}_k^2(\mu ))$. In contrast, the distant neighbors need to have only a small amount of variability to be in the null hypothesis rejection zone. This indicates that we need a decision scheme that accounts for the neighbors’ sensitivity.

Figure 2.

Sensitivity of the different KNN to variability. (A) Heatmaps showing the sensitivity of the different KNNs to variability. The left heatmap indicates the position of the simulated differential interactions. The heatmaps labeled from k = 1 to k = 9 show the positions of the pairwise interactions showing a significant difference from their kth-nearest neighbor (P-value <0.001). The right heatmap shows the majority vote heatmap of the KNNs. We noticed that the furthest neighbors give noisier predictions. (B) The distribution of the P-values of the KNN heatmaps calculated in A. Plots 1–9 are the P-values obtained using μ₁ as reference, and plots 10–18 are the P-values obtained using μ₂ as reference. (C) Plot showing the convergence of the Fisher distribution using k as the degrees of freedom (k ∈ [1, 9]). We noticed that the larger the k is, the faster the Fisher distribution converges out of the acceptance zone.

Different strategies can be adopted to combine the 2W² P-values calculated for each pairwise interaction (i, j). Traditional methods such as Fisher's combined probability test (Fisher 1925) and Stouffer's Z-test (Riley et al. 1949) or their weighted variants can be used; however, they are designed to report a significant P-value if at least one of the 2W² tests is non-null, which makes them very sensitive to changes in the farthest KNNs. Other methods, such as the maxP approach (Wilkinson 1951) are too stringent, as this method considers only the largest ordered P-value among the 2W² tests and potentially misses many differential interactions. Ideally, a weighted P-value alternative should be adopted; however, they tend to be computationally demanding. A good tradeoff is the use of the rth ordered P-value (rOP) method (Song and Tseng 2014). The rOP method considers a collection of tests to be significant if at least r of them are significant. Under the null hypothesis, the rOP tests on the rth order statistic among the sorted 2W² P-values using beta distribution with degrees of freedom α = r and β = 2W² − r + 1. In our model, the value of r is equal to the largest integer value smaller than p × W², such that p ∈ (0, 1] is the percentage of the significantly variable KNNs between the two biological conditions required for a pairwise interaction to be considered a DCI.

The spatial dependency model shows more accurate detection of DCIs compared to the spatial dependency-free models

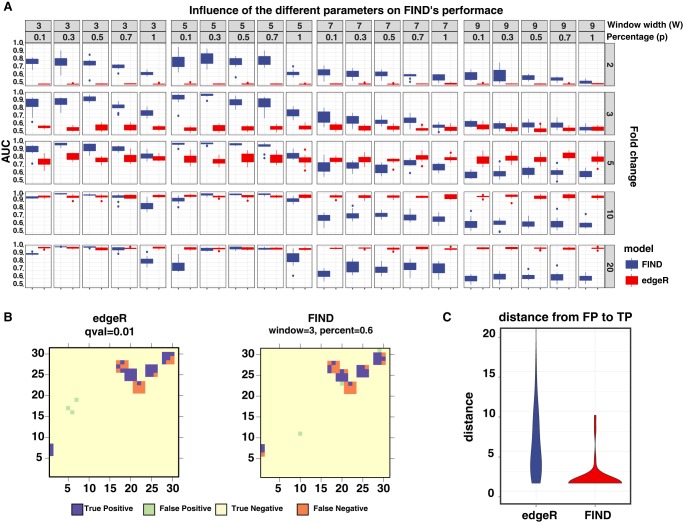
To assess the accuracy of our model, we compared its performance to the edgeR method as a representative of models that assume the independence between the Hi-C pairwise interactions. We did a simulation analysis in which we generated a Hi-C experiment with two conditions, each with two replicates. We used the counts of the K562 Hi-C at 5-kb resolution as a reference to generate the simulated interaction counts (Methods). Then, given the known positions of the differential and nondifferential interactions, we calculated the area under the curve (AUC) values to assess the performance of FIND versus edgeR given different window sizes (W), the percentage of significantly variable KNNs (P), and fold-change (FD) values. For each fixed setting, the simulation was repeated 10 times. By summarizing these results in Figure 3A, we observed that for a window less than or equal to 5 bins (25 kb), FIND outperforms edgeR. However, depending on the selected proportion of significantly differential KNNs, the performance of FIND varies. When we required all the neighboring pairwise interactions in the sliding window to be significantly variable (P = 1), which is also equivalent to the maxP statistic, we observed that FIND still maintains a good DCI detection performance but drops significantly compared to other percentage values. This strict setting could be useful to detect reliable DCIs, but it would also miss many other important DCIs. On the other hand, we noticed a lower performance if we only required a small proportion of the neighboring pairwise interactions (P < 0.5) to be differential, the result is comparable to those of Fisher's combined probability test and Stouffer's Z-test.

Figure 3.

Performance comparison between FIND and edgeR on simulated data. (A) Tile plot comparing the performance between FIND and edgeR given different window sizes (W), percentages of significantly variable KNNs (P) and fold-change values. For each fixed configuration, we ran 10 simulations and calculated the box plots shown in each tile. (B) An example simulation showing the positioning of the reported DCI by edgeR and FIND (blue and green) relative to the real signal (blue and orange) in a case in which FIND and edgeR have similar performance. We observed that regions reported by edgeR tend to be located far from the real signal. (C) Distribution of the distances of edgeR and FIND's false-positive signals relative to true DI regions. We observed that edgeR DIs tended to be more scattered in the heatmap, whereas FIND's results tended to be near the real signal.

When the window size is very large, >35 kb, FIND's performance degrades and shows generally worse performance than edgeR. This behavior can be explained by the loss of the local dependency between the interacting chromatin fibers at larger resolutions. This relationship can be seen in the 5-kb variogram in Figure 1B, in which we observed high variance between bins with increasing distance. These results indicate that FIND is suitable for high-resolution Hi-C data, whereas in the case of a low-resolution contact map, a count-based method such as edgeR can be sufficient.

As edgeR is independent from the window size and the confidence level α, it has similar performance for a fixed fold-change value. By allowing differential interaction to have increasing fold-change values, we observed that edgeR performs similarly to FIND in high fold-change regions. For example, in the case in which we allowed the DCI bins to have a fold change of 10 or more, edgeR and FIND performed similarly. This indicates that edgeR is more suitable to detect very significant changes that have a visible impact on the neighborhood. However, edgeR still misses many of the DCIs that show lower fold change but have a significant structural change in their neighborhoods.

We then looked at the case in which edgeR and FIND have comparable behavior (high fold-change values) to check which method was more reliable. In other words, how far are the false-positive values from the real signal? In Figure 3B, we show an example of the location of the wrongly predicted DCI (shown in green) to the accurately simulated DCIs (blue and orange). We clearly see that FIND's false positives are located near the real signal, whereas edgeR false positives tend to be located far away. Most of FIND's false positives are located one bin away from the real signal, while for edgeR, the false-positive predictions tend to be located far away (Fig. 3C). This observation indicates that the DCIs reported by FIND tend to be in the neighborhood of regions of high structural variability, and edgeR has more potential to detect technical noise in the Hi-C contact map, which can lead to more erroneous conclusions.

To sum up, these simulation results reveal the advantage of our method over the count-based methods for high-resolution Hi-C contact map as it uses the nearest neighbors’ information to decide about the significance of a structural change. Compared to count-based methods, this strategy avoids the detection of noisy DCIs, because it borrows information for adjacent interactions. We also showed that in high resolution Hi-C data, count-based methods may be used, but they require more cautious manipulation as detailed in Lun and Smyth (2015).

FIND shows more reliable behavior than count-based methods on real data

To assess the reliability of our model on real data, we compared the 5-kb resolution Hi-C contact maps of K562 and GM12878 cells (Rao et al. 2014). For each cell line, we used two replicates. The data were normalized using the Knight-Ruiz matrix-balancing algorithm (Rao et al. 2014). Additionally, to remove the between-replicates variability, we normalized the replicates of each condition using the MA-plot strategy (Methods).

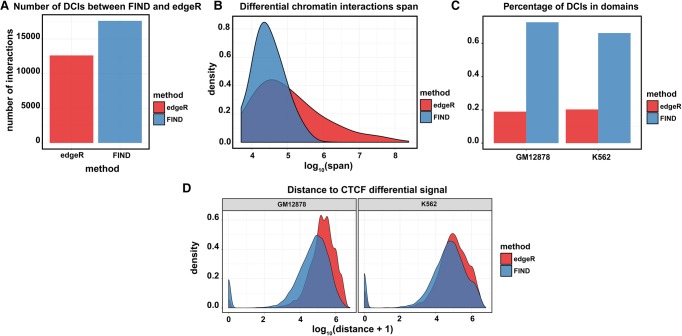
We found that FIND detects approximately 1.6 times more DCIs than edgeR (Fig. 4A). A reasonable explanation is that edgeR missed some of the differential interactions with relatively small fold change, whereas FIND can consider these interactions as true differential interactions because it is backed up by the information from the neighboring interactions.

Figure 4.

Performance comparison between FIND and edgeR with genomic characteristics. (A) The numbers of DCIs detected by FIND and edgeR. (B) The distribution of the span of the DCIs reported by edgeR and FIND. We observed that the majority of FIND's results have a span <1 Mb. (C) The proportion of the genome-wide DCIs located inside TADs for both edgeR and FIND. (D) The distances of edgeR- and FIND-reported DCIs to the CTCF differential peaks.

Several Hi-C-based comparative studies indicated that the majority of the chromatin structural changes tend to occur within topologically associated domains (TADs) (Rao et al. 2014; Dixon et al. 2015; Smith et al. 2016). Hence, we checked the span of the reported DCIs by both methods, and the results indicated that the majority of the DCIs detected by FIND have an interaction span <1 Mb (mean span 58,229.4 kb); for edgeR, approximately 20% of the interactions span >1 Mb, with a mean span of 107,555 kb (Fig. 4B; Supplemental Fig. S4). We also calculated the proportion of DCIs located within TADs (Fig. 4C; Supplemental Fig. S5). The results are consistent with Figure 4B, showing that ∼70% of the DCIs detected by FIND are located within TADs; for edgeR, only ∼20% of the DCIs are within TADs. Additionally, because CTCF is a master controller of the chromatin architecture (Rao et al. 2014; Tang et al. 2015), we expected the DCIs to be located in the neighborhoods of the differential CTCF peaks. Thus, we calculated the distance of edgeR- and FIND-detected DCIs to the differential CTCF peaks (Fig. 4D). Compared with edgeR, FIND has a larger proportion of peaks located <100 bp from the CTCF peaks. All of these results indicated that FIND tends to detect larger numbers of reliable DCIs than edgeR.

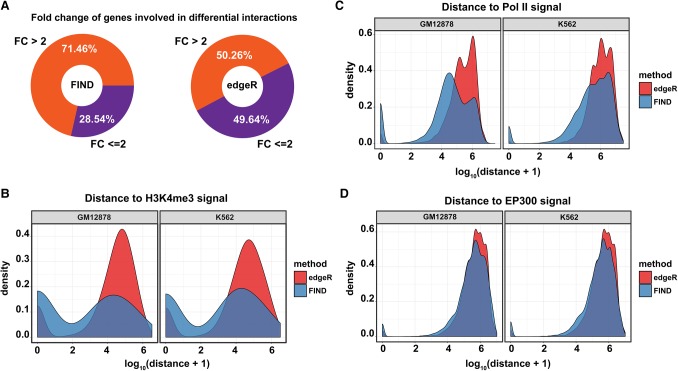
Topological changes have a large effect on the cross-talk between enhancers and promoters that can alter gene expression (Rao et al. 2014; Dixon et al. 2015). We classified genes located in the proximity of DCIs according to their expression fold change (FC) into two categories: FC ≤ 2, genes that did not show a significant difference in expression between the two cell lines, and FC > 2, genes that have a noticeable difference in expression. For FIND, 71.46% of the DCI-related genes show a significant expression change (FC ≥ 2); for edgeR, approximately 50.63% of the DCI-related genes show an expression change between the cell lines (Fig. 5A). Consistent with transcription results, DCIs detected by FIND are closer to active gene signals such as H3K4me3, Pol II binding sites, and EP300 (Fig. 5B–D). All of these results indicated that FIND tends to detect larger numbers of functional DCIs than edgeR.

Figure 5.

Comparison of performance between FIND and edgeR with transcriptional characteristics. (A) The proportion of genes with different fold changes located near the DCIs. (B) The distribution of the distances between DCIs and the H3K4me3 peaks. (C) The distribution of the distances between DCIs and the Pol II peaks. (D) The distribution of the distances between DCIs and the EP300 peaks.

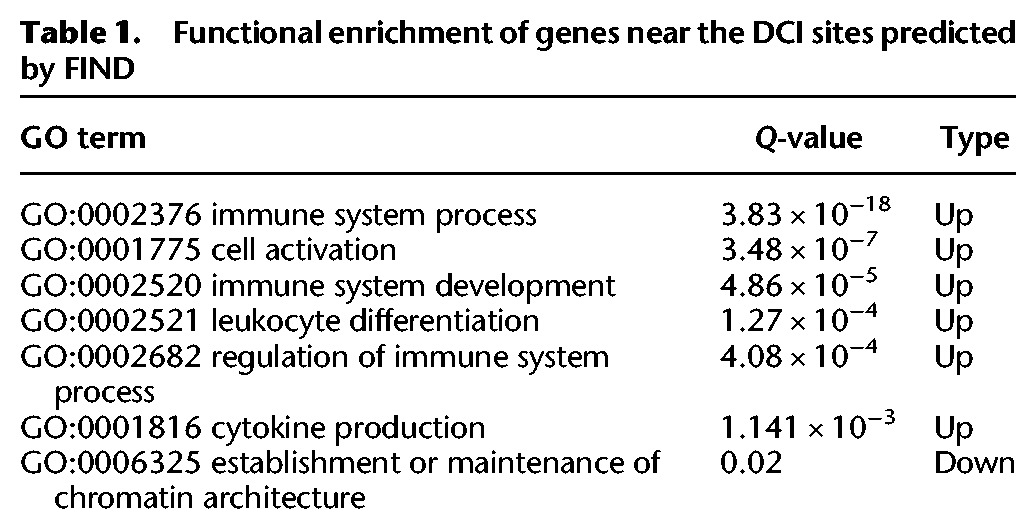
Interestingly, the functional analysis of the genes located in the proximity of DCIs (≤5 kb) detected by FIND, shows a high enrichment for GO terms related to the immune system (Table 1). Meanwhile, for edgeR, only the term “immune system process” showed a significant enrichment. These results further support the reliability of FIND. These findings are consistent with previous reports that indicate that many of the H3K4me1 peaks overlap with known autoimmune disorder SNPs in the B lymphoblast cell line GM12878 (Corradin et al. 2014).

Table 1.

Functional enrichment of genes near the DCI sites predicted by FIND

Role of chromatin structure in K562 differentiation

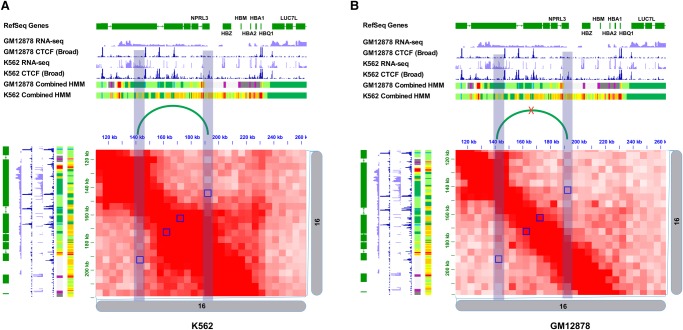
The role of chromatin loops is well characterized at the classical alpha-globin locus, which is known for its exclusive expression in erythroid cells (K562) and its silencing in lymphoblastoid cells (GM12878) (Fig. 6; Vernimmen et al. 2007; Baù et al. 2011). Genes at this locus are regulated by a cluster of remote DNase I hypersensitive sites (HSs) located approximately 30–60 kb upstream of the alpha-globin genes (Vernimmen et al. 2007), and the silencing of these genes is due to the absence of the enhancer-promoter interaction.

Figure 6.

DCIs in the alpha-globin region as detected by FIND between K562 and GM12878 cells. (A) Hi-C contact map of the K562 at the alpha-globin locus. Differential interactions (Q-value <1 × 10⁻⁴) are shown in blue squares; the CTCF signal change region is highlighted by the blue bars. (B) The corresponding region shown in the GM12878 with the same regions highlighted.

In Figure 6, we marked the different results reported by FIND using the P-value cutoff of 1 × 10⁻⁴. We notice that all the reported differently interacting regions are located around interactions that show a significant differential binding of the CTCF protein. ChromHMM tracks at this region also indicate a major change in chromatin state (Ernst and Kellis 2012), from a strong enhancer state (shown in orange in the ChromHMM track) to a heterochromatin state (shown in gray in the ChromHMM track). In addition to the alpha-globin locus, the localization of FIND's result around differential CTCF binding sites can be observed in many regions (Supplemental Fig. S6).

Job Dekker and his group used the low-throughput 5C experiment to investigate the chromatin cross-talk between selected regions in different cell lines (Sanyal et al. 2012). The comparison of our results in the proximity of the differential 5C interactions indicates that FIND'S DCIs are closer to the differential 5C peaks than edgeR ones (Supplemental Fig. S7).

Discussion

Here, we present a novel computational method that detects differential chromatin interactions between two Hi-C experiments. We argue that in high-resolution Hi-C maps, the spatial dependency between neighboring interactions should be considered. First, we used the directional semivariogram metric to verify the existence of the neighborhood dependency in Hi-C data. Then, taking this relationship into account, we developed a computational method that detects differential chromatin interactions that show a correlated change with the pairwise interactions within the surrounding window.

In our model, we consider the Hi-C matrix in the 3D space, which enabled us to consider an interaction change as a change in intensity (height). Then, we exploited a spatial Poisson process to estimate the changes in the intensities of the k-nearest neighbors around the pairwise interactions between two Hi-C conditions. We showed that this change can be estimated using a Fisher distribution. Given the Fisher cumulative distribution function (CDF), we showed that more-distant neighbors show more sensitivity to change due to the fast convergence of their associated CDF. Therefore, we used the rth ordered P-value (rOP) method to minimize the effect of this sensitivity.

To assess the performance of our method, we performed some simulation analyses in which we compared the performance of our method to the widely adopted count-based method edgeR. We showed that, in general, our method outperformed edgeR. For high fold-change interactions, we showed that there is essentially no large performance gap between our model and edgeR; however, our false positives tend to localize near the real differential interactions, whereas edgeR false positives tend to be scattered along the heatmap.

In addition to the simulation experiments, we tested our method on Hi-C interaction data comparing K562 and GM12878 cells. We showed that the DCIs detected by FIND tend to be more located inside TADs, whereas a large proportion of the edgeR results are outside TADs. Additionally, the DCIs reported by our method are located near differential CTCF binding cites and are associated with differentially expressed genes.

The increasing availability of high-resolution chromatin conformation data opens the door to understanding the principles that govern the spatial organization of the chromatin between different species and cell types. However, with the lack of differential chromatin interaction detection tools, it is hard to make significant conclusions. Using existing DCI detection methods without considering the spatial dependence between neighboring interactions may be prone to serious errors when analyzing high-resolution contact maps. Our tool, FIND, has resolved this issue, hence presenting a valuable tool for many investigators.

However, more room remains for improvement; for example, the methods can be extended to allow comparisons of more than two conditions. It would also be beneficial to be able to remove the rOP statistics step and replace it with a unified statistic.

Methods

Hi-C data analysis

We used Hi-C data published by Lieberman-Aiden's group (Rao et al. 2014). For the GM12878 cell line, we used the samples GSM1551574 and GSM1551575; for K562, we used the samples GSM1551620 and GSM1551623. Hi-C matrices were normalized using the VC-squared method available in the Juicebox tool (Durand et al. 2016). For each condition, inter-sample normalization was performed using the MA-plot approach (described below).

For data visualization, we used the R Environment for Statistical Computing (R Core Team 2016) for the generation of Figures 1 and 2 and Supplemental Figures S1–S3; for Figure 6 and Supplemental Figure S6, we used the Juicebox tool (Durand et al. 2016).

Gene expression data

The gene expression data were obtained from the ENCODE project (The ENCODE Project Consortium 2012) with accession numbers GSE78553 for GM12878 cells and GSE78625 for K562 cells.

Gene set enrichment

The gene set enrichment was done using the GAGE method (Luo et al. 2009).

Simulation analysis

To simulate the contact frequencies of the different replicates, we used the K562 Hi-C heatmap as a reference. For each pairwise interaction (i, j), we used a negative-binomial distribution with a dispersion of 1 × 10⁴ using the R function rnbinom. The nondifferential interactions are sampled from a negative binomial with a mean equal to the value of the corresponding pairwise interaction in the K562 matrix, whereas the differential interactions are sampled from a negative binomial with a mean equal to the fold change of their corresponding pairwise interaction in the K562 Hi-C contact map. We tried to make the simulated DCIs as sparsely distributed as possible by selecting a small number of interactions to be DCIs (approximately 1%). Among these DCIs, 40% showed an increase in their interaction count with a given fold-change value. The obtained new mean value (for the DCIs) is used to sample the frequency counts of the DCI region of the replicates in the second condition. Then, we applied a Gaussian smoother around the DCI bins to simulate the effect of changes in the neighbors. We also allowed the non-DCI sample to be an outlier with a probability of 10%.

Semivariogram calculation

The semivariogram calculation was done using the gstat (Pebesma 2004) package in R. The variogram (or semivariogram) measure is widely used in geostatistics to describe the degree of spatial correlation of a given spatial process. If y(x) is a spatial process defined in a two-dimensional space, the variability between all pairs of points separated by a distance h can be calculated as follows:

$$\gamma (h)=\frac{1}{2\left|N\left(h\right)\right|}\sum _x{\left[y\left(x\right)-y(x+h)\right]}^2.$$ (1)

For example, x and h ∈ ℝ² and N(h) is the set of all points separated by h, and |N(h)| indicates the size of this set.

Testing the significance of the kth-nearest neighbor intensity change

The k-nearest neighbor intensity change test is based on the k-nearest neighbor density estimator developed by Burguet et al. (Burguet et al. 2009, 2011; Burguet and Andrey 2014). In this part, we summarize their main model. If we consider the Hi-C interactions in the 3D space, each interaction can be represented by the Cartesian coordinates (i, j, f_ij), such that i and j are the genomic coordinates and f_ij is the interaction frequency. Then, from Burguet's work, we know that for a given pairwise interaction (i, j) with an interaction frequency μ, the probability of observing the kth-nearest neighbor at the distance x_ik from (i, j, μ) in the nth Hi-C replicate is

$$f(x_{n,k})=\frac{{\left(4\lambda \pi \right)}^k}{3^{k-1}(k-1)!}{x}_{n,k}^{k-1}\exp \left(-\lambda \frac{4\pi }{3}{x}_{n,k}^3\right).$$ (2)

In Equation 2, we can see that the only parameter that needs to be estimated is the density λ(μ), written as λ for clarity. Given the Hi-C matrix of the experimental condition c with n_c replicates, the density of the kth-nearest neighbor around the point μ can be estimated from the maximum likelihood of Equation 2, which gives

$${\hat{\lambda }}_k^{\left(c\right)}(\mu )=\frac{n_{c}k-1}{{\displaystyle \frac{4\pi }{3}{\sum }_{n=1}^{n_c}{x}_{n,k}^3}}.$$ (3)

By doing some variable change and algebraic manipulation (detailed in Supplemental Methods), we can show that under the null hypothesis the ratio between the kth-nearest neighbor density at μ in the first and second conditions follows a Fisher distribution with 2n₁ k and 2n₂ k degrees of freedom:

$${\hat{R}}_k(\mu )=\frac{{\hat{\lambda }}_k^{\left(2\right)}(\mu )}{{\hat{\lambda }}_k^{\left(1\right)}(\mu )}\sim FS(2n_{1}k,2n_{2}k).$$ (4)

Thus, given Equation 4 and given a confidence level α, the two-sided P-value that ${\hat{R}}_k(\mu )$ is significant will be equal to

$$P-\mathrm{value}(k)=2\times min(Pr(R_k(\mu )<{\hat{R}}_k(\mu )),Pr(R_k(\mu )>{\hat{R}}_k(\mu ))).$$ (5)

FIND's algorithm

Consider two Hi-C experiments performed under two conditions c₁ and c₂ each with n₁and n₂ replicates. For a given pairwise interaction (i, j) between two genomic bins i and j, let μ₁ be the mean interaction frequency of (i, j) in c₁, and let μ₂ be the mean interaction frequency of (i, j) in c₂. Let W be the size of the window around (i, j). The window around (i, j) will then be of size W² and will include all the pairwise interactions of their coordinates in the Cartesian product

$$\left\{i-\frac{W}{2},\dots ,i,\dots ,i+\frac{W}{2}\right\}\times \left\{j-\frac{W}{2},\dots ,j,\dots ,j+\frac{W}{2}\right\},$$ (6)

where W/2 indicates the largest integer value smaller than W/2.

Using the mean interaction frequency of (i, j) in the first biological condition μ₁ as a point of reference, we can associate with each pairwise interaction in our defined window a P-value that indicates if it significantly changes around μ₁ between the two conditions. A total of W² P-values will be obtained. Then, using the mean interaction frequency of (i, j) in the second biological condition μ₂ as a point of reference, we can also calculate W² P-values that indicate the change of the interactions in the defined window around μ₂. In total, 2W² P-values will be obtained.

The rth ordered P-value (rOP) statistic will be used to estimate the probability that r out of the 2W² tests are significant. We define r as r = p × 2W², where p ∈ (0, 1] is the percentage of the significantly variable KNNs between the two biological conditions required for a pairwise interaction to be considered as a DCI. Briefly, given 2W² P-values estimated through 2W² tests, the rOP statistic defines the following hypothesis setting HS_r:

$$H{S}_r:\left\{H_0:\bigcap _{k=1}^{2W^2}\left\{{\theta }_k=0\right\}\mathrm{versus}{H}_1:\sum _{k=1}^{2W^2}I\left\{{\theta }_k\ne 0\right\}\ge r\right\},$$ (7)

where θ_k is the effect size of the test k. If S_r is the rth order statistic of P-values, then

$$S_r\sim \text{Beta}(r,2W^2-r+1).$$ (8)

ROC calculation

We used the ROCR package to estimate the prediction performances of each of edgeR and FIND. The true-positive signals are the regions simulated to be DCI and reported to be DCI by the algorithm. The false-positive signals are the regions that are not DCI in the simulation but reported as DCI by the algorithm. The false-negative signals are the regions simulated as DCI but reported as not DCI by the algorithm. The true negatives are the regions not DCI in the simulation that are reported as not DCI by the algorithm.

MA normalization

To ensure consistency between the replicates of the same condition, we performed a between-samples normalization. The procedure is similar to the MA-plot normalization for gene expression. Briefly, for each interaction point (i, j) with interaction frequencies $f_{ij}^{\left(1\right)}$ and $f_{ij}^{\left(2\right)}$ in replicate one and replicate two, respectively, we calculated the log intensity (A) and the log ratio (M) as follows:

$$\{\begin{array}{c}A=\frac{\log 2\left(f_{ij}^{\left(1\right)}{f}_{ij}^{\left(2\right)}\right)}{2}\\ M=\log 2\left(\frac{f_{ij}^{\left(1\right)}}{f_{ij}^{\left(2\right)}}\right)\end{array}$$ (9)

The expected bias, M_bias, is then estimated by fitting a loess curve in the MA-plot. The corrected M-value, M_correct = M − M_bias, is calculated, and the rescaled values of $f_{ij}^{\left(1\right)}$ and $f_{ij}^{\left(2\right)}$ are calculated as follows:

$$\{\begin{array}{c}\widehat{f_{ij}^{\left(1\right)}}=2^{\left(A+0.5\times M_{\mathit{correct}}\right)}\\ M=2^{\left(A-0.5\times M_{\mathit{correct}}\right)}\end{array}$$ (10)

5C data processing

The five interaction matrices were downloaded from the GEO under the accession number GSE39510. Both the first and second sets of primers, ENm and ENr, were used. We considered an interaction to be differential in 5C if the interaction between two primers is absent in K562 or GM12878.

Selection of the Q-value threshold in the real data case

Two possible ways can be used to select the cutoff Q-value. One is using a hard cutoff. In this approach, it is advisable to use a Q-value that corresponds to the rOP statistic. For example, if we require that the rth P-value in each window should not be larger than 1×10⁻³, we can use a Q-value cutoff of Beta(1 × 10⁻³|α = r, β = 2W² − r + 1).

Using a hard cutoff can sometimes be very stringent and generally will remove some long-range DCIs due to the relatively weak signal of the large interactions. Moreover, some of the long-range DCIs will show a significantly different Q-value than their counterparts that have the same interaction span. Thus, we used quantile regression to model the relationship between interaction-span and Q-value (Supplemental Fig. S8). In our analysis, all the Q-values above the 99th percentile were considered, and none were larger than Beta(1 × 10⁻³|α = 13, β = 18 − 13 + 1).

Software availability

The software is published under the GNU GPL v3.0 license. The source code of FIND is available in the Supplemental Material and at https://bitbucket.org/nadhir/find.