Improved scatter correction with factor analysis for planar and SPECT imaging

Abstract

Quantitative nuclear medicine imaging is an increasingly important frontier. In order to achieve quantitative imaging, various interactions of photons with matter have to be modeled and compensated. Although correction for photon attenuation has been addressed by including x-ray CT scans (accurate), correction for Compton scatter remains an open issue. The inclusion of scattered photons within the energy window used for planar or SPECT data acquisition decreases the contrast of the image. While a number of methods for scatter correction have been proposed in the past, in this work, we propose and assess a novel, user-independent framework applying factor analysis (FA). Extensive Monte Carlo simulations for planar and tomographic imaging were performed using the SIMIND software. Furthermore, planar acquisition of two Petri dishes filled with ^99mTc solutions and a Jaszczak phantom study (Data Spectrum Corporation, Durham, NC, USA) using a dual head gamma camera were performed. In order to use FA for scatter correction, we subdivided the applied energy window into a number of sub-windows, serving as input data. FA results in two factor images (photo-peak, scatter) and two corresponding factor curves (energy spectra). Planar and tomographic Jaszczak phantom gamma camera measurements were recorded. The tomographic data (simulations and measurements) were processed for each angular position resulting in a photo-peak and a scatter data set. The reconstructed transaxial slices of the Jaszczak phantom were quantified using an ImageJ plugin. The data obtained by FA showed good agreement with the energy spectra, photo-peak, and scatter images obtained in all Monte Carlo simulated data sets. For comparison, the standard dual-energy window (DEW) approach was additionally applied for scatter correction. FA in comparison with the DEW method results in significant improvements in image accuracy for both planar and tomographic data sets. FA can be used as a user-independent approach for scatter correction in nuclear medicine.

INTRODUCTION

The development of quantitative image-generation methods is nowadays an increasingly important task for medical physicists working in the field of nuclear medicine. Past work by the research community has primarily focused on quantitative positron-emission-tomography (PET) imaging. However, using the ability to provide precise locations of physiological data from nuclear medicine studies is now possible with hybrid SPECT/CT systems.¹ The use of additional x-ray CT scans for attenuation correction and the need to perform dosimetry calculations increased interest by physicists to also obtain quantitative single photon emission tomography (SPECT) data sets. Recent work has shown comparable results to PET for SPECT data sets if similar correction methods are used.² For many clinical applications, photon attenuation is commonly the most important factor introducing distortions in image quality. Following such corrections,^3,4 a new layer of distortion appears, namely, due to Compton scattering, wherein the presence of scattered events also reduces quantitative image contrast.^5,6 Compton (incoherent) scattering is an example of inelastic scattering, where the photon transfers its energy to an electron (typically loosely bound in the outer shell) and deviates from its original direction.⁷ Scatter contribution is a function of various parameters such as photon energy, object dimension, source location, energy resolution of the imaging system, and setting of the energy window. Multiple scatter events can be found in all sections of the imaging pipeline, such as patient, bed, collimator, and scintillation crystal.⁸

An objective assessment of scatter correction methods requires knowledge of the spatial distribution of scattered or non-scattered events within the photo-peak window. Several correction techniques have been developed,^8–11 but clinically the “window-subtraction” technique is still most commonly used.¹² Here, additional energy window(s) positioned below and/or above the original photo-peak window are acquired, multiplied by a correction factor, and then subtracted from the acquisition. The chosen value of the correction factor is taken to depend only on the isotope used for imaging (no patient “form factor” is applied). For many isotopes, the correction factor is not quantified at all and is simply set to 1.0. Although the window-subtraction technique might be useful for a number of clinical applications, the implementation for all isotopes, various clinical applications, and patient shapes (from <1 kg to >250 kg weights) obviously makes it difficult to obtain reasonably correct quantitative data. One mathematical method that is used for many different clinical and non-clinical applications is factor analysis (FA). It has led to a number of clinical applications in the past, such as fully automatic separation between different compartments in renal scintigraphy,¹³ radionuclide ventriculography,¹⁴ or salivary gland scintigraphy.¹⁵ FA or holospectral imaging assumes that each pixel value has contributions from the photo-peak and the scatter data.^16–19 Applying FA, it is possible to separate these contributions from each other. The results of this analysis are two factor images, representing the spatial distribution, and two factor curves, representing a visual representation of the energy spectrum. Since we are only interested to measure photo-peak information within the energy window, this area is divided into a number of sub-energy windows and analyzed using a two-factor model. Validation of this scatter correction model was performed using Monte Carlo simulations and phantom measurements.

MATERIAL AND METHODS

Factor analysis (FA) framework

We apply a linear model of factor analysis,

$$D=V{C}^{\prime }+E,$$ (1)

where D is the data matrix of dimensions [m,n] including n scintigraphic images of a dynamic sequence with m (m > n) pixels each, V represents matrix [m,k] having k (k < n) factor images, C is the matrix [n,k] of k factor curves with n time points (C′ is the transpose of C), and E is the matrix [m,n] of errors or residuals not explained by the model.

The problem of finding the unknowns V and C is solved in two steps. The first step is primary factorisation of D (usually) by principal component analysis [from here, we let D indicate the data matrix reproduced by k principal components so that E from Eq. (1) can be left aside],

$$D=P{A}^{\prime },$$ (2)

where P and A are primary estimates of V and C. The second step is “rotation” of principal components to “physiological factors”

$$D=PT{T}^{-1}{A}^{\prime }=V{C}^{\prime },T{T}^{-1}=I(I=\text{unit matrix})$$ (3)

so that

$$V=PT\text{and}{C}^{\prime }=T^{-1}{A}^{\prime },$$ (4)

where T is a regular transformation matrix [k,k]. There is an infinite number of (even positive) solutions of transformation (4), and a unique solution can be found only if some prior information on either or both factor images and curves can be used to find (or to specify “constraints” on the solution of) the matrix T.^19–23 In our study, factor rotation [Eq. (4)] was performed using the “promax” criterion.²⁴ It is an oblique “Procrustes” rotation that maximizes a criterion based on the variance of factor curves C, with parameters that optimized separation of the photo-peak and scatter counts.

To enable factor analysis for gamma camera acquisitions, it is necessary to acquire data either in list mode or using multispectral acquisition techniques.¹⁹ Contrary to previous efforts where the scatter spectrum was determined,^7,15–18 in this work, we are interested to measure the photo-peak information (image and spectra) as accurately as possible. Therefore we divide the acquisition energy window of the imaging system into a number of sub-windows (Fig. 1). If we use, for example, an imaging system that has an energy resolution of 20% for ^99mTc, the lower and higher values of the energy window are 126 keV and 154 keV, respectively. In our approach, we define a number of sub-windows equally distributed between energy windows. After using FA, the FWHM of the photo-peak spectrum should correspond to the energy resolution of the imaging system and is used to control the result of the analysis. The data were exported to a standard computer and analyzed using a self-developed FA software written in Matlab (Mathworks GmbH, Germany).

FIG. 1.

Schematic representation of the sub-energy windows used for scatter correction with FA.

Dual energy window (DEW) scatter correction

Jaszczak et al. proposed the dual energy method for scatter correction.²⁵ Here, an additional energy window below the photo-peak window is used to monitor the number of scatter counts corrupting the total count within the photo-peak window. For the MC simulations and the gamma camera measurement, an additional energy window positioned below the energy window was chosen (120 keV ± 5%). After adjusting the size of the scatter window, the counts of the scatter window are multiplied by a factor k_DEW and then subtracted pixel-by-pixel from the photo-peak window.

More specifically, scatter correction using the DEW method was performed using the following implementation:

$$Scatterfreedata=Count{s}_{Main}-\frac{Count{s}_{SC}}{W_{SC}}\cdot W_{Main}\cdot k_{DEW}.$$

Here the counts measured within the energy window are denoted by Counts_Main, the counts in the scatter window by Counts_SC, and the sizes of the energy windows by W_Main and W_SC, respectively. In this study, k_DEW was set to 0.5.²⁶

Monte Carlo (MC) simulations of scintillation camera acquisitions

Extensive simulations involving various objects were carried out using the well-established SIMIND MC code for SPECT.^27,28 The version of the used code is coupled to a collimator routine that explicitly models collimator scatter and photon penetration. The simulations were performed by taking also the scatter within the phantom into account.

The SIMIND software package also enables separation of events in the image originated from photon interaction with and within the collimator. For example, the value “Geometrical” in the result file defines the percentage of photons that passed through the collimator hole without septal penetration, the value “Penetration” defines the percentage of photons that penetrated the septal wall, and “Scatter” defines the percentage of photons that were scattered within the collimator. The SIMIND code enables the user to change various components of the scintillation camera setup. For our purposes, the maximum scatter order was set for all applications to 5. The simulations carried out apply a point source located in the center of a water cylinder, a ^99mTc MDP bone scan, and a tomographic phantom. In this work, we focus on ^99mTc simulations and scintillation camera acquisitions (detector material: NaI, cover material: Al, detector thickness: 0.952 cm, intrinsic resolution: 0.4 cm). Using MC simulations allows one to vary the energy resolution of the imaging device. For this work, an energy resolution between 5% and 20% was chosen. Planar and tomographic acquisitions were performed by subdividing the photo-peak energy window into 28 sub-windows. After acquiring the planar data, the series of imaging data sets can be immediately utilized by our FA approach. The case of tomographic acquisition is different since prior to the reconstruction procedure, FA has to be applied. The results of this procedure are now two tomographic data sets: one for the photo-peak and the other for the Compton data sets.

Afterwards the reconstruction algorithm is applied to obtain the transaxial data sets.

MC simulation of a point source in a water cylinder

The simulations were performed using different collimators from various scintillation camera vendors. The following scintillation camera types and collimator types were used: Infinia (General Electric), Nucline SPIRIT (Mediso), Brightview (Philips), Symbia (Siemens). SIMIND allows one to calculate the fractional values for geometric, septal penetration, and collimator scatter varying the photon energy (100-500 keV) and collimators [low-energy general purpose (LEGP), low-energy high resolution (LEHR)].

MC simulation of a ^99mTc source varying the energy resolution of the acquisition system

A 10 × 10 × 10 mm ^99mTc source was simulated using the SIMIND software package. Instead of using a single photo-peak energy window, 28 sub-energy windows were used. Several simulations were performed for the same digital phantom by varying the energy resolution (5%, 10%, 15%, and 20%) of the imaging system. The size of the sub-energy window was chosen such that the entire photo-peak was covered.

The simulations were performed using different collimators from various scintillation camera vendors. The following scintillation camera types and collimator types were used: Infinia (General Electric), Nucline SPIRIT (Mediso), Brightview (Philips), Symbia (Siemens).

^99mTc MDP bone simulation

To obtain clinically realistic images, a 3D voxel-based anthropomorphic computer phantom was used for this MC simulation.²⁹ The phantom consists of a set of 128 × 128 images, where each voxel has a unique identifier that relates the voxel to a particular organ or structure that the voxel belongs to. A ^99mTc MDP bone scintigraphy study was simulated using a low-energy high-resolution collimator and a 10% energy window. The energy window was further subdivided into 28 sub-windows, and the simulated images were processed using the FA framework. For comparison, the DEW method was applied.

Tomographic simulation

A 360° SPECT acquisition (6° steps, 1⁶ events per projection angle) of a tomographic phantom was simulated using the “multiple spheres” routine of the SIMIND software package. For tomographic acquisitions, FA was performed for each angular position which resulted in photo-peak and Compton tomographic data sets. The data were reconstructed using filtered backprojection (recon filter: Hanning 1.14).

Gamma camera measurement

A standard large-field-of-view scintillation camera (Infinia Hawkeye 4, General Electric Healthcare) was used to acquire planar and tomographic phantom studies. All gamma camera studies were conducted using a LEHR collimator and 18 sub-energy windows. To perform comparison with the DEW method, an additional scatter window was acquired.

Planar imaging

Two Petri dishes, filled with two different ^99mTc-water solutions (left/right ratio = 1.96), were acquired using a 7 cm layer of paper as the scattering material. After acquisition, the data were analysed using the mean values with “Region of Interest” (ROI).

Tomographic imaging

A 360° SPECT acquisition was performed for a Jaszczak phantom (Data Spectrum Corporation, Durham, NC, USA) filled with 500 MBq ^99mTc and acquired using 40 sec/frame. The measured projection data were subsequently exported and processed off-line using our FA approach. The SPECT data set containing only the photo-peak images were transferred to a General Electric Xeleris workstation and reconstructed using the filtered-backprojection algorithm. The setting of the reconstruction filter (Butterworth) was adopted to obtain optimal visual contrast. The reconstructed non-scatter and scatter corrected slices of the Jaszczak phantom were quantified using the ImageJ plugin (originally developed by Bergmann, Medical University of Vienna, Austria) capable of objectively detecting subtle changes in image quality.³⁰ To calculate the sphere contrast, the optimal sphere position is determined using a 3D Nelder-Mead simplex algorithm. The sector contrast is calculated by using an ROI template generated from X-ray CT that is transformed to a representative SPECT slice using fiducial points in CT and SPECT images. The contrast is then calculated by using

$$contrast=\left(\frac{sphere\left(rod\right)}{background}-1\right)\times 100\%.$$

By applying this software tool, we were able to quantify the contrast (sphere and sector) and the uniformity of the Jaszczak phantom.

RESULTS

Simulation of a point source in a water cylinder

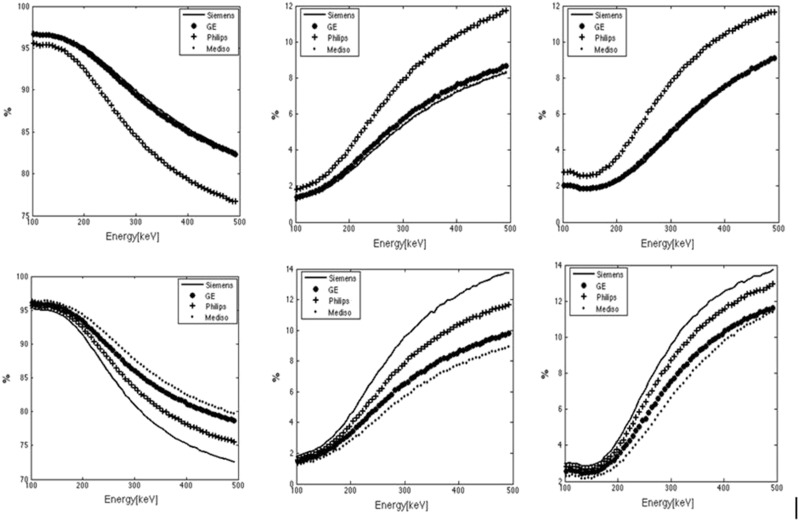
Images obtained from GE Infinia are shown in Fig. 2. Clearly, the increasing diameter of the point source and star artefacts as a function of photon energy (100, 200, 300, 400, 500 keV) can be observed. Figure 3 depicts the calculated fractional values for geometric, septal penetration, and collimator scatter obtained from a point source varying the photon energy (100-500 keV) and applying different collimators [low-energy general-purpose (LEGP), low-energy high-resolution (LEHR)] for different scintillation cameras. Despite the fact that the “types” of the collimators are the same for all vendors, large differences for scatter in the collimator are found.

FIG. 2.

MC simulations of a point source with different photon energies and a low-energy high-resolution collimator: (a) 100 keV, (b) 200 keV, (c) 300 keV, (d) 400 keV, (e) 500 keV.

FIG. 3.

Fractional contribution (%) of geometric (left), septal penetration (center), and scatter events for different collimator types: (top) low-energy general-purpose (LEGP) and (bottom) low-energy-high-resolution (LEHR), of different vendors (GE, Mediso, Philips, Siemens), varying the photon energy of a point source (100-500 keV).

MC simulations

^99mTc source varying the energy resolution of the acquisition system

The results of MC simulations for 10% energy window are shown next to the true photo-peak and Compton data obtained from SIMIND in Fig. 4. A comparison of the factor curves for photo-peak and scatter data showed good agreement with the spectral data obtained from MC simulations (Fig. 5). The energy resolution of the scintillation camera agrees with the FWHM of the resulting photo-peak spectra after our FA method for different energy resolutions.

FIG. 4.

MC simulation of a 10 × 10 × 10 mm ^99mTc source applying 10% energy resolution: Comparison of MC simulated photo-peak and Compton data sets with the resulting factor images. (a) MC simulation: photo-peak, (b) FA: photo-peak, (c) MC simulation: Compton, (d) FA: Compton.

FIG. 5.

MC simulation of a 10 × 10 × 10 mm ^99mTc source applying 10% energy resolution: Comparison of MC simulated spectral data with the factor curves.

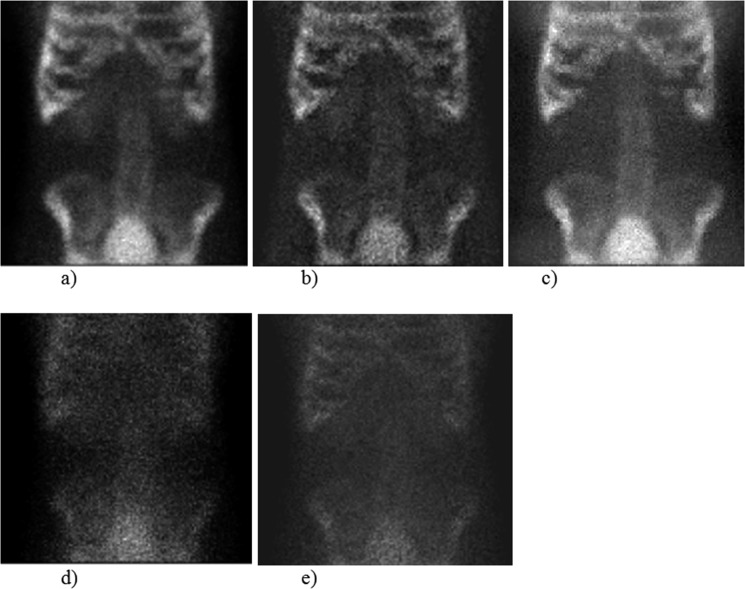
^99mTc MDP bone imaging

Photo-peak and scatter images resulting from FA show comparable results with the MC simulation and the DEW approach (Fig. 6). The energy spectra for the photo-peak and the Compton spectra energy obtained by FA correlate well with the MC simulation. The FWHM of the calculated photo-peak (9.6%) shows good agreement with the chosen 10% energy resolution of the scintillation camera (Fig. 7).

FIG. 6.

MC simulation of a ^99mTc MDP bone study using the voxel phantom: Comparison of MC simulated photo-peak and Compton region data sets with the resulting factor images. (a) MC simulation: photo-peak region, (b) FA: photo-peak region, (c) DEW method (d) MC simulation: Compton region, (e) FA: Compton region.

FIG. 7.

Comparison of the primary and scatter spectra from MC simulation and FA of the ^99mTc MDP bone study.

Tomographic phantom

The reconstructed transaxial slices for photo-peak and Compton data of the FA method are shown in comparison to MC simulations in Fig. 8.

FIG. 8.

SPECT reconstruction of a mathematical phantom. (a) MC simulation: photo-peak, (b) FA: photo-peak, (c) MC simulation: Compton, (d) FA: Compton.

Gamma camera measurements

Planar imaging

Two Petri dishes (diameter 80 mm), positioned next to each other on 55 mm scatter media (paper), were filled with two ^99mTc-water solutions resulting in a ratio of 1.96, which was chosen as the reference value. The resulting images applying non-SC, FA, and DEW methods are shown in Fig. 9. The calculated ratio for the DEW method showed a bias of 29.6%, whereas for the FA method, this bias was only 3.1%.

FIG. 9.

Two Petri dishes filled with ^99mTc. The true left to right ratio of activity of the Petri dish was 1.96. (a) Non-scatter correction, (b) FA method, (c) DEW method.

Tomographic imaging

Representative transaxial slices of the Jaszczak phantom are shown for non-SC, FA, and DEW methods in Fig. 10. The results of the contrast analysis are summarized in Tables I and II. As compared to the non-scatter corrected slices, we found improved sphere and sector contrast for both scatter correction methods. The DEW method results in an improved cold sphere contrast that ranges from −65.9 to −7 and from −23.6 to −0.2 for the sector contrast. The FA results in −51.5 to −7.5 for the cold sphere contrast, and for the cold sector contrast, it resulted in cold contrasts of −16.6 to −0.2.

FIG. 10.

Representative transaxial slices of the Jaszczak phantom (a) Non-scatter correction, (b) FA method, (c) DEW method.

TABLE I.

Jaszczak phantom: calculation of cold sphere contrast.

	Standard	FA	DEW
1	−47.7	−51.5	−65.9
2	−35.0	−52.9	−60.0
3	−28.5	−32.4	−43.5
4	−11.4	−18.7	−32.3
5	−17.3	−22.1	−27.1
6	−4.8	−7.5	−7.1

TABLE II.

Jaszczak phantom: calculation of cold sector contrast.

	Standard	FA	DEW
1	−16.6	−16.6	−23.6
2	−14.5	−13.6	−20.4
3	−7.5	−7.3	−10.4
4	−3.4	−4.1	−2.1
5	−0.2	−0.3	−0.3
6	0.2	−0.2	−0.2

DISCUSSION

Quantification of planar and tomographic data in nuclear medicine has become an increasingly important issue.^1,2 An in-depth understanding of photon-matter interactions is necessary to correct the various effects that alter and distort image quality and quantitation. A major source of error is scattered radiation, which degrades image quality and the quantitative information.^31–33 In most nuclear medicine imaging departments, the dual-energy-window (DEW) or triple-energy-window (TEW) approach is used in the clinical routine.⁸ For the DEW and TEW methods, scatter energy windows, located below and above the energy window, are additionally acquired. These acquisitions are then multiplied with a (vendor specific) correction factor and subtracted from the normal energy-window acquisition. However, since the patient shape is not included, the multiple-energy-window approach is in many cases an approximation of the reality. Although various attempts have been made to develop a more suitable scatter correction method, such as multi-energy windows using an artificial neural network framework,^8–10 the standard DEW or TEW method, due to their relative simplicity, remains as most commonly used. Furthermore, large differences in collimator characteristics (geometric, penetration, and scatter in the collimator) are found even if the vendors (GE, Mediso, Philips, and Siemens) use the same (or similar) “types” of collimators (Figs. 2 and 3). Therefore image processing (such as reconstruction) on various workstations might lead to different quantitative values since the vendor-specific scatter correction factors might differ.

A fascinating and promising mathematical tool is the FA method that can be used not only to separate clinical structures but also to correct for cross talk of two radiotracers or for scatter correction.^8,16–18

More than 20 years ago, a mathematical algorithm, “Holospectral imaging,” involving multiple energy window acquisitions of the entire spectrum was proposed to distinguish the specific contribution to the image of both primary and scattered photons and, in addition, noise.¹⁸ Following this basic idea, and to make this approach useable for clinical use, we adapted the acquisition parameters as we only aimed to determine the photo-peak and scatter distribution within the range of the energy window as accurately as possible. In detail, we implemented two main changes to use FA for scatter correction but also to control the result of the FA calculations. First, we subdivided only the energy window in a number of sub-windows (Fig. 1) and only this energy range is analyzed. Second, we also calculated the FWHM of the FA photo-peak, which has to correlate with the energy resolution of the imaging system. The number of different sub-windows remains the same for all MC simulations,²⁸ whereas for technical reasons, for the planar and tomographic scintillation camera acquisitions, 18 sub-windows were used. This data set is used as input to our FA approach, which results in two factor images (photo-peak and Compton) and two factor curves (photo-peak and Compton spectra). The result of this analysis was validated using extensive MC simulations using the SIMIND software package.²⁷ MC simulations allow the user to vary physical parameters of the scintillation camera (such as collimator, crystal thickness, and energy resolution) and the acquisition parameters (e.g., planar vs. SPECT acquisition). Furthermore, the user has the ability to obtain image and spectral information for photo-peak and scattered data. The presented scatter correction method applied to several MC simulated data such as those generated from ^99mTc point source (Fig. 4), planar ^99mTc bone study (Fig. 6), and tomographic phantom (Fig. 8) shows good agreement with the “true” MC photo-peak and Compton images. Furthermore, the FA spectral data of photo-peak and Compton are in accordance with the MC data (Figs. 5 and 7). However, it has to be noted that in the energy region below the photo-peak, deviations from the simulated data were found. Since we are dealing with a non-perfect imaging system (e.g., limited energy resolution), the data used for FA are not ideal but close to reality. These limitations might explain the variations in the different curves. Additionally, we introduce an internal quality control since the full-width at half maximum (FWHM) of the photo-peak spectra has to correlate with the FWHM of the imaging system. Validation with MC simulation was also done for tomographic data (Fig. 8). Here we have to use FA for each angular position. The results of the calculations are two tomographic data sets: one for the photo-peak and the other for the scattered data. The data were reconstructed using a nuclear medicine image processing workstation (Xeleris, GE Healthcare). The reconstructed slices agree well with the MC slices.

The same algorithm was used to perform the scatter correction of scintillation camera (Infinia, GE Healthcare) measurements. The gamma camera acquisition of two Petri dishes was analyzed using ROIs (Fig. 9). The calculated ratios show significant biases in the cases of no-SC (30.6%) and DEW (29.6%), in contrast to FA (3.1%). Validation of the proposed scatter correction for tomographic data was done with a Jaszczak phantom. The same pre-processing as mentioned above for the MC tomographic data has to be performed. After reconstruction, the resulting transaxial slices of the Jaszczak phantom were analyzed in detail by using an ImageJ plugin³⁰ that allows one to calculate the contrast (sphere and sector) and the appearance of the possible ring artefacts. We found improved contrast in the reconstructed Jaszczak phantom transaxial slices if scatter correction was applied (Tables I and II). For example, the cold contrast of the smallest sphere improves from −4.8 (NC) to −7.1 (DEW) and to −7.5 (FA). Furthermore, a higher cold sector contrast is found in the scatter correction slices: 0.2 (NC) and −0.2 (DEW and FA). It has to be noted that the results of the DEW method largely depend on the value of k_DEW, which was set to 0.5 in our study. The value of k_DEW depends on several factors such as the object and acquisition geometry.⁶ The quantitative analysis of the cold contrast of the Jaszczak phantom shows in general higher values for the DEW method than for the FA method, whereas for the hot contrast values in the Petri dish acquisition, it results in a larger bias than for the FA method. The use of the DEW approach might lead to under- and over-correction of the image data.³⁴ It has to be noted that we also found a small artifact in the FA uniformity images [Fig. 10(b)]. However, the scintillation camera system is usually optimized for standard photo-peak acquisitions. Since a much finer energy sampling, the FA method seems to be more sensitive to camera non-uniformities.⁸ However, also reducing the number of sub-energy windows and increasing the acquisition time did not improve the image uniformity of the Jaszczak phantom. Another possible reason for the uniformity artifacts might be that the uniformity correction of the scintillation camera is performed by using a uniformity map that applied the standard ±10% energy window. The correction with this, for our setting, incorrect map might be the cause for the uniformity artefacts in the Jaszczak phantom. However, also with the scatter correction methods, uniformity variations can occur.³⁵

In this work, we used FA to perform scatter correction of planar and SPECT studies. The proposed method agreed well with the data and spectral information obtained by MC simulations. Although we focused, in this work, on scintillation camera imaging (and ^99mTc), the same method can be used for other isotopes and positron-emission tomography (PET).

The implemented FA method does not need any supervised training or parameter setting since it uses just the image information to perform accurate scatter correction.

CONCLUSION

In this paper, we demonstrated, via Monte Carlo simulations and phantom studies, that factor analysis can be used without user interaction to correct for incoherent scatter.

Additionally, the quality of the correction can be supervised by comparing the FWHM of the photo-peak spectra with the FWHM of the imaging system. Although further tests in a clinical setting are necessary, our results indicate that factor analysis can improve the quantitative accuracy of planar and SPECT acquisitions.