Abstract
The cochlea is a spiral-shaped, liquid-filled organ in the inner ear that converts sound with high frequency selectivity over a wide pressure range to neurological signals that are eventually interpreted by the brain. The cochlear partition, consisting of the organ of Corti supported below by the basilar membrane and attached above to the tectorial membrane, plays a major role in the frequency analysis. In early fluid-structure interaction models of the cochlea, the mechanics of the cochlear partition were approximated by a series of single-degree-of-freedom systems representing the distributed stiffness and mass of the basilar membrane. Recent experiments suggest that the mechanical properties of the tectorial membrane may also be important for the cochlea frequency response and that separate waves may propagate along the basilar and tectorial membranes. Therefore, a two-dimensional two-compartment finite difference model of the cochlea was developed to investigate the independent coupling of the basilar and tectorial membranes to the surrounding liquid. Responses are presented for models using two- or three-degree-of-freedom stiffness, damping, and mass parameters derived from a physiologically based finite element model of the cochlear partition. Effects of changes in membrane and organ of Corti stiffnesses on the individual membrane responses are investigated.
I. INTRODUCTION
The cochlea is the organ in the inner ear which converts sound to neurological signals that can be interpreted by the brain. Classical cochlea models consist of two uncoiled, liquid-filled compartments separated by a structure representing the basilar membrane (BM) (e.g., Steele and Taber, 1979; Neely, 1981). The upper and lower compartments correspond to the scala vestibuli and the scala tympani, respectively, with the scala media included with the scala vestibuli because of the negligible mechanical impedance of the Reissner's membrane. In such a model, the BM is typically approximated by a series of uncoupled one-degree-of-freedom spring-mass-damper systems along the length of the cochlea, which are driven by the pressure difference across the BM. Excitation of the oval window at the basal end of scala vestibuli creates a pressure wave propagating in the liquid that in turn generates a slower wave, propagating as a transverse wave along the BM. This slower transverse wave peaks at a frequency specific location along the length of the membrane: The lower the frequency of the excitation sound source, the closer the peak to the apical end of the cochlea. The organ of Corti, attached to the top of the BM, is a specialized structure in mammals that transforms the mechanical vibrations produced by the traveling waves into neurological signals. Gradients in mechanical properties of the cochlear partition, which includes the BM and other attached structures (see Fig. 1), contribute to the frequency specificity of the cochlea (von Bekesy, 1960).
FIG. 1.
Schematics of (a) the 2D fluid domain, showing the two compartments separated by the cochlear partition, (b) the cochlear partition, comprised of the organ of Corti, supported below by the BM and attached above to the TM, and (c) the cochlear partition model consisting of a series of two-degree-of-freedom systems positioned along the length of the cochlea. In the figures, the label “Scala vestibuli” refers to the combined scala vestibuli and scala media compartments.
Zwislocki (1980, 1986) suggested that the tectorial membrane (TM), located along the top boundary of the organ of Corti, acts as a second series of resonators. He proposed that this secondary set of resonators can result in sharper frequency tuning and a secondary peak in the BM tuning curve. Lukashkin et al. (2010) reviewed experimental evidence highlighting the role of the TM in frequency processing. To investigate the role of the TM-BM interaction in frequency tuning, one-degree-of-freedom models of the cochlear partition were generalized to two- and three-degree-of-freedom systems in cochlea simulations (e.g., Allen, 1980; Neely and Kim, 1986; Neely, 1993; Ramamoorthy et al., 2007). In these models, the fluid-structure interaction is still typically limited to coupling between the fluid and the BM, implicitly assuming a single traveling wave.
Ghaffari et al. (2007) showed that a traveling wave with motion in the radial direction can propagate longitudinally along the TM in vitro and suggested that a second traveling wave may exist in vivo that can affect cochlear frequency tuning. Chen et al. (2011) measured a different tuning curve for the reticular lamina (at the top of the organ of Corti) than for the BM and also a phase difference between the two responses, especially evident in the active cochlea. A variety of models (Reichenbach et al., 2012; Lamb and Chadwick, 2011; Chadwick et al., 1996) have been developed to investigate multiple traveling waves propagating simultaneously along different members of the cochlear partition. In Lamb and Chadwick's (2011) two-compartment model, the TM and BM are represented by a series of two-degree-of- freedom systems along the length of the cochlea. The liquid in the upper compartment and the liquid in the lower compartment each interact with one of the two degrees of freedom representing the TM and BM, respectively. Their results indicate dual propagating waves, with distinct tuning curves and characteristic frequencies for the TM and BM. Reichenbach et al. (2012) used a three compartment model, with the intermediate compartment coupling the transverse displacements of the Reissner's and basilar membranes, to predict dual traveling waves. According to their model, the wave propagating along the BM is little affected by the Reissner's membrane except near the apex and the wave traveling along the Reissner's membrane does not significantly affect the BM for frequencies greater than 1 kHz. Chadwick et al. (1996) used a three compartment model coupled to a series of three-degree-of-freedom systems representing the transverse displacements of the TM, reticular lamina, and the BM. Their model predicts only one wave of physical interest.
In this paper, two- and three-degree-of-freedom models of the cochlear partition are used in a two-dimensional (2D), two compartment model (Fig. 1). In the model, x, y, and z are coordinates in the longitudinal, transverse, and radial directions, respectively, as indicated in Fig. 1. The two compartment model allows independent coupling of the fluid to the BM and TM in order to explore the possibility of independent tuning curves (Chen et al., 2011; Lamb and Chadwick, 2011) and the role of the TM properties and gradients on the tuning curves (Ghaffari et al., 2010; Ghaffari et al., 2007; Zwislocki, 1986). This model is similar to the model of Lamb and Chadwick (2011), except that a finite difference approach is used instead of the WKB (Wentzel-Kramers-Brillouin) approximation and the model allows for longitudinal coupling and either a two- or three-degree-of-freedom series of resonators. The same approximation as used in Lamb and Chadwick (2011) was applied, so the pressure in the lower compartment acts on the BM and the pressure in the upper compartment acts on the TM. As an extension of previous work, in this paper, effects of the stiffness and stiffness gradients of various structures within the cochlear partition on the cochlea's response to pure tone excitation are investigated. Stiffness and mass values for the cochlear partition parameters of the model are obtained from a detailed finite element model of the cochlear partition that uses properties and geometries based on anatomical features and experimental measurements of the gerbil cochlea (Nam and Fettiplace, 2010, 2012). In the two-degree-of-freedom model, the degrees of freedom are the transverse (y direction) displacements of the BM and TM, similar to the model of Lamb and Chadwick (2011). In addition, a third degree of freedom, the z-direction motion of the TM, was included in the model because it will be important for stimulating hair bundle responses when active forces are considered. Details of the cochlea fluid-structure interaction model are given in Sec. II. In Sec. III, results for two- and three-degree-of-freedom models of the cochlear partition are presented, showing the effect of the cochlear partition mechanical parameters on the pure tone response of the cochlea.
II. METHODS
A. Cochlea fluid-structure interaction model
The 2D model of the cochlea contains two rectangular liquid-filled compartments, representing the scala vestibuli/media and the scala tympani, as shown in Fig. 1(a). The compartments are separated by the cochlear partition, which comprises the BM and TM and the organ of Corti. There is an opening in the cochlear partition at the apex (at x = L), representing the helicotrema, that connects the liquids in the two compartments. The liquid in the upper compartment, the scala vestibuli/media, is excited by motion of the oval window, with velocity vs. In the model, the cochlear partition will be approximated by a series of two- or three-degree-of-freedom systems along the longitudinal x direction, discussed in more detail in Sec. II B. A schematic for two-degree-of-freedom systems is shown in Fig. 1(c).
The fluid is assumed to be an inviscid and incompressible liquid and displacements are assumed small so nonlinear terms are negligible. For these assumptions, the Navier-Stokes equation and the incompressibility condition reduce to
| (1a) |
and
| (1b) |
respectively, where v(x, y, t) is velocity vector, p(x, y, t) is the pressure, ρ is the liquid density, and the superposed dot denotes a time derivative. The divergence of Eq. (1a) results in Laplace's equation for pressure, which must be satisfied in both domains, so
| (2) |
where subscripts T and B refer to the scala vestibuli (top compartment) and scala tympani (bottom compartment), respectively.
Eight boundary conditions are needed to complete the problem statement for the fluid pressure. First, the excitation is the x direction velocity at the oval window, vs(y,t). Equation (1a) can be used to write this excitation boundary condition in terms of fluid pressure as
| (3a) |
By conservation of mass, the mass flow out the round window must equal the mass flow in the oval window minus any compression of the cochlear partition that lies between the TM and BM. For initial calculations, it was assumed that the compression of the cochlear partition is negligible and
| (3b) |
This was verified to be a reasonable assumption for the simulations presented. Rigid boundaries are assumed at the top and bottom of the cochlea, resulting in boundary conditions of the form
| (3c) |
and
| (3d) |
A solid wall boundary condition is also assumed at the apical end (Neely, 1985), so
| (3e) |
and
| (3f) |
Along the boundary with the cochlear partition, the pressure and transverse velocity in the liquid in the top and bottom compartments must match the pressure and transverse velocity of the top and bottom surfaces of the cochlear partition, respectively. The BM is the bottom surface of the cochlear partition. As in Lamb and Chadwick (2011), we assume that the top surface displacement can be approximated by the displacement of the TM. Equation (1a) is used to write the boundary condition in terms of the TM and BM displacements as
| (3g) |
and
| (3h) |
with ξy denoting the structural displacement in the positive y direction. In Eqs. (3g) and (3h), either F = 1 or , with the same value of F(x) used in both equations, where β is the ratio of the membrane to compartment widths. Using F = 1 is equivalent to assuming that the membranes have the same width as the compartments. Using , approximately accounts for the difference in widths by enforcing conservation of mass, assuming the deformation of the membrane is a half sine wave in the y-z plane (Diependaal and Viergever, 1989). To obtain a unique solution, the pressure at the helicotrema is used as the reference pressure, so
| (3i) |
A finite difference approximation is used to discretize and solve the equations for the steady state frequency response to pure tone excitation. The frequency domain equations are obtained by assuming steady-state time-harmonic motion of the form
| (4) |
where ω = 2πf is the radial frequency, f is the excitation frequency, and an overbar indicates the complex amplitude of the variable. Complex notation is used to represent the amplitude and phase of the response. It is implied that the real part of the complex quantities represent the excitation and responses.
B. Cochlear partition model
To simulate dual traveling waves on the TM and BM, it is important to have realistic properties for these membranes and for the organ of Corti. Therefore, stiffness and mass values were obtained from detailed finite element models of the gerbil cochlear partition, described in Nam and Fettiplace (2010) and Nam and Fettiplace (2012). The finite element models of the cochlear partition incorporate realistic geometrical and mechanical property data of the different cells and tissues, such as the TM and BM, outer hair cells, Deiter cells, and pillar cells. In addition, the mechanical responses of the finite element models, such as the point stiffness at different locations and the longitudinal space constant, were verified against experimental data. Because it would be computationally expensive to include the complete finite element model in the fluid-structure interaction simulations, lumped parameter models were used. Results for a parameter study are also presented, because there is still uncertainty in the mechanical property values and gradients.
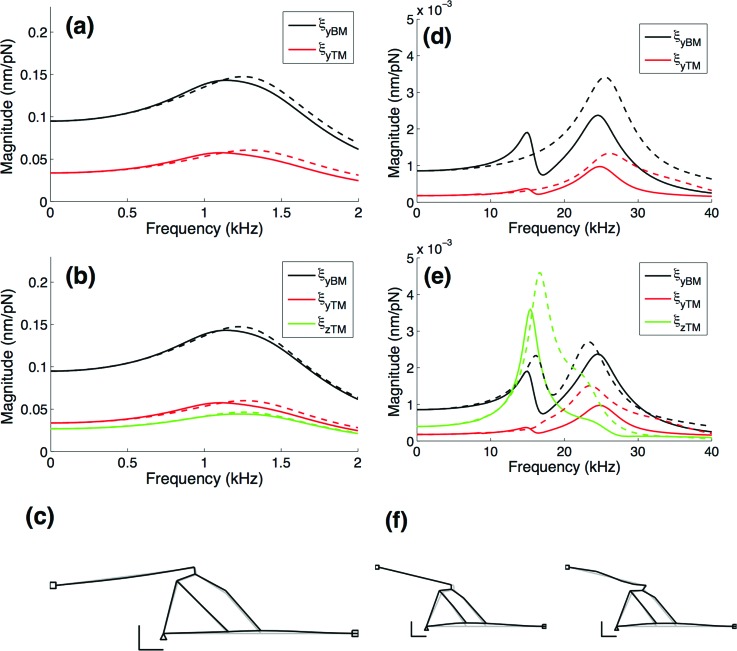
A series of either two- or three-degree-of-freedom mechanical systems are used to approximate the response of the cochlear partition, as shown schematically in Fig. 1(c) for two degrees of freedom. Parameters for these models were obtained from the Nam and Fettiplace (2012) finite element models of the gerbil cochlear partition at x = 2 and 10 mm. First, stiffness matrices were generated from the static compliances obtained by applying point forces to the finite element model at the degrees of freedom of interest. Specifically, ijth element of the compliance matrix is equal to the displacement at degree of freedom i resulting from a static unit point force applied to degree of freedom j. The stiffness matrix is the inverse of this compliance matrix. By using point forces, symmetric compliance and stiffness matrices are guaranteed by reciprocity. Diagonal mass matrices were then obtained using the general method proposed by Kim et al. (2008) with constraints added to only allow a diagonal mass matrix and using the stiffness matrix obtained from the static analysis. This method applies least squares fits to finite element model frequency response functions for the degrees of freedom of interest. To illustrate the method, a subset of the frequency response curves corresponding to the two- and three-degree-of-freedom models are shown in Fig. 2. Each frequency response function is a plot of displacement amplitude of degree of freedom i versus frequency resulting from a harmonic point force applied to degree of freedom j. Again, by reciprocity there are only n* (n + 1)/2 independent frequency response functions for the n-degree-of-freedom approximation. The frequency response functions shown are for excitation of the BM, but similar curves result from excitation of the other degrees of freedom. As seen in Figs. 2(a) and 2(b), both the two- and three-degree-of-freedom models show excellent agreement with the amplitude and phase of the responses for the single peak response at x = 10 mm. At x = 2 mm, unlike the apical result, the finite element model's frequencies response shows two peaks—one at 14 kHz and the other at 25 kHz. The two-degree-of-freedom model only approximates the primary peak of the dual peak response, while the three-degree-of-freedom model has a similar two-peak response [Figs. 2(d) and 2(e)]. The stiffness and mass values along the length of the cochlea were obtained by fitting exponential curves to the stiffness and mass values obtained from the detailed finite element models at x = 2 and 10 mm.
FIG. 2.
Comparison of frequency response functions for detailed finite element model (solid line) and two- and three-degree-of-freedom approximations (dashed line). The frequency response functions shown are for forcing at the BM, but the other frequency response functions are similar. Frequency response functions at x = 10 mm for the (a) two-degree-of-freedom model and (b) three-degree-of-freedom model both match well the amplitudes and peak frequency of the finite element response. Frequency response functions at x = 2 mm have two peaks; the two-degree-of-freedom model results shown in (d) approximate the primary peak, while the three-degree-of-freedom model results shown in (e) are able to predict the double peak. Higher order models would produce an even better agreement, but would be more computationally expressive and less intuitive. Schematics of the deformed shape for forcing at the peak frequencies are given in (c) and (f), at x = 10 mm and x = 2 mm, respectively. The deformed shape corresponding to the higher frequency peak at x = 2 mm [right schematic of (f)] shows involvement of the second mode of the TM, suggesting that the TM may have a different effect on the cochlea response in the basal region.
The two degrees of freedom used to obtain the two-degree-of-freedom model were the BM transverse (y direction) displacement at the connection to the base of the Deiters cell and the y direction displacement of the TM where it attaches to the tip of the outer hair cell bundle. Each two-degree-of-freedom system can be represented in terms of a lumped parameter spring-mass system, as shown in Fig. 1(c). The two degrees of freedom represent the y direction displacements ξyBM and ξyTM of the BM and TM, respectively. In the two-degree-of-freedom lumped model, stiffnesses, kBM and kTM, are the effective y-direction stiffnesses of the BM and TM, respectively. The effective stiffness of the organ of Corti structures connecting these two membranes is denoted by kOC. The masses, mBM and mTM, are the effective y-direction masses of the BM and TM and include contributions from the organ of Corti inertia.
Parameters obtained from this procedure for the two-degree-of-freedom approximation are given in Table I. At the basal end, the BM stiffness is higher than the TM stiffness. Due to the larger gradient along the length, the BM stiffness is lower than the TM stiffness at the apical end. Both BM and TM effective masses increase along the length, with a larger gradient for the TM. Nondimensional damping (ζBM = ζTM= 0.2 + 0.67 x) was chosen such that the membrane displacement response exhibited approximately two to three cycles between the stapes and their peaks regardless of frequency, consistent with experimental observations (Olson et al., 2012). Values for the ratio of the membrane width to compartment width (β = 0.265 e1.1x), were estimated from experimental measurements of the gerbil cochlea (Schweitzer et al., 1996) similar to Yoon et al. (2007), assuming a rectangular cross-section with constant aspect ratio.
TABLE I.
Mechanical properties for the two-degree-of-freedom approximation of the cochlear partition (x in cm). The TM stiffness gradient (−41 dB/cm, with stiffness converted to N/m) compares well with stiffness gradients (−40 dB/cm in perilymph and −34 dB/cm in endolymph) measured by Richter et al. (2007).
| Stiffness per unit area (dyne/cm3) | Height of each compartment (cm) |
| kBM = 14.2 × 107 e−7.6x | H = 0.04 |
| kTM = 7.7 × 107 e−5.5x | Length of the compartments/membranes (cm) |
| kOC = 1.7 × 107 e−4.5x | L = 1.2 |
| Liquid density (g/cm3) | |
| Mass per unit area (g/cm2) | ρ = 1 |
| mBM = 0.0017 e0.58x | Longitudinal coupling stiffness (for a 10 μm section) |
| mTM = 0.0005 e1.1x | kBM-LC = e3.7xkBM |
| kTM-LC = e3.7xkTM | |
| Nondimensional damping coefficient () | |
| ζBM = ζTM = 0.2 + 0.67 x | |
| cOC = cTM kOC/kTM | |
| Membrane to compartment width ratio () | |
| β = 0.265 e1.1x | |
The governing equation for the two-degree-of-freedom system at each x location can be written in matrix form as
| (5) |
where viscous damping in parallel with the stiffness elements has been assumed and the cBM, cTM, and cOC are the damping coefficients. The dependence of the matrix coefficients on longitudinal coordinate x is not explicitly indicated, but implied.
The coupled ordinary differential equations [Eq. (5)] become algebraic equations
| (6) |
in the frequency domain, after substitution of Eq. (4).
The three-degree-of-freedom model, in addition to the transverse displacements ξyBM and ξyTM, also includes the z-direction displacement of the TM ξzTM. A diagonal mass matrix is used, so there is one mass associated with each degree of freedom. A general symmetric stiffness matrix is used.
The frequency domain equations for the three-degree-of-freedom system can be written as
| (7) |
where viscous damping in parallel with the stiffness elements has again been assumed. In Eqs. (5)–(7), liquid in the bottom compartment is coupled to the BM and the liquid in the top compartment is coupled to the TM. The two compartments can be coupled exclusively to the BM so that the pressure difference is applied across the BM, by modifying the right-hand-side of Eqs. (5)–(7) and Eqs. (3g) and (3h).
Results for the parameters used by Lamb and Chadwick (2011) were used as a validation of the two-compartment model of the cochlea. The membrane displacement curves obtained with our model have similar amplitude and shape features as those in Fig. 2 of Lamb and Chadwick (2011), but are shifted apically by less than 1/2 mm. This shift is likely due to our 2D approximation, which is limited to constant compartment width.
III. RESPONSE OF COCHLEAR PARTITION MODEL BASED ON DETAILED FINITE ELEMENT MODELS
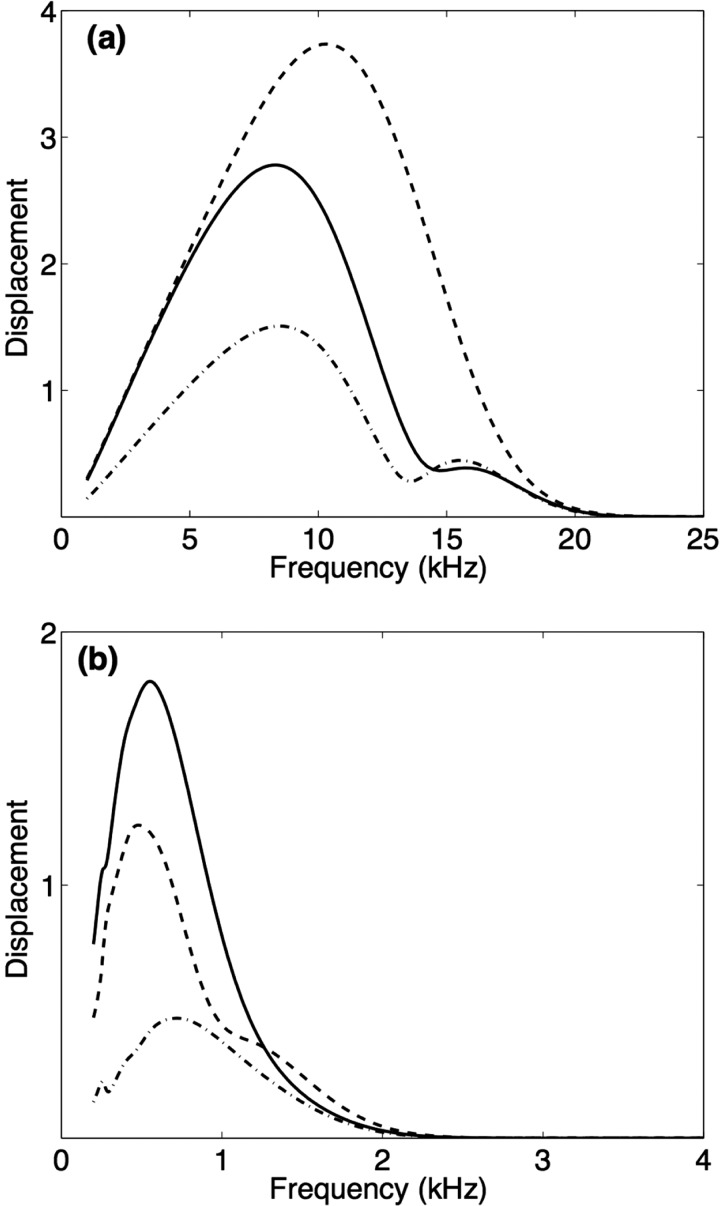
Predicted membrane displacements and fluid pressures for 1 and 10 kHz pure tone excitations, using parameters based on the detailed finite element model of the cochlear partition are given in Fig. 3. Independent coupling of the top and bottom fluid compartments to the top and bottom surfaces of the cochlear partition allows for two coupled waves traveling along the cochlear partition. The waves propagating along the BM and TM have distinct displacement peak locations [Fig. 3(a)]. For the passive response modeled here, the phase difference between the TM and BM is small (less than 0.1 cycles) at the peak location, but increases by approximately 1/2 cycle after the peak [Fig. 3(b)]. In addition, different pressures are predicted along the BM and TM surfaces [Fig. 3(c)]. For low frequencies that peak near the apical end, the BM displacement amplitude is larger and its peak occurs approximately 0.4 mm apical of the TM displacement amplitude peak. For high frequencies which peak near the basal end, the TM displacement amplitude is larger and peaks apical of the BM displacement peak. For acoustic coupling applied only through a pressure difference across the BM (results not shown), the TM displacement amplitude is always smaller than the BM displacement amplitude and the phase difference between the two membrane responses is negligible.
FIG. 3.
Response of the two-degree-of-freedom model of the cochlear partition for 1 and 10 kHz excitation plotted versus distance from the stapes. (a) BM (solid line) and TM (dashed line) displacements (re stapes). (b) Phase difference between the BM and TM displacements. The BM and TM displacements are in phase at the stapes. The amplitude of the phase difference increases after the peak displacement until the TM leads the BM by approximately 1/2 cycle. (c) Normalized pressure amplitude at the BM (solid line) and TM (dashed line) surfaces. Half the pressure difference (dotted line) is shown for comparison to one compartment models. Pressures are normalized by half the pressure difference at the stapes. When the BM and TM displacements are significantly different, the pressures on the membranes also differ.
Increasing damping will increase effective fluid mass due to the increased wavelength (Steele and Taber, 1979; Lighthill, 1981) and thereby shift the displacement amplitude peak for a given frequency toward the basal end. Therefore, a damping gradient that increases from the basal to the apical end increases the frequency range of the cochlea. To estimate the effect of the damping gradient on the frequency range, results with and without a damping gradient were compared. The difference in the characteristic frequencies between x = 2 and 8 mm decreases by 19% and 24% for the BM and TM, respectively, if the damping used for Fig. 3 is replaced by a constant nondimensional damping equal to the average value, ζBM = ζTM = 0.6. In addition, decreasing the ratio of the membrane width to compartment width, β, from apex to base also increases the frequency range, as well as the membrane displacements. The difference in the characteristic frequencies between x = 2 and 10 mm decreases by 50% and 42% for the BM and TM, respectively, if the membrane width is assumed constant and equal to the compartment width.
The two-degree-of-freedom model developed here also allows for longitudinal coupling stiffnesses for both the BM and TM. The BM longitudinal coupling stiffness was represented by springs connecting the successive BM masses, that is, the ith coupling spring kBM–LC,i connects mBM,i and mBM,i+1, as in the model used by Naidu and Mountain (2001). The magnitude of the BM longitudinal coupling was defined in terms of the proportionality constant, , for a 10 μm section (corresponding to one row of outer hair cells), where kBM and kBM–LC are the BM stiffness and longitudinal coupling stiffness, respectively. Values for the BM longitudinal coupling stiffness (kBM–LC = e3.7xkBM, with x in cm) were chosen so that the model produced space constants (ranging from 10 to 50 μm, increasing from base to apex) consistent with experimental measurements of Naidu and Mountain (2001) for BM displacements indented by a static probe. The same proportionality constant was used for the TM, when TM longitudinal coupling stiffness was included (see Table I). Neither BM nor TM longitudinal coupling stiffnesses of this magnitude significantly affected the passive response, consistent with results presented by Meaud and Grosh (2010). This was expected because the wavelength of the traveling wave is greater than the space constant. Increasing the magnitude of the BM longitudinal coupling to effectively increase the space constant by an order of magnitude did not have a significant effect on the characteristic frequency map, but did reduce the amplitude and quality factor of the response at the characteristic frequency (results not shown).
Only y direction displacements of the BM and TM are considered for the two-degree-of-freedom approximation of the cochlear partition cross-section, as these motions couple to the fluid. However, shearing motion of the outer cell hair bundles due to a tangential motion of the TM in the y-z plane is associated with active hair cell forces. Therefore, the z-direction displacement of the TM at the point it attaches to the tip of the outer hair cell bundle is added as the third degree of freedom to create the three-degree-of-freedom model of the cochlear partition cross-section. Membrane displacement amplitudes are plotted versus frequency in Fig. 4 for the three-degree-of-freedom model of the cochlear partition, for a more basal position, x = 2 mm, and a more apical location, x = 9 mm. Near the apical end, the BM transverse peak displacement has a greater amplitude and a higher frequency than that of the TM. The opposite is true near the basal end. The two-degree-of-freedom model results show similar trends in the relative TM and BM displacement peak amplitudes and positions. The tangential motion of the TM will be important when active forces are considered. Because this study is focused on passive fluid-structure interactions between two compartments and two interacting surfaces rather than active responses, the remaining results will be for the two-degree-of-freedom model.
FIG. 4.
Transverse BM (solid line), transverse TM (dashed line), and tangential TM (dashed-dotted line) displacement amplitudes (re stapes) versus frequency for the three-degree-of-freedom model of the organ of Corti at (a) x = 2 mm, a basal position, and (b) x = 9 mm, an apical location.
IV. PARAMETER STUDY FOR TWO-DEGREE-OF-FREEDOM COCHLEAR PARTITION MODEL
The two-degree-of-freedom model was used to investigate the effects of organ of Corti stiffness, TM stiffness, and TM stiffness gradient on the cochlea traveling wave response. To isolate the effects of the coupling and TM stiffnesses on the response, parameters were chosen so that the total stiffness, kBM + kTM, and mass, mBM + mTM, at each point were equal to the values obtained from the two-degree-of-freedom model reduced from the finite element model. In addition, the individual membrane frequencies were chosen to be equal at each point along the cochlea length.
In the current model, the TM and BM are separately driven by the fluid pressure in the scala vestibuli and the scala tympani, respectively. Their motions are coupled by the spring, kOC, representing the organ of Corti. The relative stiffness of the organ of Corti affects how independent the motions of the TM and BM are. Figure 5 shows a series of response curves for various levels of organ of Corti stiffness, for . When the coupling stiffness is low compared to the membrane stiffnesses (kOC = 0.04 * kBM), the TM and BM respond independently, each membrane having its own peak frequency. When the coupling is comparable to the membrane stiffnesses (kOC = 0.4 * kBM), interference occurs and second peaks are seen in both the TM and BM responses. Also notable is the shift of the two peaks so that the BM displacement peak frequency is now lower than the TM displacement peak. For coupling stiffness greater than the membrane stiffnesses (kOC = 4 * kBM), the two membranes essentially move together as expected.
FIG. 5.
Effect of the coupling strength between the TM and BM. Vertical (y direction) displacement amplitude (re stapes) of the BM (solid line) and TM (dashed line) at x = 6 mm versus frequency for the two-degree-of-freedom model of the cochlear partition for (a) kOC = 0.04 kBM, (b) kOC = 0.4 kBM, and (c) kOC = 4 kBM. For weak coupling, the traveling waves on the two membranes are uncoupled and have different frequency peaks. For intermediate coupling, the membrane interaction increases and interference can occur. For higher coupling, the membranes move together.
Figure 6 shows how the ratio of the BM to TM stiffness affects the difference in characteristic (peak) frequency of the two membranes at x = 2 and 9 mm. For Fig. 5, an intermediate coupling stiffness kOC= 0.3* (kBM + kTM) is used. When , the two-degree-of freedom structure is symmetric, so the pressure field is anti-symmetric about the cochlear partition and the BM and TM move together and therefore have the same characteristic frequency. As the BM to TM stiffness ratio increases, the characteristic frequencies of the TM and BM separate, even though the structural frequencies of the two membranes remain equal . The curves in Fig. 6 show a similar trend for the apical and basal regions.
FIG. 6.
Effect of the relative membrane stiffnesses. Normalized difference in peak frequency as a function of for both a basal location at x = 2 mm (circles) and an apical location at x = 9 mm (squares). Results shown are for a coupling stiffness kOC = 0.3 (kBM + kTM).
The peak frequencies of the BM and TM for are plotted versus distance from the stapes in Fig. 7 (solid curves). The membranes peak at different distances from the stapes for pure tone excitation even though the individual membrane frequencies are equal at each point along the cochlea length. As the exponential slope of the TM stiffness is increased, the average slopes of the curves increase (from solid line to dashed line to dotted-dashed line in Fig. 7). The effect on the BM is greater than the effect on the TM, even though only the TM stiffness is changed.
FIG. 7.
Effect of the TM stiffness gradient. Peak frequency of the BM (black line) and TM (gray line) versus position as the exponential slope of the TM stiffness is varied, with the TM stiffness at x = 6 mm held constant. All other material parameters are also held constant. The solid curve corresponds to and a coupling stiffness kOC = 0.3 (kBM + kTM). Increasing the exponential slope of the TM stiffness by 10% (dashed line) and 20% (dotted line) has a greater effect on the average slope of the BM response, even though the BM properties are unchanged.
V. DISCUSSION AND SUMMARY
A two-compartment model of the cochlea, with independent fluid coupling to the top and bottom surfaces of the cochlear partition, was developed and used to investigate how the mechanical properties of the cochlear partition affect the cochlear response to pure tone excitation. Results of this model show that BM and TM responses to pure tone excitation can have different peak locations and phases, indicative of dual propagating waves. Two conditions are required for the dual traveling waves to become distinct: (1) Different mechanical properties of the TM and BM, (2) weak coupling between the TM and BM. Lamb and Chadwick's (2011) model satisfied these conditions: To obtain half an octave frequency difference between the two membranes, the TM stiffness was given as half of the BM value and a small value for the coupling stiffness (their S12) was used. Although it is unclear if these conditions are satisfied in actual cochlea, our mechanical parameters reduced from a detailed organ of Corti finite element model (Nam and Fettiplace, 2010) indicate that the two conditions are satisfied. Interestingly, the effects were different in the apex and the base. With parameters derived from the more detailed finite element model, the BM peak was more apical than the TM peak for low frequency excitation, while the TM peak was more apical than the BM peak for high frequency excitation. Similar differences in amplitude and frequency response across the cochlear partition were observed in a previous experiment (Chen et al., 2011), but were not reproduced by the Nam and Fettiplace structural model (e.g., Nam and Fettiplace, 2010, 2012), probably because their model does not include the fluid dynamics.
There is evidence that the BM and TM stiffnesses vary monotonically and significantly from the base to the apex (Teudt and Richter, 2014; Richter et al., 2007; Gueta et al., 2006; Olson et al., 2012). On the other hand, there is little evidence that the organ of Corti stiffness may vary as much, considering that the organ of Corti stiffness may be determined by the outer hair cells and Deiter's cells (Nam and Fettiplace, 2010). As a result, in the basal region it is likely that the organ of Corti elastic coupling is relatively weaker than in the apical region. This may result in characteristically different mechanical responses in the two locations. Results in Fig. 4 predict that the independent traveling waves are more likely in the basal turn of the cochlea than in the apex.
The parameter study shows the effect of the organ of Corti stiffness, the TM stiffness, and the TM stiffness gradient on the responses of the BM and TM. In particular, the organ of Corti coupling stiffness determines the degree of coupling between the two membrane responses. The TM to BM stiffness ratio and the TM stiffness gradient affect the difference in frequency peak location and frequency range. The model indicates that gradients in both cochlear partition damping and the ratio of the BM to compartment widths significantly increase the frequency range of the cochlea. However, the longitudinal coupling of the membranes does not have a significant effect on the passive response of the cochlea. The passive responses for the two- and three-degree-of-freedom models were similar. The three-degree-of-freedom model will be needed to estimate the shearing motion of the outer cell hair bundles when active hair cell forces are included.
ACKNOWLEDGMENTS
This work was supported by NSF Grant No. CMMI-1233595.
References
- 1. Allen, J. B. (1980). “ Cochlear micromechanics—A physical model of transduction,” J. Acoust. Soc. Am. 68(6), 1660–1670. 10.1121/1.385198 [DOI] [PubMed] [Google Scholar]
- 3. Chadwick, R. S. , Dimitriadis, E. K. , and Iwasa, K. H. (1996). “ Active control of waves in a cochlear model with subpartitions,” Proc. Natl. Acad. Sci. U.S.A. 93, 2564–2569. 10.1073/pnas.93.6.2564 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Chen, F. , Zha, D. , Fridberger, A. , Zheng, J. , Choudhury, N. , Jacques, S. L. , Wang, R. K. , Shi, X. , and Nuttall, A. L. (2011). “ A differentially amplified motion in the ear for near-threshold sound detection,” Nat. Neurosci. 14(6), 770–777. 10.1038/nn.2827 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Diependaal, R. J. , and Viergever, M. A. (1989). “ Nonlinear and active two-dimensional cochlear models: Time-domain solution,” J. Acoust. Soc. Am. 85(2), 803–812. 10.1121/1.397553 [DOI] [PubMed] [Google Scholar]
- 7. Ghaffari, R. , Aranyosi, A. J. , and Freeman, D. M. (2007). “ Longitudinally propagating traveling waves of the mammalian tectorial membrane,” Proc. Natl. Acad. Sci. U.S.A. 104, 16510–16515. 10.1073/pnas.0703665104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Ghaffari, R. , Aranyosi, A. J. , Richardson, G. P. , and Freeman, D. M. (2010). “ Tectorial membrane travelling waves underlie abnormal hearing in Tectb mutant mice,” Nat. Comm. 1, 96. 10.1038/ncomms1094 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Gueta, R. , Barlam, D. , Shneck, R. Z. , and Rousso, I. (2006) “ Measurement of the mechanical properties of isolated tectorial membrane using atomic force microscopy,” Proc. Natl. Acad. Sci. U.S.A. 103(40), 14790–14795. 10.1073/pnas.0603429103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Kim, K.-S. , Kang, Y. J. , and Yoo, J. (2008). “ Structural parameters identification using improved normal frequency response function method,” Mech. Sys. Signal Process. 22, 1858–1868. 10.1016/j.ymssp.2008.02.001 [DOI] [Google Scholar]
- 11. Lamb, J. S. , and Chadwick, R. S. (2011). “ Dual traveling waves in an inner ear model with two degrees of freedom,” Phys. Rev. Lett. 107(8), 088101. 10.1103/PhysRevLett.107.088101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Lighthill, J. (1981). “ Energy flow in the cochlea,” J. Fluid Mech. 106, 149–213. 10.1017/S0022112081001560 [DOI] [Google Scholar]
- 13. Lukashkin, A. N. , Richardson, G. P. , and Russell, I. J. (2010). “ Multiple roles for the tectorial membrane in the active cochlea,” Hear. Res. 266, 26–35. 10.1016/j.heares.2009.10.005 [DOI] [PubMed] [Google Scholar]
- 14. Meaud, J. , and Grosh, K. (2010). “ The effect of tectorial membrane and basilar membrane longitudinal coupling in cochlear mechanics,” J. Acoust. Soc. Am. 127, 1411–1421. 10.1121/1.3290995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Naidu, R. C. , and Mountain, D. C. (2001). “ Longitudinal coupling in the basilar membrane,” J. Assoc. Res. Otolaryngol. 2, 257–267. 10.1007/s101620010013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Nam, J.-H. , and Fettiplace, R. (2010). “ Force transmission in the organ of Corti micromachine,” Biophys. J. 98, 2813–2821. 10.1016/j.bpj.2010.03.052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Nam, J.-H. , and Fettiplace, R. (2012). “ Optimal electrical properties of outer hair cells ensure cochlear amplification,” PLoS One 7(11), e50572. 10.1371/journal.pone.0050572 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Neely, S. T. (1981). “ Finite difference solution of a two-dimensional mathematical model of the cochlea,” J. Acoust. Soc. Am. 69(5), 1386–1393. 10.1121/1.385820 [DOI] [PubMed] [Google Scholar]
- 19. Neely, S. T. (1985). “ Mathematical modeling of cochlear mechanics,” J. Acoust. Soc. Am. 78(1), 345–352. 10.1121/1.392497 [DOI] [PubMed] [Google Scholar]
- 20. Neely, S. T. (1993). “ A model of cochlear mechanics with outer hair cell motility,” J. Acoust. Soc. Am. 94(1), 137–146. 10.1121/1.407091 [DOI] [PubMed] [Google Scholar]
- 21. Neely, S. T. , and Kim, D. O. (1986). “ A model for active elements in cochlear biomechanics,” J. Acoust. Soc. Am. 79(5), 1472–1480. 10.1121/1.393674 [DOI] [PubMed] [Google Scholar]
- 22. Olson, E. S. , Duifhuis, H. , and Steele, C. R. (2012). “ Von Békésy and cochlear mechanics,” Hear. Res. 293, 31–43. 10.1016/j.heares.2012.04.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Ramamoorthy, S. , Deo, V. , and Grosh, K. (2007). “ A mechano-electro-acoustical model for the cochlea: Responses to acoustic stimuli,” J. Acoust. Soc. Am. 121(5), 2758–2773. 10.1121/1.2713725 [DOI] [PubMed] [Google Scholar]
- 24. Reichenbach, T. , Stefanovic, A. , Fumiaki, N. , and Hudspeth, A. J. (2012). “ Waves on Reissner's membrane: A mechanism for the propagation of otoacoustic emissions from the cochlea,” Cell Reports 1, 374–384. 10.1016/j.celrep.2012.02.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Richter, C.-P. , Emadi, G. , Getnick, G. , Quesnel, A. , and Dallos, P. (2007). “ Tectorial membrane stiffness gradients,” Biophys. J. 93, 2265–2276. 10.1529/biophysj.106.094474 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Schweitzer, L. , Lutz, C. , Hobbs, M. , and Weaver, S. P. (1996). “ Anatomical correlates of the passive properties underlying the developmental shift in the frequency map of the mammalian cochlea,” Hear. Res. 97, 84–94. 10.1016/S0378-5955(96)80010-4 [DOI] [PubMed] [Google Scholar]
- 27. Steele, C. R. , and Taber, L. A. (1979). “ Comparison of WKB and finite difference calculations for a two-dimensional cochlear model,” J. Acoust. Soc. Am. 65(4), 1001–1006. 10.1121/1.382569 [DOI] [PubMed] [Google Scholar]
- 28. Teudt, I. U. , and Richter, C. P. (2014). “ Basilar membrane and tectorial membrane stiffness in the CBA/CaJ mouse,” J. Assoc. Res. Otolaryngol. 15(5), 675–694. 10.1007/s10162-014-0463-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. von Békésy, G. (1960). Experiments in Hearing, E. G. Wever, Trans. ( McGraw-Hill, New York: ), Chap. 13, pp. 535–634. [Google Scholar]
- 30. Yoon, Y.-J. , Puria, S. , and Steele, C. R. (2007). “ Intracochlear pressure and derived quantities from a three-dimensional model,” J. Acoust. Soc. Am. 122(2), 952–966. 10.1121/1.2747162 [DOI] [PubMed] [Google Scholar]
- 31. Zwislocki, J. J. (1980). “ Five decades of research on cochlear mechanics,” J. Acoust. Soc. Am. 67(5), 1679–1685. [DOI] [PubMed] [Google Scholar]
- 32. Zwislocki, J. J. (1986). “ Analysis of cochlear mechanics,” Hear. Res. 22, 155–169. 10.1016/0378-5955(86)90091-2 [DOI] [PubMed] [Google Scholar]