Abstract
Perfluorocarbon droplets that are capable of an ultrasound-mediated phase transition have applications in diagnostic and therapeutic ultrasound. Techniques to modify the droplet size distribution are of interest because of the size-dependent acoustic response of the droplets. Differential centrifugation has been used to isolate specific sizes of microbubbles. In this work, differential centrifugation was employed to isolate droplets with diameters between 1 and 3 μm and 2 and 5 μm from an initially polydisperse distribution. Further, an empirical model was developed for predicting the droplet size distribution following differential centrifugation and to facilitate the selection of centrifugation parameters for obtaining desired size distributions.
1. Introduction
Acoustic droplet vaporization (ADV) has been investigated for various diagnostic and therapeutic applications such as contrast enhancement in ultrasound imaging,1,2 vessel occlusion,1 drug delivery,3 enhancement of high intensity focused ultrasound ablation,4 and gas scavenging.5 ADV involves perfluorocarbon droplets that undergo a phase transition into gas microbubbles when they are exposed to ultrasound above a threshold pressure amplitude.1 Current techniques for fabricating perfluorocarbon droplets, such as sonication,4 high-speed mechanical shaking,1,3 and condensation,2 produce polydisperse size distributions ranging from hundreds of nanometers to tens of micrometers in diameter. However, droplets greater than approximately 8 μm in diameter are too large to pass through the pulmonary capillaries following intravenous injection,6 and droplets smaller than 3 μm in diameter require more ultrasound energy to phase transition compared to larger droplets.2,3,7 Thus, methods are needed to isolate droplets that are small enough to pass through capillary beds and are large enough to phase transition efficiently. Further, the size distribution of the droplets affects the size distribution of microbubbles produced by ADV, and thus, the microbubbles' size-dependent acoustic response.8 The droplet size also affects their biodistribution and pharmacodynamics in vivo. Size-isolation techniques can be used to tailor the size distribution of droplets for specific diagnostic and therapeutic applications of ADV.
Microfluidic production,9 microfluidic sorting,10,11 and pore-filtration12,13 have been used to generate specific size ranges of microbubbles and droplets. Microfluidic techniques have been effective in controlling particle size. However, they require custom equipment and have limited throughput despite improvements in microfluidic technology. Filtration methods are susceptible to filter clogging and have low generation rates.10,13
Previous studies have reported on differential centrifugation as a means to size-isolate microbubbles.8,14 Differential centrifugation is a rapid and robust method to isolate particles of desired size distributions. It only requires a centrifuge, which is readily available in many laboratories. The goals of the current study were to demonstrate size-isolation of perfluorocarbon droplets using differential centrifugation and develop an empirical model for predicting the size distribution of droplets after differential centrifugation.
2. Methods
Albumin-coated perfluoropentane (PFP) droplets were prepared using a protocol described previously.1 Briefly, 0.75 mL of 4 mg/mL bovine serum albumin (Sigma-Aldrich, St. Louis, MO) in phosphate buffered saline (PBS) (Sigma-Aldrich) and 0.25 mL of PFP (Strem Chemicals, Newburyport, MA) was added to 2 mL serum vials (Wheaton Industries Inc., Millville, NJ). The vials were sealed with halobutyl rubber stoppers, crimped, and shaken at 4800 rpm for 30 s (Wig-L-Bug, Dentsply Rinn, York, PA) at 5 °C. The vials were stored at 5 °C and used between 12 h and 1 week after shaking.
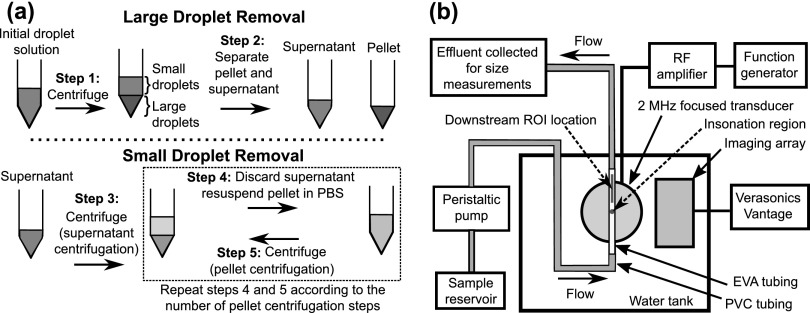
Because perfluorocarbons are denser than water, larger perfluorocarbon droplets preferentially sediment to form a pellet, while smaller droplets remain in the supernatant after centrifugation. Centrifugation (Allegra X-15R, Beckman Coulter, Inc., Brea, CA) followed by the collection of the supernatant (to isolate small droplets) will be termed a supernatant centrifugation. Centrifugation followed by the collection and resuspension of the pellet (to isolate large droplets) will be termed a pellet centrifugation. To determine how the size distribution of droplets in the supernatant and the pellet varied after centrifugation at different speeds, 1 mL of PFP droplet emulsion was diluted in PBS (1:4.8 v/v) in a 15 mL conical centrifuge tube (USA Scientific, Inc., Ocala, FL). The initial droplet size distribution was measured between 0.6 and 18 μm using a Coulter counter with a 30 μm aperture (Multisizer 4, Beckman Coulter, Inc., Brea, CA). The emulsion was then centrifuged for 1 min at a speed [measured in relative centrifugal force (RCF)] of 50 × g, 70 × g, 100 × g, 150 × g, or 230 × g [Fig. 1(a), Step 1]. The supernatant and the pellet were separated by pipetting the maximum volume of the supernatant (3.456 mL), which could be extracted without disturbing the pellet, into another 15 mL centrifuge tube [Fig. 1(a), Step 2]. The pellet after the first centrifugation was called Pellet 1 and was resuspended with 3.456 mL of PBS. The droplet size distributions in the supernatant and the resuspended Pellet 1 were measured. The resuspended Pellet 1 was centrifuged for 1 min at the same speed as the first centrifugation. The supernatant (3.456 mL) after the second centrifugation was discarded. The resultant pellet was called Pellet 2 and was resuspended in the same manner as Pellet 1. The droplet size distribution in the resuspended Pellet 2 was measured. This pellet centrifugation process was repeated three more times at the same speed to investigate how the droplet size distribution in the resultant pellet changed after each centrifugation. Experiments were performed in triplicate for each centrifugation speed.
Fig. 1.
(Color online) Schematics of the (a) differential centrifugation procedure and (b) setup used for conducting acoustic droplet vaporization experiments. The setup schematic shows the nominal insonation region as a dark blue circle and the ROI location for measuring echogenicity as a red rectangle.
A schematic of the differential centrifugation process is shown in Fig. 1(a). Larger perfluorocarbon droplets were removed by centrifuging the initial droplet solution and collecting the supernatant (Steps 1 and 2). Subsequently, smaller droplets were removed by centrifuging the supernatant and collecting the resultant pellet (Steps 3 to 5). The pellet centrifugation process (Steps 4 and 5) was performed multiple times to further modify the droplet size distribution.
An empirical model was developed to enable prediction of the droplet size distribution after differential centrifugation. The model uses a priori measurements of the droplet size distributions of the initial droplet solution, the supernatant, and the pellet after the first centrifugation. These measurements are used to calculate the supernatant ratio (SR) and the pellet ratio (PR), which are the fraction of droplets from the initial droplet solution that are in the supernatant and pellet, respectively, after the first centrifugation. In general, SR and PR depend on parameters, such as the centrifugation speed, centrifugation duration, geometry of the centrifuge tube, diluent fluid, and total volume of the fluid being centrifuged. In this study, the centrifugation speed was varied, while all other experimental parameters were kept constant. Thus, SR and PR depended only on the centrifugation speed and are expressed as and , where and are centrifugation speeds used for the supernatant and pellet centrifugations, respectively. and are computed using the following:
| (1) |
| (2) |
where is the droplet diameter, is the number-weighted size distribution of the droplets in the supernatant after the first centrifugation at a speed of [Fig. 1(a)], B is the number-weighted size distribution of endogenous particles in the diluent, I is the number-weighted size distribution of droplets in the initial droplet solution before centrifugation, and P1 is the number-weighted size distribution of droplets in the resuspended Pellet 1 after centrifugation at a speed of [Fig. 1(a)]. Note that and are normalized by I. The size distributions , B, I, and for all the centrifugation speeds investigated were measured experimentally using a Coulter counter. The predicted number-weighted size distribution of droplets after differential centrifugation is obtained from the empirical model according to the following equation:
| (3) |
where is the non-centrifuged number-weighted size distribution of droplets that will undergo differential centrifugation and n is the number of pellet centrifugation repetitions [Fig. 1(a)]. Note that by normalizing and by I, Eq. (3) can be used to predict size distributions of differentially centrifuged droplets from any initial size distribution, given by NC.
The empirical model was used to guide the preparation of two size-isolated droplet distributions. The first distribution (referred to as the 2 μm distribution) was estimated numerically by inputting the and corresponding to the centrifugation speed of 230 × g (i.e., = = 230 × g) and four pellet centrifugation repetitions (i.e., n = 4) in Eq. (3). This distribution was predicted to have droplets between approximately 1 and 3 μm in diameter. It was prepared experimentally by employing a centrifugation speed of 230 × g for all steps in the differential centrifugation process [Fig. 1(a), Steps 1, 3, and 5] and repeating the pellet centrifugation process four times [Fig. 1(a), Steps 4 and 5]. The second distribution (referred to as the 3.5 μm distribution) was estimated numerically by inputting the and corresponding to the centrifugation speed of 100 × g (i.e., = = 100 × g) and five pellet centrifugation repetitions (i.e., n = 5) in Eq. (3). This distribution was predicted to have droplets between approximately 2 and 5 μm in diameter. It was prepared experimentally by employing a speed of 100 × g for steps 1, 3, and 5 and repeating the pellet centrifugation process five times. Experiments were performed in triplicate for each size-isolated droplet distribution. The nominal upper and lower cutoffs of the size distributions were defined as the diameters at which there was a 90% reduction from the peak value of the volume-weighted size distribution. The mean diameters and coefficients of variation of the empirically modeled and experimentally measured size distributions were calculated. The polydispersity index, defined as the ratio of the volume-weighted mean diameter to the number-weighted mean diameter, was used to assess size uniformity.8 The mean diameters, coefficients of variation, and polydispersity indices between the empirically modeled and experimentally measured size distributions were compared using the Student's t-test in QuickCalcs (GraphPad, La Jolla, CA).
The ADV pressure threshold of the size-isolated droplets was determined using a previously reported technique based on changes in echogenicity.1 The droplets were diluted in PBS such that the volume of the non-centrifuged droplets at 2 and 3.5 μm approximately matched the volumes of the 2 and 3.5 μm droplet distributions, respectively (i.e., 1:30 v/v for the size-isolated droplets, and 1:225 v/v for the non-centrifuged droplets). The dilutions were calculated based on measurements of the stock droplet size distributions and concentrations using the Coulter counter. The droplets were pumped through an in vitro flow phantom [Fig. 1(b)] at 5 mL/min using a peristaltic pump (Mettler Toledo, Columbus, OH). The flow phantom consisted of polyvinyl chloride tubing (McMaster-Carr, Aurora, OH) and ethyl vinyl alcohol (EVA) tubing (McMaster) immersed in a tank of degassed water, maintained at 37 °C. ADV was initiated by a calibrated single-element, 2 MHz focused transducer (H106, Sonic Concepts, Bothell, WA) with an aperture diameter of 6.3 cm and a focal distance of 6.4 cm. The transducer was focused on the EVA tubing (1 mm inner diameter). A pulse repetition frequency of 100 Hz and a pulse duration of 5 μs were employed. To monitor the formation of microbubbles, B-mode images of the insonified droplets were collected with an ultrasound research scanner (Vantage 256, Verasonics, Kirkland, WA), equipped with a linear array transducer (L7-4, 5 MHz center frequency, Philips, Bothell, WA). The peak negative pressure of the 2 MHz transducer was increased from 0 to 6.9 MPa, in steps of 0.53 MPa. All reported pressures are based on free-field measurements performed using a membrane hydrophone (0.4 mm in diameter, Precision Acoustics, Dorchester, UK) and an ultrasound power meter (UPM-DT-10, Ohmic Instruments Co., Easton, MD).4 A B-mode image was acquired at each of the 14 pressure settings. For each B-mode image, a region of interest (ROI) was defined within the lumen of the EVA tube. The ROI extended from 6 to 14 mm downstream of the 2 MHz insonation region and was 0.9 mm across the lumen diameter of the EVA tube. Grayscale values in the ROI for each pressure setting were normalized by the maximum grayscale value obtained across all fourteen of the ROIs. The mean of the normalized grayscale values within each ROI was calculated. A piecewise linear fit was applied to the normalized mean gray scale values as a function of the peak negative pressure. The pressure amplitude corresponding to the intersection of the first two lines of the piecewise linear fit was defined as the ADV threshold.1,5
The fraction of droplets that were not phase transitioned was determined by collecting the effluent from the flow phantom [Fig. 1(b)] in the absence of ultrasound exposure and after ultrasound exposure at a peak negative pressure of 5.4 MPa. The fraction of surviving droplets was computed as the ratio of the number density of droplets in the effluent after ultrasound exposure to the number density of droplets in the effluent in the absence of ultrasound exposure at each diameter. Measurements of the ADV threshold and the fraction of surviving droplets were repeated for three separate samples of each of the three droplet distributions. The ADV thresholds of the three droplet distributions were compared using the analysis of variance in matlab® (Mathworks, Inc., Natick, MA).
3. Results and Discussion
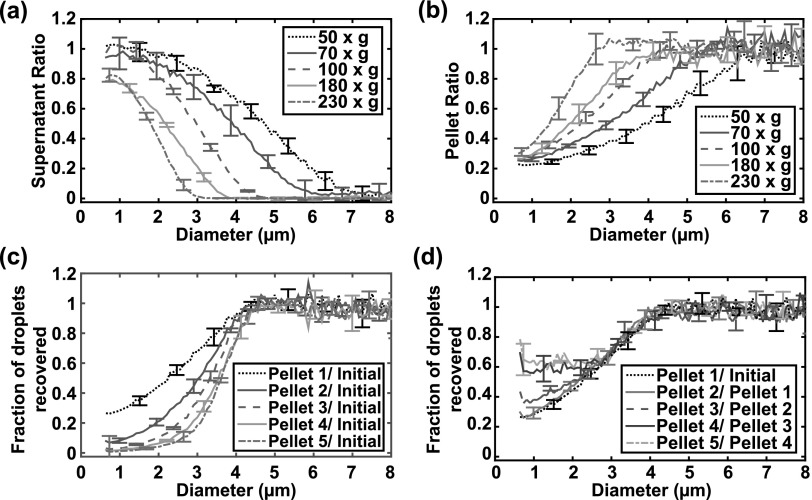
The SRs and the PRs calculated for the five centrifugation speeds employed in this study are shown in Figs. 2(a) and 2(b). Increasing the centrifugation speed reduced the fraction of larger droplets in the supernatant [Fig. 2(a)] and decreased the upper cutoff of the droplet size distribution. In contrast, increasing the centrifugation speed increased the fraction of larger droplets in the pellet [Fig. 2(b)]. However, more than 20% of the smaller droplets remained in the pellet after the first centrifugation for all speeds. Centrifuging the pellet multiple times at the same speed progressively reduced the fraction of smaller droplets and resulted in a steeper transition in the fraction of surviving droplets recovered from 0 to 1 [Fig. 2(c)]. The fraction of droplets recovered in the resultant pellet after each centrifugation step was calculated and found to be similar for each centrifugation step, except for droplets less than 2.5 μm in diameter [Fig. 2(d)]. Specifically, the curves of the fraction of droplets recovered for Pellet 3/Pellet 2, Pellet 4/Pellet 3, and Pellet 5/Pellet 4 diverged from those for Pellet 1/Initial and Pellet 2/Pellet 1. This divergence was likely because the number of particle counts was close to the noise floor of the Coulter counter, resulting in false positive counts.
Fig. 2.
(Color online) Fraction of droplets in the supernatant and pellet as a function of the centrifugation speeds and number of pellet centrifugations. (a) The ratio of the droplet size distribution in the supernatant to the initial size distribution (supernatant ratio, SR), and (b) the ratio of the droplet size distribution in the pellet to the initial size distribution (pellet ratio, PR) as a function of the droplet diameter and centrifugation speed. (c) The fraction of droplets recovered in the pellet relative to initial distribution after the first centrifugation (Pellet 1/Initial), second centrifugation (Pellet 2/Initial), third centrifugation (Pellet 3/Initial), fourth centrifugation (Pellet 4/Initial), and fifth centrifugation (Pellet 5/Initial) at 100 × g. Note that each additional centrifugation resulted in a steeper transition from zero droplets recovered to all droplets recovered. (d) The fraction of droplets recovered in the pellet after each centrifugation step, defined as the ratio of the droplet size distribution in the pellet from the subsequent centrifugation to that of the previous centrifugation. The fraction of droplets recovered after each step was consistent until the absolute number of droplets approached the noise level of the Coulter counter. The mean ± standard deviation of three samples is shown for each condition.
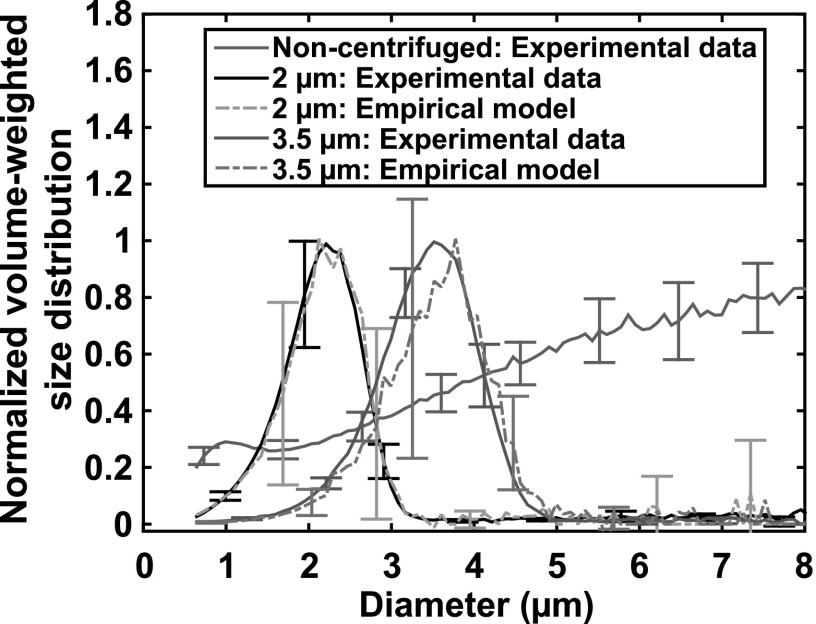
The normalized volume-weighted size distributions of the non-centrifuged droplets and the two size-isolated droplet distributions obtained using differential centrifugation are shown in Fig. 3. The upper and lower cutoffs of the experimentally measured 2 μm droplet distribution were 1.0 and 3.1 μm, respectively, and those of the 3.5 μm droplet distribution were 2.0 and 4.6 μm, respectively. The droplet number densities between 1.0 and 3.1 μm from the non-centrifuged distribution and the 2 μm distribution were 5.2 × 109 ± 0.04 × 109 droplets/mL and 2.5 × 108 ± 0.3 × 108 droplets/mL, respectively. The droplet number densities between 2.0 and 4.6 μm from the non-centrifuged distribution and the 3.5 μm distribution were 1.4 × 109 ± 0.03 × 109 droplets/mL and 7.6 × 107 ± 0.5 × 107 droplets/mL, respectively. Note that the final step of the differential centrifugation protocol resuspended the pellet with a volume of fluid equivalent to the supernatant volume that was removed. This process allows the droplet concentrations above to be compared directly to determine the fraction of recovered droplets between the cutoff diameters (approximately 5% for both size-isolation protocols). The final pellet could alternatively be resuspended with a smaller volume of fluid to increase the droplet concentration.
Fig. 3.
(Color online) The experimentally measured and empirically modeled normalized volume-weighted size distributions of size-isolated droplets and non-centrifuged droplets. The size distributions were normalized to the maximum value of each volume-weighted size distribution. The non-centrifuged droplets had a maximum volume greater than 8 μm. The 2 μm size-isolated droplet distribution was produced by using a speed of 230 × g for all centrifugation steps in the differential centrifugation process and four pellet centrifugation steps. The 3.5 μm size-isolated droplet distribution was obtained by employing a speed of 100 × g for all centrifugation steps and five pellet centrifugations. The mean ± standard deviation of three samples is reported for each size distribution. For the empirical model, the standard deviation was determined by error propagation of the experimental inputs to the model.
After the size-isolation process, 97% of the total volume of the 2 μm droplets was between 1.0 and 3.1 μm, whereas only 6% of the total volume of non-centrifuged droplets was within the same size range. Furthermore, 94% of the total volume of the 3.5 μm droplets was between 2.0 and 4.6 μm, whereas only 11% of the total volume of non-centrifuged droplets was within the same size range. To further quantify the efficacy of the size-isolation process, Table 1 summarizes the volume-weighted mean diameters, coefficients of variation, and polydispersity indices of the three droplet distributions. The differences in the mean diameters, coefficients of variation, and polydispersity indices between the experimentally measured and empirically modeled size distributions were not statistically significant (p > 0.05) for both size-isolated droplet distributions. The similarity between the results of the empirical model and experimental measurements indicates that the model can facilitate a priori determination of the desired size distribution of the perfluorocarbon droplets in a systematic manner.
Table 1.
Summary of parameters derived from experimentally measured and empirically modeled droplet size distributions. The uncertainty represents the standard deviation of three measurements.
| Droplet distribution | Volume-weighted mean diameter (μm) | Coefficient of variation (CV) (%) | Polydispersity index | |
|---|---|---|---|---|
| Non-centrifuged | Experimental | 9.75 ± 0.28 | 44.0 ± 1.39 | 6.83 ± 0.22 |
| 2 μm isolated | Experimental | 2.14 ± 0.02 | 23.3 ± 1.04 | 1.34 ± 0.03 |
| Empirical | 2.16 ± 0.01 | 23.3 ± 0.08 | 1.36 ± 0.01 | |
| 3.5 μm isolated | Experimental | 3.47 ± 0.07 | 23.2 ± 1.97 | 1.35 ± 0.06 |
| Empirical | 3.58 ± 0.01 | 23.0 ± 0.08 | 1.33 ± 0.02 |
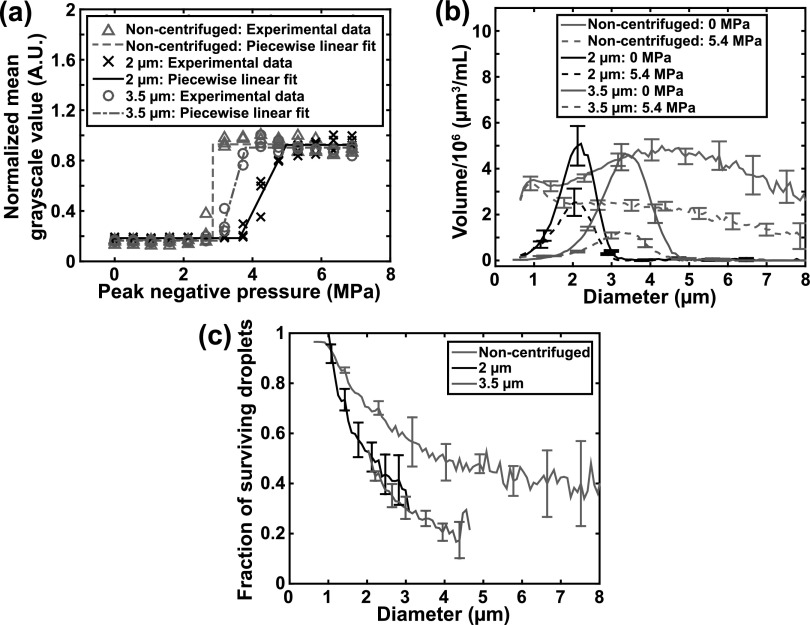
The ADV thresholds were determined using the piecewise linear fits, as shown in Fig. 4(a). The ADV thresholds of the 2 μm droplet distribution, 3.5 μm droplet distribution, and non-centrifuged droplets were 3.7 ± 0.4 MPa, 3.3 ± 0.2 MPa, and 3.0 ± 0.1 MPa, respectively. The differences in the ADV thresholds between the three droplet distributions were not statistically significant (p > 0.05). However, the trend that distributions with larger droplets have lower pressure thresholds is consistent with the superharmonic focusing theory of ADV.3,7 The volume-weighted size distributions of the droplets in the effluent with and without ultrasound exposure at 5.4 MPa (peak negative pressure) are shown in Fig. 4(b). The fraction of surviving droplets after the 5.4 MPa insonation is shown in Fig. 4(c). The fraction of surviving droplets after ultrasound exposure progressively increased as the droplet diameter decreased [Fig. 4(c)], which is consistent with the findings of previous work that reported that smaller droplets are more difficult to phase transition than larger droplets.2,3,7 Additionally, the fraction of surviving size-isolated droplets after ultrasound exposure was less than that of non-centrifuged droplets between 1 and 5 μm in diameter [Fig. 4(c)], using the experimental setup in this study. Note that because there are larger droplets in the non-centrifuged distribution, there are likely larger microbubbles as well. Microbubble-induced acoustic shadowing in B-mode images was substantially more apparent when insonifying non-centrifuged droplets as compared to size-isolated droplets (data not shown). Acoustic shadowing is an indicator that the in situ pressure in portions of the tube may have been reduced for the non-centrifuged droplets. This possible reduction in in situ pressure may have resulted in fewer droplets undergoing ADV, and therefore, a greater fraction of surviving droplets for the non-centrifuged distribution as compared to those for the size-isolated distributions.
Fig. 4.
(Color online) The acoustic response of non-centrifuged and size-isolated droplets. (a) The acoustic droplet vaporization pressure threshold was determined from the piecewise linear fits to the normalized echogenicity data as a function of the peak negative pressure. Individual data points from the triplicate measurements are shown. (b) The volume-weighted size distribution of non-centrifuged and size-isolated droplets without ultrasound exposure (0 MPa) and with ultrasound exposure (5.4 MPa peak negative pressure). Mean ± standard deviation of three samples is shown. (c) The fraction of surviving droplets after ultrasound exposure at 5.4 MPa peak negative pressure. Mean ± standard deviation of three samples is shown.
In principle, the technique reported in this paper could be used to isolate droplets of any size; however, there may be limitations in implementing the experiments. The centrifuge may need to be set to higher centrifugation speeds to isolate submicron droplets. The stability of the droplets at centrifugation speeds above 230 × g was not tested. Additionally, a device that is capable of measuring the size distribution and concentration of nanometer-sized droplets would be needed. An additional challenge would be determining whether the small particles measured are droplets containing perfluorocarbon or particulate impurities. Another limitation arises from the concentration of droplets in the solutions being centrifuged. As the droplet concentration increases, the viscosity of the diluent and thus the drag forces on the droplets during centrifugation changes.8,15 A change in the rheological parameters could change the shape of the SR and PR curves. Therefore, if the concentration of droplets changes significantly after each centrifugation step [Fig. 1(a)], then even for a fixed centrifugation speed the shape of the Supernatant Ratio and Pellet Ratio curves may change. Such changes would confound the application of the model reported in this study. Changes in the shape of these curves were not observed in this study, which used solutions with droplet concentrations ranging from 108 to 1010 droplets/mL [Fig. 2(d)].
4. Conclusion
Differential centrifugation was used to size-isolate perfluoropentane droplets from a polydisperse emulsion. An empirical model was developed and validated for predicting the droplet size distribution obtained from differential centrifugation. The empirical model can facilitate the selection of suitable centrifugation parameters to obtain a predetermined size distribution of perfluorocarbon droplets for various applications in ultrasound imaging and therapy.
Acknowledgments
The authors would like to thank Kyle Rich and T. Douglas Mast, Ph.D., for use and assistance with the ultrasound power meter for this study, as well as Himanshu Shekhar, Ph.D., and Christy K. Holland, Ph.D., for use and assistance with the hydrophone calibration system. The authors also thank Christy K. Holland for use of the Multisizer 4. The project described was supported in part by the National Center for Advancing Translational Sciences of the National Institutes of Health, under award number 1KL2 TR001426-01.
References and links
- 1. Kripfgans O. D., Fowlkes J. B., Miller D. L., Eldevik O. P., and Carson P. L., “ Acoustic droplet vaporization for therapeutic and diagnostic applications,” Ultrasound Med. Biol. 26(7), 1177–1189 (2000). 10.1016/S0301-5629(00)00262-3 [DOI] [PubMed] [Google Scholar]
- 2. Sheeran P. S., Wong V. P., Luois S., McFarland R. J., Ross W. D., Feingold S., Matsunaga T. O., and Dayton P. A., “ Decafluorobutane as a phase-change contrast agent for low-energy extravascular ultrasonic imaging,” Ultrasound Med. Biol. 37(9), 1518–1530 (2011). 10.1016/j.ultrasmedbio.2011.05.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Fabiilli M. L., Haworth K. J., Sebastian I. E., Kripfgans O. D., Carson P. L., and Fowlkes J. B., “ Delivery of chlorambucil using an acoustically-triggered perfluoropentane emulsion,” Ultrasound Med. Biol. 36(8), 1364–1375 (2010). 10.1016/j.ultrasmedbio.2010.04.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Kopechek J. A., Park E. J., Zhang Y. Z., Vykhodtseva N. I., McDannold N. J., and Porter T. M., “ Cavitation-enhanced mr-guided focused ultrasound ablation of rabbit tumors in vivo using phase shift nanoemulsions,” Phys. Med. Biol. 59(13), 3465–3481 (2014). 10.1088/0031-9155/59/13/3465 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Radhakrishnan K., Holland C. K., and Haworth K. J., “ Scavenging dissolved oxygen via acoustic droplet vaporization,” Ultrason. Sonochem. 31, 394–403 (2016). 10.1016/j.ultsonch.2016.01.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. de Jong N., ten Cate F. J., Vletter W. B., and Roelandt J. R., “ Quantification of transpulmonary echocontrast effects,” Ultrasound Med. Biol. 19(4), 279–288 (1993). 10.1016/0301-5629(93)90100-3 [DOI] [PubMed] [Google Scholar]
- 7. Shpak O., Verweij M., Vos H. J., de Jong N., Lohse D., and Versluis M., “ Acoustic droplet vaporization is initiated by superharmonic focusing,” Proc. Natl. Acad. Sci. U.S.A. 111(5), 1697–1702 (2014). 10.1073/pnas.1312171111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Feshitan J. A., Chen C. C., Kwan J. J., and Borden M. A., “ Microbubble size isolation by differential centrifugation,” J. Colloid Interface Sci. 329(2), 316–324 (2009). 10.1016/j.jcis.2008.09.066 [DOI] [PubMed] [Google Scholar]
- 9. Fabiilli M. L., Silpe J., Rush C., Lemmerhirt D., Tang E., Vasey G., and Kripfgans O. D., “ High throughput production of uniformly-sized fluorocarbon emulsions for ultrasonic therapy using a silicon-based microfluidic system,” IEEE Int. Ultrason. Symp. 1770–1773 (2014). 10.1109/ULTSYM.2014.0439 [DOI] [Google Scholar]
- 10. Segers T. and Versluis M., “ Acoustic bubble sorting for ultrasound contrast agent enrichment,” Lab Chip 14(10), 1705–1714 (2014). 10.1039/c3lc51296g [DOI] [PubMed] [Google Scholar]
- 11. Bardin D., Martz T. D., Sheeran P. S., Shih R., Dayton P. A., and Lee A. P., “ High-speed, clinical-scale microfluidic generation of stable phase-change droplets for gas embolotherapy,” Lab Chip 11(23), 3990–3998 (2011). 10.1039/c1lc20615j [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Kripfgans O. D., Orifici C. M., Carson P. L., Ives K. A., Eldevik O. P., and Fowlkes J. B., “ Acoustic droplet vaporization for temporal and spatial control of tissue occlusion: A kidney study,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 52(7), 1101–1110 (2005). 10.1109/TUFFC.2005.1503996 [DOI] [PubMed] [Google Scholar]
- 13. Cheung K., Couture O., Bevan P. D., Cherin E., Williams R., Burns P. N., and Foster F. S., “ In vitro characterization of the subharmonic ultrasound signal from definity microbubbles at high frequencies,” Phys. Med. Biol. 53(5), 1209–1223 (2008). 10.1088/0031-9155/53/5/004 [DOI] [PubMed] [Google Scholar]
- 14. Shekhar H., Rychak J. J., and Doyley M. M., “ Modifying the size distribution of microbubble contrast agents for high-frequency subharmonic imaging,” Med. Phys. 40(8), 082903 (2013). 10.1118/1.4813017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Kvale S., Jakobsen H. A., Asbjornsen O. A., and Omtveit T., “ Size fractionation of gas-filled microspheres by flotation,” Separ. Technol. 6(4), 219–226 (1996). 10.1016/S0956-9618(96)00157-9 [DOI] [Google Scholar]