Abstract
Otoacoustic emissions (OAEs) provide an acoustic fingerprint of the inner ear, and changes in this fingerprint may indicate changes in cochlear function arising from efferent modulation, aging, noise trauma, and/or exposure to harmful agents. However, the reproducibility and diagnostic power of OAE measurements is compromised by the variable acoustics of the ear canal, in particular, by multiple reflections and the emergence of standing waves at relevant frequencies. Even when stimulus levels are controlled using methods that circumvent standing-wave problems (e.g., forward-pressure-level calibration), distortion-product otoacoustic emission (DPOAE) levels vary with probe location by 10–15 dB near half-wave resonant frequencies. The method presented here estimates the initial outgoing OAE pressure wave at the eardrum from measurements of the conventional OAE, allowing one to separate the emitted OAE from the many reflections trapped in the ear canal. The emitted pressure level (EPL) represents the OAE level that would be recorded were the ear canal replaced by an infinite tube with no reflections. When DPOAEs are expressed using EPL, their variation with probe location decreases to the test–retest repeatability of measurements obtained at similar probe positions. EPL provides a powerful way to reduce the variability of OAE measurements and improve their ability to detect cochlear changes.
I. INTRODUCTION
Recordings of otoacoustic emissions (OAEs) offer a noninvasive means of monitoring and assessing the health of the cochlea's outer hair cells and related aspects of inner-ear mechanics. For example, because emission levels tend to fluctuate before significant changes in hearing sensitivity appear, OAEs provide a harbinger of impending sensory hearing loss due to sound exposure, ototoxic drugs, and aging (Ahmed et al., 2001; Campbell, 2004; Lapsley Miller and Marshall, 2007; Marshall et al., 2009; Rao and Long, 2011; Poling et al., 2014). Because basal regions of the cochlea are the most susceptible to damage, OAE changes are often first observed and most prominent at high frequencies. Unfortunately, the clinical application of these findings has been hampered by large test–retest differences across measurement sessions, differences that are particularly acute at high frequencies (reviewed in Konrad-Martin et al., 2016). Here, we show that the repeatability of OAE measurements can be substantially improved by correcting for the effects of ear-canal acoustics (e.g., standing waves) on both the evoking sound stimulus and the resulting OAE pressures. We propose a new OAE metric—emitted pressure—that, when combined with an appropriate stimulus calibration method, substantially reduces the effects of ear-canal acoustics on OAE measurements, particularly at high frequencies. Although we illustrate the ideas using measurements of distortion-product otoacoustic emissions (DPOAEs), the concepts apply to any type of OAE.
A. Stimulus calibration and standing waves
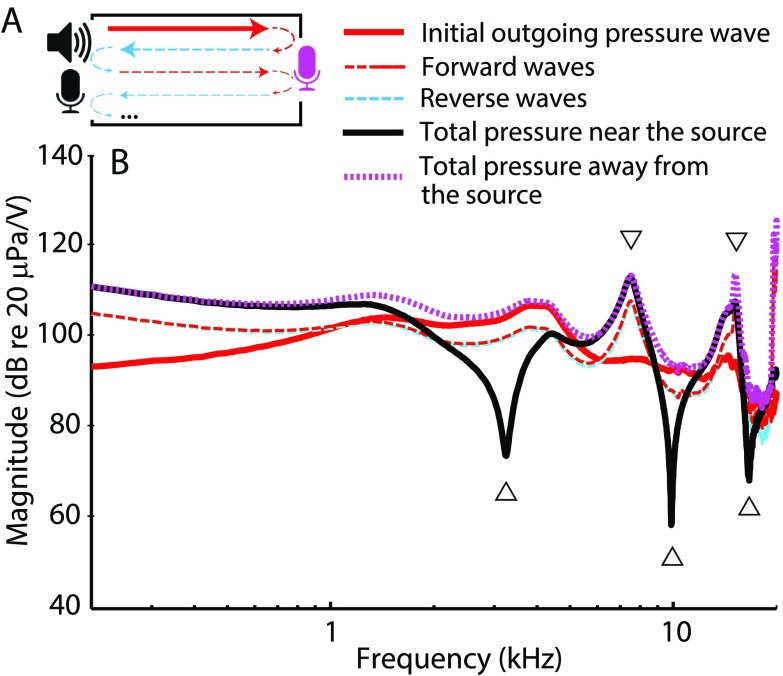
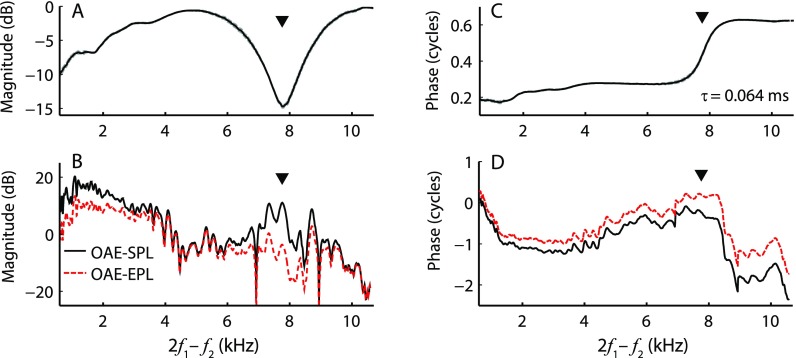
The reliability and repeatability of any hearing test hinges on appropriate stimulus calibration. Most current OAE measurement systems employ in-the-ear calibration procedures that compensate for individual differences in ear-canal acoustics with the goal of equalizing the total stimulus pressure at the OAE probe microphone. [We refer to calibration procedures that control the total pressure at the probe microphone as calibration based on sound-pressure level (SPL).] However, because of reflections that occur within the enclosed ear-canal space,1 the total pressure measured at the microphone may underestimate the pressure at the tympanic membrane (TM) by as much as 20 dB near the quarter-wave nulls (Siegel, 1994). We illustrate this schematically in Fig. 1, where the ear canal is idealized as a closed tube. The total pressure measured at any position along the tube represents the sum of the forward-going waves (i.e., the waves traveling away from the source) and the reverse-going waves [those traveling toward the source, see Fig. 1(A)]. Multiple waves traveling in the two directions arise by reflection at the ends of the tube. The total pressure measured near the sound source depends on the relative phases of the forward and reverse waves at that location. At certain frequencies, the waves combine out of phase and largely cancel one another [see Fig. 1(B), upward triangles and solid back curve]. Cancellation creates so-called standing-wave pressure nodes, which occur at odd multiples2 of the quarter-wave null frequency (fλ/4), given by fλ/4 = c/4L, where L is the length of the residual ear-canal space and c is the speed of sound in air. At the other end of the canal (i.e., at the TM), the forward and reverse waves combine with similar phases, and no cancellation at fλ/4 occurs in the total pressure [Fig. 1(B), dotted magenta line]. Thus, total-pressure (SPL-based) calibrations result in a significant underestimation of the TM pressure near quarter-wave frequencies in a manner that depends strongly on probe position relative to the TM. For instance, Souza et al. (2014) demonstrated that shifting the probe position within the ear canal by a few millimeters causes behavioral thresholds referenced to total pressure to vary by as much as 20 dB at frequencies greater than 3–4 kHz. Similarly, the variability in OAE measurements increases when probe refitting is used in conjunction with SPL-based calibration (Zhao and Stephens, 1999; Beattie et al., 2003; Mills et al., 2007; Wagner et al., 2008; Keppler et al., 2010; Piłka et al., 2014).
FIG. 1.
(Color online) Inter-relations between pressures measured in a tube closed with a flat metal plate at one end and with an OAE probe (sound source and microphone) at the other. To generate the pressures shown, the sound source was driven using a voltage waveform consisting of a constant-amplitude chirp. Because of interference between waves reflected within the cavity [dashed lines in (A) and (B)], the total pressure measured anywhere in the tube—whether near the sound source [solid black line (B)] or at the opposite end [dotted magenta line (B)]—differs from the pressure measured in an anechoic tube of the same characteristic impedance [initial outgoing wave, solid red line in (A) and (B)]. Half-wave resonances (downward triangles) boost the total pressure measured at both ends, while quarter-wave nulls (upward triangles) affect the pressure measured near the sound source when the forward and reverse waves are out of phase.
To help alleviate standing-wave problems, alternative in situ stimulus calibration methods have been proposed. One such method reduces interference effects by defining the relevant stimulus not as the total pressure but as the sum of all forward-going waves in the ear canal [Fig. (B), dashed and solid red lines; Scheperle et al., 2008]. The resulting complex stimulus pressure has been called the “forward pressure” and its level expressed using forward-pressure level (FPL). The complex forward pressure () can be obtained from the total pressure () using the formula
| (1) |
where R is the ear-canal pressure reflectance measured at the probe microphone. Although reflectance measurements in ear canals and other tubes of non-uniform geometry can be challenging (for a recent review see Rosowski et al., 2013), methods based on determination of the Thévenin-equivalent source parameters of the probe generally provide sufficient accuracy to reveal the benefits of FPL-based stimulus calibration (Lewis et al., 2009; Scheperle et al., 2011). For example, hearing thresholds referenced to FPL, unlike those expressed in SPL, are largely insensitive to changes in probe location, implying that FPL-based calibrations account well for variations in the length of an individual's residual ear-canal space (Souza et al., 2014).
Stimulus calibrations based on forward rather than total pressure decrease the dependence of OAE levels on probe location but do not eliminate it (Scheperle et al., 2008). For example, Scheperle et al. (2008) found that DPOAE levels measured at two probe positions in the ear canal differed, on average, by 2–3 dB for distortion-product (DP) frequencies (i.e., 2f1 − f2) between 0.6 and 3.8 kHz and by up to 6 dB at frequencies near 5.3 kHz, the highest frequency measured.3 We suggest that these changes represent the effects of ear-canal acoustics not on the stimulus, which have largely been removed by using FPL-based calibration, but on the emission itself. We base our suggestion on Fig. 1, reconsidered in the context of an OAE measurement. The speaker now represents the vibrating TM emitting an OAE [Fig. 1(A), solid red arrow]. The OAE pressure wave propagates toward the probe microphone [Fig. 1(A), magenta mic], where it reflects back toward the TM. The reflected OAE wave subsequently undergoes another reflection at the TM back toward the probe, and the process continues in a series of multiple reflections that gradually diminish in amplitude due to energy dissipation [Fig. 1(A), dashed arrows]. Because the total pressure measured at any point represents the sum of all forward and reverse waves trapped in the residual ear-canal space, the total OAE measured at the microphone differs from the initial OAE wave emitted at the TM [Fig. 1(B), dotted magenta line vs solid red line). Closing the ear canal with the probe assembly not only boosts the total OAE pressure at low frequencies due to increased load impedance4 (Withnell et al., 1998; Boul and Lineton, 2010), it also affects the pressure at higher frequencies, specifically near the half-wave resonances [multiples of fλ/2 = c/2L; down-pointing triangles in Fig. 1(B)]. Thus, even when the evoking stimuli are compensated for ear-canal acoustics, OAE pressures measured at the microphone still vary with probe location. The largest changes are expected near the half-wave resonant frequencies (fλ/2 ∼ 8 kHz in adults), where emission levels could be boosted by as much as 10 dB.
B. Emitted pressure
Rendering OAE measurements independent of probe location evidently requires removing the confounding effects of ear-canal acoustics both from the evoking stimulus and from the resulting OAE. To achieve the latter, we propose a new OAE metric that defines the OAE not as the total emission pressure measured at the microphone but as the initial outgoing OAE wave at the TM [Fig. 1(A), red arrow]. By definition, the initial outgoing wave is free of reflections—it represents the total OAE pressure that would be measured at the TM if the ear canal were replaced by an anechoic (e.g., infinite) tube with the same characteristic impedance. We refer to the initial outgoing pressure wave as the “emitted pressure” and to its level as the emitted pressure level (EPL).
Using a scattering-matrix representation of the residual ear-canal space, we derive formulas that extract the emitted pressure from the total OAE pressure measured at the microphone (see the Appendix). In the simplest case, when the ear-canal space can be approximated by a uniform reflectionless tube (i.e., a tube in which reflections occur at the ends but not within the tube itself), the complex emitted OAE pressure (OAEEPL) becomes
| (2) |
where OAESPL is the total emission pressure measured with the probe microphone (i.e., the conventional OAE), is the ear-canal reflectance, is the pressure reflectance of the probe, and T is the ear-canal transmission coefficient (approximated here as e-iωτ, where ω is the angular frequency and τ is the one-way ear-canal delay).5 As a useful shorthand, we refer to the quantity as the total-to-emitted pressure conversion function. Because all of the parameters included in the conversion function are readily available from FPL-based calibration routines, the implementation of emitted pressure is as simple as adding Eq. (2) to the data-acquisition software.
In this study, we test the dependence of stimulus calibration and OAE pressure on ear-canal acoustics by measuring DPOAEs across a broad frequency range at two probe positions in the ear canal (deep and shallow). We compare both total- and forward-pressure calibrations, extending the findings of Scheperle et al. (2008) to higher frequencies. After validating Eq. (2) using measurements in a simple tube, we test the prediction that OAEEPL remains independent of probe position when OAEs are evoked using FPL-calibrated stimuli. We find that the use of emitted pressure significantly improves the repeatability of OAE measurements across multiple test sessions.
II. METHODS
A. Subjects
Subjects were eight normal-hearing young adults (22–30 yrs old, six females), all with no history of ear disease, normal otoscopic exam, and normal audiometric thresholds (<15 dB hearing level) for frequencies in the range 0.5–16 kHz. Of the two ears in each subject, the ear that emitted the higher DPOAE levels at high frequencies was chosen for testing (six right ears and two left). All procedures were approved by the human studies committee at the Massachusetts Eye and Ear Infirmary.
B. Instrumentation and stimulus calibration
Stimulus waveforms were generated and responses acquired and averaged digitally using a Babyface Audio Interface (48 kHz sampling rate) and an ER10X OAE probe system (Etymōtic Research, Elk Grove Village, IL). The microphone signal was amplified (20 dB) and high-pass-filtered (cutoff frequency of 100 Hz). Thévenin-equivalent probe parameters (source pressure, PS, and impedance, ZS) were obtained daily at room temperature using constant-attenuation chirp responses measured in the ER10X calibrator [brass tube; inner diameter (i.d.) 7.9 mm; tube lengths = 70, 62, 54, 37, and 28 mm] for each sound source separately (see Scheperle et al., 2008; Souza et al., 2014 for details). Measurements were repeated until the so-called “calibration error” (calculated over 2–8 kHz range) was less than 1 (typically ∼0.03). In some measurements (Sec. II D) an ER7C probe microphone system (Etymōtic Research) was used (preamplifier gain set at 0 dB). Microphone output was corrected for the mic sensitivity measured as described in Siegel (2007). The data-acquisition hardware was controlled using custom software written in Matlab (Mathworks, Natick, MA).
All measurements were performed in a sound-attenuating chamber. The OAE probe was suspended from the chamber ceiling, and the probe cable was secured against the subject's head with a headband. The OAE probe was sealed to the ear canal with a rubber tip supplied by OAE-probe manufacturer. Before each DPOAE test, wideband chirp responses were collected in the ear canal. These responses were used to (a) estimate the first half-wave resonant frequency, fλ/2; (b) judge the probe seal; (c) calibrate the DPOAE stimuli in situ; and (d) derive ear-canal load and surge impedance to calculate the pressure reflection coefficients [, and , respectively; see Eqs. (1) and (2); procedures detailed in Souza et al., 2014]. Accurate estimation of fλ/2 was facilitated by normalizing the ear-canal chirp response by the chirp response of a 15 -m coiled copper tube (i.d. 7.9 mm; Souza et al., 2014). This normalization removes irregularities in the earphone frequency response that can obscure identification of fλ/2. The half-wave resonant frequency was used to estimate the one-way ear canal delay using the equation, τ = 1/(2fλ/2).6 We regarded the probe as adequately sealed in the ear canal when the low-frequency ear-canal absorbance was less than 0.29 and the low-frequency admittance angle was greater than 44°(averaged over 0.2–0.5 kHz, adapted from Groon et al., 2015). The stimulus voltages fed to the speakers were calibrated to produce a constant FPL-based calibration [Eq. (1)]. Additional DPOAE runs were collected with the stimulus voltages calibrated to produce a constant total sound pressure at the OAE probe microphone (SPL-based calibration), as conventionally done in many OAE measurement systems. The pressure reflectance of the ear canal (R) and of the OAE probe source (RS) were derived from the Thévenin source parameters and from the measured ear-canal responses to the chirp stimuli [see Eqs. (2) and (7) in Souza et al. (2014), respectively]. The surge impedance of the ear canal was determined using an empirically optimized procedure detailed elsewhere (Rasetshwane and Neely, 2011; Souza et al., 2014).
C. DPOAE measurements and analysis
DPOAEs were recorded at frequencies fDP = 2f1 − f2 (0.6–10.6 kHz) with primary tone levels L1, L2 of 62, 52 dB (SPL or FPL) at a fixed primary frequency ratio, f2/f1, of 1.22. The primary frequencies were swept upward at a rate of 1 octave/s, and each primary tone was played through a separate speaker. The swept-tone paradigm (also used for stimulus-frequency otoacoustic emissions, SFOAEs) allows rapid OAE measurements with high frequency resolution (e.g., Long et al., 2008; Kalluri and Shera, 2013). The full range of tested frequencies was divided into three overlapping segments having f2 {start, stop} frequencies of {0.96, 2.6}, {2.4, 6.6}, and {6.1, 16.5} kHz, respectively, resulting in ∼0.1 octave overlap between the sweeps. To expedite the data collection, the three primary sweeps were presented concurrently, each lasting ∼1.44 s.7 Fast data collection helped to minimize possible changes in DPOAE levels due to probe slippage. Data collection was stopped after accumulating 96 artifact-free measurements (see Kalluri and Shera, 2013 for a description of a real-time artifact rejection algorithm for swept-tone OAEs). Phase-rotation averaging was employed to cancel out the f1 and f2 primaries from the measured response (Whitehead et al., 1996).
DPOAE amplitude and phase were estimated using a least-squares fitting (LSF) procedure (Long et al., 2008; Abdala et al., 2015). In the LSF technique, models of the DPOAE and primary tones are fit to the measured time waveforms by minimizing the sum of the squared residuals between the model and the data. The LSF analysis is conducted on short segments (frames) of overlapping Hann-windowed data with specified duration. Window durations were adjusted to account for the sweep rate and to accommodate the frequency-dependent latency of the reflection component of the total DPOAE8 (Shera and Guinan, 1999; Abdala et al., 2015). Prior to unwrapping, DPOAE phase at fDP was corrected for the phase variation of the primaries by subtracting 2ϕ1−ϕ2, where ϕ1 and ϕ2 are the phases of either the forward or total stimulus pressures (depending on the calibration routine employed) at the frequencies f1 and f2, respectively.9 Group delays were calculated as the negative slope of the OAE phase (in cycles) vs frequency functions. The measurement noise floor was estimated by applying the LSF analysis to the difference waveform obtained by subtracting adjacent sweep pairs. Although we have no reason to doubt the validity of our DPOAE data collection and analysis procedures, we note that the results presented here depend not on absolute values but on changes (e.g., due to probe position and/or calibration procedure) between OAEs obtained using the same swept tones and LSF routines.
DPOAEs were measured using both FPL- and SPL-calibrated stimuli at each of two different probe positions: First, with the OAE probe sealed near the entrance of the ear canal (shallow insertion depth) and, subsequently, with the probe pushed deeper (by about ∼3 mm) into the ear canal (deep insertion). The probe position was adjusted (sometimes involving reinsertion and changing a tip size) until a good seal was obtained. Changes in probe position were evaluated acoustically using changes in fλ/2. Differences between DPOAE levels and phase-gradient group delays obtained at the two probe positions were compared for (i) DPOAEs collected using SPL- and FPL-calibrated stimuli and (ii) for DPOAEs expressed conventionally as total sound pressure at the probe microphone (OAESPL) and as emitted pressure at the TM (OAEEPL). Following the measurements at the deep position, the probe was returned to the shallow position, taking care to match the previous (shallow) value of fλ/2 (±100 Hz), and another set of DPOAE measurements was obtained (using FPL-calibrated stimuli only). Differences between DPOAE levels and phase-gradient group delays at the two shallow probe positions (bracketing the deep position) were used to estimate test–retest repeatability and served as a reference for assessing the significance of changes observed between the deep and shallow positions. To ensure the reliable measurement of DPOAE changes near the half-wave resonance, we required that DPOAE levels (in dB SPL) near fλ/2 have a signal-to-noise (SNR) of at least 10 dB.
Total OAE pressures measured at the OAE probe microphone (OAESPL) were converted to emitted pressure at the TM (OAEEPL) using Eq. (2). Conversion functions computed from the measured calibration parameters, , R, and T, were derived separately for each of the two sound sources in the ER10X probe. Because the conversion functions for the two sound sources were almost indistinguishable in any given ear,10 the calibration parameters for the two sources were averaged before obtaining a single, final conversion function used in subsequent analysis.
D. Tube measurements
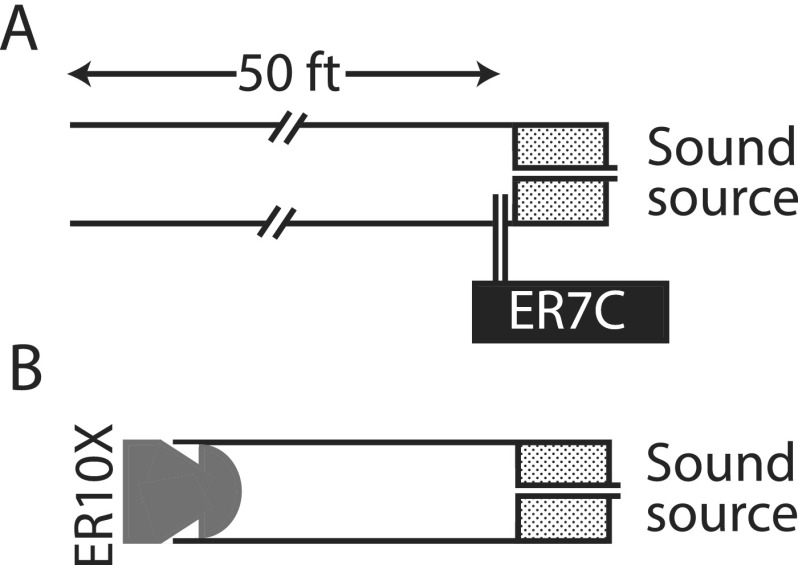
To test the consistency of our measurements and model we obtained direct and indirect measurements of emitted pressure in two tubes. Illustrated in Fig. 2, the measurement configuration consisted of two brass tubes: a long (15-m) open tube and a short (∼30 mm) closed tube of the same diameter (i.d., 7.9 mm). Both tubes were terminated with a sound source that served as an analog of the OAE source at the TM. The sound source (a modified Audax TW010F1, Meniscus, Grand Rapids, MI, coupled via 16 ga flexible tubing to a foam tip sealed to the end of the tube) was driven by a constant-voltage chirp stimulus (∼50 dB SPL). In the long (effectively anechoic) tube, the emitted pressure produced by the sound source was measured directly using a probe microphone (ER7C, Etymōtic Research) placed near the foam tip [Fig. 2(A)]. In the short tube, driven in the same way, the total pressure at the opposite end of the tube was measured using the ER10X probe [Fig. 2(B)], just as done in human ears. Prior to each measurement, the closed-tube parameters necessary to compute the total-to-emitted pressure conversion function were derived as described in Secs. II B and II C. In total, six measurements were obtained in each cavity, reinserting the speaker foam tip, ER7C probe tip, or ER10X probe tip before each measurement. While the positions of the speaker foam tip and the ER7C were kept as similar as possible between the measurements,11 the position of the ER10X in the closed tube was purposely varied to obtain measurements at six different insertion depths.
FIG. 2.
Cartoon of the experimental setup for pressure measurements in simple tubes. In (A), the sound source (Audax) was placed in a long anechoic tube and the pressure near the source was measured with a probe-tube microphone (ER7C). In such conditions, the pressure measured with the ER7C approximates the emitted pressure (i.e., the initial outgoing going wave at the sound source). In (B), the sound source was inserted into a brass tube terminated with an OAE probe assembly (ER10X). The total pressure generated by the sound source was recorded with the ER10X microphone and transformed to an estimate of emitted pressure using Eq. (2).
III. RESULTS
A. Compensating for the effects of ear-canal acoustics on OAE measurements
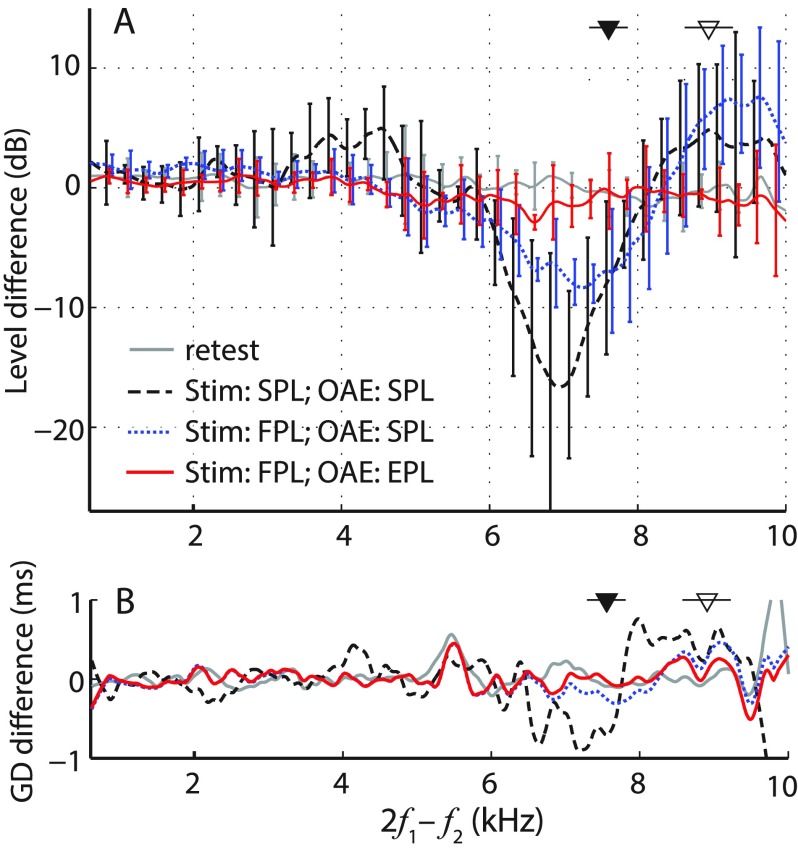
We tested whether EPL can compensate for ear-canal standing waves and improve the test–retest repeatability of OAE measurements. Before describing our results in detail, we preview the main result. Figure 3 demonstrates that when combined with FPL stimulus calibration, the conversion to EPL renders OAE measurements insensitive to the location of the ear-canal probe. The figure shows average changes due to probe position (deep vs shallow) in DPOAE level and group delay obtained using different measurement approaches (see legend). DPOAEs measured with FPL-calibrated stimuli and converted to EPL are nearly independent of probe position (Fig. 3; red solid line). The observed differences in levels and group delays are comparable to the test–retest repeatability of the DPOAE measurements at the shallow location (<2 dB, gray solid line).
FIG. 3.
(Color online) Mean differences (±1 SD) in measured DPOAE levels (A) and group delays (B) due to changes in probe insertion depth (deep minus shallow, n = 5). Data with a SNR less than 6 dB were excluded from the calculations (16%–19% of the data, depending on the curve), and the results were gently smoothed (post-averaging). For clarity, error bars for the level data are shown at intervals of 0.25 kHz and are omitted entirely for the group-delay data, for which the SDs averaged around 1–2 ms. Dashed black and dotted blue lines show differences for DPOAEs (measured with SPL- and FPL-calibrated stimuli, respectively) expressed as total pressure (SPL). The solid red line shows differences for DPOAEs (measured with FPL-calibrated stimuli) expressed as EPL. For comparison, the gray line shows the test–retest repeatability of DPOAEs obtained at the same probe position. Triangles indicate mean fλ/2 (±1 SD) for shallow (filled) and deep (open) probe insertion depths.
In contrast, conventional DPOAE levels (i.e., the total OAE pressure expressed as SPL) vary by ∼10 dB with probe position at frequencies near the half-wave resonance (see triangles), even when the stimuli are calibrated using FPL [Fig. 3(A); dotted blue line]. [In this report, DPOAE data are always plotted versus DP frequency (2f1−f2) rather than versus f2 (see note 3).] The confounding effects of ear-canal acoustics on OAE measurements are further exacerbated by the use of SPL-based stimulus calibration—in this case, DPOAE levels vary by more than 15 dB near the half-wave resonance frequencies and significant changes are seen even at lower frequencies [fDP ∼ 3–4 kHz; Fig. 3(A); dashed black line]. The use of SPL-based calibration routines also increases the sensitivity of DPOAE group delay to probe insertion depth [Fig. 3(B), dashed black line].
Our results demonstrate that compensating for the effects of ear-canal acoustics on both the evoking stimuli and the resulting emissions allows OAE measurements to be made reproducibly across test sessions, independent of probe placement in the ear canal, over frequencies spanning most of the range of human hearing. In Secs. III B and III C, we validate the use of emitted pressure in measurements made in simple tubes and then discuss the results obtained in human subjects in more detail.
B. Validation in simple tubes
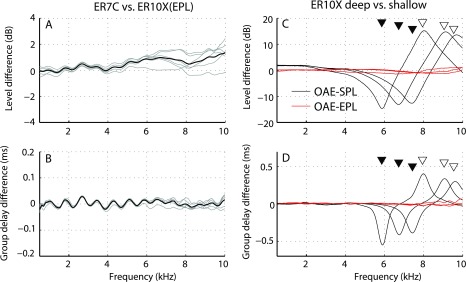
Before applying the method in human subjects, we tested the integrity of our framework by making measurements in tubes (Fig. 2). Specifically, we compared direct measurements of emitted pressure in an anechoic tube to estimates derived from measurements in a closed tube using Eq. (2). (In an anechoic tube, the total and emitted pressures at the sound source are the same.) Figure 4 demonstrates that estimates of emitted pressure (OAEEPL) obtained from the closed tube agree well with those measured directly in the anechoic tube, generally matching within ±2 dB in level and ±0.03 ms in group delay, close to the test–retest repeatability of the measurements [Figs. 4(A) and 4(B), means in black, six individual measurements in gray]. Small discrepancies between measured and estimated pressures may reflect errors in the source and microphone calibrations, as well as possible changes in resonance conditions between the tube cavity and flexible tubing connecting the speaker to the foam tip [e.g., the “wiggles” in Figs. 4(A) and 4(B)]. Some variability is also expected because of our limited ability to control the exact position of the ER7C probe position relative to the sound source, where the pressure distribution is non-uniform due to the presence of evanescent waves.
FIG. 4.
(Color online) Validating the conversion to emitted pressure using measurements in simple tubes. Panels (A) and (B) show differences in levels and group delays, respectively, between emitted pressures derived from measurements in the short tube with the ER10X [using Eq. (2)] and measured in the long tube with the ER7C (see setup in Fig. 2). Gray lines show individual measurements; black lines, the means. Ideally, level and group delays differences are zero. Panels (C) and (D) show the difference in levels and group delays between “OAEs” measured with the ER10X at pairs of shallow and deep probe placements. Black lines show differences between OAEs expressed in conventional form as total pressure; red lines show corresponding differences in emitted pressure. Triangles mark the half-wave resonant frequencies for shallow (open symbols) and deep (closed symbols) probe positions. Paired measurements are indicated by triangles placed on the same horizontal line.
The six measurements of total pressure (OAESPL) obtained at different probe insertion depths in the closed cavity were paired to form three sets of “deep” and “shallow” probe placements. Figures 4(C) and 4(D) show the changes in total pressure and group delay (black lines) due to changes in probe placement for each of the three pairs of measurements. At low frequencies (<3 kHz), total pressures increase at deeper insertion depths because the cavity (or load) impedance varies inversely with tube length and frequency (see note 4). This dependence on insertion depth can be partially corrected for using measured changes in load impedance at low frequencies (Scheperle et al., 2008). However, near the half-wave resonance frequencies, fλ/2, marked for the shallow and deep measurements in each pair using closed and open triangles, respectively, the pressures vary with probe position by as much as 15 dB in magnitude and 0.5 ms in group delay. By contrast, the red lines in Figs. 4(C) and 4(D) show that conversion to emitted pressure (OAEEPL) almost completely eliminates the dependence on probe position.
At least in simple tubes, these results demonstrate that Eq. (2) for the emitted pressure OAEEPL accurately extracts the initial outgoing pressure wave emitted by the sound source in a way not susceptible to changes in acoustic load caused by shifting the probe position relative to the sound source.
C. Application to human subjects
We obtained usable data from five of eight subjects tested. Data from the remaining three subjects did not meet our SNR criterion near fλ/2 at either the shallow or the deep probe placement (see Sec. II). Additionally, in one of the three excluded subjects (ID029) we were unable to obtain an adequate acoustic seal at the shallow probe placement.
1. Conversion of conventional OAEs to emitted pressure
Figure 5 shows example DPOAE measurements displayed both as total pressure (i.e., OAESPL, the conventional OAE) and as emitted pressure (OAEEPL). The OAE measurements were obtained using FPL-calibrated stimuli. The top panels show the magnitude and phase of the conversion function derived from the calibration procedure, and the bottom panels show the results of the conversion. The transformation from total to emitted pressure has large effects on OAE magnitude both at low frequencies, where the ear canal can be approximated as a simple volume, and near fλ/2 (downward triangle in Fig. 5), where standing-wave interference is significant. The phase of the emitted pressure manifests both a shallower overall slope, due to compensation for the one-way ear-canal delay, and significant changes near fλ/2 specific to the correction for standing waves [Fig. 5(C), triangle]. We obtained similar conversion functions in the tube tests (Sec. III B, data not shown), suggesting that the ear canal is reasonably well approximated by a uniform tube.
FIG. 5.
(Color online) Total and emitted DPOAE pressures in one subject. (A) and (C) show the magnitude and phase, respectively, of the total-to-emitted pressure conversion function computed from Eq. (2). (B) shows total and EPLs expressed in dB SPL (solid black line) and dB EPL (dashed red line), respectively. (D) shows the corresponding phases. The conversion from total to emitted pressure decreases emission levels at low frequencies and near the half-wave resonance (marked with a triangle in each panel). The dashed lines (barely visible) in (A) and (C) represent the functions computed from calibration parameters measured for each of the two earphones separately; the solid lines were obtained using parameters averaged between the two speakers.
Although the conversion from total to emitted pressure generally reduces absolute OAE levels, it does not affect the SNR, which is determined at the time of OAE measurement. Thus, when noise in the conversion function itself can be neglected—that is, when the SNR of the calibration measurements is large compared to that of the OAE measurements—then the effective EPL noise floor can be estimated by applying the same conversion [Eq. (2)] to the measured noise. Of course, the noise floor obtained in this way should not be interpreted as “emitted noise” from the TM. Indeed, unlike OAEs, the measurement noise does not consist entirely—or even primarily—of sound emanating from the TM. At low frequencies, much of the measurement noise is body or subject noise (e.g., breathing), which can enter the ear canal by other routes, and at higher frequencies most of the noise is electronic (e.g., amplifier noise), unrelated to the acoustics of the ear canal.
2. Changes in ear-canal acoustics with probe insertion depth
Significant changes in half-wave resonant frequency with insertion depth allow us to explore the sensitivity of DPOAE measurements to probe placement. When the probe was moved from its initial shallow position toward the TM, the mean value of fλ/2 across the five ears shifted from 7.61 [standard deviation (SD) 0.26] kHz to 8.96 (0.33) kHz (p < 0.001, paired t-test). After the probe was returned to the shallow position to obtain retest data, fλ/2 averaged 7.61 (0.32) kHz, a value statistically indistinguishable from the initial shallow placement (p > 0.9). The frequency of the quarter-wave null (fλ/4) also shifted significantly when the probe was advanced toward the TM, changing from 3.31 (0.72) kHz to 3.89 (0.93) kHz (p < 0.05), while no significant difference was observed between the two shallow positions (p = 0.08). Thus, we presume that any differences in the DPOAEs measured at the two shallow positions arise primarily from measurement noise and/or intrinsic fluctuations in DPOAE levels over time, rather than from changes in the residual ear-canal length.
We used the value of fλ/2 to obtain acoustic estimates of changes in probe insertion depth as well as one-way ear-canal delays. For the shallow insertion depth the probe was on average 23.2 (SD 0.8) mm away from the TM while for the deep insertion depth this distance decreased by on average by 3.5 (0.2) mm. The one-way ear-canal delay averaged 65.8 (2.3) μs and 55.9 (2.1) μs for shallow and deep insertion depths, respectively. Our estimates of one-way ear-canal delays are similar to the estimates of Rasetshwane and Neely (2011) derived from time-domain reflectance measurements.
The magnitude of the ear-canal pressure reflectance had a broad minimum (with |R| ∼ 0.6) in the range 1–5 kHz, similar to previous reports (e.g., Stinson, 1990; Keefe et al., 1993; Voss and Allen, 1994; Rasetshwane and Neely, 2011; Souza et al., 2014). In most cases, the reflectance did not vary with probe insertion depth by more than ±0.15 at frequencies below ∼10 kHz (mean change always <0.12), which is similar to the variation of test-retest measurements (change usually within ±0.15 and mean always <0.09). However, at frequencies greater than 10 kHz, |R| changed with probe insertion depth more than expected based on retest measurements, and in some instances |R| exceeded 1, implying errors in the measurements or a violation of the assumptions. Values of |R| exceeding 1 at high frequencies were also reported in Souza et al. (2014) for normal human ears, in Merchant et al. (2016) for temporal bone preparations, and in Lewis and Easterday (2016) for measurements in ear simulators. Lewis and Easterday (2016) suggest that the sensitivity of |R| to probe placement at high frequencies may be due to the impedance mismatch created at the plane of the sound source in the ear canal. Although these anomalies in measurements of |R| likely had only minor effects on the conversion to emitted pressure (which was applied for fDP ≤ 10 kHz), they could have influenced the FPL stimulus calibration at higher frequencies, since f2 was swept up to 16 kHz. Errors in stimulus calibration can introduce an apparent sensitivity of emitted pressure to the probe insertion depth.
3. Sensitivity of DPOAE magnitude and phase to probe insertion depth
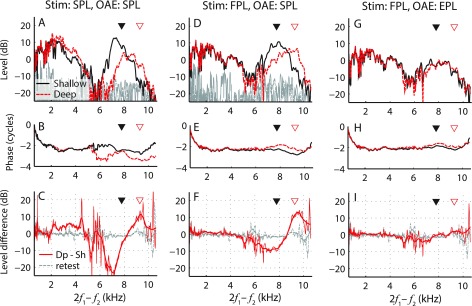
Figure 6 shows DPOAEs collected at two probe positions for one example subject. When DPOAEs are evoked using SPL-calibrated stimuli [Figs. 6(A) and 6(B)], clear changes in DPOAE magnitude and phase occur when the probe is moved toward the TM (solid black curves vs dashed red curves). DPOAE magnitudes change across the entire tested frequency range [Fig. 6(C), red curves], with the largest changes occurring near the values of fλ/2 (triangles); by contrast, only small changes are observed in the retest data (gray). The dependence of DPOAE level on probe position seen here reflects the combined effects of ear-canal acoustics on both the evoking stimuli and on the emission itself. For instance, the SPL-calibration overcompensates the stimuli level near the quarter-wave null, resulting in stronger stimulation of the cochlea (e.g., Siegel and Hirohata, 1994; Scheperle et al., 2008; Chen et al., 2014). This may explain the increase in DPOAE levels near 2–4 kHz at the deep probe placement, where the f1 frequency (2.6–5.2 kHz) was near fλ/4 (shifted from 2.6 to 3.4 kHz; see Sec. IV).
FIG. 6.
(Color online) DPOAE magnitudes (upper panels) and phases (middle panels) measured at shallow (black solid line) and deep (red dashed line) probe insertion depths in one subject (036). In the bottom panels, the red lines show changes in the DPOAE level resulting from manipulating the probe position (thick lines show the data after gentle smoothing). The three columns show data obtained using different combinations of stimulus calibration procedures (SPL vs FPL) and/or DPOAE pressure metrics (SPL vs EPL). For comparison, the dashed gray lines show the test–retest variability in the DPOAE level (dB SPL) at the shallow position obtained with FPL stimulus (bottom panels). Triangles mark the half-wave resonant frequencies for each probe position. Noise levels (in dB SPL) are shown in gray when appropriate (upper panels).
DPOAEs evoked using FPL-calibrated stimuli are less sensitive to changes in insertion depth, at least for frequencies below 5 kHz [Figs. 6(D) and 6(E)]. At low frequencies (<3 kHz), the increase in DPOAE levels at the deeper insertion depth can be explained by the change in the ear-canal load impedance, approximated as a simple volume [e.g., see Fig. 4(C), black line; also see Scheperle et al., 2008). However, near the values of fλ/2, DPOAE levels changed by over 10 dB [Fig. 6(F), red line]. Although DPOAE phase appears less sensitive to probe position than in data obtained with SPL-calibration, small changes in phase slope are evident near fλ/2 [Fig. 6(E), triangles], similar to the observations made in the tube [Fig. 4(D)]. When the probe was returned to the shallow position (retest data), the phase curve consistently shifted back to its initial position [Fig. 6(E), black line, retest data not shown]. Because FPL calibration allows delivery of stimuli that excite the cochlea in a way largely independent of probe position, the changes in DPOAE pressure (OAESPL) evident in Figs. 6(E) and 6(F)] presumably arise primarily from the acoustical effects of the residual ear-canal space on the OAEs themselves, rather than on the evoking stimuli.
Converting the conventional DPOAEs shown in Figs. 6(D) and 6(E) to emitted pressure (OAEEPL) substantially reduces the sensitivity of both magnitude [Fig. 6(G)] and phase [Fig. 6(H)] to probe placement. Indeed, when expressed using emitted pressure, DPOAE level changes [Fig. 6(I), red line] are similar to the test–retest repeatability of the measurement (gray line). Thus, the transformation to EPL reduces the dependence of DPOAE measurements on probe position, consistent with the observations in the simple tubes [Figs. 4(C) and 4(D)]. As already summarized in Fig. 3, we obtained similar results in the other four subjects.
IV. DISCUSSION
A. Effects of ear-canal acoustics on stimulus and emission
To attenuate environmental noise reaching the microphone, OAEs are usually measured with the probe sealed in the ear-canal entrance using a foam or rubber tip. Unfortunately, reflections within the ear-canal space produce standing waves (e.g., Lawton and Stinson, 1986) that create problems for stimulus calibration. (Table I estimates the frequency ranges affected by standing-wave interference in several common species.) For example, in-the-ear calibration procedures that maintain a constant total sound pressure at the probe microphone can produce variations in pressure at the TM of as much as 20 dB due to interference between forward and reverse waves at frequencies near the quarter-wave nulls [Fig. 1(B); Siegel, 1994; Siegel and Hirohata, 1994]. These effects manifest themselves most simply when stimulus and response are at the same frequency; for example, as reduced behavioral thresholds or increased SFOAE amplitudes near fλ/4 (Lewis et al., 2009; Chen et al., 2014; Souza et al., 2014). Interpretation of the effects of quarter-wave nulls on DPOAE measurements is more complicated, since DPOAE levels depend on both the absolute and the relative levels of the two evoking tones (L1 and L2), which are altered differently when either f1 and/or f2 approach fλ/4 (Whitehead et al., 1995). As a result, changes in DPOAE levels due to calibration errors near fλ/4 are less easily predictable.
TABLE I.
The range of frequencies of significant standing wave effects (≥ fλ/4) estimated based on average ear-canal (EC) lengths for different species (as summarized in Rosowski, 1994; Qi et al., 2006; Ravicz et al., 2007). These estimates are calculated assuming the ear canal is left intact and the OAE probe is sealed near the ear canal entrance.
| Species | EC length (mm) | Standing waves effects (kHz) |
|---|---|---|
| Human (adult) | 25–30 | ≥ 3.4–2.8 |
| Human (newborn) | 13–23 | ≥ 6.5–3.7 |
| Chinchilla | 30 | ≥ 2.8 |
| Cat | 15 | ≥ 5.6 |
| Ferret | 10–12 | ≥ 8.6–7.1 |
| Guinea pig | 9 | ≥ 9.5 |
| Gerbil | 4a | ≥ 21.3 |
| Mouse | 6 | ≥ 14.3 |
Length of the bony ear canal (i.e., excluding cartilaginous part).
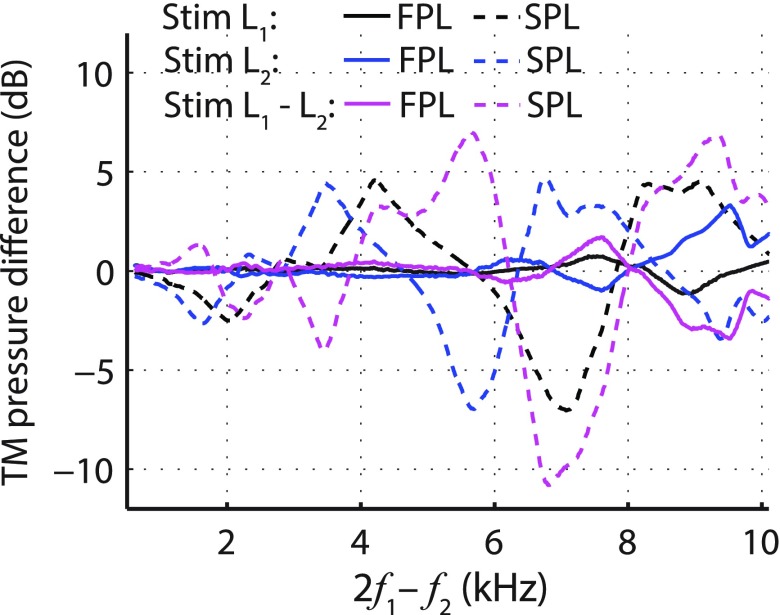
Figure 7 illustrates how the estimated levels of the two primary tones at the TM vary with probe insertion depth. The pressure at the TM was approximated by the sum of the magnitudes of the forward and reverse waves (Lewis et al., 2009). When using SPL-calibration (dashed lines), the greatest variation in stimulus pressures occurs for fDP > 3 kHz, which coincides with the region where the largest changes in DPOAE levels are noted for SPL-calibrated stimuli [Fig. 3(A), dashed black line]. In the individual data, DPOAE levels are often affected at even lower frequencies [e.g., fDP ∼ 2 kHz, Fig. 6(C)], but the sign of the shift varies across subjects and the changes tend to cancel in the mean [Fig. 3(A), dashed black line between 2 and 3 kHz]. These findings are similar to those of Scheperle et al. (2008) and Zebian et al. (2011b), who noted that when using SPL-calibrated stimuli DPOAE levels are most sensitive to probe insertion depth at fDP frequencies from ∼2 kHz to the highest frequencies tested (5 and 6.4 kHz, respectively). The shift in DPOAE levels correlates well with both the shift in the estimated L1 (average correlation coefficient of 0.6; SD 0.03; one-sample t-test p < 0.001) and the difference L1−L2 (0.46; 028; p < 0.03) but not with the shift in L2 (−0.1; 0.35; p > 0.05). This agrees with observations that DPOAE levels are more sensitive to changes in L1 than in L2 (Gaskill and Brown, 1990; Whitehead et al., 1995).
FIG. 7.
(Color online) Mean level differences (deep minus shallow) for estimates of the pressure at the TM obtained by summing the magnitudes of the forward and reverse pressure waves (Lewis et al., 2009). Measurements at the two insertion depths were made with stimuli calibrated using forward (FPL, solid line) and total (SPL, dashed line) pressure in five subjects. Line colors code TM level differences for different primaries: Black is the lower frequency primary tone (L1); blue is the higher frequency primary tone (L2); and magenta is the level difference (L1−L2). All data are plotted versus fDP to facilitate comparison with Fig. 3.
When using FPL-calibration, by contrast, the estimated primary tones at the TM vary little with insertion depth (Fig. 7, solid lines). Maximal changes in L2 of a few dB occur for fDP near 9–10 kHz (i.e., for f2 > 10 kHz), where the estimated ear-canal reflectance depends on insertion depth and sometimes takes on unphysical values (e.g., |R| > 1, see also Souza et al., 2014; Lewis and Easterday, 2016; Merchant et al., 2016). At these higher frequencies, FPL-calibration is presumably less accurate. Despite the near constancy of the primary tone levels at the TM, DPOAE levels change by as much as 10 dB with insertion depth (Fig. 3, dotted blue line), even at frequencies where no changes in the primaries are expected (e.g., fDP < 9 kHz). These results obtained with FPL calibration suggest that the DPOAE level changes arise through the effects of ear-canal acoustics on the emission itself.
The acoustics of the closed ear canal boost the total OAE pressure both at low frequencies and near the half-wave resonance frequencies, whose values depend on the length of the residual ear-canal space [i.e., on the probe insertion depth; see Fig. 4(C), black line]. However, when DPOAEs measured with FPL-calibrated stimuli are converted to emitted pressure (i.e., to OAEEPL), the emissions become independent of probe position across the whole frequency range tested (Fig. 3, solid red line). Changes in OAEEPL with probe insertion depth are comparable to test–retest changes measured after removing and refitting the probe in (almost) the same position (Fig. 3, gray line). During the probe refitting, we took care to match the fλ/2 values for the two measurements within 100 Hz, resulting in mean retest differences less than 2 dB. These changes are similar to the variability in DPOAE levels obtained in sequential, repeated measurements performed without removing the probe (Piłka et al., 2014). In addition, we tried to minimize possible DPOAE changes due to slow modulations in middle-ear static pressure or the cochlear processes involved in OAE generation (e.g., outer-hair-cell operating points) by making the required measurements in each subject during a relatively short period of time. However, small changes arising from effects unrelated to ear-canal acoustics cannot be excluded and would not be corrected by conversion to emitted pressure (see Sec. IV F).
In summary, the acoustics of the residual ear-canal space have their largest effects on stimulus pressures near fλ/4 and on OAE pressures near fλ/2 (and also at low-frequencies). Because they grow in a complicated, nonlinear way with stimulus level (e.g., Brass and Kemp, 1993; Dorn et al., 2001), OAEs cannot easily be corrected post hoc for ear-canal effects on stimulus calibration. For example, applying emitted-pressure corrections to OAEs measured using SPL-calibrated stimuli still yields emission measurements that depend on probe position (data not shown). In contrast, the effects of ear-canal acoustics on the OAEs themselves can be removed after the measurement via the conversion to emitted pressure [Figs. 5(A) and 5(C)].
B. OAE test repeatability and performance: Clinical implications
The sensitivity of OAEs for detecting changes in cochlear health in subjects exposed to noise, ototoxic drugs, or other harmful agents is limited by the test–retest repeatability of the OAE measurements (Konrad-Martin et al., 2012). Probe removal and refitting during repeated testing is known to increase the variability of serial OAE measurements (Zhao and Stephens, 1999; Beattie et al., 2003; Mills et al., 2007; Wagner et al., 2008; Keppler et al., 2010; Piłka et al., 2014). Piłka et al. (2014) demonstrated that probe refitting increases measurement variability at all frequencies, but effects are largest at fDP > 5 kHz, where mean DPOAE levels changed by 6–7 dB, compared with the ∼2 dB shifts observed at lower frequencies. The increased variability with probe refitting may reflect the contaminating influence of ear-canal standing waves on both the stimulus and the OAE pressures. At high frequencies, even small (2–3 mm) changes in probe position can result in 10–20 dB shifts in DPOAE levels when commonly used SPL-based calibration routines are employed [Fig. 6(A); Scheperle et al., 2008; Zebian et al., 2011b]. Thus, much of the substantial variability seen in serial DPOAE measurements (e.g., Dreisbach et al., 2006; Sockalingam et al., 2007) may result from mismatches in probe position across measurement sessions.
The effects of ear-canal acoustics on conventional OAE pressures may explain why the use of FPL-based rather than SPL-based calibrations provides, at best, only a moderate boost to DPOAE test performance in identifying impaired ears or predicting hearing thresholds (Burke et al., 2010; Rogers et al., 2010; Kirby et al., 2011). Because the conversion to OAEEPL largely eliminates standing-wave effects from DPOAE measurements, and thereby decreases spurious variability across repeated sessions, the use of emitted pressure (in combination with FPL-calibration) has the potential to improve the sensitivity of OAE measurements to changes in cochlear or middle-ear status. We expect the greatest improvements in applications, such as longitudinal monitoring, where probe refitting is unavoidable. Alternatively, close attention to maintaining the position of the probe relative to the TM (e.g., by matching values of fλ/2 across serial sessions) would improve the test–retest repeatability of OAEs. However, unlike the conversion to emitted pressure, simply matching values of fλ/2 across sessions provides no compensation for absolute OAE levels or phases (e.g., for comparisons across subjects).
C. Application to other OAE types
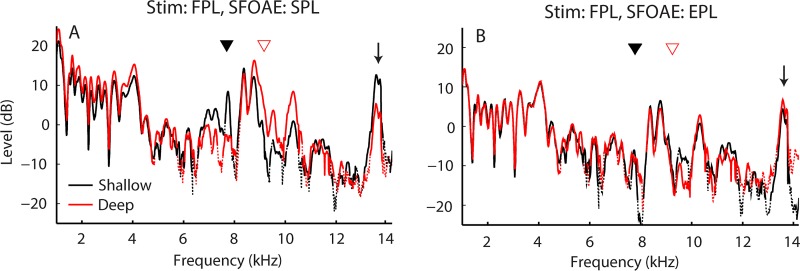
Although we focus here on the application of emitted pressure to DPOAE measurements, the conversion to emitted pressure can be applied to any type of OAE whenever the ear-canal and probe-source reflectances are known. Figure 8 shows an example of applying emitted pressure to SFOAEs.12 The SFOAEs were evoked using FPL-calibrated tones at two probe locations in the ear canal (black lines vs red lines). When expressed in the conventional way [OAESPL, Fig. 8(A)], the measurements show a dependence on insertion depth similar to that seen with DPOAEs (i.e., level shifts of 2–3 dB at low frequencies and ∼10 dB near fλ/2). In contrast, SFOAEs expressed as emitted pressure are nearly unaffected by probe position [Fig. 8(B)], even at frequencies above 10 kHz (see the arrow).
FIG. 8.
(Color online) SFOAEs measured in one ear at shallow (black line) and deep (red line) probe positions both before [(A), left] and after [(B), right] conversion to EPL. Data segments with SNR <6 dB are shown using dotted lines. SFOAEs were measured using the interleaved suppression method at frequencies swept from 1 to 16 kHz at 1 oct/s (Kalluri and Shera, 2013). Probe and suppressor levels were 37 and 57 dB FPL, respectively. Triangles mark the half-wave resonances and the arrow indicates the frequency of a strong spontaneous OAE. Data are from the same ear as the DPOAE data shown in Fig. 5.
Similarly, the use of emitted pressure appears equally effective at removing the dependence on ear-canal acoustics from transient-evoked otoacoustic emissions (TEOAEs), at least for the one subject tested so far (same as in Fig. 8, data not shown). For simplicity, we employed FPL-shaped clicks for the measurement of TEOAEs (Scheperle et al., 2011). However, the calibration of transient stimuli needs to be carefully considered based on the duration of the stimulus. For example, when the duration of the transient is comparable to or less than the round-trip ear-canal delay, calibration procedures based on the steady-state response, such as FPL, are likely inappropriate. Instead, calibrations that equalize the initial outgoing stimulus pressure (the “emitted stimulus”) may be the better choice (e.g., Goodman et al., 2009).
D. Effects of the OAE probe system
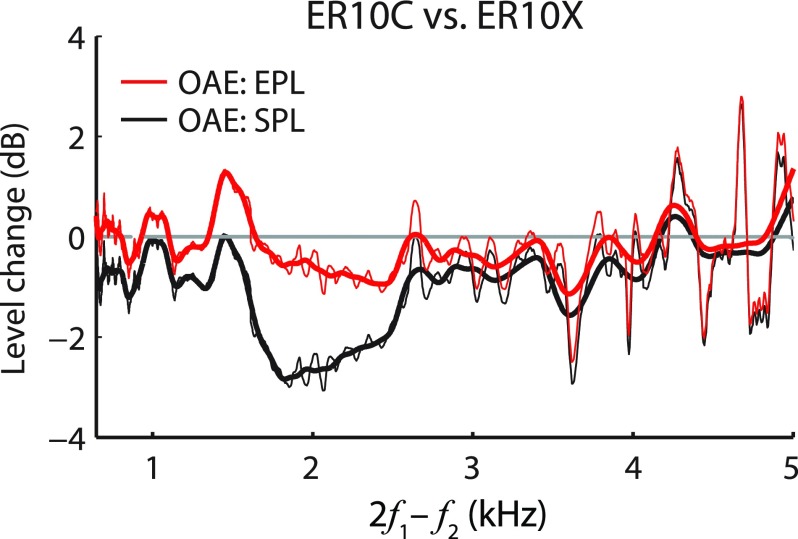
Studies by Thornton et al. (1994) and Mills et al. (2007) demonstrated large differences between OAEs measured with different commercially available probe systems. Many of the differences observed in these studies probably arose from the lack of compensation for the levels and/or spectral content of the stimuli produced by the two systems. However, theoretical studies indicate that the acoustic load presented by the probe system can alter the measured emissions (Matthews, 1983; Jurzitza and Hemmert, 1992), and experimental observations support that prediction (Zwicker, 1990; Nakajima et al., 1994; Withnell et al., 1998; Boul and Lineton, 2010). If the effects of probe impedance on measured OAE pressures are predominantly acoustic—that is, if the use of different probes does not significantly alter intracochlear emission generation (see Sec. IV F)—then the conversion to emitted pressure should compensate for them. To explore this, we measured DPOAEs using two different probe systems in the same subjects (see Fig. 9). The two probe systems (ER10X and ER10C) differ in their Thévenin-equivalent source impedances (by ±6 dB over the 0.5–8 kHz range). Both probes were inserted in the ear canal to similar depths (as judged by the value of fλ/2) and were calibrated using FPL. Differences in DPOAE levels measured with the two probes reached ∼3 dB near the DP frequencies of about 2 kHz (Fig. 9, black line), where the probe reflectances were most dissimilar (∼4 dB), but fell to less than 1 dB following the conversion to EPL (red line). Although limited, these data corroborate our expectation that the use of emitted pressure reduces the variability of OAEs measured using different probe systems.
FIG. 9.
(Color online) Level differences between DPOAEs measured using two different probe systems (ER10C and ER10X). Black lines show level differences expressed in SPL (black); red lines show level differences in EPL. The thick lines are smoothed versions of the thin lines. The measurements were made using FPL-calibrated stimuli and are shown only for f2 < 8 kHz to avoid contamination by system distortion in the ER10C probe (Richmond et al., 2011). The probes were inserted to similar depths in the ear canal as judged by the values of fλ/2 (7.7 kHz for the ER10C, 8.1 kHz for the ER10X).
E. Alternative methods for removing ear-canal acoustics from OAEs
With the goal of compensating both for the impedance of the sound system and for possible differences across animals, Fahey and Allen (1986) expressed DPOAEs measured in cats as Thévenin-equivalent OAE pressures at the probe microphone rather than as total pressures (OAESPL). The Thévenin-equivalent OAE pressure at the microphone (OAETh-mic) can be computed from the measured OAE pressure (OAESPL) using the following expression:13
| (3) |
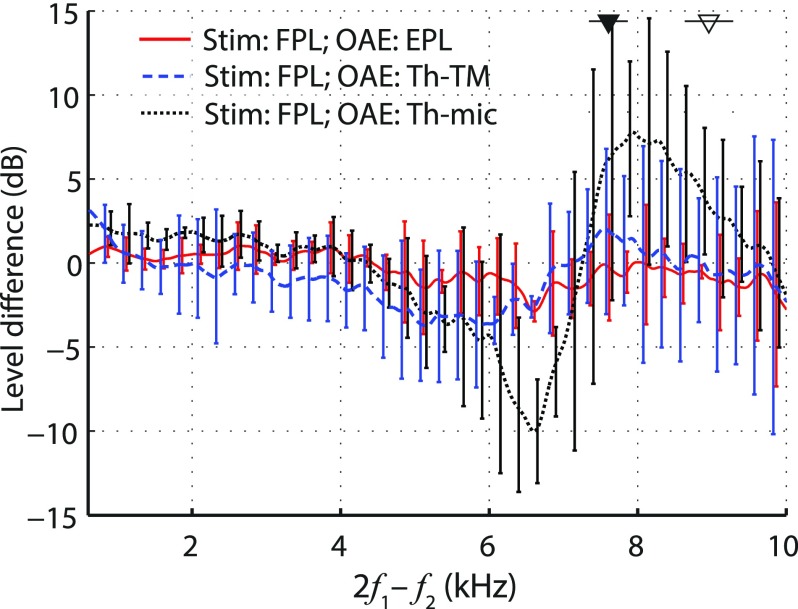
where R and are the ear-canal and probe source reflectances, respectively. Although expressing OAE pressures as Thévenin-equivalents at the microphone compensates for differences between OAE probes, it does not compensate for differences in ear-canal acoustics; the acoustics of the ear canal are lumped into the Thévenin source impedance of the preparation. When the microphone can be placed acoustically close to the TM—as in the measurements of Fahey and Allen (1986), where it was placed ∼4 mm from the cat TM—OAETh-mic provides a good alternative to OAESPL. However, OAETh-mic becomes problematic both in human ears, where probe placement close to the TM is not possible, and, more generally, whenever small changes in probe position produce large changes in ear-canal impedance due to standing waves (Rabinowitz, 1981; Voss and Allen, 1994). Indeed, Fig. 10 shows that OAETh-mic varies substantially with insertion depth in human ears (dotted black line).
FIG. 10.
(Color online) Mean differences (±1 SD) in measured DPOAE levels due to changes in probe insertion depth (deep minus shallow). The red line, taken from Fig. 3, shows the level difference expressed in EPL. The other two lines show level differences computed using DPOAEs expressed as Thévenin-equivalent DPOAE source pressures at either the microphone (black dotted line) or the TM (dashed blue line). Stimulus levels were set using FPL.
To compensate for ear-canal acoustics as well as OAE probe parameters, the Thévenin-equivalent OAE pressure needs to be computed at the plane of the TM instead of at the microphone inlet. Using the scattering matrix representation of the ear canal (see the Appendix) and the same reflectionless-duct approximation used to obtain Eq. (2), the Thévenin-equivalent OAE pressure at the TM (OAETh-TM) becomes
| (4) |
where T is the ear-canal transmission coefficient appearing in Eq. (2). OAETh-TM is related to the emitted pressure (OAEEPL) through the equation
| (5) |
Note that whereas OAEEPL depends on the characteristic impedance of the ear canal (i.e., on its cross-sectional area), OAETh-TM is entirely independent of the acoustic load presented to the TM by the ear canal and probe. In principle, therefore, OAETh-TM provides a better metric than OAEEPL for comparing OAEs across subjects, for whom ear-canal diameters vary. In our measurements, OAETh-TM did show the expected decrease in sensitivity to probe position (Fig. 10, dashed blue line) compared to OAESPL or OAETh-mic. In our (small) sample, however, OAETh-TM tended to perform worse than OAEEPL in the mid frequency range (solid red line). Surprisingly, we also found more variability in the ability of OAETh-TM to correct for ear-canal acoustics across subjects (see the size of the error bars), although both methods performed similarly in the test cavities (data not shown). Despite theoretical expectations, the slightly poorer performance of OAETh-TM relative to OAEEPL suggests that OAETh-TM is more susceptible to errors in determination of the in situ ear-canal and probe reflectances.
F. Limitations
The approximations used when deriving Eq. (2) for the total-to-emitted pressure conversion function represent the ear canal by a lossless, reflectionless tube with the same cross-sectional area at the two ends. In effect, Eq. (2) assumes that reflections and losses within the ear canal (e.g., due to reflections from the curved walls of the canal) can safely be ignored. Similar assumptions are employed when justifying the use of forward pressure [Eq. (1)]. Although we have generalized the EPL formula to the case where the ear canal can be modeled as an arbitrary two-port network (see the Appendix), determining the necessary two-port parameters in a subject's ear canal presents a challenge. In most subjects, the combination of forward-pressure calibration and conversion to emitted pressure using Eq. (2) largely eliminates the dependence of DPOAE measurements on probe position, suggesting that the approximations of the model have only a minor effect on the utility of the procedure.
In one subject, however, the conversion to EPL significantly reduced sensitivity to probe position but did not eliminate it: ∼10 dB level shifts remained at low frequencies. Interestingly, in this subject (033, whose measurements were excluded from the analysis due to poor SNR near fλ/2 at the deep probe placement), the increase in surge impedance between the shallow and deep probe placements was substantially larger than found in the other subjects. The large increase in surge impedance—by a factor of 2.5, compared to a mean of 1.2 (range 0.9–1.5) for the other 7 subjects—suggests a correspondingly large decrease in canal cross-sectional area (by ∼22.6 mm2) between the shallow and deep positions, consistent with an abrupt tapering of the ear canal near its entrance (e.g., Johansen, 1975; Stinson and Lawton, 1989; Egolf et al., 1993). We suspect that reflections from structures other than the TM (e.g., from the curved canal walls or rapid changes in area) contributed to the reflectance R since the shape of the “exposed” ear canal changed with the probe insertion depth (Stinson, 1990), in violation of the assumptions underlying Eqs. (1) and (2).
Our experience with subject 033, although perhaps an outlier, serves as a reminder that reliable application of forward and emitted pressure relies on robust methods for measuring reflectance and other parameters of ear-canal acoustics. Recent studies propose promising improvements (e.g., Lewis and Neely, 2015; Lewis and Easterday, 2016). In the meantime, problems such as those encountered in subject 033 might be reduced by monitoring (and minimizing) changes in ear-canal surge impedance across sessions. Deep probe placements (i.e., within the bony part of the ear canal) are recommended for routine measurements, since the residual ear-canal space then presumably best approximates a lossless, reflectionless tube, at least in adults.14
Other factors that can contribute to errors in the application of forward and emitted pressure include acoustic leaks and/or static pressurization of the residual ear-canal space. The criteria we adopted here to ensure a satisfactory probe seal were sensitive to leaks with effective diameters greater than about 0.5 mm (0.02 in Groon et al., 2015), and thus we cannot exclude the possibility of smaller leaks. On physical grounds, small leaks are especially likely at shallow probe placements; consistent with this, in all subjects the low-frequency absorbance decreased and the angle of the low-frequency admittance increased after moving the probe closer toward the TM. In the absence of leaks, moving the probe toward the TM can increase the static pressure in the residual ear-canal space, stiffening the TM and reducing middle-ear transmission at low frequencies (e.g., Hauser et al., 1993). Because the conversion to emitted pressure worked as intended in most subjects, largely eliminating the dependence of DPOAE levels on probe location in the ear canal, possible errors due to leaks or static pressure seem unlikely to have had a significant impact on our results.
Finally, the conversion to emitted (and/or Thévenin-equivalent) OAE pressure can compensate for ear-canal and probe acoustics only to the extent that the intracochlear mechanisms that generate OAEs are themselves independent of the ear-canal load. For heuristic reasons, we equated the emitted OAE pressure with the OAE that would be measured at the TM if the ear-canal were an infinite (anechoic) tube with the same cross-sectional area as the canal. But this description may not be entirely correct. Because of cochlear nonlinearities, the ear-canal load can affect the process of emission generation and, as a result, the effects of the load cannot be entirely removed by applying a simple, multiplicative conversion function. For example, spontaneous otoacoustic emission (SOAE) frequencies, and not simply their amplitudes, are known to depend slightly on the ear-canal load (e.g., Kemp, 1981; Schloth, 1983; Hauser et al., 1993; de Kleine et al., 2000; Boul and Lineton, 2010), a consequence of the dependence of SOAE generation on the effective reflection coefficient at the stapes (Shera, 2003). As our success at representing OAE measurements using emitted pressure illustrates, however, such effects are expected to be negligible in most applications.
G. Summary
In summary, we have shown that
-
(1)
Conventional DPOAEs evoked using stimuli calibrated for total pressure depend sensitively on the position of the measurement probe in the ear canal, especially at emission frequencies greater than 3–4 kHz. The largest changes with probe position occur near the half-wave resonant frequencies of the ear canal (6–10 kHz), where changes in the DPOAE level can be as much as 20 dB and changes in group delay can approach 1 ms.
-
(2)
Stimulus calibration procedures that compensate for ear-canal standing waves (e.g., by employing forward rather than total pressure) reduce the sensitivity to probe position. However, at emission frequencies greater than 5–6 kHz, DPOAE levels measured at different probe positions can still vary by up to 10 dB.
-
(3)
Converting conventional DPOAEs to emitted pressure, when combined with forward-pressure calibration of the evoking stimuli, reduces the dependence on probe position to the test–retest variability across the entire frequency range. Together, FPL-based stimulus calibration and post hoc conversion to EPL effectively remove the confounding effects of ear-canal acoustics on DPOAE measurements. Similar results apply to other types of OAEs.
ACKNOWLEDGMENTS
Supported by NIH Grant No. R01 DC003687 (to C.A.S.). Portions of this report were presented at the 171st ASA Meeting, Salt Lake City, UT. We thank Stephen Neely and Jonathan Siegel for many helpful discussions and Carolina Abdala and the anonymous reviewers for thoughtful comments on the manuscript.
APPENDIX: EMITTED AND THÉVENIN-EQUIVALENT OAE PRESSURES
In this appendix we use a scattering-matrix formalism to derive expressions for both the emitted pressure and the Thévenin-equivalent OAE pressure in a one-dimensional duct (or transmission line) of variable cross-sectional area, adopted as a model of the residual ear-canal space. We obtain the approximate formulas used in the text by assuming that the duct is internally “reflectionless” (i.e., that reflections may occur at the ends of the duct due to the boundary or loading conditions applied there, but not within the duct itself).
A. Emitted pressure
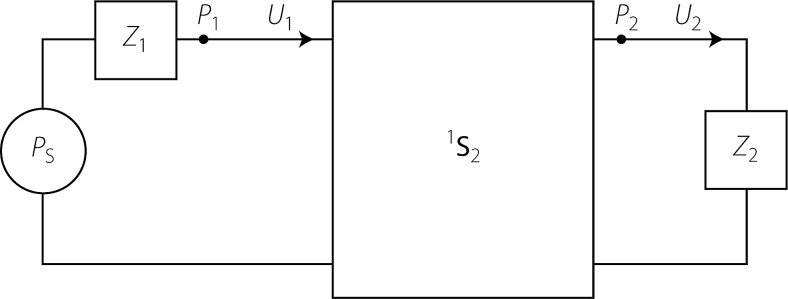
Consider the general two-port system shown in Fig. 11. The pressures , , and are total pressures. The volume velocities and are defined positive out of the source (i.e., in this case, to the right; see arrows). Let the characteristic impedance at port be denoted , and define right- and leftward traveling waves ( and , respectively) using the equations . The corresponding scattering matrix
| (A1) |
is then defined by the equation
| (A2) |
At each port, the equivalent load reflectances are given by
| (A3) |
Note that reciprocity requires that
| (A4) |
These formulas are reviewed in Shera and Zweig (1992, Appendix A).
FIG. 11.
Generic two-port represented by the scattering matrix 1S2. The two-port is terminated with load impedances Z1 and Z2 and driven by a Thévenin source pressure, PS.
To derive the formula for emitted pressure, we first find in terms of (i.e., the total pressure at port 2 in terms of the outgoing pressure at port 1). From the scattering matrix
| (A5) |
Since we have
| (A6) |
Solving this for gives
| (A7) |
Thus
| (A8) |
As the next step of the derivation, we find (i.e., the “total” outgoing wave at port 1) in terms of , the “initial” outgoing wave (or emitted pressure). The formula is
| (A9) |
where is the total reflectance of the two-port measured looking from port 1 into port 2. According to Shera and Zweig [1992, Eq. (A17)], the formula for the net reflectance of the two-port terminated in the one-port reflectance is
| (A10) |
Note that if either or is zero, then , as expected. Combining Eqs. (A8) and (A9) gives in terms of ,
| (A11) |
Substituting in the value of and solving for the initial wave in terms of the total pressure yields
| (A12) |
For future convenience it proves helpful to rewrite Eq. (A12) in terms of the net reflectance seen looking toward port 1 from port 2. By analogy with Eq. (A10) this reflectance is
| (A13) |
Solving Eq. (A13) for and using the result in Eq. (A12) yields our expression for the emitted pressure
| (A14) |
It may sometimes make sense to compute the initial outgoing wave as it appears at port 2, rather than at port 1. The two pressures are related by
1. A special case
For the results presented in the main text, we simplify Eq. (A14) for the emitted pressure by assuming that the residual ear-canal space can be well approximated by a reflectionless duct or transmission line. In this special case, the scattering matrix has the form
| (A15) |
where Equation (A14) then becomes
| (A16) |
An approximate expression for valid in a one-dimensional duct of slowly varying cross-sectional area can be found by using the Wentzel-Kramers-Brillouin approximation to solve the Webster horn equation. The result is
| (A17) |
where k is the wavenumber and L is the length of the duct [see Shera and Zweig, 1992, Eq. (C5)]. For the computations in the text, we ignore possible variations in (i.e., in the cross-sectional area) along the canal and adopt the further simplification that , where ω is the angular frequency and τ is the one-way transmission delay. After translation using the notation key given in Sec. C below, Eq. (A16) appears in the main text as Eq. (2) for the emitted pressure (OAEEPL).
B. Thévenin-equivalent OAE pressure
To find the Thévenin-equivalent emission (or source) pressure, , as a function of the measured pressure , we use the fact that the initial outgoing pressure wave equals the total pressure measured at port 1 when the source is loaded by an infinite (anechoic) tube of characteristic impedance . By the voltage-divider equation
| (A18) |
Solving for and expressing the result in terms of gives
| (A19) |
Substituting values of and from Eqs. (A13) and (A14) yields
| (A20) |
In a reflectionless tube (, this reduces to
| (A21) |
Note that , by reciprocity [Eq. (A4)]. After translation using the key below, Eq. (A21) appears in the main text as Eq. (5) for the Thévenin OAE source pressure at the TM (OAETh-TM).
C. Translation to ear-canal measurement of OAEs
The following notational translations are useful when applying Eqs. (A14) or (A16) to find the emitted pressure (“initial outgoing OAE”) at the TM and/or when applying Eqs. (A20) or (A21) to find the Thévenin-equivalent OAE pressure at the TM:
Port 1 → TM
Port 2 → OAE probe microphone
→ scattering matrix of ear-canal space
→ emitted OAE pressure at the TM (OAEEPL)
→ Thévenin-equivalent OAE pressure at the TM (OAETh-TM)
→ total OAE pressure measured at the microphone
→ load reflectance measured at the microphone
→ Thévenin source reflectance of the OAE probe
→ , where is the one-way canal delay
Footnotes
The reflection coefficients at both closed ends (near the ear tip and TM) are typically high (∼0.9 and ∼0.9–0.6, respectively, e.g., Souza et al., 2014; Zebian et al., 2011a).
Due to the curvature and more complex geometry of the human ear canal, higher-order nulls can be slightly offset from exact odd multiples of fλ/4 (Stinson, 1990).
Because the largest DPOAE components originate close to the f2 place in the cochlea, DPOAEs are commonly reported and plotted versus f2 rather than versus fDP (e.g., 2f1−f2). Here, however, we are most concerned with the effects of ear-canal acoustics on DPOAEs, and it is therefore more informative to use the emission frequency itself. As in all studies referenced here, the f2/f1 ratio was ∼1.2, and the reader can easily convert fDP to the corresponding value of f2 if preferred.
At low frequencies the impedance of the ear canal can be approximated by the impedance of a closed tube, such as Z , where z0 is the characteristic impedance of the tube, k is the wave number, and L is the length of the tube. Because of the inverse proportionality between Z and L, the OAE pressure increases when the OAE probe is moved toward the TM.
As defined by Eqs. (1) and (2), the forward and emitted pressures refer to sound emitted by two different sources, specifically by the OAE-probe (FPL) and by the TM (EPL), respectively. If the terms were applied to sound produced by a single source, then the emitted pressure would be the initial outgoing wave, whereas the forward pressure would be the sum of all outgoing waves (i.e., the initial outgoing pressure wave as well as all subsequent forward going reflections and re-reflections). Emitted and forward pressure are equivalent in an infinite, reflectionless tube.
The one-way ear canal delay can also be estimated from the time-domain representation of the ear-canal reflectance (Rasetshwane and Neely, 2011).
In pilot experiments, we found no significant differences between DPOAEs measured using either (1) the three concurrent primary sweeps described in the text; (2) a single sweep covering the entire frequency range at the same rate; or (3) discrete primary tones stepped with a resolution of 200 points/octave. Thus, the frequency separation we employed between the concurrently presented primary pairs (∼1.4 octaves) appears sufficient to prevent mutual suppression and/or other significant interaction effects on the measured DPOAE.
The goal was to keep constant the number of SFOAE group-delay periods in each analysis window across the frequency range. A power-law fit to human SFOAE group delay (NSFOAE, in stimulus periods) was used as a starting point, where NSFOAE = βfα with β = 11 and α = 0.37 (see Shera et al., 2002). The window length was adjusted with fDP (kHz) such as twin = log2[(N/β + fDPα)(1/α)/fDP]/b where N represents the desired change in OAE group delay (in periods) within the analysis window and b is the sweep rate (in octaves/millisecond). For N = 1/6, twin decreased from 70.7 ms (equivalent to bandwidth, twinb, of 0.06 octaves) to 25.1 ms (0.025 octaves). These parameters provided good estimates of DPOAE fine-structure (as assessed by comparing them to DPOAEs measured using discrete frequency steps with high resolution) while maintaining relatively low levels of noise. These variations in window duration over the range of measured fDP frequencies agrees well with those proposed by Abdala et al. (2015; inset in Fig. 11).
Because both the amplitudes and phases of the primaries were calibrated in situ, the phase 2ϕ1−ϕ2 was nearly constant across frequency, and the phase correction was therefore not essential. We included it here to emphasize the importance of correcting for the DPOAE phase using the phase of 2ϕ1−ϕ2 evaluated for primaries expressed in appropriate units (FPL and SPL).
Averaged across subjects and frequencies, the mean difference between the magnitude of conversion function derived from each of the two earphones was -0.065 dB (SD = 0.414 dB) and -0.032 dB (0.451 dB) for the shallow and deep probe placements, respectively.
It was not possible to visually confirm the exact placement of the ER7C probe tip relative to the speaker foam tip in the anechoic tube. Thus, to avoid a bias in a single direction, we reinserted both ER7C and speaker tips before each measurement.
In the case of evoked OAEs, taking full advantage of the conversion to emitted pressure requires using a stimulus calibration method that reduces sensitivity to standing waves, such as forward-pressure calibration (or see Souza et al., 2014, for alternative methods). In this respect, the most straightforward application might therefore be to SOAEs—with SOAEs there is no stimulus and thus no need to worry about standing-wave effects on the evoking sound. Thus, SOAEs might have advantages over evoked OAEs for validating the use of emitted pressure by varying probe position. However, in normal human subjects, SOAEs are most abundant at frequencies less than 5 kHz (e.g., Talmadge et al., 1993), and thus most SOAEs occur at frequencies below the typical value of fλ/2 where changes in OAE pressures with probe position are relatively small [∼2–3 dB, see Fig. 3(A) dotted blue line].
Fahey and Allen (1986) define the OAE Thévenin-equivalent pressure as . We rewrite it using reflection coefficients rather than impedances for consistency with other equations in the text.
In newborns, where the ear canal remains unossified (McLellan and Webb, 1957), sound absorption may be higher even for deep probe placements.
References
- 1. Abdala, C. , Luo, P. , and Shera, C. A. (2015). “ Optimizing swept-tone protocols for recording distortion-product otoacoustic emissions in adults and newborns,” J. Acoust. Soc. Am. 138, 3785–3799. 10.1121/1.4937611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Ahmed, H. O. , Dennis, J. H. , Badran, O. , Ismail, M. , Ballal, S. G. , Ashoor, A. , and Jerwood, D. (2001). “ High-frequency (10–18 kHz) hearing thresholds: Reliability, and effects of age and occupational noise exposure,” Occup. Med. 51, 245–258. 10.1093/occmed/51.4.245 [DOI] [PubMed] [Google Scholar]
- 3. Beattie, R. C. , Kenworthy, O. T. , and Luna, C. A. (2003). “ Immediate and short-term reliability of distortion-product otoacoustic emissions,” Int. J. Audiol. 42, 348–354. 10.3109/14992020309101328 [DOI] [PubMed] [Google Scholar]
- 4. Boul, A. , and Lineton, B. (2010). “ Spontaneous otoacoustic emissions measured using an open ear-canal recording technique,” Hear. Res. 269, 112–121. 10.1016/j.heares.2010.06.020 [DOI] [PubMed] [Google Scholar]
- 5. Brass, D. , and Kemp, D. T. (1993). “ Suppression of stimulus frequency otoacoustic emissions,” J. Acoust. Soc. Am. 93, 920–939. 10.1121/1.405453 [DOI] [PubMed] [Google Scholar]
- 6. Burke, S. R. , Rogers, A. R. , Neely, S. T. , Kopun, J. G. , Tan, H. , and Gorga, M. P. (2010). “ Influence of calibration method on distortion-product otoacoustic emission measurements: I. Test performance,” Ear Hear. 31, 533–545. 10.1097/AUD.0b013e3181d86b3d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Campbell, K. (2004). “Audiologic monitoring for ototoxicity,” in Ototoxicity, edited by Roland P. and Rutka J. ( BC Decker, New York: ), pp. 153–160. [Google Scholar]
- 8. Chen, S. , Zhang, H. , Wang, L. , and Li, G. (2014). “ An in-situ calibration method and the effects on stimulus frequency otoacoustic emissions,” Biomed. Eng. Online 13, 95–111. 10.1186/1475-925X-13-95 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. de Kleine, E. , Wit, H. P. , van Dijk, P. , and Avan, P. (2000). “ The behavior of spontaneous otoacoustic emissions during and after postural changes,” J. Acoust. Soc. Am. 107, 3308–3316. 10.1121/1.429403 [DOI] [PubMed] [Google Scholar]
- 10. Dorn, P. A. , Konrad-Martin, D. , Neely, S. T. , Keefe, D. H. , Cyr, E. , and Gorga, M. P. (2001). “ Distortion product otoacoustic emission input/output functions in normal-hearing and hearing-impaired human ears,” J. Acoust. Soc. Am. 110, 3119–3131. 10.1121/1.1417524 [DOI] [PubMed] [Google Scholar]
- 11. Dreisbach, L. E. , Long, K. M. , and Lees, S. E. (2006). “ Repeatability of high-frequency distortion-product otoacoustic emissions in normal-hearing adults,” Ear Hear. 27, 466–479. 10.1097/01.aud.0000233892.37803.1a [DOI] [PubMed] [Google Scholar]
- 12. Egolf, D. P. , Nelson, D. K. , Howell, H. C. III , and Larson, V. D. (1993). “ Quantifying ear-canal geometry with multiple computer-assisted tomographic scans,” J. Acoust. Soc. Am. 93, 2809–2819. 10.1121/1.405802 [DOI] [PubMed] [Google Scholar]
- 13. Fahey, P. , and Allen, J. (1986). “Characterization of cubic intermodulation distortion products in the cat external auditory meatus,” in Peripheral Auditory Mechanisms, edited by Allen J. B., Hall J. L., Hubbard A., Neely S. T., and Tubis A. ( Springer, New York: ), pp. 314–321. [Google Scholar]
- 14. Gaskill, S. A. , and Brown, A. M. (1990). “ The behavior of the acoustic distortion product, 2f1−f2, from the human ear and its relation to auditory sensitivity,” J. Acoust. Soc. Am. 88, 821–839. 10.1121/1.399732 [DOI] [PubMed] [Google Scholar]
- 15. Goodman, S. S. , Fitzpatrick, D. F. , Ellison, J. C. , Jesteadt, W. , and Keefe, D. H. (2009). “ High-frequency click-evoked otoacoustic emissions and behavioral thresholds in humans,” J. Acoust. Soc. Am. 125, 1014–1032. 10.1121/1.3056566 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Groon, K. A. , Rasetshwane, D. M. , Kopun, J. G. , Gorga, M. P. , and Neely, S. T. (2015). “ Air-leak effects on ear-canal acoustic absorbance,” Ear Hear. 36, 155–163. 10.1097/AUD.0000000000000077 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Hauser, R. , Probst, R. , and Harris, F. P. (1993). “ Effects of atmospheric pressure variation on spontaneous, transiently evoked, and distortion product otoacoustic emissions in normal human ears,” Hear. Res. 69, 133–145. 10.1016/0378-5955(93)90101-6 [DOI] [PubMed] [Google Scholar]
- 18. Johansen, P. A. (1975). “ Measurement of the human ear canal,” Acustica 33, 349–351. [Google Scholar]
- 19. Jurzitza, D. , and Hemmert, W. (1992). “ Quantitative measurements of simultaneous evoked otoacoustic emissions,” Acoustica 77, 93–99. [Google Scholar]
- 20. Kalluri, R. , and Shera, C. A. (2013). “ Measuring stimulus-frequency otoacoustic emissions using swept tones,” J. Acoust. Soc. Am. 134, 356–368. 10.1121/1.4807505 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Keefe, D. H. , Bulen, J. C. , Arehart, K. H. , and Burns, E. M. (1993). “ Ear-canal impedance and reflection coefficient in human infants and adults,” J. Acoust. Soc. Am. 94, 2617–2638. 10.1121/1.407347 [DOI] [PubMed] [Google Scholar]
- 22. Kemp, D. (1981). “Physiologically active cochlear micromechanics—one source of tinnitus,” in Tinnitus, edited by Evered D. and Lawrenson G. ( Pitman, London: ), pp. 55–81. [DOI] [PubMed] [Google Scholar]
- 23. Keppler, H. , Dhooge, I. , Maes, L. , D'Haenens, W. , Bockstael, A. , Philips, B. , Swinnen, F. , and Vinck, B. (2010). “ Transient-evoked and distortion product otoacoustic emissions: A short-term test-retest reliability study,” Int. J. Audiol. 49, 99–109. 10.3109/14992020903300431 [DOI] [PubMed] [Google Scholar]
- 24. Kirby, B. J. , Kopun, J. G. , Tan, H. , Neely, S. T. , and Gorga, M. P. (2011). “ Do ‘optimal’ conditions improve distortion product otoacoustic emission test performance?,” Ear Hear. 32, 230–237. 10.1097/AUD.0b013e3181fa5da2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Konrad-Martin, D. , Poling, G. L. , Dreisbach, L. E. , Reavis, K. M. , McMillan, G. P. , Lapsley Miller, J. A. , and Marshall, L. (2016). “ Serial monitoring of otoacoustic emissions in clinical trials,” Otol. Neurotol. 37, e286–e294. 10.1097/MAO.0000000000001134 [DOI] [PubMed] [Google Scholar]
- 26. Konrad-Martin, D. , Reavis, K. M. , McMillan, G. P. , and Dille, M. F. (2012). “ Multivariate DPOAE metrics for identifying changes in hearing: Perspectives from ototoxicity monitoring,” Int. J. Audiol. 51(1), S51–S62. 10.3109/14992027.2011.635713 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Lapsley Miller, J. A. , and Marshall, L. (2007). “Otoacoustic emissions as a preclinical measure of noise-induced hearing loss and susceptibility to noise-induced hearing loss,” in Otoacoustic Emissions: Clinical Applications, 3rd ed., edited by Robinette M. S. and Glattke T. J. ( Thieme, New York: ), pp. 321–341. [Google Scholar]
- 28. Lawton, B. W. , and Stinson, M. R. (1986). “ Standing wave patterns in the human ear canal used for estimation of acoustic energy reflectance at the eardrum,” J. Acoust. Soc. Am. 79, 1003–1009. 10.1121/1.393372 [DOI] [PubMed] [Google Scholar]
- 29. Lewis, J. D. , and Easterday, M. (2016). “ Contributions to high-frequency reflectance from the change in diameter between sound-delivery tube and ear canal,” J. Acoust. Soc. Am. 139, 1996. 10.1121/1.4949852 [DOI] [Google Scholar]
- 30. Lewis, J. D. , McCreery, R. W. , Neely, S. T. , and Stelmachowicz, P. G. (2009). “ Comparison of in-situ calibration methods for quantifying input to the middle ear,” J. Acoust. Soc. Am. 126, 3114–3124. 10.1121/1.3243310 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Lewis, J. D. , and Neely, S. T. (2015). “ Non-invasive estimation of middle-ear input impedance and efficiency,” J. Acoust. Soc. Am. 138, 977–993. 10.1121/1.4927408 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Long, G. R. , Talmadge, C. L. , and Lee, J. (2008). “ Measuring distortion product otoacoustic emissions using continuously sweeping primaries,” J. Acoust. Soc. Am. 124, 1613–1626. 10.1121/1.2949505 [DOI] [PubMed] [Google Scholar]
- 33. Marshall, L. , Lapsley Miller, J. A. , Heller, L. M. , Wolgemuth, K. S. , Hughes, L. M. , Smith, S. D. , and Kopke, R. D. (2009). “ Detecting incipient inner-ear damage from impulse noise with otoacoustic emissions,” J. Acoust. Soc. Am. 125, 995–1013. 10.1121/1.3050304 [DOI] [PubMed] [Google Scholar]
- 34. Matthews, J. W. (1983). “Modeling reverse middle ear transmission of acoustic distortion signals,” in Mechanics of Hearing: Proceedings of the IUTAM/ICA Symposium, edited by Boer E. and Viergever M. A., Delft University of Technology, The Netherlands (July 13–15). [Google Scholar]
- 35. McLellan, M. S. , and Webb, C. H. (1957). “ Ear studies in the newborn infant: Natural appearance and incidence of obscuring by vernix, cleansing of vernix, and description of drum and canal after cleansing,” J. Pediatr. 51, 672–677. 10.1016/S0022-3476(57)80102-4 [DOI] [PubMed] [Google Scholar]
- 36. Merchant, G. R. , Merchant, S. N. , Rosowski, J. J. , and Nakajima, H. H. (2016). “ Controlled exploration of the effects of conductive hearing loss on wideband acoustic immittance in human cadaveric preparations,” Hear. Res. 341, 19–30. 10.1016/j.heares.2016.07.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Mills, D. M. , Feeney, M. P. , Drake, E. J. , Folsom, R. C. , Sheppard, L. , and Seixas, N. S. (2007). “ Developing standards for distortion product otoacoustic emission measurements,” J. Acoust. Soc. Am. 122, 2203–2214. 10.1121/1.2770543 [DOI] [PubMed] [Google Scholar]
- 38. Nakajima, H. H. , Olson, E. S. , Mountain, D. C. , and Hubbard, A. E. (1994). “ Electrically evoked otoacoustic emissions from the apical turns of the gerbil cochlea,” J. Acoust. Soc. Am. 96, 786–794. 10.1121/1.410316 [DOI] [PubMed] [Google Scholar]
- 39. Piłka, E. , Jędrzejczak, W. W. , Trzaskowski, B. , and Skarżyński, H. (2014). “ Variability of distortion product otoacoustic emissions at 10, 12 and 16 kHz: A preliminary study,” J. Hear. Sci. 4(4), 59–64. [Google Scholar]
- 40. Poling, G. L. , Siegel, J. H. , Lee, J. , and Dhar, S. (2014). “ Characteristics of the 2f1−f2 distortion product otoacoustic emission in a normal hearing population,” J. Acoust. Soc. Am. 135, 287–299. 10.1121/1.4845415 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Qi, L. , Liu, H. , Lutfy, J. , Funnell, W. R. , and Daniel, S. J. (2006). “ A nonlinear finite-element model of the newborn ear canal,” J. Acoust. Soc. Am. 120, 3789–3798. 10.1121/1.2363944 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Rabinowitz, W. M. (1981). “ Measurement of the acoustic input immittance of the human ear,” J. Acoust. Soc. Am. 70, 1025–1035. 10.1121/1.386953 [DOI] [PubMed] [Google Scholar]
- 42. Rao, A. , and Long, G. R. (2011). “ Effects of aspirin on distortion product fine structure: Interpreted by the two-source model for distortion product otoacoustic emissions generation,” J. Acoust. Soc. Am. 129, 792–800. 10.1121/1.3523308 [DOI] [PubMed] [Google Scholar]
- 43. Rasetshwane, D. M. , and Neely, S. T. (2011). “ Inverse solution of ear-canal area function from reflectance,” J. Acoust. Soc. Am. 130, 3873–3881. 10.1121/1.3654019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Ravicz, M. E. , Olson, E. S. , and Rosowski, J. (2007). “ Sound pressure distribution and power flow within the gerbil ear canal from 100 Hz to 80 kHz,” J. Acoust. Soc. Am. 122, 2154–2173. 10.1121/1.2769625 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Richmond, S. A. , Kopun, J. G. , Neely, S. T. , Tan, H. , and Gorga, M. P. (2011). “ Distribution of standing-wave errors in real-ear sound-level measurements,” J. Acoust. Soc. Am. 129, 3134–3140. 10.1121/1.3569726 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Rogers, A. R. , Burke, S. R. , Kopun, J. G. , Tan, H. , Neely, S. T. , and Gorga, M. P. (2010). “ Influence of calibration method on distortion-product otoacoustic emission measurements: II. Threshold prediction,” Ear Hear. 31, 546–554. 10.1097/AUD.0b013e3181d86b59 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Rosowski, J. (1994). “ Outer and middle ear,” in Comparative Hearing: Mammals, edited by Popper A. N. and Fay R. R. (Springer, Verlag: ), pp. 172–248. [Google Scholar]
- 46. Rosowski, J. J. , Stenfelt, S. , and Lilly, D. (2013). “ An overview of wideband immittance measurements techniques and terminology: You say absorbance, I say reflectance,” Ear Hear. 34(1), 9S–16S. 10.1097/AUD.0b013e31829d5a14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Scheperle, R. A. , Goodman, S. S. , and Neely, S. T. (2011). “ Further assessment of forward pressure level for in situ calibration,” J. Acoust. Soc. Am. 130, 3882–3892. 10.1121/1.3655878 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Scheperle, R. A. , Neely, S. T. , Kopun, J. G. , and Gorga, M. P. (2008). “ Influence of in situ, sound-level calibration on distortion-product otoacoustic emission variability,” J. Acoust. Soc. Am. 124, 288–300. 10.1121/1.2931953 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Schloth, E. (1983). “ Relation between spectral composition of spontaneous otoacoustic emissions and fine-structure of threshold in quiet,” Acustica 53, 250–256. [Google Scholar]
- 50. Shera, C. A. (2003). “ Mammalian spontaneous otoacoustic emissions are amplitude-stabilized cochlear standing waves,” J. Acoust. Soc. Am. 114, 244–262. 10.1121/1.1575750 [DOI] [PubMed] [Google Scholar]
- 51. Shera, C. A. , and Guinan, J. J., Jr. (1999). “ Evoked otoacoustic emissions arise by two fundamentally different mechanisms: A taxonomy for mammalian OAEs,” J. Acoust. Soc. Am. 105, 782–798. 10.1121/1.426948 [DOI] [PubMed] [Google Scholar]
- 52. Shera, C. A. , Guinan, J. J., Jr. , and Oxenham, A. J. (2002). “ Revised estimates of human cochlear tuning from otoacoustic and behavioral measurements,” Proc. Natl. Acad. Sci. U.S.A. 99, 3318–3323. 10.1073/pnas.032675099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Shera, C. A. , and Zweig, G. (1992). “ Analyzing reverse middle-ear transmission: Noninvasive Gedanken experiments,” J. Acoust. Soc. Am. 92, 1371–1381. 10.1121/1.403930 [DOI] [PubMed] [Google Scholar]
- 54. Siegel, J. H. (1994). “ Ear-canal standing waves and high-frequency sound calibration using otoacoustic emission probes,” J. Acoust. Soc. Am. 95, 2589–2597. 10.1121/1.409829 [DOI] [Google Scholar]
- 55. Siegel, J. H. (2007). “Calibration of otoacoustic emission probes,” in Otoacoustic Emissions: Clinical Applications, 3rd ed., edited by Robinette M. S. and Glattke T. J. ( Thieme, New York: ), pp. 403–429. [Google Scholar]
- 56. Siegel, J. H. , and Hirohata, E. T. (1994). “ Sound calibration and distortion product otoacoustic emissions at high frequencies,” Hear Res. 80, 146–152. 10.1016/0378-5955(94)90106-6 [DOI] [PubMed] [Google Scholar]
- 57. Sockalingam, R. , Lee Choi, J. , Choi, D. , and Kei, J. (2007). “ Test-retest reliability of distortion-product otoacoustic emissions in children with normal hearing: A preliminary study,” Int. J. Audiol. 46, 351–354. 10.1080/14992020701311168 [DOI] [PubMed] [Google Scholar]
- 58. Souza, N. N. , Dhar, S. , Neely, S. T. , and Siegel, J. H. (2014). “ Comparison of nine methods to estimate ear-canal stimulus levels,” J. Acoust. Soc. Am. 136, 1768–1787. 10.1121/1.4894787 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Stinson, M. R. (1990). “ Revision of estimates of acoustic energy reflectance at the human eardrum,” J. Acoust. Soc. Am. 88, 1773–1778. 10.1121/1.400198 [DOI] [PubMed] [Google Scholar]
- 60. Stinson, M. R. , and Lawton, B. W. (1989). “ Specification of the geometry of the human ear canal for the prediction of sound-pressure level distribution,” J. Acoust. Soc. Am. 85, 2492–2503. 10.1121/1.397744 [DOI] [PubMed] [Google Scholar]
- 61. Talmadge, C. L. , Long, G. R. , Murphy, W. J. , and Tubis, A. (1993). “ New off-line method for detecting spontaneous otoacoustic emissions in human subjects,” Hear. Res. 71, 170–182. 10.1016/0378-5955(93)90032-V [DOI] [PubMed] [Google Scholar]
- 62. Thornton, A. R. , Kimm, L. , Kennedy, C. R. , and Cafarelli-Dees, D. (1994). “ A comparison of neonatal evoked otoacoustic emissions obtained using two types of apparatus,” Br. J. Audiol. 28, 99–109. 10.3109/03005369409077920 [DOI] [PubMed] [Google Scholar]
- 63. Voss, S. E. , and Allen, J. B. (1994). “ Measurement of acoustic impedance and reflectance in the human ear canal,” J. Acoust. Soc. Am. 95, 372–384. 10.1121/1.408329 [DOI] [PubMed] [Google Scholar]
- 64. Wagner, W. , Heppelmann, G. , Vonthein, R. , and Zenner, H. P. (2008). “ Test-retest repeatability of distortion product otoacoustic emissions,” Ear. Hear. 29, 378–391. 10.1097/AUD.0b013e31816906e7 [DOI] [PubMed] [Google Scholar]
- 65. Whitehead, M. L. , Stagner, B. B. , Lonsbury-Martin, B. L. , and Martin, G. K. (1995). “ Effects of ear-canal standing waves on measurements of distortion-product otoacoustic emissions,” J. Acoust. Soc. Am. 98, 3200–3214. 10.1121/1.413810 [DOI] [PubMed] [Google Scholar]
- 66. Whitehead, M. L. , Stagner, B. B. , Martin, G. K. , and Lonsbury-Martin, B. L. (1996). “ Visualization of the onset of distortion-product otoacoustic emissions, and measurement of their latency,” J. Acoust. Soc. Am. 100, 1663–1679. 10.1121/1.416065 [DOI] [PubMed] [Google Scholar]
- 67. Withnell, R. H. , Kirk, D. L. , and Yates, G. K. (1998). “ Otoacoustic emissions measured with a physically open recording system,” J. Acoust. Soc. Am. 104, 350–355. 10.1121/1.423292 [DOI] [PubMed] [Google Scholar]
- 68. Zebian, M. , Fedtke, T. , and Hensel, J. (2011a). “ Otoacoustic emission retrograde standing waves caused by eartip foams,” Appl. Acoust. 72, 470–476. 10.1016/j.apacoust.2011.02.001 [DOI] [Google Scholar]
- 69. Zebian, M. , Hensel, J. , Fedtke, T. , and Vollbort, S. (2011b). “ Interpretation of distortion product otoacoustic emissions at higher frequencies,” J. Hear. Sci. 1, 49–51. [Google Scholar]
- 70. Zhao, F. , and Stephens, D. (1999). “ Test-retest variability of distortion-product otoacoustic emissions in human ears with normal hearing,” Scand. Audiol. 28, 171–178. 10.1080/010503999424743 [DOI] [PubMed] [Google Scholar]
- 71. Zwicker, E. (1990). “ On the influence of acoustical probe impedance on evoked otoacoustic emissions,” Hear. Res. 47, 185–190. 10.1016/0378-5955(90)90150-N [DOI] [PubMed] [Google Scholar]