Syllable-constituent perception by hearing-aid users: Common factors in quiet and noise

Abstract

The abilities of 59 adult hearing-aid users to hear phonetic details were assessed by measuring their abilities to identify syllable constituents in quiet and in differing levels of noise (12-talker babble) while wearing their aids. The set of sounds consisted of 109 frequently occurring syllable constituents (45 onsets, 28 nuclei, and 36 codas) spoken in varied phonetic contexts by eight talkers. In nominal quiet, a speech-to-noise ratio (SNR) of 40 dB, scores of individual listeners ranged from about 23% to 85% correct. Averaged over the range of SNRs commonly encountered in noisy situations, scores of individual listeners ranged from about 10% to 71% correct. The scores in quiet and in noise were very strongly correlated, R = 0.96. This high correlation implies that common factors play primary roles in the perception of phonetic details in quiet and in noise. Otherwise said, hearing-aid users' problems perceiving phonetic details in noise appear to be tied to their problems perceiving phonetic details in quiet and vice versa.

I. INTRODUCTION

Early workers at Bell Telephone Laboratories (BTL) established that the intelligibility of various speech materials is highly correlated with syllable intelligibility. They used this correlation to develop the Articulation Index (AI) method of predicting the intelligibility of speech materials subjected to filtering and noise (Allen, 1996; French and Steinberg, 1947). The AI is an estimate of the proportion of the acoustic information that underlies speech perception that is available to the listener. Among the findings at BTL was the important fact that nearly perfect sentence intelligibility and almost as good word intelligibility only required a syllable intelligibility of about 70% and an AI of 0.5. The clear implication of this early research at Bell Telephone Laboratories was that the acoustic information that supports syllable intelligibility is fundamental to speech perception, but that only about 50% of that information is needed for successful perception of words, phrases, and sentences as the use of context makes some of the information redundant. These results were based on average scores of normal hearing adults listening to speech distorted by noise or filtering. Following in this tradition, investigators at Communication Disorders Technology, Inc (CDT) have developed a Speech Perception Assessment and Training System (SPATS) that utilizes the measurement and training of the intelligibility of 109 syllable constituents shown to be of importance in the phonetic structure of spoken English. The details of this flexible system have been described elsewhere (Miller et al., 2008a; Miller et al., 2008b; Watson and Miller, 2013). The developers of the SPATS software believe that failures in the identification of syllable constituents may be more readily associated with severity and patterns of hearing loss than the more abstract concepts such as phonemes or speech features. (For further details on the constituent analysis of the syllable, see Hall, 2006.) As part of a study of the efficacy of speech perception training for hearing-aid users, data have been collected that, when appropriately analyzed, provide a unique comparison of the accuracy of identification of 109 syllable constituents by hearing-aid users in quiet and in noise. It is our hypothesis that such perception is fundamental to the perception of words and sentences in a manner similar to that described by the pioneering work at BTL. While this pioneering work did not include analyses of individual differences, it is our hypothesis that individual differences in the perception of phonetic details such as syllable perception, syllable-constituent perception, or phoneme perception will correlate well with word, phrase, and sentence perception once the individual differences in the use of context in perception of the more redundant signals (words, phrases, and sentences) is accounted for. However, the exploration of this more general hypothesis is a matter for future research. While there are many interesting questions about syllable-constituent perception and how it is affected by hearing loss, we became particularly interested in the relation between syllable-constituent identification in quiet and in noise because early results, from a small number of listeners, indicated that scores in quiet and in noise were highly correlated. This trend seemed to be in conflict with other data, based on words that indicated that speech perception in noise could not be predicted from speech perception in quiet as exemplified by the work of Wilson and McArdle (2005) and Wilson (2011). The early trends also seemed to be in conflict with the view that the problems faced by hearing-aid users with the perception of speech in noise is for the most part unrelated to problems that they may have with speech perception in quiet. Therefore, it was decided to determine whether the trends seen with the first few listeners held up as more listeners were studied. The focus of the present paper is solely on the overall relation between the perception of phonetic details in quiet and in noise as measured by the identification of syllable constituents. A high correlation between the two would indicate that this perception is based on common factors in quiet and in noise, while a low correlation would indicate that this perception is differently based in quiet and noise. If a high correlation between the two can be confirmed, then other analyses are planned to elucidate the relations between syllable-constituent identification, the use of context, and the identification of words in sentences.

The general strategy used in the present paper is as follows: (1) represent each listener's measured performances in quiet and noise by fitted logistic functions, (2) evaluate how well these fitted functions represent each listener's observed data points, (3) evaluate and compare the reasonableness of the use of the fitted functions to estimate, by interpolation, each listener's performance at the speech-to-noise ratios (SNRs) of −5, 0, 5, 10, and 15 dB as these are the SNRs commonly encountered in real-life, noisy situations in which people try to communicate with speech (Pearsons et al., 1977; Olsen, 1998; Smeds et al., 2015), and (4) based on these interpolations characterize and interpret the observed relations between the identification of syllable constituents in quiet and noise by the hearing-aid users.

II. LISTENERS

A. General

The participant hearing-aid users are part of what will be a larger group participating in an ongoing study entitled, “Multi-site study of the efficacy of speech-perception training for hearing-aid users,” C. S. Watson, PI. These listeners are being recruited and tested at five participating sites, and a description of this project can be found in Miller et al. (2015). The 59 listeners whose data are described in this report met the following inclusion criteria: (1) adult between 35 and 89 year of age, (2) native speaker of English, (3) sensorineural hearing loss with pure tone average (PTA) at 500, 1000, and 2000 Hz less than 75 dB hearing level (HL) in each ear, (4) hearing-aid user for at least 3 months, (5) no significant conductive loss, (6) no current otologic pathology, (7) no disease or medication that may affect hearing or performance, (8) no history of neurologic disease including stroke, (9) hearing aids in working order, (10) normal or corrected normal vision (Snellen (20/50)), (11) reading level at or above the 4th grade, (12) score above 85 on the Wechsler Adult Intelligence Scale (WAIS), (13) score above 20 on the Saint Louis University Mental Status Examination (SLUMS), and (14) ability to perform project tasks. All listeners signed informed consent forms as approved by each site's Institutional Review Board (IRB).

B. Sexes and ages

Of these 59 listeners, 24 were females and 35 were males, and their ages ranged from 51 to 86 years with a mean of 72 years.

C. Audiograms

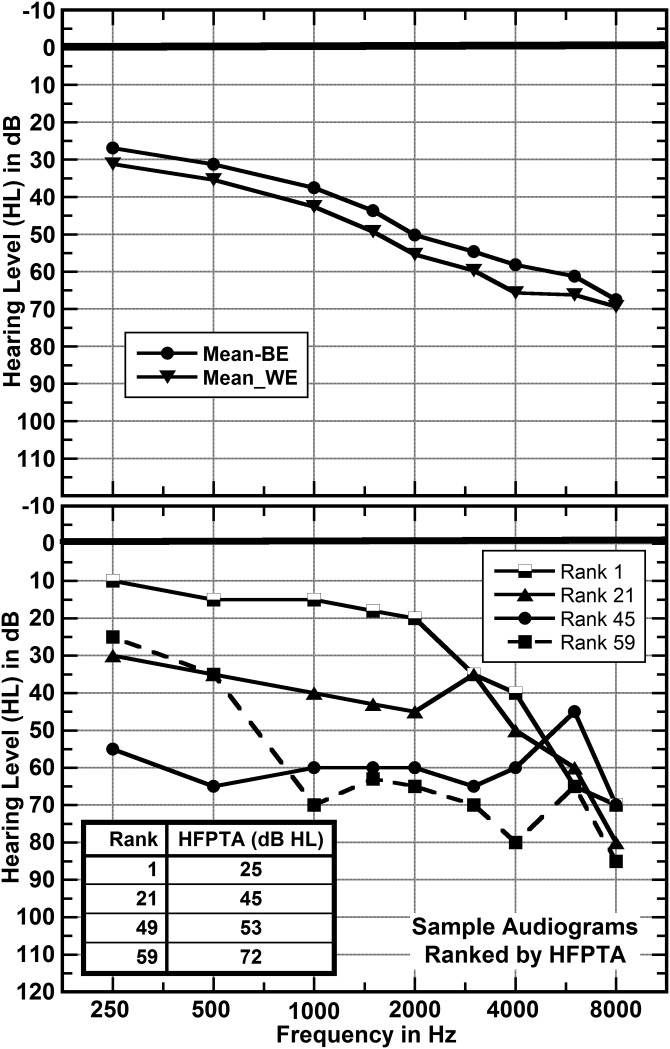
Pure-tone thresholds were measured by air conduction for the right and left ears prior to participation in the study. An initial evaluation of these thresholds was made by calculating the high-frequency pure tone average (HFPTA). Wilson (2011) defines HFPTA to be the average HL at the test frequencies of 1000, 2000, and 4000 Hz. The HFPTAs in the listeners' better ears ranged from 25 to 72 dB HL with a mean of 49 dB HL, and in the poorer ears ranged from 32 to 80 dB HL with a mean of 55 dB HL. The difference in HFPTA between the better and worse ears ranged from 0 to 23 dB with a mean of 6 dB and a mode of 2 dB. The average thresholds of the better ears and of the worse ears are displayed on the upper panel of Fig. 1. These average audiograms fall off at about 9.8 dB per octave over the range 500 to 4000 Hz and at lower rates between 250 and 500 Hz and above 4000 Hz. The statistics of the hearing levels at the better and worse ears are given in Tables I and II. Additionally, there are notable individual differences in the shapes and severities of the audiometric losses. These differences are exemplified on the lower panel of Fig. 1.

FIG. 1.

Average audiograms for the better and worse ears of the 59 participants are shown on the upper panel. Better ear audiograms are shown in the lower panel for four individual listeners ranked by their HFPTAs.

TABLE I.

Statistics for better-ear thresholds (dB HL).

Hz	Average	Standard Deviation	Minimum	Maximum	Range
250	27.0	16.14	5	65	60
500	31.4	16.19	5	65	60
1000	37.6	15.85	5	70	65
1500	43.8	13.85	12.5	75	62.5
2000	50.3	14.12	20	85	65
3000	55.6	12.09	35	75	40
4000	59.2	11.15	35	80	45
6000	61.1	14.36	20	95	75
8000	67.7	14.72	30	95	65
HFPTA	49.0	11.25	27	73	46

TABLE II.

Statistics for Worse-Ear Thresholds (dB HL).

Hz	Average	Standard Deviation	Minimum	Maximum	Range
250	31.1	17.17	5	80	75
500	35.3	16.75	5	65	60
1000	42.6	16.17	10	70	60
1500	49.2	12.43	15	73	58
2000	55.3	13.77	20	85	65
3000	59.5	13.86	30	110	80
4000	65.8	12.13	45	105	60
6000	66.3	13.45	40	105	65
8000	69.2	15.12	15	100	85
HFPTA	54.6	11.35	32	80	48

It can be seen that while there is generally increasing HL with frequency, the exact pattern varies from listener to listener. The variation in individual audiogram shapes is even greater when all 59 listeners are considered.

D. Hearing aids

Among the 59 study participants, 97% were wearing bilateral hearing aids and the remainder were wearing unilateral hearing aids. Eighty percent of the hearing aids consisted of behind-the-ear aids; the remainder were in-the-ear or in-the-canal style. All testing and training was conducted with the hearing aids at the user's customary volume and/or program settings. Consistent hearing-aid function was verified throughout the study, as follows. At each visit, the participant was asked to report any hearing-aid malfunction. If a change in hearing aid status was noted, testing was postponed and the participant was referred to the dispensing audiologist for repair. If no concerns were noted, the hearing aids were visually inspected by the tester for damage or blockage. Batteries were checked and replaced if necessary. Functional amplification was evaluated in two ways. First, coupler output was measured as a function of frequency at a range of input levels, using the appropriate coupler (HA1 or HA2) for the style of aid. Second, the real ear aided response was measured for input levels of 50, 65, and 80 dB sound pressure level (SPL). Because the study aimed to sample representative hearing-aid wearers, no adjustments were made to the hearing aids by the study audiologists, and the wearer used the hearing aid during training as they did during everyday listening. An abbreviated set of coupler measurements was completed at the beginning of each listening visit. Measurements ±5 dB re: baseline results were required to demonstrate stable aid function and proceed with training. Accordingly, the aided auditory experience was considered to be stable over the course of participation.

III. METHODS

A. General

The data reported here were collected as part of the initial phase of speech perception training described by Miller et al. (2015). This involved orientation to and practice with the tasks so that the data could be considered reflective of performance early in the training. All of the listeners of this study had exactly the same exposure to orientation materials, training trials, and testing trials. However, there were individual differences in how many sessions and hours were needed to complete the orientation, initial training and testing. This resulted from differences in the lengths of scheduled sessions and differences in the speeds with which individual listeners completed the initial orientation, training, and testing materials. For an average listener this required six to seven visits to the site and approximately 13 h of initial orientation, training and testing.

B. Syllable-constituent intelligibility in quiet and noise

1. Test materials

The descriptions of the syllable constituents that follow are abbreviated. More detailed information regarding these speech sounds can be found in Miller et al. (2008a); Miller et al. (2008c); and Watson and Miller (2013). Within each constituent category, individual constituents were ranked separately for textual frequency of occurrence and lexical frequency of occurrence. These ranks were then averaged and individual sounds re-ranked based on the averages. The ranks, so derived, are shown in Tables III, IV, and V.

TABLE III.

Showing the 45 onsets used in SPATS.

Rank	Onset	Rank	Onset	Rank	Onset	Rank	Onset
1	#Vwla	12	p-	24	th(v)-b	35	dr-
2	s-	13	l-	25	br-	36	kw-
3	r-	14	n-	26	gr-	37	fl-
4	k-	15	pr-	27	kr-	38	sl-
5	b-	16	g-c	28	sp-	39	kl-
6	m-	17	v-	29	pl-	40	sw-
7	h-	18	st-	30	th-	41	sm-
8	d-	19	sh-	31	y-	42	gl-
9	t-	20	fr-	32	sk-	43	sn-
10	w-	21	j-	33	bl-	44	skr-
11	f-	22	tr-	34	str-	45	z-
		23	ch-

^aVwl stands for a glottal release into a nucleus.

^bth(v) stands for /ð/.

^cg- stands for /ʤ/.

TABLE IV.

Showing the 28 nuclei used in SPATS.

Rank	Nucleus	Rank	Nucleus	Rank	Nucleus	Rank	Nucleus
1	hid	8	hayed	15	how'd	22	held
2	heed	9	hide	16	hewed	23	Hal'd
3	herd	10	hawed	17	hared	24	hold
4	had	11	who'd	18	haired	25	hauled
5	head	12	hulled	19	hood	26	hired
6	hud	13	hoed	20	hilled	26	hailed
7	hod	14	hoard	21	hoid	28	heeled

TABLE V.

Showing the 36 codas used in SPATS.

Rank	Coda	Rank	Coda	Rank	Coda	Rank	Coda
1	Vwla	10	-m	19	-bz	28	-ch
2	-z	11	-nt	20	-ks	29	-sts
3	-n	12	-v	21	-p	30	-pt
4	-d	13	-k	22	-dz	31	-ngz
5	-t	14	-nz	23	-mz	32	-vz
6	=l	15	-ts	24	-f	33	-ps
7	-ng	16	-f	25	-kt	34	-sh
8	-s	17	-st	26	-th	35	-g
9	-nd	18	-ns	27	-j	36	-b

^aVwl stands for syllables ending without final consonant(s).

a. Syllable onsets.

The 45 syllable onsets included in SPATS are shown in Table III.

These are spoken by eight talkers and combined with 4 nuclei (/i/, /a/, /u/, and /ɝ/) as described in Miller et al. (2008a). Thus, each onset category is represented by 32 tokens. In these tests the listeners are not asked to identify the entire syllable, only each syllable's onset. Here a single test consists of two presentations of each of the 45 onsets. Each onset is selected without replacement until all 45 onsets are presented and then the process is repeated. After an onset is selected, a talker is selected randomly without replacement, and then a nucleus is selected without replacement. This procedure guarantees that in the long run all tokens are equally likely to be selected. The response screen (not shown) displays all 45 onsets in an arrangement that reflects the manner, voicing, and place of articulation of each onset (Miller et al., 2008a). Since all 45 onsets are equally likely, chance performance on an onset test is 100(1/45) or 2.22%.

b. Syllable nuclei.

The 28 syllable nuclei included in SPATS are shown in Table IV.

These are spoken by eight talkers in an /h_d/ context, as described in Miller et al. (2008a). Thus, each nucleus is represented by eight tokens. In these tests the listeners are asked to identify the entire syllable, but these syllables differ only in their nuclei. A single test consists of two presentations of each of the 28 nuclei. Each nucleus is selected without replacement until all 28 nuclei are presented and then the process is repeated. After a nucleus is selected, a talker is selected randomly without replacement. This procedure guarantees that in the long run all tokens are equally likely to be selected. The response screen (not shown) represents all 28 nuclei arranged in a manner that reflects the similarities between the usual oral monophthongs and diphthongs, rhotic diphthongs, and lateral diphthongs (vowels combined with dark el) as described in Miller et al. (2008a). Since all 28 nuclei are equally likely, chance performance on a nucleus test is 100(1/28) or 3.57%. Note that in the SPATS tests of the ability to identify nuclei, only one phonetic context (hNd) was used while the tests for onsets and codas require that these constituents be identified in several phonetic contexts. This was done as a matter of convenience so that it would not be necessary to teach the users abstract representations of vowel-like sounds. In the case of onsets and codas such abstract representations are not needed because there is generally a close connection between the English spellings of these sounds and their phonetic representations. Whether the results for nuclei as compared to the results for onsets and codas are strongly influenced by these differences in procedures is a matter for future research.

c. Syllable codas.

The 36 syllable codas included in SPATS are shown in Table V. These are spoken by eight talkers and in most cases combined with five nuclei, /i/. /a/, /u/, /ɝ/, and /ɛɫ/ as described in Miller et al. (2008a).

Most coda categories are represented by 40 tokens (eight talkers times five nuclei). The category called vowel is represented by only 24 tokens (eight talkers times three nuclei /i, a, u/), and the categories /ɝ/, and /ɛɫ/ are each represented by eight tokens, one from each talker In these tests the listeners are not asked to identify the entire syllable, only each syllable's coda. Here a single test consists of two presentations of each of the 36 codas. Each coda is selected without replacement until all 36 codas are presented and then the process is repeated. After a coda is selected, a talker is selected randomly without replacement, and then a nucleus is selected without replacement. This procedure guarantees that in the long run all tokens within each category are equally likely to be selected. The response screen (not shown) represents all 36 codas arranged in a manner that reflects the manner, voicing, and place of articulation of each coda (Miller et al., 2008a). Since all 36 codas are equally likely, chance performance on a coda test is 100(1/36) or 2.78%.

2. Test conditions

All sounds are presented by a loudspeaker calibrated to present sounds at 65 dBC as measured in the region of the listener's head. Listeners are tested in quiet rooms facing the loudspeaker at a distance of approximately 4.75 ft while wearing their own hearing aids with their usual settings. In the SPATS program, the overall level of the speech-plus-noise is held constant at 65 dBC as the SNR is changed.

3. Test procedures for individual constituent classes: Onsets, nuclei, and codas

The intelligibilities of 45 syllable onsets, 28 syllable nuclei, and 36 syllable codas were separately measured in a noise background of 12-talker babble. Quiet is defined as an SNR of 40 dB, and the percent correct at this SNR is said to be the percent correct in quiet, PC_q. Intelligibility in noise is measured using an adaptive technique that finds the SNR required to reach a target percent correct (TPC, Kaernbach, 1991). One objective of the experimental design is to characterize each listener's overall ability to identify phonetic details (syllable constituents) in both quiet and noise during initial speech perception training. It was reasoned that this is most efficiently done by collecting data that allow estimation of the s-shaped psychometric function that describes each listener's performance as a function of SNR. Since the psychometric function is usually treated as being symmetrical around its inflection point, it was decided to carefully measure three points on the upper branch of the s-shaped function. As will be shown, a properly selected trio of points can define a logistic function, which in turn serves as the s-shaped function of interest. The three points on the upper branch of the s-shaped function are separately selected for each class of syllable constituent (onsets, nuclei, and codas) and for each listener. The first point is the percent correct identification at an SNR of 40 dB. This point is chosen because, in the case of energetic auditory masking, maximum performance is usually reached at SNRs less than or near to 40 dB. Therefore, the percent correct at an SNR of 40 dB reasonably represents performance in quiet. The TPCs were individually selected for each listener and constituent type based on the percentage difference between chance and the individual's score in quiet (SNR = 40 dB). The second point on the psychometric function corresponds to the TPC at 80% of that distance above chance, which is denoted “TPC_0.8” and its corresponding SNR is denoted “SNR_0.8” The third point on the psychometric function corresponds to the TPC that is 50% of that distance above chance, which is denoted “TPC_0.5” and its corresponding SNR is denoted by “SNR_0.5.” By way of review, each listener's performance for each constituent class (onsets, nuclei, and codas) is characterized by three pairs of numbers: one pair for quiet (SNR = 40, PC_q); a second pair corresponding to 80% of the distance between chance and PCq (PC_0.8,SNR_0.8); and a third pair at half-way between chance and PC_q (SNR_0.5, PC_0.5). The TPCs are defined by Eqs. (1) and (2),

$${\text{TPC}}_{0.8}=0.8({\text{PC}}_{\mathrm{q}}–{\text{PC}}_{\text{chance}})+{\text{PC}}_{\text{chance}}$$ (1)

and

$${\text{TPC}}_{0.5}=0.5({\text{PC}}_{\mathrm{q}}–{\text{PC}}_{\text{chance}})+{\text{PC}}_{\text{chance}},$$ (2)

where PC_chance is defined by Eq. (4), below.

4. Combining scores for onsets, nuclei, and codas to get overall scores

In finding an average (X_oa) based on measurements of each of several groups, it is common to weight the measurement for each group by the proportion of cases in each group. For syllable constituents there are 45 onsets, 28 nuclei, and 36 codas. The average of these measures weighted by the items in each group is given by Eq. (3),

$${\mathrm{X}}_{\text{oa}}-(45/10{9)\mathrm{X}}_{\text{onsets}}+(28/109){\mathrm{X}}_{\text{nuclei}}+(36/109){\mathrm{X}}_{\text{codas}}.$$ (3)

Each listener's overall performance (PC_oa) for syllable constituents is obtained by weighting the resulting SNRs and PCs for the individual constituent classes by the proportion of the total number of items in each class. The general form for finding the weighted average of the percent corrects associated with each of the three constituent classes is given in Eq. (4). It can be seen that the results for the three constituent classes are weighted in proportion to the relative size of each class,

$${\text{PC}}_{\text{oa}}=\left[(45/109){\text{PC}}_{\text{onsets}}+(28/109){\text{PC}}_{\text{nuclei}}+(36/109){\text{PC}}_{\text{codas}}\right].$$ (4)

It is noted for the special case where each of the 109 constituents is presented equally often, this equation simplifies to 100 times the ratio of the total number of correct responses to the total number of trials as shown in Eq. (5),

$$\text{PCoa}=100({\mathrm{N}}_{\text{correct}}/{\mathrm{N}}_{\text{presentations}}).$$ (5)

However, for cases where the number presentations per constituent vary as between onsets, nuclei, and codas, then the more complicated formula of Eq. (4) must be used. Table VI gives an example of these scores for a typical listener (53c13). The entries in the right-most columns of Table VI are found by calculating the weighted averages of the entries in the corresponding cells to the left as exemplified in the footnote of Table VI.

TABLE VI.

Calculation of overall scores.^a

Measure	Onsets		Nuclei		Codas		All Constituents
	SNR	PC	SNR	PC	SNR	PC	SNR	PC
TPC0.5	3	33	−7	42	1	13	−0.23	28.71
TPC0.8	25	51	−7	65	3	20	9.51	44.36
Quiet	40	63	40	89	40	24	40.00	54.49

^aRight-hand columns are weighted averages of the left-hand columns. For example, −23 = [(45/109)(3) + (28/109)(−7) + (36/109)(1)]. See text for explanation.

For example, the entry in the top-right cell under the heading “All Constituents” is found by multiplying the corresponding entries under Onsets by (45/109), under Nuclei by (28/109), and under Codas by (36/109), and then summing these products to find their weighted average. For each listener, these operations result in overall scores in quiet (PC_q for SNR = 40), and SNRs for two targets (TPCs). PC_q is the percent correct in quiet (SNR = 40 dB). The overall PC_chance is the weighted average of the chance scores for onsets, nuclei and codas as shown in Eq. (6),

$${\text{PC}}_{\text{chance}}=\left[(45/109)2.22\%+(28/109)3.57\%+(36/109)2.78\%\right]=2.75\%.$$ (6)

5. Data used to define each of the three observed points

To appreciate the fitting processes described below, one needs to understand the amount of data used to define the three observed points for each hearing-aid user. For the measurement of the Percent Correct in quiet (PC_q), each point is based on 90 trials for onsets, 56 trials for nuclei, and 72 trials for codas, a total of 218 trials. Note that for these tests in quiet, each constituent presented 2 times and Eqs. (3) and (4) produce identical results The adaptive procedure involves 135 trials for onsets, 112 trials for nuclei, and 108 trials for codas. The SNRs to be associated with each TPC were calculated based on the second half of each adaptive run. Thus, each SNR for each listener is based on the last 68 trials of an adaptive test with onsets, the last 56 trials of an adaptive test with nuclei, and the last 54 trials of an adaptive test with codas, a total of 178 trials. In these cases only Eq. (3) results in appropriately weighted averages across the three constituent types. It is also noted here that the weighted averages of TPC's and the weighted averages of the measured PC's are in almost perfect agreement. For the 59 hearing-aid users,the mean difference between the programmed TPC_0.5's and the observed PCs is −0.1% and the correlation between the two is 0.98. For the TPC_0.8, the mean difference between programmed and observed values is 0.2% and the correlation between the two is 0.99. In summary, the three data pairs of the combined measures were used to fit the three observed points for each individual listener. These were (1) the proportion of correct identifications of the 109 syllable constituents in quiet (PC_q) at an SNR of 40 dB; (2) the combined TPC_0.8 and SNR_0.8 for the 109 constituents; and (3) the combined TPC_0.5 and the SNR_0.5 for the 109 constituents.

C. Interpolation method

The logistic function has three free parameters: (1) an upper asymptote, ua, (2) a slope parameter, s, and (3) the point-of-inflection parameter, b. The point-of-inflection parameter, b, gives an estimate of the SNR at which the upper branch of the s-shaped function transitions to the lower branch of that function. A fourth important parameter, the lower asymptote, la, is fixed and determined by the percent correct that can be achieved by chance, 2.75%. The logistic function is shown by Eq. (7),

$$\text{PC}=\left[\text{la}+(\text{ua}-\text{la})(1/(1+{\mathrm{e}}^{-\mathrm{s}(\text{SNR}\hspace{0.17em}–\hspace{0.17em}\mathrm{b})}))\right].$$ (7)

For each listener the logistic function is fitted to the three overall points using the Solver algorithm of Microsoft Excel. The criterion for the best fit is the minimization of the squared error between the three observed points and the three fitted points. Finally, by interpolation along the fitted logistic function PC values are found for the SNRs of −5, 0, 5, 10, and 15 dB. The average of these five PC values is called PCn or the average percent correct in noise. PC(5) is taken as the fitted score at the SNR of 5 dB, which Smeds et al. (2015) found to be the average SNR encountered by hearing-aid users in noisy situations. For a discussion of issues related to the fitting of the observed data with the logistic function see the Appendix. Here it is noted that the only constraint used in fitting the logistic is that the lower asymptote must equal chance (2.75%). It is also assumed that the fitted logistic functions accurately describe the observed points and provide a creditable basis for interpolation (see Sec. IV).

IV. RESULTS

A. Average logistic functions for onsets, nuclei, and codas and their weighted average

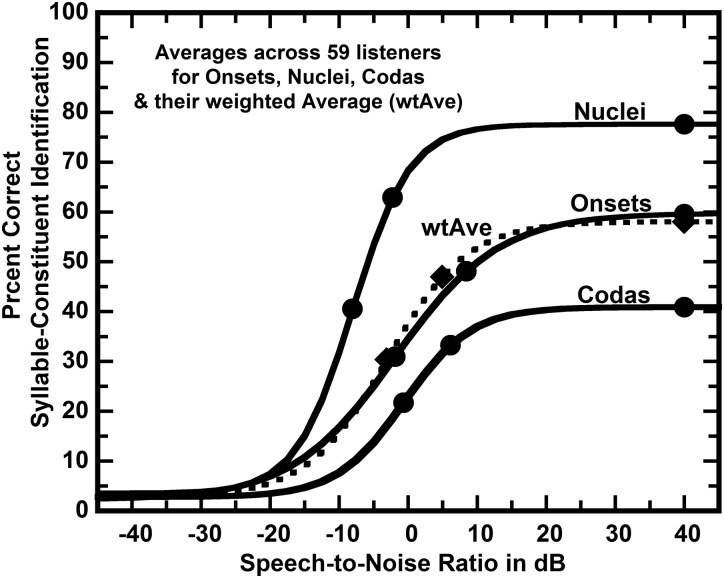
As a further illustration of the methods used, the three data points for each subject are averaged across listeners for onsets, nuclei, and codas separately and then their weighted averages are found. This process results in four sets of three points: A set for onsets, a set for nuclei, a set for codas, and a set for all constituents, found as the weighted averages of the first three sets. Each of these four sets is then fit by a logistic function. These are shown in Fig. 2 to illustrate the methods used for each individual listener in the analysis of individual differences that follows. It can be seen that the weighted average, or overall percent correct, is very similar to the percent correct for onsets alone. Additionally, for hearing-aid users, onsets are more difficult than nuclei, and codas are more difficult than onsets.

FIG. 2.

Percent correct syllable-constituent identification as a function of SNR averaged across all 59 listeners. The weighted average of the scores for nuclei, onsets, and codas is shown by the dotted line. It is each individual's weighted average that is reported in the remainder of the paper.

B. Examples of logistic fits and interpolated points for individual hearing-aid users

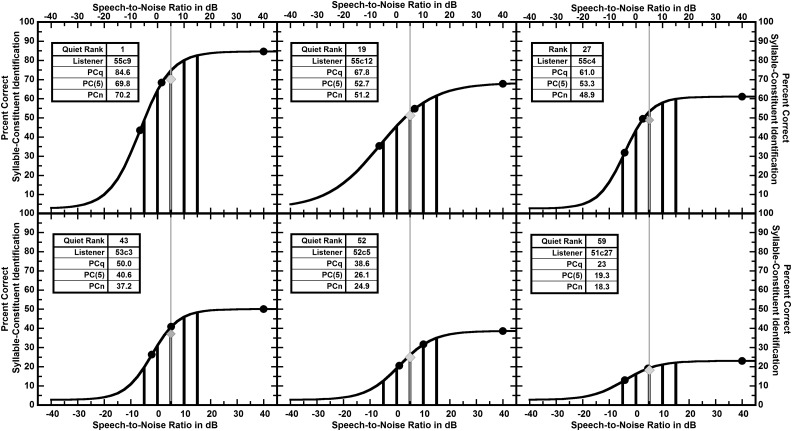
The use of interpolation along the fitted logistics to estimate the percent correct scores (PCs) in the region of commonly encountered SNRs is justified by inspection of each individual's data as exemplified in Fig. 3 and also can be viewed for each of the 59 listeners at the link provided in the supplemental material.¹ Note that the observed points, filled circles, are well represented by the fitted logistics. Also note that interpolated points, shown by the intersection of the vertical lines with the fitted curves, are close to neighboring observed points or between observed points that are reasonably connected by the fitted logistic. For these reasons, it is argued that interpolated PCs are very likely to be accurate.

FIG. 3.

Data points (filled circles), fitted logistics (curves), and interpolated points over the range of commonly encountered SNRs (thick vertical lines) are shown for a sample of six listeners selected so that their scores in quiet (PCq's) are spaced at about 12% intervals. The averages of the interpolated points (PCn's) are shown as grey diamonds. The thin grey vertical lines are at an SNR of 5 dB (Smeds et al., 2015), the average SNR encountered by hearing-aid users. Each listener's percent correct at the SNR of 5 dB (PC(5)) is given by the intersection of the vertical grey line and the fitted logistic. Note that the interpolated points are near to or between the observed points. These graphs are typical of those for all of the 59 listeners, which can be viewed at the link provided in the supplementary material.

C. Individual differences among hearing-aid users in identifying syllable constituents in quiet and in noise

1. In quiet

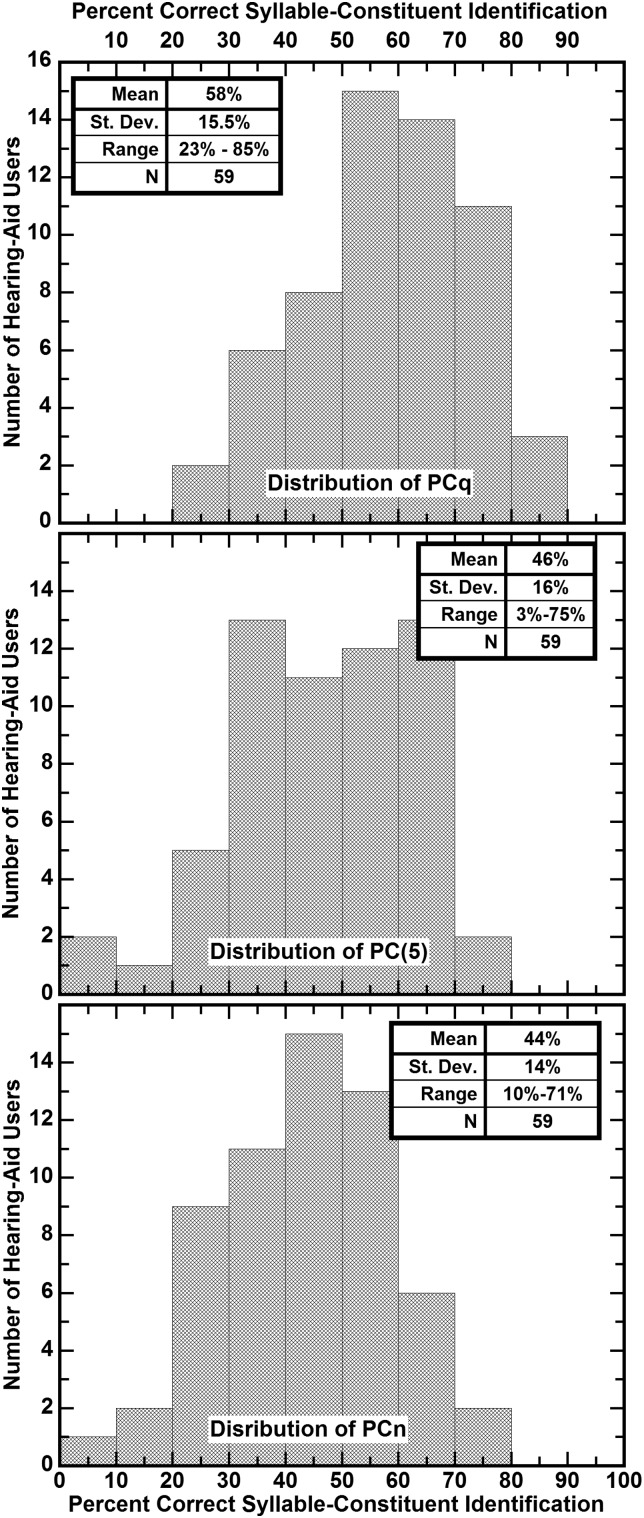
The distribution of individual differences in percent correct scores among hearing-aid users when listening in quiet is shown on the upper panel of Fig. 4. Clearly these listeners vary greatly in their abilities to identify syllable constituents with scores ranging from 23% to 85% correct. The mean score is 58% correct with a standard deviation of 15.5% correct.

FIG. 4.

The distribution of the 59 scores for syllable-constituent identification in quiet, PCq (upper panel), at an SNR of 5 dB, PC(5) (middle panel), and the average score for SNRs of −5, 0, 5, 10, and 15 dB, PCn (bottom panel).

2. In noise

The distribution of individual differences in percent correct scores among hearing-aid users when listening at an SNR of 5 dB is shown on the middle panel of Fig. 4. Again these listeners vary greatly in their abilities to identify syllable-constituents at this SNR with scores ranging from 3% to 75%. The mean score is 46% correct with a standard deviation of 16%. The distribution of individual differences in their average scores over SNRs ranging from −5 to 15 dB, PCn, is shown on the bottom panel of Fig. 4. Again these listeners vary greatly in their average performances in commonly encountered SNRs with scores ranging from 10% to 71%. The mean score is 44% with a standard deviation of 14%.

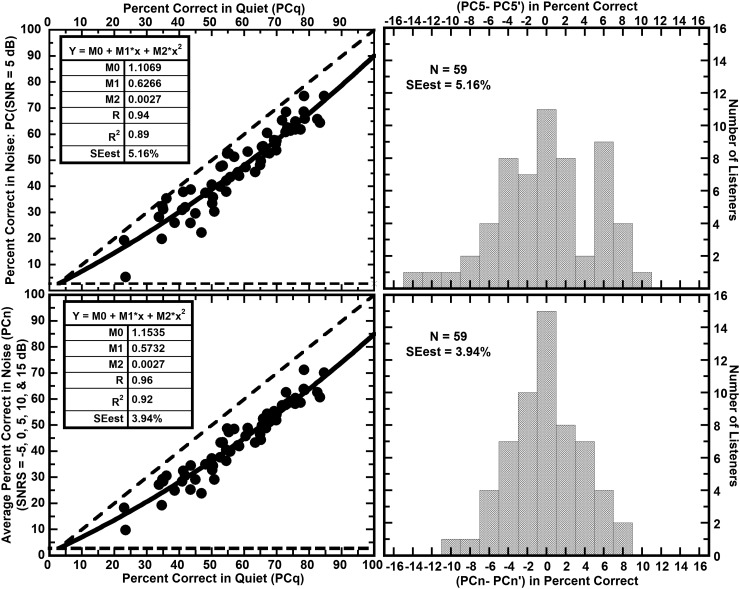
D. The relation between syllable-constituent identification in quiet and noise

The principal finding of this paper is encapsulated by the graphs shown in Fig. 5. The upper-left panel shows the relation between PC(5), the percent correct at an SNR of 5 dB and PCq. The percent correct in quiet correlates very highly (R = 0.94) with PC(5) and the standard error of the estimate is 5.16%. The lower-left panel shows the same relation when the syllable-constituent identification scores in noise are averaged over the range of commonly encountered SNRs, −5 to +15 dB. The process of averaging appears to slightly improve the stability of the PCn and to improve the correlation between scores in quiet and in noise to 0.96 with a standard error of the estimate of 3.94%. Also note that the best fitting polynomials relating identification in noise with identification in quiet have highly similar parameters in both cases. Clearly, syllable-constituent perception in noise is highly correlated with the same performance in quiet. A more detailed description of the bases of the high correlations between the identification of syllable constituents in quiet and noise and of the allocation of variance reduction in PCn to the parameters of the fitted logistics is given in the Appendix.

FIG. 5.

The relation between syllable-constituent identification in quiet and in noise. The upper-left panel shows the scatter plot of the percent correct at an SNR of 5 dB, PC(5), against the percent correct in quiet, PCq. The lower left panel shows the scatter plot of the percent correct over the range of commonly encountered SNRs that range from −5 to 15 dB (PCn) against the percent correct in quiet, PCq. The inset tables give the relevant correlational statistics. The dashed lines show limits on the percent correct as determined by chance and the assumption that the score in quiet sets an upper limit on the score in noise. The right-hand panels show the distributions of differences between observed and fitted scores.

E. Correlation between performance in noise and quiet when the only constraints are that the scores in noise can neither exceed the scores in quiet nor be less than chance

It is reasonable to assume that the score in quiet, PCq, sets an upper limit on the score in noise, PCn. It is, therefore, reasonable to ask how much of the correlation between PCq and PCn reported above is due to that constraint. If the only constraints on each individual's performance in noise are that performance in noise cannot exceed that in quiet and cannot be less than that expected by chance, one can calculate the expected correlation between performance in noise and in quiet. The correlations between the average percent correct in noise, PCn, and the percent correct in quiet, PCq, were calculated as follows. In each of 25 replications, each of the 59 observed scores in quiet were correlated with noise scores drawn randomly from a rectangular distribution of possible scores falling between chance and the observed score in quiet. The results were very clear. Using the same methods as used for the data described in Sec. IV B above, the correlations ranged from 0.21 to 0.53 with an average correlation of 0.37. On average the random replications accounted for 14% of the variation in the noise scores while the observed correlation of 0.96 accounted for 92% of the variation in the noise scores. Clearly, the observed correlation between scores in quiet and noise is not merely a consequence of the former serving as an upper limit on the latter.

F. Correlation between performance in noise and quiet when the only constraints are that the score in quiet sets an upper limit on the score in noise and the psychometric (logistic) function is monotonic

It could be argued that the monotonic psychometric functions also contribute to the observed correlation between syllable-constituent identification in quiet and noise. Therefore, additional simulations were run that include both the constraint imposed by the score in quiet being an upper limit of performance and the constraint imposed by the monotonicity of the psychometric function. This condition was modeled with the logistic functions as follows. For each simulation it was assumed that there were 59 hypothetical listeners with the same PCq's as those found for the 59 real listeners reported above. The values of TPC_0.8 and TPC_0.5 were assigned to the hypothetical listeners exactly as they were for the actual listeners. However, the values of SNR_0.8 were randomly selected from a wide range, −3 to 35 dB, emulating the possibility that some listeners are able to hear “deep” into the noise, while others are very susceptible to even small amounts of noise. The values of SNR_0.5 were then randomly selected from a range that is consistent with the ratios of SNR_0.5 to SNR_0.8 exhibited by the 59 real listeners. Twenty-five Monte Carlo replications of this simulation were completed. The 25 correlations ranged from 0.12 to 0.51 with a mean of 0.34. On average these random replications accounted for 12% of the variation in the noise scores while the observed correlation of 0.96 accounted for 92% of the variation in the noise scores. Clearly, the observed scores in noise are much more strongly influenced by the observed scores in quiet than implied by providing both an upper limit on the performance in noise and a monotonic psychometric function. It is noted that this second type of simulation yielded differing results depending on exactly how the values of SNR_0.5 were chosen relative to the random values of SNR_0.8. Nonetheless, the simulated values always resulted in much lower correlations between PCq and PCn than were found in the actual data. In summary, the constraints considered here make only minor contributions to the high correlations observed in the data of our listeners.

G. Relations of fitted logistic parameters to PCq

1. The relation of the upper asymptote (ua) to PCq

The average fitted value of the ua was greater than PCq, the percent correct at an SNR of 40 dB, by 0.17%. The correlation between the two values was 0.99. This close relation is the result of the pattern of the three fitted points as the fitting procedure did not constrain the value of ua to equal PCq.

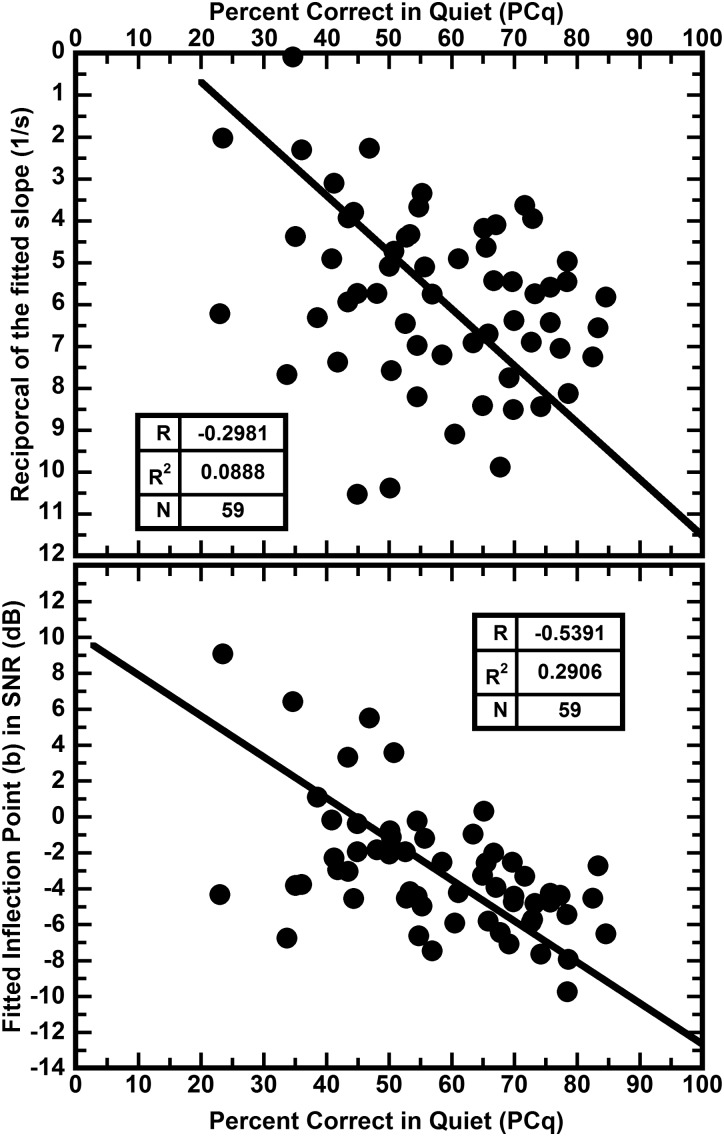
2. The relation of the fitted slope (s) and the fitted inflection point (b) to PCq

These relations are shown in the upper and lower panels of Fig. 6. The upper panel shows that there is a weak tendency for the slope to decrease as PCq increases. The lower panel shows that the SNR at the fitted inflection point decreases as the PCq increases. Both relations combine to increase the score in noise as the score in quiet increases.

FIG. 6.

Showing the relation between the fitted slopes (upper panel) and inflection points (lower panel) of the logistic and the identification scores in quiet. Model II regression lines are shown (Sokal and Rohlf, 1995). The upper panel shows that there is a weak tendency for the slope to decrease as PCq increases. The lower panel shows that the SNR at the fitted inflection point decreases as the PCq increases. Both relations combine to increase the score in noise as the score in quiet increases.

H. Syllable-constituent identification, better-ear pure-tone averages, and listener ages

1. Correlations between PTAs and PCs for syllable constituents

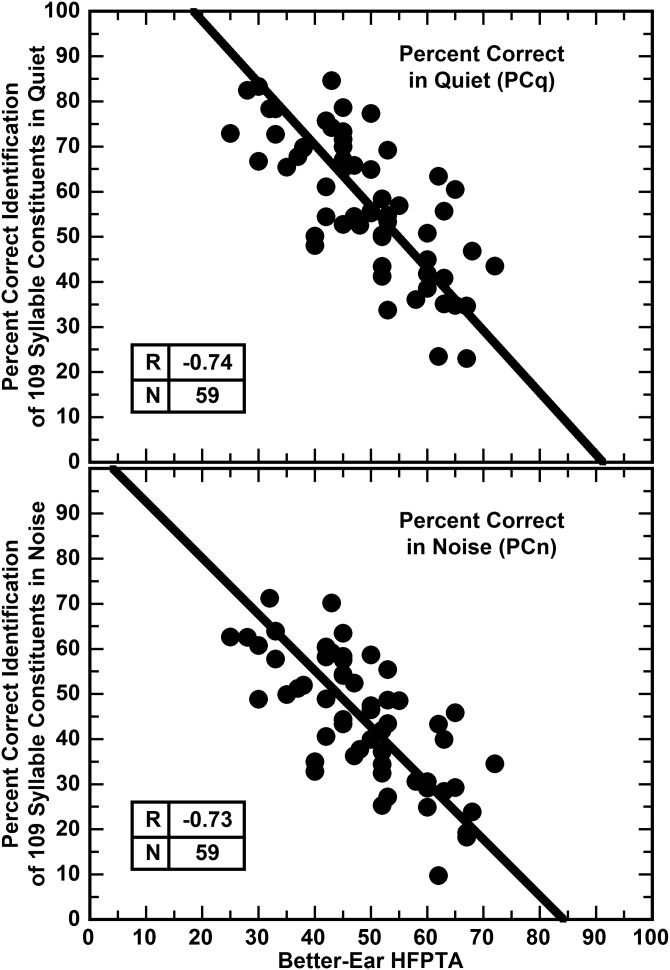
Correlations between three commonly used PTAs and syllable-constituent identification are now described. All of the PTAs are based on better-ear pure tone thresholds measured without hearing aids, whereas the syllable constituent scores were obtained with listeners wearing their aids as usually configured. The better-ear HFPTA, the average threshold in dB HL at 1000, 2000, and 4000 Hz (Wilson, 2011), has correlations of −0.74 with PC_q and −0.73 with PC_n as shown on the upper and lower panels of Fig. 7.

FIG. 7.

Scatter plots of syllable-constituent identification in quiet, PC_q, (upper panel) and syllable-constituent identification in noise, PC_n, (lower panel) against the high frequency pure tone average, HFPTA, are shown for the 59 hearing-aid users. The model II regression lines (Sokal and Rohlf, 1995) are shown. The corresponding correlations are shown in the inset tables on each panel. The y-intercept on the lower panel suggests that the loss of the ability to identify syllable constituents in noise begins with HFPTAs as low as 5 dB HL. It is also apparent that considerable variance remains after allowing for the HFPTA.

While not shown, the better-ear four-frequency PTA, PTA4, the average HL at 500, 1000, 2000, and 4000 Hz, has correlations with PC_q and PC_n of −0.71 and −0.70, respectively. Also, the traditional three-tone PTA, the average HL at 500, 1000, and 2000 Hz, has correlations of −0.67 and −0.64 for quiet and noise, respectively.

2. Correlations between listener ages and PCs for syllable constituents

The ages of the listeners ranged from 51 to 86 years and do not correlate well with the syllable-constituent identification scores being −0.05 with PCq and −0.10 with PCn. Also using the best combination of both age and HFPTA in a multiple regression does not improve the observed correlations over those found with HFPTA alone.

3. Discussion of relations between PTAs and syllable-constituent scores

The fact that aided, syllable-constituent identification is related to the unaided audiogram probably depends on two factors. The first is that it is likely that the more severe the audiometric loss the more difficult it becomes to achieve appropriate amplification. This is plausible because (1) it becomes more difficult to achieve the needed gains for high frequencies and (2) the associated reduced dynamic ranges may require under amplification of soft sounds and the use of compression algorithms that may interfere with syllable-constituent recognition. The second factor underlying the relationship between syllable-constituent identification and hearing sensitivity is that greater audiometric loss implies the existence of more extensive cochlear and/or neural damage patterns that in turn may reduce the speech information that is available to the listener. Further research is needed to clarify these issues.

V. GENERAL DISCUSSION

A. The generality of the relation between speech perception in quiet and in noise

The findings reported here, like all scientific findings, need to be replicated and the limits of their generality need exploration. On the one hand, it is likely that such correlations will only be found when materials like syllable constituents are presented in situations that provide little context to aid in their perception. For example, it has been shown that the perception of words in noise cannot be well predicted by the perception of words in quiet (Wilson and McArdle, 2005; Wilson, 2011). It seems unlikely that high correlations will be observed between speech perception in quiet and in noise with larger speech units such as words, phrases, and sentences because the identification of these larger units depends not only on the identification of smaller units such as syllable constituents but also on the use of context provided by them and the situation (Boothroyd and Nittrouer, 1988; Bronkhurst et al., 1993; Bronkhurst et al., 2002; Miller et al., 2015). Further, it is believed that there are large individual differences in listeners' abilities to use context. In other words, listeners' abilities to understand words, phrases and sentences depend on exactly how the identification of speech elements interacts with the use of context to produce the observed performance. However, while it seems unlikely because of the interactions between hearing of speech sounds and the use of context, it may be that if the same procedures and analyses as used here are applied to words and sentences then similar high correlations might be found between scores in quiet and scores in noise. In this way, appropriate recommendations as to the necessity of measurements in both quiet and noise will evolve.

B. A possible approach to modeling the relation between syllable-constituent identification in quiet and noise

The papers of Trevino and Allen (2013) and Toscano and Allen (2014) indicate that intelligibility of individual tokens of speech sound varies in quiet and noise. This implies that a listener's performance at any SNR is based on the proportion of presented tokens that are intelligible at that SNR. Therefore, a listener's logistic function would have an upper asymptote determined by the proportion of tokens that are above threshold in the quiet. The inflection point would be determined by the mean threshold SNR of the tokens that are identifiable in quiet, and slopes would be determined by variance in the ease of recognition.

VI. SUMMARY AND CONCLUSIONS

• (1)The abilities of 59 hearing-aid users to identify 109 syllable-constituents is characterized by measurements of the percent correct in quiet (SNR = 40 dB) and by measurement of the SNR required to reach a Target Percent Correct (TPC) at two other points selected to be on the upper branch of the s-shaped functions that describe their performances as a function of SNR. A fourth datum used to characterize listener's performance is the percent correct that can be achieved by chance.
• (2)It is shown that the measured points are accurately represented by fitted logistic functions
• (3)It is further demonstrated that the fitted functions can be creditably used to calculate interpolated percent corrects at five SNRs commonly encountered by hearing-aid users in noisy environments.
• (4)It is also demonstrated that hearing-aid users exhibit large individual differences in syllable-constituent identification both in quiet and in noise.
• (5)It is then demonstrated that the correlation between syllable-constituent identification in quiet and in noise is very high, being 0.93 or 0.96 depending on the choice of metric used to characterize performance in noise.
• (6)It is also shown that there are moderate correlations between the performances in quiet and noise with hearing aids and better-ear PTAs that characterize each listener's magnitude of hearing loss, measured without hearing aids. In contrast, the ages of these listeners are not correlated with syllable-constituent identification.
• (7)Taken as a whole, the results presented herein lead to the conclusion that the abilities of hearing-aid users to identify phonetic details (syllable constituents) in quiet and in noise are a consequence of factors common to those two conditions. The audibility and discriminability of the acoustic cues that underlie such identification and the ability to use these cues for the identification of syllable constituents are likely to be the hypothesized common factors. In general, hearing-aid users differ greatly in their abilities to recognize the phonetic details of speech. Some of the variance can be explained by hearing loss as measured by the audiogram, and it is likely that additional variance will be explained by the gains or other measures of the hearing aids. Other aspects of hearing loss, not reflected in the audiogram, as well as individual differences in phonetic identification skills or cognitive measures that are independent of hearing loss (Kidd et al., 2007) may also play roles in syllable-constituent identification. No matter the reasons for these individual differences, this aspect of speech perception by hearing-aid users in noise is highly predictable from that in quiet and vice versa. Difficulty in the perception of phonetic details by hearing-impaired people in quiet and noise appears to be related to common factors as there is no indication of a special difficulty in syllable-constituent perception in noise that cannot be traced to the difficulty of the same task in quiet.

APPENDIX: FITTING THE LOGISTICS TO THE DATA AND THE RELATION BETWEEN PCn AND THE OBSERVED DATA POINTS

A. Fitting the logistic to the three observed data points

This section is designed to clarify the curve-fitting techniques. It is known that the only requirement for a perfect fit of the logistic to three data points is that the points fall in a monotonic pattern. However, the kind of fits reported here can be found if and only if the three points are arranged in a monotonic increasing pattern with a decreasing slope. This is true because the three points must be consistent with being the upper branch of a logistic that approaches its upper asymptote before or near the SNR of 40 dB if the fits are to be reasonable representations of the psychometric function. Also, the fits cannot be considered to be reasonable if their parameters violate common, well-known constraints on the variables being related. In the case of the present paper, the percent-correct scores cannot be negative nor can they exceed 100. Also it would not be reasonable to find an inflection point at an SNR less than about −20 dB or greater than about +20 dB. Nor, for example, would a fit be reasonable if a large SNR of greater than about 40 dB is required to closely approach the upper asymptote or if a similarly large negative SNR was required to closely approach the lower asymptote.

Obviously unreasonable fits would be found if the three observed points, as defined in this paper, were to fall in a monotonic pattern with an increasing slope. In this case the fitting procedure would treat them as being on the lower branch of the logistic and the upper asymptote might be found to be well above 100% and a large SNR, well above 40 dB, might be required before the curve approaches close to its upper asymptote. Similarly unreasonable fits might be found if three observed points were to fall in a monotonic increasing pattern with a constant slope. In this case the upper asymptote might fall well above PCq.

As can be seen in Fig. 3 and in the archival link in the supplemental material,¹ the fitted logistic functions appear to be reasonable in terms of our general knowledge of psychometric functions for speech sounds. It is also clear that each set of the three measured points fall in a monotonic increasing pattern with a decreasing slope that is consistent with being the upper branch of the logistic.

Finally, it needs to be stressed that the free parameters of the logistic, ua, b, and s are determined by the pattern of the three points and not on the value of any one measured point. This is because the only constraint on the fitting procedure was that the lower asymptote was set to chance. So while we refer to the percent correct at an SNR of 40 dB as the percent correct in quiet that measurement is not used to set the value of the parameter ua. Similarly, while SNR_0.5 is measured as an estimate of the inflection point of the logistic, b, that single measure did not define the parameter b. Rather, the fitting process finds a value of b based on the pattern all three points. Here, fits of the logistic to the three data points were made with only one constraint, the lower asymptote of the logistic must be equal to chance performance on our syllable-constituent tasks. Why then are the fits to the data so reasonable if the fitting procedure has only the one constraint as described above? It is because in every case, for each of the 59 listeners, the three data points fall into monotonic increasing pattern with a decreasing slope. In brief, the data were perfectly consistent with being an upper branch of the logistic that closely approaches its upper asymptote before or very near to an SNR of 40 dB.

Does this mean that the data are error free? No, rather it means that the errors are not large enough to cause the data points to deviate from the monotonic increasing pattern with decreasing slope as is consistent with being the upper branch of the logistic function. Does this mean that the fitted parameters are equal to the “true” parameters for each listener? No, the fitting procedure finds the parameters for each logistic that minimizes the sum of squared error and, therefore, adjusts the parameters to fit small random errors in the data. In spite of this problem, the fits provide an excellent description of the observed data points and support the interpolations made using the fitted logistic functions. It is likely that better estimates of each listener's true parameters could be obtained by methods that sample more than three points along the psychometric function. With equally precise data at more points along the psychometric function the random errors will probably preclude such perfect fits as observed here, but accurate estimates of each listener's true parameters become more likely as the small random errors at each measured point are likely to cancel out with some above and others below their expected values.

B. Relation of syllable-constituent identification in noise, PCn, to the three measured data points

1. The problem

One inconsistency noted is that the correlations of PCq with SNR_0.5 and of PCq and with SNR_0.8 are not high, being 0.53 and 0.28, respectively. These moderate to low correlations seem to be in conflict with the high correlations between PCq and PCn reported in the text of this paper. Here it is argued that this apparent conflict does not in fact obviate the high correlation between PCq and PCn. The reason is that identification of syllable-constituents in noise does not depend solely on the relations between PCq and SNR_0.5 and SNR_0.8, but rather it depends on the pattern of the three measured points in the two dimensional space of PC by SNR. These patterns determine the trajectory of the fitted logistic through the region of commonly encountered SNRs, −5 to 15 dB. This trajectory or path, in turn, determines the PCn, which is an average of five points on the logistic. Below in part B2 of this appendix, correlational analyses are presented that confirm this point of view.

2. How PCn is determined by the pattern of the three measured points

The three measured points in PC by SNR space determine the three free parameters of the fitted logistic: The upper asymptote (ua), the inflection point (b), and the slope (s). Here it is shown that a linear combination of ua, b, and the natural logarithm of the reciprocal of the slope parameter, LN(1/s), can be found that predicts the PCn almost perfectly. In other words, the PCn for syllable constituents depends on the upper asymptote of the fitted logistic, on the inflection point of the fitted logistic, and on the logarithm of the reciprocal of the slope of the fitted logistic. And by way of repetition, these three parameters, in turn, depend on the pattern of the three measured points in PC by SNR space.

It is found by least squares that the best linear combination of the three logistic parameters to predict PCn is given by Eq. (A1),

$$PC{n}^{\prime }=M0+M1(ua)+M2(b)+M3(LN(1/s)),$$ (A1)

where

$$\mathrm{M}0=-3.3677,\hspace{0.17em}\mathrm{M}1=0.7447,\hspace{0.17em}\mathrm{M}2=-1.8597,\hspace{0.17em}\text{and}\hspace{0.17em}\mathrm{M}3=-1.3253.$$

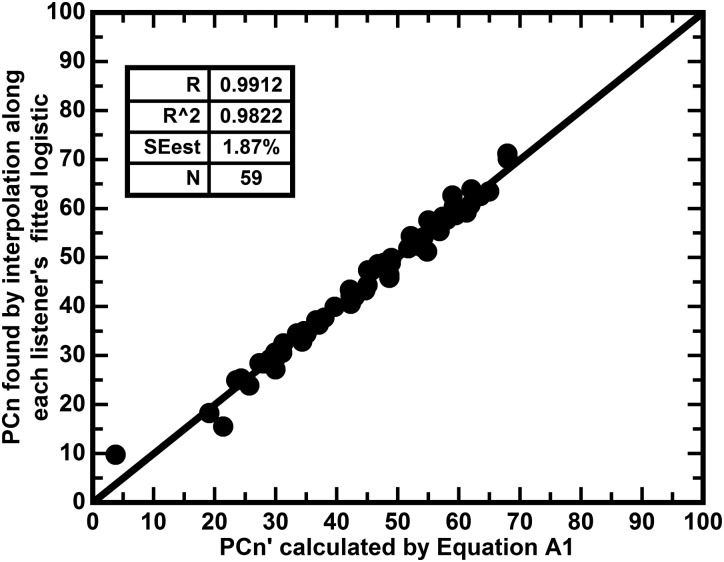
The correlation between PCn′ found by Eq. (A1) and the PCn found by interpolation along each listeners fitted logistic is 0.9912 and the resulting scatter plot is shown in Fig. 8. This figure proves that in the case of syllable-constituent identification the score in noise can be easily calculated based on the pattern of three measured points in the PC by SNR space.

FIG. 8.

Showing the multiple correlation between PCn measured by interpolation and PCn′ found by the best linear combination of the fitted parameters ua, b, and LN(1/s) as shown in Eq. (A1). Clearly, the patterns of the three measured points in the PC by SNR space allow accurate estimation of syllable-constituent identification in noise as 98.26% of the variance in PCn is accounted for and the standard error of the estimate is only 1.87%.

Next the first order correlations of the three free parameters of the fitted logistics with PCn are explored. As will be shown, the upper asymptote (ua) has the highest correlation with PCn being, by now familiar, 0.96. The next highest is correlation is that of b, the SNR at the inflection point, with PCn being 0.72. The logarithm of the fitted slope has the lowest correlation with PCn being 0.36. To be consistent with Fig. 8, the first order correlations are shown as plots of PCn versus PCn′ in Figs. 9, 10, and 11.

FIG. 9.

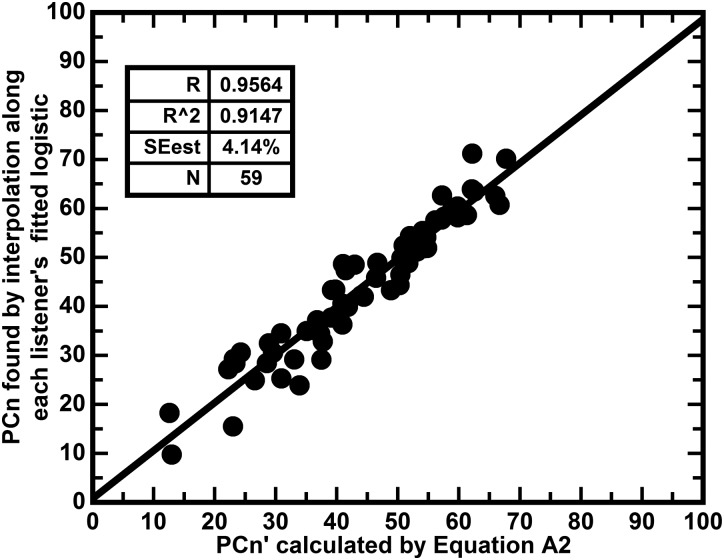
Showing the correlation between PCn′ calculated by Eq. (A2) and the PCn found by interpolation along each listener's fitted logistic. It can be seen that this relation is slightly less constrained than that shown in Fig. 8. While the multiple R accounts for 98.3% of the variance in PCn, when only ua is used the R accounts for 91.5% of the variance in PCn. This difference is mirrored in the standard errors of the estimates.

FIG. 10.

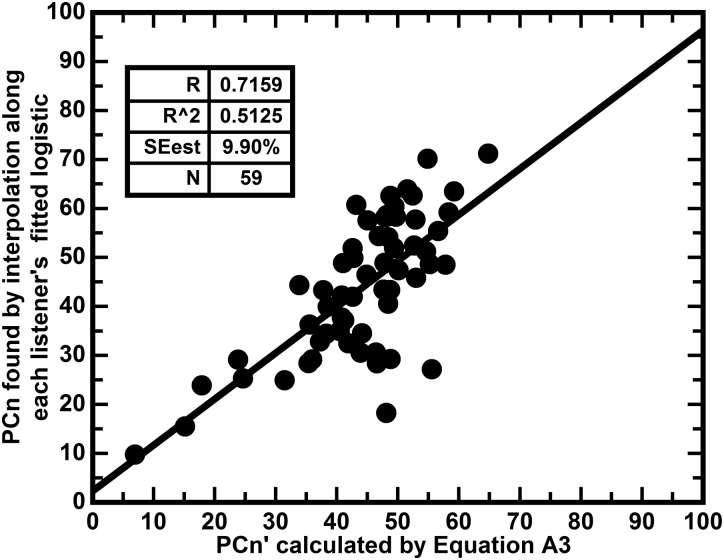
Showing the relation between PCn′ calculated from Eq. (A3) and PCn. The inflection point accounts for 61.25% of the variance in PCn. However, as will be shown, it only adds about 6.24% to the variance in PCn that is accounted for by the correlation with the upper asymptote, ua. Although it cannot be seen in this plot, as the inflection point increases in SNR, PCn declines.

FIG. 11.

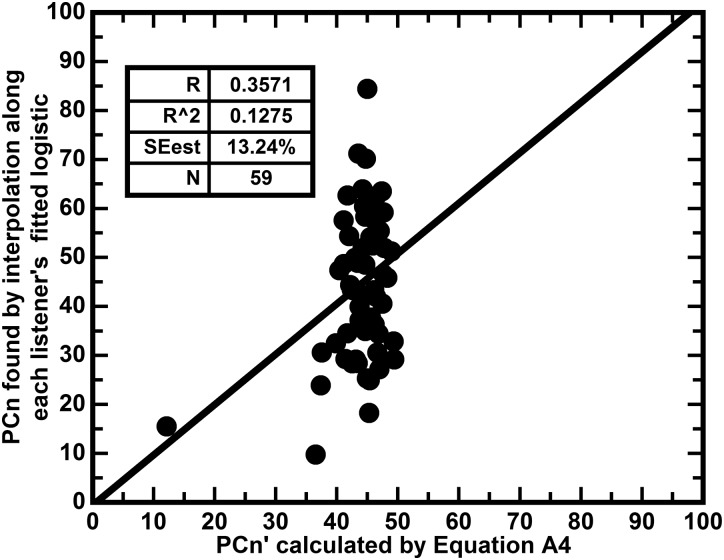
Showing the relation between PCn′ calculated by Eq. (A4) and PCn. The slope has little influence on PCn except for a few cases. As will be shown, the slope accounts for only 12.75% of the variance in PCn, but only adds a 0.51% reduction in the variance in PCn accounted for by the upper asymptote and the inflection point. Although not shown, the steeper the slope the lower PCn.

a. Correlation of the fitted upper asymptote with PCn.

It is found that the fitted ua correlates highly with PCn (0.9564) as would be expected from our previous work correlating PCq with PCn. The equation that best predicts PCn′ is Eq. (A2),

$$PCn\prime =-8.0161+0.8952(ua).$$ (A2)

b. Correlation of the fitted inflection point, b, with PCn.

The fitted inflection point, b, has a strong correlation (0.7135) with PCn and Eq. (A3) gives the least squares regression of PCn′ on b,

$$PC{n}^{\prime }=34.8340-3.0727(b).$$ (A3)

c. Correlation of LN(1/s) with PCn.

The logarithm of the reciprocal of the slope parameter of the logistic has a low (0.3571), but interesting, correlation with PCn. This relation is captured by Eq. (A4),

$$PC{n}^{\prime }=30.9586+7.8460\left(LN\left(\frac{1}{s}\right)\right).$$ (A4)

3. Summary of the factors contributing to PCn

PCn is determined by the pattern of the three measured points in the space of PC by SNR. This pattern determines the three fitted parameters of each listener's fitted logistic. Table VII summarizes the contribution of each these parameters to the determination of PCn.

TABLE VII.

Showing Logistic Parameters Relations with PCn.

Logistic Parameter(s)	R	R2	SEest	PCn Variance Explained
Slope [LN(1/s)]	0.3175	0.1275	13.24%	12.75%
Inflection Pt. (b)	0.7158	0.5125	9.90%	51.25%
Upper Asymptote-(ua)	0.9564	0.9147	4.14%	91.47%
ua and ba	0.9885	0.9771	2.34%	97.71%
ua, b, and LN(1/3)	0.9912	0.9822	1.87%	98.22%

^aGraph and analysis not shown in text.

The upper asymptote accounts for most of the variance in PCn. The addition of the inflection point gives a further reduction in the unexplained variance of 6.24%, while the addition of slope further reduces the unexplained variance by 0.51%. In other words, for the case of syllable-constituent perception, and based on the present data, the amount of the variation in performance in noise that is independent of the variation in quiet, but dependent on the inflection point and the slope of the logistic is about 6.75%. Finally, another 1.87% of the variance in PCn is due to unknown factors. No matter the exact allocation of variance reductions, it is clear that performance in noise is largely determined by performance in quiet and that this relation is determined by the pattern of the three measured points in PC by SNR space.