Full four-dimensional and reciprocal Mueller matrix bidirectional reflectance distribution function of sintered polytetrafluoroethylene

Abstract

We measured the Mueller matrix bidirectional reflectance distribution function (BRDF) of a sintered polytetrafluoroethylene (PTFE) sample over the scattering hemisphere for six incident angles (0° to 75° in 15° steps) and for four wavelengths (351 nm, 532 nm, 633 nm, and 1064 nm). The data for each wavelength were fit to a phenomenological description for the Mueller matrix BRDF that is an extension of the bidirectional surface scattering modes developed by Koenderink and van Doorn [J. Opt. Soc. Am. A 15, 2903 (1998)] for unpolarized BRDF. This description is designed to be complete, to obey the appropriate reciprocity conditions, and to provide a full description of the Mueller matrix BRDF as a function of incident and scattering directions for each wavelength. The description was further extended by linearizing the surface scattering mode coefficients with wavelength. This data set and its parameterization provides a comprehensive on-demand description of the reflectance properties for this commonly used diffuse reflectance reference material over a wide range of wavelengths.

1. INTRODUCTION

Having high reflectance from the near ultraviolet to the near infrared and being relatively Lambertian, pressed polytetrafluoroethylene (PTFE) powder was developed as a reference standard for diffuse reflectance and was used for constructing integrating spheres for irradiance averaging devices and uniform radiance sources [1–3]. A sintered, machinable version of the material, was developed and sold initially under the trade name Spectralon, then later Fluorilon-99W, Zenith, Spectralex, OP.DI.MA, and others¹ [4]. Much of its reflectance properties are well documented. Many studies considered the like-and crossed-polarized reflectance properties in the plane of incidence [5–10]. Mueller matrix properties in the plane of incidence are reported in [11–15]. A small number of measurements are reported out of the plane of incidence [16, 17], while [1–4, 11] considered the wavelength dependence of the optical properties. These works leave gaps in the availability of information, especially for out-of-plane geometries and for its polarization properties. These properties are needed to sufficiently model many applications of this material. Having a full four-dimensional (incident and scattering direction) description of the scattering properties, including polarization, over a wide wavelength range should close the gap on the ability to fully utilize this material and to understand errors that can arise in measurements due to its residual non-ideal properties.

In this work, we performed full Mueller matrix bidirectional reflectance distribution function (BRDF) measurements for a sintered PTFE sample, covering the hemisphere with over 300 sampled points at each of six incident angles ranging from normal incidence to 75° and for four wavelengths (351 nm, 532 nm, 633 nm, and 1064 nm). Making the assumption that the sample is isotropic, these data are sufficient to describe the reflectance for any incident and scattering direction. In 1998, Koenderink and van Doorn (KvD) [18] developed a phenomenological description of the unpolarized BRDF, which was designed to describe it in a manner that ensures reciprocity and the symmetries imposed by the isotropic nature of the sample and allowing for rapid on-demand evaluation of the BRDF in arbitrary geometries. We extend that description to allow for all of the Mueller matrix BRDF elements. Thus, we provide a description that allows for an on-demand evaluation of the Mueller matrix BRDF for any scattering geometry.

In Sec. 2, we describe the KvD surface scattering mode description and extend it to all elements of the Mueller matrix. In Sec. 3, we describe the measurements of the sintered PTFE sample. The results of those measurements and the fits to the extended KvD description are given in Sec. 4. In Sec. 5, we discuss the results by describing some metrics for the scattering behavior that are evaluated using the extended KvD representation of the data.

2. THEORY

Koenderink and van Doorn developed a phenomenological model for the unpolarized BRDF that, by construction, is complete and obeys reciprocity, using symmetrized products of Zernike polynmials [18]. That is, they show that the unpolarized BRDF can be expressed by a set of coefficients $a_{11,nm}^{kl}$ with

$$f_{\mathrm{r},11}({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}},{\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}})=\sum _{\mathit{nkml}}{a}_{11,nm}^{kl}{H}_{nm}^{kl}({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}},{\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}}),$$ (1)

where the bidirectional surface scattering modes are

$$H_{nm}^{kl}({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}},{\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}})=\frac{K_n^k({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}})K_m^l({\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}})+K_n^k({\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}})K_m^l({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}})}{{(2+2{\delta }_{nm}{\delta }_{kl})}^{1/2}},$$ (2)

where the Zernike polynomials are given by

$$K_n^k(\theta ,\varphi )=\sqrt{\frac{n+1}{\pi }}{R}_n^k\left(\sqrt{2}sin\frac{\theta }{2}\right){\text{az}}_k(\varphi ),$$ (3)

and where

$${\text{az}}_k(\varphi )=\{\begin{array}{cc}-sink\varphi ,& k<0\\ 1/\sqrt{2},& k=0\\ cosk\varphi ,& k>0.\end{array}$$ (4)

The radial Zernike polynomials are given by

$$R_n^m(\rho )=\sum _{s=0}^{(n-\mid m\mid )/2}{\left(+1\right)}^s\frac{\left(n-s\right)!}{s!\left(\frac{n-m}{2}-s\right)!\left(\frac{n-m}{2}-s\right)!}{\rho }^{n-2s}.$$ (5)

The subscript 11 in the BRDF f_r,11 and the coefficients $a_{11,nm}^{kl}$ in Eq. (2) indicates that they refer to the unpolarized 11 element of the Mueller matrix. The integer indices m and n vary from 0 to ∞ and can usually be truncated significantly, while the indices l and k vary from −m to m or −n to n, respectively, in steps of 2. KvD chose to express the argument to the radial Zernike function (see Eq. 3) as

$${\rho }_j=\sqrt{2}sin({\theta }_j/2)$$ (6)

in order to map points on the unit circle uniformly with solid angle on the hemisphere. It should be noted that one can also map points on the unit circle uniformly on the projected hemisphere, so that,

$${\rho }_j=sin{\theta }_j.$$ (7)

Other projections from the unit circle to the hemisphere can also be chosen. However, to be consistent with KvD, we keep the convention of Eq. (6). The denominator in Eq. (2) and the prefactor in Eq. (3) ensure that the surface scattering modes are orthonormal as defined in [18].

For isotropic media, the BRDF only depends upon Δϕ_ir = ϕ_r − ϕ_i, and KvD further showed that the BRDF can be expanded as

$$f_{\mathrm{r},11}({\theta }_{\mathrm{i}},{\theta }_{\mathrm{r}},\mathrm{\Delta }{\varphi }_{\text{ir}})=\sum _{\mathit{nmk}}{a}_{11,nm}^k{I}_{nm}^k({\theta }_{\mathrm{i}},{\theta }_{\mathrm{r}},\mathrm{\Delta }{\varphi }_{\text{ir}}),$$ (8)

where the isotropic surface scattering modes are

$$I_{nm}^k({\theta }_{\mathrm{i}},{\theta }_{\mathrm{r}},\mathrm{\Delta }{\varphi }_{\text{ir}})=\frac{1}{2\pi }{\left[\frac{(n+1)(m+1)}{A_{nm}^k}\right]}^{1/2}\times \left[R_n^k\left(\sqrt{2}sin\frac{{\theta }_{\mathrm{i}}}{2}\right)R_n^k\left(\sqrt{2}sin\frac{{\theta }_{\mathrm{r}}}{2}\right)+R_m^k\left(\sqrt{2}sin\frac{{\theta }_{\mathrm{i}}}{2}\right)R_n^k\left(\sqrt{2}sin\frac{{\theta }_{\mathrm{r}}}{2}\right)\right]\times cosk\mathrm{\Delta }{\varphi }_{\text{ir}},$$ (9)

and

$$A_{nm}^k=\{\begin{array}{ll}4\hfill & \text{if}(n=0)\text{or}((n=m)\text{and}(k=0))\hfill \\ 2\hfill & \text{if}((n=m)\text{or}(k=0))\hfill \\ 1\hfill & \text{otherwise.}\hfill \end{array}$$ (10)

Lastly, they point out that for the isotropic case the indices n, m, and k are restricted: n ≥ 0, 0 ≤ m ≤ n, 0 ≤ k ≤ m, and both n − k and m − k must be even. The expansions given in Eqs. (2) and (8) are complete for the BRDF of an anisotropic and an isotropic medium, respectively, provided there are no singularities. In practice, the sums are truncated, yielding a relatively small number of coefficients.

The polarization properties of the BRDF are best represented by describing the BRDF as a Mueller matrix, f_r(θ_r, ϕ_r, θ_i, ϕ_i) [19]. That is, the Mueller matrix BRDF is the linear relationship between the incident Stokes irradiance and the scattered Stokes radiance. In order to perform an expansion based upon Zernike polynomials, we need to choose the basis for the Mueller matrix carefully in order to avoid singularities. For example, in an s and p basis, defined as perpendicular and parallel, respectively, to the plane containing the direction of propagation and the surface normal (with different planes for incident and scattering directions), there exists a singularity along the surface normal. In a ⊥ and || basis, defined as perpendicular and parallel, respectively, to the plane containing both the incident and scattering directions of propagation, there exists a singularity in the retroreflection direction. These basis set singularities cause singularities in the Mueller matrix in out-of-plane geometries, which make it difficult to expand some matrix elements in a Zernike basis. Therefore, we chose an x and y basis set, defined as the same as p and s, respectively, when ϕ_i = 0 and ϕ_r = 0, but which rotate by ϕ_i and ϕ_r, respectively, to remove the singularity existing in the s-p basis at the surface normal. We consider y, x, and the direction of propagation to form a right-handed triplet. The x-y basis is the natural basis in a back-focal-plane microscope scatterometer. Here, we define the four elements of Stokes vectors by

$$\begin{gathered} S_1=I_y+I_x, \\ {S}_2=I_y-I_x, \\ {S}_3=I_{y+x}-I_{y-x}, \\ {S}_4=I_{\mathrm{l}}-I_{\mathrm{r}}, \end{gathered}$$ (11)

where I_y, I_x, etc. are intensity-like quantities (e.g., irradiance or radiance). I_l and I_r are intensities for left and right circular polarizations, where we use the convention that right-handed polarization refers to the electric field rotating clockwise when viewing into the beam.

We now extend the formalism of KvD to include the other elements of the Mueller matrix. As for the unpolarized BRDF, there is a reciprocity condition for the Mueller matrix BRDF f_r [20]. In this case, we have

$${\mathbf{f}}_{\mathrm{r}}({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}},{\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}})=\mathbf{A}{[{\mathbf{f}}_{\mathrm{r}}({\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}},{\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}})]}^{\mathrm{T}}\mathbf{A},$$ (12)

where A = diag(1, 1, −1, 1) relates a Stokes vector to its time-reversed counterpart. Thus, there is the requirement that the i j-th element obeys

$$f_{\mathrm{r},ij}({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}},{\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}})=\pm f_{\mathrm{r},ji}({\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}},{\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}}),$$ (13)

where the sign is chosen to be positive for i j = 11, 22, 33, 44, 12, 14, or 24 and negative for i j = 13, 23, or 34.

For the other diagonal Mueller matrix elements, we can use the same basis set as the 11 element in Eq. (2), since the surface scattering modes $H_{nm}^{kl}({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}},{\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}})$ obey Eq. (13). That is,

$$f_{\mathrm{r},ii}({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}},{\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}})=\sum _{\mathit{nkml}}{a}_{ii,nm}^{kl}{H}_{nm}^{kl}({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}},{\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}}).$$ (14)

For the off-diagonal Mueller matrix elements, we note that the functions $K_n^k({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}})K_m^l({\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}})$ form a complete orthogonal basis for the functions on (θ_i, ϕ_i, θ_r, ϕ_r). We enforce reciprocity by requiring that, for i < j, the upper elements be

$$f_{\mathrm{r},ij}({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}},{\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}})=\sum _{\mathit{nkml}}{a}_{ii,nm}^{kl}{K}_n^k({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}})K_m^l({\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}}),$$ (15)

and the lower elements be

$$f_{\mathrm{r},ji}({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}},{\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}})=\pm \sum _{\mathit{nkml}}{a}_{ij,nm}^{kl}{K}_m^l({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}})K_n^k({\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}}),$$ (16)

where the choice of signs is the same as for Eq. (13). The restrictions on the indices nm, kl are the same as for Eq. (2).

As above, when the material is isotropic and non-chiral, some simplications can be made. However, since most of the Mueller matrix elements are not rotationally symmetric in the x-y basis at normal incidence or viewing, we choose to keep the Eqs. (14), (15), and (16), but restrict the combinations of indices that can contribute and require some coefficients to be identical. For all of the Mueller matrix elements, n −m must be even (that is, n and m must be both odd or both even). For the diagonal elements, we chose n ≤ m to avoid redundancy. Also, the Zernike polynomials require that |k| ≤ n and |l| ≤ m.

The rest of the restrictions imposed by isotropy and non-chirality are on the allowable values of k and l and depend upon matrix element. These are determined by ensuring that the Mueller matrix is even or odd with respect to the plane of incidence when the radiation is incident in the x-z plane and ensuring that the azimuthal dependence of the matrix element at normal incidence or viewing is correct. These rules can be summarized as follows:

• For the elements 22 and 33, all values k > 0 and l > 0, such that k ≤ n ≤ m and l ≤ m, are allowed. Values k < 0 and l < 0 are also allowed, but $a_{ii,nm}^{(-k)(-l)}=a_{ii,nm}^{kl}$. In addition, kl can be 00 and 40.

• For the element 44, all values k > 0 and l > 0, such that k ≤ n ≤ m and l ≤ m, are allowed. Values k < 0 and l < 0 are also allowed, but $a_{ii,nm}^{(-k)(-l)}=a_{ii,nm}^{kl}$. In addition, kl can be 00.

• For elements 12 and 34 (and their transpose pairs), all values k > 0 and l > 0, such that k ≤ n and l ≤ m, are allowed. In addition, kl can be 02 and 20.

• For elements 13 and 24 (and their transpose pairs), all values of kl for which k < 0 and l > 0 or k > 0 and l < 0, such that |k| ≤ n and |l| ≤ m, are allowed. In addition, kl can be 02̄ and 2̄0. (2̄ = −2)

• For element 23 (and its transpose pair), all values of kl for which k < 0 and l > 0 or k > 0 and l < 0, such that |k| ≤ n and |l| ≤ m, are allowed. In addition, kl can be 04̄ and 40̄.

• And, for element 14 (and its transpose pair), all values for which k < 0 and l > 0 or k > 0 and l < 0, such that |k| ≤ n and |l| ≤ m, are allowed. Neither k nor l can be 0.

If the parameters describing the Mueller matrix BRDF vary slowly with wavelength λ, we can approximate the coefficients as depending linearly on the wavelength, at least for some small spectral region. That is, we can further expand the Mueller matrix BRDF to include the dependence on λ. For the unpolarized 11 element, we let

$$f_{\mathrm{r},11}({\theta }_{\mathrm{i}},{\theta }_{\mathrm{r}},\mathrm{\Delta }{\varphi }_{\text{ir}})=\sum _{\mathit{nmkp}}{a}_{11,nm}^{kp}{\lambda }^p{I}_{nm}^k({\theta }_{\mathrm{i}},{\theta }_{\mathrm{r}},\mathrm{\Delta }{\varphi }_{\text{ir}}).$$ (17)

for the other diagonal elements, we let

$$f_{\mathrm{r},ii}({\theta }_{\mathrm{i}},{\theta }_{\mathrm{r}},\mathrm{\Delta }{\varphi }_{\text{ir}})=\sum _{\mathit{nmklp}}{a}_{ii,nm}^{\mathit{klp}}{\lambda }^p{H}_{nm}^{kl}({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}},{\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}}),$$ (18)

and for the off-diagonal elements, we let

$$f_{\mathrm{r},ij}({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}},{\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}})=\sum _{\mathit{nkmlp}}{a}_{ij,nm}^{\mathit{klp}}{\lambda }^p{K}_n^k({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}})K_m^l({\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}}),$$ (19)

and

$$f_{\mathrm{r},ji}({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}},{\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}})=\pm \sum _{\mathit{nkmlp}}{a}_{ij,nm}^{\mathit{klp}}{\lambda }^p{K}_m^l({\theta }_{\mathrm{i}},{\varphi }_{\mathrm{i}})K_n^k({\theta }_{\mathrm{r}},{\varphi }_{\mathrm{r}}),$$ (20)

where the coefficients $a_{ii,nm}^{kp}$ and $a_{ij,nm}^{\mathit{klp}}$ obey the same restrictions as $a_{ii,nm}^k$ and $a_{ij,nm}^{kl}$, respectively, and we let p be 0 or 1.

We determine expansion coefficients by performing linear least-square fits of the data of interest to the model. The 11 element of the Mueller matrix BRDF is fit directly. All of the other elements are normalized by the 11 element before fitting. Each of the diagonal elements are fit separately. Each transpose pair of off-diagonal elements are fit simultaneously. For multi-wavelength fits, the unpolarized BRDF (f_r,11) is first normalized, so that the normal incidence directional-hemispherical reflectance is 1. Afterwards, the directional-hemispherical reflectance, which is not linear in wavelength, can be returned to the BRDF by scalar multiplication.

3. MEASUREMENT

Measurements were carried out using the laser-based goniometric optical scatter instrument (GOSI) at NIST [21]. GOSI measures the Mueller matrix BRDF for any pair of incident and scattering directions at a number of laser wavelengths. Four laser sources were used for these measurements: a continuous wave (cw) Nd-doped yttrium-aluminum-garnet (Nd:YAG) laser operating at 1064 nm, a cw HeNe laser operating at 633 nm, a frequency-doubled cw Nd:YAG laser operating at 532 nm, and a frequency-doubled mode-locked Ti:sapphire laser operating at 351 nm (fundamental at 702 nm). The solid angle subtended by the receiver was 1.114 × 10⁻⁴ sr. Data were taken for six incident angles (0°, 15°, 30°, 45°, 60°, and 75°), measuring the scatter on a uniform grid in projected directional cosine space, with directional cosine spacing of 0.1, so that there were 304 scattering directions measured for each incident angle. Points were removed from each wavelength’s dataset if the receiver was blocking the incident beam.

Mueller matrix measurements were performed using a rotating-retarder polarization state generator and a rotating-retarder polarization state analyzer. Sixteen measurements in a 4 × 4 grid were performed at each scattering geometry. The reduction matrix converting the sixteen measurements to the Mueller matrix was determined using the method of Compain et al. [22]. This method uses a high quality polarizer (in this case a Glan-Taylor polarizer) in transmission and a diattenuator-retarder (in this case a silicon wafer with a nominal 1000 nm thermally-grown SiO₂ layer) in reflection. While the method calls for one full Mueller matrix measurement from each of the two references and one without any sample present, we perform measurements of the polarizer in transmission for 18 different rotations (0° to 170°), measurements of the diattenuator-retarder for 18 angles of incidence (30° to 75°), and 18 measurements without any reference. Thus, there was significant redundancy in our calibration process that allows us to determine various figures of merit for the accuracy of subsequent measurements. For example, the standard deviation of all the reference measurements across all elements of the normalized Mueller matrix were 0.0043 (for 351 nm), 0.0014 (for 532 nm), 0.0023 (for 633 nm), and 0.0052 (for 1064 nm). We believe we can use these standard deviations as standard uncertainties in subsequent measurements. Since the natural coordinate system for the laboratory is that defined by the scattering plane containing incident and scattering directions, data are acquired in that coordinate system and numerically converted to the x-y coordinate system.

The actual Mueller matrix BRDF data have larger random uncertainties, mostly due to laser speckle; these can be estimated by observing the point-to-point variations in the data. The apparent noise is higher for the 1064 nm results, partly because of the longer wavelength, but also since the focussing of the system had been changed so that the spot size at the sample was smaller.

The sample was an 8 mm thick, 50 mm diameter coupon of sintered PTFE obtained commercially. The material was unsupported, and the back was left open during the measurements. Previous measurements on similar samples [13] showed some non-ideal behavior in sintered PTFE. In particular, there was a small amount of anisotropy observed, and some Mueller matrix elements, that should have been zero in the plane of incidence, especially 23 and 32, were not zero, but averaged to zero, when the sample was rotated. All measurements taken with the evenly spaced scattering directions had a fixed plane of incidence that was maintained between wavelengths.

Another set of data was obtained at 532 nm, where approximately 1800 (similar to those described above) incident and scattering direction pairs were randomly chosen uniformly in projected directional cosine space. In order to avoid obscuration by parts of the instrument and to not have too large an illumination area on the sample, θ_i and θ_r were restricted to angles less than 75°. This secondary set of data was intended to help assess the uncertainties in the fitting parameters, since selecting a subset of points would not bias the results in any way. That is, selecting every other three data points produces three separate sets of data, from which separate expansions could be determined. Because the incident directions were randomized in ϕ_i, this set also helps to assess the affects of sample anisotropy on the results.

4. RESULTS

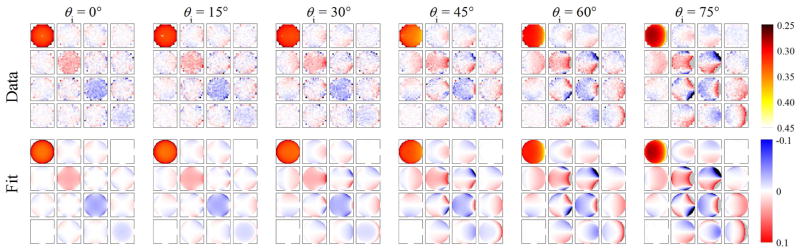
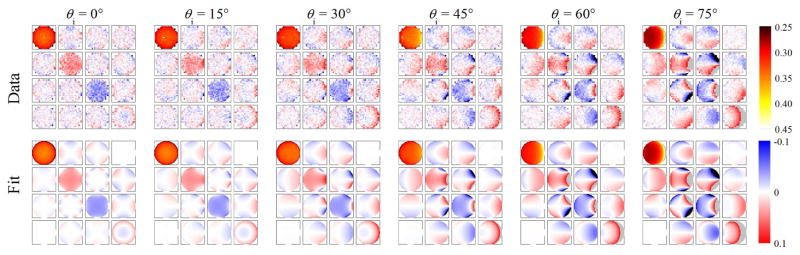
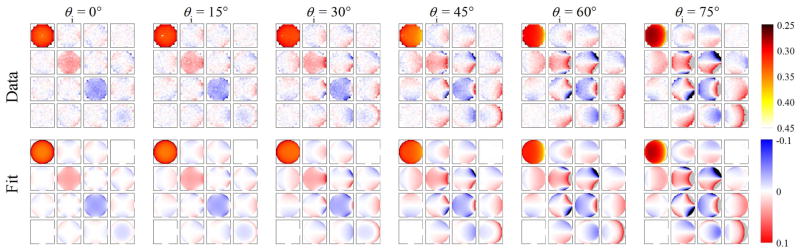
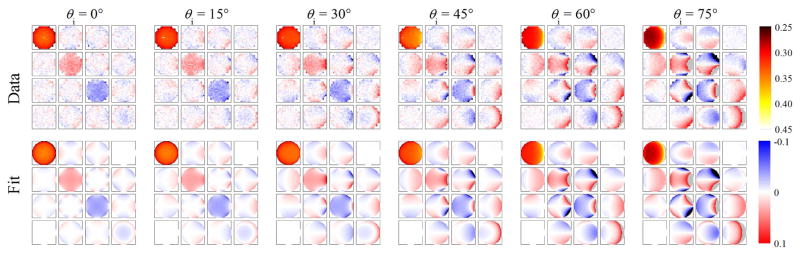
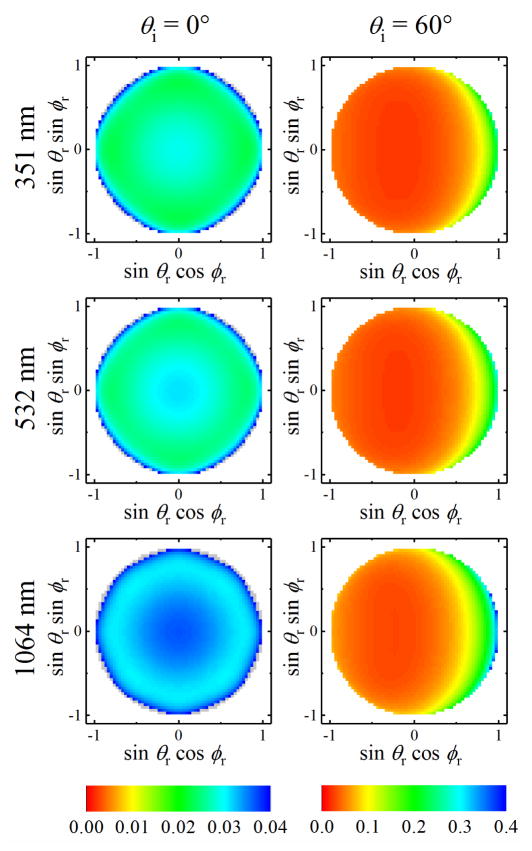
The results of the measurements are shown in Figs. 1 – 4 for 351 nm, 532 nm, 633 nm, and 1064 nm, respectively. The results are shown in projected directional cosine space, with the plane of incidence being a horizontal line through the center of each circle. The radial coordinate of each circle represents sin θ_r. The data for each wavelength were initially fit to obtain the coefficients $a_{11,nm}^{kl}$ (with orders up to 7) and $a_{ij,mn}^{kl}$ (with orders up to 4). There were noticeable and consistent trends of the Mueller matrix BRDF with wavelength. We also attempted to fit all of the data to obtain the coefficients $a_{11,mn}^{\mathit{klp}},a_{ii,mn}^{\mathit{klp}}$ and $a_{mn,ij}^{\mathit{klp}}$. The results of this latter fit are shown with each of the data sets in Figs. 1, 2, 3, and 4. The overall root-mean-square deviation for the fits were 0.004 sr⁻¹ for the 11 element, 0.010 for elements 12, 13, and 14. 0.013 for elements 22, 23, and 24, 0.014 for element 33, 0.012 for element 34, and 0.011 for element 44. Since the element 14 (together with its transpose pair) has the least structure and is easiest to fit, the root-mean-square deviation is believed to be nearly entirely from the speckle noise and the small anisotropy of the sample. The single wavelength fits were somewhat better than the multi-wavelenth fits, but the results are not shown in the figures, since the differences are difficult to distinguish by eye. Further comparison will be shown later in the Discussion.

Fig. 1.

The Mueller matrix BRDF at 351 nm shown in projected directional cosine space (vertical and horizontal scales −1 to 1). Each column corresponds to an incident angle. The top row shows the measured data, while the second row shows the fit to the phenomenological model for an isotropic medium with a linear wavelength dependence. The 11 element is on a scale from (black) 0.25 sr⁻¹ to (white) 0.45 sr⁻¹, while the other elements are shown normalized on a scale from (blue) −0.1 to (red) 0.1. Some regions are saturated on this scale. See Supplementary Information for tabulated data.

Fig. 4.

The Mueller matrix BRDF at 1064 nm shown in projected directional cosine space (vertical and horizontal scales −1 to 1). Each column corresponds to an incident angle. The top row shows the measured data, while the second row shows the fit to the phenomenological model for an isotropic medium with a linear wavelength dependence. The 11 element is on a scale from (black) 0.25 sr⁻¹ to (white) 0.45 sr⁻¹, while the other elements are shown normalized on a scale from (blue) −0.1 to (red) 0.1. Some regions are saturated on this scale. See Supplementary Information for tabulated data.

Fig. 2.

The Mueller matrix BRDF at 532 nm shown in projected directional cosine space (vertical and horizontal scales −1 to 1). Each column corresponds to an incident angle. The top row shows the measured data, while the second row shows the fit to the phenomenological model for an isotropic medium with a linear wavelength dependence. The 11 element is on a scale from (black) 0.25 sr⁻¹ to (white) 0.45 sr⁻¹, while the other elements are shown normalized on a scale from (blue) −0.1 to (red) 0.1. Some regions are saturated on this scale. See Supplementary Information for tabulated data.

Fig. 3.

The Mueller matrix BRDF at 633 nm shown in projected directional cosine space (vertical and horizontal scales −1 to 1). Each column corresponds to an incident angle. The top row shows the measured data, while the second row shows the fit to the phenomenological model for an isotropic medium with a linear wavelength dependence. The 11 element is on a scale from (black) 0.25 sr⁻¹ to (white) 0.45 sr⁻¹, while the other elements are shown normalized on a scale from (blue) −0.1 to (red) 0.1. Some regions are saturated on this scale. See Supplementary Information for tabulated data.

The BRDF data, the coefficients $a_{11,mn}^{kl}$ and $a_{ij,mn}^{kl}$ determined for each wavelength, and the coefficients $a_{11,mn}^{\mathit{klp}}$ and $a_{ij,mn}^{\mathit{klp}}$ determined for all of the wavelengths taken together are provided in the Supplementary Information. These coefficients can be used for on-demand evaluation of the Mueller matrix BRDF for any wavelength in the range of the data. Since the data were normalized to unit reflectance before the multi-wavelength fits, determination of the BRDF from the coefficients $a_{11,mn}^{\mathit{klp}}$ needs to account for the spectral reflectance of PTFE, which could not be linearized. We assumed the reflectance of the sample were those given by the manufacturer as 0.976 (for 351 nm), 0.984 (for 532 nm), 0.984 (for 633 nm), and 0.983 (for 1064 nm). The Supplementary Information contains C++ code that evaluates the Mueller matrix BRDF using the tabulated coefficients. These codes have been incorporated into the SCATMECH library of scattering models [23] and the Modeled Integrated Scatter Tool (MIST) [24].

5. DISCUSSION

By describing the data by its surface scattering mode expansion, we accomplish a number of goals. The first, that the BRDF can be evaluated on demand for arbitrary geometry or wavelength, has already been mentioned. Because we have truncated the expansion to only include those orders which we believe are significant, it also serves to remove noise in the data. The expansion also forces the scattering pattern to have the required symmetry. Finally, for polarimetric data, it removes noise in a manner which should better reflect the properties that would be non-linear in the Mueller matrix.

As an example, we evaluate the Gil-Bernabeu depolarization parameter [25]

$$D=\frac{1}{\sqrt{3}{f}_{\mathrm{r},11}}\sum _{ij\ne 11}{f}_{\mathrm{r},ij}^2$$ (21)

for three wavelengths (532 nm and 633 nm were very close to one another, so the latter is not shown) and two incident angles using the wavelength-dependent expansion. The results are shown in Fig. 5. Note that, while the parameter is typically called the depolarization parameter, higher levels of depolarization yield smaller parameter values. These data show an increasing degree of depolarization observed as the wavelength is shortened. Furthermore, there is a change in the width of the forward-scattering feature, which is less depolarizing (higher depolarization factor). Subtle flaws in the model can also be observed: the normal incidence depolarization shows a small four-fold symmetric pattern, which is a result of all of the matrix elements being fit separately and some of them forced to have four fold symmetry. Furthermore, we have only included Zernike orders up to 4. The example shown in Fig. 5 is representative of a value that is non-linear in the Mueller matrix. If we were to evaluate the depolarization parameter of the data directly, we would observe less depolarization, because the speckle pattern is fully polarized and the measured degree of polarization increases as the size of the detector decreases. By having a suitable smoothening procedure, such as the surface scattering mode expansion of the data, we can extract these values without this bias.

Fig. 5.

The Gil-Bernabeu depolarization parameter determined from the model shown in projected cosine space for 351 nm, 532 nm, and 1064 nm and for normal incidence and for 60° incidence.

Figure 6 shows the co- and cross-polarized BRDFs in the plane of incidence calculated for θ_i = 45° for the four wavelengths and for both the single-wavelengh fits and the multi-wavelength fit. The cross-polarized BRDF is much flatter than the co-polarized part and there is larger s→s scattering than p→p scattering. For the most part, there is good agreement between the single-wavelength fits and the multi-wavelength fits, with the largest deviation observable for the crossed polarized elements in the forward scattering regime for 351 nm. Since 351 nm is at a point where there is beginning to be some absorption, this may be due to the scattering behavior changing or it may be due to the larger errors of the single-wavelength fits. At angles past 75°, the different curves have different behavior, either at the same wavelength or between wavelengths. This effect is due to a combination of the orders used to fit the data and the use of 75° as the maximum incident angle. As a result, it is expected that the model fits will have limited applicability for either incident or scattering polar angles greater than 75°.

Fig. 6.

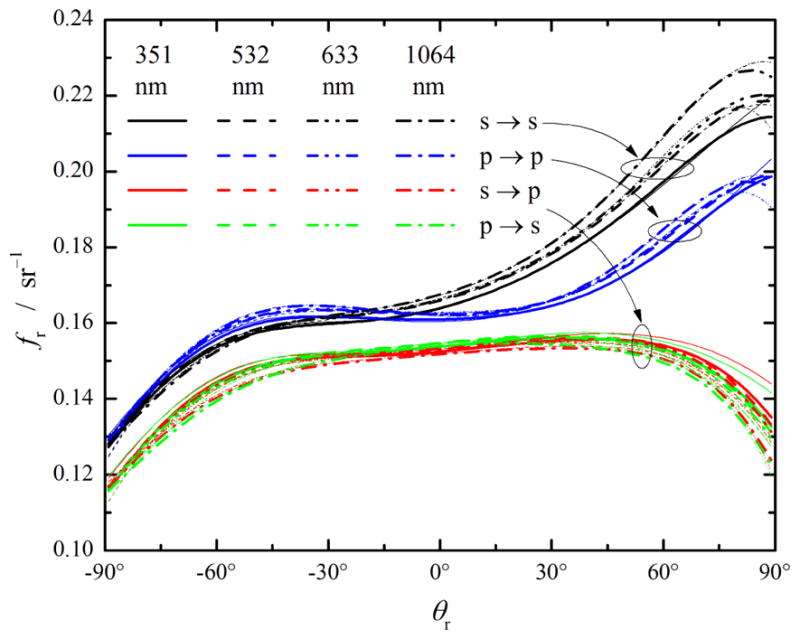
Calculated co- and cross-polarized BRDF in the plane of incidence for θ_i = 45° using (thin lines) the fits to each wavelength separately and (thick lines) the fits to all of the wavelengths simultaneously. The components are (black) s→s, (red) s→p, (green) p→s, and (blue) p→p. The wavelengths are (solid) 351 nm, (dashed) 532 nm, (dash-dot-dot) 633 nm, and (dash-dot) 1064 nm.

Figure 7 shows a comparison of the calculated co- and cross-polarized BRDF in the plane of incidence for θ_i = 45° and λ = 532 nm, obtained from the data shown in Fig. 2 and those obtained from the randomly sampled incident and scattering directions. Since the total number of randomly sampled data points measured was approximately the same as the number of evenly sampled data points, and because the randomly sampled points were down-sampled by three, one should expect that the uncertainty in the curves determined from the randomly sampled points to be approximately 1.7 greater than that for the evenly sampled points. Furthermore, the evenly sampled points had scattering polar angles exceeding 75°, while the randomly sampled points were limited to scattering angles less than 75°, so one should expect the results to not be reliable for θ_r < −75° or θ_r > 75°. Some of the systematic differences for θ_r > 50° may be due to the fact that the sample exhibited some anisotropy, which was not compensated by fitting the evenly sampled points to an isotropic model. The average absolute value of the fractional deviation between the fits to the randomly sampled data and the fit for the evenly spaced data for −60° ≤ θ_r ≤ 60° was 0.59 %, while the maximum average fractional deviation between them was 2.6 %. The average of the standard deviation of the fractional difference between fits to the randomly sampled data over the sampled angle range is 0.52 %.

Fig. 7.

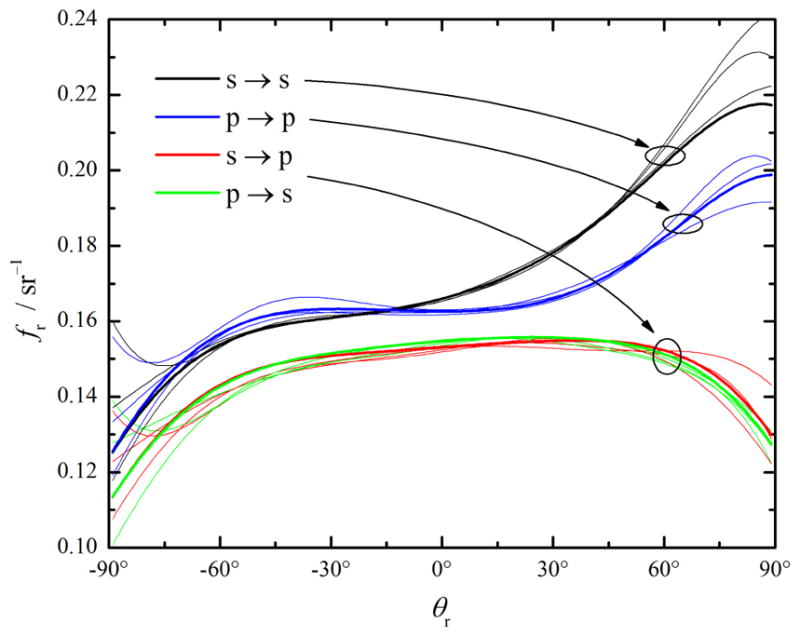
Calculated co- and cross-polarized BRDF in the plane of incidence for θ_i = 45° and λ = 532 nm using (thin lines) the fits to the three independent sets of random incident and scattering direction pairs and (thick lines) the fit to the data shown in Fig. 2. The components are (black) s→s, (red) s→p, (green) p→s, and (blue) p→p.

The results described here are in reasonable agreement with other work on this material, especially given that there is minor variation between specimens of the same material. [4–8, 10–16] Some conspicuous discrepancies are due to differences in polarization basis, which will change the sign of Mueller matrix elements. [14] Also, some works display f_r,11 cos θ_r rather than f_r,11 and to normalize to values at θ_r = 0. [14, 15]

The surface scattering mode approach for describing the scattering from sintered PTFE is an entirely phenomenological description of the scattering properties. Its only physical requirements are that reciprocity be obeyed and that the material behaves as if it were isotropic and non-chiral. Thus, in this manuscript, we do not describe the physical process that causes the material to scatter, nor do we extract physical parameters such as the scattering phase function. Other work has discussed radiative transfer models for this material [13].