Detecting genetic association through shortest paths in a bi-directed graph

Abstract

Genome-wide association studies (GWASs) commonly use marginal association tests for each single nucleotide polymorphism (SNP). Because these tests treat SNPs as independent, their power will be suboptimal for detecting SNPs hidden by linkage disequilibrium (LD). One way to improve power is to use a multiple regression model. However, the large number of SNPs preclude simultaneous fitting with multiple regression, and subset regression is infeasible because of an exorbitant number of candidate subsets. We therefore propose a new method for detecting hidden SNPs having significant yet weak marginal association in a multiple regression model. Our method begins by constructing a bi-directed graph locally around each SNP that demonstrates a moderately sized marginal association signal, the focal SNPs. Vertexes correspond to SNPs, and adjacency between vertexes is defined by an LD measure. Subsequently, the method collects from each graph all shortest paths to the focal SNP. Finally, for each shortest path the method fits a multiple regression model to all of the SNPs lying in the path and tests the significance of the regression coefficient corresponding to the terminal SNP in the path. Simulation studies show that the proposed method can detect susceptibility SNPs hidden by LD that go undetected with marginal-association testing or with existing multivariate methods, including lasso. When applied to real GWAS data from the Alzheimer's Disease Neuroimaging Initiative (ADNI), our method detected two groups of SNPs: one in a region containing the apolipoprotein E (APOE) gene, and another in a region close to the semaphorin 5A (SEMA5A) gene.

1 Introduction

In genome-wide association studies (GWASs), researchers routinely use univariate regression to analyze each single nucleotide polymorphism (SNP). Although GWASs have led to the discovery of many new SNPs that are involved in disease development and/or progression of clinical characteristics, the genetic architecture of many human traits remains largely unknown (Manolio 2013). This is referred to as a missing heritability problem (Manolio et al. 2009, Maher 2008), for which several explanations have been proposed. These include gene-environment interaction; gene-gene interaction; and the contributions of rarer variants, structural variants, and many variants with small effects. Researchers are attempting to develop statistical methods to test such challenging scientific hypotheses. Linkage disequilibrium (LD) may also contribute to missing heritability (Ehret et al. 2012). The univariate regression approach—or marginal association testing—works for SNP panels designed to capture causal variants under the assumption of a single causal variant or unlinked multiple causal variants (de Bakker et al. 2005, Eberle et al. 2007, Spencer et al. 2009). If this assumption is violated, marginal association testing, which treats SNPs as independent and does not fully take LD into account, may fail to achieve adequate statistical power. For example, if multiple causal SNPs in a region are in LD, the marginal association signal can be weakened due to cancellation of effects (Eberle et al. 2007). (See “Supplementary Information Section 4” for an illustration under a bivariate model.) We refer to this as the hidden signal problem. It differs from the case of an untyped causal variant, where the true causal variant is not included in the panel of SNPs tested. The hidden signal problem can occur even if all causal variants are included in the data. Therefore, an association signal hidden by LD may be undetectable, even with genotype imputation, when a marginal association test is employed.

Simultaneous analysis using multiple regression may be effective if the number of candidate SNPs is small. However, because GWAS data contain a large number of SNPs, fitting them simultaneously with a multiple regression model is impossible. A two-marker test based on bivariate regression is applicable to the above problem: Kim et al. (2010), Slavin et al. (2011), and Wang et al. (2012) proposed using two adjacent SNPs, and Howey and Cordell (2014) recently proposed a different two-marker test, an artificial imputation (AI) test. All of these two-marker tests are motivated by the goal of improving statistical power under a scenario in which a single causal variant exists and coverage by the marker (tag) SNPs is poor. Another applicable method is the multiple marker test based on a sliding window approach, as implemented in the UNPHASED method (Dudbridge 2008, Dudbridge et al. 2011); this approach tests the effect of a haplotype comprising multiple SNPs. The sliding window approach tests the combined, group effect of a set of nearby SNPs. However, it is not necessary that nearby SNPs possess similar effects. Taking a wider window may avoid missing causal SNPs, but it concomitantly increases the number of tested SNPs, thereby expending degrees of freedom—in particular, when most of the SNPs in a group are neutral— so that statistical power is greatly decreased.

In this paper, we describe a new method that can detect SNPs hidden by LD. To account for LD, we fit a multiple regression model for each SNP one-at-a-time (which we call the focal SNP) by incorporating other, adjacent SNPs that are in LD with the focal SNP. We develop a SNP selection method based on a bi-directed graph (Cox and Wermuth 1996, Kauermann 1996, Drton and Perlman 2007) to narrow the field of candidate SNPs to be incorporated into the model. Adjacency is defined by using a measure of LD. Then, in the bi-directed graph, all shortest paths to the focal SNP are identified and saved. Finally, the multiple regression model is fitted to all of the SNPs lying in each shortest path, and significance of the regression coefficient corresponding to the terminal SNP (the SNP farthest from the focal SNP) in each path is tested. The rationale for seeking the shortest paths is that the regression coefficient of the terminal SNP has nonzero effect in a noiseless setting (see Proposition 2). Our method aims to detect SNPs that have weak marginal association but show strong association in a multiple regression model after adjustment is made for confounding due to multiple nearby SNPs. We develop a conservative multiple testing procedure to control the family-wise error rate in testing the regression coefficients of the terminal SNPs in each graph. Simulation studies and application to real GWAS data from the Alzheimer's Disease Neuroimaging Initiative (ADNI) demonstrate that the proposed method can detect disease susceptibility SNPs hidden by LD that go undetected with the marginal association test or with existing multivariate methods.

2 Material and Methods

2.1 The proposed bi-directed graph approach

Suppose that we have observations consisting of n subjects with p SNPs X = (X₁, … , X_p), where X_j = (X_1j, … , X_nj)^T with X_ij ∈ {0, 1, 2} (i.e. the minor allele count) for i = 1, … , n and j = 1, … , p, together with quantitative phenotype data y = (y₁, … , y_n)^T. Let M = {1,… , p}. For a subset A ⊂ M, we denote by X_A the sub-column matrix of X in which the indexes run through the subset A. Similar notation is used for vectors throughout. In standard SNP-GWAS analysis, the effect of each SNP is investigated by testing the null hypothesis that the regression coefficient β_j of jth SNP is zero in a marginal model,

$$y=1{\beta }_0+X_j{\beta }_j+\varepsilon ,$$

where β₀ is the intercept, 1 denotes an n-vector with all components being unity, and ∊ ∼ N(0, σ²I). When the marginal effect is weak, the standard marginal testing approach is expected to be underpowered. The existence of multiple causal SNPs that are in LD may weaken the marginal association signal (See “Supplementary Information Section 4”). In this situation, controlling for the correlation structure due to LD should improve the detection power. Therefore, we consider testing for the effect of the jth SNP conditional on a set of other SNPs, A ⊂ M \ {j}. Specifically, we test the null hypothesis that β_j, the regression coefficient of jth SNP, is zero in a multiple linear regression model,

$$y=1{\beta }_0+X_j{\beta }_j+X_A{\beta }_A+\varepsilon ,$$

where β_A is the vector of regression coefficients corresponding to X_A and ∊ ∼ N(0, σ²I). Let β̂_j,A be the regression coefficient estimated by least squares in the above multiple regression model. If A = ∅, the above test reduces to the standard marginal association test. To detect SNPs whose effect is hidden by LD, testing for the effect of β̂_j,A with a non-empty set A ⊂ M \ {j} may produce higher power than the marginal association test. However, there exist numerous choices for A, so with GWAS data, where p is large, it is difficult to compute β̂_j,A for all possible subsets A ⊂ M. Even if all combinations of A are computable, we face a multiple testing burden in evaluating β̂_j,A, i.e. testing the null hypothesis

$$\forall A\subset M\backslash \{j\}:{\beta }_{j,A}=0.$$

It is unclear how to carry out a multiple testing correction. There are $\left(\begin{array}{c}p-1\\ m\end{array}\right)$ possibilities of β̂_j,A for A with |A| = m for a given m < n. For example, consider p = 500, 000 SNPs. Then, for m = 2, 3, and 4 (i.e. two, three, and four conditioning SNPs), we have roughly 1.2 × 10¹¹, 2 × 10¹⁶, and 3 × 10²¹ possibilities, respectively. If all tests are independent, then the Bonferroni correction is appropriate. However, the independence assumption is violated by the correlation among tests due to LD as well as the repeated tests of the jth SNP simply by altering the set of conditioning SNPs. Therefore, the naive Bonferroni approach should lead to unrealistically stringent multiple testing correction.

To deal with this challenging problem, we utilize a bi-directed graph (Drton and Perlman 2007) for SNPs with adjacency defined by the pairwise correlation between SNPs. For a given matrix X, let Q_X = I − P_X, where P_X is the projection onto the column space of X. Then, for an n-dimensional vector x, Q_Xx is the residual from regression of x onto X. Hereafter, we assume that n-dimensional vectors are standardized: specifically, assume that x satisfies both x^T1 = 0 and ║x║² = 1. For two standardized n-dimensional vectors x₁ and x₂, the inner-product $x_1^T{x}_2={\sum }_{i=1}^n{x}_{1i}{x}_{2i}$ equals the sample correlation. Centering of an n-vector X_j is obtained by x_j = Q₁X_j = X_j − P₁X_j, then $x_j^{T}1=0$ holds. In some circumstances, we have covariates Z, such as age, gender, and known genetic variants, whose effects on y need to be removed according to prior scientific knowledge. In such cases, we consider x_j = Q_(1,Z)X_j.

We denote the bi-directed graph by G = (V, E) having a vertex set V = {0} ∪ M and an edge set E ⊂ V × V. Hence |V| = 1 + p. Let the vertex 0 be the phenotype, i.e. x₀ = μ = E(y|X). The remaining vertexes belonging to M correspond to the p SNPs. Two arbitrary vertexes j and k in V are adjacent if and only if (j, k) ∈ E; Otherwise, they are not adjacent. Here, we say that two vertexes j and k (j ≠ k) in V are adjacent if

$$x_j^T{x}_k\ne 0.$$ (1)

Adjacent vertexes are said to be spouses, and they are joined by a bi-directed edge j ↔ k. Therefore, absence of an edge between vertexes j and k corresponds to $x_j^T{x}_k=0$, whereas the presence of an edge corresponds to $x_j^T{x}_k\ne 0$. A path from vertex j to vertex k is a sequence of adjacent edges connecting j and k for which the corresponding sequence of vertexes contains no repetitions. We refer to the first and the last vertexes as the terminals of the path, and all other vertexes as intermediate vertexes. For two standardized SNP vectors, x_j and x_k, coded as 0, 1, 2, $x_j^T{x}_k$ coincides with the Wellek–Ziegler correlation coefficient, which measures the magnitude of LD — just as with the Pearson correlation coefficient for haploid data — even if the SNPs are unphased. In fact, the population version of the Wellek–Ziegler correlation coefficient coincides with the population Pearson correlation coefficient for haploid data under Hardy–Weinberg equilibrium (Wellek and Ziegler 2009). With real GWAS data, a value of adjacency $x_j^T{x}_k$ exactly equal to zero is not practical in finite samples. In practice, we introduce a non-zero cutoff value for judging an adjacency of zero in our bi-directed graph.

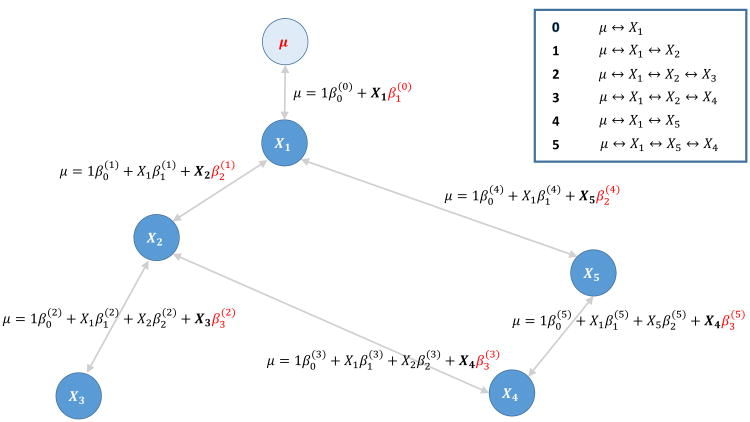
Our proposed approach is based on the shortest paths to μ in a bi-directed graph constructed locally for each SNP that shows (weak) association with y with a moderate p-value cutoff α₁ — we call these SNPs of interest focal SNPs. Using the shortest paths, we can narrow the candidates for A, thereby rendering computation feasible and reducing the multiple testing burden. The motivation behind our proposal is given in the “Appendix”. Centered around each focal SNP, say SNP X₁, which has p₁ nearby SNPs, we compute $\left(\begin{array}{c}{p}_1\\ 2\end{array}\right)$ Wellek–Ziegler correlation coefficients. Subsequently, we collect all of the shortest paths starting from x₁ in the bi-directed graph. (We regard the focal SNPs with moderate marginal signals as being adjacent to μ.) An illustration of constructing the bi-directed graph is given in Figure 1. If one of the shortest paths is μ ↔ X₁ ↔ X₂ ↔ ⋯ ↔ X_l ↔ X_l+1, we test the null hypothesis β_l+1 = 0 for the terminal SNP, with the test based on the multiple regression model,

Figure 1.

Illustration of the proposed shortest path test. The focal SNP, X₁, shows (weak) marginal association with μ = E(y|X) based on a moderate p-value cutoff (path 0). A bi-directed graph around SNP X₁ is constructed with adjacency defined by the magnitude of linkage disequilibrium, and all shortest paths to X₁ are collected. In this example, there are five shortest paths numbered 1–5, as shown in the top right. For each of five shortest paths, the SNP corresponding to the terminal vertex is tested for association in a multiple regression model including all SNPs in the path. The fitted multiple regression model is described for each shortest path. The tested SNP and its regression coefficient are emphasized in bold and in red, respectively. Conservative multiple testing is adapted in order to take the number of shortest paths into account.

$$y=1{\beta }_0+X_1{\beta }_1+X_2{\beta }_2+\cdots +X_l{\beta }_l+X_{l+1}{\beta }_{l+1}+\varepsilon .$$ (2)

If X₁ and μ are truly adjacent, then the path is the shortest between μ and SNP X_l+1. Then, Proposition 2 in the “Appendix” ensures that E(β̂_{l+1,{1,…,l}}|X) ≠ 0 where β̂_{l+1,{1,…,l}} is the least-squares estimator in (2). However, the adjacency between X₁ and μ is arbitrarily determined by some moderate p-value cutoff. Furthermore, the above statement only mentions nonzero effects but takes no account of stochastic noise. We overcome these issues by testing hypotheses for the β̂_{l+1,{1,…,l}}. We employ a conservative testing approach for the terminal SNP in each shortest path as described in Section 2.2. For binary phenotypes, we use the multiple logistic regression model with the Wald test.

2.2 Algorithm description

Here, we describe the proposed algorithm in detail.

1. Initialization Set a p-value cutoff α₁ for screening, and a desired family-wise error rate α (e.g. 5%).

2. Marginal association test Conduct marginal association tests for all SNPs k ∈ M = {1, … , p} under the marginal model β₀ + X_kβ_k, which yields p-values P_k, k ∈ M. Let H = {k ∈ M : P_k < α₁} be the set of SNPs of interest, the focal SNPs.

3. Test in bi-directed graph For each k ∈ H, set SNP k as the focal SNP. Denote its nearby SNPs by N(k) ⊂ M including the focal SNP (SNP k) itself, where nearby SNPs are determined by a 100 kb window (see Section 5) both upstream and downstream of the kth SNP. Build a bi-directed graph where adjacency between two vertexes l,m ∈ N(k) is declared if ${\rho }_{lm}^2\in [a_{min},a_{max}]$. Here a_min and a_max (a_min < a_max) are pre-specified cutoff values, and ρ_lm is the Wellek–Ziegler correlation coefficient (Pearson correlation coefficient for SNP genotypes coded 0,1,2) between the lth and mth SNPs. Denote the resulting bi-directed graph by G_k.

3.1. Collection of shortest paths to centered SNP k Collect all shortest paths from the focal SNP k to each vertex in G_k and denote the set of all shortest paths by A(k).

• 3.1.1. Fit multiple regression model for each shortest path For each shortest path e ∈ A(k), fit the multiple regression model,

  $$\mu =1{\beta }_0+X_k{\beta }_k+X_{e\_}{\beta }_{e\_}+X_{t(e)}{\beta }_{t(e)},$$

  where t(e) represents the other terminal vertex of the path e (other than k), and e₋ denotes the index set where the terminal vertex t(e) is removed from the index set e. Obtain the p-value, P_{t(e)|{k,e−}}, for testing the null hypothesis, β_t(e) = 0.

• 3.1.2. Conservative multiple test correction Declare SNP t(e) as significant if P_{t(e)|{k,e−}} < α/(α₁p|A(k)|) where |A(k)| is the number of elements of A(k).

In Step 3.1.2, the factor α₁p|A(k)| can be interpreted as the number of tests accounting for marginal association screening in Step 2. Under the null hypothesis of no effect of all SNPs, the family-wise error rate in detecting any SNPs as declared significant in 3.1.2 is never greater than the nominal level α : a proof is given in “Supplementary Information Section 3”. We propose to declare adjacency between two SNPs l and m with correlation ρ_lm if $a_{min}\le {\rho }_{lm}^2\le a_{max}$ holds. The cutoff a_min eliminates uncorrelated pairs, and a_max avoids multicollinearity in the multiple regression fit (as described in the “Appendix”. If there are covariates, we slightly modify the proposed algorithm by adding the covariates to all regression models as with usual covariate adjustment. We investigate appropriate values of a_min and α₁ in simulation studies where we set a_max = 0.8 throughout. We implemented the proposed method in R (R Core Team 2015) with input of the result from PLINK's marginal association testing, such as by using the -- assoc option, where the shortest paths in the bi-directed graph were collected by using the get.all.shortest.paths function implemented in the R package igraph (Csardi and Nepusz 2006).

3 Simulation studies

To examine the performance of the proposed method, we conducted studies with simulated data that mimic real SNP-GWAS data. We investigated type I error and statistical power. Data were simulated by sampling individuals from the general population. We used HAPGEN v2.2.0 (Su et al. 2011) with input consisting of haplotype data comprising 73,832 SNPs from the HapMap3 east Asian population (JPT+CHB). We compared our proposed method with three other methods: the marginal association test in PLINK with the -- assoc option, SnipSnip, and UNPHASED with option - window 5 - zero 0.2.

3.1 Type I error

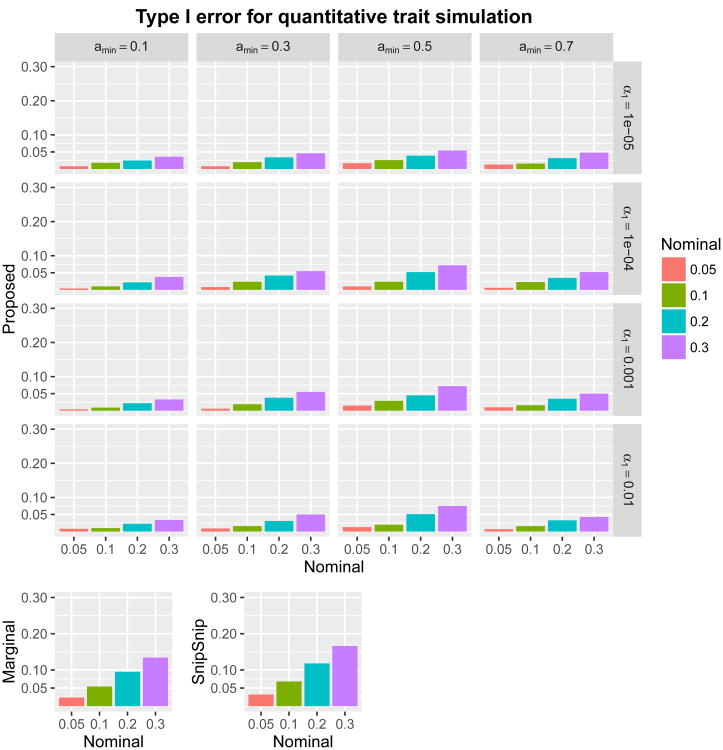
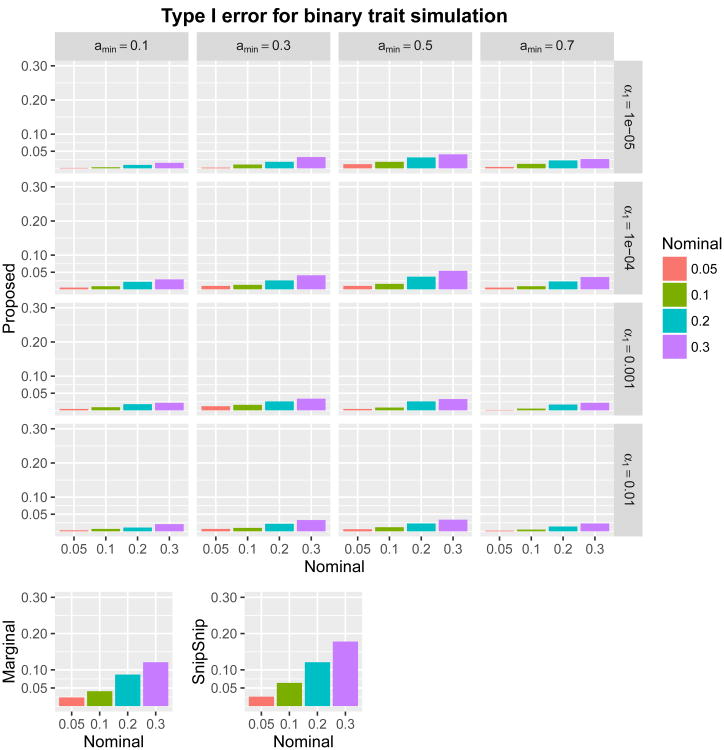
For type I error simulations, we generated by HAPGEN 1,000 datasets of the 73,832 SNPs for 1,000 subjects. We considered both quantitative and binary traits. For quantitative traits, we generated the phenotype independently and identically from a standard normal distribution. For binary traits, we randomly assigned the value of 0 (control) to one-half (500) of the subjects and assigned the value 1 (case) to the other half. We then applied the proposed method with various parameters. We also ran the marginal association test and the SnipSnip procedure for comparison (we did not include UNPHASED in type I error simulations because its computational cost running on 73,832 SNPs is prohibitive). We considered four nominal levels of the family-wise error rate: α = 30, 20, 10, and 5%. Because we assumed that no SNPs were causal, type I error was defined by whether ‘any’ SNPs were detected (declared significant) in each replicate. For marginal association testing and SnipSnip, we used Bonferroni correction with 73,832 SNPs. For the proposed method, we considered all 16 combinations of (a_min, α₁) ∈ {0.1,0.3,0.5,0.7} × {0.01,0.001,0.0001,0.00001}. The results are given in Figures 2 and 3. All methods maintained type I error rate at or below the nominal level. Regardless of the values of a_min and α₁, the proposed method was conservative, as expected. Mean and maximum shortest path length, as well as number of shortest paths, are given in “Supplementary Information Section 5”. These summary measures tended to decrease as α₁ decreased or a_min increased, and a_min = 0.3 tended to produce longer path lengths than a_min = 0.1.

Figure 2.

Type I error rates from quantitative trait simulations comparing the proposed method with (a_min, α₁) ∈ {0.1,0.3,0.5,0.7} × {0.01,0.001,0.0001,0.00001}, the marginal association test, and SnipSnip. Nominal family-wise error rates are α = 30, 20, 10, and 5%.

Figure 3.

Type I error rates from binary trait simulations comparing the proposed method with (a_min, α₁) ∈ {0.1,0.3,0.5,0.7} × {0.01,0.001,0.0001,0.00001}, the marginal association test, and SnipSnip. Nominal family-wise error rates are α = 30, 20, 10, and 5%.

3.2 Power

For power simulations, we extracted a region on chromosome 10 ranging from 2,001,233 to 3,499,300 (in NCBI Build 36 base pair position) consisting of 1,273 SNPs. Phenotype data for each sampled subject with these 1,273 SNPs was generated according to a regression model assuming the causal SNPs were the five SNPs listed in Table 1, which also shows the correlation structure. We considered six scenarios with different true regression coefficients based on the values of the ${\beta }_j^{\ast }$ given in Table 1. We multiplied ${\beta }_j^{\ast }$ by a constant m > 0 to define the jth true regression coefficient. Nominal family-wise error rate α was fixed at 0.05 and total number of SNPs was assumed to be 1,000,000 in all simulations.

Table 1.

Causal SNPs for power simulations. Upper table: Wellek–Ziegler correlation coefficients (×100) and minor allele frequency (%) for five causal SNPs, rs9423671, rs9423711, rs2388264, rs11251392, and rs17155640, whose indexes in the 1,273 SNPs ordered in base pair position are 457, 476, 492, 533, and 534, respectively. Lower table: Regression models considered in power simulations. Five regressions of the form ${\beta }_0+{\sum }_{j=1}^5{x}_{i,j}{\beta }_{0,j}$ were used, where the true regression coefficients β_0j for the six scenarios were set as ${\beta }_j^{\ast }$ multiplied by a constant m > 0, and empty cells indicate that the true coefficient was zero.

	rs9423671	rs9423711	rs2388264	rs11251392	rs17155640
rs9423671		82	70	–42	–19
rs9423711			87	–42	–32
rs2388264				–35	–42
rs11251392					–61
rs17155640
MAF(%)	32	26	26	38	37
Scenario	${\beta }_1^{\ast }$	${\beta }_2^{\ast }$	${\beta }_3^{\ast }$	${\beta }_4^{\ast }$	${\beta }_5^{\ast }$
1			0.20
2	–0.40		0.50
3		–0.60	0.70
4	0.40	–0.70	0.50
5	–0.20		0.50	0.40	0.30
6	0.50	–0.50	0.50	0.50	0.50

Quantitative traits

We generated by HAPGEN 1,000 simulated datasets of the 1,273 SNPs for n = 1000 subjects, and then we generated phenotype data y_i for subject i according to the linear regression model with the five causal SNPs given in Table 1:

$$y_i=\sum _{j=1}^5{X}_{i,j}{\beta }_{0,j}+{\varepsilon }_i,$$

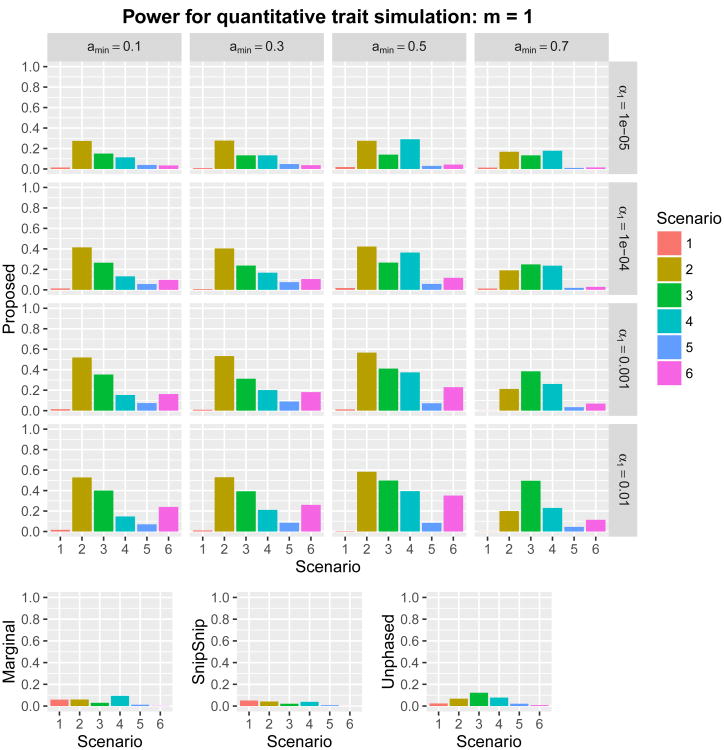
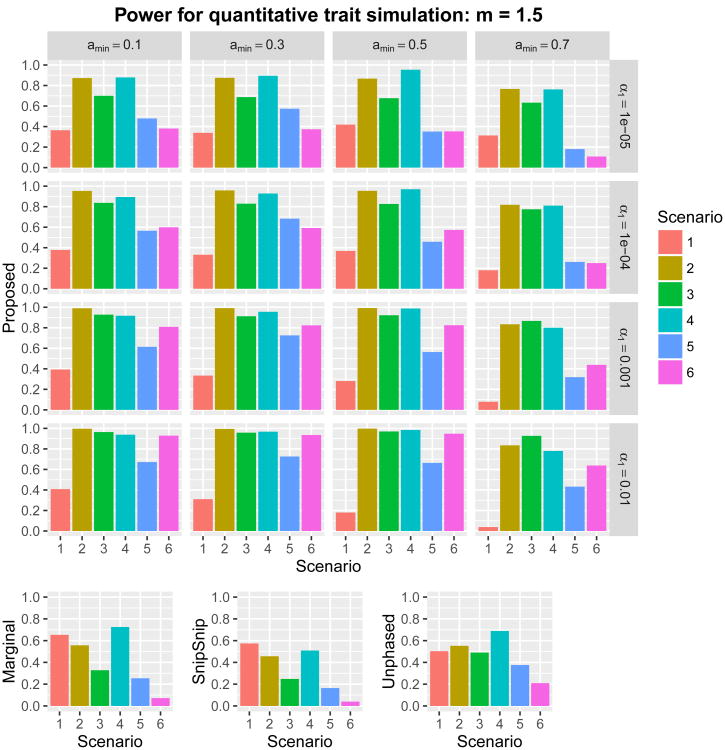
where X_i,j denotes the minor allele count (0, 1, or 2) at the jth causal SNP (j = 1, … , 5), β_0,j represents the jth regression coefficient, and ∊_i is an independently and identically distributed standard normal error for the ith subject. Using each of the six sets of regression coefficients ${\beta }_j^{\ast }$ in Table 1, we set ${\beta }_{0,j}=m{\beta }_j^{\ast }$ for a given constant m > 0. Two scenarios, m = 1 and m = 1.5, were considered. Consequently, we carried out twelve power simulations. The proposed method was examined at 16 combinations of the parameters (a_min, α₁) ∈ {0.1, 0.3, 0.5, 0.7} × {0.01, 0.001, 0.0001, 0.00001}. The power of overall detection for the region, with m = 1 and m = 1.5, is given in Figures 4 and 5, respectively. We report the proportion of runs where any SNP within a 110 kb window upstream of the first causal SNP and downstream of the last causal SNP was significant. Scenario 1 assumes a single causal SNP, implying that the marginal association test works well. The marginal association test gave the highest power among the methods (see also “Supplementary Information Section 4”). Further insights are obtained by looking at the other simulations. Scenarios 2–6 were designed so that the marginal association test is underpowered due to the presence of more than one causal SNP. Overall, irrespective of the choice of parameters a_min and α₁, the proposed test gave higher power than the three other methods. Using a_min = 0.7 or α₁ ≤ 0.0001 gave lower power. The optimal choice of (a_min, α₁) depended on the underlying genetic architecture, as no single pair of (a_min, α₁) gave the best performance among the candidate parameters across scenarios 2–6. Mean and maximum shortest path length and number of shortest paths in the bi-directed graphs are given in “Supplementary Information Section 5”. These summary measures varied across scenarios, but tended to decrease as α₁ decreased. In general, a_min = 0.3 tended to give longer shortest-path length and greater numbers of shortest paths. Shortest-path length and number of shortest paths may influence statistical power through multiplicity of tests. However, no obvious relation between these summary measures and power was observed.

Figure 4.

Power with m = 1 for six scenarios in quantitative trait simulations with 16 combinations of (a_min, α₁) ∈ {0.1,0.3,0.5,0.7} × {0.01,0.001,0.0001,0.00001}. Nominal family-wide error rate was set at α = 0.05. The ordinate is the proportion of runs where any SNP within a 110 kb window upstream of the first causal SNP and downstream of the last causal SNP was significant.

Figure 5.

Power with m = 1.5 for six scenarios in quantitative trait simulations with 16 combinations of (a_min, α₁) ∈ {0.1,0.3,0.5,0.7} × {0.01,0.001,0.0001,0.00001}. Nominal family-wide error rate was set at α = 0.05. The ordinate is the proportion of runs where any SNP within a 110 kb window upstream of the first causal SNP and downstream of the last causal SNP was significant.

Binary traits

For simulations with binary traits, we considered case-control data. We generated case-control samples with 1,000 cases and 1,000 controls. Samples were collected by repeatedly sampling from the general population, as described below in detail. A binary phenotype y_i ∈ {0,1} for each individual from the general population was generated according to the logistic regression model

$${\mu }_i=P(y_i=1|x_i)=1/\{1+exp(-{\beta }_0-\sum _{j=1}^5{X}_{i,j}{\beta }_{0,j})\},$$

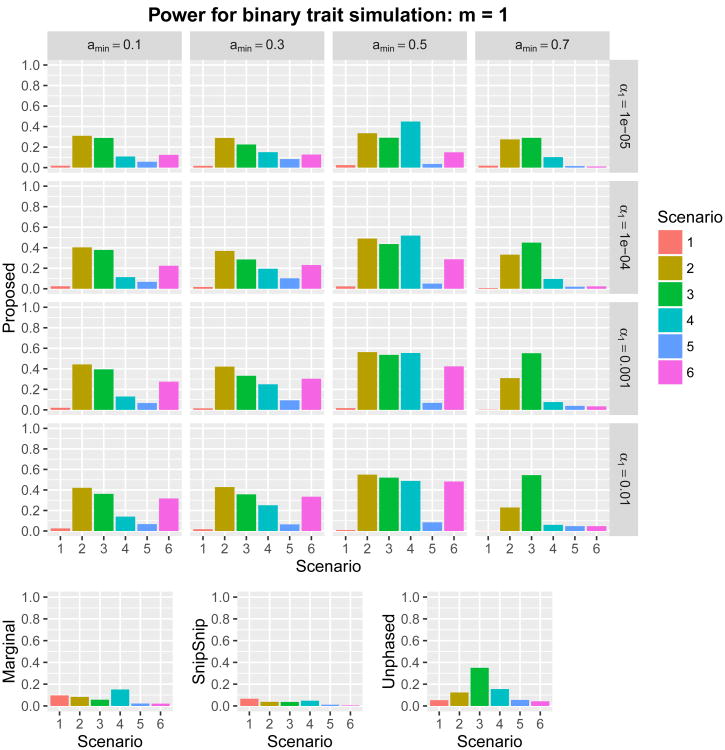
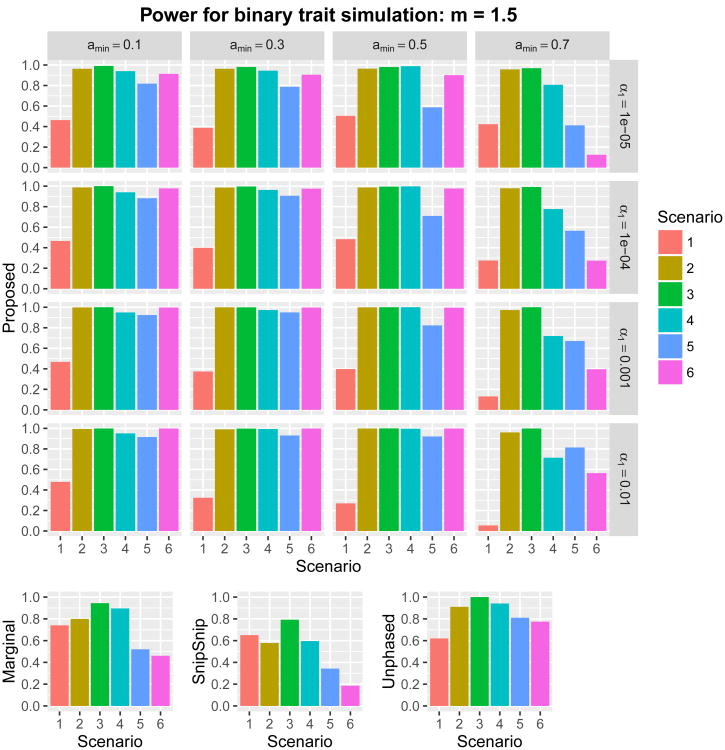
where X_i,j denotes the minor allele count (0, 1, or 2) at the jth causal SNP (j = 1, … , 5); β_0,j represents the jth regression coefficient; and β₀ is the intercept, which was determined to produce a prevalence of roughly 1%. Using each of the six regression coefficients ${\beta }_j^{\ast }$ in Table 1, we set ${\beta }_{0,j}=1.4\times m{\beta }_j^{\ast }$ for a given constant m > 0. We considered two scenarios, m = 1 and m = 1.5. We then carried out twelve power simulations. For each replicate, we generated 1,000 subjects with genotype data at these 1,273 SNPs. Subsequently, a binary phenotype was assigned to each subject according to the above logistic regression model. The sampling of 1,000 subjects was repeated until 1,000 cases and 1,000 controls were collected. We simulated 1,000 such datasets. The proposed method was examined at 16 combinations of the parameters (a_min, α₁) ∈ {0.1,0.3,0.5,0.7} × {0.01, 0.001, 0.0001, 0.00001}. The power of overall detection in the region for m = 1 and m = 1.5 is given in Figures 6 and 7, respectively. The results were roughly consistent with the quantitative power simulations, and the optimal choice of (a_min, α₁) depended on the underlying genetic architecture.

Figure 6.

Power with m = 1 for six scenarios in binary trait simulations with 16 combinations of (a_min, α₁) ∈ {0.1, 0.3, 0.5, 0.7} × {0.01, 0.001, 0.0001, 0.00001}. Nominal family-wide error rate was set at α = 0.05. The ordinate is the proportion of runs where any SNP within a 110 kb window upstream of the first causal SNP and downstream of the last causal SNP was significant.

Figure 7.

Power with m = 1.5 for six scenarios in binary trait simulations with 16 combinations of (a_min, α₁) ∈ {0.1,0.3,0.5,0.7} × {0.01,0.001,0.0001,0.00001}. Nominal family-wide error rate was set at α = 0.05. The ordinate is the proportion of runs where any SNP within a 110 kb window upstream of the first causal SNP and downstream of the last causal SNP was significant.

4 Application to ADNI-GWAS data

We applied our proposed method to the ADNI-GWAS dataset obtained from the publicly available data of the Alzheimer's Disease Neuroimage Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 as a public-private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessments can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer's disease (AD). For up-to-date information, see www.adni-info.org. ADNI is an ongoing, longitudinal study with primary purpose being to explore the genetic and neuroimaging information associated with late-onset Alzheimer's disease (LOAD). The study investigators recruited elderly subjects older than 65 years of age comprising about 400 subjects with mild cognitive impairment (MCI), about 200 subjects with Alzheimer's disease (AD), and about 200 healthy controls. Each subject was followed for at least 3 years. During the study period, the subjects were assessed with magnetic resonance imaging (MRI) measures and psychiatric evaluation to determine the diagnosis status at each time point.

The ADNI-GWAS data were obtained from 818 DNA samples of ADNI1 participants using the Illumina Human 610-Quad genotyping array (Shen et al. 2014). The data initially included 620,901 SNPs. We included the apolipoprotein E (APOE) SNPs rs429358 and rs7412 in our analysis. We used data from 684 non-Hispanic Caucasian samples after we excluded one pair showing cryptic relatedness (revealed by the PLINK pairwise π̂ statistic being greater than 0.125) (Purcell et al. 2007), and we excluded subjects whose reported sex did not match the sex inferred from X-chromosome SNPs. We then applied further quality control measures by excluding SNPs with missing genotype rate > 0.1, Hardy–Weinberg equilibrium test P < 10⁻⁶, and MAF < 5%; the total number of remaining SNPs was 528,984. There were 166 controls and numbers of cases with early MCI (EMCI), late MCI (LMCI), or AD were 67, 110, and 341, respectively. We classified the MCI cases into two sub-categories, EMCI and LMCI, following the procedure in the report ‘Multistate modeling of ADNI progression’ that is included with the ADNIMERGE R package provided by ADNI. We then scored the controls and cases of EMCI, LMCI, and AD as 0, 2, 3, and 4, respectively, which was treated as a quantitative trait in our analysis (we assigned score 1 to cases with significant memory concern [SMC], but the ADNI1 cohort did not contain any subjects with SMC — see http://adni.loni.usc.edu/study-design/background-rationale/ — and no subjects having score 1 were present in the ADNI-GWAS data). We also considered adjustment for the covariates sex and age in the proposed method. With covariate adjustment, p-values increased only slightly and the same SNPs were significant, so we only report results without covariate adjustment.

We applied our method with the same 16 combinations of (a_min, α₁) as in the simulation studies ({0.1, 0.3, 0.5, 0.7} × {0.01, 0.001, 0.0001, 0.00001}). The nominal family-wise error rate was set as α = 0.05, in which the number of SNPs, 528,984, was used as the multiple testing correction factor. In Tables 2–5, we show the significant shortest paths and the SNPs contained in them. We so not show shortest paths containing SNPs with genome-wide significance (i.e., those with marginal association p-value less than 0.05/528,984), so that only SNPs undetected by marginal association scans are shown (a full list of results is given in “Supplementary Information Section 5”). Without paths containing genome-wide significant SNPs, four combinations of (a_min, α₁) remained: (0.1, 0.01), (0.1, 0.001), (0.1, 0.0001), and (0.3, 0.001). All SNPs detected with (0.1, 0.0001) were also contained among the significant results with (0.1, 0.01) and (0.1, 0.001), which implies that α₁ = 0.0001 is too stringent a threshold, as was observed in our simulation studies. The ADNI-GWAS application also implies that a_min = 0.7 is unlikely to provide high power, again as observed in our simulation studies.

Table 2.

Significant shortest paths at a_min = 0.1 and α₁ = 0.01. Paths that include genome-wide significant SNPs were excluded. P_marg, marginal association p-value. P_mult, multiple regression p-value applied to each path. SNPs in each path are ordered so that the first SNP is adjacent to the phenotype and the last SNP is tested for association. SNPs tested in each path are emphasized in bold.

Significant path	CHR	SNP	BP	Pmarg	Pmult
1	19	rs440277	50053064	3.8e-03	4.5e-01
1	19	rs387976	50070900	8.8e-02	4.1e-02
1	19	rs157580	50087106	5.2e-05	2.0e-11
1	19	rs8106922	50093506	1.3e-04	1.3e-08
2	19	rs440277	50053064	3.8e-03	1.7e-01
2	19	rs387976	50070900	8.8e-02	4.3e-02
2	19	rs157580	50087106	5.2e-05	1.3e-11
2	19	rs405509	50100676	7.7e-04	1.6e-08
4	19	rs157580	50087106	5.2e-05	9.2e-11
4	19	rs8106922	50093506	1.3e-04	3.9e-10
5	19	rs157580	50087106	5.2e-05	1.2e-10
5	19	rs405509	50100676	7.7e-04	2.5e-09
8	19	rs8106922	50093506	1.3e-04	3.9e-10
8	19	rs157580	50087106	5.2e-05	9.2e-11
11	19	rs8106922	50093506	1.3e-04	1.2e-01
11	19	rs405509	50100676	7.7e-04	1.6e-02
11	19	rs439401	50106291	1.3e-05	2.3e-09
12	19	rs405509	50100676	7.7e-04	2.5e-09
12	19	rs157580	50087106	5.2e-05	1.2e-10
18	19	rs405509	50100676	7.7e-04	6.1e-08
18	19	rs439401	50106291	1.3e-05	1.2e-09
20	19	rs439401	50106291	1.3e-05	5.8e-02
20	19	rs157580	50087106	5.2e-05	1.1e-04
20	19	rs8106922	50093506	1.3e-04	1.1e-09
21	19	rs439401	50106291	1.3e-05	1.2e-09
21	19	rs405509	50100676	7.7e-04	6.1e-08

Table 5.

Significant shortest paths at a_min = 0.3 and α₁ = 0.001. Paths that include genome-wide significant SNPs were excluded. P_marg, marginal association p-value. P_mult, multiple regression p-value applied to each path. SNPs in each path are ordered so that the first SNP is adjacent to the phenotype and the last SNP is tested for association. SNPs tested in each path are emphasized in bold.

Significant path	CHR	SNP	BP	Pmarg	Pmult
1	5	rs2963327	8987159	2.0e-04	8.1e-08
1	5	rs2963345	8962508	3.2e-03	7.1e-03
1	5	rs6870451	8991885	9.3e-02	1.4e-06
2	5	rs2963327	8987159	2.0e-04	7.8e-08
2	5	rs2963344	8962428	3.7e-03	1.1e-02
2	5	rs6870451	8991885	9.3e-02	2.0e-06
3	5	rs2963327	8987159	2.0e-04	7.7e-08
3	5	rs2963345	8962508	3.2e-03	8.0e-03
3	5	rs11955429	8994715	7.8e-02	1.6e-06
4	5	rs2963327	8987159	2.0e-04	7.0e-08
4	5	rs2963344	8962428	3.7e-03	1.3e-02
4	5	rs11955429	8994715	7.8e-02	2.3e-06
5	5	rs2963337	8988632	1.5e-04	4.0e-08
5	5	rs2963345	8962508	3.2e-03	7.0e-03
5	5	rs6870451	8991885	9.3e-02	8.6e-07
6	5	rs2963337	8988632	1.5e-04	3.9e-08
6	5	rs2963344	8962428	3.7e-03	1.1e-02
6	5	rs6870451	8991885	9.3e-02	1.3e-06
7	5	rs2963337	8988632	1.5e-04	3.8e-08
7	5	rs2963345	8962508	3.2e-03	7.9e-03
7	5	rs11955429	8994715	7.8e-02	9.9e-07
8	5	rs2963337	8988632	1.5e-04	3.5e-08
8	5	rs2963344	8962428	3.7e-03	1.2e-02
8	5	rs11955429	8994715	7.8e-02	1.4e-06

As seen in Tables 2–5, SNPs with weak marginal signals showed enhanced association signals with multiple regression. The results varied with the choice of parameters (a_min, α₁), but SNPs on chromosome 19 were detected in most of the scenarios. The noteworthy regions contain APOE4 SNPs, which are also genome-wide significant even with the marginal association test, SnipSnip, and UNPHASED, as seen in Table 6. We also applied lasso (Tibshirani 1996) by using the PUMA software (Hoffman et al. 2013) with the default setting and optimal model chosen according to AIC (Akaike information criterion). The SNPs detected with lasso are shown in “Supplementary Information Section 5” along with p-values from PUMA (PUMA p-values are a ranking measure, not the usual measure of statistical significance). Six unique SNPs on chromosome 5 given in Tables 3 and 5 are more interesting as they were not detected by the marginal association test, SnipSnip, UNPHASED, or lasso. The gene closest to these unique SNPs on chromosome 5 is semaphorin 5A (SEMA5A). The Ensembl Variant Effect Predictor (McLaren et al. 2010) predicted that these SNPs are intergenic and function as modifiers. The SEMA5A gene was previously reported to be a susceptibility locus for Parkinson's disease (Maraganore et al. 2005, Lin et al. 2009) and for autism (Melin et al. 2006). SEMA5A is involved in axonal guidance during neural development.

Table 6.

SNPs that were significant by the marginal association test, Snip-Snip, and UNPHASED; family-wise error rate was 5% using Bonferroni correction based on the number of SNPs, 528,984.

CHR	SNP	BP	Pmarg	PSnipSnip	PUnphased
19	rs387976	50070900	8.9e-02	6.0e-01	1.5e-09
19	rs11667640	50071631	2.0e-02	3.4e-02	1.9e-12
19	rs6859	50073874	1.9e-02	9.4e-02	5.8e-11
19	rs157580	50087106	5.2e-05	1.2e-10	1.0e-18
19	rs2075650	50087459	1.9e-11	6.3e-09	5.3e-19
19	rs8106922	50093506	1.3e-04	3.9e-10	5.0e-21
19	rs405509	50100676	7.7e-04	2.5e-09	2.5e-22
19	rs429358	50103781	9.5e-23	1.5e-18	5.6e-20

Table 3.

Significant shortest paths at a_min = 0.1 and α₁ = 0.001. Paths that include genome-wide significant SNPs were excluded. P_marg, marginal association p-value. P_mult, multiple regression p-value applied to each path. SNPs in each path are ordered so that the first SNP is adjacent to the phenotype and the last SNP is tested for association. SNPs tested in each path are emphasized in bold.

Significant path	CHR	SNP	BP	Pmarg	Pmult
1	5	rs2963337	8988632	1.5e-04	4.0e-08
1	5	rs2963345	8962508	3.2e-03	7.0e-03
1	5	rs6870451	8991885	9.3e-02	8.6e-07
2	5	rs2963337	8988632	1.5e-04	3.8e-08
2	5	rs2963345	8962508	3.2e-03	7.9e-03
2	5	rs11955429	8994715	7.8e-02	9.9e-07
4	19	rs157580	50087106	5.2e-05	9.2e-11
4	19	rs8106922	50093506	1.3e-04	3.9e-10
5	19	rs157580	50087106	5.2e-05	1.2e-10
5	19	rs405509	50100676	7.7e-04	2.5e-09
8	19	rs8106922	50093506	1.3e-04	3.9e-10
8	19	rs157580	50087106	5.2e-05	9.2e-11
11	19	rs8106922	50093506	1.3e-04	1.2e-01
11	19	rs405509	50100676	7.7e-04	1.6e-02
11	19	rs439401	50106291	1.3e-05	2.3e-09
12	19	rs405509	50100676	7.7e-04	2.5e-09
12	19	rs157580	50087106	5.2e-05	1.2e-10
18	19	rs405509	50100676	7.7e-04	6.1e-08
18	19	rs439401	50106291	1.3e-05	1.2e-09
20	19	rs439401	50106291	1.3e-05	5.8e-02
20	19	rs157580	50087106	5.2e-05	1.1e-04
20	19	rs8106922	50093506	1.3e-04	1.1e-09
21	19	rs439401	50106291	1.3e-05	1.2e-09
21	19	rs405509	50100676	7.7e-04	6.1e-08

5 Discussion

We present herein a new conservative multiple testing method for detecting genetic association signals hidden by LD. Our proposed bi-directed graph approach can be applied to high-dimensional genome-wide SNP data. Despite the conservativeness of our proposed method, simulation studies confirmed that the method has higher power than existing methods. In an application to ADNI-GWAS data, our method detected new susceptibility SNPs on chromosome 5 that were originally undetected by existing methods, including lasso. The negative results with lasso are expected because lasso is a variant of stagewise regression (Efron et al. 2004); in view of lasso's iterative model update process (c.f. the coordinate descent algorithm (Friedman et al. 2010)), a SNP is entered into the model only if the absolute value of the correlation between that SNP and the residual of the current model is larger than some threshold as achieved by the soft-thresholding function. This in turn implies that a SNP weakly correlated with the current residual will never be included in the model. Hidden SNPs having large effects conditional on other SNPs will be included only if the current model contains those other SNPs. However, if the conditioning SNPs have only weak or moderately sized marginal signals, non-informative SNPs will be entered by chance into the model long before the conditioning SNPs are entered. Consequently, the non-informative SNPs result in a model with unnecessarily high dimension, wasting degrees of freedom, and model building will terminate before the important, hidden SNP is included. In contrast, our method avoids including too many non-informative SNPs among the conditioning SNPs by restricting to the shortest paths in a ‘local’ bi-directed graph, making the hypothesis test more powerful.

Our theoretical consideration of the presence of multiple causal variants that are in LD is also new. So far, designing GWASs (in particular, selecting tag SNPs) has been based chiefly on statistical power analyses that assume causal variants exist separately in unlinked loci (de Bakker et al. 2005, Eberle et al. 2007, Spencer et al. 2009). Conclusions from existing studies based on the GWAS design may therefore not be generalizable to situations with multiple causal variants that are in LD. One consequence is that current SNP panels are suboptimal in this situation; hence, additional studies of statistical power are needed. However, power calculations turn out to be much more complicated than in situations with multiple causal variants that are not in LD: it remains unknown which of various genetic models and statistical methods is optimal.

Although our proposed method attempts to detect hidden SNPs that are difficult to detect with GWAS data (Eberle et al. 2007), detection should be distinguished from true association. Even though a particular combination of detected SNPs produces the highest power, it does not necessarily indicate that these are the causal SNPs. Subsequent, careful examination based on biological background and function is also necessary.

There are several possible directions for future work to improve our method. First, our proposed test is slightly conservative as shown in type I error simulations. This is because the method is based on Bonferroni-type control of multiplicity of shortest paths. There is inevitably overlap in the SNPs to be tested, resulting in redundancy. Development of a less conservative method of type I error control may further improve the statistical power. Second, our method has two tuning parameters (a_min, α₁); although the choice influences the result, we could not determine an optimal choice that could be used in all simulation scenarios. Because the optimal parameters seemed to depend on underlying genetic architecture, which is unknown, we recommend trying multiple sets of (a_min, α₁) in practice. Simulation studies suggested that the the two parameters be in the ranges a_min ∈ [0.1, 0.5] and α₁ ∈ [0.01, 0.001], which produced improved performance over existing methods. Application to the ADNI-GWAS data also supported this choice of ranges. Based on our experience with applications to other real GWAS data (not shown), we found that a_min = 0.3 and α₁ = 0.001 tended to allow detection of SNPs that had gone undetected with existing methods.

Our method builds a bi-directed graph locally within a fixed-size window centered (focused) around each SNP across the genome. This approach may fail in the presence of long-distance LD, which is not ignorable in real human data (Pritchard and Przeworski 2001). However, use of a wider window size incurs both computational and multiple testing burdens as the number of shortest paths increases exponentially. As observed in simulation studies, the LD between two SNPs needs to be high for them to be adjacent in the bi-directed graph. The cutoff a_min approximately corresponds to that for r². According to the relationship between average r² and genetic distance in human data given in Figure 2 of (Pritchard and Przeworski 2001), the average of r² is much lower than 0.1 for a 0.1 cM distance between SNPs. Thus, our choice of a 100 kb window could be reasonable on average in practice, although exceptions surely exist. We will continue applying our method to real human genetic data to explore the optimal choices of the parameters in future research. R code that implements our method for SNP-GWAS data in PLINK binary format is available from the authors upon request.

Table 4.

Significant shortest paths at a_min = 0.1 and α₁ = 0.0001. Paths that include genome-wide significant SNPs were excluded. P_marg, marginal association p-value. P_mult, multiple regression p-value applied to each path. SNPs in each path are ordered so that the first SNP is adjacent to the phenotype and the last SNP is tested for association. SNPs tested in each path are emphasized in bold.

Significant path	CHR	SNP	BP	Pmarg	Pmult
2	19	rs157580	50087106	5.2e-05	9.2e-11
2	19	rs8106922	50093506	1.3e-04	3.9e-10
3	19	rs157580	50087106	5.2e-05	1.2e-10
3	19	rs405509	50100676	7.7e-04	2.5e-09
7	19	rs439401	50106291	1.3e-05	5.8e-02
7	19	rs157580	50087106	5.2e-05	1.1e-04
7	19	rs8106922	50093506	1.3e-04	1.1e-09
8	19	rs439401	50106291	1.3e-05	1.2e-09
8	19	rs405509	50100676	7.7e-04	6.1e-08

Appendix. Motivation for the bi-directed graph approach

Here we describe the theoretical background behind our proposed method. First, we relate the bi-directed graph with the least-squares estimator β̂_j,A in the model y = x_jβ_j + Σ_k∈Ax_kβ_k + ∊. Let X_A = (x_k : k ∈ A). To this end, we exploit the following representation (Rao and Yanai 1979, Ueki and Kawasaki 2013):

$${\widehat{\beta }}_{j,A}={\Vert Q_{X_A}{x}_j\Vert }^{-2}{y}^T(Q_{X_A}{x}_j).$$

Its expectation and variance are given by

$$E({\widehat{\beta }}_{j,A}|X)={\Vert Q_{X_A}{x}_j\Vert }^{-2}{\mu }^T(Q_{X_A}{x}_j)$$

and var (β̂_j,A|X) = σ²║Q_XAx_j║⁻², respectively. Consequently, in order to evaluate whether E(β̂_j,A|X) = 0 or not, it suffices to investigate the quantity

$${\mu }^T(Q_{X_A}{x}_j).$$

The following result, whose proof is given in “Supplementary Information Section 1”, helps us to screen SNPs to be entered into the conditioning set A for β̂_j,A. It is essentially the equivalence between pairwise and global Markov properties in a bi-directed graph for a multivariate Gaussian distribution (Kauermann 1996, Drton and Perlman 2007).

Proposition 1. If there is no path between vertexes 0 (i.e. μ = E(y|X)) and j ∈ M = V \ {0} with intermediate vertexes being any subset from a vertex set {j₁, … , j_l} ⊂ M \ {j} = V \ {0, j} (allowing the empty set), then for any A ⊂ {j₁, … , j_l}, we have μ^T(Q_XAx_j) = 0.

Proposition 1 implies that, for the discovery of SNP j such that E(β̂_j,A|X) ≠ 0 for some A, we can ignore the SNPs having no paths to μ = E(y|X). Conversely, we can focus on SNPs having paths to SNPs that are adjacent to μ. The adjacency with μ corresponds to the presence of a marginal association signal as in a standard GWAS scan. In typical GWAS, however, SNPs often show weak marginal signals. Our target is the SNPs with low marginal association signals. To this end, we focus on SNPs that show a moderate marginal signal (e.g. marginal p-value less than a cutoff), and then build a bi-directed graph around each of those SNPs. In samples from the general population, LD between two SNPs far apart is expected to be low. We exploit this LD structure in application to GWASs. Namely, it suffices to consider SNPs for the conditioning set A that are close to the focal SNP to be tested for the effect; SNPs far away can be excluded from the candidates for A. As a consequence, we build a bi-directed graph locally, e.g. 100 kb (kilo base pair) window both upstream and downstream of each SNP.

We note that Proposition 1 does not guarantee its complementary statement — that is, that the existence of a path between μ (vertex 0) and SNP j with intermediate vertexes {j₁, … , j_l} implies the existence of some subset A ⊂ {j₁, … , j_l} such that E(β̂_j,A|X) ≠ 0. In fact, the complement of Proposition 1 does not always hold. For instance, if there are two distinct vertexes j and k whose corresponding SNPs satisfy x_j = x_k = μ, then there is a path between vertexes 0 and j with an intermediate vertex k. We can easily obtain the result that μ^T(Q_xkx_j) = 0 as Q_xkx_j is the residual of x_j from regression onto x_k. More generally, if x_j is represented by a linear combination of X_A (i.e. there is a vector γ_A ∈ ℝ^|A| such that x_j = X_Aγ_A), then μ^TQ_XAx_j = 0. From the relationship with the regression coefficient of x_j in multiple regression of μ on (x_j, X_A), this corresponds to perfect multicollinearity. Consequently, we still have the possibility that μ^TQ_XAx_j = 0 using the SNPs on the paths to μ with terminal vertex j and intermediate vertexes A. In what follows, we explore a way of eliminating such redundant paths.

In the causal-inference literature, assumptions such as faithfulness are usually imposed to ensure that the complement of Proposition 1 is true. However, rather than assuming such conditions, we explore conditions under which the complementary result of Proposition 1 holds. Define the length of the path between vertexes a and b with intermediate vertexes {j₁, … , j_l} by the number of edges on the path, i.e., l. The length between two adjacent vertexes a and b is defined to be zero. We declare that the path between vertexes a and b with length l ≥ 0 is the shortest if and only if there is no path between a and b whose length is less than l. This definition permits the existence of multiple shortest paths with equal length.

We then have the following result, which complements Proposition 1.

Proposition 2. Suppose that there is at least one path between vertexes 0 and j, and that the set of intermediate vertexes of one of the shortest paths is {j₁, … , j_l} ⊂ M\{j} = V \ {0, j}. Then, we have μ^T(Q_X{j1,…,jt}x_j) = 0.

The proof is given in “Supplementary Information Section 2”. For the discovery of SNP j such that E(β̂_j,A|X) ≠ 0 for some A, Proposition 2 suggests that we should incorporate into the conditioning set A the intermediate vertexes of the shortest paths between μ = E(y|X) and j. In the above example for two distinct vertexes j and k whose corresponding SNPs satisfy x_j = x_k = μ, the length of the path between vertexes 0 and j with an intermediate vertex k is one, which is not the shortest because vertexes 0 and j are adjacent. That is, the path between 0 and j (whose length is zero) is the shortest path. Proposition 2 states that μ^Tx_j ≠ 0 (the shortest path) is guaranteed but μ^TQ_xkx_j ≠ 0 is not guaranteed (not the shortest path). Note that Proposition 2 does not eliminate the possibility that the non-shortest path gives μ^TQ_Ax_j ≠ 0. Therefore, it is possible that our proposed method misses some non-shortest paths that give a large nonzero effect. Nevertheless, we consider that restricting the search to the shortest paths is useful because the shortest paths produce parsimonious regression models with low degrees of freedom. This narrows the candidate models to be considered, thereby improving statistical power.

Because Propositions 1 and 2 are based on the bi-directed graph with which adjacency is based on the Wellek–Ziegler correlation (which can take value zero), it is not practical in real data applications. To resolve this, we introduce cutoff values for the Wellek–Ziegler correlation between SNPs to declare adjacency in the bi-directed graph. Specifically, for given correlation cutoffs a_min and a_max, if ${(x_j^T{x}_k)}^2\in [a_{min},a_{max}]\subset [0,1]$, we declare that SNPs j and k are adjacent; otherwise, we declare that they are not adjacent. We now derive a_max empirically as follows. Consider a simple multicollinear case of two SNPs x₁ and x₂ such that $x_1^T{x}_2\approx 1$ and $x_2^T\mu \ne 0$, and hence the residual Q_x2x₁ ≈ 0. Then, on the path μ ↔ x₂ ↔ x₁, we will have that $x_1^T{Q}_{x_2}\mu \approx 0$ — i.e. the effect of x₁ has been removed by x₂. Because the test statistic for testing the null hypothesis β₁ = 0 in the regression model μ = x₁β₁+x₂β₂ is proportional to the correlation between y and Q_x2x₁ (Remark 1 in Ueki and Kawasaki 2013), the inclusion of x₂, which is highly-correlated with x₁, renders the test underpowered due to the above-mentioned effect removal. A similar consideration can be found in Howey and Cordell (2014), who noted that the power of their proposed AI test tends to improve by choosing a partner SNP such that the correlation with the anchor SNP is neither high nor low. Even with multiple x₂, the test statistic for testing the null hypothesis β₁ = 0 is proportional to the correlation between y and Q_x2x₁ (Ueki and Kawasaki 2013), so multicollinearity leads to underpowered detection due to effect removal. In that case, the cutoff a_max avoids the inclusion of highly correlated SNPs simultaneously, and it is expected that multicollinearity will be alleviated.