An Exponential Tilt Mixture Model for Time-to-Event Data to Evaluate Treatment Effect Heterogeneity in Randomized Clinical Trials

Abstract

Evaluating the effect of a treatment on a time-to-event outcome is the focus of many randomized clinical trials. It is often observed that the treatment effect is heterogeneous, where only a subgroup of the patients may respond to the treatment due to some unknown mechanism such as genetic polymorphism. In this paper, we propose a semiparametric exponential tilt mixture model to estimate the proportion of patients who respond to the treatment and to assess the treatment effect. Our model is a natural extension of parametric mixture models to a semiparametric setting with a time-to-event outcome. We propose a nonparametric maximum likelihood estimation approach for inference and establish related asymptotic properties. Our method is illustrated by a randomized clinical trial on biodegradable polymer-delivered chemotherapy for malignant gliomas patients.

1. Introduction

Survival time is a primary endpoint for assessing the treatment effect in many randomized clinical trials. It is often observed that the treatment may only be effective to a subgroup of the population due to some unknown mechanism such as genetic polymorphism. For patients in that subgroup, which we call responders, their survival time is associated with the treatment assignment. For patients not in that subgroup, which we call nonresponders, their survival time follows the same distribution regardless of the treatment assignment. One such example is from a randomized trial conducted by Brem et al. (1995). Two hundred and twenty two recurrent brain malignant gliomas patients were randomized to receive either biodegradable polymer-delivered bis-chloroethylnitrosourea (BCNU), a chemotherapy, or placebo wafers at the time of primary surgical resection. The histograms of survival time comparing the BCNU treated group and the placebo group are shown in Figure 1. The histogram for the BCNU group appears to be a mixture of two uni-mode distributions, where one of the two modes is at roughly the same location as the mode for the placebo group. Therefore, the BCNU treatment effect on patients’ survival appears to be heterogeneous: the distribution of survival time in the treatment group is a mixture of two uni-mode distributions, one for nonresponders and the other for responders. Clinically, three questions are of great interest. First, what is the proportion of responders in the population? Second, how to estimate the treatment effect for responders? Third, how to test the existence of treatment effect?

Figure 1.

Histograms of the BCNU data.

One approach to analyze data with a mixture structure is by using finite (parametric) mixture models (Pearson, 1894), where each mixture component was assumed to follow a parametric distribution and the EM algorithm was used to find maximum likelihood estimates of the distributional parameter and the mixture proportion. Larson and Dinse (1985) and McLachlan (1996) extended the parametric mixture models to handle survival data with censored observations. See McLachlan and McGiffin (1994) for a review of the development in this field. More recently, semiparametric models have become an interesting alternative because of the more flexible model framework and weaker model assumptions. The proportional hazards model, which is the most frequently used semiparametric model for survival data, has been extended to handle mixture data (Rosen and Tanner, 1999; Chen and Little, 1999). However, one concern of using the proportional hazards mixture model is that it does not have clear connections to parametric mixture models except for the Weibull mixture model.

For completely observed data, another interesting semiparametric model, referred to as the Exponential Tilt Mixture Model (ETMM), has been proposed by Qin (1999) and Zou et al. (2002). This model is based on the Exponential Tilt Model (ETM), which assumes a log-linear function for the density ratio of two mixture components, leaving the baseline density unspecified. The ETM accommodates a broad class of parametric models because the density ratio functions from many parametric models, such as normal model, gamma model, and lognormal model, have very simple forms that can be easily modeled by a log-linear function. Built upon the ETM, the ETMM can be viewed as a natural generalization of parametric mixture models. The ETM without a mixture structure has been extended to censored, time-to-event data (Shen et al., 2007; Wang et al., 2011). However, to our knowledge, the extension of ETMM to time-to-event outcome has not been studied yet.

One important issue for mixture models is testing for the existence of treatment effect. This hypothesis testing problem is not regular because the parameter space is degenerated under the null hypothesis. The asymptotic distribution of the regular likelihood ratio test statistic is very complicated (Hartigan, 1985; Chen and Chen, 2001). Alternatively, Chen (1998) proposed a penalized likelihood ratio test, which solved the degenerate problem by adding a penalizing term to the likelihood function. The asymptotic distribution of the test statistic turned out to be much simpler. However, there is no clear standard on how to choose an appropriate penalizing function. Lemdani and Pons (1995) and Liang and Rathouz (1999) proposed another testing method based on the following observation: although jointly testing for two parameters, the mixture proportion and the distributional parameter of the mixture component, is not regular, the test for one parameter given the other is regular. By utilizing this nice property, they proposed testing statistics with very simple asymptotic distributions for binomial mixture models.

In this paper, we extend the ETMM to censored, time-to-event data. We propose a nonparametric maximum likelihood estimation (NPMLE) approach to estimate model parameters and study the associated asymptotic properties. We also develop a statistical testing procedure to assess the existence of treatment effect based on the ETMM. The application of our methods is illustrated by using the BCNU data.

2. Materials and Methods

2.1Exponential Tilt Mixture Model (ETMM)

Let F₀(.) be the distribution of survival time in the control group. As for the treatment group, to characterize the heterogeneous treatment effect for responders and nonresponders, we assume the survival time follows a mixture distribution: λF₀(t) + (1 − λ)F₁(t), where 1 − λ is the proportion of responders and F₀(.) is the distribution of survival time for responders after receiving the treatment. We consider an ETM for the treatment effect on responders: dF₁(t) ∝ dF₀(t)exp{h(t,β)}, where h(t, β) is a prespecified parametric function with a vector of parameters β. Our model is semiparametric because F₀(.) is completely unspecified. The ETMM can be regarded as a semiparametric generalization of parametric mixture models. For example, it reduces to the normal mixture model with two mixture components if F0 is a normal distribution and h(t,β) = β₁t + β₂t².

2.2Parameter Estimation

We assume the survival time and the censoring time are independent given treatment assignment and further assume the censoring time to be discrete with a finite number of values c_01,…, c_0d0, c_0d0+1 = ∞ for the control group and c_11,…, c_1d1, c_1d1+1 = ∞ for the treatment group. Let c_z = (c_z1,…c_zdz)^T, z = 0,1. Suppose the observed data consist of n (= n₀ + n₁) uncensored, independent observations x₁,…,x_n, where the first n₀ observations come from the placebo group with density dF₀(.) and the next n₁ come from the treatment group with density λdF₀(.) + (1 − λ)dF₁(.). The data also contain m₀ censored, independent observations from the placebo group and m₁ censored, independent observations from the treatment group, with m_zj observations censored at time c_zj (j = 1,…, d_z, z = 0,1, m_z1 + … + m_zdz = m_z). Let N₀ (= n₀ + m₀) and N₁ (= n₁ + m₁) be the numbers of observations in the two groups and N (= N₀ + N₀) be the total number of observations. Furthermore, let ρ₀ = N₀/N, ρ₁ = N₁/N. In this subsection, we assume there is a treatment effect so that λ < 1. We will discuss the test for the existence of treatment effect in Section 2.3. Our parameters of interest include the mixture proportion λ and the distributional parameter β characterizing the difference between the two mixture components. Now consider discrete distributions with point masses only at the observed failure times and let p_i = F₀([x_i]). The nonparametric log-likelihood function (Vardi, 1985; Owen, 2001) is:

$$\begin{array}{c}l(\theta ,F_0)=\sum _{i=1}^{n}log{p}_i+\sum _{i=n_0+1}^{n}log\left(\lambda +(1-\lambda )\frac{exp\{h(x_i,\beta )\}}{\mathrm{\sum }{p}_{i}exp\{h(x_i,\beta )\}}\right)+\sum _{j=1}^{d_0}{m}_{0j}\text{log}\sum _{i=1}^n{p}_{i}I\{x_i>c_{0j}\}\\ +\sum _{j=1}^{d_1}{m}_{1j}log\sum _{i=1}^n{p}_i\left(\lambda +(1-\lambda )\frac{exp\{h(x_i,\beta )\}}{\mathrm{\sum }{p}_{i}exp\{h(x_i,\beta )\}}\right)I\{x_i>c_{1j}\},\end{array}$$ (1)

with a constraint ${\mathrm{\sum }}_{i=1}^n{p}_i=1$. Let θ = (λ, β^T) ^T, and define the profile likelihood of θ as pl_N(θ) = max_F0l(θ, F₀). The NPMLE of θ is obtained by maximizing pl_N(θ), that is, θ̂ = argmaxpl_N(θ). One appealing feature of the NPMLE method is that it does not have the problem of “unbounded likelihood.” Day (1969) pointed out that, for normal mixture models, the global MLE may not exist because the likelihood goes to infinity if one mixture component concentrates on a single sample point. This problem does not arise in our nonparametric likelihood approach. By considering discrete distributions, the point mass at any sample point is at most one, which yields a bounded likelihood. In practice, pl_N(θ) can be obtained via the EM algorithm (Dempster et al., 1977), see Supplementary Materials for the details. Then, θ̂ can be obtained via a Newton-Raphson method by maximizing pl_N(θ). The asymptotic properties of θ̂ are as follows:

Proposition 1

Assume that all the elements in ∂h(x, β)/∂β,∂²h(x,β)/∂β², and (∂h(x, β)/∂β)(∂h(x,β)/∂β)^T are continuous and bounded by some function κ(x) for x ∈ (0, ∝) in a neighborhood of the true value of β satisfying ${\int }_0^{\infty }\kappa (x)d{F}_0<\infty$ and ${\int }_0^{\infty }\kappa (x)d{F}_1<\infty$. We have

1. θ̂ is a consistent estimator of θ

2. $\sqrt{N}(\widehat{\theta }-\theta )\to N(0,U^{-1})$

where θ is the true parameter value and $U=-\underset{N\to \infty }{lim}\frac{1}{N}\frac{{\partial }^{2}p{l}_N(\theta )}{\partial {\theta }^2}$ is the Fisher information.

Proof

See Supplementary Materials.

To estimate survival probabilities for responders and nonresponders at a give time point t₀, it is natural to consider the following estimators

$$\left(\begin{array}{c}{\widehat{S}}_0(t_0)\\ {\widehat{S}}_1(t_0)\end{array}\right)=\left(\begin{array}{c}{\sum }_{i=1}^n{\widehat{p}}_{i}I\{x_i>t_0\}\\ {\sum }_{i=1}^n{\widehat{p}}_{i}exp\{h(x_i,\widehat{\beta })\}I\{x_i>t_0\}/{\sum }_{i=1}^n{\widehat{p}}_{i}exp\{h(x_i,\widehat{\beta })\}\end{array}\right),$$

where p̂_i is the p̂_i’s that maximize l(θ,F₀) in equation (1). Proposition 2 shows that the survival probability estimators (Ŝ₀(t₀) for nonresponders and Ŝ₁(t₀) for responders in the treatment group) are asymptotically linear, which can be used to calculate standard errors of the estimators and to construct pointwise confidence intervals for survival functions.

Proposition 2

Under the same conditions as in Proposition 1,

$$\sqrt{N}\left\{\left(\begin{array}{c}{\widehat{S}}_0(t_0)\\ {\widehat{S}}_1(t_0)\end{array}\right)-\left(\begin{array}{c}{S}_0(t)\\ S_1(t)\end{array}\right)\right\}=\frac{1}{\sqrt{N}}\sum _{i=1}^N\phi (t_0,x_i,{\delta }_i,z_i,\theta ,\eta )+{\mathrm{o}}_p(1),$$

where the expression of φ(t₀, x_i, δ_i, z_i, θ, η) is defined in equation (S5) in Supplementary Materials.

Proof

See Supplementary Materials.

2.3 Testing the Existence of Treatment Effect

There are two equivalent ways to express the null hypothesis for testing the existence of treatment effect. One way, expressed as λ = 1, is to test whether the data come from a mixture of two distributions or from a single distribution. The other way, expressed as β = 0, is to test whether the two mixture components are the same. The diversity in expressing the null hypothesis indicates the irregularity of this testing problem. Under the null hypothesis, the joint parameter space for (λ, β) is degenerated. It includes two lines: λ = 1 and β is arbitrary, and β = 0 and λ is arbitrary. The asymptotic distribution for the regular likelihood ratio statistic is very complicated.

In this subsection, we propose a simple solution to this problem based on the observation that under the null hypothesis, if we fix one parameter, testing for the other parameter is regular. The idea is analogous to Lemdani and Pons (1995); Liang and Rathouz (1999) used for parametric mixture models. Two tests can be constructed: one is the likelihood ratio test for β with a fixed λ; the other is the likelihood ratio test for λ for with a fixed β. These two tests correspond to the two different yet equivalent expressions of the null hypothesis: β = 0 and λ = 1. Since λ is simply a scaler and easy to be set to a fixed value, for convenient, we will focus on testing β = 0 for a fixed λ.

Proposition 3

Under the same conditions as in Proposition 1, for any given 0 ≤ λ < 1, ${\mathit{LRT}}_{\lambda }(\lambda )=2[p{l}_N(\lambda ,{\widehat{\beta }}_{\lambda })-p{l}_N(0)]\to {\chi }_1^2$, where β̂_λ is the NPMLE of β for a given λ and pl_N(0) is the profile likelihood under the null hypothesis.

Proof

See Supplementary Materials.

In practice, it is also of interest to estimate the proportions of nonresponders and responders by constructing a 95% confidence interval for λ. However, the regular Wald confidence interval constructed from Proposition 2 may underestimate λ because it always excludes one based on the assumption of λ < 1 we made in the proposition. Alternatively, we consider the following procedure:

1. Perform the test in Proposition 3. If the p-value is smaller than 0.05, go to step 2; otherwise, go to step 3.

2. Construct the regular Wald confidence interval, which is (exp {G_0.025}/(1 + exp{G_0.025}), exp {G_0.975}/{1 + exp{G_0.975})).

3. Construct the confidence interval as (exp {G_0.05}/(1 + exp{G_0.05}),1].

   where G_q is the q quantile of the asymptotic distribution of log[λ̂/(1 – λ̂)]. When λ < 1, the confidence intervals in both Step 2 and Step 3 can cover λ with probability 0.95. When λ = 1, there is 95% of the chance to choose the interval in Step 3, which always contains one. Thus, the aforementioned procedure can always cover the true value of λ with probability 0.95.

3. Results

3.1 Simulations

The first set of simulations evaluates the finite sample performance of the estimator for the mixture proportion λ. We considered the first three simulation scenarios listed in Table 1. Specifically, λ was chosen as 0.25, 0.50 or 0.75, representing different proportions of responders in the treatment group. Observations in the placebo group were simulated from a log-normal distribution F₀(.) ~ LN(3.2, 0.9²), and those in the treatment group were simulated from λF₀(.) + (1 − λ)F₁(.), where F₁(.)~LN(3.7, 0.2²). The simulation setting is similar to the BCNU data in the sense that the distribution of survival time for responders in the treatment group has larger mean and smaller variance than that for nonresponders. We assumed censoring to occur at 6 fixed time points, the 30%, 40%, 50%, 60%, 70%, and 80% quantiles of F₀. The censoring probabilities were 14% for the placebo group and 16% to 20% for the treatment group, depending on the mixture proportion. Seperate simulations were run for N₀ = N₁ = 150 or 500. Under each setting, 1,000 independent data sets were simulated. We considered the following two specifications of the h(.) function in the ETM:

$$\begin{array}{c}h(t,\beta )={\beta }_{1}log(t)+{\beta }_2{\{log(t)\}}^2\\ h(t,\beta )={\beta }_{1}t+{\beta }_{2}log(t)+{\beta }_3{\{log(t)\}}^2\end{array}$$

Table 1.

Simulation scenarios.

Scenario	F0	F1	λ
(i)	LN (3.2, 0.92)	LN (3.7, 0.22)	0.25
(ii)	LN (3.2, 0.92)	LN (3.7, 0.22)	0.50
(iii)	LN (3.2, 0.92)	LN (3.7, 0.22)	0.75
(iv)	LN (3.2, 0.92)	LN (3.2, 0.92)	—

The first h(.) function is proportional to the density ratio for log-normal distributions. The corresponding ETM, which we call the log-normal ETM, reduces to a log-normal model when F0 is a lognormal distribution. The second h(.) function is a more general expression that incorporates density ratios for log-normal, exponential, and gamma distributions. The corresponding ETM is called the general ETM. Simulation results are summarized in Table 2.

Table 2.

Simulation results for estimating λ.

Simulation	N0 = N1	Log-normal ETM				General ETM Scenario
		Bias	SSE	SEE	CP	Bias	SSE	SEE	CP
(i)	150	−0.002	0.061	0.056	0.94	−0.012	0.063	0.058	0.95
	500	−0.002	0.031	0.031	0.95	−0.005	0.031	0.031	0.96
(ii)	150	−0.014	0.093	0.078	0.94	−0.035	0.112	0.083	0.94
	500	−0.002	0.041	0.042	0.95	−0.006	0.042	0.043	0.95
(iii)	150	−0.100	0.211	0.219	0.88	−0.150	0.253	0.173	0.89
	500	−0.011	0.065	0.066	0.92	−0.024	0.095	0.063	0.91

NOTE: Bias is the mean difference between λ̂ and the true value, SSE is the standard error of λ̂, SEE is the square-root of the mean of the variance estimate of λ̂, and CP is the coverage probability of the 95% confidence interval of λ.

For λ = 0.25 or 0.50, estimates from both the log-normal ETM and the general ETM are virtually unbiased. Coverage probabilities are also close to the desired value 0.95. For λ = 0.75 and when sample size is small (N₀ = N₁ = 150), biases are large and coverage probabilities are lower than 0.95. This is due to the limited number of responders in the data. The estimation becomes better when the sample size increases to 500.

The second set of simulations evaluates the performance of the testing statistic LRT_λ(λ) proposed in Section 2.3. We considered the same three scenarios as in the first set of simulations. In addition, we considered a null scenario where both F₀(.)and F₁(.)~LN(3.2, 0.9²). The simulation scenarios are listed in Table 1. We used the log-normal ETM as our working model and considered five choices of λ in LRT_λ(λ): 0.00, 0.25, 0.50, 0.75, and 0.90. Results are summarized in Table 3.

Table 3.

Empirical Type I error/power for testing the existence of treatment effect

Scenario	N0 = N1	LRTλ(0)	LRTλ(0.25)	LRTλ(0.5)	LRTλ(0.75)	LRTλ(0.9)
(i)	150	1.00	1.00	1.00	1.00	1.00
	500	1.00	1.00	1.00	1.00	1.00
(ii)	150	0.86	0.94	0.99	1.00	0.99
	500	1.00	1.00	1.00	1.00	1.00
(iii)	150	0.28	0.32	0.52	0.77	0.70
	500	0.75	0.78	0.87	0.99	1.00
(iv)	150	0.04	0.04	0.05	0.09	0.15
	500	0.05	0.05	0.05	0.06	0.11

The power appears to be higher for larger λ. For example, the empirical power is 1.00 for λ = 0.90 in simulation scenario (iii) with N₀ = N₁ = 500. But the power for λ = 0.00 is only 0.75. However, the test statistic with larger λ is also less stable. The type I error is larger than the expected value when λ = 0.75 or 0.90 and N₀ = N₁ = 150.

3.2 Data Analysis

Malignant gliomas are a common type of malignant primary brain tumors. Despite of the disproportionately high morbidity and mortality, drug treatment is hampered by the difficulty in crossing the blood-brain barrier and the severe complications from systemic exposure to drugs targeted for the brain. To overcome these problems, a method was developed to incorporate BCNU, a very effective chemotherapeutic drug, into biodegradable polymers. Implantation of the BCNU- incorporated polymers at the tumor site allows local sustained release of BCNU with minimal systemic exposure. In a clinical trial conducted by Brem et al. (1995), two hundred and twenty two patients with recurrent malignant brain tumors were randomized into a BCNU-treatment group and a control group. Patients’ survival time was recorded. In this section, we evaluate the effectiveness of BCNU treatment and estimate the proportion of patients that benefited from the treatment.

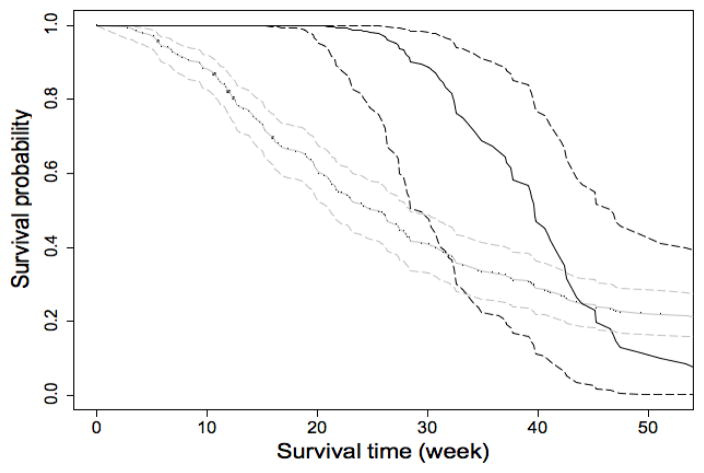
We consider two ETMs: the log-normal ETM and the general ETM. The results are summarized in Table 4. Since the likelihood ratio test comparing the two ETMs is not significant (p-value = 0.168), we choose the log-normal ETM as our working model. Based on this model, we test the hypothesis of no treatment effect (β = 0) using the test statistic LRTλ(λ) described in Proposition 3. Fixing λ at 0.00, 0.25, 0.50, 0.75, or 0.90, we obtain the p-value as 0.38, 0.36, 0.29, 0.10, or 0.12. The test with smaller λ seems to be less powerful, which is consistent with our simulation findings in Section 3. Since none of the tests is significant at 5% level, we follow Step 3 of the procedure described in Section 2.3 to calculate a 95% confidence interval for λ as (0.595, 1]. The survival function estimates for the first year of follow-up comparing treatment responders vs. nonresponders are shown in Figure 2. The survival fraction for treatment responders is significantly higher than that for nonresponders in the first thirty weeks. But after that period, the survival fractions for the two subgroups become close.

Table 4.

Analysis results for the BCNU data. SE is the estimated standard error of λ̂.

	λ̂	SE	95% Confidence Interval	Log-likelihood
Log-normal ETM	0.804	0.099	(0.595,1]	−1151.355
General ETM	0.738	0.111	(0.524,1]	−1150.405

Figure 2.

Estimated survival probabilities (solid curves) along with 95% confidence intervals (dashed curves) for the BCNU data. The black curves are for responders in the treatment group, and the gray curves are for nonresponders.

4. Conclusion

In this paper, we investigate the treatment effect heterogeneity problem in randomized clinical trials, where the survival time for only a subgroup of the population is affected by the treatment. To deal with this problem, we extend the ETMM to time-to-event outcome. We also develop a testing procedure for the existence of treatment effect. To characterize the magnitude of heterogeneity, we proposed a unified confidence interval for the mixture proportion.

One limitation of our method is that it assumes a sufficiently long follow-up period. In case of a short follow-up period with patients censored by the end of the study, a new parameter to characterize the survival fraction by the end of the study can be introduced. Statistical inference procedure and theoretical proofs will need to be modified correspondingly. Similar approach has been taken in Wang et al. (2011, 2014). Another limitation of our method is that the censoring time is assumed to be discrete. Extending our method to continuous censoring time is challenging due to the technical complexity in studying asymptotic properties of model parameters. More advanced theoretical tools, such as the modern empirical process, may be required. But the derivations is primarily of mathematical interest because censoring time can be approximated by a sufficiently fine set of discrete points in practice.

The power of lLRT_λ(λ) depends on the choice of λ. Based on simulations, we recommend to use λ = 0.50, which balances the sensitivity and stability. More powerful tests may be derived by taking the supreme over λ. For binomial mixture model, Lemdani and Pons (1995) showed that the supreme test _λ∈[0,e]LRT_λ(λ), 0 < e < 1 has the same asymptotic distribution as LRT_λ(λ) for a given λ. The asymptotic distribution of the supreme test under the ETMM is more complicated. But the empirical distribution may be obtained using a resampling method.

Abbreviations

ETM

Exponential Tilt Model

ETMM

Exponential Tilt Mixture Model

NPMLE

NonParametric Maximum Likelihood Estimation

BCNU

bis-chloroethylnitrosourea