Characterization of Compton-scatter imaging with an analytical simulation method

Abstract

By collimating the photons scattered when a megavoltage therapy beam interacts with the patient, a Compton-scatter image may be formed without the delivery of an extra dose. To characterize and assess the potential of the technique, an analytical model for simulating scatter images was developed and validated against Monte Carlo (MC). For three phantoms, the scatter images collected during irradiation with a 6 MV flattening-filter-free therapy beam were simulated. Images, profiles, and spectra were compared for different phantoms and different irradiation angles. The proposed analytical method simulates accurate scatter images up to 1000 times faster than MC. Minor differences between MC and analytical simulated images are attributed to limitations in the isotropic superposition/convolution algorithm used to analytically model multiple-order scattering. For a detector placed at 90° relative to the treatment beam, the simulated scattered photon energy spectrum peaks at 140–220 keV, and 40–50% of the photons are the result of multiple scattering. The high energy photons originate at the beam entrance. Increasing the angle between source and detector increases the average energy of the collected photons and decreases the relative contribution of multiple scattered photons. Multiple scattered photons cause blurring in the image. For an ideal 5 mm diameter pinhole collimator placed 18.5 cm from the isocenter, 10 cGy of deposited dose (2 Hz imaging rate for 1200 MU min⁻¹ treatment delivery) is expected to generate an average 1000 photons per mm² at the detector. For the considered lung tumor CT phantom, the contrast is high enough to clearly identify the lung tumor in the scatter image. Increasing the treatment beam size perpendicular to the detector plane decreases the contrast, although the scatter subject contrast is expected to be greater than the megavoltage transmission image contrast. With the analytical method, real-time tumor tracking may be possible through comparison of simulated and acquired patient images.

1. Introduction

Real-time tumor tracking with gantry-mounted kV, fixed kV, and/or MV portal imaging systems is limited by additional imaging dose and/or constrained imaging angles. Imaging of the Compton-scattered, therapy-beam photons is a promising alternative method for tumor tracking because images may be acquired from many angles without delivery of additional dose (Redler et al 2015), but further characterization of the technique is required.

Compton scattering is the most important photon interaction for megavoltage therapy photon beams, and scattering dominates for low atomic number (Z < 8) materials over the ~0.026–24 MeV energy range (Khan and Gibbons 2014). During Compton scattering, an incident photon scatters into a different direction with a longer wavelength, and its lost energy is contributed to the kinetic energy of an electron. The other scattering process— coherent scattering—is negligible over the considered energy range, and any further mention of scattering is in reference to Compton scatter. The scatter probability and scattered photon energy can be analytically calculated based on the incident photon energy, the scattering angle, and the electron density of the material. An image may be formed by identifying the origin of the scattered photons through proper collimation (Lale 1959, Farmer and Collins 1971, Clarke et al 1976, Harding and Tischler 1986), by mapping energies to spatial coordinates (Norton 1994; Lenti 2008), with a Compton camera (Mundy and Herman 2010), or through coded-aperture techniques (MacCabe et al 2013). Of these, pinhole collimation (Redler et al 2015) is a conceptually simple technique that is amenable to experiment and simulation.

A number of applications have been proposed for scatter images. Because the intensity of the image is proportional to electron density, researchers proposed (Odeblad and Norhagen 1956) and showed (Lale 1959, Farmer and Collins 1971, Clarke et al 1976, Harding and Tischler 1986) that scatter images may be used to create volumetric electron density maps of 3D objects and tissues, although steps must be taken to reduce the contribution from multiple scattering (Farmer and Collins 1971) and correct for attenuation (Lale 1959, Clarke and Van Dyk 1973, Battista et al 1977). The high fluence (and resulting dose) required for these measurements and the development of kilovoltage computed tomography (CT) made scatter electron density mapping obsolete (Battista and Bronskill 1981). Because the intensity is dependent on the number of incident photons, scatter imaging may also provide a method for quantitatively measuring the delivered 3D dose (Mundy and Herman 2010).

More recently, scatter imaging has been proposed as a possible technique for real-time tracking of tumor motion during radiotherapy treatment (Redler et al 2015, Yan et al 2016). Because photons are scattered in all directions, scatter imagers can be placed at many points surrounding a patient to provide imaging at different viewing angles. Rather than using an external kV x-ray source (Yan et al 2016), the focus of this work is to analyze the images generated by collecting photons scattered from the treatment beam itself (Redler et al 2015). Preliminary experimental and Monte Carlo (MC) simulated images generated by megavoltage therapy beam irradiation have been analyzed by our group with the focus of applying scatter imaging to track lung tumors during stereotactic body radiation therapy treatment (Redler et al 2015). Because the therapeutic beam is the source of the scattered photons, no additional imaging dose is deposited. Scatter imaging is particularly applicable to hypofractionated treatments because millimeter accuracy and tumor motion corrections are required, and the large deposited dose (and delivery rates in excess of 1200 MU min⁻¹) may generate images with adequate signal-to-noise ratios at short enough acquisition times for real-time guidance. To assess the proposed scatter imaging technique, we developed an analytical method for simulating scatter images. Through this model, the underlying physical processes and image features can be better understood. The analytical method development is also motivated by the desire for a simulation technique that is computationally faster than the previously-used MC simulations. In addition, scattering affects other techniques such as SPECT and PET imaging (Zaidi and Koral 2004, Hutton et al 2011). Development of an analytical scatter modeling technique may improve reconstruction algorithms for these different imaging modalities.

The paper is organized as follows. The analytical simulation method is described briefly (a complete, detailed description is given in the appendix). Using three phantoms, the analytical method is validated through comparison to MC simulations. Through validation, the scatter imaging technique is characterized and assessed as a possible tumor tracking method.

2. Methods

The simulation methods described here assume that only photons passing through a hole (an ideal pinhole collimator) located above the phantom reach the detector. Combined with the knowledge that photons travel along straight lines, an image may be formed by imposing this pinhole restriction.

2.1. Analytical Compton-scatter image simulation

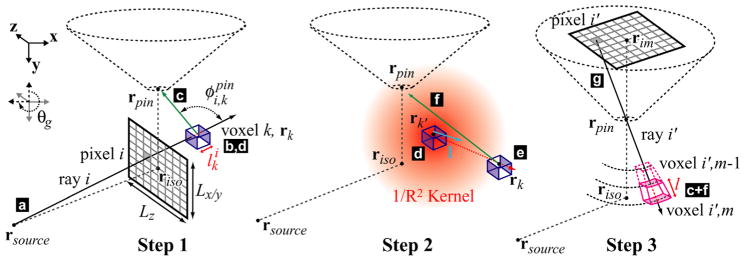
The analytical scatter images were calculated in a multi-step process that models initial attenuation of the therapy beam photons, repeated scattering and attenuation between collision events, and attenuation as the exiting photons travel from the final scattering interaction to the detector. A general description of the algorithm is given here, and each step is described in more detail in the appendix. First, attenuation of the therapy beam photons is calculated through ray-tracing, and the number of these source photons that reach each irradiated voxel within the CT volume is determined. Next, based on the number of incident photons, two quantities are calculated and associated with each voxel: the number and spectrum of photons primary (n = 1) Compton-scattered into the solid angle of the pinhole (Ω_pin) and the total number and spectrum of photons primary-scattered in all directions (Ω_4π). To calculate multiple scattering (n > 1), the total photons (Ω_4π) from the primary scattering are propagated in all directions through kernel convolution/superposition. Attenuation is approximated during kernel photon propagation using Taylor expansions (Boyer and Mok 1986, Wong et al 1996). This propagation is followed by a scattering step in which the total number of scattered photons are used to seed the next round of propagation, and the fraction of the total photons scattered into the pinhole solid angle (Ω_pin) is recorded for each voxel. The kernel propagation and scattering is repeated five times (2nd-through 6th-order scattering). Finally, in the last step, the higher order and the primary-scattered Ω_pin photons from each voxel are attenuated along collection rays emanating to the pinhole and summed to give the scatter image for an ideal pinhole collimator and detector combination.

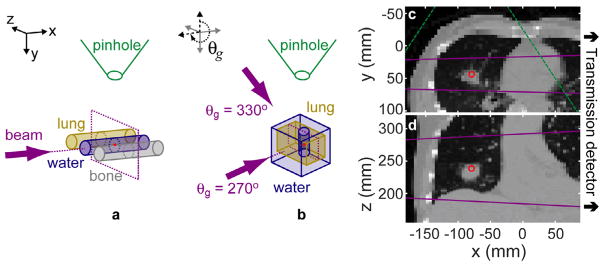
The coordinate system (see figure 1) is defined in relation to a head-first, supine patient lying on a treatment couch such that the x, y, and z unit vectors correspond to patient right-to-left, anterior-to-posterior (A–P), and inferior-to-superior axes, respectively. Here, the treatment couch position is fixed so that a gantry rotation moves the beam around the z axis. The pinhole is always positioned along the –y axis (at gantry angle, θ_g = 0°).

Figure 1.

The 3C phantom (a) consists of three 2.8 cm diameter, 7 cm long cylinders (ρ_lung = 0.29, ρ_water = 1.00, ρ_bone = 1.824 g cm⁻³) with center-to-center spacing of 5.1 cm. The LT phantom (b) is formed by a vertical 2.8 cm diameter water cylinder of 7 cm length centered within a 9 × 9 × 11 cm³ lung box. The lung is surrounded on top, bottom, and back by a 2 cm layer of water and 4 cm of water in front (at the θ_g = 270° beam entrance). For variable LT source/gantry angles, the phantom and detector are fixed, and the source is rotated around the z axis (e.g. the θ_g = 330° beam direction is specified). The LTCT phantom axial (c) and coronal (d) slices are shown. The CT is down-sampled to a voxel size of 4.69 × 4.57 × 2 mm³. The isocenter is marked (red point). The beam direction ((a) and (b): arrows) and size ((c) and (d): lines) are marked (purple). The pinhole position ((a) and (b)) and field of view ((c): dashed lines) are marked (green). For all simulations, the source, pinhole, and detector plane were placed 100, 18.5, and 37 cm, respectively, from isocenter. The schematics in (a) and (b) are not to scale.

The therapy beam spectrum is modeled with a typical, clinical 6 MV flattening-filter-free (FFF) x-ray beam, and an ideal pinhole collimator is used to collect the scattered photons. For the simulation input, the only necessary pinhole parameters are the position (r_pin) and the diameter. r_pin is in the same xy plane as the source (linear accelerator target) and treatment isocenter, and is 18.5 cm from the isocenter with the vector between pinhole and isocenter oriented 90° from the source-isocenter vector, unless otherwise noted. The pinhole area is calculated using a 5 mm diameter.

2.2. Validation by MC

To validate the analytical model, MC simulations were performed with MC n-Particle v6.0 (MCNP6) (Goorley et al 2012) using the same geometries and phantoms as used for the analytical simulations. An ideal pinhole collimator was simulated by turning off all photon transport in a plane above the phantom except through the pinhole. A radiography tally (with card name ‘FIR’) was used to collect the scatter image. For the FIR tally, each particle collision creates a set of deterministic photon psuedoparticles directed at each FIR pixel. These psuedoparticles are weighted based on the probability that the collision generates photons directed into the solid angle of the FIR pixel. The psuedoparticles undergo attenuation through the material between collision and pixel. Thus, although the interactions and particle transport are based on MC simulation, the image is formed based on psuedoparticles. This FIR tally technique is a method for generating images of scarce events. In the course of the MCNP simulations, ~100 true particles (of the 8 × 10⁶ source particles required for convergence of the LTCT image, 160 photons entered the pinhole) were scattered into the pinhole while the FIR psuedoparticles created converged images, as determined by <5% associated standard deviation errors. Each event in a pinhole-collimated FIR tally deposits a circular spot of intensity in the image due to the pinhole masking. As the number of particles increases, the tally converges to a smooth image. Although coherent scattering contributes negligibly to the fully converged image (the coherent scattering cross section is small—it contributes ~10% to the total attenuation coefficient at its contribution maximum at ~25 keV, a low energy relative to the 200 keV simulated scatter photon spectrum—and the forward-peaked distribution means that photons undergoing coherent scattering essentially continue on the same path), when undersampled, coherent scattering manifests as high intensity spots overlaid on the image. This is due to the forward-peaked angular distribution, which means that for the rare events in which a photon traveling towards the detector is coherently scattered, the generated image spot has a much higher intensity per event than for Compton scattering. Thus, there is an intermediate period in the simulation during which the Compton scatter contribution has converged but the undersampled coherent scattering leaves spots in the image. To increase the speed of convergence, coherent scattering was turned off in the MCNP simulations. Comparison of fully converged MCNP images simulated with and without coherent scattering reveals negligible differences: for the LT phantom, the difference in image pixel intensities divided by the image maximum was ≤2%.

2.3. Material properties—μ, ρ, Z/A

The material type of each CT voxel was assigned based on the Hounsfield Unit (HU): air (HU < −940), lung (−940 ≤ HU < −200), water (−200 ≤ HU < 120), or bone (HU ≥ 120). The density of each CT voxel, ρ, was mapped based on the HU using the clinically calibrated relationship for the specific CT scanner.

For the MCNP simulations, each voxel was assigned a density and an atomic mass composition according to the PNNL compendium (McConn et al 2011) based on its material type.

For the analytical simulations, from the material type, the Z/A (atomic number/atomic mass) and energy-dependent mass attenuation coefficient μ(hν)/ρ associated with each voxel were drawn from NIST (Hubbell and Seltzer 1996). Air was replaced with vacuum. μ(hν)/ρ was linearly interpolated (on log–log scales) to give the value for energy bin j, μ_j/ρ. The relative electron density was calculated as ρ_e = (Z/A) ρ/ρ_w, where ρ_w is the electron density of water.

2.4. Phantoms

The scatter images resulting from irradiating three different phantoms were simulated: the three cylinder phantom (3C) irradiated with a 15 × 15 cm² beam (L_x/y × L_z), simple lung tumor phantom (LT) irradiated with an 8 × 8 cm² beam, and lung tumor CT (LTCT) irradiated with a 5 × 10 cm² beam. The phantoms are shown in figure 1. As a simple test case, the 3C phantom is composed of three cylinders of lung-, water-, and bone-like material. The LT phantom consists of a solid water cylinder surrounded by lung-like tissue and an entrance, exit, top, and bottom wall of water-like material. The LTCT was interpolated down to a 4.7 × 4.6 × 2 mm³ voxel size to increase the speed of MCNP simulations. By analyzing the simple 3C scatter image, intensity proportionality to electron density may be assessed. The 3C and LT phantoms have been used previously to show agreement between experimental and MC simulated scatter images (Redler et al 2015). Therefore, analytically simulated 3C and LT images may be transitively compared to experimental images via MC validation.

2.5. Computer hardware

The MC simulations were performed on a workstation with 16 GB of RAM and a 6 core (2 threads per core) Intel Xeon E5-1660 3.70 GHz CPU. The analytical simulations were performed with 8 GB of RAM and a 4 core Intel Core i7-4770 3.40 GHz CPU.

3. Results

3.1. Analytical versus MCNP simulated images

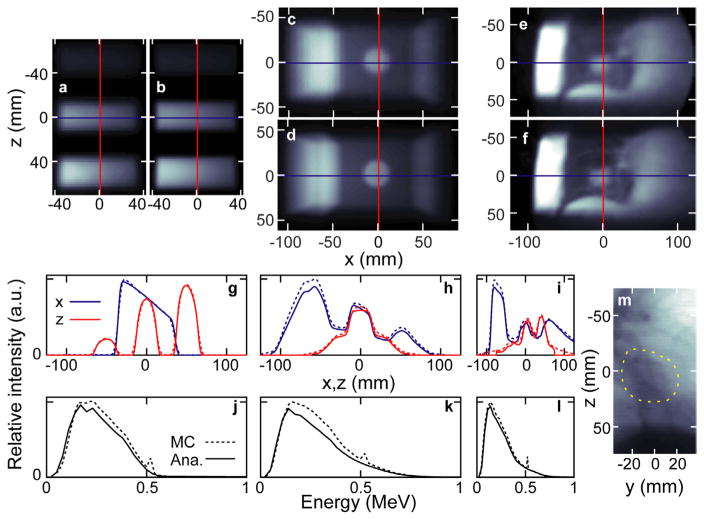
A comparison of the MCNP and analytically simulated scatter images (I) is shown for all three phantoms in figure 2. Line profiles show that all features observed in the MCNP images are reproduced in the analytically simulated images. Quantitative pixel-by-pixel comparison shows that, for the pixels in the MCNP images with greater than 10% of the maximum value (I_MC/max(I_MC) > 10%), (I_ana − I_MC)/max(I_MC) has a standard deviation and maximum of 3.1 and 12% for the 3C phantom, 2.9 and 15% for the LT phantom, and 2.4 and 11% for the LTCT. The largest discrepancies between the analytical and MCNP simulated scatter images are at the beam entrance (left side of image), where the analytical simulations under-predict the image intensity by up to 15% relative to the MCNP.

Figure 2.

The MCNP ((a), (c) and (e)) and analytical method ((b), (d) and (f)) simulated scatter images are shown for the three phantoms: 3C, LT, and LTCT (left to right, respectively). The absolute profiles from each above image (corresponding to the overlaid lines in (a)–(f)) along the x and z dimensions are shown in panels (g)–(i). The unnormalized spectra of the above simulated images are shown in (j)–(l). The 6 MV FFF transmission image (at 50 cm from isocenter) simulated for the LTCT is shown in (m) with the tumor circled (dashed line).

The 3C, LT, and LTCT MCNP-simulated images shown in figures 2(a), (c) and (e) required 7.3, 17.9, and 287.5 h, respectively, to simulate statistically acceptable images (relative error ≤ 0.05 for 1.7 × 1.7 mm² pixels with image intensity ≥ 10% of the maximum) on two threads of the MCNP computer used here. Using the above-specified computing hardware, the corresponding analytically-simulated images required 0.45, 0.39, and 0.27 h of calculation in MATLAB.

For the 3C case, despite the higher attenuation of incident and scattered photons, the bone-like cylinder generates the highest intensity image compared to water-like and lung-like materials. Integrating a 19 × 19 mm² square at the center of each cylinder image gives normalized intensity of 0.28, 1.00, 1.25 for the lung, water, and bone in I_ana compared to 0.3, 0.99, 1.29 in I_MC. Relative to water, the electron densities of lung and bone are 0.29 and 1.71. The tumor in both the LT phantom and LTCT are clearly visible in the scattered images. The image intensity decreases along the beam direction in all three phantom images. The MCNP and analytically simulated energy spectra agree (figures 2(j), (k) and (l)), although the LT phantom and LTCT analytical spectra exhibit lower magnitudes at higher energies compared to the MCNP. Negligible intensity (0.1% of photons in the LTCT MCNP case) is observed above 780 keV. The spectra are peaked at 140–220 keV. Assuming all the photons entering the pinhole come from a point at r_iso (i.e. the pinhole is far from the phantom), the integrated intensity of each I_MC and I_ana is 0.437 and 0.401 (3C), 1.79 and 1.52 (LT), and 1.82 and 1.68 (LTCT) photons per steradian per (source photons per cm²) at r_iso. For example, from the 3C analytical results, if there is 1 source photon in the 15 × 15 cm² beam and the 0.25 cm radius pinhole is 18.5 cm from r_iso, then 0.401 sr⁻¹ cm² × π(0.25)²/18.5² sr × 1 photon/(15 × 15 cm²) = 1.0 × 10⁻⁶ photons are scattered into the pinhole.

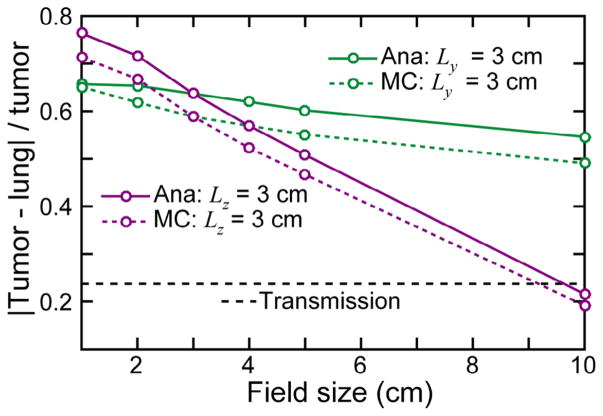
3.2. Scatter image contrast

The tumor contrast relative to the surrounding lung was calculated for the LTCT simulated images and plotted in figure 3. The contrast is calculated as |Ī_tumor − Ī_lung|/Ī_tumor, where Ī is the average intensity in an area assigned to either the interior portion of the tumor or the surrounding lung. As the in-plane field size (L_z, perpendicular to the pinhole axis) is increased from 1 to 10 cm, there is a small drop in the contrast (by 0.16 and 0.10 for the MC and analytical images, respectively). A much larger drop in contrast (by 0.52 and 0.55, MC and analytical) is observed with increasing A–P field size (L_y, along the pinhole axis). Of the simulated field sizes, the highest contrast (0.71, MC; 0.76 analytical) is observed in the 1 × 3 cm² (L_y × L_z) case. The field-size dependent contrast effects are consistent in the analytical and MC simulations. The tumor-lung contrast in the MV transmission image (figure 2(m)) is 0.24.

Figure 3.

The tumor contrast is reported for the LTCT phantom as a function of A–P (y axis in figure 1(c)) and sup–inf (z axis in figure 1(d)) beam field size. The contrast for the MV transmission image (figure 2(m)) is also plotted for comparison.

3.3. Angular dependence

The LT phantom images simulated for gantry angles of θ_g = 330, 300, 240, and 210° (source-isocenter-pinhole angles of 30, 60, 120, and 150° —see figure 1(b)) are shown in figure 4. As with the θ_g = 270° case (figure 2), the line profiles show good agreement between I_ana and I_MC. There is a complicated relationship between source-isocenter-pinhole angle and number of photons that reach the pinhole. Compared to the θ_g = 270° case (figure 2), the integrated I_ana intensity for the other four angles considered here is 2.38, 1.97, 2.19, and 4.53 photons per steradian per (source photons per cm²). As the source-isocenter-pinhole angle increases, the mean energy of the spectrum increases.

Figure 4.

The MCNP ((a)–(d)) and analytically ((e)–(h)) simulated scatter images are shown for the LT phantom irradiated at different source angles: from left to right θ_g = 330, 300, 240, 210°. The absolute profiles from each above image (corresponding to the overlaid lines in (a)–(h)) along the x and z dimensions are shown in panels (i)–(l). The unnormalized spectra of the above simulated images are shown in (m)–(p).

3.4. Spatial energy dependence

A false-color analytically simulated scatter image is shown in figure 5. After binning the photon energies into three ranges, the intensity of each scattered photon energy bin is visualized with three colors. As the source-voxel-pinhole angle decreases, Compton-scattering angle ( ${\varphi }_{i,k}^{\text{pin}}$) increases and scattered photon energy decreases. Thus, the photons from the front face of the LTCT have the highest energy, while those at the back have the lowest. Low energy photons appear at the top and bottom edge of the image, beyond the irradiating field boundaries, due to multiple-scatter.

Figure 5.

A false-color, energy-resolved image of the LTCT analytically simulated scatter image is shown in (a). The component images ((b)–(d)) are formed by summing energy-resolved images over the 0–190, 190–325, and >325 keV energy ranges, respectively.

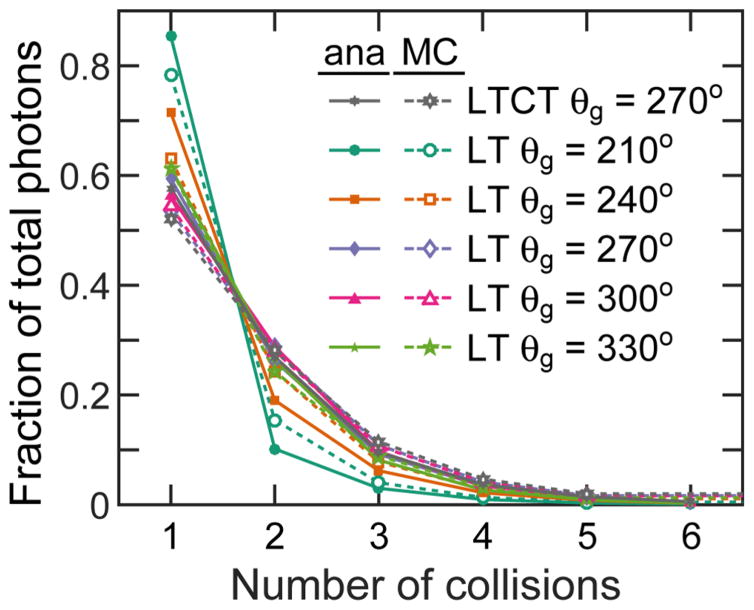
3.5. Multiple scattering

The number of photons that reach the pinhole as a result of nth order scattering are shown in figure 6 for both the LT and LTCT cases (for θ_g = 270°). The ratios of analytically-simulated photons match those from MCNP. In both phantoms, 50–60% of photons that reach the pinhole are primary-scattered. The ratio then drops off exponentially, and the 5th order scattering only contributes ≤2%. For obtuse (120° and 150°) source-isocenter-pinhole angles (θ_g = 240° and 210°), the 1st order scattering contributes a larger fraction (up to 80%) of the total photons that enter the pinhole. Because the n = 1 and 2 collisions generate 80–96% of the imaged photons in all the considered cases, the lines connecting n = 1 and n = 2 data points cross n ~ 1.5 between 0.4 and 0.48.

Figure 6.

The fraction of photons that pass through the pinhole after 1–6 collisions is plotted for different phantoms and source beam angles. The MC and analytically simulated results are shown.

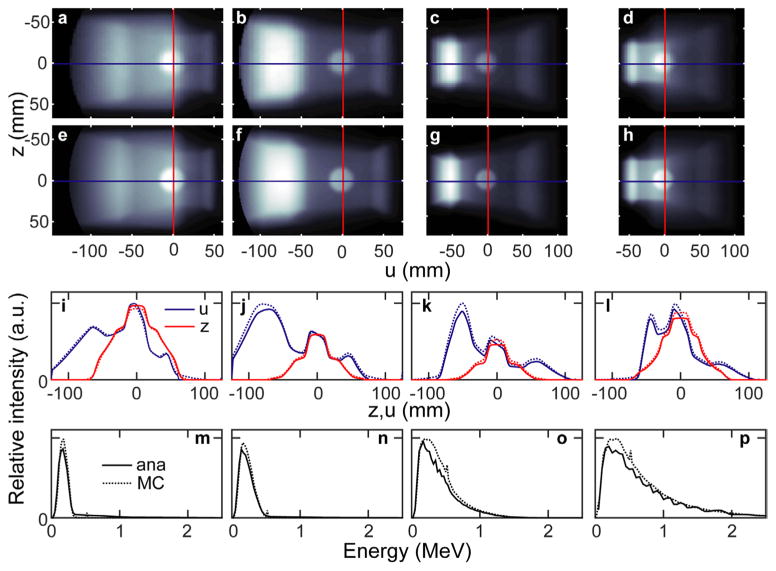
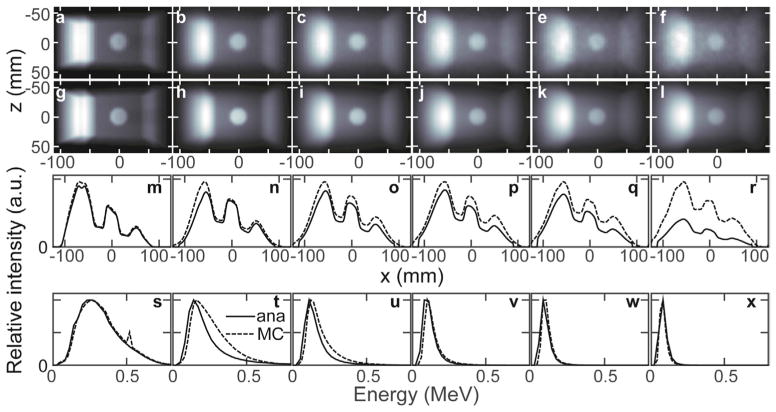
Figure 7 plots the images, line profiles, and spectra associated with each nth order scattering round simulated for irradiation of the LT phantom. Qualitatively, increasing the scattering order blurs the image and causes a more homogeneous distribution of intensity. The primary images $I_{\text{ana}}^{n=1}$ and $I_{\text{MC}}^{n=1}$ match well, as do their spectra. The entrance intensity discrepancy (I_MC > I_ana on the left side of the image) results from differences in the higher order scattering images ( $I_{\text{ana}}^{n>1}$). The 1 < n ≤ 3 analytical spectra have lower intensity than the MCNP spectra above 150 keV. The 511 keV positron-annihilation peak is present in the n = 1 MCNP spectrum, but not in the analytically-simulated nor higher-order MCNP spectra. Pair production was not included in the analytically simulated method because its contribution is <1% of the total collected photons. If desired, inclusion of pair production is straightforward: photons incident at each voxel are converted to 511 keV emitted photons based on the known pair production cross sections.

Figure 7.

The collision-number separated MCNP ((a)–(f)) and analytically ((g)–(l)) simulated LT phantom (θ_g = 270°) scatter images are shown. From left-to-right, the images formed by n = 1, 2, 3, 4, 5 and 6 order–scattered photons are shown. The MCNP image f is formed for collisions 6 ≤ n <100, which may explain the profile amplitude discrepancy in (r). The absolute profiles from each above image along the x dimensions (z = 0.85 mm) are shown in panels (m)–(r). The normalized spectra of the above simulated images are shown in (s)–(x).

4. Discussion

Figures 2, 4 and 6 demonstrate Compton-scattered images simulated using a fast, MC-validated, analytical algorithm. Through these simulations, scatter imaging is characterized to understand the underlying mechanism, information content, expected contrast, scattered photon energies, anticipated fluence, and the manifestation of multiple scattering.

Scatter photons are generated when the therapeutic beam interacts with matter. Therefore, scatter images may be obtained and used to determine which structures have been irradiated. For each of the shown images, the radiation source is to the left, the imaging pinhole is placed at 90° perpendicular to the beam axis (unless otherwise noted, as in figure 4), and the portal transmission image is collected to the right. The scatter image intensity is higher on the left side of the images because the treatment beam is attenuated from left-to-right as it penetrates the phantoms. As shown in the presented simulated images, scatter imaging has the potential to provide high-contrast images collected at arbitrary angles relative to the treatment beam. Because photons are scattered in all directions, the detector may be placed anywhere except for positions where it will (i) block the beam or (ii) be flooded by direct, transmitted beam photons. Unlike portal transmission imaging, which only gives a beam’s eye view of the cumulative attenuation experienced by the beam over its entire path length, scatter imaging can provide multiple simultaneous views of the irradiated volume. As shown in figures 2 + 5, the scatter images may be collected at multiple views from multiple angles. The LTCT phantom scatter image provides a high contrast image with a discernable lung tumor, a feature that is difficult to identify in the transmission image (figures 2(m) and 3). Because of the orthogonal view provided by the scatter image, the features in the 3C and LT phantoms lost in the null-space of their transmission images (not shown) are discernable in the scatter images. Scatter images may potentially be used for tumor tracking. For example, if the lung tumor in figure 2(e) and (f) leaves the beam (due to breathing motion, for example), then it will not appear on the image.

Because scattered photons only originate from irradiated volumes (with the exception of multiple-order scattering), the imaged volume and resulting contrast depend on the field size, as is shown in figure 3. Increasing the field size above and below the tumor (in this case, A–P, along the y axis of figure 1(c)) generates increased scattered photons from lung tissue above and below the tumor without additional photons from the tumor, and contrast decreases. Increasing the field size sup–inf (along the z axis, figure 1(d)) is clearly observed in the scatter image—a larger area in the image field-of-view ‘lights up’—but the tumor-lung contrast is only slightly decreased (due to multiple-scattering photons).

The results presented here not only show what scatter images will look like, but they also indicate the expected energy and number of scattered photons, information important for selecting the proper collimator and detector. When placed at 90° relative to the 6 MV FFF beam, the detected scatter energy spectrum peaks at 140–220 keV, drops abruptly at lower energies, and trails off more gradually to 700–800 keV. The energy of a scattered photon depends on the incident energy and scattering angle. For large field-of-view collimator/detector pairs, the size of the irradiated object will affect the collected scattered photon spectrum because more extreme primary scattering angles are imaged. The three investigated phantoms span fields-of-view ranging from 80 to 200 mm (along the beam direction), and the 3C phantom displays a spectrum with a much lower intensity high-energy tail because of its smaller size. Although the irradiated object size (or detector field-of-view) will affect the collected scatter photon spectrum, the angle between photon source and detector axes is expected to be a more important factor in dictating the scatter spectrum. When the detector is placed at an acute angle relative to the beam, the scattered photons are of lower energy, up to 350 keV (figures 4(m) and (n)). For obtuse source-isocenter-pinhole angles, the scattered photons are of higher energy, up to >2 MeV (figures 4(o) and (p)). The scatter images also exhibit spatial energy-dependence, as shown in figure 5. When the source-voxel-pinhole angle is larger, the Compton-scattering angle is smaller, and higher energy photons are scattered into the pinhole. No portion of the image is monoenergetic, however, due to the polyenergetic source spectrum and the importance of multiple scattering events. Due to the relatively high energy of the scatter image photons, collimators and detectors developed for nuclear imaging applications are expected to be better suited to scatter image collection than diagnostic x-ray setups (2.5 cm of lead transmits 8% of 800 keV photons).

For the 6 MV FFF beam considered here, 10 cGy of dose is calculated by MCNP to be deposited in water at d_max by 1.95 × 10¹⁰ photons cm⁻² (10 × 10 cm² field, central axis, 100 cm SSD). For the LT phantom with the pinhole placed 90° relative to the beam at 18.5 cm from isocenter, the simulations predict that 1.7 × 10⁷ photons will pass through the 5 mm diameter pinhole to deliver an average 1 × 10³ photons per mm² at the imaging plane (1:1 magnification ratio from isocenter to imaging plane). For the same collimator geometry and deposited dose, an average of 6 × 10² photons are expected per mm² for the LTCT phantom. Based on the relatively low expected photon fluence, low noise detectors and long (hundreds of milliseconds) integration times are expected to be necessary for image collection. At a high 1200 MU min⁻¹ dose rate, ~10 cGy will be delivered in 0.5 s. Thus, imaging at 2 Hz is expected to generate ~1 × 10³ photons per mm² per frame. Further experimental work and more sophisticated simulations (with realistic collimators) are required to assess whether this photon fluence results in images of sufficient quality for real-time tumor tracking.

Of the photons that contribute to the scatter image, 40–50% are from multiple scattered photons (figure 6), although increasing the source-isocenter-pinhole angle above 90° decreases the contribution. The multiple scattering redistributes initially scattered photons throughout the phantom, and the left-to-right exponential drop in intensity—caused by attenuation of the primary irradiating beam—is washed out with increased scattering order. The higher-order scatter images still report on the underlying density (the tumor insert is still discernable) because the multiple scattering is also linear in the electron density. But the n > 1 scatter images appear blurred and lose contrast (the difference in peak/valley intensity decreases in figures 7(m)–(r)) because the photons incident at each voxel no longer originate from a known source (r_source). For primary-scattered photons, there are clear origin boundaries as defined by the therapy field edges. For higher-order scattering, photons leak out of the field volume (the low energy blurring at the top and bottom of figure 5(a)).

Two possible applications of scattering imaging—volumetrically measuring the phantom electron density and spatially quantifying deposited dose—are detrimentally affected by the blurring caused by multiple scattering because the intensity of scatter from a voxel of interest also depends on the surrounding voxels. To improve the accuracy of electron density determination, many attempts have been made to reduce the contribution from multiple scattering by localizing the scattering volume with a narrow beam and focused collimator (Lale 1959, 1968), energy-discrimination (Clarke and Van Dyk 1969, Farmer and Collins 1971, Battista et al 1977), and/or collecting at reduced scattering angles(Battista and Bronskill 1978). Despite these advances, multiple scattering and attenuation have limited electron density determination to a 4.3% standard deviation (for 0.11 Gy of delivered dose) (Battista and Bronskill 1981). As an example of this difficulty, although a simple, homogeneous phantom was simulated in the 3C case, multiple scattering and attenuation results in a relative scatter image intensity that does not linearly correlate with material electron density (the bone-like material has an electron density 1.71 times higher than water, but a scatter image intensity only 1.25–1.29 times higher). This discrepancy is largely attributed to the higher attenuation in bone versus water. Although Compton scattering is the predominant attenuation interaction over the simulated scatter image spectral range—and the mass attenuation coefficients are nearly identical for water and bone—the increased scattering (linearly proportional to electron density) is shadowed by the decreased transmission into and out of the bone (exponentially related to density). Quantification of deposited dose based on scatter image intensity has not been tested, possibly because it is also complicated by the multiple-scattering blurring. Energy-discriminating Compton cameras may be able to perform a statistical determination, although processing may take days of computation (Mundy and Herman 2010). The analytical simulation method described here may provide a faster iterative route through which agreement of experimental and simulated images would allow for 3D quantification of deposited dose, even when multiple scattering is present.

In addition to characterizing the scatter imaging technique, the results also serve to validate the presented analytical model: the scatter images simulated with the presented analytical method closely match those simulated with MC. The MC and analytical method primary scatter images and spectra match well, as is expected given the similarity in how they are calculated. In the MC case, the primary scatter image is generated by deterministic psudeoparticles after collisions in the phantom. In the analytical method, the percentage of photons scattered is calculated analytically, and incident and outgoing attenuation is calculated through ray-tracing. Differences in the primary images can be attributed to pinhole blurring—MCNP uses ray tracing through an explicit pinhole while the analytical technique relies on post-processing convolution of the ideal image with a pinhole function— and the discretized nature of both the source and scattered spectra used in the analytical method; the analytical method uses a finite set of photon energies, while the MC simulation allows for a complete sampling (see appendix figure A2). This discretization is also the cause of the jagged spectrum analytically simulated for the θ_g = 240 and 210° (figures 4(o) and (p)).

The discrepancy between MC and analytically simulated images is largely due to approximations in the convolution/ superposition technique used for higher-order scattering in the analytical method. For the convolution/ superposition technique there are two major assumptions. The first is that the attenuation between successive scattering events is approximated by the Taylor expansion given in appendix equation (A.11): the material between voxels is first assumed to be water, and then corrections are made based on the density of the originating voxel (r_k′) and the scattering voxel (r_k) and the distance between. The r_k′ and r_k material corrections assume that the voxels have the same atomic composition (and therefore μ/ρ attenuation curve) as water, which is valid for lung and bone above 100 keV. Based on the approximations, the biggest errors are expected in highly heterogeneous materials and near interfaces (Boyer and Mok 1986). From figures 2(e), (f) and (i), the analytical technique appears to faithfully reproduce features and intensities despite the heterogeneous nature of the lung tissue. The lung tissue scatter intensity is under-predicted by the analytical technique, which may be a result of the approximation.

The analytical technique convolution/superposition method also assumes that the scattered photons are scattered isotropically. But, the scattering probability and energy of scattered photon are both scattering-angle dependent (appendix equations (A.2) and (A.3)). The manifestation of this isotropic approximation is that the analytical spectrum intensity for the n = 2 and 3 order scattering is too low at high energies (hv′ > 150 MeV). The isotropic approximation becomes more valid at higher scattering order, and the spectrum discrepancy is not observed for n ≥ 4.

For the three phantoms investigated here and using similar computer processors, the analytical simulation is up to 1000 times faster to compute than the MC simulation. This speed advantage increases with the complexity and resolution of the phantom because the MCNP simulation time is highly dependent on these factors while the analytical simulation time is not. The analytical simulations were completed in ~30 min in MATLAB without the parallelization toolbox. Almost all of the computations in the analytical simulation method are parallelizable (ray-tracing, FFT), which suggests that the algorithm might be re-written using a faster coding language and implemented on a parallelized GPU cluster to achieve sub-minute (possibly sub-second) computational times.

The proposed goal of the presented scatter imaging technique is to track lung tumor motion during high dose-rate irradiation. This application is well-suited because scatter imaging contrast relies on electron density differences, which are most drastic in lung tumor cases. And, tracking of breathing motion is particularly important during high-dose rate deliveries (>2 times higher than conventional 400–600 MU min⁻¹ dose rates), where high signal-to-noise scatter images may possibly be acquired fast enough for tracking. Aside from previously-proposed, potential 3D dose tracking uses (Mundy and Herman 2010), which may be challenged by computational time and attenuation, there are other possible applications of scatter imaging. For example, beam alignment during cranial, head and neck, or tangential breast treatment might be verified based on air in sinuses, trachea, or lung, respectively. Unwanted beam passage through (air in) bowels might be identified during abdominal treatments. Additionally, the high photoelectric cross section of contrast agents and fiducials might attenuate low energy scatter photons enough to make them discernable on scatter images.

The analytical and MC simulation methods described here assume an ideal pinhole collimator (no septal nor collimator penetration) and an ideal, noiseless detector that collects all incident photons. In reality, a finite thickness collimator is expected to transmit some of the high energy photons. Given the low solid angle represented by the pinhole relative to the full detector area, even a modest collimator transmission probability will create a substantial background, and thick collimators—similar to those proven to be effective in nuclear imaging— will be required. Collimator penetration is expected to cause a broad, inverse-squared background in the image. Septal penetration is expected to blur the image and cause a decrease in spatial resolution. The energy-response of the detector will cause a low-energy weighting of the image, which may help to maintain image quality even if high energy photons leak through the collimator. The full manifestation of these realistic effects is unknown, but preliminary experimental images suggest that quality images are achievable with low dose deposition (Redler et al 2015). Due to the similarities in expected photon energies, many of the extensive technologies developed for medium energy (<400 keV) nuclear imaging may be adapted for scatter imaging. Although preliminary results used a relatively thin ~0.7 cm thick lead pinhole collimator and a planar x-ray cassette (Redler et al 2015), optimized systems are expected to couple ~2–3 cm thick lead collimators to classic segmented crystal arrays. Although energy discrimination is desirable, the high instantaneous photon fluence (the linear accelerator is pulsed) dictates that pulse height analysis will require fast processing, which may not be achievable even with direct conversion crystals, such as CdZnTe. Thus, integrated detection schemes may be required.

Despite the current absence of realistic collimator and septal penetration in the described analytical simulation technique, the method provides a fast and accurate algorithm for generating the ideal image. From the ideal image, the potential information content, expected photon energies, and underlying physics can be assessed. Therefore, we consider the described technique as a necessary step for fully characterizing scatter imaging.

Although it is used here for scatter imaging, the analytical simulation technique may possibly be applied more generally to model Compton scattering within complex phantoms regardless of the origin of the source photons, such as for SPECT, PET, and proton prompt gamma imaging (Zaidi and Koral 2004, Hutton et al 2011).

5. Conclusion

Compton-scattered photons carry information about the irradiated volume. By localizing the origin of these photons with a pinhole collimator, images may be formed that reveal the treatment beam path through the patient anatomy. Unlike other forms of tumor-tracking imaging, Compton-scatter imaging does not require additional ionizing radiation (compare to on-board imaging) and simultaneous images may be collected from multiple angles and positions (compare to portal imaging). Here, a computationally fast—up to 1000 × faster than MC—analytical method for simulating scatter images is described and validated with three phantoms through comparison to MC. The analytical method described here may serve to generate simulated images for real-time comparison to experimental scatter images for the purpose of tumor tracking. The method may also find application to other imaging techniques where modeling Compton scattering is important.

Appendix. Analytical Compton-scatter image simulation

The analytically simulated scatter images were calculated in a multi-step process: source photon deposition, Compton scattering, and signal photon collection. The detailed steps and equations underlying the analytical simulation method are described below and in figures A1 and 2.

A.1. Source photon deposition

For simplicity, an isotropic point source is assumed and defined at r_source. Field size is defined and centered at the isocenter, r_iso, as a rectangle of dimensions L_x/y × L_z normal to the vector (r_iso − r_source). L_z is the field length along the z axis while L_x/y is the length along the cos(θ_G) x + sin(θ_G) y direction. The rectangular field is split into rectangular pixels. Rays are generated that originate at r_source and travel through the center of each field pixel. These beamlet rays carry the source photons through the attenuating CT volume. Each ray carries N_0,Ωi photons, where the 0 subscript indicates that the photons originate at the source, and Ω_i represents the solid angle of field pixel (and associated ray) i. The energy of these photons is distributed discretely over the source spectrum such that summing over the j energy bins gives $N_{0,\mathrm{\Omega }i}={\sum }_j{N}_{0,\mathrm{\Omega }i}^j$. The spectrum of source photons is shown in figure A3, which is a typical output spectrum for a Truebeam 6 MV FFF therapeutic x-ray beam. The number of photons carried by each ray (N_0,Ωi) is proportional to the solid angle represented by each ray. The total number of photons in the full beam is normalized to 1. Thus the number of photons collected per pixel in the final scattered image represents the number expected per source photon in an irradiating field of size L_x/y × L_z. Multiplying by the beam area gives the number of photons expected per source photon fluence. The photon fluence (photons m⁻²) for ray i reaching voxel k at a distance R from r_source (R = |r_k − r_source|) is given by N_0,Ωi/Ω_iR². Because each ray carries a number of photons proportional to its represented solid angle, the fluence of each ray is the same as the fluence for the total beam, N₀/Ω₀R².

Each ray i is traced through the CT volume, and the interaction length, $l_i^k(\mathrm{m})$, with each CT voxel k is calculated (Siddon 1985). The source photons of energy j that reach voxel k is then given by:

$$N_{0,\mathrm{\Omega }i}^j({\mathbf{r}}_k)=N_{0,\mathrm{\Omega }i}^j\text{exp}\left[\sum _{m=1}^M-{\mu }_j({\mathbf{r}}_m)l_i^m\right]$$ (A.1)

where the sum represents the cumulative attenuation of the photons at energy j over the pixels m (= 1, 2,…, M) that ray i intersects before reaching the pixel of interest, k. Along its path, the ray intersects with M voxels before reaching voxel k. μ_j(r_m) is the attenuation coefficient (m⁻¹) (described below) for voxel m at energy j.

By allowing the rays to pass completely through the CT volume, a transmission image can be calculated based on equation (A.1).

Figure A1.

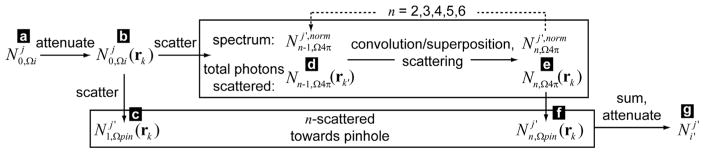
The analytical simulation method is described with an illustration. The variables corresponding to each letter label are given in figure A2. In Step 1, each ray (indicated by (a), of solid angle Ω_i) is traced through the phantom and attenuated. The number of photons reaching each voxel (b) is recorded. The number and energy of photons scattered towards the pinhole is recorded (c). The total number of n = 1 scattered photons and their average spectrum (d) are used as the starting point of Step 2, in which propagation of (d) is modeled with a convolution/superposition algorithm. The total number and spectrum of photons that scatter from the n − 1 round (into the n round, (e)) is used to seed progressive rounds, while the fraction of photons scattered towards the pinhole is recorded (f). Finally, all of the photons scattered by each voxel are summed ((c) + (f)) in Step 3, and attenuated by tracing along rays that pass through the pinhole to each detector pixel (g).

Figure A2.

The analytical simulation method is described with a flow chart (letter labels are consistent with figure A1). In Step 1, (a)–(d) (n = 1) are calculated. In Step 2, convolution/superposition is used in a loop to calculate (e) and (f) for n = 2–6. For each loop, the scattered photons (e) are used as the starting point (d) for the next iteration. In Step 3, (g) is calculated by summing over (c) and (f) (n = 2–6).

A.2. Compton scattering

As is shown below and previously (Clarke and Van Dyk 1969, Farmer and Collins 1974, Battista et al 1977, Battista and Bronskill 1978), multiple-order Compton scattering must be considered. Primary scattering (one collision) generates some photons that undergo secondary scattering (the second collision) that in turn may successively undergo higher-order scattering. Thus, for each considered scattering order n, two quantities are calculated: $N_{n,\mathrm{\Omega }\text{pin}}^j({\mathbf{r}}_k)$, the number of photons of energy j scattered by voxel k into the solid angle subtended by the pinhole, and N_n,Ω4π(r_k), the total number of photons (of all energies) scattered by voxel k into all directions. $N_{n,\mathrm{\Omega }\text{pin}}^j({\mathbf{r}}_k)$ is recorded and cumulatively summed after each scattering round n so that the image may be generated in the final step, while N_n,Ω4π(r_k) is used to seed the next wave of scattering. The primary photons scattered towards the pinhole, $N_{1,\mathrm{\Omega }\text{pin}}^j({\mathbf{r}}_k)$, are explicitly calculated using ray-tracing. To reduce memory requirements and increase computational speed, a generalized isotropic approximation is used to calculate multiple-order scattering.

A.2.1. Primary Compton scattering in the direction of the pinhole

For each irradiated voxel, the solid angle subtended by the pinhole relative to the voxel, ${\mathrm{\Omega }}_k^{\text{pin}}$, is calculated. For each ray and intersected voxel, the Compton-scattering angle (π minus the angle between source-voxel-pinhole), ${\varphi }_{i,k}^{\text{pin}}$, is calculated. For each energy j in the source photon spectrum, voxel k, and ray i, the pinhole-scattered photon energy (MeV):

$$h{\nu }_{i,j,k}^{\prime }=\frac{h{\nu }_j}{1+{\alpha }_j\left(1-\text{cos}{\varphi }_{i,k}^{\text{pin}}\right)},$$ (A.2)

and pinhole-scattered Compton cross section (m² sr⁻¹ per electron):

$$\frac{{\mathrm{d}}_{\mathrm{e}}{\sigma }_{i,j,k}^{\text{pin}}}{\mathrm{d}{\mathrm{\Omega }}_{\varphi }}=\frac{r_0^2}{2}{\left(\frac{h{\nu }_{i,j,k}^{\prime }}{h{\nu }_j}\right)}^2\left(\frac{h{\nu }_j}{h{\nu }_{i,j,k}^{\prime }}+\frac{h{\nu }_{i,j,k}^{\prime }}{h{\nu }_j}-{\text{sin}}^2{\varphi }_{i,k}^{\text{pin}}\right),$$ (A.3)

are calculated using the Compton and Klein–Nishina cross section equations, where the classical electron radius, r₀ = 2.818 × 10⁻¹⁵ m, and α_j = hν_j/511 keV. The number of photons of final energy hν′ scattered towards the pinhole by each pixel k from all the source rays is calculated by multiplying (first term in parentheses below) the number of incident photons of energy bin j (equation (A.1)) by the electron density relative to water (ρ_e), the electron density of water (ρ_w), Compton cross section (equation (A.3)), the pinhole solid angle, and the interaction length between ray and voxel:

$$N_{1,\mathrm{\Omega }\text{pin}}^{j^{\prime }}({\mathbf{r}}_k)=\left(\sum _j\sum _i{N}_{0,\mathrm{\Omega }i}^j({\mathbf{r}}_k)·{\rho }_{\mathrm{e}}({\mathbf{r}}_k)·{\rho }_{\mathrm{w}}·\frac{{\mathrm{d}}_e{\sigma }_{i,j,k}^{\text{pin}}}{\mathrm{d}{\mathrm{\Omega }}_{\varphi }}·{\mathrm{\Omega }}_k^{\text{pin}}·l_i^k\right)\left(\frac{1}{{\displaystyle \sum _i}{N}_{0,\mathrm{\Omega }i}·l_i^k}\frac{N_0}{{\mathrm{\Omega }}_0{R}^2}{V}_{\text{vox}}\right).$$ (A.4)

Because the rays are discrete lines interacting with an ordered grid of voxels, the first parenthetical term above results in artefactual geometric patterns—aliasing—in the number of photons reaching each voxel. To correct for this streaking, the second term is included in equation (A.4). Rather than use the rays to carry photons to each voxel, the rays are instead only used to determine the attenuation along the path from source to voxel. The second term in parentheses represents normalizing by the discrete (number of photons multiplied by interaction length) contribution from all rays, and replacing it with the continuous fluence, N₀/Ω₀R², multiplied by the voxel volume, V_vox.

Figure A3.

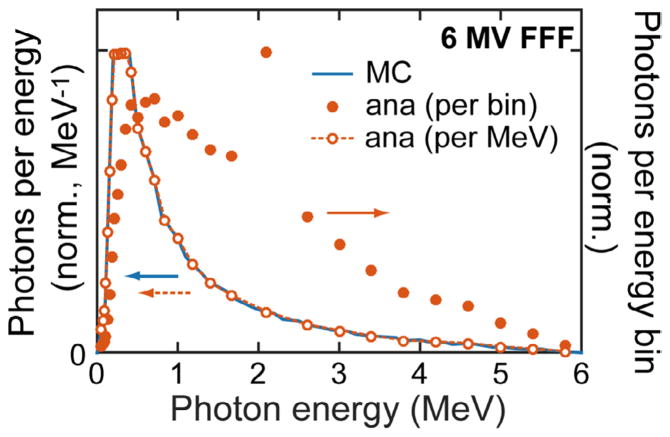
The 6MV FFF treatment beam source spectrum (used for the MC simulations) and source photons per energy bin (analytical simulations) are shown. To reduce the computational time and memory requirements, non-uniform source photon energy bins ( $N_0^j$) were used (solid dots, right axis). When divided by the energy bin width (photons/bin → photons/MeV), the analytical source photon distribution spectrum matches the desired 6 MV FFF spectrum. The energy bin centered at 2.1 MeV has a larger width—and amplitude—than the surrounding bins.

Rather than tracking the resulting scattered photons based on their initial energy (hv_j), the scattered photons are discretely binned into energy bins j′ based on their final energy given by equation (A.2).

Thus, for each voxel, the number and energy of photons primary-scattered (the photons undergo a single collision, n = 1) towards the pinhole are recorded, but ray-tracing to the pinhole to determine the transmitted fraction is not yet performed; this is calculated in the final step. Increasing the pinhole area results in a linear increase in the solid angle and, thus, a linear increase in the number of photons scattered into its direction.

A.2.2. Total primary Compton scattering

To calculate the total number of photons scattered in all directions (not just towards the pinhole), the Klein–Nishina Compton cross section integrated over all angles was calculated for each incident photon of energy j:

$${{}_e\sigma }_j=2\pi r_0^2\left\{\frac{1+{\alpha }_j}{{\alpha }_j^2}\left[\frac{2(1+{\alpha }_j)}{1+2{\alpha }_j}-\frac{ln\left(1+2{\alpha }_j\right)}{{\alpha }_j}\right]+\frac{ln\left(1+2{\alpha }_j\right)}{2{\alpha }_j}-\frac{1+3{\alpha }_j}{{\left(1+2{\alpha }_j\right)}^2}\right\}.$$ (A.5)

Similar to equation (A.4), the number of total source photons scattered by voxel k is given by summing over all the incident photon energies:

$$N_{1,k,\mathrm{\Omega }4\pi }=\left(\sum _j\sum _i{N}_{0,\mathrm{\Omega }i}^j({\mathbf{r}}_k)·{\rho }_{\mathrm{e}}({\mathbf{r}}_k)·{\rho }_w·{{}_e\sigma }_j·l_i^k\right)\left(\frac{1}{{\displaystyle \sum _i}{N}_{0,\mathrm{\Omega }i}·l_i^k}\frac{N_0}{{\mathrm{\Omega }}_0{R}^2}{V}_{\text{vox}}\right).$$ (A.6)

These photons are scattered in all directions. Keeping track of the direction and energy of each scattered photon at each voxel is too memory-intensive. The spectrum of primary scattered photons only depends on the incident photons’ energy. Therefore the relative, normalized spectrum summed over all possible ϕ (scattered in all directions) can be approximately calculated by summing the differential Compton cross section weighted by the number of photons of energy j

$$N_{1,\mathrm{\Omega }4\pi }^{j^{\prime },\text{norm}}=\frac{1}{N_{0_e}{\sigma }_j}\sum _j\sum _{\varphi =0,1,\dots ,180°}{N}_0^j\frac{{\mathrm{d}}_e{\sigma }_j}{\mathrm{d}{\mathrm{\Omega }}_{\varphi }}2\pi \text{sin}\varphi ·\mathrm{\Delta }\varphi$$ (A.7)

where d_eσ_j/dΩ_ϕ is calculated by replacing ${\varphi }_{i,k}^{\text{pin}}$ in equations (A.2) and (A.3) with the full range of possible scattering angles, ϕ = [0°, 180°], Δϕ = 1°. The prefactor normalizes the result such that ${\displaystyle \sum _{j^{\prime }}}{N}_{1,\mathrm{\Omega }4\pi }^{j^{\prime },\text{norm}}=1$. As with equation (A.4), the spectrum is discretized based on its scattered energy, hν′, into energy bin j′. Equation (A.7) is an approximation as it ignores beam hardening (the initial source spectrum ( $N_0^j$) is assumed to reach each voxel).

Furthermore, from equations (A.6) and (A.7), the number of primary photons scattered by voxel k in energy bin j is given by multiplying the total scattered photons by the fraction in that energy bin:

$$N_{1,\mathrm{\Omega }4\pi }^{j^{\prime }}\left({\mathbf{r}}_k\right)=N_{1,\mathrm{\Omega }4\pi }\left({\mathbf{r}}_k\right)·N_{1,\mathrm{\Omega }4\pi }^{j^{\prime },\text{norm}}.$$ (A.8)

In reality, the scattered photon spectrum is anisotropic and dependent on the direction of incident and emitted radiation. For the computationally-fast kernel treatment described below, the spectrum is assumed to be isotropic. This assumption is a source of error, as described in the discussion.

A.2.3. Higher order Compton scattering

With the total number of photons scattered at each voxel k′ from the previous (n − 1) order scattering, the scattering at voxel k in the current order n is given by:

$$N_{n,\mathrm{\Omega }4\pi }({\mathbf{r}}_k)=\langle {}_e\sigma \rangle ·{\rho }_{\mathrm{e}}({\mathbf{r}}_k)·{\rho }_{\mathrm{w}}\left\{N_{n-1,\mathrm{\Omega }4\pi }\left({\mathbf{r}}_{k^{\prime }}\right)\otimes K\left({\mathbf{r}}_k-{\mathbf{r}}_{k^{\prime }}\right)·V_{\text{vox}}·{\int }_{\mathbf{l}={\mathbf{r}}_{k^{\prime }}}^{\mathbf{l}={\mathbf{r}}_k}\langle \mu (\mathbf{l})\rangle {\widehat{\mathbf{r}}}_{k-k^{\prime }}\mathrm{d}\mathbf{l}\right\}.$$ (A.9)

〈_eσ〉 is the spectrum-weighted Compton cross section, where the triangular bracket indicates $\langle g\rangle ={\displaystyle \sum _j}{g}_j{N}_{n-1,\mathrm{\Omega }4\pi }^{j,\text{norm}}$ for arbitrary variable g. The pre-bracket terms represent the likelihood that a photon will scatter at voxel k if it reaches it. The bracketed term calculates the number of photons that reach voxel k from all other voxels k′; N_n−1 is the total number of photons distributed over the full volume of voxel k′, the kernel propagates these photons, and the line integral term represents the attenuation between voxels k′ and k along the unit vector r̂_k−k′ = (r_k − r_k′)/|r_k − r_k′| with spectrum-weighted attenuation coefficient given by 〈μ〉. The kernel, K, only depends on the relative position between n − 1 scattering voxel k′ and n scattering voxel k. K is a 3D matrix where the value at r_k − r_k′ = 0 is zeroed out:

$$K({\mathbf{r}}_k-{\mathbf{r}}_{k^{\prime }})=\frac{B}{4\pi {\mid {\mathbf{r}}_k-{\mathbf{r}}_{k^{\prime }}\mid }^2};B=\{\begin{array}{cc}\frac{{\displaystyle \sum _j}4\pi \frac{d{{}_e\sigma }_j\left({\varphi }_k\right)}{d{\mathrm{\Omega }}_{\varphi }}{N}_0^j}{{{}_e\sigma }_j{N}_0},& n=2\\ 1,& n>2\end{array}.$$ (A.10)

For n = 2, the incident photons (N_1,Ω4π (r_k′ ) voxel k′) are generated by source photons (n = 0) primary scattering at voxels k′ (n = 1). By approximating that the beam is a parallel beam travelling along direction r_iso − r_source, then the angle of Compton scattering can be determined and incorporated into K (for n = 2). For this assumption, the angle-specific Compton scattering is calculated, spectrum-weighted, normalized, and multiplied by the expected inverse square fall-off with distance (B, n = 2). For n > 2, the direction of incoming beams is scrambled by the previous kernel treatment, and the kernel simply propagates with the inverse square (B = 1). The above processes approximate the exact solution from a MC-like simulation, which would require explicit tracking of each photon’s incident and final direction through successive scattering rounds.

The explicit calculation of the attenuation between voxels through the integral term in equation (A.9) is not possible with a kernel convolution/superposition. The attenuation is instead approximated with Taylor expansions (Boyer and Mok 1986, Wong et al 1996) based on the properties of the originating voxels r_k′, the final voxels r_k, and the distance between r_k − r_k′:

$${\int }_{\mathbf{l}={\mathbf{r}}_{k^{\prime }}}^{\mathbf{l}={\mathbf{r}}_k}\langle \mu (\mathbf{l})\rangle {\widehat{\mathbf{r}}}_{k-k^{\prime }}\mathrm{d}\mathbf{l}\approx \langle exp(-{\mu }^{\mathrm{w}}\mid {\mathbf{r}}_k-{\mathbf{r}}_{k^{\prime }}\mid )\rangle \times \left\{1+\left[1-\frac{{\rho }_{\mathrm{e}}({\mathbf{r}}_k)}{2}-\frac{{\rho }_{\mathrm{e}}({\mathbf{r}}_{k^{\prime }})}{2}\right]\langle {\mu }^{\mathrm{w}}\rangle \mid {\mathbf{r}}_k-{\mathbf{r}}_{k^{\prime }}\mid +{[1-{\rho }_{\mathrm{e}}({\mathbf{r}}_{k^{\prime }})]}^2\langle {({\mu }^{\mathrm{w}})}^2\rangle \frac{{\mid {\mathbf{r}}_k-{\mathbf{r}}_{k^{\prime }}\mid }^2}{2}\right\}$$ (A.11)

where the largest component (left term) is based on calculating the attenuation as if the material is water with attenuation factor ${\mu }_j^{\mathrm{w}}$, and corrections are based on the density of the originating and final voxels (the atomic composition is assumed to be the same as water).

A fast Fourier Transform was used to calculate the convolution in equation (A.9) after zero-padding to double the length of each dimension (to prevent a circular FT).

The spectrum of the photons generated by equation (A.9) is calculated with equation (A.7) after replacing $N_0^j\to N_{n-1,\mathrm{\Omega }4\pi }^{j,\text{norm}}$ and $N_{1,\mathrm{\Omega }4\pi }^{j^{\prime },\text{norm}}\to N_{n,\mathrm{\Omega }4\pi }^{j^{\prime },\text{norm}}$. Thus, each n − 1 photon of energy bin j is scattered into a spectrum of energy bin j′ photons with amplitudes given by the angle-dependent differential Compton cross-section.

Finally, under an isotropic approximation, for scattering round n, the number of photons scattered by voxel k towards the pinhole is proportional to the pinhole-subtended solid angle divided by 4π:

$$N_{n,\mathrm{\Omega }\text{pin}}({\mathbf{r}}_k)=N_{n,\mathrm{\Omega }4\pi }({\mathbf{r}}_k)·{\mathrm{\Omega }}_k^{\text{pin}}/4\pi .$$ (A.12)

The process of kernel propagation and scattering (equations (A.9)–(A.11)) was repeated for n = 2, 3.. 6.

A.3. Signal photon collection

After the above calculations, the total number of photons scattered towards the pinhole by voxel k with energy in bin j′ is given by:

$$N_{\mathrm{\Omega }\text{pin}}^{j^{\prime }}({\mathit{r}}_k)=N_{1,\mathrm{\Omega }\text{pin}}^{j^{\prime }}({\mathit{r}}_k)+\sum _{n=2}^6{N}_{n,\mathrm{\Omega }\text{pin}}({\mathit{r}}_k)N_{n,\mathrm{\Omega }4\pi }^{j^{\prime },\text{norm}}.$$ (A.13)

To attenuate and collect these photons, a new set of rays i′ was generated that pass from the center of each imaging pixel (also identified by i′) through r_pin and into the CT volume. The number of photons per voxel was converted into a photon density, ${\rho }_{\mathrm{\Omega }\text{pin}}^{j^{\prime }}({\mathit{r}}_k)=N_{\mathrm{\Omega }\text{pin}}^{j^{\prime }}({\mathit{r}}_k)/V_{\text{vox}}$ and interpolated onto spherical coordinates with grid points defined along the rays i′. Rather than use the rectangular voxel indices k or k′, the spherical coordinate voxels are identified by their defining, intersecting ray i′ and their distance from the pinhole, indicated with index m. Each ray i′ passes through the center of M spherical coordinate voxels, where voxel i′, m = M is furthest from r_pin and voxel i′,m = 1 is closest. The distance between successive voxels along any ray i′ is chosen to be constant, and, by definition, is also the interaction length ray i′ with the spherical coordinate voxel i′,m: l = |r_i′,m − r_i′,m±1|. With this spherical interpolation, the number of photons of energy bin j′ reaching each imaging pixel can now be calculated by summing and attenuating along each collection ray:

$$N_{i^{\prime }}^{j^{\prime }}=\sum _{m=1}^M{\rho }_{\mathrm{\Omega }\text{pin}}^{j^{\prime }}({\mathit{r}}_{i^{\prime },m})·V_{\text{vox}}^m\text{exp}\left[\sum _{m^{\prime }=1}^{m-1}-{\mu }_{j^{\prime }}({\mathbf{r}}_{i^{\prime },m^{\prime }})l\right].$$ (A.14)

Here, the photon density is converted to number of photons by multiplying by the spherical coordinate voxel volume. The exponential attenuation between the scattering voxel and the pinhole is summed over the interceding distance and material. Finally, to approximate the blurring caused by the pinhole, the image was convolved with a binary, 5 mm diameter circular step function.