3D Image-Based Navigators for Coronary MR Angiography

Abstract

Purpose

To develop a method for acquiring whole-heart 3D image-based navigators (iNAV) with isotropic resolution for tracking and correction of localized motion in coronary magnetic resonance angiography (CMRA).

Methods

To monitor motion in all regions of the heart during a free-breathing scan, a variable-density (VD) cones trajectory was designed to collect a 3D iNAV every heartbeat in 176 ms with 4.4 mm isotropic spatial resolution. The undersampled 3D iNAV data were reconstructed with efficient self-consistent parallel imaging reconstruction (ESPIRiT). 3D translational and nonrigid motion-correction methods using 3D iNAVs were compared to previous translational and nonrigid methods using 2D iNAVs.

Results

Five subjects were scanned with a 3D cones CMRA sequence, accompanied by both 2D and 3D iNAVs. The quality of the right and left anterior descending coronary arteries was assessed on 2D and 3D iNAV-based motion-corrected images using a vessel sharpness metric and qualitative reader scoring. This assessment showed that nonrigid motion correction based on 3D iNAVs produced results that were noninferior to correction based on 2D iNAVs.

Conclusion

The ability to acquire isotropic-resolution 3D iNAVs every heartbeat during a CMRA scan was demonstrated. Such iNAVs enabled direct measurement of localized motion for nonrigid motion correction in free-breathing whole-heart CMRA.

Introduction

Motion is a major challenge for magnetic resonance imaging (MRI), particularly in the torso where oscillatory respiratory motion can create ghosting artifacts or image blurring. For cardiac imaging, respiratory-based motion is often reduced by imaging subjects during a breath-hold. While breath-holding is effective, it is not a realistic solution for whole-heart coronary MR angiography (CMRA) with scan times on the order of minutes. Long cardiac scans are commonly gated according to the respiratory cycle, storing data falling within a specified acceptance window (1). However, gating on average extends scan times by a factor of two to three.

To avoid a prolonged scan time, acquired data can be processed retrospectively to reduce respiratory motion artifacts. Such processing has been performed with 1D navigators and with 2D image-based navigators (iNAVs) that track the respiratory-based motion. Following the scan, data is corrected by applying linear phase terms in k-space (2–4).

Recently, the use of 3D affine transformations has been investigated. This has been achieved by first grouping acquired data into bins based on the respiratory cycle, then applying unique 3D affine transformations to each bin (5–7). The 3D affine methods can improve the image quality over translational methods, but the correction is based on general motion trends obtained from information over multiple heartbeats. An advantage of translational methods over binned affine correction methods is the ability to apply motion correction for a particular heartbeat based only on motion tracking information obtained in that same heartbeat. Translational correction has also been extended to correct nonrigid motion by using an autofocus method to reconstruct various regions of the heart with different translational motion trajectories (8).

Recent work has examined acquiring low, anisotropic-resolution 3D Cartesian iNAVs every heartbeat (9,10) to track 3D translational motion. Not only do 3D iNAVs enable the tracking of 3D translational information directly from the heart, but if acquired with sufficient fidelity, they enable the tracking of nonrigid motion. By capitalizing on the time efficiency of non-Cartesian imaging and iterative reconstruction, we demonstrate that isotropic resolution 3D iNAVs can be obtained using a variable-density (VD) 3D cones acquisition to provide navigators with substantially higher resolution than previously investigated Cartesian methods. We also demonstrate preliminary feasibility of using 3D iNAVs for nonrigid 3D motion correction on a per-heartbeat basis.

Method

CMRA Method

We previously developed a free-breathing, ECG-triggered, whole-heart CMRA method based on a segmented 3D cones k-space trajectory (4). Figure 1a shows the timing diagram of this method. To achieve 100% acquisition efficiency, we tracked respiratory motion in three orthogonal directions by acquiring both a sagittal and a coronal 2D spiral iNAV every heartbeat. These 2D iNAVs were gradient-echo (GRE) acquisitions that preceded and followed the alternating-TR (ATR) SSFP (11) 3D cones sequence.

Figure 1.

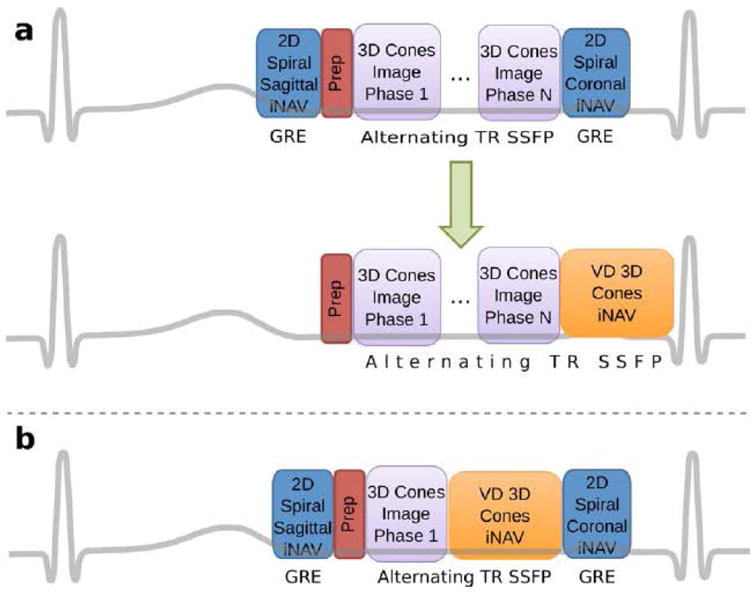
(a) The orthogonal 2D spiral iNAVs in the previous implementation of the 3D cones CMRA pulse sequence (top) can be replaced by a single variable-density 3D cones iNAV (bottom). (b) To compare retrospective motion correction with the 2D and 3D iNAVs, both were collected in a single scan.

In this work, we propose to replace the two orthogonal 2D iNAVs with a single whole-heart 3D iNAV, as illustrated in Fig. 1b. The 3D iNAVs image the same volumetric region as the segmented full-resolution acquisition, continuing the ATR SSFP sequence to maintain similar image contrast.

3D iNAV Design

3D iNAVs with high, isotropic spatial resolution are desirable for extracting 3D motion estimates, although the iNAV resolution need not match the resolution of the full-resolution scan. By interpolating the iNAVs, they can satisfactorily provide motion information for retrospective correction. This has been demonstrated with 2D iNAVs acquired with 3.2 mm resolution that provided motion correction for images acquired with 1.2 mm isotropic resolution (4).

Previous investigations of 3D iNAVs used 3D Cartesian trajectories with anisotropic spatial resolutions of 56 × 18 × 1 mm³ and 5 × 5 × 10 mm³. In the first case, 13 readouts were acquired during SSFP catalyzation (9). In the second case, higher spatial resolution was obtained by acquiring twice as many readouts and using SENSE reconstruction (10).

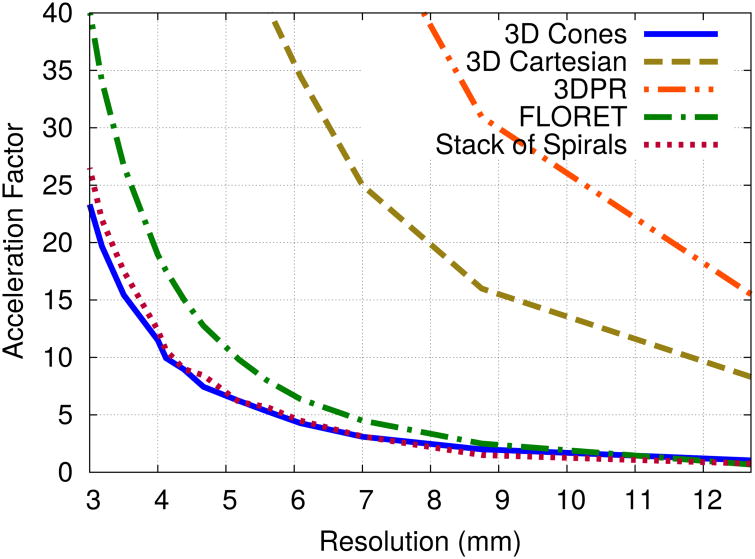
Non-Cartesian trajectories such as 3D cones (12), stack-of-spirals, and FLORET (13), offer the benefit of time-efficient imaging to improve the spatial resolution of 3D iNAVs over a Cartesian trajectory. Figure 2 plots the acceleration factors needed for various trajectories to encode a 28×28×14 cm³ FOV with 32 readouts (2.8 ms readout duration each). Compared to 3D Cartesian and 3D projection reconstruction (3DPR), the 3D cones, stack-of-spirals, and 2-hub FLORET (14) trajectories require significantly fewer readouts. Because FLORET cannot be designed for an anisotropic FOV, more readouts are required compared to 3D cones and stack-of-spirals. For spatial resolution better than 5 mm, the 3D cones trajectory is slightly more efficient than the stack-of-spirals trajectory. The 3D cones trajectory also offers additional motion robustness compared to the stack-of-spirals trajectory as every readout samples the center of k-space.

Figure 2.

The acceleration factors required to acquire 28×28×14 cm³ FOV 3D iNAVs in 176 ms with the alternating-TR SSFP sequence as a function of spatial resolution for 3D Cones, 3D Cartesian, 3DPR, stack-of-spirals and FLORET trajectories (FLORET prescribed for 28 × 28 × 28 cm³ FOV).

We therefore base our design on a 3D cones trajectory in which a 3D iNAV is collected in 176 ms using 32 readouts. This duration is similar to the 160 ms acquisition of the 3D stack-of-spiral fat navigator implemented by Keegan et al. (15).

As shown in Fig. 2, a 176-ms 3D cones acquisition without scan acceleration can achieve a spatial resolution of only 12.7 mm. To improve the resolution, we use scan acceleration via parallel imaging and a variable-density (VD) version of 3D cones (16). The VD 3D cones trajectory is designed with a k-space sampling density that is a polynomial of order p; i.e.,

$$f(\mathit{k})=(1-f_{\mathrm{o}}){(1-|\mathit{k}|/k_{\mathit{\text{max}}})}^p+f_{\mathrm{o}}|\mathit{k}|\in [0,k_{\mathit{\text{max}}}]$$ (1)

where f represents the relative sampling density compared to a standard 3D cones trajectory (f = 1 for a fully sampled trajectory), and f_o is the relative sampling density at k_max. Higher values of p and lower values of f_o increase the amount of k-space undersampling and therefore increase the scan acceleration.

For image reconstruction of the 3D iNAVs, we use a fast wavelet-based algorithm adapted for VD 3D cones (16, 17). Because the 3D iNAVs are acquired over the same FOV as the fully sampled, segmented dataset, the calibration data is extracted from the central region of the fully sampled dataset. The coil sensitivity maps for ESPIRiT are computed using the Software Toolbox and Programming Library for Compressed Sensing and Parallel Imaging (18,19).

Motion Correction with 3D iNAVs

The process of CMRA image reconstruction with 3D iNAV-based motion correction (Supporting Figure S1) first involves the iterative reconstruction of the 3D iNAVs, as described above. Motion information is then derived from these 3D iNAVs. The type of motion correction determines how the motion information from the 3D iNAVs is combined with the segmented 3D cones acquisition in the final step of the process.

3D translational motion correction based on 2D iNAVs assumes that bulk respiratory motion of the heart can be determined from two orthogonal slices through the heart (4). This has produced positive results, but the motion tracking information from each slice is susceptible to through-plane motion effects, which may manifest erroneously as motion in orthogonal directions.

With 3D iNAVs, numerous methods of motion correction are possible. The simplest is to prescribe a region of interest (ROI) covering the heart, and track the translational motion of the heart from beat to beat. To test the feasibility of nonrigid motion correction, an autofocus method, previously shown to improve motion correction with 2D iNAVs (8), is used with 3D iNAVs. This method reconstructs a bank of motion-compensated images and uses a gradient entropy metric to determine the best fitting motion for each pixel in the full image. In the 2D iNAV case, cardiac motion outside of the iNAV planes is not measured directly. The method assumes that localized motion in all regions of the heart are proportional to a single “global” motion trajectory obtained from the 2D iNAVs. A relatively large search space of 405 scaled versions of this global motion trajectory serve as candidate motion trajectories.

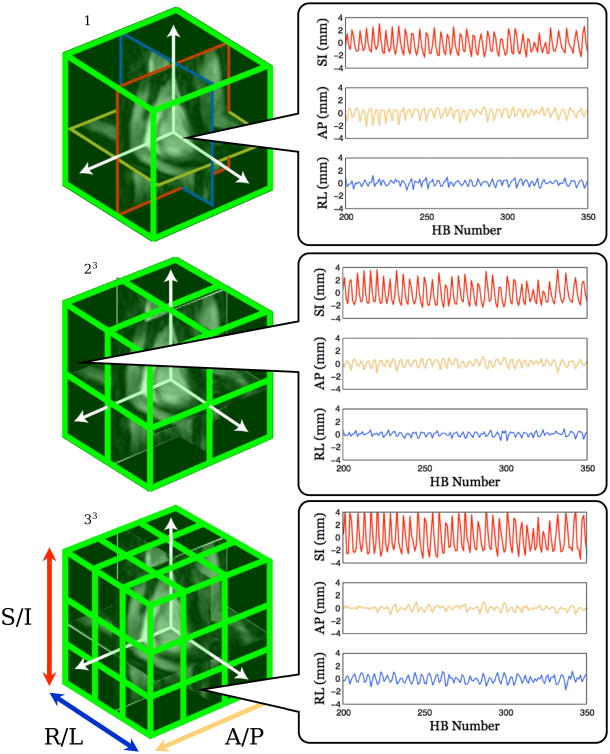
With 3D iNAVs, direct measurement of localized motion within different regions of the heart is theoretically possible, which would improve the efficiency of the autofocus method by reducing the motion search space. To test this, images are first cropped to an ROI encompassing the entire heart, and a reference 3D iNAV is selected at end-expiration. A B-spline-based nonrigid registration method (Insight Toolkit) registers each 3D iNAV to the selected reference image, yielding a 3D deformation field for each heartbeat. A mutual information metric is used for image registration. 3D translational motion trajectory estimates are obtained by averaging these deformation fields within localized regions, using a multi-resolution approach. In three resolution steps, the ROI is divided into 1, 8, and 27 equally sized rectangular volumes as shown in Fig. 3. For each ROI, the mean superior/inferior, anterior/posterior, and right/left translations are computed. A total of 36 candidate translational motion trajectories result from the various ROIs, and for completeness, we include an additional zero-valued motion trajectory to represent the motion of static structures.

Figure 3.

An illustration of the multi-resolution motion information extracted from the 3D iNAVs used for autofocus motion correction. A total of 37 candidate motion trajectories as a function of heartbeat (HB) are used, including a zero-motion trajectory. Three of these trajectories are shown (right).

Experiments

Imaging was performed on a GE Signa 1.5 T Excite scanner with an 8-channel cardiac coil. Data were acquired with a 3D cones ATR SSFP sequence imaging a single cardiac phase (4). The timing parameters were TE/TR₁/TR₂ = 0.57/1.15/4.33 ms and the flip angle was 70°. All 3D trajectories were designed to encode a 28 × 28 × 14 cm³ FOV with a 2.8 ms readout waveform duration. 2D and 3D iNAVs were acquired in each scan as illustrated in Fig. 1c. 2D iNAVs were obtained with 3.2 mm in-plane resolution and 8 mm slice thickness.

Five healthy volunteer subjects with written consent approved by the Institutional Review Board were scanned with ages ranging from 26 to 40. Two experiments were performed: 1) a multiple resolution 3D iNAV test, and 2) a motion-correction comparison test. All subjects underwent the motion-correction test comparison while two of the five subjects were involved in the resolution test.

Prescribed 3D iNAV Resolution Test

Various VD 3D cones trajectories were designed for 32 readout iNAV acquisitions. Six trajectories were tested with isotropic spatial resolutions of 12.7, 8.8, 6.1, 5.2, 4.4, and 3.5 mm, corresponding to acceleration factors of 1, 2, 4.3, 6.2, 9, and 15.4, respectively. Table 1 gives the k-space sampling density function parameters for these six trajectories. At each resolution, an image from a fully sampled trajectory was acquired to serve as a reference to the 3D iNAV. The fully sampled trajectory was segmented over multiple heartbeats during a free-breathing scan, and 2D iNAVs were used for motion correction. The 3D iNAV-based on the VD cones trajectory was acquired in a single heartbeat.

Table 1.

3D iNAV Design - k-space sampling density parameters and scan acceleration for different spatial resolutions. 32-readout, VD 3D cones trajectory.

Resolution (mm)	p	fo	Acceleration
12.7	1.0	1.00	1
8.8	2.0	0.65	2
6.1	1.8	0.39	4.3
5.2	2.0	0.31	6.2
4.4	3.1	0.26	9
3.5	3.0	0.19	15.4

Motion-Correction Comparison Test

In the second experiment, the segmented 3D cones acquisition obtained whole-heart images with 1.2 mm isotropic spatial resolution while the 3D iNAV acquisition obtained images with 4.4 mm isotropic resolution using an acceleration factor of 9.

The following four motion-correction methods, based on either 2D or 3D iNAVs, were applied retrospectively to reconstruct the 1.2-mm resolution coronary angiograms: 1) 2D iNAV-based 3D translational motion correction (4); 2) 2D iNAV-based autofocus correction, using 405 candidate motion trajectory estimates from scaled motion (8); 3) 3D iNAV-based 3D translational motion correction from bulk motion estimates; and 4) 3D iNAV-based autofocus correction using 37 candidate motion trajectory estimates derived from the nonrigid B-splined-based registration method.

The motion-correction quality in the images was measured with a gradient-based image edge profile acutance (IEPA) metric that assesses the sharpness of cross-sectional profiles across a boundary (20). The method measures the signal difference between selected points inside and outside a boundary. The CoroEval software (21), which provides functionality for segmenting coronary arteries and calculating line profiles across the lumen at 1 mm intervals was modified to add a feature for calculating IEPA. IEPA values were calculated by processing a pair of three points inside and outside the lumen boundary along ten transverse radial profiles. Each artery was equally divided into five segments and the mean IEPA over each segment was determined. The whole-heart 1.2 mm images were oversampled to a resolution of 0.3 mm before processing the IEPA values, which were calculated in the right coronary (RCA) for each motion-correction method. For the IEPA metric, higher values correspond to a sharper object depiction.

Qualitative scores were also obtained through blinded reading by two board-certified cardiologists with experience in CMRA. For each artery, five sets of images were displayed side by side in a randomized order, corresponding to the different motion-correction methods. The readers divided each artery into three equal-length segments and assigned scores to each. Images were judged on a 4-point scale: 4 - Good, 3 - Moderate, 2 - Poor, 1 - Non-diagnostic image quality. In total, 150 segments were analyzed per reader.

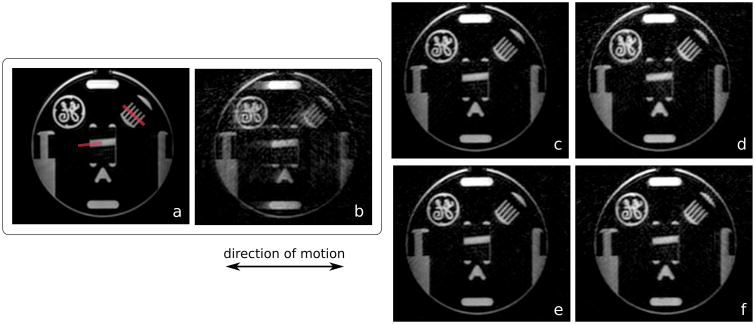
To validate the motion-correction methods under controlled conditions, a study was performed with a resolution phantom. The scanner table was programmed to move periodically over a range of 25 mm with a period of 4.5 s. IEPA measurements were made in the phantom to compare the correction methods.

Results

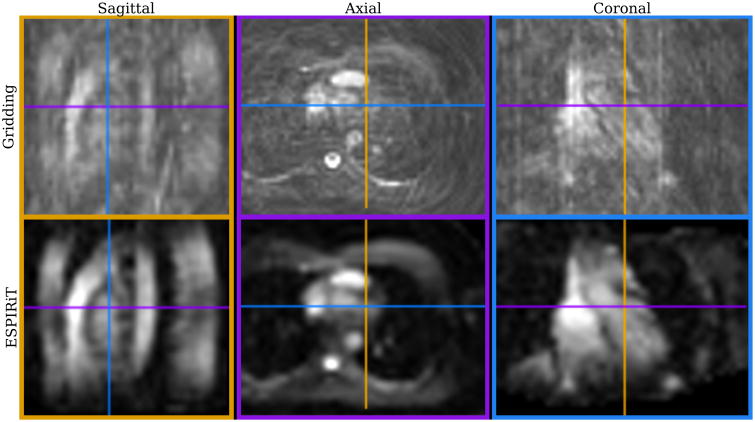
Figure 4 shows three cross sections of a single 3D iNAV with 4.4 mm isotropic resolution. The initial gridding and the corresponding ESPIRiT reconstructions are displayed. A significant amount of aliasing is present in the gridded image due to the high acceleration factor of 9. ESPIRiT significantly reduces the aliasing artifacts, revealing contrast and features useful for motion estimation. (A video showing beat-to-beat 3D iNAVs is included as Supporting Information.)

Figure 4.

A single-heartbeat, 4.4 mm isotropic resolution 3D iNAV reconstructed with gridding (top) and ESPIRiT (bottom) in sagittal (left), axial (center), and coronal (right) planes.

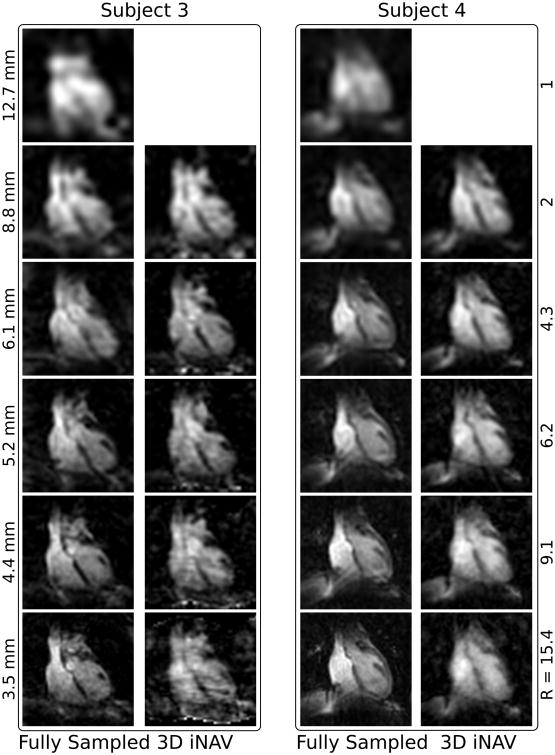
A comparison of 3D iNAVs to fully sampled images is shown in Fig. 5 for multiple spatial resolutions in two subjects. Up to a resolution of 4.4 mm (acceleration factor 9), the 3D iNAVs exhibit similar image quality as the corresponding fully sampled images. At 3.5 mm resolution, blurring and aliasing artifacts corrupt the image quality as ESPIRiT does not sufficiently handle the very high acceleration factor of 15.4.

Figure 5.

A comparison of segmented, motion corrected, fully sampled images reconstructed with gridding (left) and 3D iNAVs reconstructed with ESPIRiT (right) acquired with identical isotropic spatial resolutions in two subjects. The resolution of the images are 12.7, 8.8, 6.1, 5.2, 4.4, and 3.5 mm with corresponding acceleration factors of 1, 2, 4.3, 6.2, 9.1, and 15.4 (top to bottom).

The phantom experiment results are displayed in Fig. 6. IEPA measurements were made in two locations in the phantom (red lines in Fig. 6a)–one along the interface near the center, and a second across five lines in the comb structure. As expected, the uncorrected image had the lowest average IEPA values of 0.116 along the interface and 0.103 in the comb. The image of the stationary phantom had the highest average IEPA values of 0.347 along the interface and 0.315 in the comb. The values for the correction methods were 0.239, 0.261, 0.230, and 0.235 at the interface, and 0.214, 0.238, 0.224, and 0.229 in the comb, corresponding to 2D iNAV-based translational, 2D iNAV-based autofocus, 3D iNAV-based translational, and 3D iNAV-based autofocus motion correction, respectively.

Figure 6.

Reformatted maximum intensity projection images of a resolution phantom. In b-f, the phantom moved periodically over an extent of 25 mm. No motion was present in a. The images were reconstructed with no motion correction (b) and 2D iNAV-based 3D translational (c), 3D iNAV-based 3D translational (d), 2D iNAV-based autofocus (e), and 3D iNAV-based autofocus motion correction (f).

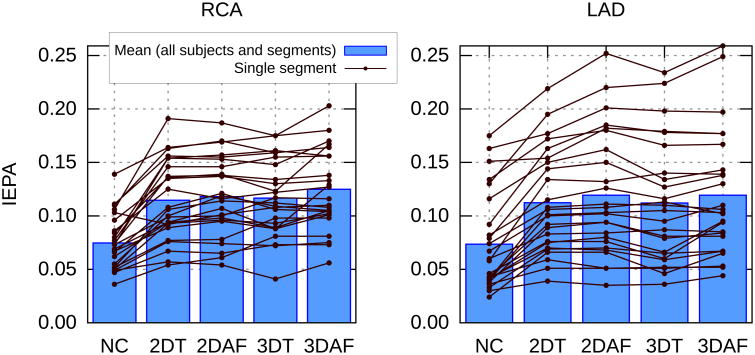
For each subject, the IEPA values for each of the five segments of the RCA and LAD (segment 1 being the most proximal) are displayed in Fig. 7. Each line represents one segment of an artery reconstructed with each of the correction methods. The boxes represent the average value over all segments for each of the correction methods.

Figure 7.

IEPA measurements in the right coronary artery (RCA) and left anterior descending artery (LAD) for images reconstructed with no motion correction (NC), 2D iNAV-based 3D translational (2DT), 2D iNAV-based autofocus (2DAF), 3D iNAV-based 3D translational (3DT), 3D iNAV-based autofocus (3DAF) motion correction. Each artery from each subject was divided into five equal segments. The segments are shown by the lines. The boxes are the mean values over all segments and all subjects for each correction method.

The P-value for a repeated measures ANOVA for changes between the different reconstruction methods was statistically significant (P < 0.05). Given the significance of the ANOVA, paired t-tests were performed to compare the IEPA measurements of the 3D iNAV-based autofocusing method with the other correction methods. In the RCA, the IEPA values with 3D iNAV-based autofocusing were significantly higher than all four other cases. In the LAD, 3D iNAV-based autofocusing gave IEPA values that were significantly higher compared to no correction and 3D iNAV translational correction.

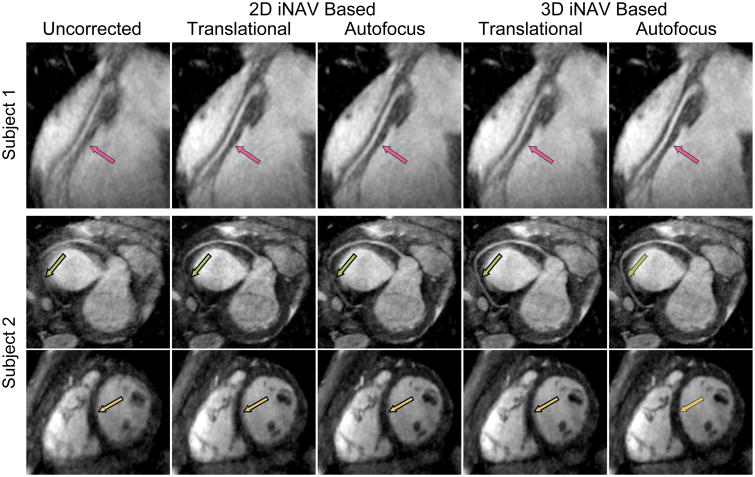
Figure 8 presents images reconstructed with the various motion-correction methods for two subjects. In the RCA of subject 1, the 3D iNAV-based autofocus image had the highest vessel sharpness in all segments. In the images showing the RCA of subject 2, the distal segment of the artery is depicted more clearly for the 3D-iNAV-based motion-correction methods than the 2D-iNAV-based motion-correction methods. Although a sharpness metric was not calculated in the ventricular wall signal, in the short-axis view of the heart in the same subject, the sharpness of the ventricular septum appears to be greatest for the 3D iNAV-based autofocus reconstruction.

Figure 8.

Reformatted maximum intensity projection images of three subjects reconstructed with no motion correction, 3D translational motion correction based on 2D iNAVs, 2D autofocus motion correction, 3D translational motion correction based on 3D iNAVs, and autofocus motion correction based on 3D iNAVs (left to right).

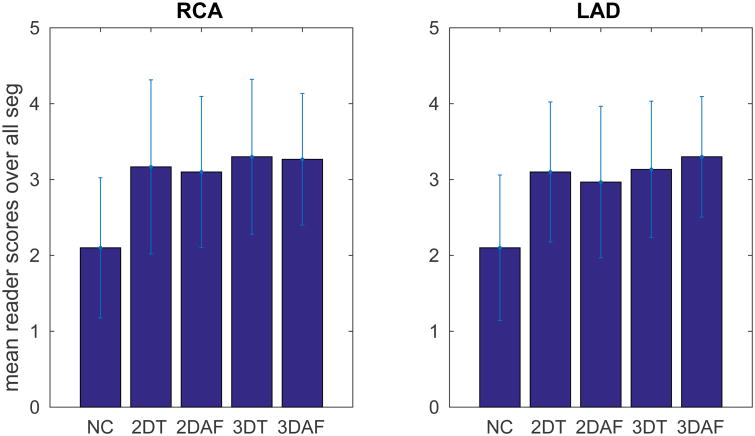
The mean reader scores over all segments are shown in Fig. 9. The P-value for a repeated measures ANOVA for the reader scores obtained for the different reconstruction methods was statistically significant (P < 0.05). Given the significance of the ANOVA, paired t-tests were performed to compare the reader scores of the 3D iNAV-based autofocusing method with the other correction methods, and a P-value threshold of 0.0125 was used (Bonferroni corrected from 0.05). The only comparisons with statistical significance were between 3D iNAV-based autofocusing compared to 2D iNAV-based autofocusing in the LAD and compared to no correction in both the RCA and LAD.

Figure 9.

Mean qualitative reader scores of the RCA and LAD for images reconstructed with no motion correction (NC), 2D iNAV based 3D translational (2DT), 2D iNAV based auto-focus (2DAF), 3D iNAV based 3D translational (3DT), 3D iNAV based autofocus (3DAF) motion correction. The quality scores are: 1 - non-diagnostic, 2 - poor, 3 - moderate, 4 -good.

Discussion

We demonstrated a method for acquiring a 3D iNAV every heartbeat using a VD 3D cones trajectory and iterative image reconstruction. This method produced 3D iNAVs with substantially higher isotropic spatial resolution than those previously achieved. Although acquired at lower temporal resolution than 2D iNAVs, 3D iNAVs produced useful information to correct for motion. The 3D iNAVs were prescribed to the same FOV as the main imaging segment, which simplified the scan setup compared to 2D iNAVs.

While the phantom study demonstrated the near equivalence of all the methods to correct for translational motion, the utility of the 3D iNAVs in-vivo was shown by extracting nonrigid motion information from the 3D iNAVs with the calculation of deformation maps, which were used for autofocus motion correction. The degree of image quality improvement from translational motion correction to nonrigid motion correction was less than from no correction to translational correction. This is in agreement with previous work modeling coronary artery motion based on respiration, showing that the translational motion component is dominant (22).

Based on the assessment results, nonrigid motion correction using 3D iNAV-based autofocusing produced results that were noninferior to those of other correction methods. IEPA indicated better sharpness with 3D iNAV-based autofocusing in the RCA while reader scores indicated better quality in the LAD, but only compared to 2D iNAV-based autofocusing. At this early stage however, these are preliminary results on a small sample size that demonstrate mainly the feasibility of processing 3D iNAVs for motion correction.

Although the 3D-iNAV-based method provided higher vessel sharpness values than the 2D-iNAV-based method in the RCA, the 2D-iNAV-based method had the highest IEPA value in a substantial number of segments. This was possibly due to the 2D-iNAV-based method using a much larger motion search space to determine the optimal motion trajectory at each pixel. With 3D iNAVs, we used 37 candidate motion trajectories, an 11-fold reduction in trajectories compared to the 405 used with 2D iNAVs. This smaller search space correspondingly reduced the autofocus processing time while providing good quality motion correction. Improved image quality with 3D iNAVs may be possible by expanding the search space with scaled versions of the motion trajectories. In the current implementation, the reduced auto-focus processing time was counteracted by the long reconstruction time with ESPIRiT. On a Linux system with dual 2.6 GHz Xeon x5650 CPUs and 72 GB RAM, the total processing time was approximately 4 hours and was dominated by reconstructing the 508 3D iNAVs with ESPIRiT. This time, however, can be reduced with more efficient programming and distributed computing.

In this study, both 2D and 3D iNAVs were acquired in the scans to compare the motion-correction methods on the same data. This required the navigators to be acquired at different points in the cardiac cycle. Taking the midpoint of the segmented acquisition as a reference point, the time to the midpoint of the iNAV acquisitions were -129 and 274 ms for the 2D iNAVs and 138 ms for the 3D iNAV. Depending on the heart rate, the different delays could cause differences in the performances of the motion-correction methods.

Motion occurring over the duration of the 176 ms 3D iNAV acquisition can also be detrimental. Another potential approach to 3D iNAVs would be to combine design elements of the 3D iNAV trajectory with the segmented trajectory and reconstruct low-resolution images each heartbeat. This would reduce discrepancies between the 3D iNAVs and the segmented data.

The autofocus method is not the only means to provide nonrigid motion correction. A 3D affine model could also be generated from the 3D iNAVs to correct the images in a manner similar to the work with respiratory bins (5–7). However, with 3D iNAVs, the 3D affine model would be generated on a per-heartbeat basis.

The motion-correction methods described in this work are based on linear phase modulation in k-space. The generalized reconstruction by inversion of coupled systems (GRICS) method, compatible with VD 3D cones imaging, utilizes a matrix equation relating the motion-corrupted image to the ideal image and appropriately inverting the equation to reconstruct the corrected image (23). This method, which has been demonstrated for free-breathing MRI, relies on possessing an appropriate motion model in which 3D iNAVs could be highly beneficial as they directly give localized displacement fields.

A set of 3D iNAVs with various spatial resolutions was tested, but there is not yet a clear objective method for determining the ideal 3D iNAV. Because aliasing is a function of the subject size, it is more likely the case that the ideal 3D iNAV parameters would be subject dependent. To track dominant superior/inferior motion better, it may be more effective for the 3D iNAV to have higher spatial resolution in that direction.

More generally, for all forms of retrospective image-based motion correction, the question still remains of the necessary spatial resolution to adequately capture motion. Improvements can be made to improve both the spatial and temporal resolution of the 3D iNAVs. Currently, the 3D iNAVs are only undersampled spatially. With scan times of over 500 heartbeats, there is considerable temporal redundancy that could be exploited with some form of low-rank reconstruction (24,25). Also, the FOV of the 3D iNAV is set to encompass the entire chest in the axial plane. Using an outer volume suppression pulse (26,27), the FOV could be reduced, lowering the required acceleration factors. For example, the 4.4 mm 3D iNAV acquired over a 14 cm³ FOV would require an acceleration factor of 4.9 with 3D cones compared to 9 which was used in this study. Additionally, increasing the acquired data redundancy with more coil elements would likely improve the parallel imaging reconstruction of the 3D iNAVs.

Conclusion

A VD 3D cones trajectory with iterative image reconstruction enabled rapid 3D iNAV acquisition of the entire heart with improved isotropic spatial resolution. By collecting a 3D iNAV every heartbeat, 3D motion of the heart was measured during a free-breathing CMRA acquisition to track localized motion in all regions of the heart, providing 100% acquisition efficiency and nonrigid motion correction. A small comparative study on normal subjects demonstrated the feasibility of performing nonrigid motion correction using autofocusing with 3D iNAVs. At this stage, such correction demonstrated noninferiority in its performance as compared to methods based on 2D iNAVs.

While this work demonstrated the feasibility of obtaining and processing such 3D iNAVs, opportunities exist to improve their image quality with more sophisticated data acquisition and image reconstruction. Also, other motion-detection and motion-correction algorithms could be applied to take advantage of the full three-dimensional information available with 3D iNAVs.

Supplementary Material

Supp Video

Supporting Figure S1: The CMRA image reconstruction process using ESPIRiT for 3D iNAV reconstruction and retrospective motion correction for the full-resolution data.

Video. Beat-to-beat 3D iNAVs