Abstract
Objective
MRI measures of network integrity may be useful disease markers in cerebral small vessel disease (SVD). We compared the sensitivity and reproducibility of MRI derived structural and functional network measures in healthy controls and SVD subjects.
Methods
Diffusion tractography and resting state fMRI were used to create connectivity matrices from 26 subjects with symptomatic MRI confirmed lacunar stroke and 19 controls. Matrices were constructed at multiple scales based on a multi-resolution cortical atlas and at multiple thresholds for the matrix density. Network parameters were calculated over the multiple resolutions and thresholds. In addition the reproducibility of structural and functional network parameters was determined in a subset of the subjects (15 SVD, 10 controls) who were scanned twice.
Results
Structural networks showed a highly significant loss of network integrity in SVD cases compared to controls, for all network measures. In contrast functional networks showed no difference between SVD and controls. Structural network measures were highly reproducible in both cases and controls, with ICC values consistently over 0.8. In contrast functional network measures showed much poorer reproducibility with ICC values in the range 0.4–0.6 overall, and even lower in SVD cases.
Conclusions
Structural networks identify impaired network integrity, and are highly reproducible, in SVD, supporting their use as markers of SVD disease severity. In contrast, functional networks showed low reproducibility, particularly in SVD cases, and were unable to detect differences between SVD cases and controls with this sample size.
Keywords: Small vessel disease, MRI, Network analysis, Reproducibility diffusion imaging, Functional connectivity
Highlights
-
•
Diffusion based networks are reproducible in both small vessel disease and controls.
-
•
Functional connectivity in controls is less reproducible.
-
•
Functional connectivity in small vessel disease is not reproducible.
-
•
This limits the ability of whole brain functional networks to distinguish groups.
1. Introduction
Cerebral Small Vessel Disease (SVD) is the most common pathology underlying vascular cognitive decline and dementia (Pantoni, 2010). A number of features can be seen on MRI imaging including lacunar infarcts, T2-white matter hyperintensities, cerebral microbleeds, and more diffuse white matter changes seen on Diffusion Tensor Imaging (DTI) (Schmidt et al., 2010). It has been suggested that damage to white matter tracts leads to disruption of complex networks connecting cortical and sub-cortical regions (Lo et al., 2010; Reijmer et al., 2013). Recently it has become possible to estimate the disruption of such networks using MRI techniques. Structural networks can be constructed via tractography using DTI datasets and these have been shown to be abnormal in patients with SVD, with the extent of disruption correlating with cognitive decline (Lawrence et al., 2014). Mediation analysis has suggested conventional MRI markers of SVD cause cognitive decline via structural network disruption, and recently the degree of network disruption was found to be a significant predicator of future dementia risk (Lawrence et al., 2014). Network integrity can also be assessed using functional connectivity, which utilises resting-state blood oxygen level dependent (BOLD) MRI. Temporal correlations of signal fluctuations in different cortical regions are assessed, and provide an estimate of brain connectivity of these regions (Biswal et al., 1995). Abnormalities of functional connectivity have been reported in SVD, and it has been suggested they may correlate with cognitive impairment (Farràs-Permanyer et al., 2015).
In this study we compared functional and structural connectivity measures in SVD compared with age matched controls, and re-scanned both patients and controls on a further occasion to determine reproducibility of both measures.
2. Methods
2.1. Participants
The study was approved by East of England - Cambridge East research ethics committee (reference: 14/EE/0014). All participants provided written, informed consent. Twenty-six participants with symptomatic SVD were recruited from acute and outpatient stroke services at a single teaching hospital. Inclusion criteria were: 1) history of clinical lacunar stroke syndrome (Bamford et al., 1991) with MRI evidence of an anatomically appropriate lacunar infarct, 2) presence of confluent White Matter Hyperintensities (Fazekas scale ≥ 2) (Fazekas et al., 1987). Exclusion criteria were any cause of stroke other than small vessel disease specifically: 1) evidence of larger subcortical infarctions (>1.5 cm) on MRI as these are often embolic; 2) cortical infarction on MRI; 3) large artery disease - carotid, vertebral or intracranial stenosis >50%; 4) cardioembolic source for embolism (moderate or higher risk according to the Trial of Org 10172 in Acute Stroke Treatment criteria (Adams Jr et al., 1993). In addition patients with any major central nervous system disease other than SVD. In addition 19 stroke-free control subjects were recruited, for these the exclusion criteria were: 1) a medical history of stroke; 2) any major central nervous system disease.
2.2. MRI acquisition
Participants were imaged on a 3 T Verio MRI system (Siemens AG, Erlangen, Germany) employing a 32-channel receive-only head coil. In addition to conventional sequences (1 mm volumetric T1 weighted MPRAGE, 0.9375 × 0.9375 × 2 mm T2 weighted FLAIR, 0.86 × 0.86 × 5 mm T2* weighted gradient echo) for SVD marker identification and brain volume estimation, the following whole brain sequences were acquired:
-
1.
Axial single shot T2*-weighted EPI sequence with diffusion-weighted images (b = 1000 s·mm−2) obtained in 63 non-collinear directions on the whole sphere. Eight non-diffusion weighted images (b = 0 s·mm−2) were acquired. TE/TR: 106/11700 ms, GRAPPA: 2, acquisition matrix 128 × 128, FOV: 256 × 256 mm, 63 contiguous 2 mm slices. Acquisition time 14.5 min.
-
2.
Gradient recalled echo fieldmap, TR: 688 ms, TE1: 5.19 ms, TE2: 7.65 ms, flip angle: 60°. Geometry, slice order and phase encoding identical to 1.
-
3.
Eleven minute axial multi-echo EPI resting state acquisition during which subjects were instructed to attend to a fixation cross. TR: 2430 ms, TE1/2/3: 13/31/48 ms, Flip angle: 90°, GRAPPA: 2, acquisition matrix: 64 × 64, FOV: 240 × 240 mm, 34 slices of 3.8 mm thickness, 10% slice gap. Reconstructed voxel dimensions: 3.75 × 3.75 × 4.18 mm. 269 volumes were acquired.
2.3. Test-retest reproducibility
To investigate the reproducibility of our MRI measures we acquired a second set of MRI data for a subset of participants. Fifteen SVD and 10 control participants were rescanned within 6 months of the original scan.
2.4. MRI processing
2.4.1. Cortical segmentation
Cortical reconstruction and volumetric segmentation of the T1-weighted images was performed using the Freesurfer suite (http://surfer.nmr.mgh.harvard.edu; version 5.3 (Fischl and Dale, 2000; Fischl et al., 2002)). Subcortical structures are segmented and the grey-white matter boundary estimated and refined. The cortical surface is parcellated into 33 regions per hemisphere on the basis of cortical folding patterns (Desikan et al., 2006).
2.4.2. Diffusion and rs-fMRI pre-processing
The diffusion data was pre-processed to produce a diffusion tensor for each voxel using FSL (Jenkinson et al., 2012) and other algorithms implemented in Python, details can be found in Appendix A.
The rs-fMRI data was analysed using the methods proposed by Kundu et al. (2012), this was followed by a pipeline involving steps from SPM (Friston et al., 1995) and CONN (Whitfield-Gabrieli and Nieto-Castanon, 2012) to remove residual effects of noise, movement and the confounding effects of CSF and WM signal, a signal time-course can then be obtained; see Appendix A for more details.
2.5. Network construction
2.5.1. Network nodes definition
Network nodes were defined from the Desikan-Killiany parcellation of cerebral cortex (Desikan et al., 2006). For the structural analysis the nodes are based on the white-grey matter surface, the ROIs were single voxel dilated with 26-connectivity to capture connectivity where streamlines terminated close to grey matter. For functional connectivity the measure of interest is the signal from the cortical region volume itself, so this is the ROI.
To investigate the effects of atlas resolution we employed a hierarchical multiresolution atlas (Daducci et al., 2012). The atlas was created according to Cammoun et al. (2012), the original Desikan-Killiany 68 GM-WM ROIs were partitioned to create a fine resolution atlas of approximately equal area regions (1.5 cm2, n = 998). Then successive merges of neighbouring regions were employed to produce multiple atlas resolutions. Due to the low functional imaging resolution we omit the finest resolution atlas and investigate networks constructed at four atlas resolutions: 68, 114, 219 and 448 nodes.
2.5.2. Network connection definition
For the structural data whole brain deterministic tractography was conducted on the principal directions of the tensors. Streamlines were generated and two cortical regions A, B were connected where one or more streamlines terminating in region A also terminated in region B. The strength of this connection was weighted by the number and length of streamlines between the two regions. Details of the tractography processing and weighting are found in Appendix A.
The corresponding measure for the functional data is simply the correlation coefficient between the signal time-courses over the 269 volumes for any 2 regions.
2.6. Brain network analysis
Network analysis produces a number of measures of network integrity. We focussed on weighted global efficiency (EGlobal), weighted clustering coefficient (Cw) and the total network strength (TNS) as these have previously been shown to be sensitive to structural network differences between SVD cases and controls in (Lawrence et al., 2014). Details on how these parameters are derived is in Appendix A.
2.7. Thresholding of connectivity matrices
There is a correlation coefficient between every pair of nodes in functional analysis and a threshold is required to distinguish connections from statistical noise. In contrast, structural networks are sparse with most pairs of nodes having no connection. Further, for structural data the distribution of connection weights decays exponentially such that the number of streamlines is very low for most connections (Hagmann et al., 2007). Thresholding is also commonly carried out in structural networks to reduce the impact of low-weight false positives resulting from the effects of noise on the tractography algorithm.
In both cases there is no optimal threshold and commonly a range of thresholds are considered. In this study we adopt common thresholding schemes across functional and structural modalities and the different resolutions, for the functional data a fixed edge density is chosen, and the correlation coefficient value varied between subjects to achieve this. For the structural data a fixed edge weight is chosen, and the edge density will differ between subjects. At each resolution for each modality the most restrictive threshold (based on edge density for the rs-fMRI data and edge weight for the diffusion data) was chosen such that 50% of subjects had 95% connectivity of their network. In other words it was possible to access 95% of nodes using the supra-threshold connections. The least restrictive threshold was chosen such that 95% of subjects had 95% connectivity of their network. Twelve thresholds (including these end points) were then equally distributed between the extremes. An additional summary statistic was calculated as the area under the curve (AUC) across all thresholds.
2.8. Statistical analysis
Analyses were conducted in R v3.3.2 (https://www.r-project.org/) using additional functions from the psych package (http://personality-project.org/r/psych, v1.69).
We assess the effects of SVD on the network measures of interest across thresholds and atlas resolutions using ordinary least squares linear regression and Hedge's g, a measure of standardised effect size for the effect of group. These analyses allow the inclusion of confounding variables in addition to the effect of interest (group). The Hedge's g analysis achieves this by attributing the maximum amount of variance to the confounding variables before testing for the effect of group.
Spearman's Rho rank correlation coefficient was calculated to assess whether functional and structural connectivity data was correlated. To reduce dimensionality of the analysis only the AUC data was used in this analysis across each network parameter and atlas.
We assessed test-retest reproducibility for our network measures (EGlobal, Cw, and TNS) using the Intra-class correlation coefficient (ICC), specifically ICC(2,1) according to the definition of Shrout and Fleiss (1979).
For the reproducibility analyses variability in the interval between the scans and variability in the time of day for each scan might act as confounds. These quantities were compared between the SVD and control groups using the Student's unpaired t-test. The Pearson correlation coefficient was used to test the relationship between them and the difference between the network parameters at the two time points.
3. Results
The demographics for the entire group of participants and those who had test/retest scanning are shown in Table 1. The groups were matched for age and gender. The distribution of radiological markers of small vessel disease in the cases and controls is shown in Table 2.
Table 1.
Demographics for the two groups, and for the subgroups who had repeat scanning.
Values given are either mean (SD) or number (%). In the group test column T indicates the t-test was used, X indicates the chi-squared test was used, the number in brackets is the degrees of freedom in the test.
| Whole group |
Test-retest subgroup |
|||||
|---|---|---|---|---|---|---|
| Controls (n = 19) | SVD (n = 26) | Group test | Controls (n = 10) | SVD (n = 15) | Group test | |
| Age (years) | 67.81 (2.71) | 65.86 (11.71) | T(28.6) = 0.82, p = 0.4 | 67.67 (2.92) | 65.33 (13.22) | T(16) = 0.66, p = 0.5 |
| Male gender | 16 (84.21%) | 15 (57.69%) | X(1) = 2.47, p = 0.12 | 9 (90.00%) | 10 (66.67%) | X(1) = 0.74, p = 0.4 |
| Hypercholesterolemia | 7 (36.84%) | 15 (57.69%) | X(1) = 1.17, p = 0.3 | 5 (50.00%) | 8 (53.33%) | X(1) = 0.00, p = 1 |
| Diabetes mellitus | 1 (5.26%) | 3 (11.54%) | X(1) = 0.04, p = 0.8 | 0 (0.00%) | 2 (13.33%) | X(1) = 0.20, p = 0.7 |
| Hypertension | 9 (47.37%) | 18 (69.23%) | X(1) = 1.37, p = 0.2 | 3 (30.00%) | 11 (73.33%) | X(1) = 2.98, p = 0.084 |
| Body mass index (kg/m2) | 27.64 (4.19) | 27.48 (5.07) | T(33.9) = 0.10, p = 0.9 | 25.30 (2.74) | 28.61 (4.14) | T(14.4) = −2.07, p = 0.057 |
| Smoking: current | 1 (5.26%) | 3 (11.54%) | X(2) = 2.17, p = 0.3 | 1 (10.00%) | 3 (20.00%) | X(2) = 0.60, p = 0.7 |
| Smoking: ex | 9 (47.37%) | 7 (26.92%) | – | 3 (30.00%) | 5 (33.33%) | – |
| Modified Rankin scale | ||||||
| 0 | 19 (100.00%) | 5 (19.23%) | X(3) = 28.77, <0.0001 | 10 (100.00%) | 5 (33.33%) | X(3) = 11.11, p = 0.011 |
| 1 | 0 (0.00%) | 9 (34.62%) | – | 0 (0.00%) | 5 (33.33%) | – |
| 2 | 0 (0.00%) | 5 (19.23%) | – | 0 (0.00%) | 1 (6.67%) | – |
| 3 | 0 (0.00%) | 7 (26.92%) | – | 0 (0.00%) | 4 (26.67%) | – |
Table 2.
MRI markers determined from the conventional images, these are Fazekas scale white matter hyperintensity visual rating scale, number of microbleeds, number of lacunes and white matter hyperintensity volume. These indicate the level of damage to the brain of the SVD subjects. The one SVD patient with Fazekas score 0 had multiple lacunar infarcts.
| Group | Fazekas scale (score, number) | No. microbleeds (range, median) | No. lacunes (range, median) | White matter hyperintensity volume (mean ± SD) ml |
|---|---|---|---|---|
| SVD | 0, 1 1, 0 2, 10 3, 15 |
0–84, 0.5 | 1–17, 6 | 33 ± 34 |
| Controls | 0, 6 1, 7 2, 6 3, 0 |
0–1, 0 | 0–3, 0 | 3 ± 3 |
For the functional data the range of edge densities associated with the thresholds was 0.142–0.355 for the lowest resolution atlas and 0.04–0.1 for the highest. The equivalent ranges for the structural data were 0.074–0.221 and 0.011–0.036.
3.1. Comparison of structural and network measures between cases and controls
Although it was found that there were no significant differences in any of the demographic variables between groups, gender and hypertension approached difference. It was decided to include these in the linear regression and Hedge's g analysis as potential confounds. For the structural network data there was a significant difference between SVD cases and controls across the vast majority of atlas, threshold and parameter combinations for network parameters EGlobal and TNS, and those non-significant combinations approached significance (maximum p-value 0.083). Cw showed a different pattern where only a few of the atlas/threshold combinations showed a significant difference between the groups. In contrast the functional network analysis showed no difference between groups for any network parameter, threshold or parameter combination as evidenced by the large p-values associated with all thresholds and atlases. Table 3 shows means and p-values for the three network parameters across all atlas resolutions and thresholds. p-Values are uncorrected for multiple comparisons and were selected to provide best and worst case scenarios for each of the parameters and imaging modalities across the range of atlas resolutions and thresholds. The relative ability of the structural and functional networks to differentiate between SVD and controls is illustrated in Fig. 1. This shows the effect size for the difference between SVD cases and controls for the functional and structural data for each of the three network measures.
Table 3.
Network parameters in cases and controls for both structural and functional networks.
The table shows the means (±SD) of the three network parameters used in this study along with the p-value from the regression model network measure ~ gender + hypertension + group. The best (lowest p) and worst (highest p) case scenarios for each parameter are shown. The p-values given are not corrected for multiple comparisons.
| Structural networks | Atlas | Threshold | Controls | SVD | p-Value |
|---|---|---|---|---|---|
| E(Global) | |||||
| Best-case | N68 | Th8 | 19.61 (±2.63) | 16.87 (±3.03) | 0.026 |
| Worst-case | N114 | Th11 | 10.29 (±1.24) | 8.92 (±1.92) | 0.083 |
| Cw | |||||
| Best-case | N68 | Th3 | 15.51 (±1.51) | 13.52 (±2.10) | 0.021 |
| Worst-case | N219 | Th11 | 3.37 (±0.93) | 5.71 (±1.41) | 0.559 |
| TNS | |||||
| Best-case | N68 | Th0 | 10,743 (±1148) | 9261 (±1571) | 0.017 |
| Worst-case | N114 | Th11 | 10,897 (±1503) | 9265 (±1981) | 0.064 |
| Functional networks | Atlas | Threshold | Controls | SVD | p-Value |
|---|---|---|---|---|---|
| E(Global) | |||||
| Best-case | N68 | Th11 | 0.342 (±0.030) | 0.347 (±0.030) | 0.49 |
| Worst-case | N114 | Th0 | 0.453 (±0.038) | 0.450 (±0.036) | 0.988 |
| Cw | |||||
| Best-case | N68 | Th9 | 0.487 (±0.047) | 0.470 (±0.045) | 0.383 |
| Worst-case | N114 | Th4 | 0.502 (±0.052) | 0.495 (±0.047) | 0.993 |
| TNS | |||||
| Best-case | N114 | Th0 | 10,484 (±849) | 10,455 (±763) | 0.817 |
| Worst-case | N68 | Th11 | 275 (±19) | 274 (±18) | 0.9 |
Fig. 1.
Differences between SVD and controls for functional and structural network data.
The three columns represent global efficiency (E(Global)), weighted clustering coefficient (Cw) and total network strength (TNS) respectively. Part A shows a row for each of the atlas resolutions and in each graph the x-axis overs the range of thresholds used. B summarises area under the curve data, across all density thresholds for each parameter. Structural data is shown in black and functional data n in grey. The y-axis shows the size of the differences between SVD cases and controls. The functional data has a g close to zero, whereas the value for the structural data is much higher. If sample size were increased the p-values from a group comparison and the confidence intervals shown here may reduce, however the effect size will show little change.
The magnitude of the difference between SVD cases and controls for both global efficiency and TNS showed no resolution or threshold dependence; however for the weighted clustering coefficient there was a slight dependence on threshold for both functional and structural networks as shown in Fig. 1.
3.2. Relationship between functional and structural connectivity parameters
There was no significant correlation between the structural and functional data for the three network parameters across any atlas resolution. Analysis was performed for all subjects and the control and SVD groups separately; the maximum Spearman's Rho across all analyses was 0.31, with an associated minimum p-value (uncorrected) of 0.11, this data is shown in Appendix B, Fig. B1.
3.3. Test/retest data
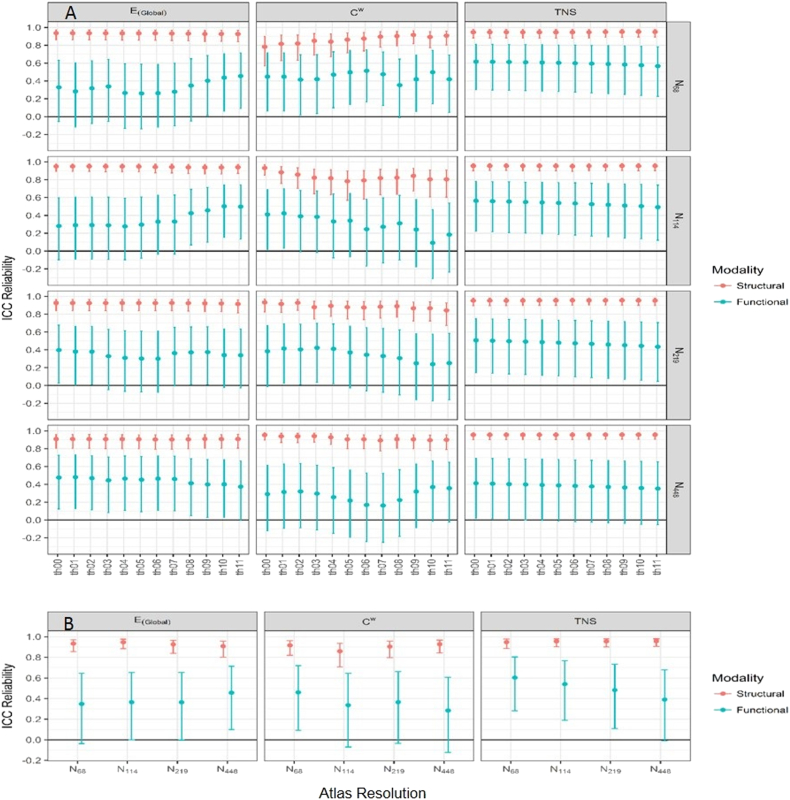
This was first examined in all subjects. The structural data was highly reproducible with ICC values consistently over 0.8. In contrast the functional data showed much poorer reproducibility with ICC values in the range 0.4–0.6 for most analyses. Fig. 2 shows a comparison of the ICC obtained from the test/retest data for the structural and functional data for the three network parameters (EGlobal, Cw, and TNS) and for the four atlas resolutions. The bottom row in Fig. 2 shows the AUC data and that the ICC was largely independent of the threshold used. Appendix B Table B1a shows the ICC and 95% confidence intervals for the structural data over the range of atlas sizes and network parameters, B1b shows the same for the functional data.
Fig. 2.
Comparison of reproducibility of structural and functional network measures.
Structural (red) and functional (blue) data at various thresholds and atlas resolutions. The error bars represent the 95% confidence interval. The three columns represent global efficiency (E(Global)), weighted clustering coefficient (Cw) and total network strength (TNS), the four rows in A represent the four atlas scales. B shows the ICC represented across the range of density thresholds as the area under the curve as a function of atlas resolution used. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
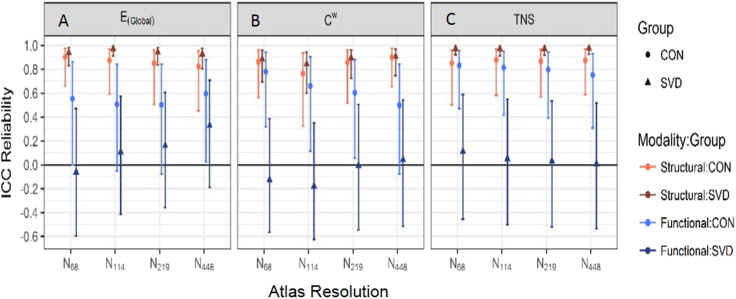
We then evaluated reproducibility separately in cases and controls (Fig. 3). For the structural network measures reproducibility was similarly high in cases and controls. In contrast for functional networks reproducibility was higher in controls than cases, although even in controls it was much lower than with structural networks. In SVD cases reproducibility of functional networks was very poor, with ICCs tending towards zero. A tabular representation of this data can be found in Appendix B in Tables B2a–d and ICC values for all thresholds and resolutions are shown in Fig. B2.
Fig. 3.
Comparison of reproducibility of structural and functional network measures divided into SVD cases and controls.
ICC for the structural (red) and functional (blue) data for each subject group represented as the AUC data for each atlas resolution. For each group the controls are shown with circular markers and a lighter colour than the SVD subjects (triangular markers). The error bars represent the 95% confidence interval. Graph A represents global efficiency (E(Global)), B weighted clustering coefficient (Cw) and C total network strength (TNS). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
The difference in time of day between the scans for retest data was 177 (SD ± 84) minutes for controls and 128 (±109) for the SVD group (p = 0.21). There was a longer delay between scans in the control group than in SVD subjects (12 ± 4 weeks vs. 5 ± 10 weeks, p = 0.003). Neither of these parameters showed any significant correlation with the variation between the repeated measures for any network parameter.
4. Discussion
Growing evidence suggests MRI markers may offer useful surrogate markers to predict risk of dementia in individual patients, and also as a surrogate disease marker to test potential therapeutic interventions with sample sizes much smaller than those needed for phase 3 trials with clinical endpoints such as stroke and dementia (Gregoire et al., 2012; Lambert et al., 2017). Recent data suggest a number of these MRI markers of SVD cause cognitive impairment via network disruption (Lawrence et al., 2014), and therefore MRI network analysis may represent a useful method to integrate information from these different markers into a single measure which can be used in risk prediction. Both structural and functional networks have been suggested as methods to obtain this network data, but to date no studies have compared structural and functional connectivity measures in patients with SVD. Furthermore their comparative reproducibility in SVD has not been determined.
The work investigated the effect of differing atlas scales and thresholds on the results, as can be seen from Fig. 1, Fig. 2, Fig. 3 these variations have, if anything, a very small effect on the results obtained. Certainly in all cases the uncertainty in the parameter estimates is greater than any variation caused by changes in either the atlas scale or threshold used. Although there are hints (for example the reproducibility of E(Global) for the SVD patients and functional networks) that there may be an effect of atlas scale there is no consistent pattern and no statistical evidence that this effect is other than chance. There is more variation in the results with the threshold used, however, again there is no consistent pattern seen. In general it appears that, in this data, the effect of atlas size and threshold used is small and does not affect either the ability of the techniques to separate the groups or their reproducibility.
Using structural networks we found significant differences in network integrity between patients with SVD and normal controls for both EGlobal and TNS, as reported previously (Lawrence et al., 2014). It should be noted that the gender and hypertension proportions in the two groups approach significance for difference and that these were included in the analysis models, compared to models without these variables the group effect size seen was reduced and the p-values associated with the group comparisons were increased, particularly for Cw which lost most of its discriminatory power when the confounds were included (range of p-values without confounds 0.001–0.101). However, overall the structural data are able to distinguish the two groups. In contrast we were unable to show any difference in network integrity when estimated using functional connectivity measures. Furthermore our study indicated while structural network measures were very reproducible over time in both controls and cases, functional connectivity measures were much less reproducible and, particularly, reproducibility in SVD cases was poor. These results demonstrate that structural networks are a better marker of the extent of white matter damage in patients with SVD.
A recent review of the reproducibility of structural networks in healthy controls (Welton et al., 2015) reported excellent or good reproducibility with ICC values for E(Global) ranging from 0.37 to 0.94 and for Cw from 0.48–0.93. However, the reproducibility of structural network measures in SVD has not been reported. The results presented here show that structural networks are highly reproducible in SVD, with ICC comparable with others seen in work on controls. Although there are methodological variations between the various studies, the results here show that for structural networks the atlas resolution and threshold used have little effect on reproducibility. That this pattern of high reproducibility is seen in both cases and controls suggests that the disease does not affect the precision of the measurements.
Several papers have also investigated the reproducibility of rs-fMRI data in controls, but no previous studies have looked at this in SVD. Termenon et al. (2016) investigated graph theory analysis reproducibility in data from the human connectome project. They varied the atlas resolution, network density and number of subjects in the analysis to produce a number of network parameters. Looking at global efficiency specifically these variations had a maximum ICC value of approximately 0.45, it was also found that 40 subjects are needed to give an ICC significantly different from zero.
Welton et al. (2015) also investigated rs-fMRI as well as diffusion based structural connectivity. Two rs-fMRI studies are quoted using different atlases and thresholding techniques with 26 and 33 subjects respectively. The following ICC values were reported from the two studies: Global efficiency: 0.60, 0.67; Clustering coefficient: 0.27, 0.59; Characteristic path length: 0.54, 0.61. These results from control data are similar to the results presented here, suggesting that the poor reproducibility in the SVD data is due to the disease rather than the methods used.
Possible explanations for the poor reproducibility of functional connectivity in the SVD group are that the standard pathways for functional connectivity are being destroyed in the disease and replaced by a more ad hoc system and that the vascular pathology effects the BOLD haemodynamic response to reduce its reproducibility, reducing the correlations seen between brain regions (Williams et al., 2017; Mark et al., 2015), or that the processing techniques used are less appropriate for the diseased brain due to atrophy and the presence of lesions reducing the quality of registrations and the atlas definitions between scans; however no systematic differences in image quality or registration quality were seen.
The analysis methods chosen may also have an effect on the results, for example the use of probabilistic tractography may change the networks seen, however, deterministic tractography is a well-used method in network analysis and has been used in our previous work in similar groups (Lawrence et al., 2014). Probabilistic tractography or spherical deconvolution methods may be applied in future work on this dataset to assess their impact on the results. In practise the use of the magnitude of the correlations seen had no effect on the results as no negative correlations were large enough to survive the thresholding. The weighting scheme used will also have an effect on the results, again we chose one that removes a known bias in our methods and is compatible with previous work. There is a difference in the methodology used for choosing the thresholds, for the structural data the edge weight is thresholded, whereas for the functional data the threshold is the edge density. This methodological approach could be responsible for the differences seen in reproducibility. However, there is no equivalency between edge weight thresholds between the techniques. In addition, it is important to preserve the relative sizes of the largest connected components for the structural and functional connectivity matrices at the various thresholds to ensure compatibility of analysis with regard to breakdown of brain connectivity. As a result the edge densities of the two techniques will differ due to the structure of the connectivity matrices. Lastly the use of full correlations rather than partial will have an effect, however recent work has suggested that full correlations are appropriate in data of this type (Kim et al., 2015).
Our results have important implications for the use of network measures in SVD. Previous work has shown network disruption correlates with the degree of cognitive impairment and predicts those individuals who progress to dementia (Tuladhar et al., 2016). This has led to the suggestion that MRI measures of network disruption may be useful in identifying those individuals who are likely to progress to dementia; this is important as previous studies have shown that only a subgroup of those with lacunar stroke and confluent WMH will show rapid progressive cognitive decline. Our results confirm that structural networks can identify differences between SVD cases and controls, and provide new data demonstrating the high reproducibility of the technique, which is important if it is to be used in risk prediction. In contrast, functional networks, which have also been suggested as disease markers in SVD, showed low reproducibility and were unable to detect differences between SVD cases and controls, demonstrating that they are unlikely to be a useful disease marker in SVD.
Author contributions
Andrew Lawrence, study concept and design, acquisition of data, analysis and interpretation of data, drafting or revising the manuscript for intellectual content, obtained funding.
Daniel Tozer, analysis and interpretation of data, drafting or revising the manuscript for intellectual content.
Emmanuel Stamatakis, analysis and interpretation of data, drafting or revising the manuscript for intellectual content.
Hugh Markus, study concept and design, analysis and interpretation of data, drafting or revising the manuscript for intellectual content, obtained funding, overall supervision.
Author disclosures
Andrew Lawrence – Reports no disclosures.
Daniel Tozer – Reports no disclosures.
Emmanuel Stamatakis – Reports no disclosures.
Hugh Markus – Reports no disclosures.
Funding sources
This work and Andrew Lawrence are supported by a project grant from Alzheimer's Research UK (ARUK-PG2013-2; ARUK-EXT2015B-1).
Hugh Markus is supported by a NIHR Senior Investigator award. We acknowledge infrastructural support by the Cambridge University Hospitals NIHR Comprehensive Biomedical Research Centre. The funders played no role in the design or carrying out of the study.
Acknowledgements
The authors would like to thank Dr. Manfred Kitzbichler (University of Cambridge) for his help in implementing the multi echo processing.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.nicl.2018.02.013.
Contributor Information
Daniel J. Tozer, Email: djt54@medschl.cam.ac.uk.
Emmanuel A. Stamatakis, Email: eas46@cam.ac.uk.
Hugh S. Markus, Email: hsm32@medschl.cam.ac.uk.
Appendix A. Supplementary data
Supplementary data, including further details of the analysis methods used and extra results including correlations of the functional and structural network parameters and group specific reproducibility analysis.
References
- Adams H.P., Jr., Bendixen B.H., Kappelle L.J., Biller J., Love B.B., Gordon D.L. Classification of subtype of acute ischemic stroke. Definitions for use in a multicenter clinical trial. TOAST. Trial of Org 10172 in Acute Stroke Treatment. Stroke. 1993;24:35–41. doi: 10.1161/01.str.24.1.35. [DOI] [PubMed] [Google Scholar]
- Bamford J., Sandercock P., Dennis M., Burn J., Warlow C. Classification and natural history of clinically identifiable subtypes of cerebral infarction. Lancet. 1991;337:1521–1526. doi: 10.1016/0140-6736(91)93206-o. [DOI] [PubMed] [Google Scholar]
- Biswal B., Yetkin F.Z., Haughton V.M., Hyde J.S. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn. Reson. Med. 1995;34:537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- Cammoun L., Gigandet X., Meskaldji D., Thiran J.P., Sporns O., Do K.Q. Mapping the human connectome at multiple scales with diffusion spectrum MRI. J. Neurosci. Methods. 2012;203:386–397. doi: 10.1016/j.jneumeth.2011.09.031. [DOI] [PubMed] [Google Scholar]
- Daducci A., Gerhard S., Griffa A., Lemkaddem A., Cammoun L., Gigandet X. The connectome mapper: an open-source processing pipeline to map connectomes with MRI. PLoS One. 2012;7 doi: 10.1371/journal.pone.0048121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desikan R.S., Ségonne F., Fischl B., Quinn B.T., Dickerson B.C., Blacker D. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage. 2006;31:968–980. doi: 10.1016/j.neuroimage.2006.01.021. [DOI] [PubMed] [Google Scholar]
- Farràs-Permanyer L., Guàrdia-Olmos J., Peró-Cebollero M. Mild cognitive impairment and fMRI studies of brain functional connectivity: the state of the art. Front. Psychol. 2015;6:1095. doi: 10.3389/fpsyg.2015.01095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fazekas F., Chawluk J.B., Alavi A., Hurtig H.I., Zimmerman R.A. MR signal abnormalities at 1.5 T in Alzheimer's dementia and normal aging. Am. J. Roentgenol. 1987;149:351–356. doi: 10.2214/ajr.149.2.351. [DOI] [PubMed] [Google Scholar]
- Fischl B., Dale A.M. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc. Natl. Acad. Sci. U. S. A. 2000;97:11050–11055. doi: 10.1073/pnas.200033797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B., Salat D.H., Busa E., Albert M., Dieterich M., Haselgrove C. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33:341–355. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
- Friston K.J., Holmes A.P., Worsley K.J., Poline J.B., Frith C., Frackowiak R.S.J. Statistical parametric maps in functional imaging: a general linear approach. Hum. Brain Mapp. 1995;2:189–210. [Google Scholar]
- Gregoire S., Smith K., Jäger H., Benjamin M., Kallis C., Brown M. Cerebral microbleeds and long-term cognitive outcome: longitudinal cohort study of stroke clinic patients. Cerebrovasc. Dis. 2012;33:430–435. doi: 10.1159/000336237. [DOI] [PubMed] [Google Scholar]
- Hagmann P., Kurant M., Gigandet X., Thiran P., Wedeen V.J., Meuli R. Mapping human whole-brain structural networks with diffusion MRI. PLoS One. 2007;2 doi: 10.1371/journal.pone.0000597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M., Beckmann C.F., Behrens T.E., Woolrich M.W., Smith S.M. FSL. NeuroImage. 2012;62:782–790. doi: 10.1016/j.neuroimage.2011.09.015. [DOI] [PubMed] [Google Scholar]
- Kim J., Wozniak J.R., Mueller B.A., Pan W. Testing group differences in brain functional connectivity: using correlations or partial correlations? Brain Connect. 2015;5:214–231. doi: 10.1089/brain.2014.0319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kundu P., Inati S.J., Evans J.W., Luh W.-M., bandettini P.A. Differentiating BOLD and non-BOLD signals in fMRI time series using multi-echo EPI. NeuroImage. 2012;60:1759–1770. doi: 10.1016/j.neuroimage.2011.12.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lambert C., Zeestraten W., Williams O., Benjamin P., Lawrence A., Morris R. Use of MRI to identify preclinical vascular dementia in symptomatic small vessel disease. Lancet. 2017;389(supplement 1):S58. doi: 10.1016/j.nicl.2018.06.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawrence A.J., Chung A.W., Morris R.G., Markus H.S., Barrick T.R. Structural network efficiency is associated with cognitive impairment in small-vessel disease. Neurology. 2014;83:304–311. doi: 10.1212/WNL.0000000000000612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lo C.Y., Wang P.N., Chou K.H., Wang J., He Y., Lin C.P. Diffusion tensor tractography reveals abnormal topological organization in structural cortical networks in Alzheimer's disease. J. Neurosci. 2010;30:16876–16885. doi: 10.1523/JNEUROSCI.4136-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mark C.I., Mazerolle E.L., Chen J.J. Metabolic and vascular origins of the BOLD effect: implications for imaging pathology and resting-state brain function. J. Magn. Reson. Imaging. 2015;42:231–246. doi: 10.1002/jmri.24786. [DOI] [PubMed] [Google Scholar]
- Pantoni L. Cerebral small vessel disease: from pathogenesis and clinical characteristics to therapeutic challenges. Lancet Neurol. 2010;9:689–701. doi: 10.1016/S1474-4422(10)70104-6. [DOI] [PubMed] [Google Scholar]
- Reijmer Y.D., Leemans A., Brundel M., Kappelle L.J., Biessels G.J., Utrecht Vascular Cognitive Impairment Study Group Disruption of the cerebral white matter network is related to slowing of information processing speed in patients with type 2 diabetes. Diabetes. 2013;62:2112–2115. doi: 10.2337/db12-1644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt R., Ropele S., Ferro J., Madureira S., Verdelho A., Petrovic K. Diffusion weighted imaging and cognition in the leukoariosis and disability in the elderly study. Stroke. 2010;41 doi: 10.1161/STROKEAHA.109.576629. [DOI] [PubMed] [Google Scholar]
- Shrout P.E., Fleiss J.L. Intraclass correlations: uses in assessing rater reliability. Psychol. Bull. 1979;86:420–428. doi: 10.1037//0033-2909.86.2.420. [DOI] [PubMed] [Google Scholar]
- Termenon M., Jaillard A., Delon-Martin C., Achard S. Reliability of graph analysis of resting state fMRI using test-retest dataset from the human connectome project. NeuroImage. 2016;142:172–187. doi: 10.1016/j.neuroimage.2016.05.062. [DOI] [PubMed] [Google Scholar]
- Tuladhar A.M., van Uden I.W.M., Rutten-Jacobs L.C.A., Lawrence A., van der Holst H., van Norden A. Structural network efficiency predicts conversion to dementia. Neurology. 2016;86:112–119. doi: 10.1212/WNL.0000000000002502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welton T., Kent D.A., Auer D.P., Dineen R.A. Reproducibility of graph-theoretic brain network metrics: a systematic review. Brain Connect. 2015;5:193–202. doi: 10.1089/brain.2014.0313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitfield-Gabrieli S., Nieto-Castanon A. Conn: a functional connectivity toolbox for correlated and anticorrelated brain networks. Brain Connect. 2012;2:125–141. doi: 10.1089/brain.2012.0073. [DOI] [PubMed] [Google Scholar]
- Williams R.J., Goodyear B.G., Peca S., McCreary C.R., Frayne R., Smith E.E. Identification of neurovascular changes associated with cerebral amyloid angiopathy from subject-specific hemodynamic response functions. J. Cereb. Blood Flow Metab. 2017;37:3433–3445. doi: 10.1177/0271678X17691056. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary data, including further details of the analysis methods used and extra results including correlations of the functional and structural network parameters and group specific reproducibility analysis.