Solvent interactions determine carbohydrate conformation

Abstract

The relationship between the three-dimensional structures of oligosaccharides and polysaccharides and their biological properties has been the focus of many recent studies. The overall conformation of an oligosaccharide depends primarily on the orientation of the torsion angles (φ, ψ, and ω) between glycosyl residues. Numerous experimental studies have shown that in glucopyranosides the ω-torsion angle (O₆-C₆-C₅-O₅) displays a preference for gauche orientations, in disagreement with predictions based on gas-phase quantum mechanics calculations. In contrast, the ω-angle in galactopyranosides displays a high proportion of the anti-orientation. For oligosaccharides containing glycosidic linkages at the 6-position (1→6 linked), variations in rotamer population have a direct effect on the oligosaccharides' structure and function, and yet the physical origin of these conformational preferences remains unclear. Although it is generally recognized that the gauche effect in carbohydrates is a solvent-dependent phenomenon, the mechanism through which solvent induces the gauche preference is not understood. In the present work, quantum mechanics and solvated molecular dynamics calculations were performed on two representative carbohydrates, methyl α-d-glucopyranoside and methyl α-d-galactopyranoside. We show that correct reproduction of the experimental rotamer distributions about the ω-angles is obtained only after explicit water is included in the molecular dynamics simulations. The primary role of the water appears to be to disrupt the hydrogen bonding within the carbohydrate, thereby allowing the rotamer populations to be determined by internal electronic and steric repulsions between the oxygen atoms. The results reported here provide a quantitative explanation of the conformational behavior of (1→6)-linked carbohydrates.

The phenomenon of carbohydrate recognition is critical to many biological functions, including the response of the immune system to bacterial pathogens, the attachment of viral influenza particles to host cells, and the hyperacute rejection of tissue transplants from nonhuman sources. Understanding the conformational properties of carbohydrates is essential for the elucidation of their mechanisms of action, which may aid in the design of carbohydrate-based vaccines, antiviral drugs, and other therapeutic agents. A significant amount of research has gone into the study of the three-dimensional structures and dynamics of oligosaccharides and polysaccharides for these reasons (1–18).

Unlike polypeptides and proteins, oligosaccharides do not contain secondary-structural motifs and do not form well-organized tertiary structures in solution. Rather, oligosaccharides often populate multiple conformational families, thus requiring both temporal and spatial descriptors to quantify their conformational properties. Experimental methods such as NMR spectroscopy and x-ray crystallography have a long history of application to carbohydrates. However, these methods generally result in a single three-dimensional model for the oligosaccharide, which fails to adequately describe its dynamic properties.

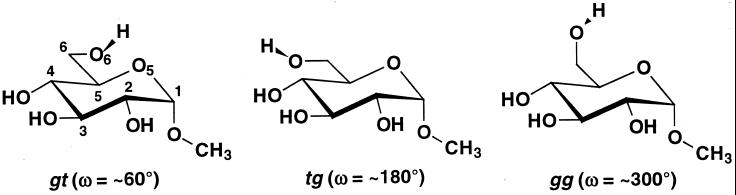
Molecular dynamics (MD) simulations applied to oligosaccharides and oligosaccharide-protein complexes can result in good agreement with experimental data (18–20). MD simulations offer the advantage of providing insight into the extent and the influence that internal molecular motion has on the oligosaccharide, a property that is difficult to determine experimentally. A problem that has plagued theoretical modeling to date arises in the case of oligosaccharides containing (1→6) glycosidic linkages. The 1→6 linkage differs from other glycosidic linkages in that it contains an additional rotatable bond, which may be characterized by the O₆-C₆-C₅-O₅ torsion angle (ω-angle). Although three stable staggered rotamers are possible for the ω-angle [gauche-trans (gt), trans-gauche (tg), and gauche-gauche (gg), referring to the orientations of the ω-angle and the O₆-C₆-C₅-C₄ angle, respectively (Fig. 1)], the conformational families about the C₅—C₆ bond display a bias for gauche orientations. Weaknesses in the force fields used in the MD simulations, combined with insufficient simulation lengths, contribute to the inability of current MD methods to generate conformational ensembles that display the correct rotamer populations for this linkage.

Figure 1.

The gt, tg, and gg rotamers of methyl α-d-glucopyranoside (1). Methyl α-d-galactopyranoside (2) differs from 1 in configuration at C₄.

Regardless of the residue attached to the O₆ atom of gluco- or mannopyranosides (mannopyranosides differ from glucopyranosides in configuration at C₂), their mono- and disaccharides display approximately equal populations of gt and gg rotamers with a nearly complete absence of the tg rotamer, both in the solid (7, 21) and the solution phases (4, 5, 22). This feature was exemplified in a statistical analysis of 101 x-ray structures of glucopyranosyl derivatives, which yielded a rotamer population distribution of 40:0:60 (gt/tg/gg) (21). Specific examples of solution-phase rotamer distributions include those for methyl α-d-glucopyranoside (1) and methyl α-d-glucopyranosyl-(1→6)-α-d-glucopyranoside, which possess populations of 38:5:57 and 29:1:70, respectively (4, 5). In contrast, galactopyranosides (which differ in configuration at C₄ from glucopyranosides) display a markedly different rotamer distribution about the C₅—C₆ bond, possessing a large tg component at the expense of the gg rotamer. For example, in solution methyl α-d-galactopyranoside (2) and methyl α-d-galactopyranosyl-(1→6)-α-d-galactopyranoside display rotamer populations of 47:39:14 and 53:31:16, respectively (4, 5).

The propensity for the ω-angle to adopt gauche conformations in glucopyranosides has been attributed to the gauche effect. In structural terms, the gauche effect has been defined as the tendency for a molecule to adopt the structure that has the maximum number of gauche interactions between the adjacent electron pairs and/or polar bonds (23). This definition is demonstrative in nature and does not attempt to explain the physics behind the phenomenon. An alternative and widely cited definition defines the gauche effect as an internal stereoelectronic or hyperconjugative property of X-C-C-Y fragments, where X and Y are electronegative atoms, and as such is akin to the proposed origin of the anomeric effect (12, 24, 25). The drawback of this electronic definition is that it is extremely difficult to quantify, partly because of the inability to separate the stereoelectronic effect from that arising from steric repulsion and hydrogen bonding (22, 26). Furthermore, this definition does not explain why the tg and gg populations differ between 1 and 2.

The presence of the tg conformation in galactopyranosides often is rationalized as arising from solvent effects (12) or unfavorable 1,3-diaxial interactions (22). According to the argument based on 1,3-interactions, electronic and steric repulsion arising between the O₄ and O₆ atoms in galactopyranosides destabilize the gg rotamer (5, 22). The equivalent interaction in glucopyranosides has been invoked to explain the low population of the tg rotamer (22). Although this rationalization offers a qualitative explanation of the phenomenon, it is in conflict with theoretical studies that indicate that internal hydrogen bonding between the O₄ and O₆ hydroxyl groups leads to low energy conformers, regardless of the fact that they contain 1,3-diaxial interactions (14, 27–29). To develop a comprehensive explanation for the physical origin of the rotamer preference about the ω-angle, we have performed quantum mechanics (QM) and molecular mechanics (MM) calculations in the gas phase, as well as MD simulations in water of the representative carbohydrates 1 and 2. The theoretical results reported here are consistent with the published NMR and x-ray data for the conformational preferences of these carbohydrates and their related saccharides and provide an understanding of the underlying forces that determine the conformational preferences of 1→6 linkages in carbohydrates.

Methods

QM calculations were performed by using restricted closed shell Hartree-Fock (HF) and Becke's three parameters with Lee–Yang–Parr functionals (B3LYP) (30, 31) levels of theory, as implemented in the GAUSSIAN94 program suite (32). Both full and constrained geometry optimizations were carried out at the HF/6–31G(d) level of theory. Relative conformational energies were then obtained by performing single-point energy calculations at the B3-LYP/6–31++G(2d,2p) level of theory. This theory level was selected because it reduces basis set superposition error (33, 34).

All MM and MD calculations were performed by using the sander module in the AMBER 5.0 program suite (35). The Parm96 force-field parameters, augmented with the glycam (36) parameters for carbohydrates, were used throughout the MM and MD calculations. The force-field parameters associated with the ω-angle were parameterized to reproduce the gas-phase ab initio data of several carbohydrate analogs (data not presented). Consistent with the philosophy of maintaining parameter transferability, the resultant parameters (Table 1, which is published as supporting information on the PNAS web site, www.pnas.org) are generally applicable to monosaccharides. The atomic partial charges were determined from an ensemble of MD conformations (37) and computed from HF/6–31G(d) quantum molecular electrostatic potentials by using the resp algorithm as reported (38). In contrast to the traditional amber formalism, we found it necessary to treat all 1–4 and greater electrostatic and van der Waals interactions equally, using a unit scale factor throughout. The dielectric constant was set to unity and a residue-based cutoff of 8 Å was used for nonbonded interactions. MD simulations were performed under isothermal-isobaric periodic boundary conditions, in which the carbohydrate was immersed in a theoretical box of 260 TIP3P (39) waters with approximate dimensions of 17 Å × 18 Å × 21 Å. The shake (40) algorithm was applied to all hydrogen-containing bonds, consistent with the use of TIP3P waters. The MD simulations were initiated from the experimentally observed gt conformation (5). Initial conjugate-gradient energy minimization was performed on all systems studied, by using a 0.01 kcal⋅mol⁻¹⋅Å convergence criterion in the energy gradient. The energy minimizations were followed by a period of heating (200 ps), during which the temperature of the system was increased from 0 to 300 K. After the heating, production dynamics were performed for 50 ns at 300 K and a pressure of 1 atmosphere.

In both the QM and MM calculations, the rotational energy curves were determined by driving the ω-torsion angle from 0° to 330° in 30° increments, while allowing the rest of the geometry to relax. All conformations possessed low-energy counterclockwise arrangements of hydrogen bonds between the secondary hydroxyl groups (27). Two rotational potential energy curves were produced per carbohydrate. In one curve, the formation of an internal hydrogen bond between the hydroxyl group at C₆ and either the ring oxygen atom or the hydroxyl group at C₄ was disallowed, generating curves that display repulsive oxygen⋅⋅⋅oxygen interactions, referred to as the repulsive energy curves. This was accomplished by maintaining the C₅-C₆-O₆-H in a trans conformation as necessary. In the second set of rotational energy curves, an internal hydrogen bond between the hydroxyl group at C₆ and either the ring oxygen atom or the hydroxyl group at C₄ was introduced, generating the attractive energy curves.

Results

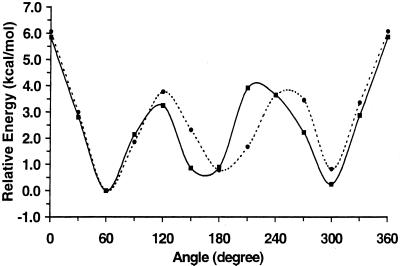
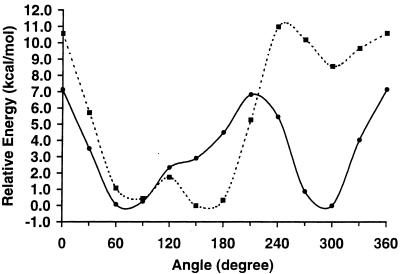
The attractive and repulsive QM potential energy curves for the rotation of the ω-angle for 1 and 2 are presented in Figs. 2 and 3, respectively. It is apparent that when these carbohydrates are allowed to form intramolecular hydrogen bonds, their rotational curves are very similar, giving rise to the three staggered rotamers with approximately equal stabilities (Fig. 2). For 1, allowing the constrained geometries of the three minima to fully relax to their most stable conformations results in relative energies (and ω-angles in parentheses) of 0.000 (gt, 58.7°), 0.227 (tg, 166.5°), and 0.242 (gg, 302.6°) kcal⋅mol⁻¹. Calculating a Boltzmann population distribution from these relative rotamer energies, at a temperature of 298 K, yielded a population distribution of 43:29:28. Performing the same procedure for 2 gave values of 0.000 (gt, 60.6°), 0.739 (tg, 172.4°), and 0.854 (gg, 304.9°) kcal⋅mol⁻¹, and yielded a population distribution of 66:19:15. For comparison, experimental homonuclear J-coupling data suggest a rotamer distribution of 38:5:57 for 1 and 47:39:14 for 2 (5).

Figure 2.

The attractive QM potential energy curves for ω-angle rotation in 1 (solid line) and 2 (dashed line).

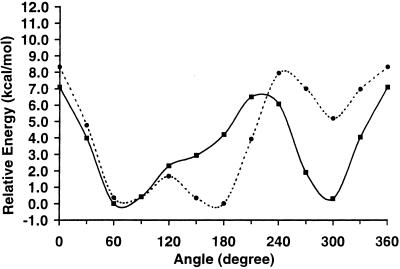
Figure 3.

The repulsive QM potential energy curves for ω-angle rotation in 1 (solid line) and 2 (dashed line).

Unlike the attractive energy curves, the higher energy repulsive curves, shown in Fig. 3, display marked differences between the two carbohydrates, with a clear preference for only two of the three rotamers for both 1 and 2. Allowing the constrained geometries of each staggered rotamer present in the repulsive energy curves to relax fully yielded relative energies of 0.000 (gt, 69.6°) and 0.521 (gg, 294.6°) kcal⋅mol⁻¹ for 1. [The tg rotamer is not a stationary point on the potential energy surface at the HF/6–31G(d) level of theory.] A Boltzmann population analysis of these energies gives a distribution of 62:0:37, which is qualitatively similar to the experimentally determined distribution of 38:5:57 (5). Performing a full energy minimization on the rotamers present in the repulsive energy curves of 2 yielded relative energies of 0.211 (gt, 72.3°), 0.000 (tg, 172.4°), and 5.642 (gg, 302.2°) kcal⋅mol⁻¹ and a Boltzmann population distribution of 41:59:0, which may be compared with the experimentally determined distribution of 47:39:14 (5). Although the qualitative agreement is clear, the QM-determined rotamer distributions reverse the population ordering of the two major rotamers (gt and gg for 1, and gt and tg for 2), relative to the experimental populations for each carbohydrate, and fail to correctly predict the population of the minor rotamer.

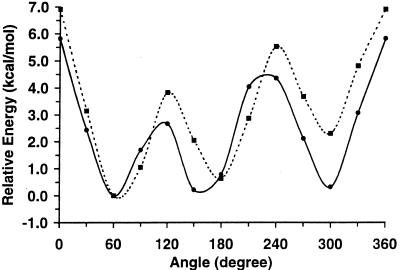
The MM attractive and repulsive energy curves, presented in Figs. 4 and 5, display good agreement with the relevant QM-generated curves. Having thus determined that the glycam force-field parameters were able to reproduce the QM gas-phase data, fully solvated MD simulations were performed on 1 and 2. The 50-ns MD trajectories of 1 and 2, as well as the resulting ω-angle histograms, are presented in Figs. 6 and 7, respectively. These simulations are 1–2 orders of magnitude longer than previously reported simulations on fully solvated carbohydrates (10, 11, 16, 18, 28, 41–46).

Figure 4.

The amber/glycam attractive potential energy curves for the ω-angle rotation in 1 (solid line) and 2 (dashed line).

Figure 5.

The amber/glycam repulsive potential energy curves for the ω-angle rotation in 1 (solid line) and 2 (dashed line).

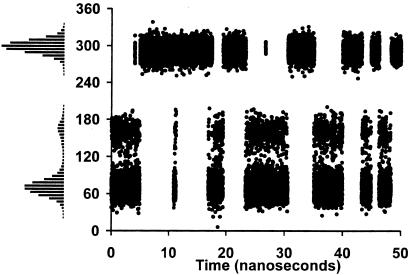
Figure 6.

A 50-ns MD trajectory of the ω-angle and the resulting histogram for 1.

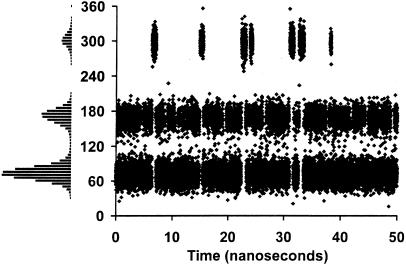
Figure 7.

A 50-ns MD trajectory of the ω-angle and the resulting histogram for 2.

The MD trajectory for 1 displays the three expected rotamers, with gg and gt significantly more populated than tg. Frequent short-lived transitions between the gt and tg conformers were observed, whereas the first dynamically stable gg rotamer occurred only after ≈5 ns. From the transition frequencies in the MD data, the conformational lifetime of the gg rotamer can be estimated to be ≈5 ns. The transition frequencies between the three rotamers are consistent with the gas-phase repulsive energy curve, which displays a minimum at ≈60° (ω-angle), a shoulder at ≈160°, and another minimum at ≈300°, with large energy barriers between the gt and gg rotamers. The trajectory for 2 displays a remarkably different profile than seen for 1, showing infrequent and short-lived transitions to the gg rotamer, with the gt and tg being the more populated rotamers. These populations are also qualitatively consistent with the gas-phase repulsive energy curve, which exhibits low energy minima at ≈80° and 170°, and a higher energy minimum at 300°, with a small energy barrier between the gt and tg rotamers and a larger barrier between the gt and gg minima. Based on these simulations, the population distribution for the ω-angle in 1 was computed to be 40:6:54, whereas for 2 a population ratio of 64:28:8 was obtained. These ratios are in excellent agreement with the experimentally determined populations (5).

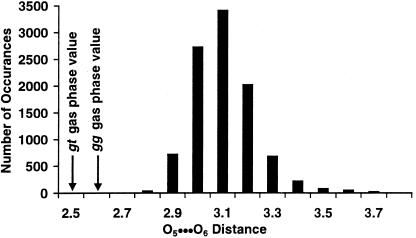
A histogram of the O₅⋅⋅⋅O₆ distances, shown in Fig. 8, was generated for 1 to ascertain the extent that internal hydrogen bonds between O₆—H and O₅ persisted during the simulations. The O₅⋅⋅⋅O₆ distances present in the energy minimized gas-phase MM calculation, in which intermolecular hydrogen bonds are present, have values of 2.5 Å (gg) and 2.6 Å (gt) and are clearly not populated in the simulation.

Figure 8.

The histogram of the intramolecular hydrogen bond distances from the MD trajectory of 1.

Discussion

If the gauche effect arises from stereoelectronic effects (24, 25, 47), then it might be expected that the gas-phase data from the QM studies of 1 and 2 would assist in explaining the experimentally observed rotational preferences in these carbohydrates. Examination of the rotational energy curves for low-energy conformations of 1 and 2, in which internal hydrogen bonds involving O₆ are present, leads to the conclusion that both carbohydrates should display significant populations of each staggered rotamer (gg, gt, and tg), in contrast to the experimental results. This observation alone does not dismiss a possible role for stereoelectronic effects, but demonstrates the difficulty in using theoretical gas-phase results to understand solution-phase chemistry.

It is reasonable to assume that hydrogen bond formation with the solvent may compete effectively with the intramolecular hydrogen bonds in the solute, which are seen in the gas phase. The repulsive energy curves remove the influence that intramolecular hydrogen bonding has on the carbohydrate's conformation, and as such give a model for the influence of solvation, but only to the extent that the solvation totally removes internal hydrogen bonding. The general shapes of the repulsive energy curves are consistent with expectations based on 1,3-diaxial destabilization. However, gas-phase electronic and steric repulsions alone incorrectly predict the relative populational ordering between the gt:gg and gt:tg conformers for 1 and 2, respectively. This is not surprising given that multiple carbohydrate-solute configurations are possible for each rotamer, leading to differential stabilization of the rotamers, a feature that is ignored in the QM calculations.

Therefore, we turned our attention to studying the carbohydrates in a more representative environment, by performing fully solvated MD simulations. We anticipated that the MD simulations would provide an opportunity to sample multiple carbohydrate-water configurations. Excellent agreement was obtained between the experimental rotamer populations and those obtained from the MD trajectories for both 1 and 2. We have shown that a classical force field has reproduced both the experimental conformer populations about the ω-angle, in solution, and the associated QM gas-phase data. The simulations clearly show that water plays a central role in determining the conformational properties of 1→6-linked carbohydrates. Water competitively forms intermolecular hydrogen bonds with the carbohydrate, and in doing so, weakens the intramolecular hydrogen bond networks. Saliently, the populations from the MD trajectories correlate strongly with those expected on the basis of the QM repulsive energy curves. Therefore, electrostatic and steric repulsion appear to be an underlying feature in determining the conformational preference of 1→6 linkages, when the solvent is able to disrupt the internal hydrogen bonds.

In summary, it is clear that the populations of the gt, tg, and gg rotamers are not explained by the gas-phase rotational energy profiles. Correct reproduction of the experimental rotamer distributions about the ω-angles was obtained only after explicit water was included in MD simulations. Because the simulations are based on force-field parameters derived from gas-phase data (36), interactions with the explicitly included water must be responsible for the resultant gauche population preference. The primary role of the water appears to be to weaken the internal hydrogen bonds of the carbohydrates. Additional factors, such as dipolar interactions between the carbohydrate and solvent and energies associated with the cavity formation in the solvent, may contribute to a lesser extent.

Abbreviations

gg

gauche-gauche

gt

gauche-trans

tg

trans-gauche

HF

Hartree–Fock

MD

molecular dynamics

MM

molecular mechanics

ω-angle

O6-C6-C5-O5 angle

QM

quantum mechanics