Improved Algorithmic Complexity for the 3SEQ Recombination Detection Algorithm

Abstract

Identifying recombinant sequences in an era of large genomic databases is challenging as it requires an efficient algorithm to identify candidate recombinants and parents, as well as appropriate statistical methods to correct for the large number of comparisons performed. In 2007, a computation was introduced for an exact nonparametric mosaicism statistic that gave high-precision P values for putative recombinants. This exact computation meant that multiple-comparisons corrected P values also had high precision, which is crucial when performing millions or billions of tests in large databases. Here, we introduce an improvement to the algorithmic complexity of this computation from O(mn³) to O(mn²), where m and n are the numbers of recombination-informative sites in the candidate recombinant. This new computation allows for recombination analysis to be performed in alignments with thousands of polymorphic sites. Benchmark runs are presented on viral genome sequence alignments, new features are introduced, and applications outside recombination analysis are discussed.

Determining whether genomic regions are undergoing homologous recombination is important in all parts of biology and genetics. Indeed, recombination has profound consequences for a population’s evolutionary trajectory, and it changes our understanding of the evolutionary history of a population as described through phylogenetics (Schierup and Hein 2000; Posada and Crandall 2002). Identifying recombination is especially important in large genomic analyses, as the larger the region being analyzed the higher the chance that recombination will be detected even in a small sample. Over the past three decades, methods of identifying recombination from sequence data have focused on detection of clustered polymorphism, excessive homoplasy, low linkage disequilibrium, mosaicism, and incongruent phylogenies (Posada et al. 2002). Some of these statistical signals have advantages over others in terms of false positive rate, statistical power, speed, and the size of the data set that can be analyzed. An analysis of sensitivity and specificity can be found in Posada and Crandall (Posada and Crandall 2001) and a guide to choosing an appropriate method for a given data set can be found in Martin et al. (2011).

In modern sequence analysis, a major challenge in recombination detection is the size of the data sets themselves. Beyond the computational burden, critical but often underappreciated statistical issues arise through the extremely large number of compared nucleotide sequence patterns. With this many comparisons being performed, truly nonrecombinant sequences can exhibit nucleotide patterns that appear recombinant by chance. For this reason, statistical corrections for multiple comparisons are essential to guard against calling spurious recombinants. In an algorithm called 3SEQ, Boni et al. (2007) presented an exact mosaicism statistic for calling recombinants. Critically, the exactness of the computation (e.g., calculating P values to a precision of 10⁻²⁰ or 10⁻³⁰) allows these mosaic signals to remain statistically significant, even when billions of comparisons are being performed and adjusted for multiple comparison. This means that the exact mosaicism statistic implemented in the 3SEQ software maintains good power properties even on large data sets when statistical correction factors for multiple comparisons are on the order of 10¹⁰ or more.

Recombination detection methods that detect mosaic signals always take a triplet approach or a quartet approach, positing one sequence as the candidate recombinant, two sequences as the parents, and possibly a fourth sequence as an outgroup. With the parental sequences labeled P and Q and the candidate recombinant labeled C, these methods normally use “recombination informative” sites, or simply informative sites, to determine if C is a mosaic of P and Q. In 3SEQ, nucleotide positions on C are labeled informative if the nucleotide in C is identical to one parental sequence but different from the other. If the sequence of m informative sites identical to P and n informative sites identical to Q appears nonrandom or clustered, this is an indication that recombination may have occurred. When read from left to right along the sequence, the informative sites can be used to draw a random walk on a set of axes with m up-steps and n down-steps; this is called a hypergeometric random walk (HGRW). A strong descent or ascent in the middle of a HGRW indicates that one type of informative site exhibits clustering, and the properties of the random walk can be used to compute exact probabilities of this occurring. See figure 1 for an example. In this letter, we present a new and faster method of computing these probabilities.

Fig. 1.

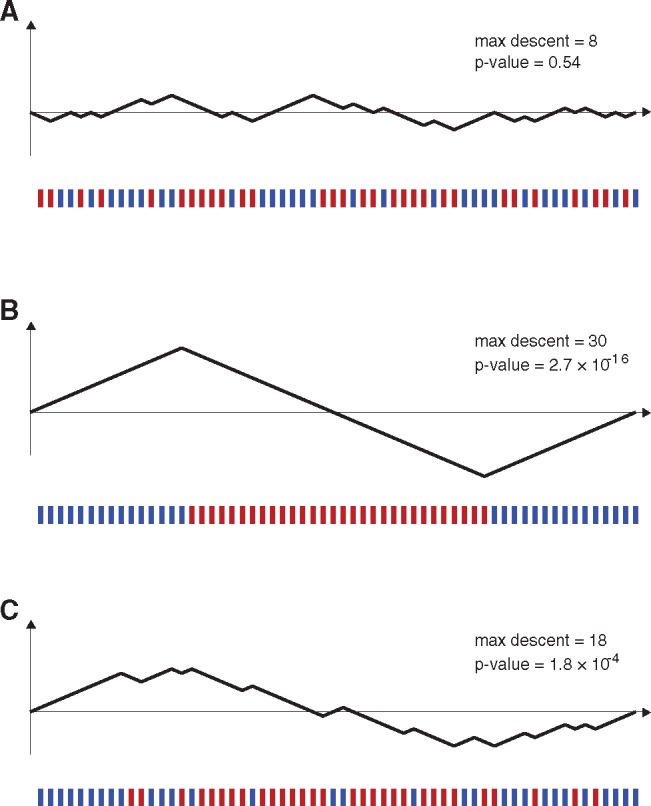
Relationship between ordering of informative sites along a genome and a hypergeometric random walk. Below each set of axes, the 30 red bars and 30 blue bars show positions on a genome (informative sites) where a putative recombinant sequence is identical to parent P but different from parent Q (blue bars), or identical to parent Q but different from parent P (red bars). Each blue site can be mapped to an up-step in a random walk and each red site can be mapped to a down-step in a random walk, and there is a one-to-one correspondence between the space of informative-site arrangements and the space of hypergeometric random walks. (A) A random arrangement of informative sites, which does not visually suggest that the sequence is a mosaic of putative parents P and Q. The arrangement of sites maps to a random walk which stays fairly close to the horizontal axis. This walk’s maximum descent is eight steps, and ∼54% of HGRWs with 30 up-steps and 30 down-steps have a maximum descent of eight steps or greater. (B) A nonrandom arrangement of informative sites that clearly suggests that the candidate sequence is a mosaic of the two parental sequences P and Q. The probability of all the red sites appearing consecutively is 31! × 30!/60! which is 2.62 × 10⁻¹⁶. (C) An arrangement of red sites and blue sites that suggests the red sites may be clustered in the middle. When mapping the site arrangement to a hypergeometric random walk, the random walk has a maximum descent of 18 steps. The P value for a maximum descent of 18 steps cannot be written down in closed form but can be calculated from recursion (4). The P value for this maximum descent and for this arrangement of informative sites is 1.8 × 10⁻⁴.

Improved Complexity

The central feature of 3SEQ was a reduction of an O(2 ^m+n) space-complexity problem into an O(mn³) problem, for computing the probability x_{m, n, k} that a HGRW with m up-steps and n down-steps achieves a maximum descent of size k exactly. The descent does not need to be k consecutive down steps. The computations were done via auxiliary variables y_{m, n, k, j}: the probability that a HGRW with m up-steps and n down-steps achieves a maximum descent of size k exactly and the minimum value achieved by the random walk is exactly j units below the origin. The y-variables can be computed recursively (Boni et al. 2007) by building a table of size mn³. The x-variables are then computed as follows:

$${\mathbf{x}}_{m,n,k}=\sum _{j=0}^k{\mathbf{y}}_{m,n,k,j}.$$ (1)

By separating out the first and last term in the sum above, and using the y-variable recursions, a nearly direct recursion can be written for the x-variables:

$${\mathbf{x}}_{m,n,k}=\frac{m}{m+n}{\mathbf{x}}_{m-1,n,k}+\frac{n}{m+n}{\mathbf{x}}_{m,n-1,k}+\frac{n}{m+n}{\mathbf{y}}_{m,n-1,k-1,k-1}-\frac{n}{m+n}{\mathbf{y}}_{m,n-1,k,k}.$$ (2)

The P value for observing a maximum descent of size at least k is defined by

$${\mathbf{p}}_{m,n,k}=\sum _{l=k}^n{\mathbf{x}}_{m,n,l},$$ (3)

and recursions for the p-variables reduce to:

$${\mathbf{p}}_{m,n,k}=\frac{m}{m+n}{\mathbf{p}}_{m-1,n,k}+\frac{n}{m+n}{\mathbf{p}}_{m,n-1,k}+\frac{n}{m+n}{\mathbf{y}}_{m,n-1,k-1,k-1}.$$ (4)

The y-variables in equation (2) above—since the last two indices are equal—can be computed recursively by building one table of size mn². The p-variables can be recursively computed by building a second table of size mn². This means that the entire computational procedure of P values can be done with space complexity O(mn²) instead of the original O(mn³) presented in Boni et al. (2007). All computations were verified against the original approach.

This new approach allows larger probability tables to be built more quickly. Using the 2007 recursions, a table of size 700 × 700 × 700 was built in 9 h and used 5.1-GB RAM (2.6 GHz processor; 16-GB RAM). Using the recursions above, a table of 1,600 × 1,600 × 1,600 was built in 1 h and 42 min in a 10.4-GB memory footprint. Two other noteworthy improvements were made to the algorithm: 1) faster breakpoint calculations by using polymorphic sites only in breakpoint searches, and 2) a repeated subsampling feature that allows for comparison of data sets of different sizes; with this feature one can randomly subsample M sequences from multiple databases or sequence collections, and repeat the process to see how often these subsets exhibit recombination. The new source code and manual can be downloaded from http://mol.ax/3seq. When a P value falls outside the bounds of the table being used, the software substitutes in Hogan–Siegmund approximations (Hogan and Siegmund 1986) for the queried P value.

New Applications

The 3SEQ maximum descent statistic describes clustering patterns in sequences of binary outcomes, and is therefore not confined to recombination analysis. The statistic can be viewed as a generalization of the Mann–Whitney U statistic, in the sense that outcomes of one type (of a binary outcome variable) do not necessarily have to cluster or rank at the beginning or end of a sequence of data points. The maximum descent of a HGRW can be used to describe the clustering of one particular binary outcome in the middle of a sequence of binary outcomes; in other words, it is a 1D nonparametric clustering statistic. In recombination analysis, this is the clustering of one kind of informative site among all the informative sites (Han et al. 2010). To make use of this statistic easier for those working outside the field of recombination, we developed a web calculator (fig. 2) that computes exact P values for clustering in a sequence of binary outcomes, available at http://mol.ax/delta. For example, the sequence “AAAAABBBBABBBABBBAAAA” can be typed in and the calculator reports that the clustering of Bs in the middle of the sequence is significant at P = 0.0055.

Fig. 2.

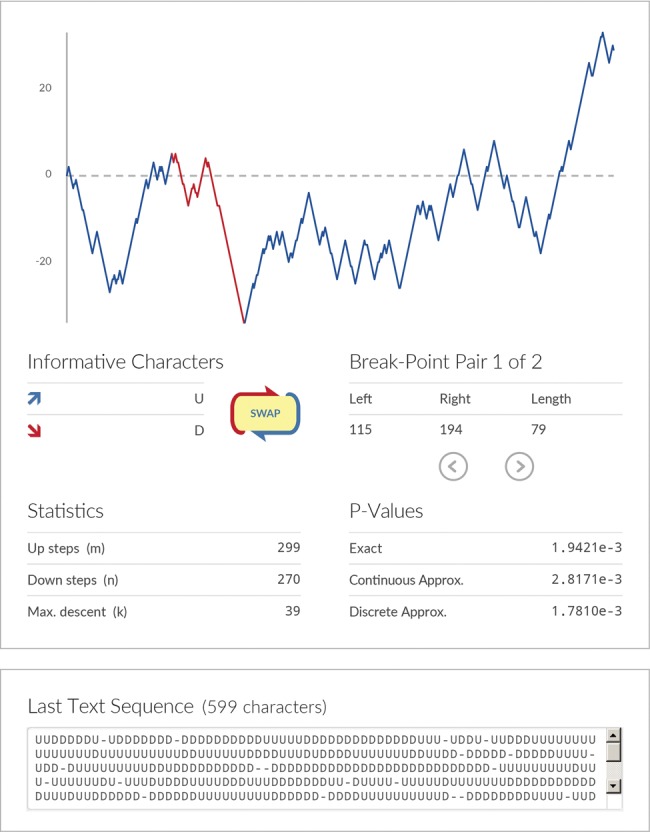
Screenshot of new online tool that can be used to calculate P values testing the hypothesis of whether one binary outcome clusters in the middle of a (1D) sequence of binary outcomes. One input method is simply typing two characters in a text box (above, “U” for up and “D” for down) and letting the calculator return a P value showing whether one type of character is clustered in the middle. To test whether the other type of character is clustered, the “SWAP” button can be used. The hypergeometric walk is shown graphically. The exact P value, computed with the methods in this article, is shown. The two Hogan–Siegmund approximations for this P value are also shown.

We list two practical example uses of our nonparametric clustering statistic. First, seasonality can be assessed nonparametrically. If a particular population behavior or climatic characteristic (e.g., rain or no rain) can be noted to occur or not occur every day, then an ordered sequence of the days in the year will show if the occurrence of one of the behaviors is clustered and thus if this feature was seasonal in that one year. As a second example, when a process is expected to behave at an intermediate range or when an observation is expected to be made at intermediate values only, this pattern can be tested for nonparametrically. Dengue virus does not cause severity for all ages equally. One’s first dengue infection, occurring during childhood, is typically nonsevere; secondary infections, seen in older children and teenagers, have a higher chance of severity, whereas tertiary and subsequent infections, those that would occur in older age groups, are thought to be rare and/or subclinical (Gubler 1998; Wikramaratna et al. 2010). Thus, disease severity in a surveillance system should be seen in the intermediate age ranges, and this can be tested for nonparametrically by noting if each age band is overrepresented or underrepresented in the pool of patients experiencing dengue-like severe disease in a hospital. In fact, since all that is required here is a symptoms description, the identification of a vulnerable age range can be done for any set of symptoms.

Results and Discussion

To illustrate improved runtimes and memory usage of the new 3SEQ algorithm, we searched for recombinants among large sequence data sets of dengue virus serotype 2, Ebola virus, the coronavirus responsible for Middle-East Respiratory Syndrome (MERS) and Zika virus; see table 1. Full-length Zika virus sequences were downloaded from the NCBI Viral Variation Resource (Brister et al. 2014) and aligned with Muscle v3.8 (Edgar 2004). Full-length sequences of Ebola virus, dengue virus serotype 2, and the coronavirus responsible for Middle-East Respiratory Syndrome (MERS) were downloaded from NCBI and aligned with the online NCBI alignment tools. Ebola virus sequences were restricted to human viruses sampled in Africa after December 1, 2013. Dengue virus serotype 2 was chosen to include a particularly large and polymorphic alignment. As negative controls, we considered segments PB2 and NS from avian influenza A virus, subtype H5N1, originally analyzed in Boni et al. (2010); only sequences from the Influenza Genome Sequencing Project were included (Ghedin et al. 2005) and identical sequences were removed (when identical sequences were not removed, results using the new version of 3SEQ were identical to the results in table 1 of Boni et al. 2010).

Table 1.

Computation Times for Large Alignments of Viral Genomes.

Gene/Genome	Number of Distinct Sequences	Sequence Length (nt)	Number of Polymorphic Sites	% of Triplets with Exact P Values	Dunn–Sidak Corrected P Value	Number of Identified Recombinant Sequences Longer Than 500 nt	Run Time
Avian influenza A/H5N1. PB2 segment	112	2,409	844	100	0.0016	0	11 s
Avian influenza A/H5N1, NS segment	160	906	298	100	1	0	24 s
MERS-CoV, whole genome	164	30,130	1,150	100	1.72×10−11	100	1.5 min
Zika virus, whole genome	157	11,192	2,792	>99.9	1.44×10−37	6	2 min
Ebola virus, 2013–2015 epidemic, whole genome	982	18,980	2,535	100	6.49×10−12	0	8.5 h
Dengue virus, serotype 2, whole genome	1,108	11,349	6,151	99.4	0	36	15.5 h

Note.—Computations were done on a 2.6-GHz linux laptop with 16-GB RAM. The P value table used was 1,200 × 1,200 × 1,200, which has a memory footprint of 2.2 GB.

The new version of the software—run with a P value table of size 1,200 × 1,200 × 1,200—had faster computation times than the previous version and was able to comfortably accommodate alignments with thousands of polymorphic sites. Table 1 shows the results of all runs. Note that because 3SEQ evaluates all triplets in a data set, the run time of the algorithm scales as the cube of the number of sequences and linearly with the alignment length. As informative sites can sometimes be clustered in short regions of the genome, 3SEQ will report these short segments as recombinant. For this reason, an additional column is included in table 1 showing the number of sequences that were identified as recombinant with both inherited regions being longer than 500 nt; if one of the recombinant regions is very short, it is difficult to confirm the recombination results with a phylogenetic analysis of the two identified parental segments.

Starting with the analysis on the two negative control data sets, no recombinant segments longer than 500 nt were detected in either avian influenza alignment. Both of these runs took <30 s. The genomic alignments of MERS and Zika virus contained 1,150 and 2,792 polymorphic sites, respectively, and >99.9% triplets were able to be tested for mosaicism with exact P values. These runs took <2 min. As expected from a recent analysis by Dudas and Rambaut (Dudas and Rambaut 2015), the MERS sequence data set was highly recombinant, with 100 out of 164 sequences being identified as such. For Zika, 6 out of 157 virus sequences were identified as recombinant, consistent with earlier analyses supporting the presence of recombination in the evolutionary history of Zika (Faye et al. 2014; Zhu et al. 2016); details of the recombinants, parents, and breakpoints are included in the Supplementary Material online. The Ebola virus and dengue virus alignments each contained around 1,000 sequences. The Ebola virus data showed no evidence of recombination. The dengue alignment was the most diverse of all the tested data sets with 6,151 polymorphic sites; 99.4% of the triplets in this data set were able to be evaluated with exact P values. A total of 36 out of 1,108 dengue sequences were identified as recombinant (see Supplementary Material online). Several previous analyses of dengue virus have shown evidence for intraserotype recombination in dengue (Holmes et al. 1999; Worobey et al. 1999; Uzcategui et al. 2001; Aaskov et al. 2007; Waman et al. 2016, 2017). The results presented here, as well as those of Waman et al. (2017), suggest that recombination in dengue is infrequent.

In general, when recombinants are identified by a mosaicism statistic like the one used by 3SEQ, a phylogenetic analysis should be performed to ensure that the recombination signal is preserved when the entire evolutionary history of the sample is taken into account. The size of modern data sets presents two challenges here. First, as the number of available sequences increases, the choice for phylogenetic inference tools drifts to more approximate methods, as thorough explorations of tree space become computationally expensive for large numbers of sequences. This reduces our confidence in phylogenetic incongruence signals that we observe in these data. Second, genome-level analyses in highly recombining organisms are likely to result in a subdivision of the genome into many nonrecombinant blocks. Inferring phylogenies for all blocks individually will be computationally expensive, as will the subsequent analysis of identifying specific phylogenetic incongruences among the trees. The next generation of recombination detection methods should focus on these computational challenges.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.