Mutation-Driven Parallel Evolution during Viral Adaptation

Abstract

Convergent evolution has been demonstrated across all levels of biological organization, from parallel nucleotide substitutions to convergent evolution of complex phenotypes, but whether instances of convergence are the result of selection repeatedly finding the same optimal solution to a recurring problem or are the product of mutational biases remains unsettled. We generated 20 replicate lineages allowed to fix a single mutation from each of four bacteriophage genotypes under identical selective regimes to test for parallel changes within and across genotypes at the levels of mutational effect distributions and gene, protein, amino acid, and nucleotide changes. All four genotypes shared a distribution of beneficial mutational effects best approximated by a distribution with a finite upper bound. Parallel adaptation was high at the protein, gene, amino acid, and nucleotide levels, both within and among phage genotypes, with the most common first-step mutation in each background fixing on an average in 7 of 20 replicates and half of the substitutions in two of the four genotypes occurring at shared sites. Remarkably, the mutation of largest beneficial effect that fixed for each genotype was never the most common, as would be expected if parallelism were driven by selection. In fact, the mutation of smallest benefit for each genotype fixed in a total of 7 of 80 lineages, equally as often as the mutation of largest benefit, leading us to conclude that adaptation was largely mutation-driven, such that mutational biases led to frequent parallel fixation of mutations of suboptimal effect.

Introduction

Convergent or parallel evolution is the acquisition of similar changes across multiple independently evolving populations. Parallelism has been reported over a range of biological scales, from identical nucleotide and amino acid substitutions occurring within experimentally evolved lineages of the same genotype (Wichman et al. 1999; Rokyta et al. 2005; Toprak et al. 2012; Miller et al. 2016) and across diverged genotypes (Bollback and Huelsenbeck 2009; Rokyta et al. 2009; Miller et al. 2016) to parallel adaptive changes at the gene level (Colosimo et al. 2005; Woods et al. 2006; Tenaillon et al. 2012; Miller et al. 2016), parallel patterns of fitness improvement (Kryazhimskiy et al. 2014), and convergent changes observed in complex phenotypes within natural populations of species and across entire higher order taxa (Zhang and Kumar 1997; Zhang 2003; Zhen et al. 2012; Ujvari et al. 2015; Natarajan et al. 2016). The extent to which molecular adaptation is predictable and repeatable, rather than being driven by stochastic forces and mutational contingency, is a topic of ongoing debate, as evidence has at times offered support for either a random or a deterministic view of evolution, and instances of parallel evolution have often been cited in arguments for determinism (Gould 1989; Morris 2003). Rates of parallelism across independently adapting populations, however, depend upon the mutational and fixation biases (differences in the probabilities of particular mutations arising and variable probabilities of mutational fixation) of the system and the extent to which mutational effects are determined by genetic background (Chevin et al. 2010; Streisfeld and Rausher 2010; Storz 2016; Stoltzfus and McCandlish 2017).

Mutational biases alter the likelihood of individual mutations arising, and fixation biases (i.e., antagonistic pleiotropy) may limit the fixation probability of certain classes of mutations that experience different magnitudes of deleterious pleiotropy (Streisfeld and Rausher 2010). These two forces may act together to increase the probability of convergence across independent lineages by limiting the number of available beneficial mutations (Storz 2016). Conversely, sign epistasis (the case where the sign of a mutation’s effect depends upon its genetic context) may decrease the likelihood of parallel fixation across divergent lineages, as mutations beneficial on one background may be deleterious in others (Weinreich et al. 2005; Salverda et al. 2011; Pearson et al. 2012; de Visser and Krug 2014; Natarajan et al. 2016).

The distribution of beneficial fitness effects is also a determinant of the frequency of parallel evolution, as the abundance or scarcity of mutations of very large effect will skew the probability of parallel fixation events (Schenk et al. 2012). Many attempts to theoretically model the genetics of adaptation assume that effect sizes for new beneficial mutations are drawn from an exponential distribution (Gillespie 1984, 1991; Gerrish and Lenski 1998; Orr 2002, 2003; Rokyta, Beisel, et al. 2006). However, extreme value theory shows that this distribution may belong to any of the families of distributions whose right tails can be represented by the generalized Pareto distribution (GPD), including the Fréchet (heavy-tailed distributions), the Weibull (right-truncated tails), and the Gumbel (including the exponential distribution) (Beisel et al. 2007). Results from recent attempts to fit a distribution to experimental results have been mixed, with some data showing support for the Gumbel (Kassen and Bataillon 2006; MacLean et al. 2009), the Weibull (Rokyta et al. 2008; Bataillon et al. 2011; Bank et al. 2014), and the Fréchet (Schenk et al. 2012; Foll et al. 2014). Additional experimental work is needed before any general conclusions can be reached, but most recent results lend support primarily for a distribution belonging to the Weibull domain. Such a distribution with a finite upper bound yields a lower probability of parallel evolution, whereas distributions from the Gumbel and Fréchet domains yield greater levels of predictability (Joyce et al. 2008; Schenk et al. 2012).

Patterns of convergence are often offered as strong evidence of adaptation (Losos 2011), but contention remains over whether parallelism is driven primarily by selection repeatedly finding the same solution to common evolutionary challenges (i.e., selectionism) or is the result of mutational biases (i.e., mutationism) (Lenormand et al. 2016). In haploid organisms, the substitution rate, K, can be generally calculated as $K=N\mu \lambda$, a product of the population size, N, the mutation rate, μ, and the probability that a mutation is fixed once it has arisen, λ, which is a function of selection (Kimura 1983; Streisfeld and Rausher 2010). However, differential rates of mutation or fixation probability among loci or different classes of mutations alter the substitution rates of individual mutations, and even modest mutational biases have been shown to influence the trajectory of adaptation (Yampolsky and Stoltzfus 2001; Stoltzfus 2006; Streisfeld and Rausher 2010; Nei 2013). Mutations with the highest substitution rates are the most likely to occur in parallel. A high substitution rate depends on both the fitness effect and the mutation rate for that change. Raising either, or both, will increase the chances of parallel changes. If mutation bias is an important directional force in adaptive molecular evolution, then the mutations that confer the greatest fitness benefit may not necessarily have the highest fixation probability.

We present the results from 20 replicate first-step experimental adaptations for each of four related strains of microvirid bacteriophages. We estimated the distributions of mutational fitness effects for each phage genotype to test for a parallel pattern of fitness effects. We also measured the frequency of parallel adaptation at the levels of mutational effect sizes and gene, protein, amino acid, and nucleotide changes in an effort to characterize patterns of parallelism and the underlying processes that drive them.

Results and Discussion

Parallel Distributions of Fitness Effects

We identified the first fixed mutation in each of 20 replicate lineages for each of four single-stranded DNA (ssDNA) microvirid bacteriophages: ID11 (20 replicate adaptations originally performed by Rokyta et al. [2005]), ID8, NC13, and WA13. Populations experienced selection acting on phage growth rate on Escherichia coli C hosts at 37^∘ C (see Materials and Methods). ID11, ID8, and NC13 belong to the G4-like clade of microvirid phages, and WA13 belongs to the α3-like clade, as described by Rokyta et al. (2005). Between seven and ten unique mutations fixed within each set of 20 replicates of each genotype (table 1). At least seven large-effect beneficial mutations are therefore available to each of the four genotypes, and likely an even larger number of mutations of smaller effect, indicating some degree of parallelism in the genotype-fitness landscape for all four genotypes with regard to the number of possible adaptive trajectories available from any suboptimal point in sequence space.

Table 1.

Summary of Observed Mutations and Fitnesses.

Genotype	Nucleotide	Change	Gene	Residue	Change	No. of Occurences	wa	SE	sb
ID11	2534	G → T	J	20	V → L	1	20.1	0.32	0.30
	3665	C → T	F	355	P → S	5	19.7	0.21	0.28
	3850	G → A	F	416	M → I	3	19.1	0.40	0.24
	3857	A → G	F	419	T → A	1	18.8	0.41	0.22
	3567	A → G	F	322	N → S	1	18.3	0.42	0.19
	2520	C → T	J	15	A → V	6	18.2	0.45	0.18
	3543	C → T	F	314	A → V	1	17.6	0.37	0.14
	3864	A → G	F	421	D → G	1	17.3	0.39	0.13
	2609	G → T	F	3	V → F	1	17.1	0.39	0.11
ID8	4496	G → A	G	172	V → I	3	19.1	0.52	0.61
	3742	A → G	F	393	I → V	1	17.8	0.52	0.50
	4493	A → G	G	171	T → A	8	17.7	0.35	0.49
	4494	C → T	G	171	T → I	2	16.9	0.59	0.43
	4011	A → G	G	10	N → S	4	16.4	0.40	0.38
	3587	C → T	F	340	A → V	1	16.2	0.30	0.30
	4951	G → A	H	142	G → D	1	14.1	0.37	0.19
NC13	4775	C → T	H	71	A → V	2	20.6	0.51	0.47
	3779	A → G	F	393	I → V	1	20.2	0.35	0.44
	4533	G → A	G	172	V → I	3	20.1	0.51	0.44
	4048	A → G	G	10	N → S	2	19.8	0.52	0.41
	4039	C → T	G	7	S → F	1	18.6	0.48	0.33
	3408	A → G	F	269	N → S	1	18.6	0.43	0.33
	4404	A → G	G	129	T → A	6	18.1	0.38	0.29
	4531	C → T	G	171	T → I	4	16.7	0.45	0.19
WA13	5238	G → C	H	50	A → P	1	21.5	0.33	0.64
	3702	C → T	F	203	T → I	7	21.1	0.29	0.60
	5299	C → T	H	70	T → M	1	21.0	0.37	0.59
	3234	C → T	F	47	A → V	3	20.5	0.38	0.56
	4048	G → T	F	319	L → F	1	20.1	0.25	0.53
	3951	C → T	F	287	A → V	1	19.8	0.28	0.50
	5289	C → T	H	67	P → S	2	19.8	0.32	0.50
	3401	G → C	F	104	D → H	2	18.9	0.30	0.44
	4023	C → T	F	311	T → I	1	18.6	0.28	0.41
	2962	C → T	D	148	A → V	1	17.1	0.35	0.30

^aFitness measured in log₂ doublings per hour.

^bSelection coefficient relative to wild-type fitness.

We next analyzed the distribution of beneficial fitness effects for each phage genotype. The shape of the distribution of beneficial fitness effects is a critical assumption in models of adaptation (Sanjuán et al. 2004; Kassen and Bataillon 2006; Beisel et al. 2007; Joyce et al. 2008; Martin and Lenormand 2008; Neidhart et al. 2014). This distribution is generally assumed to belong to a family of probability distributions known as the Gumbel domain of attraction. Extreme value theory, however, predicts that the tail distribution describing beneficial fitness effects may also belong to the Fréchet (heavy-tailed distributions) or the Weibull (right-truncated tails) domains (Joyce et al. 2008; Neidhart et al. 2014). The tails for each of these three domains can be described by the generalized Pareto distribution (GPD) (Joyce et al. 2008). The probability density function of the distribution of beneficial fitness effects is determined by shape parameter κ and scale parameter τ. A κ of 0 yields a distribution in the Gumbel domain, specifically the exponential distribution. $\kappa <0$ results in a member of the Weibull domain with a finite upper bound, and $\kappa >0$ gives a heavy-tailed distribution in the Fréchet domain.

Beisel et al. (2007) and Rokyta et al. (2008) proposed a likelihood-ratio test (LRT) framework, designed explicitly for experiments like ours, to test whether an experimentally observed sample of beneficial mutations have fitness effects that are consistent with having been drawn from a distribution in the Gumbel domain of attraction (see Materials and Methods). The LRT generates estimates of κ and τ, as well as P values based on 10,000 parametric bootstrap replicates, and it has sufficient power to accurately reject the exponential distribution even for mutational samples as small as those reported here, particularly when $\kappa <0$. Rokyta et al. (2008) also described an approximate method for estimating κ (see Materials and Methods). These methods account for beneficial mutations of small effect that were not observed in our sets of 20 replicate lineages by measuring fitness effects relative to the mutation of smallest effect that fixed in each genotype rather than measuring selection coefficients relative to wild-type fitness. This gives the same distribution as the overall distribution of beneficial fitness effects, assuming we observed all available mutations above this threshold (Beisel et al. 2007). Application of the LRT and approximate κ estimation methods to our data (tables 1 and 2) resulted in the rejection of the exponential distribution for ID8, NC13, and WA13. Approximate estimates of κ ranged from −1.32 to −0.66 with upper 95% confidence intervals <0 for all four backgrounds, even when effect sizes were shifted relative to the second and third smallest effect mutant for NC13 and WA13 and the mutation of smallest effect for ID8 and ID11.

Table 2.

Summary of Statistical Results for Test of Distribution Fit.

Phage	Obs.	Shifta	Ho: κ = 0 $(\widehat{\tau })$	HA: $\kappa \ne 0$$(\widehat{\kappa },\widehat{\tau })$	Likelihood Ratio Test			Approximate Method
					$-2\hspace{0.17em}\text{log}\hspace{0.17em}\Lambda$	df	P	$\widehat{\kappa }$	df	95% CIb
ID11	9	1	0.38	$(-1.0,0.73)$	5.40	8	0.13	–0.66	7	$(-1.99,-0.43)$
ID8	7	1	0.81	$(-1.0,1.25)$	6.77	6	0.04	–0.76	5	$(-2.34,-0.37)$
NC13	8	1	0.72	$(-1.0,1.0)$	10.83	8	$<{10}^{-4}$	–1.32	6	$(-3.28,-0.71)$
		2	0.43	$(-1.0,0.65)$	8.12	7	0.02	–1.08	5	$(-2.94,-0.56)$
		3	0.35	$(-1.0,0.52)$	7.08	6	0.03	–1.03	4	$(-3.17,-0.50)$
WA13	10	1	0.76	$(-1.0,1.11)$	11.08	9	0.002	–1.06	8	$(-2.46,-0.59)$
		2	0.45	$(-1.0,0.75)$	7.65	8	0.03	–0.80	7	$(-1.99,-0.43)$
		3	0.41	$(-1.0,0.66)$	7.29	7	0.03	–0.80	6	$(-2.18,-0.41)$

^aThis designates the threshold used for the analysis. 1 indicates the fitness of the lowest fitness mutant; 2, the second lowest; 3, the third lowest. Shifting further than shown results in a failure to reject at the 5% significance level.

^b95% confidence intervals were constructed by assuming that $2(n-1)\widehat{\kappa }/\kappa$ follows a ${\chi }^2$ with $2(n-1)$ degrees of freedom.

We found three new empirical instances of beneficial effect distributions belonging to the Weibull domain, as well as a case (ID11) for which we approximated κ as −0.66, but were unable to reject the Gumbel. The Gumbel domain was previously rejected for this set of ID11 mutations by Rokyta et al. (2008), but a new set of assays was used to measure fitness for the ID11 mutants to ensure consistency with the results for the newly evolved ID8, NC13, and WA13 genotypes. The rank order of effects for each ID11 mutation remained largely unchanged with the new measurements, but statistical significance was not achieved when the new data were analyzed (P = 0.13).

Overall, ID11, ID8, NC13, and WA13 exhibited a parallel distribution of beneficial effects, with estimates of κ being <0 for all four genotypes. Despite assumptions about the shape of the beneficial tail of the overall distribution of mutational effects being critical to many models of adaptation, empirical attempts to determine its shape have been uncommon. Experiments that have been reported have returned a mixture of results, with some distributions consistent with the Gumbel (Kassen and Bataillon 2006; MacLean et al. 2009), the Weibull (Rokyta et al. 2008; Bataillon et al. 2011; Bank et al. 2014; Foll et al. 2014), and the Fréchet (Schenk et al. 2012; Foll et al. 2014). Reports of distributions belonging to the Frechet´ domain have typically been observed for populations subjected to antibiotic drugs or another similarly harsh environment, resulting in a very low initial fitness and yielding a distribution featuring a few mutations of very large effect. Distributions belonging to the Weibull domain have been reported in cases where starting population genotypes are closer to an optimum. Foll et al. (2014) found that influenza virus exhibited a distribution of beneficial effects in the Weibull domain, but the presence of neuraminidase inhibitor oseltamivir resulted in a distribution from the Frechet´ domain. Our results provided strong evidence that the distribution of beneficial fitness effects may generally belong to the Weibull domain of distributions with finite upper bounds when initial fitness is not extremely low. Joyce et al. (2008) showed that the probability of parallel evolution decreases as κ decreases, meaning that a distribution of beneficial effects from the Weibull domain will yield a lower rate of parallelism than an exponential or heavy-tailed distribution.

Convergent Changes in Capsid Genes

Adaptive convergence was high at the gene and protein level. Of 80 total replicates, 65 fixed mutations in the two major structural proteins of the capsid, with 32 mutations fixing in the coat protein (F) and 33 in the spike protein (G) (table 1), despite those two genes only comprising 30–33% of the total genome. Of 80 amino acid substitutions, 56 resulted in a hydrophobic, aliphatic residue, and the most frequent mutation in three backgrounds resulted in the substitution of a threonine residue (polar, uncharged) with a nonpolar, aliphatic residue.

These results are consistent with other studies of $\Phi$X174, which have often found an abundance of large-effect mutations affecting F and G. Nearly half of the unique mutations observed by Pepin et al. (2008) during the experimental adaptation of $\Phi$X174 to novel E. coli hosts affected the capsid protein, with many of them occurring in parallel in independent lineages. Likewise, nearly half of the unique mutations observed by Wichman et al. (1999) fixed in gene F, several of them occurring in both of their experimental lineages. High levels of convergence affecting specific genes have also been observed in more complex systems. For example, Tenaillon et al. (2012) found that over half of 115 replicate lineages of E. coli fixed mutations in ybaL gene, and Tishkoff et al. (2007) found four independent convergent changes in the human lactase gene in European and African populations.

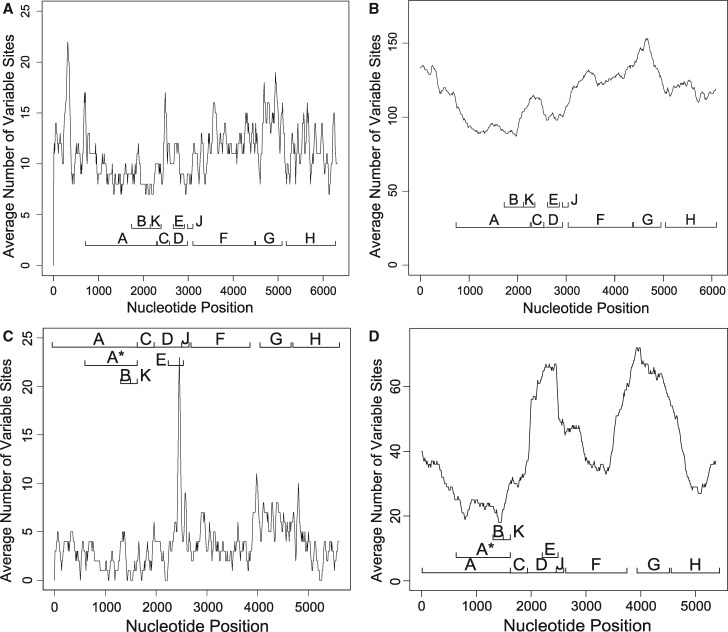
To test whether the disproportionate representation of mutations in genes F and G may be a result of genomic variation in mutation rates we performed an analysis using the set of 11 natural phage isolates belonging to the $\alpha 3$-like clade of microvirid phages described by Rokyta, Burch, et al. (2006), including the isolate of WA13 used here, and a set of 17 wild G4-like phages, including the wild-type isolates of ID11, ID8, and NC13, wherein we measured the average number of variable nucleotide sites between each pair of genotypes within each clade across a sliding window of 50 or 500 nt, measured every 10 nt across the genome (fig. 1). Although the evolution of these phages will have been influenced by neutral evolution and widely variable selective pressures, our results demonstrated heterogeneity in rates of divergence and mutation across different regions of the genome. The spike gene G displayed on an average a higher rate of divergence than other loci, so the large number of mutations fixed in G may be a result of locally variable mutation rates, but F was not highly variable, so convergent mutation in F cannot be explained by regional mutation rates.

Fig. 1.

Average number of variable sites among all pairs of the 11 $\alpha 3$-like (A and B) and 17 wild G4-like (C and D) phage genotypes isolated and described by Rokyta, Burch, et al. (2006), measured across snapshots of size 50 nt (A and C) and 500 nt (B and D) taken every 10 nt across the entire genome. The locations of each gene are labeled. ID11, ID8, and NC13 belong to the G4 clade, whereas WA13 belongs to the clad of $\alpha 3$-like phages. Gene G, which was the most frequently mutated gene among the 60 replicate G4-like lineages, is also the most divergent gene among the analyzed G4-like natural isolates.

Under any particular selective pressure, the vast majority of genes may not contribute to fitness-related variation, potentially resulting in a concentration of beneficial mutations within just a handful of genes or loci. Our results, and those of other $\Phi$X174 studies, indicated that improvement of growth rate generally takes the form of changes in the same genes and proteins, specifically the spike and capsid proteins. Although other molecular strategies for fitness improvement exist, (as indicated by mutations affecting the DNA binding protein, J, the pilot protein, H, and the scaffolding protein, D) adaptation was largely constrained to large-effect mutations affecting the structure of the phage capsid, leading to high rates of parallel mutations affecting capsid genes.

Structural Hotspots in Adaptation

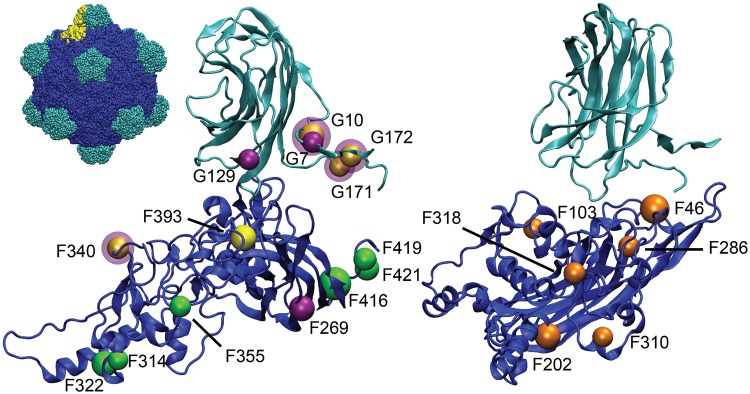
The locations of the capsid mutations (sites in coat protein F and spike protein G) that fixed in the G4 genotypes (ID8, ID11, and NC13) were clustered significantly more closely together than would be expected for a set of randomly chosen mutations of equal size (fig. 2). In particular, residues 171 and 172 of the spike protein were the subject of 20 fixation events, including two unique amino acid changes at residue 171. We calculated the average distance from each alpha carbon in the set of 19 observed G4 mutation sites to its first-, second-, and third nearest neighbor from among the other sites (table 3). We then compared these data for the observed mutations to a set of the same calculations for 10,000 randomly chosen sets of 19 sites within the coat-spike complex (see Materials and Methods). The sample size of WA13 mutations was not large enough for a separate analysis.

Fig. 2.

Locations of observed mutations in G4 lineages (left) and WA13 (right). Coat protein (F) shown in blue, spike protein (G) shown in teal. Full capsid is shown in the top left, with a single copy each of F and G highlighted in yellow. Of the G4 lineages, the sites of mutations that fixed in ID11 are shown in green, mutations in ID8 are shown in yellow, and mutations in NC13 are shown in purple. A purple halo around a yellow site indicates a site shared between ID8 and NC13. G4 mutations are significantly clustered, with the first-, second-, and third nearest neighbors of each mutation being significantly closer together than expected for a set of random mutations.

Table 3.

Average Distance between Mutations (Å).

	Observed	Variable Sites	Random
First nearest	5.93	14.71	10.40
Second nearest	10.31	17.91	14.02
Third nearest	13.15	21.24	16.73

The average distance between each observed mutation and its first nearest neighbor (5.93 Å) was significantly smaller than that of a set of randomly chosen sites (10.39 Å; t-test, two-sided, unequal variance, $P<{10}^{-5}$; 95% confidence interval, 8.39 Å, 12.36 Å; table 3). Of 10,000 simulated sets of random mutations, the smallest average first nearest neighbor distance was 6.36 Å, a clear indication that sites of observed substitutions were significantly clustered in adaptive hotspots of the proteins. Repeated convergent changes within particular regions of genes is perhaps not surprising given the high degree of mutational heterogeneity within genes observed across 50 nt sliding comparisons of the genomes of wild phage isolates (fig. 1). To test whether the mutational clustering we observed within the 3D capsid may simply be in regions of 1D DNA sequence with a higher local mutation rate (though proximity on the protein structure does not translate to proximity along a sequence), we also measured the average distance from each observed coat and spike mutation to the first-, second-, and third nearest neighbor from among all 150 variable sites within the set of 17 G4-like natural phage genomes described by Rokyta, Burch, et al. (2006). Each of those measurements was significantly larger than the average distance from the observed mutations to a random set of residues (14.71, 17.91, and 21.24Å for the first-, second-, and third nearest neighbor among variable sites, t-test, two-sided, unequal variance, $P<{10}^{-5}$, table 3), so the regions of protein structure that were hotspots for beneficial mutations in our lineages were not located near residues encoded by regions of DNA sequence within each gene that may be subject to elevated rates of mutation. We therefore found strong evidence not just of convergence among divergent genotypes at the level of changes affecting the same genes and proteins, but of convergence at particular regions of the capsid proteins resulting from selection.

Previous results have shown that amino acid substitutions at protein–protein interfaces within the capsid can have large effects on growth rate and capsid stabilities (Wichman et al. 1999; Holder and Bull 2001; Sackman and Rokyta 2013; McGee et al. 2014). Doore and Fane (2015), for example, found that compensatory mutations repairing disrupted protein–protein interactions were critical for the recovery of an extremely low fitness $\Phi$X174/G4 hybrid phage. Many of the mutations that fixed in our experimental lineages were located at or near coat–spike, coat–coat, and spike–spike interfaces, and our data provided new evidence that mutation affecting the interaction of capsid subunits is a common strategy for molecular adaptation across multiple phage genotypes and is often the first step in adaptation to a novel environment.

Parallel Nucleotide Substitution within and between Genotypes

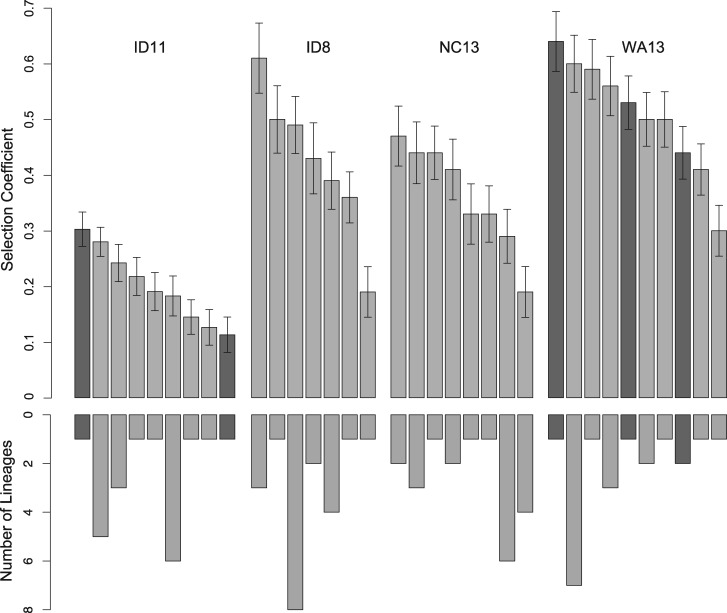
Overall, 31 unique mutations fixed in 80 replicate lineages. Nine unique mutations fixed in the ID11 lineages, seven in ID8, eight in NC13, and ten in WA13. Parallel adaptation was frequent within sets of replicates. The most common mutation on each background fixed an average of 7 times out of 20 replicates (fig. 3 and table 1).

Fig. 3.

Selection coefficients (s) for each of the unique mutations to fix in the 20 replicates of each genotype, and the number of lineages in which they occurred. Dark gray indicates substitutions resulting in transversions and light gray indicates transitions. For all four genotypes, the most fit mutation was never the most frequent. For NC13, half of all lineages fixed one of the two lowest fitness mutations.

ID11, ID8, and NC13 share between 96% and 98% sequence identity, and WA13 shares only $\sim 55\%$ sequence identity with the three other genotypes. ID8 and NC13 shared four mutations in common, resulting in amino acid substitutions at residue 393 in the coat protein, F, and at residues 10, 171, and 172 in the spike protein, G (table 1). Half of each of the ID8 and NC13 replicates fixed mutations at one of these four shared sites. The lack of sign epistasis (such that the sign of a mutation’s effect is conditional upon genetic background) at these sites was surprising given that ID8 and NC13 differ at 4% of nucleotide sites. ID11 and WA13 did not share any substitutions with any other background, despite a closer relationship between ID11 and NC13 (2% nucleotide divergence). Epistasis has been demonstrated in microvirid phages (Rokyta and Wichman 2009; Sackman and Rokyta 2013; Doore and Fane 2015; Sackman et al. 2015; Doore et al. 2017) and likely caused the lack of parallel substitutions between WA13 and other genotypes, as fitness effects on other backgrounds would have little correlation with effects on the highly divergent WA13 background. WA13 nonetheless exhibited frequent parallelism among replicates and exhibited a high degree of parallelism with the G4 genotypes at the level of gene and protein changes and at the level of mutational effects.

Parallel fixation of identical nucleotide and amino acid substitutions was frequent overall within each genotype, in general agreement with other similar experimental evolution studies (Rokyta et al. 2008; Bollback and Huelsenbeck 2009; Toprak et al. 2012; McGee et al. 2016). Surprisingly, however, a large proportion of ID8 and NC13 replicates fixed shared identical substitutions, despite their level of divergence and the prevalence of sign epistasis within the bacteriophage genome (Rokyta et al. 2011; Caudle et al. 2014; Doore and Fane 2015). Overall, our results are indicative of adaptive landscapes with a small number of large-effect steps available from each starting point in an adaptive walk, yielding moderately predictable evolutionary trajectories over many replicates initiated from the same genotype. Parallel evolution was common at every level analyzed, both within and among genotypes.

Probability of Parallel Evolution

Orr (2005) showed that the probability of parallel evolution, or the likelihood that any two identical populations fix the same mutation, is $P=2/(n+1)$, where n is the number of unique beneficial mutations available to a starting wild-type sequence. Orr’s model assumes that selection is strong, that n is small, and that mutational effect sizes are drawn from a distribution that conforms to the expectations of extreme value theory (Orr 2005). Joyce et al. (2008) extended this prediction to account for differences in the distribution of beneficial mutational effects by incorporating the value of the GPD shape parameter, κ. Under this framework, the probability of parallel evolution is approximately $2(1-\kappa )/[(1-2\kappa )(n-1)]$ (Joyce et al. 2008), and this prediction should be on an average robust even when mutation rates are not constant among loci (Rokyta et al. 2005).

If we assume that all available beneficial mutations were observed in each set of 20 replicate populations, we can calculate expected probabilities of parallel evolution for each genotype. Using the prediction of Orr (2005), for ID11, n = 9; ID8, n = 7; NC13, n = 8; WA13, n = 10. Our predicted probabilities of parallel evolution are 0.2, 0.25, 0.22, and 0.18 for ID11, ID8, NC13, and WA13, respectively. To estimate P experimentally for each genotype, we randomly paired all 20 replicate lineages without replacement and recorded the frequency of randomly paired lineages possessing identical substitutions within each set of ten random pairings. P was estimated in this fashion by averaging this frequency over 1,000 bootstrap data sets. Our observed estimates of parallel evolution were $\widehat{P}=0.15$ for ID11, $\widehat{P}=0.20$ for ID8, $\widehat{P}=0.14$ for NC13, and $\widehat{P}=0.15$ for WA13, with 95% confidence intervals generated from the bootstrap distribution of 0.0–0.4 for ID11, ID8, and NC13 and 0.0–0.3 for WA13.

Although the expected values of P derived from the formula of Orr (2005) fall within the 95% confidence intervals for all four genotypes, all four experimental estimates of P were lower than expected, likely because our estimates of n fail to account for low-fitness beneficial mutations available to each background that failed to fix in any population. Our results nonetheless provide some support for Orr’s theoretical prediction (Orr 2005) and the prediction that parallel evolution should (and does) occur at a high rate. However, Joyce et al. (2008) showed that the probability of parallel evolution decreases as κ decreases. Using their formula, the probability of parallel evolution is 0.18, 0.23, 0.18, and 0.15 for ID11, ID8, NC13, and WA13, respectively, closer to our observed estimates of the rate of parallel evolution. The distribution of beneficial fitness effects for all four genotypes is best described by a member of the Weibull family of right-truncated distributions, yielding a reduced rate of parallel evolution relative to the prediction of Orr (2005), which was formulated for fitness effects drawn from an exponential distribution. Despite the downward adjusted rate of parallel evolution resulting from the shape of the distribution of fitness effects, parallelism was still frequent. We have thus far demonstrated a high level of parallelism within and across genotypes at the level of mutational effects and for adaptive evolution at the levels of genes, proteins, and amino acid and nucleotide substitutions as well as a predictability in the overall rate of parallel adaptation.

Mutation Bias Drives Parallel Evolution

Absent stochastic effects and mutational biases, the most highly fit mutant in each background should be the most frequently fixed (Haldane 1927), a pattern that is exacerbated by clonal interference (Gerrish and Lenski 1998). However, our results differed significantly from this expectation. The most fit mutant failed to fix most frequently in all four genotypes (table 1 and fig. 3). In fact, the least fit mutation in each genotype fixed in a total of 7 of 80 replicates, the same frequency as for the most fit mutation for each genotype. By contrast, the most frequent mutation in each genotype fixed in a total of 27 of the 80 replicates, even though the mutations of largest fitness effect in ID11, ID8, and NC13 conferred a significantly greater benefit than the most frequently fixed mutation in each genotype (Welch two-sample t-tests, P < 0.01 for ID11, P = 0.04 for ID8, $P<{10}^{-3}$ for NC13, P = 0.30 for WA13, table 1). The pooled standard errors (SE) for our fitness measurements were 0.37, 0.43, 0.45, and 0.32 doublings per hour for ID11, ID8, NC13, and WA13, respectively, whereas the average fitness difference between each mutation and its nearest-ranked neighbors was 0.48 doublings per hour. The fitness for the majority of mutations is >1 SE from the next-ranked mutations, including in the cases of the most fit and most frequent mutations for ID11, ID8, and NC13, so we can be reasonably certain of the ranked orders of mutational effects.

The second-, third-, and fourth largest effect substitutions that fixed in ID11 were the three most common. The most fit mutant, though, only fixed once in 20 replicates. The most fit WA13 mutation likewise fixed only once. This discrepancy is likely caused by a known bias favoring transitions over transversions (Rokyta et al. 2005; Stoltzfus and Norris 2016; Storz 2016; Stoltzfus and McCandlish 2017). The most highly fit WA13 and ID11 mutants were both transversions, and fixed less frequently as a result. Very little pattern is discernible from the fixations in ID8 and NC13. The two largest effect ID8 mutations only fixed in a total of four replicates. Half of the 20 NC13 lineages fixed one of the two mutations with the smallest effect. No transversions fixed in ID8 or NC13, ruling out this simple explanation of these results.

The probability that a particular locus contributes a mutation that fixes is dependent upon the locus-specific mutation rate and the probability that a particular mutation fixes after arising in the population, which is an increasing function of the mutation’s selection coefficient, s (Lenormand et al. 2016; Bailey et al. 2017). Selection in this system acts only on the phenotype of interest, growth rate, which serves as our measurement of fitness. As such, there can be no fixation bias arising from deleterious pleiotropic effects, since all possible effects of a mutation are already incorporated into our measurement of fitness. Parallel evolution can be driven by interference dynamics (Bailey et al. 2017), but our selection scheme minimizes the likelihood of clonal interference via small bottleneck sizes between passages (McGee et al. 2016), and interference dynamics, had they been present, would actually have amplified the likelihood of fixation of higher fitness mutants, contrary to our observation of repeated fixation of smaller effect mutations. Therefore, the apparent lack of correlation between frequency of occurrence and the magnitude of a mutation’s selection coefficient can only be attributable to mutation bias affecting the rates at which specific mutations are generated during DNA replication or caused by DNA damage. Transition bias is not applicable to the results for ID8 and NC13, but the mutation rate is certainly not equal at all sites in the genome, as suggested by the differential rates of divergence among natural phage isolates across regions of the genome (fig. 1), resulting in differential frequencies of particular mutations (Chevin et al. 2010; Lenormand et al. 2016; Bailey et al. 2017). Mutation bias has been previously observed to affect evolutionary outcomes in experimental (Couce et al. 2015) and natural systems (Galen et al. 2015). In the case of our results, not only did mutational biases impact the outcomes of adaptation but they also repeatedly drove populations toward suboptimal outcomes with a frequency contrary to expectations based on selection coefficients alone.

Conclusions

We demonstrated conclusively that parallel adaptation was frequent across every biological level, both within and among genotypes. All four genotypes exhibited a similar distribution of beneficial effects characterized by a finite upper bound, contributing to a growing consensus of empirical results demonstrating that the distribution of beneficial mutational effects is right-truncated when fitness is not extremely low. Each genotype found convergent molecular strategies for improving growth rate, with 80% of all substitutions affecting just two genes and evidence of significant clustering of mutations near protein interfaces within the capsid structure. Parallelism was also exceptionally common at the nucleotide level within genotypes, with the most common mutation fixed an average of 7 times in each set of 20 replicates. Additionally, the NC13 and ID8 lineages shared fixed substitutions in half of their lineages, despite having 4% nucleotide divergence and a presumably high prevalence of sign epistasis (Rokyta and Wichman 2009; Sackman and Rokyta 2013; Doore and Fane 2015). The patterns of abundant parallel adaptation characterizing every level of organization, however, could not be satisfactorily explained by selection alone.

The magnitudes of selective benefit of many mutations conflicted with their frequencies of fixation within each set of 20 replicates. The mutation in each genotype with the smallest effect on fitness fixed on an average as often as the mutation of largest effect, which only fixed once each in two genotypes. Transition bias accounted for some of the skewed fixation patterns, but additional unknown site-specific biases clearly affected the substitution rates of particular mutations. We thus demonstrated conclusively that while selection was responsible for limiting the first step of adaptation to a beneficial subset of all possible mutations, the parallel fixation of new mutations was in large part mutation-driven, leading to the frequent fixation of suboptimal adaptive substitutions.

Materials and Methods

Selection Experiments

ID8, ID11, NC13, and WA13 were originally isolated and described by Rokyta, Burch, et al. (2006) (GenBank accession numbers: DQ079898, AY751298, DQ079901, DQ079873). They are microvirid bacteriophages with circular, single-stranded DNA genomes of $\sim 5,500$ nucleotides encoding 11 genes. Selection experiments were performed as described by Rokyta et al. (2005) and McGee et al. (2016). Unique isolates were used to initiate each replicate lineage. Isolates were evolved via serial flask passaging at 37 °C on Escherichia coli hosts in an orbital shaking water bath at 200 rpm.

Each passage was initiated by inoculating $\sim {10}^8$ hosts with $\sim {10}^5$ phage, which were grown for 40 min. Population sizes were therefore kept large enough to minimize the waiting period for a beneficial mutation while minimize the potential for clonal interference. Growth was terminated with CHCl₃. Samples were centrifuged, and a fraction of the supernatant was used to initiate the following passage. Population size and fitness (growth rate) were determined at each passage by agar plating at the start and end of each passage.

Passaging was continued until a spike in population fitness, measured on a log₂ scale as population doublings per hour, indicated fixation of a new mutation. This was performed 20 times for each genotype, yielding a set of 20 first-step mutations for each genotype. The 20 replicate adaptations of ID11 were originally performed by Rokyta et al. (2005), but new fitness values were generated by assays so that data would be consistent with assay data from the three new genotypes. The 20 replicate adaptations of ID8 were originally described by McGee et al. (2016).

Sequencing

We sequenced the entire genome of the final population of each lineage. Whole population sequencing allowed us to determine the identity of fixed mutations following apparent increases in population fitness. Individual isolates used for fitness assays were taken from final population passages and sequenced to confirm they contained only the mutation of interest.

Fitness Assays

Fitness measurements were determined through assays similar to the above-described passaging protocol. Sequence-confirmed isolates of the wild-types and each single-mutant were assayed over 5–10 replicates to determine fitness.

Sliding Window Analysis and Measurement of Mutational Clustering

A Python script (Python Software Foundation, https://www.python.org/; last accessed October 11, 2017) was used to measure the average pairwise number of variable sites among the sets of 11 $\alpha 3$-like and G4-like phage isolates described by Rokyta, Burch, et al. (2006) within a sliding window of 50 and 500 nt across the phage genomes. For the purposes of this analysis, the ID2 genotype putatively belonging to the G4 clade was ignored, as it has been previously demonstrated that a large section of the ID2 genome is unrelated to other G4 genotypes (Sackman and Rokyta 2013), and the genomes of $\phi$K and $\alpha 3$ were also left out of the analysis due to a very high level of divergence between those two genomes and the other members of the $\alpha 3$ clade. Another Python script was used to measure the distances from the alpha carbon of each observed G4 mutation to their first-, second-, and third nearest neighbors, using the published structure for G4 (PDB structure 1GFF). The same script was used to calculate the same distances for 10,000 equal-sized sets of randomly chosen mutations. 95% confidence intervals were calculated from the distance distributions from that set of 10,000 simulations. A mutation at residue 3 in capsid protein F was left out of the analysis because the first several residues of F are not included in the published structure of G4. The analysis was then performed using all 150 variable amino acid residues within the sequences of the coat (F) and spike (G) proteins of the G4-like clade of phages, again ignoring the sequences of ID2, and for 10,000 sets of 150 randomly chosen residues from across the protein structures.

LRT and Approximate Estimation of κ

The likelihood-ratio test (LRT) framework and method for estimating GPD shape parameter κ are described by Beisel et al. (2007) and Rokyta et al. (2008). Statistical methods were employed exactly as described. The LRT framework tests whether an experimental sample of beneficial mutations have fitness effects that are consistent with having been drawn from a distribution in the Gumbel domain of attraction. Negative twice the difference in the log likelihoods, $-2\hspace{0.17em}\text{log}\hspace{0.17em}\Lambda$, is calculated based on the GPD, testing the null model that the beneficial fitness effects of mutations available to an adapting sequence are drawn from the exponential distribution (κ = 0) against the alternative that the distribution belongs to the Weibull or Fréchet domain ($\kappa \ne 0$). Data are shifted for the LRT such that empirical effect sizes are measured relative to the effect of the least fit mutation rather than the wild-type fitness to reduce possible bias introduced by missing small-effect beneficial mutations in our sample of 20 replicates. Κ is stable with respect to shifts in the value of this threshold. The LRT generates estimates of κ and τ, as well as P values based on 10,000 parametric bootstrap replicates.

Rokyta et al. (2008) also show that for an ordered sample of size n from the GPD, $X_{(1)},X_{(2)}\mathrm{\dots },X_{(n)}$, where $X_{(n)}$ is the largest value from the sample and $X_{(1)}$ is the smallest, $\widehat{\kappa }$ can be estimated by

$$\widehat{\kappa }=\frac{1}{n-1}\sum _{i=1}^{n-1}\mathrm{l}\mathrm{n}(1-X_{(i)}/X_{(n)}).$$ (1)

Approximate confidence intervals for estimates of $\widehat{\kappa }$ can be generated by assuming that $2(n-1)\widehat{\kappa }/\kappa$ follows a X² with $2(n-1)$ degrees of freedom (Rokyta et al. 2008). All analyses were performed using R (R Development Core Team 2010).