Abstract
We present a new Bayesian method for estimating demographic and phylogenetic history using population genomic data. Several key innovations are introduced that allow the study of diverse models within an Isolation-with-Migration framework. The new method implements a 2-step analysis, with an initial Markov chain Monte Carlo (MCMC) phase that samples simple coalescent trees, followed by the calculation of the joint posterior density for the parameters of a demographic model. In step 1, the MCMC sampling phase, the method uses a reduced state space, consisting of coalescent trees without migration paths, and a simple importance sampling distribution without the demography of interest. Once obtained, a single sample of trees can be used in step 2 to calculate the joint posterior density for model parameters under multiple diverse demographic models, without having to repeat MCMC runs. Because migration paths are not included in the state space of the MCMC phase, but rather are handled by analytic integration in step 2 of the analysis, the method is scalable to a large number of loci with excellent MCMC mixing properties. With an implementation of the new method in the computer program MIST, we demonstrate the method’s accuracy, scalability, and other advantages using simulated data and DNA sequences of two common chimpanzee subspecies: Pan troglodytes (P. t.) troglodytes and P. t. verus.
Keywords: isolation-with-migration model, importance sampling, Markov chain representation, model comparison, likelihood ratio test
Introduction
In the study of diverging populations and species, a common goal is to disentangle the conflicting signals of prolonged genetic drift, which elevates divergence, and gene exchange, which removes it. A widely used conceptual framework for such divergence problems is the Isolation-with-Migration (IM) model, which accounts for genetic drift with parameters for effective population size and splitting time, and for gene exchange with migration rate terms (fig. 1a). IM models have been widely used to study the evolutionary divergence of a very wide range of organisms (Moodley et al. 2009; Won and Hey 2005; Berner et al. 2009; Hey 2010a; Geraldes et al. 2008; Cong et al. 2015; Pinho and Hey 2010).
Fig. 1.
(A) An example of a demographic model with a genealogy. A 2-population isolation with migration (IM) model includes six parameters: population sizes, and θa, migration rates, m1 and m2, and splitting time Ts. The graph in black lines depicts a genealogy (G) including coalescent events at time t1 and t2, respectively, (vertical paths of genes) and migration events (horizontal paths). (B) The coalescent tree (λ1) of genealogy G includes the same coalescent events on G. (C) A coalescent tree λ2 whose probability is same as that of λ1. (D) Genealogy and coalescent tree with population labels.
To connect data, in the form of aligned gene or genome sequences, to the parameters of an IM model, virtually all methods use some form of integration over latent genealogies (Felsenstein 1988; Griffiths 1989). A genealogy includes both a coalescent tree, that is an ultrametric binary tree that describes a possible history of common ancestry of a sample of gene copies, and a history of migration events between populations for each of the branches in the tree (Beerli and Felsenstein 1999). Genealogies are not part of the data, nor typically part of the final results. However, because we can calculate the probability of aligned sequences given a genealogy (using a mutation model) and because we can calculate the probability of a genealogy given a demographic model (e.g., the parameters for an IM model), likelihood or Bayesian methods for fitting demographic models to aligned DNA sequences all include some kind of machinery for integrating over genealogies (Kuhner et al. 1995; Wilson and Balding 1998; Nielsen and Wakeley 2001; Nielsen 2000; Lopes et al. 2009; Hey and Nielsen 2007; Bahlo and Griffiths 2000; Griffiths and Tavaré 1994).
In principle, genealogy sampling under IM models can enable a rich model-based approach to demographic and phylogenetic analyses. However on the practical side, inference methods that use IM models frequently face significant computational and statistical challenges. Because of the inclusion of migration events, the space of possible genealogies for a given data set is vastly larger than the space of coalescent trees for the same data. As a practical matter it is difficult to develop a method that adequately samples the space of genealogies, particularly for larger data sets. Likelihood and Bayesian methods for fitting complex demographic models are generally slow and typically cannot be applied to large population genomic data sets (Kuhner 2008).
Recently, progress has been made on separating the migration events from the genealogy to allow for calculating the probability distribution of a simpler coalescent tree under an IM model (Zhu and Yang 2012; Andersen et al. 2014; Hobolth et al. 2011). By representing the history of coalescence and migration using a Markov chain, it becomes possible to integrate over all possible migration histories to calculate the prior probability of a coalescent tree. For example, Zhu and Yang (2012) developed a maximum likelihood estimation under an IM model for three DNA sequences using the probability of a coalescent tree.
Here, we address several problems associated with genealogy-sampling approaches to demographic inference and present a new Bayesian Markov chain Monte Carlo (MCMC) method for demographic/phylogenetic models including IM models. Our new approach allows for the study of large numbers of loci and can be used for a wide range of demographic models, while allowing for likelihood ratio tests (LRTs) of nested models using a posterior density, proportional to the likelihood, that is joint for all parameters in the model.
To improve the MCMC process and to facilitate the integration over genealogies, we decompose a genealogy G into (1) coalescent tree, a simple bifurcating tree, λ (fig. 1b), and (2) the remaining information , which includes horizontal migration paths of genes between populations. We derive explicit formulas for the probability distribution of a coalescent tree using a Markov chain as a representation of genealogy and matrix exponentiation. For efficient MCMC simulations of coalescent trees, we employed importance sampling in which trees are sampled from a tractable probability distribution (called an importance sampling distribution), rather than from the coalescent probability conditional on the demographic model of interest. Then in the numerical integration over λ, each value of λ is weighted by the inverse of its importance sampling distribution. This adjustment accounts for having sampled from the importance sampling distribution and yields an approximation converging to the exact integration over λ as more trees are sampled (Robert and Casella 2013). For the importance sampling distribution, we consider posterior probability distributions in which priors on λ are free of the underlying demographic model. Because the coalescent trees do not include migration events and are not constrained by demographic epochs, the MCMC simulation is largely free of mixing difficulties and works well with large numbers of loci.
The computer program, MIST (for “model inference from sampled trees”), implements the new method for multiple processes in parallel. The program MIST is freely available at https://github.com/yujin-chung/MIST.git Using simulated DNA sequences, we demonstrate the use of importance sampling distributions and assess the performance of the method in terms of accuracy and computing time. We also demonstrate the application of different demographic models to a single MCMC sample, by using models with and without an unsampled “ghost” population. We also examined false positives of LRTs for migration rates when data show low divergence. Finally, we apply the method to population genomic samples from two subspecies of common chimpanzees (Prado-Martinez et al. 2013), Pan troglodytes (P. t.) troglodytes and P. t. verus, and compare the results to those from previous other studies.
New Method
The new method is described for a basic 2-population isolation with migration (IM) model (fig. 1a) with the sizes of two sampling populations and their common ancestral population (θ1, θ2, and θa), two migration rates between two sampling populations (m1 and m2), and the splitting time of two populations from their common ancestral population (TS). A 2-population IM model with six parameters () is easily adapted to variations of this model, such as those shown in figure 2. Also it should not be difficult to extend the approach to models for data that have been sampled from more than two populations (Hey 2010b).
Fig. 2.
The new method schematic. In step 1 coalescent trees for the aligned DNA sequences are sampled from an MCMC simulation using an importance sampling distribution of trees that is free of a demographic model of interest. In step 2, the set of sampled coalescent trees is used for the approximation of the joint posterior density under a demographic model of interest. Optimization of the joint posterior density provides an estimate of model parameters. The same set of trees from step 1 can be used repeatedly to study different demographic models.
Following Felsenstein (1988), the likelihood of can be obtained by integrating out all possible genealogies in the model:
| (1) |
where is the probability of genetic data D given genealogy and is coalescent probability of genealogy given a demographic model. Considering a Bayesian approach, the posterior distribution of demographic parameters , given genetic data, is
where is a prior distribution under which parameters are independent and uniformly distributed (i.e., is constant over a specified range of values for ).
In considering how to ameliorate the difficulties of working with genealogies it is important to note two things about how a history of migration events impacts the data. First, from a coalescent perspective, the effect of migration events in the true history of a set of genes is to shape the times of common ancestry of those genes. Second, the calculation of the likelihood depends only on the vertical branch lengths and topology of G and not on the migration events in G. We can decompose a genealogy into two parts, a coalescent tree λ and migration events , such that (fig. 1a). Migration will have shaped the coalescent tree, but when the coalescent tree is known, the data are independent of : . Then using this fact, the integration in equation (1) separates into two integrations:
| (2) |
where
| (3) |
Expression (2) is our target, the posterior density for the model parameters. Below we provide a formula for computing analytically the integration over , in equation (3) and we develop a new MCMC approach using importance sampling to approximate the integration over λ in equation (2).
Exact Integration over Migrations: Markov Chain Representation
The exact integration over migration paths in equation (3) is done by computing transition probabilities in a Markov chain representation of a genealogy G. To reduce the state space of the Markov chain representation of a genealogy G, we introduce a simplified genealogy in which sampled gene copies are labeled only by the population they were sampled from. We define a function ϱ that replaces the tip labels on G or λ by the label of their respective sampled population. The genealogy or coalescent tree with population labels is denoted as or , respectively. For example, λ1 and λ2 in figure 1 have different individual tip labels, but are converted to the same coalescent tree with population labels: . Moreover, the probabilities of λ1 and λ2 are the same: . In general, all trees that can be converted into the same coalescent tree using population labels, will share the same probability (see Lemma in the supplementary note, Supplementary Material online), and this needs only to be calculated once. Using this property and the following Theorem 1, we compute from .
Theorem 1 Consider a m-population IM model with parameters . Let be the collection of coalescent trees that are converted into the same coalescent tree with population labels λp. Then its size is
| (4) |
where V is the set of vertices of λp that has two tips as descendants (so called "cherry"), ni is the number of samples from population i () andis 2 if the two descendants (tips) of v have the same labels; 1 otherwise. The probability density ofis
The proof of Theorem 1 is provided in the supplementary note, Supplementary Material online.
To compute we use a Markov chain representation of Gp in which time is separated into multiple epochs bounded by coalescent times and population splitting times. For example, in figure 1d, two epochs, and , are defined by two coalescent events at time t1 and t2, respectively. The genealogy in each time epoch can be expressed as a sequence of transitions (Asmussen 2003) among transient states (migration events) and into absorbing states (coalescent events). A state s of a Markov chain is a subset of , where a in denotes the number of lineages with label l in population q and k is the total number of kinds of lineages’ labels. Note that tips on Gp or λp may have the same labels, but ancestral lineages have distinct labels. In figure 1, the lineages on genealogy Gp have labels 1 to 4 and all transient states in each epoch are in table 1. The initial state of Gp at time 0 is s2, the state right before the first coalescent event at time t1 is s4, and the state right after the event is . If a state has an element of zero number of lineages for some l and q, then, for an efficient expression, we consider the states with and without the element with no lineage are identical. For example, .
Table 1.
The Possible Transient States of Markov Chains As Representatives of Gp in Epoch and , Respectively.
| Epoch 1(0, t1] | ||
|---|---|---|
| State | Notation | |
| Pop1 | Pop2 | |
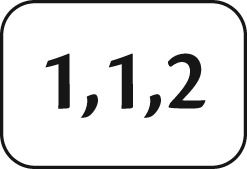 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
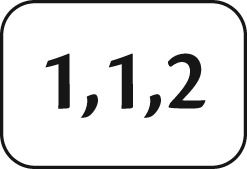 |
|
| Epoch 2(t1, t2] | ||
| State | Notation | |
| Pop1 | Pop2 | |
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
Note.—The left column in each table visualizes the state of (1) three lineages: two with same label 1 and one with label 2 in Epoch 1 and (2) two lineages with label 1 and 3 in Epoch 2. The right column in each table shows the corresponding notation of a Markov chain state.
In general, the transition rate from state si to state sj is as follows:
if (i.e., a lineage with label l moves from population p to q), then , where is the migration rate from population p to population q backward in time, and the set difference is defined by
-
if sj = A (the absorbing state), , and either X1 or X2 is not an empty set (i.e., two lineages with the same label l or different labels l and coalesce), then
;
if i = j, then ;
otherwise, .
For example, the state change from to s3 in table 1 means that a lineage with label 1 migrates from population 1 to 2. The transition rate for the event is , since and . Similarly, the formulas are applied for every transition event. The transition rate matrices Q1 and Q2 for Gp in epoch and , respectively, are below:
and
where , and diagonal elements are set to the negative sum of the corresponding row. Then the probability of state change from si to sj during time t1 is , where eQ is a matrix exponential and is (i, j) entry of matrix Q.
Because the coalescent tree λp does not include information about the populations in which coalescent events occurred, computing requires that we consider all the possibilities. The possible states right before the first coalescent event are s1 (all lineages in Population 1), s3 (the coalescing lineages only in Population 1), s4 (the coalescing lineages only in Population 2), and s6 (all lineages in Population 2). The corresponding states right after the event are , and , respectively. The probability of the case that s4 is the state right before the first event is . In a similar way, we compute the probability of each possible way and the probability of λp takes account of all possible cases:
Using this approach, we can compute the probability of any coalescent tree under an IM model.
A ranked tree topology is a topology with ordered internal nodes (Semple and Steel 2003), and for coalescent trees that share a ranked topology, the corresponding possible transition rate matrices are the same. For efficient computation, we have a list of ranked tree topologies with population labels, and save the matrix decomposition of possible transition rate matrices for reuse. In this way, by using population labels, we can reduce the state space of a Markov chain as well as the redundant computation of matrix decomposition.
IM Model Estimation Based on Importance Sampling of Trees
Importance sampling is a widely used approach for working with a distribution of interest by using another distribution that is more tractable (Robert and Casella 2013). In our case we desire coalescent trees sampled from equation (3) using MCMC, but will use a far more accessible distribution to simplify the MCMC phase of the analysis. If q is a probability density from which we can generate trees easily, then we can write
| (5) |
where if . The distribution q is called an importance sampling distribution. The above integration can be estimated using n draws from by the expression,
| (6) |
We consider two distinct posterior distributions as importance sampling distributions, neither of which depends on an underlying demographic model. The first assumes a uniform improper prior, , on the space of coalescent trees, which consists of a finite set of tree topologies and an infinite set of each of the branch lengths. This prior is noninformative and does not assume any demographic model. It follows that the sampled coalescent trees are drawn from a posterior distribution that is strictly proportional to the likelihood of the DNA sequences: With the infinite-sites mutation model for calculating the likelihood, the posterior density is a proper probability distribution and, more specifically, is a mixture of the product of gamma distributions (see the supplementary note, Supplementary Material online). When this posterior density is applied as an importance sampling distribution, the ratio in the integrand of equation (5), , is proportional to . Therefore, with a sample of , the approximation in equation (6) is simplified as
By using this importance sampling distribution q1 with improper prior f1, we sample coalescent trees mostly where the likelihood is large and hence we expect this importance sampler to be efficient.
The second type of importance sampling distribution that we consider assumes a simple single population model for which the single population size parameter, θ, is integrated out analytically. The explicit form of the prior is
where is a constant, k is the number of tips on λ, for , coalescent times on λ and , the upper incomplete gamma function. With this importance sampling distribution, , the posterior density of demographic parameters in equation (6) can be approximated as follows:
where .
In overview (fig. 2), the method has two steps: in step 1, coalescent trees are sampled from an MCMC simulation under an importance sampling distribution, independent of a demographic model of interest; while in step 2 the joint posterior probability of the demographic model of interest is calculated. Once the sample of coalescent trees has been obtained, they are used to build a function for the joint posterior density of the demographic model of interest, which in turn is used to find the maximum a posteriori (MAP) estimate of the model parameters. We used a differential evolution algorithm (Price et al. 2005) to maximize the joint posterior density, but other methods can be used. By using in step 1 a posterior distribution as an importance sampling distribution, that is free of the underlying demographic model, it is possible to study diverse demographic models without having to repeat step 1. For example, with data from two populations, the same coalescent trees sampled in step 1 can be used to examine the data under an IM model, an isolation model, an islands with migration model and an IM model with an unsampled “ghost” population (fig. 2). Another benefit is that by analytically integrating over all possible migration paths in step 2, sampling variance of migration paths is not a source of variance in parameter estimation or model choice as it is in methods that sample migration paths from an MCMC simulation.
Multiple Loci and Parameterization of Mutation Rates
We consider two parameterizations of the mutation process, one in which all loci experience the same mutation rate per site, and a second model in which each locus has its own mutation rate. The constant mutation rate model, in which the mutation rate experience by a locus is proportional to its length, is quite straightforward to implement in the MCMC sampling, even for very large numbers of loci. Under this constant mutation rate model, demographic parameters and coalescent times are scaled by the mean of per-site mutation rate. Therefore, the mutation rate is not estimated through an MCMC simulation and the approximated posterior density is as follows:
| (7) |
where is the jth sampled tree for locus i from importance sampling distribution q1. Although n coalescent trees are given for each locus, the approximation of the posterior density in equation (7) is computed from joint samples of coalescent trees for loci. This is different from other MCMC-based genealogy samplers, which generate n joint samples of genealogies for loci and some demographic parameters. In such cases the estimation of demographic parameters is computed from n joint samples of genealogies, regardless of the number of loci. In contrast, under our new method with the same amount of sampled trees (n trees per locus), estimates of demographic parameters are based effectively on joint samples. Because the number of joint samples increases exponentially with the number of loci, , and polynomially increases with the number of sample size per locus with the degree of , we expect the method to perform well even for small values of n (i.e., small numbers of sampled coalescent trees).
Under the locus-specific mutation rate model, each locus has a mutation rate scalar and the product of all mutation scalars is constrained to be 1, with demographic parameters scaled by the geometric mean of the mutation rates across loci (Hey and Nielsen 2004). Under this approach the posterior density is approximated as
Compared with the constant mutation rate model, the locus-specific mutation rate model includes mutation scalars in the Markov chain state space and requires more iterations in MCMC simulation. The posterior surface to explore in MCMC simulation is the joint probability of mutation scalars and coalescent trees. With many loci, the joint surface would be more difficult to explore, whereas in the constant mutation rate model the number of loci does not affect the number of MCMC iterations.
Results
Performance of the New Method
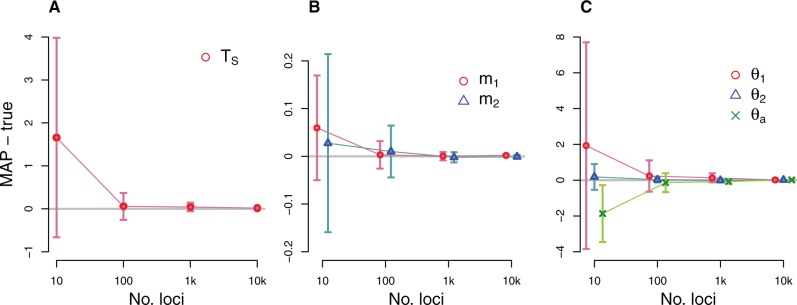
We evaluated the performance of the new method using computer simulations. We used ms (Hudson 2002) to simulate two gene copies from each of 2-population IM model with , and TS = 2 (fig. 1a), and varied the number of loci, including 10, 100, 1,000, and 10,000. For each case, 20 replicates were generated. We assumed an infinite sites mutation model (Kimura 1969) and no recombination within loci, but free recombination between loci. We also assumed that all loci have the same mutation rate. For each analysis we sampled 1,000 coalescent trees per locus after 100,000 burn-in iterations and 100 thinning iterations from the MCMC simulation. Convergence diagnostics were monitored (see supplementary Notes and supplementary figs. S1 and S2, Supplementary Material online). In step 2, the upper bounds of population sizes, migration rates and splitting time were 20, 10, and 10, respectively. The optimization of the joint posterior density yielded joint MAP estimates for all six model parameters.
As shown in figure 3, the new method provides consistent and asymptotically unbiased estimations. The mean of each parameter estimate became closer to the true value (the absolute bias ranges between 0.009 and 0.016 on 10,000-locus data) and the standard errors (range: 0.0028–0.0699 on 10,000-locus data) were also substantially reduced as the number of loci increases. The mean squared errors (MSEs) consisting of bias and variance of estimators were strictly decreasing with the number of loci (see supplementary table S1, Supplementary Material online). The overall accuracy of all parameter estimations was quite high with just 100 loci, and estimates were very close to the true values with 1,000 or more loci.
Fig. 3.
Simulation results illustrating the performance of the new method for a 2-population IM model. The true IM model has parameters TS = 2, and . DNA sequences were simulated over a range of loci numbers. For each plot, the x axis for numbers of loci is on a log scale. The difference between the true value and the mean of the estimated values are plotted (gray horizontal line at 0), and vertical dashed lines indicate standard errors. The average of MAP estimations from 20 replicates, each with 1,000 coalescent trees per locus sampled in step 1, are compared with the true parameters. (a) The average difference between MAP estimates and the true splitting time. (b) The average differences for migration parameters. (c) The average differences for the population size parameters for sampled and ancestral populations.
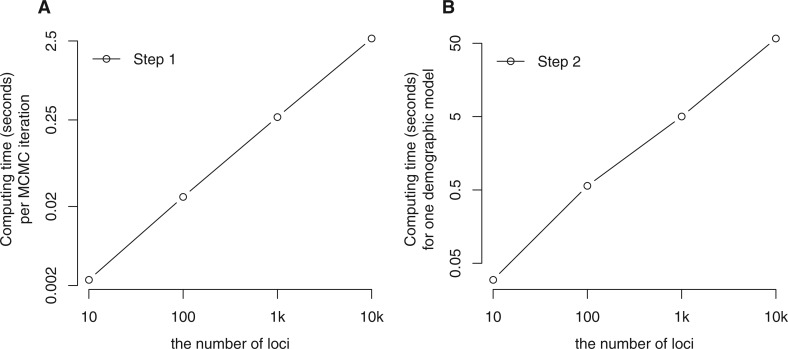
We also assessed the performance of MIST in terms of computing time. At each iteration of MCMC simulation in step 1, one coalescent tree of four gene copies from each locus is simulated. Thus, the CPU time in serial computing of each iteration is proportional to the number of loci (fig. 4a). In step 2, when the posterior probability of a given demographic model is approximated from a set of coalescent trees, a matrix decomposition is required to compute the probability of a coalescent tree. To avoid repeated computation, matrix decomposition is done for each ranked tree topology with population labels. In this simulation study, there are seven possible ranked tree topology with population labels when two gene copies were sampled from each population. Then we need to do matrix decomposition for these trees no matter how many loci are analyzed and how many trees are sampled from an MCMC simulation. In our analyses, the computing time of matrix decomposition was constant as 0.02 s for the case of four sequences. Given the result of matrix decomposition, the CPU time of computing the posterior probability is proportional to the number of loci in a serial computation (fig. 4b). In parallel computing, the computing time of both steps is substantially reduced (see supplementary table S2, Supplementary Material online) and this method is appropriate to analyze many loci.
Fig. 4.
The average CPU time for a single CPU (serial computation) in Step 1 and Step 2 of the new method as a function of the number of loci with four gene copies. (a) The mean CPU time for one iteration of MCMC simulation (Step 1), including proposal and evaluation of an update for each locus. Both axes are on a log scale. (b) The mean CPU time for completing the posterior probability calculation (Step 2) for a single set of demographic parameter values, given sampled coalescent trees from multiple loci. Both axes are on a log scale.
Evaluation of Importance Samplers
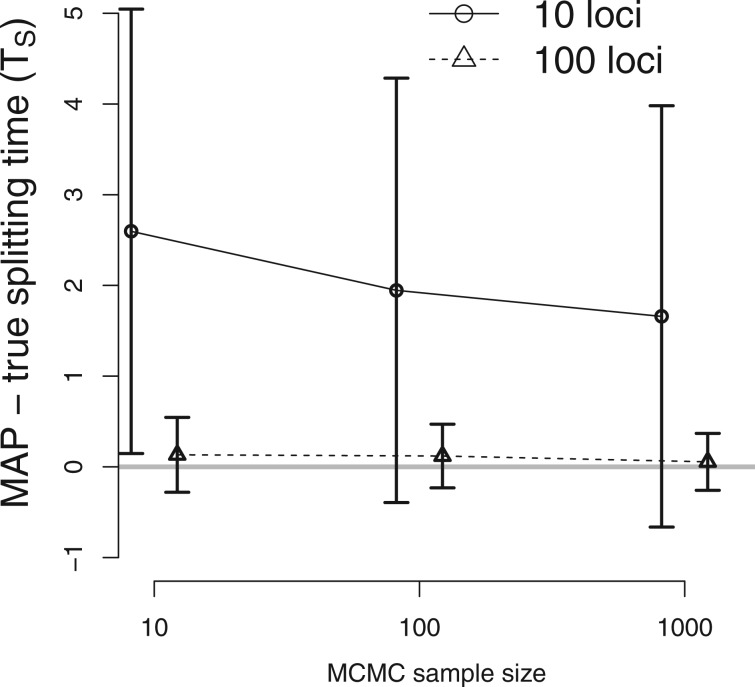
In order to assess the effect of MCMC sample size (i.e., the number of sampled coalescent trees per locus), we returned to the simulated data used for the analysis in figure 3 and generated 10 and 100 coalescent trees per locus after 100,000 burn-in iterations and 100 thinning iterations through MCMC simulations separately. Demographic parameters were estimated from sets of coalescent trees with different sizes to evaluate the performance of the new method as a function of sample size. As expected, larger samples and more loci lead to better estimates, however the accuracy of the estimates were fairly insensitive to the number of sampled coalescent trees, with estimates based on 10 trees per locus being nearly as good as those for samples of 100 or more (fig. 5; supplementary fig. S3, Supplementary Material online). The reason for this good performance with small MCMC sample size is that joint samples were used to approximate the posterior density of from n coalescent trees sampled from each of loci (eq. 7). Thus, the number of joint samples increases exponentially with the number of loci and increases polynomially with the order of the number of loci as the MCMC sample size per locus increases. Therefore, the new method using importance sampling requires a much smaller size of MCMC samples than standard MCMC samplers.
Fig. 5.
The performance of the new method as a function of MCMC sample size. The true IM model has parameters TS = 2, , and . The difference between the true splitting time and the mean of the estimated values are plotted (gray horizontal line at 0), and vertical lines indicate standard errors. DNA sequences were simulated for 10 loci ( and real line) and 100 loci ( and dashed line). The x axis for MCMC sample size is on a log scale. The estimates of other parameters are shown on supplementary figure S3, Supplementary Material online.
We also compared the performance when using the importance sampling distribution assuming an improper prior, , with the performance when using a single population model for the importance sampling distribution, . We analyzed the same simulated data sets that resulted in figure 3, but using importance sampling distribution with an upper bound of 20 for the single population size. As before, we sampled 1,000 coalescent trees per locus following 100,000 burn-in iterations. The accuracy of the estimates made using (see supplementary fig. S4, Supplementary Material online) are very similar to those found using the improper prior (fig. 3). However, the efficiency of the importance sampling distribution q2 depends on the upper bound for the single population size (see supplementary fig. S5, Supplementary Material online). For example, when a small upper bound is assumed, trees with short branches would be mostly sampled (see supplementary fig. S6, Supplementary Material online). In this case, a much larger MCMC sample size is required to achieve the same performance with that using the improper prior.
Demographic Model Inference with and without Ghost Population
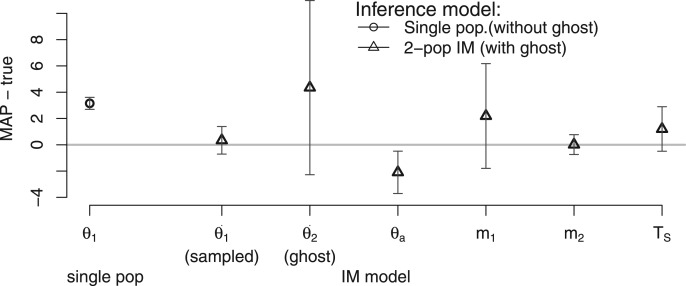
Once a sample of coalescent trees has been obtained, it can be used for analyses under multiple different demographic models, without having to resort to additional MCMC simulations. As an example, we analyzed simulated data sampled from a single population under both a single population model and a two-population IM model. For the simulation we generated 20 data sets, each with 50 loci and four gene copies from a single population which shares migrants with another unsampled population, a so-called “ghost” population. Thus both the sampled and unsampled populations occur in an IM model (fig. 1a) with parameters, (sampled population), (ghost), and TS = 4. In step 1, 10,000 coalescent trees for each locus were sampled after 100,000 burn-in iterations and 100 thinning iterations from MCMC simulation. In step 2, the same set of coalescent trees was used repeatedly to infer two evolutionary scenarios: (1) a single population that has not shared migrants with other populations; and (2) an IM model in figure 1a where the population of size θ2 was considered as “ghost”.
Under the single population model, the population size estimate of 4.15 was much larger than the true size of 1 (fig. 6). When an IM model was inferred, the estimated sampled population size was 1.338, much closer to the true value, and overall the estimates of the IM model parameters were accurate (fig. 6). Since we did not sample the ghost population, the standard error for the ghost population size was large, but the confidence interval contains the true value. For model comparison, we used Akaike’s information criterion (AIC), and in 18 out of 20 replicates the IM model was selected rather than a single population model (see supplementary table S3, Supplementary Material online).
Fig. 6.
Estimation of demographic model with and without ghost population. The true simulation model is a 2-population IM model (, TS = 4) and we simulated DNA sequences from the population of size θ1. That is, the other population of size θ2 is a “ghost” population. Two demographic models were estimated: a single population model ( and IM model with ghost population ( Symbols represent the average difference over 20 replicates between MAPs and the true value. Bars represent the standard errors of parameter estimations.
False Positives of Likelihood Ratio Tests
The new method maximizes the joint posterior distribution, which is proportional to the joint likelihood when the prior distribution on demographic parameters is constant. Thus when working with uniform priors, and given a single sample of coalescent trees in step 1, the method can compare the maximum joint likelihoods, L0 and L1, under null (nested) and alternative (full) models, respectively (see also Nielsen and Wakeley 2001; Hey and Nielsen 2007).
Recently, a widely used method (implemented in IMa2) for LRTs for nested IM model comparisons (Hey and Nielsen 2007) was shown to exhibit high false positive rates when actual divergence is low and the amount of data is not large (Cruickshank and Hahn 2014). The cause of the high false positive rate was later shown to be largely due to the LRT being based on a marginal density that was not joint with the splitting time parameter and population sizes in the IM model. Hey et al. (2015) were able to generate a fully joint surface for a reduced model of three parameters, and showed that the observed distribution of the LRT test statistic followed the asymptotic distribution much more closely, and that the high false positive rate was much closer to target rate. Thus, because our new method estimates a joint posterior density in all demographic parameters, we were particularly interested in its LRT performance under the small data, low divergence context that exhibited high false positive rates for Cruickshank and Hahn (2014). We simulated 2, 10, 100, and 1,000 loci of two gene copies from each of two populations under recently diverged isolation models with and or . We considered two low values for TS, including a value of effectively zero, , and a value of which was used by Cruickshank and Hahn (2014) and Hey et al. (2015). For each case we simulated 100 replicates. In step 1, 1,000 coalescent trees for each locus were sampled after 100,000 burn-in and 100 thinning iterations. In step 2, the joint likelihoods are maximized under an isolation model (no migration) with same population sizes (null model) and an IM model with same population sizes and same migration rates (alternative model) using the same set of trees. We computed the LRT statistic for each case. The difference in the number of parameters between two models is 1.
Typically, when comparing two models that differ by one parameter the appropriate asymptotic distribution of LRT statistic is the -distribution with 1 degree of freedom. However for the present case of the true parameter value equal to zero and on the boundary of the parameter space, the asymptotic distribution is a mixture distribution of zero with probability 0.5 and with probability 0.5 (Chernoff 1954; Self and Liang 1987). That is, we expect a half of LRTs to be zero when . Therefore, we examined the proportion of zero LRTs and the false positive rates using two critical values, 2.705 and 3.841, from the mixture and original distributions with significance level 5%.
Table 2 shows the false positive rates and the proportion of zero values of LRTs. When the true splitting time is near zero, the results show a false positive rate close to the expected rate. On 1,000-locus data sets, the LRT statistic seems to follow the mixture distribution (see supplementary fig. S10, Supplementary Material online): the false positive rate is 2% and 52% of data sets have zero LRTs. In this case, the original test with distribution shows conservative results. Although the false positive rate on 100-locus case is elevated, those on smaller data sets are 5% or less. The proportions of zero LRTs on 100-locus or smaller data sets are 12–34%, lower than the expected proportion of 50%. When the true model has a splitting time of , the MAPs of the parameters under isolation model and IM model, respectively, come closer to the true values with more loci (see supplementary table S5, Supplementary Material online). However, we observed some elevation of false positives (table 3), though much smaller than when TS is not in the joint distribution (Cruickshank and Hahn 2014), with LRT values seeming to depart from the mixture distribution which is the limiting distribution of LRT when the number of loci goes to the infinity (see supplementary fig. S10, Supplementary Material online). The false positive rates on 2-locus and 100-locus cases are smaller than 5% but larger than 5% on 10-locus and 1000-locus cases. The proportions of zero LRTs range from 28% to 34%. When the null hypothesis is rejected, migration rate and splitting time are always overestimated and the population size is underestimated (see supplementary fig. S9, Supplementary Material online). This pattern indicates that the divergence of sequences under IM models with such large splitting time and migration rate is similar to that of the simulation model of zero migration rate and small splitting time.
Table 2.
False Positive Rates under Very Low Divergence.
| No. loci | 2 | 10 | 100 | 1,000 |
|---|---|---|---|---|
| False positive rate (mixture) | 0.01 | 0.05 | 0.11 | 0.02 |
| False positive rate () | 0.01 | 0.02 | 0.05 | 0.01 |
| Proportion of zero LRTs | 0.25 | 0.12 | 0.34 | 0.52 |
Note.—False positive rates of LRTs for migration rate are computed when the mixture distribution or an original are considered as a null distribution. The proportions of zero values of LRTs are computed as well. The true simulation model is the 2-population isolation models with and , respectively. The number of loci varies from 2 to 1,000, and two gene copies are simulated from each population.
Table 3.
False Positive Rates under Intermediate Divergence.
| No. loci | 2 | 10 | 100 | 1,000 |
|---|---|---|---|---|
| False positive rate (mixture) | 0.03 | 0.14 | 0.03 | 0.13 |
| False positive rate () | 0.01 | 0.06 | 0.03 | 0.10 |
| Proportion of zero LRTs | 0.34 | 0.29 | 0.33 | 0.28 |
Note.—False positive rates of LRTs for migration rate are computed when the mixture distribution or an original are considered as a null distribution. The proportions of zero values of LRTs are computed as well. The true simulation model is the 2-population isolation model with and . The number of loci varies from 2 to 1,000, and two gene copies are simulated from each population.
Evolutionary History of Western and Central Common Chimpanzees
We applied the new method to the demographic history of two common chimpanzee subspecies, Pan troglodytes (P. t.) troglodytes from Central Africa and P. t. verus from West Africa. These subspecies have been studied previously using IM models with small numbers of loci (Won and Hey 2005; Hey 2010a; Becquet and Przeworski 2007). These and other studies (Wegmann and Excoffier 2010; Caswell et al. 2008) reported finding a signal of gene exchange between the subspecies with a divergence times of several hundred thousand years.
We aligned three sequences from each of two subspecies from the great ape genome project (Prado-Martinez et al. 2013) by using the human genome reference (version 18). We partitioned the whole genome into nonoverlapping segments of size 10,000 bps and selected 1,000 segments at random. In order to minimize a potential influence from recombination within a locus, each segment was separated into haplotype blocks using the four-gamete criterion (Hudson and Kaplan 1985) and one block was selected at random from each segment. The average length of 1,000 loci was 4,206 base pairs. In step 1 of the analysis, an improper prior was assumed and 3,000 coalescent trees, scaled by per-site mutation rate, were sampled every 100 iterations after a burn-in of 100,000 iterations for each locus. Several MCMC diagnostics was carried out to ensure convergence (see supplementary Note and Supplementary figs. S7 and S8, Supplementary Material online). In step 2, we estimated three population sizes of each of P. t. troglodytes and P. t. verus and their common ancestor, two migration rates and divergence time of them. The upper bounds for population sizes, divergence time and migration rates were 0.1, 0.01, and 1000, respectively. We used 48 CPUs for the step 1 analysis and it took around 3 h. The step 2 analysis took around 17 h on 196 CPUs.
The estimated demographic parameter values by MIST were (P. t. troglodytes), (P. t. verus), , and =2.573e-10. Using a per-site mutation rate per generation of and assuming 20 years per generation, we converted the estimates on a demographic scale. Table 4 shows the converted estimates obtained with MIST using 1,000 loci together with estimates from previous studies that used an IM model. These include Won and Hey (2005) and Hey (2010a) who used a 6-parameter IM model with 48 and 73 loci, respectively, and Becquet and Przeworski (2007) who analyzed 68 loci using a 5-parameter IM model with a single symmetric migration rate. All of these studies are broadly consistent with each other and suggest a model in which P. t. troglodytes is estimated to be about four times larger than that θ2 of P.t. verus, with gene flow occurring since their separation several hundred thousand years ago. Our new estimate of the migration rate m1 from P. t. verus to P. t. troglodytes (forward in time) is larger than previously reported (), but our estimate of m2 for the opposite direction is very close to zero (), which is consistent with Won and Hey (2005). In contrast Hey (2010a) reported a significant migration rate m2 under a 2-population IM model and Becquet and Przeworski (2007) reported a bidirectional rate of where . Overall the estimated model under the new method is consistent with results from previous studies. It is useful to note that all of these previous studies generated estimates from the marginal posterior distributions, whereas our analysis using MIST provides an estimate based on the full joint posterior density.
Table 4.
Estimation of Demography for Two Chimpanzee Subspecies.
| Methods | MIST | Won & Hey (2005)a | Hey (2010a)b | Becquet et al. (2007)c | |
| No. loci | 1,000 | 50 | 73 | 68 | |
| P. t. troglodytes (Ptt) Ne | 27,081.38 | 27,900 | 27,832.67 | 33,000 | |
| P. t. verus (Ptv) Ne | 6,342.3 | 7,600 | 7191.48 | 9,750 | |
| Common ancestor Ne | 10,808.71 | 5,300 | 8,399.21 | 15,000 | |
| Splitting time (years) | 347,732 | 422,000 | 410,000 | 439,000 | |
| Migration rate per generation | |||||
| from Ptt to Ptv | 1.621e-5 | 9.2115e-6 | 9.108e-6 | – | |
| from Ptv to Ptt | 5.147e-18 | 1.1842e-7 | 7.0496e-6 | – | |
Note.—Maximum a posteriori estimates of demography for P. t. troglodytes and P. t. verus from 3,000 loci of six sequences are compared with the estimates of previous studies. Model parameter estimates are shown on a demographic scale, using a per-site mutation rate per generation of and assuming 20 years per generation. Migration rates are backward in time.
IMa2(Hey and Nielsen 2007) was applied
Geometric mean of mutation rate per locus per generation of 7.808e-6 and 15 years per generation were assumed
Geometric mean of mutation rate per locus of 9.108e-6 and 20 years per generation were used.
MIMAR (Becquet and Przeworski 2007) was applied. The per-site mutation rate per generation of and 20 years per generation assumed.
Discussion
MCMC-based Isolation-with-Migration analyses have come to play a critical role in the analysis of population structure and of recent speciation events (Gronau et al. 2011; Pinho and Hey 2010; Schraiber and Akey 2015; Payseur and Rieseberg 2016; Hey and Pinho 2012). The innovations presented here will enable the inclusion of larger portions of the genome, and provide a path for studying a wider range of demographic and phylogenetic models.
A major roadblock for existing MCMC based approaches that allow for extensive gene flow and population splitting is the non-independence of loci in demographic models with multiple time epochs. It is the updating of these epochs (e.g., splitting time Ts) that must be done jointly for all loci, and that causes low acceptance rates in the Markov chain simulation when there are large numbers of loci (Wang and Hey 2010). By using importance sampling of coalescent trees and removing the underlying demographic model from the MCMC phase of the study, the MCMC update and sampling processes in the new method can treat loci independently.
Another major hurdle for MCMC-based methods that include migration over wide time periods are the complexities and time required to appropriately update genealogies that include migration paths. Our new approach includes an exact accounting of all possible migration path histories in the second phase of the analysis, allowing for the removal of migration paths from the MCMC phase and allowing for the importance sampling approach that does not rely upon an underlying demographic model.
With a simpler Markov chain simulation that treats loci independently, we have no need for the use of metropolis-coupling (Geyer 1991) or parallel tempering methods (Swendsen and Wang 1986) that rely upon running multiple heated chains. In our experience a single Markov chain simulation for as many as 10,000 loci proceeds smoothly without mixing difficulty.
The emphasis on problems with large numbers of loci and small numbers of gene copies per locus is appropriate for many demographic problems, for which the optimal sampling effort favors more loci over more gene copies per locus (Felsenstein 2006; Hey 2010b; Cruickshank and Hahn 2014; Hey et al. 2015). The new method is designed to scale well with the number of loci, but limited to low numbers of gene copies per locus because the computing times and required memory size grows exponentially with the number of gene copies per locus (see supplementary table S4, Supplementary Material online). In the calculation of the posterior probability in the second step of the analyses, MIST implemented the new method employs transition rate matrices that are constructed for the unique ranked tree topologies with population labels among the sampled coalescent trees. The number of ranked tree topologies exponentially increases with the number of gene copies (Semple and Steel 2003) and the sizes of transition rate matrices for each ranked tree topology are exponentially growing with the number of gene copies as well (Andersen et al. 2014). For example, there are 7,248 unique ranked tree topologies on eight gene copies, whereas seven unique ranked tree topologies on four gene copies. The CPU times and physical memory usages in step two rapidly increased from 4 to 8 gene copies (see supplementary table S4, Supplementary Material online).
The new method is also unique in efficiently providing the joint MAP estimate of any given demographic model and for allowing model comparisons based on joint MAP estimates obtained under different models. In the case of Bayesian methods that sample demographic parameter values from an MCMC simulation, it has generally not been feasible to estimate a posterior density in many dimensions, and most analyses are limited to estimates of a marginal posterior density for each parameter using histograms built from the sampled parameter values. For example, LRTs of migration rates using IMa2 exhibit high false positive rates in cases of low divergence and small sample sizes (Cruickshank and Hahn 2014), and this has been shown to largely be a consequence of using marginal distributions (Hey et al. 2015).
By sampling only coalescent trees, the new method does not rely upon histograms of sampled parameter values, but instead generates a function equation (6) that is an estimate of the joint distribution over all demographic parameters. LRTs of migration rates using the new method show false positive rates close to those expected of the limiting case for the null distribution of the LRT statistic, even for very low divergence.
Supplementary Material
Supplementary data are available at Molecular Biology and Evolution online.
Supplementary Material
Acknowledgments
We thank Vitor Sousa for helpful discussion on an early version of the new method and Arun Sethuraman for writing a part of codes of MIST. This research was supported under NIH grant R01GM078204 to J.H.
References
- Andersen LN, Mailund T, Hobolth A.. 2014. Efficient computation in the im model. J Math Biol. 686: 1423–1451. [DOI] [PubMed] [Google Scholar]
- Asmussen S. (2003). Applied probability and queues. New York, NY: Springer-Verlag. [Google Scholar]
- Bahlo M, Griffiths RC.. 2000. Inference from gene trees in a subdivided population. Theor Popul Biol. 572:79–95. [DOI] [PubMed] [Google Scholar]
- Becquet C, Przeworski M.. 2007. A new approach to estimate parameters of speciation models with application to apes. Genome Res. 1710:1505–1519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beerli P, Felsenstein J.. 1999. Maximum-likelihood estimation of migration rates and effective population numbers in two populations using a coalescent approach. Genetics 1522:763–773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berner D, Grandchamp AC, Hendry AP.. 2009. Variable progress toward ecological speciation in parapatry: stickleback across eight lake-stream transitions. Evolution 637:1740–1753. [DOI] [PubMed] [Google Scholar]
- Caswell JL, Mallick S, Richter DJ, Neubauer J, Schirmer C, Gnerre S, Reich D.. 2008. Analysis of chimpanzee history based on genome sequence alignments. PLoS Genet. 44:e1000057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chernoff H. 1954. On the distribution of the likelihood ratio. Ann Math Statist. 253:573–578. [Google Scholar]
- Cong Q, Borek D, Otwinowski Z, Grishin NV.. 2015. Tiger swallowtail genome reveals mechanisms for speciation and caterpillar chemical defense. Cell Rep. 106:910–919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cruickshank TE, Hahn MW.. 2014. Reanalysis suggests that genomic islands of speciation are due to reduced diversity, not reduced gene flow. Mol Ecol. 2313:3133–3157. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. 1988. Phylogenies from molecular sequences: inference and reliability. Annu Rev Genet. 221:521–565. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. 2006. Accuracy of coalescent likelihood estimates: do we need more sites, more sequences, or more loci?. Mol Biol Evol. 233:691–700. [DOI] [PubMed] [Google Scholar]
- Geraldes A, Basset P, Gibson B, Smith KL, Harr B, Yu HT, Bulatova N, Ziv Y, Nachman MW.. 2008. Inferring the history of speciation in house mice from autosomal, x-linked, y-linked and mitochondrial genes. Mol Ecol. 1724:5349–5363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geyer CJ. (1991). Markov chain Monte Carlo maximum likelihood. Computing Science and Statistics. Proceedings of the 23rd Symposium on the Interface, p. 156–163.
- Griffiths RC. 1989. Genealogical-tree probabilities in the infinitely-many-site model. J Math Biol. 276:667–680. [DOI] [PubMed] [Google Scholar]
- Griffiths RC, Tavaré S.. 1994. Simulating probability distributions in the coalescent. Theor Popul Biol. 46:131–159. [Google Scholar]
- Gronau I, Hubisz M, Gulko B, Danko C, Siepel A.. 2011. Bayesian inference of ancient human demography from individual genome sequences. Nat Genet. 4310:1031–1034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hey J. 2010a. The divergence of chimpanzee species and subspecies as revealed in multipopulation isolation-with-migration analyses. Mol Biol Evol. 274:921–933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hey J. 2010b. Isolation with migration models for more than two populations. Mol Biol Evol. 274:905–920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hey J, Nielsen R.. 2004. Multilocus methods for estimating population sizes, migration rates and divergence time, with applications to the divergence of Drosophila pseudoobscura and D. persimilis. Genetics 1672:747–760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hey J, Nielsen R.. 2007. Integration within the Felsenstein equation for improved Markov chain Monte Carlo methods in population genetics. Proc Natl Acad Sci USA 1048:2785–2790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hey J, Pinho C.. 2012. Population genetics and objectivity in species diagnosis. Evolution 665:1413–1429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hey J, Chung Y, Sethuraman A.. 2015. On the occurrence of false positives in tests of migration under an isolation-with-migration model. Mol Ecol. 2420:5078–5083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hobolth A, Andersen LN, Mailund T.. 2011. On computing the coalescence time density in an isolation-with-migration model with few samples. Genetics 1874:1241–1243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson RR. 2002. Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics 182:337–338. [DOI] [PubMed] [Google Scholar]
- Hudson RR, Kaplan NL.. 1985. Statistical properties of the number of recombination events in the history of a sample of DNA sequences. Genetics 1111:147–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M. 1969. The number of heterozygous nucleotide sites maintained in a finite population due to steady flux of mutations. Genetics 61:893–903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhner MK. 2008. Coalescent genealogy samplers: windows into population history. Trends Ecol Evol. 242:86–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhner MK, Yamato J, Felsenstein J.. 1995. Estimating effective population size and mutation rate from sequence data using metropolis-hastings sampling. Genetics 1404:1421–1430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopes JS, Balding D, Beaumont MA.. 2009. PopABC: a program to infer historical demographic parameters. Bioinformatics 2520:2747–2749. [DOI] [PubMed] [Google Scholar]
- Moodley Y, Linz B, Yamaoka Y, Windsor HM, Breurec S, Wu JY, Maady A, Bernhöft S, Thiberge JM, Phuanukoonnon S, et al. 2009. The peopling of the pacific from a bacterial perspective. Science 3235913:527–530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen R. 2000. Estimation of population parameters and recombination rates from single nucleotide polymorphisms. Genetics 1542:931–942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen R, Wakeley J.. 2001. Distinguishing migration from isolation: a Markov chain Monte Carlo approach. Genetics 1582:885–896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payseur BA, Rieseberg LH.. 2016. A genomic perspective on hybridization and speciation. Mol Ecol. 2511:2337–2360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinho C, Hey J.. 2010. Divergence with gene flow: models and data. Annu Rev Ecol Evol Syst. 411:215–230. [Google Scholar]
- Prado-Martinez J, Sudmant PH, Kidd JM, Li H, Kelley JL, Lorente-Galdos B, Veeramah KR, Woerner AE, O’Connor TD, Santpere G, et al. 2013. Great ape genetic diversity and population history. Nature 499:471–475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price K, Storn R, Lampinen J. (2005). Differential evolution: a practical approach to global optimization. New York: Springer. [Google Scholar]
- Robert CP, Casella G. (2013). Monte Carlo statistical methods. New York: Springer Science & Business Media. [Google Scholar]
- Schraiber JG, Akey JM.. 2015. Methods and models for unravelling human evolutionary history. Nat Rev Genet. 1612:727–740. [DOI] [PubMed] [Google Scholar]
- Self SG, Liang KY.. 1987. Asymptotic properties of maximum likelihood estimators and likelihood ratio tests under nonstandard conditions. J Am Stat Assoc. 82398:605–610. [Google Scholar]
- Semple C, Steel M. (2003). Phylogenetics. New York, NY: Oxford University Press. [Google Scholar]
- Swendsen RH, Wang JS.. 1986. Replica Monte Carlo simulation of spin-glasses. Phys Rev Lett. 5721:2607. [DOI] [PubMed] [Google Scholar]
- Wang Y, Hey J.. 2010. Estimating divergence parameters with small samples from a large number of loci. Genetics 1842:363–379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wegmann D, Excoffier L.. 2010. Bayesian inference of the demographic history of chimpanzees. Mol Biol Evol. 276:1425–1435. [DOI] [PubMed] [Google Scholar]
- Wilson IJ, Balding DJ.. 1998. Genealogical inference from microsatellite data. Genetics 1501:499–510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Won YJ, Hey J.. 2005. Divergence population genetics of chimpanzees. Mol Biol Evol. 222:297–307. [DOI] [PubMed] [Google Scholar]
- Zhu T, Yang Z.. 2012. Maximum likelihood implementation of an isolation-with-migration model with three species for testing speciation with gene flow. Mol Biol Evol. 2910:3131–3142. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.