Bad Clade Deletion Supertrees: A Fast and Accurate Supertree Algorithm

Abstract

Supertree methods merge a set of overlapping phylogenetic trees into a supertree containing all taxa of the input trees. The challenge in supertree reconstruction is the way of dealing with conflicting information in the input trees. Many different algorithms for different objective functions have been suggested to resolve these conflicts. In particular, there exist methods based on encoding the source trees in a matrix, where the supertree is constructed applying a local search heuristic to optimize the respective objective function. We present a novel heuristic supertree algorithm called Bad Clade Deletion (BCD) supertrees. It uses minimum cuts to delete a locally minimal number of columns from such a matrix representation so that it is compatible. This is the complement problem to Matrix Representation with Compatibility (Maximum Split Fit). Our algorithm has guaranteed polynomial worst-case running time and performs swiftly in practice. Different from local search heuristics, it guarantees to return the directed perfect phylogeny for the input matrix, corresponding to the parent tree of the input trees, if one exists. Comparing supertrees to model trees for simulated data, BCD shows a better accuracy (F₁ score) than the state-of-the-art algorithms SuperFine (up to 3%) and Matrix Representation with Parsimony (up to 7%); at the same time, BCD is up to 7 times faster than SuperFine, and up to 600 times faster than Matrix Representation with Parsimony. Finally, using the BCD supertree as a starting tree for a combined Maximum Likelihood analysis using RAxML, we reach significantly improved accuracy (1% higher F₁ score) and running time (1.7-fold speedup).

Introduction

When reconstructing large scale phylogenies from molecular data, it is common practice to combine multiple loci (e.g. genes); as not every loci is available for every taxon, methods have to deal with incomplete data. Doing so is possible on different levels (Schmidt 2003; Kupczok et al. 2010): Low-level approaches (total evidence, supermatrix, superalignment, combined analysis) combine multiple genes on the sequence level by concatenating the alignments of the different genes; gaps in the resulting data matrix correspond to missing data. The resulting supermatrix can be analyzed by conventional tree reconstruction methods such as Maximum Parsimony (MP) (Fitch 1971), Maximum likelihood (ML) (Felsenstein 1981) or Bayesian inference (Yang and Rannala 1997). Medium-level strategies combine the loci on a further processed analysis stage than concatenating the raw sequence data, but do not estimate a complete tree for each locus. Such stages can e.g. be quartets (Strimmer and von Haeseler 1996; Schmidt et al. 2002) or distance matrices (Criscuolo et al. 2006). High-level approaches estimate a phylogenetic tree for each gene independently, and these gene trees are combined using a supertree method. These methods assemble phylogenetic trees with nonidentical but overlapping taxon sets into one supertree that contains all taxa of the source trees. Constructing a supertree from nonconflicting source trees is easy (Aho et al. 1981), whereas resolving such conflicts in a reasonable way, usually results in NP-hard optimization problems. Many supertree approaches have been proposed over the years; some of them may return multiple supertrees which than have to be combined (Baum 1992; Ragan 1992), or may return supertrees not containing all taxa (Scornavacca et al. 2008). See Bininda-Emonds (2004) for early methods, and (Ross and Rodrigo 2004; Chen et al. 2006; Criscuolo et al. 2006; Cotton and Wilkinson 2007; Holland et al. 2007; Scornavacca et al. 2008; Steel and Rodrigo 2008; Bansal et al. 2010; Ranwez et al. 2010; Snir and Rao 2010; McMorris and Wilkinson 2011; Swenson et al. 2012; Berry et al. 2013; Brinkmeyer et al. 2013; Markin and Eulenstein 2016; Vachaspati and Warnow 2016) for recent ones. One basic principle that many supertree methods share is a Matrix Representation of the source trees. A Matrix Representation (MR) encodes inner nodes (or branches) of all source trees as partial binary characters in a matrix, which is then analyzed using an optimization or agreement criterion to yield the supertree. Matrix Representation with Parsimony (MRP) (Baum 1992; Ragan 1992) was among the earliest methods proposed but remains the most frequently used. Despite its computational complexity (Foulds and Graham 1982), heuristics have been developed that allow data sets with several hundred taxa to be analyzed in reasonable time. On the theoretical side, MRP has certain undesirable properties, such as introducing clades into the supertree that are contradicted by all source trees (Bininda-Emonds and Bryant 1998; Pisani and Wilkinson 2002; Wilkinson, Pisani, et al. 2005), and its nonconvergence to the true tree for arbitrarily large sets of input trees (Steel and Rodrigo 2008). Matrix Representation with Flipping (MRF) (Chen et al. 2006) tries to resolve incompatibilities by flipping “0/1”-entries in the matrix. Finding a tree that with a minimum number of flips is again NP-hard but also W[2]-hard, and has no constant factor approximation unless P = NP (Böcker et al. 2011). Brinkmeyer et al. (2013) introduced a top-down heuristic FlipCut for MRF, which has guaranteed polynomial running time, and outperformed other polynomial-time supertree methods (Semple and Steel 2000; Page 2002; Willson 2004; Scornavacca et al. 2008) with regards to supertree accuracy and running time (Brinkmeyer et al. 2010, 2013). Matrix representation with Compatibility (MRC) (Purvis 1995; Rodrigo 1996; Ross and Rodrigo 2004), also known as Maximum Split Fit (SFIT) (Creevey and Mcinerney 2005), searches for the largest compatible subset of matrix columns in the MR. The MRC problem is again NP-hard, and it is likely that no PTAS exists (Badger et al. 2004; Böcker et al. 2011). MRC can be reduced to the Maximum Clique problem on the compatibility graph, or to the Maximum Independent Set problem on the incompatibility graph of the matrix. MRC (SFIT) generalizes asymmetric median consensus methods Wilkinson, Cotton, et al. (2005). Swenson et al. (2012) introduced the meta-method SuperFine which uses the Greedy Strict Consensus Merger (GSCM) (Huson, Vawter, et al. 1999; Roshan et al. 2003) as preprocessing to improve an arbitrary supertree method. SuperFine with MRP was superior to the other evaluated SuperFine variants, namely SuperFine with Quartets MaxCut (QMC) (Snir and Rao 2010) and SuperFine with Matrix Representation with Likelihood (MRL) (Nguyen et al. 2012). To this end, “SuperFine” will refer to the “SuperFine with MRP” method throughout the rest of this paper.

Conflicts in the source trees are either caused by estimation (sampling) errors, or by differing evolutionary processes of the combined genes. The later problem is known as the gene tree species tree reconciliation problem. Classical supertree and supermatrix methods where complemented by methods that incorporate evolutionary processes such as the coalescent process (Liu et al. 2009, 2010; Larget et al. 2010; Liu and Yu 2011; Mirarab et al. 2014; Whidden et al. 2014; Allman et al. 2016). Reconciliation approaches model the evolutionary process more thoroughly than standard supermatrix and supertree methods, but do not scale well with the number of taxa.

For NP-hard tree reconstruction methods (e.g. ML and MP), local search heuristics, such as hill climbing, have to be used to estimate phylogenetic trees in reasonable time. The starting tree for a local search heuristic is crucial for its accuracy and running time. ML implementations, which are widely used for the supermatrix approach commonly use Neighbor Joining and related methods to quickly find a starting tree of sufficient quality.

For large scale phylogenies, these local search heuristics may no longer converge in reasonable time. Furthermore, Sievers et al. (2013) observed that the quality of multiple sequence alignments decreases with increasing number of taxa. Combining overlapping input data with supertree methods does not require a multiple sequence alignment nor a ML analysis for all taxa simultaneously. In this context, supertree methods can be used as part of divide-and-conquer meta-techniques (Huson, Nettles, et al. 1999; Huson, Vawter, et al. 1999; Roshan et al. 2004; Nelesen et al. 2012), which break down a large phylogenetic problem into smaller subproblems that are computationally easier to solve. The subproblem results are combined using a supertree method. Different from combining incomplete gene-based source trees, conflicts between the source trees will mainly result from sampling errors for this approach.

New Approach

Here, we introduce the Bad Clade Deletion (BCD) supertree algorithm, a polynomial time top-down heuristic that minimizes the number of column (character) deletions of a MR (Baum-Regan encoding), so that the resulting matrix allows for a directed perfect phylogeny (Pe’er et al. 2004). Minimizing the number of columns to delete (minimum vertex cover on the incompatibility graph) is complementary to maximizing the number of characters to keep (maximum independent set), which is the objective function of MRC (SFIT). Hence, the optimal solution for one of these problems is also an optimal solution for the other one; both optimization problems are NP-hard, but not identical with respect to parameterized complexity and approximability. BCD modifies FlipCut for this objective function and inherits its worst-case running time (O(mn³)), but is even faster in practice. We integrate meta-information (bootstrap values, branch lengths) and reliable clades into BCD, to further improve its speed and accuracy. In detail, we use the Greedy Strict Consensus Merger Fleischauer and Böcker (2016) to calculate the set of reliable clades.

BCD computes supertrees without branch length, but reports the weighted split fit for each clade in a supertree. This cannot be interpreted as evolutionary distance, but provides information about confidence of a clade. For a fixed supertree topology, branch length can be estimated using, for example, the method of Binet et al. (2016).

In our in-depth evaluation using simulated data, BCD outperforms MRP (up to 7%) and SuperFine (up to 3%) with respect to F₁ score. At the same time, BCD is up to 7 times faster than SuperFine and up to 600 times faster than MRP; this combination of accuracy and speed has never before been achieved by a supertree method. Finally, using a BCD supertree as the starting tree for a combined ML analysis can improve results: In our evaluation, the ML analysis was 1.7 times faster and reached a 1% higher F₁ score when using the BCD starting tree instead of the default starting tree, resulting in the most accurate trees over all evaluated methods.

Results

Evaluation Setup

To thoroughly evaluate BCD Supertrees, we compare it under multiple criteria, on different simulated and biological data sets, against commonly used (low- and high level) tree reconstruction approaches. We further compare multiple Combined Analysis runs with different supertrees (SuperFine, MRP and BCD) as starting tree, to demonstrate that supertrees can improve a Combined Analysis.

In our method evaluation, we ignore the roots for all accuracy measurements, comparing the induced splits (and not the induced clades).

Evaluation Criteria for Simulated Data

For simulated data, we can compare estimated trees to the known, true model tree. Estimating false negative (FN) rates and false positive (FP) rates is common practice to measure the accuracy of estimated trees: FN splits are not in the estimated tree but should be; and FP splits are in the estimated tree but not in the model tree. Splits present both in the model tree and the estimated tree are true positives (TP). Given a fully resolved model tree, FN and FP rates provide information about the resolution of the estimated trees. For a fully resolved tree, FN = FP.

A tree estimation method may return a tree with many FPs but few FNs, or vice versa. To compare different methods, we use the well-known F₁ score (harmonic mean of precision and recall) as a single criterion to evaluate accuracy,

$$F_1=\frac{2TP}{2TP+FP+FN}.$$

To visualize results for multiple data replicates, we use boxplots. Data replicates are independent and may have highly varying complexity; even for highly overlapping boxes, it is possible that one method constantly outperforms another one for every data replicate. To evaluate whether quality differences are significant, we compare ranks of F₁ scores using the Wilcoxon signed-rank test with α = 0.05. We calculate pairwise significance for up to 16 different methods/configurations, resulting in 120 significance tests. To correct for multiple testing, we accept difference with P values below $\frac{0.05}{120}\approx 0.0004$ (Bonferroni correction). Full tables are available in the Supplementary Material online. For data sets with a small number of replicates, the Wilcoxon signed-rank test may reject significant differences. In these cases (e.g. SMIDGenOG-5500 with only 10 replicates), we report the absolute number of “wins”; see also the Supplementary Material online.

Evaluation Criteria for Biological Data

For biological data, the “true tree” to compare against is unknown; to this end, we resort to other evaluation criteria: For supermatrix data sets, we evaluate the estimated trees against the sequence data (supermatrix), using both the parsimony score) and the log-likelihood score. We use RAxML to optimize branch length and calculate the log-likelihood. For nonbinary trees, we resolved all polytomies randomly; this may discriminate against methods that return highly unresolved trees.

The supertree data sets do not even contain sequence data to compare against. To this end, we compare estimated supertrees against the source trees. It is common practice to compute the sum of false negatives/positives ratios over all source trees:

$$\begin{array}{cc}SFN\text{rate}\hfill & =\frac{\sum _{T\in \mathcal{T}}|\mathcal{S}(T)\mathrm{\setminus }\mathcal{S}(T^{\prime })|}{\sum _{T\in \mathcal{T}}|\mathcal{S}(T)|}\hfill \\ SFP\text{rate}\hfill & =\frac{\sum _{T\in \mathcal{T}}|\mathcal{S}(T^{\prime })\mathrm{\setminus }\mathcal{S}(T)|}{\sum _{T\in \mathcal{T}}|\mathcal{S}(T^{\prime })|}\hfill \end{array}$$

where $T\prime$ is the supertree, $\mathcal{T}$ is the set of source trees, and $\mathcal{S}(T)$ is the set of splits induced by some tree T. Note that optimal values of SFN rate and SFP rate depend on the source trees: For conflicting source trees, it is not possible to find a supertree with both SFN rate = 0 and SFP rate = 0.

Swenson et al. (2011) showed that SFN rate and SFP rate do not correlate well with true FN rate andFP rate and, in some cases, may actually be positively misleading. Here, we made similar findings: For most simulated data sets, neither the best estimated tree nor the model tree has the best SFN rate or SFP rate. Furthermore, SFN rate and SFP rate behave differently for each simulated data set (see supplementary figs. S6–S8, Supplementary Material online). Therefore, results of source tree-based evaluation criteria have to be interpreted with some care. Finally, the “MRP score” is the parsimony score of the supertree against the matrix representation of the source trees; results for this score have the same qualitative characteristics as to those for SFN and SFP rates, and are deferred to the Supplementary Material online.

Simulated Data Sets

SMIDGen Outgroup

The simulated SMIDGen Outgroup (SMIDGenOG) data set (Fleischauer and Böcker 2016) was generated following the SMIDGen protocol (Swenson et al. 2010). Each replicate consists of multiple clade-based source trees using a densely-sampled subset of taxa from one clade of the model tree, plus a single scaffold source tree which uses a sparsely-sampled subset of taxa of the complete model tree. Taxa in the clade-based source trees are closely related, whereas the scaffold source trees contain a (possibly small) subset of taxa, among all taxa in the model tree. For the clade-based source trees, the subset of taxa was chosen using a birth-death process, so a clade-based source tree does not necessarily contain all taxa of that clade, and not every clade of the model tree necessarily results in a clade-based source tree. Furthermore, one clade may result in more than one source tree, or a clade and a subclade may be chosen, potentially resulting in contradicting information in the clade-based source trees, see below. Different from the original SMIDGen protocol, source trees are rooted using suitable outgroups. Following Swenson et al. (2010), a different “evolution rate” (slow, medium, fast) was chosen for each clade-based source tree, resulting in a tree-wide branch length multiplier of 0.1, 1.0 and 2.0. The scaffold source tree always uses slow evolution rate. For each subset of taxa, we simulated a multiple sequence alignment using model tree branch lengths and Seq-Gen (Rambaut and Grassly 1997). Finally, source trees and bootstrap values were computed using RAxML. We generate 30 replicate model trees with 1000 taxa. For each replicate and each scaffold factor (20%, 50%, 75%, 100%), we generate 30 clade-based source trees plus one scaffold source tree with the desired percentage of taxa (scaffold factor) from the model tree. See supplementary figure S1 and the Supplementary Material online for details.

The resulting source tree sets contain between 8% and 15% contradicting clades compared with the model tree. A single source tree contains between 0% and 35% contradicting clades (see supplementary table S1, Supplementary Material online, for details).

SMIDGenOG-5500

SMIDGenOG-5500 is a large-scale simulated data set. The 10 replicates contain an average number of 5,500 taxa in the model tree, and between 37104 and 62495 clades in the source trees. We again use densely-sampled clade-based source trees, and sparsely-sampled scaffold source trees as described earlier. Since computation time of source trees using ML increases rapidly with the number of taxa, this data set does not contain different scaffold factors. For each replicate, we created 500 clade-based source trees with size between 75 and 125 taxa, and 5 scaffold source trees with 100 taxa each. This corresponds to reasonable values for a divide-and-conquer approach. We only generate 25 bootstrap replicates, again due to running time constraints. See the Supplementary Material online for details.

Biological Data Sets

We use data from three large-scale supermatrix studies on bees (1,376 taxa, 19 source trees, see Hedtke et al. 2013), saxifragales (950 taxa, 51 source trees, see Soltis et al. 2013), and legumes (2,228 taxa, 38 source trees, see McMahon and Sanderson 2006). To generate source trees for the supermatrix data sets, we split the combined alignment into its components. For every resulting alignment with more than three taxa, we calculated an ML source tree with bootstrap values, using RAxML with GTR-GAMMA default settings and 100 bootstrap replicates. Combined Analysis trees were calculated using ML (CA-ML) for the bees (Hedtke et al. 2013) and saxifragales data sets (Soltis et al. 2013), whereas the legumes Combined Analysis tree is a Maximum Parsimony tree (CA-MP) (McMahon and Sanderson 2006). Furthermore, we evaluate methods on five supertree data sets, namely placental mammals (116 taxa, 726 source trees, see Beck et al. 2006), marsupials (267 taxa, 158 source trees, see Cardillo et al. 2004), seabirds (121 taxa, 7 source trees, see Kennedy and Page 2002), primates (203 taxa, 112 source trees, see Purvis 1995) and mammalian phylogenomics (OMM, 33 taxa, 12,958 source trees, see Ranwez et al. 2010). Most of these data sets where previously used to evaluate supertree methods; all data sets have rooted source trees.

Evaluated Methods

We evaluate the performance of our new BCD method by comparing it to Matrix Representation with Parsimony (MRP), SuperFine(+MRP), the novel FastRFS and the Combined Analysis using ML (CA-ML) (see table 1). For MRP, we use the majority consensus in those cases where more than one most parsimonious tree is found, as this variant performed better than the strict consensus in our evaluations. Previous evaluations clearly suggest that other supertree methods (Semple and Steel 2000; Page 2002; Willson 2004; Creevey and Mcinerney 2005; Chen et al. 2006; Criscuolo et al. 2006; Scornavacca et al. 2008; Bansal et al. 2010; Ranwez et al. 2010; Snir and Rao 2010; Swenson et al. 2012; Brinkmeyer et al. 2013) are inferior to MRP and SuperFine(+MRP) with respect to supertree accuracy (e.g. FN-,FP rate and Robinson Foulds Distance) and, in some cases, also running time (Kupczok et al. 2010; Swenson et al. 2010, 2011, 2012; Brinkmeyer et al. 2011, 2013). We do not evaluate weighted MRP Ronquist (1996), as the above-mentioned evaluation studies indicate that it is not more accurate than SuperFine but often slower than CA-ML. Hence it is part of BCD and Superfine, we also report results of the GSCM.

Table 1.

Overview of the Methods We Compare in Our Evaluation and Their Major Differences.

Method (Implementation)	Combination	Algorithm	Objective Function
GSCM (Swenson et al. 2012)	High-Level (Supertree)	Deterministic, polynomial time	None
BCD	High-Level (Supertree)	Deterministic, polynomial time	Minimizes the number character deletions in the matrix representation of the source trees (complementary to MRC/SFIT).
FastRFS (Vachaspati and Warnow 2016)	High-Level (Supertree)	Deterministic, polynomial time	Minimizes the robinson foulds distance to the source trees (constrained search space).
MRP (Swofford 2002)	High-Level (Supertree)	Local search heuristic	Minimizes the number of character-state changes in the matrix representation of the source trees.
SuperFine (Swenson et al. 2012)	High-Level (Supertree)	Local search heuristic	Minimizes the number of character-state changes in the matrix representation of the source trees (after dividing the problem into subproblems).
CA-ML (Stamatakis 2006)	Low-Level (Supermatrix)	Local search heuristic	Maximizes the likelihood for a given supermatrix.
CA-MP (Swofford 2002)	Low-Level (Supermatrix)	Local search heuristic	Minimizes the number of character-state changes for a given supermatrix.

SMIDGenOG Results

We now describe results for the SMIDGen Outgroup data set with 30 replicates and 1000 taxa in the model tree. We found that using the GSCM “guide tree” consistently improves BCD supertree accuracy (supplementary figs. S11–S13, Supplementary Material online); on large data sets, it also reduces running times. In the following, we omit results for BCD without GSCM. We repeated our analysis for smaller data sets with 500 and 100 taxa model trees, as well as the original SMIDGen and the SuperTriplets data set, but found no significant differences (supplementary figs. S11, S12, S2, S3 and S4, Supplementary Material online). Further we evaluated BCD on the SuperTriplets data set (see supplementary figs. S18–S20, Supplementary Material online). Finally, we found that the FlipCut supertree method, being the predecessor of BCD, performs considerably worse than BCD (supplementary figs. S2–S4, Supplementary Material online); to this end, we will not consider FlipCut in the following.

Accuracy

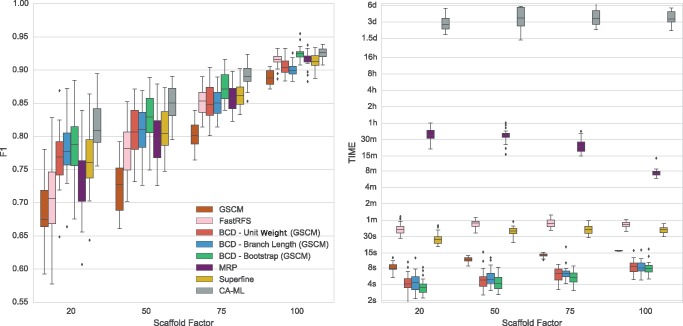
Using GSCM as an independent supertree method shows the by far worst overall performance (F₁ score) of all methods (fig. 1), but shows best FP rate which qualifies it as a preprocessing method (supplementary fig. S13c and d, Supplementary Material online). BCD (Unit Weight and Branch Length) already beats MRP for scaffold factors 20% and 50%. For scaffold factor 75%, the difference to MRP is not significant, and for scaffold factor 100% it performs worse than MRP. The differences between BCD Unit Weight and BCD Branch Length are not significant. BCD Bootstrap performs significantly better than any other evaluated supertree method, for all scaffold factors. CA-ML shows the overall best performance (significant for scaffold factors 20%, 50%, 75%). For scaffold factor 100%, the difference between BCD Bootstrap and CA-ML is not significant. Whereas SuperFine has a significantly higher F₁ score than MRP for scaffold factors 20% and 50%, it performs equally for scaffold factor 75% and 100%. FastRFS results quality depends on the scaffold factor: While it performs much worse than MRP for small scaffold factors, it is almost on par with MRP and SuperFine for scaffold factor 100%. Nevertheless, the small difference to SuperFine and MRP is significant.

Fig. 1.

F ₁ score (left) and running times (right) of the evaluated tree reconstruction methods on the simulated SMIDGen Outgroup (1,000 Taxa) data set. Running times are on a logarithmic scale. On the x-axis are the different scaffold factors plotted.

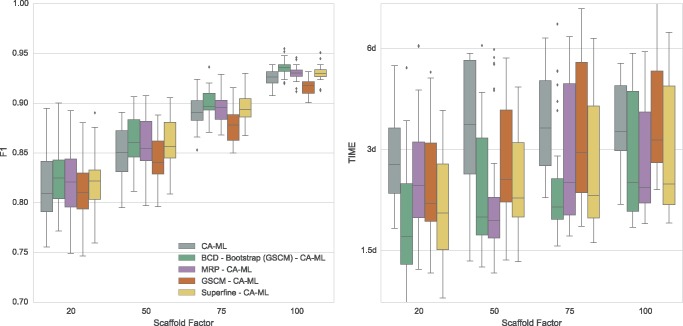
Comparing CA-ML with different starting trees demonstrates that supertrees can be used to improve CA-ML trees (see fig. 2). Here, all CA-ML trees show a significantly better F₁ score than the supertree methods. We found that a better starting tree results in a better CA-ML tree: CA-ML using the BCD Bootstrap supertree as starting tree has a significantly higher F₁ score than the default CA-ML tree, for all scaffold factors. The trees with the overall best F₁ score on the SMIDGenOG data set were estimated using CA-ML with the BCD Bootstrap starting tree.

Fig. 2.

Performance of different supertrees as a starting tree for CA-ML with RAxML regarding F₁ score (left) and running times (right) on the simulated SMIDGen Outgroup (1,000 Taxa) data set. Running times are on a logarithmic scale. On the x-axis are the different scaffold factors plotted.

Running Time

With running times between 4 and 8 s (including GSCM preprocessing), all BCD variants are much faster than all other evaluated methods (fig. 1). Note that BCD (including GSCM preprocessing) is faster than the GSCM implementation used by SuperFine. SuperFine needs ∼30 s on an average for one replicate of this data set; FastRFS need at most 1 min. MRP is by far the slowest supertree method, with running times of 40 min for scaffold factor 20%, and 8 min for scaffold factor 100%. Local search heuristics for MRP seem to converge faster for data with large scaffold trees, whereas the increased number of characters appears to increase the running time of the other methods. CA-ML with default starting tree requires between 2 and 6 days, whereas BCD requires between 4 and 8 s. Running times of CA-ML decrease with increasing starting tree accuracy, and CA-ML with BCD starting tree is up to 2 times faster than CA-ML with default starting tree (see fig. 2).

SMIDGenOG-5500 Results

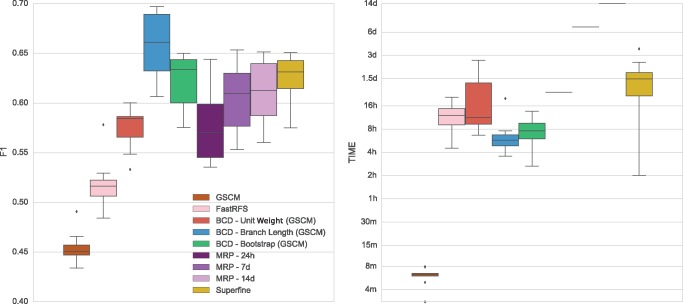
MRP did not finish in reasonable time; hence, we report its results after 1 day, 7 days and 14 days of running time. In view of the small number of replicates, we refrain from reporting significance.

Accuracy

BCD Branch Length reaches the overall best accuracy, outperforming all other methods for 10 of 10 replicates. BCD Bootstrap accuracy is considerably worse, which might be attributed to the small number of bootstrap replicates, see the discussion below; it outperforms MRP and SuperFine in 8 of 10 cases. GSCM is consistently outperformed by all other methods. In all cases, FastRFS shows a lower F₁ score than all methods but BCD Unit Weight with GSCM (for which it is outperformed in 9 of 10 cases) and GSCM (fig. 3).

Fig. 3.

F ₁ score (left) and running times (right) of MRP, SuperFine, GSCM, FastRFS and BCD on the simulated SMIDGen Outgroup (5,500 Taxa) data set. MRP did not finish after 14 days of computation; we report MRP results after 1 day, 7 days and 14 days. Running times are shown on a logarithmic scale.

Running Time

This data set clearly demonstrates the benefit of polynomial time algorithms, see figure 3: MRP did not finish after 14 days of computation, whereas BCD requires ∼7 h. FastRFS requires about ∼12 h. SuperFine needs >2 days, and will fall back to MRP computation when the GSCM preprocessing is not effective.

Results on Biological Data Sets

Accuracy

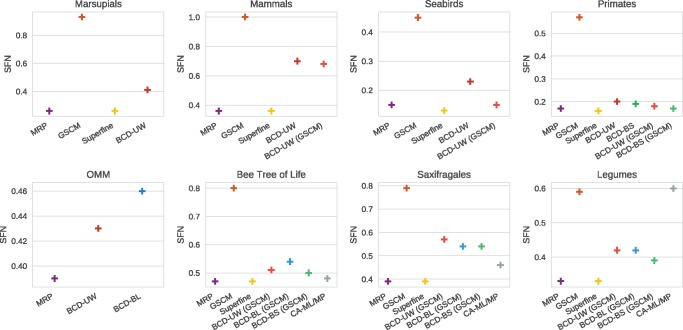
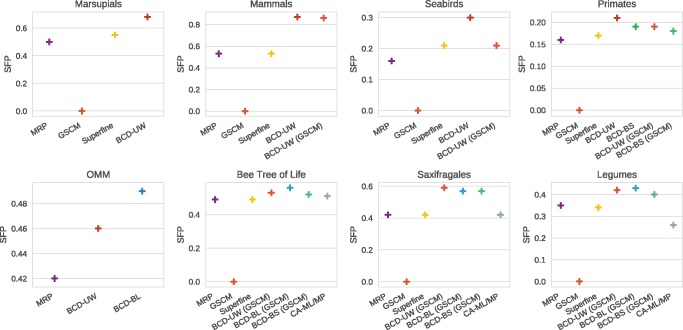
Next, we describe SFN rate and SFP rate results for all biological data sets, see figures 4 and 5. Recall that low SFN and SFP rates do not necessarily correspond to a supertree of good quality, see the Supplementary Material online for details. Bootstrap values and branch lengths are available for all supermatrix data sets (bees, saxifragales and legumes). Further, bootstrap values are available for the primates’ data set, whereas branch length are available for the OMM data set. All other supertree data sets contain neither bootstrap values nor branch length, prohibiting the use of BCD Bootstrap (BCD-BS) and BCD Branch Length (BCD-BL). By definition, the GSCM tree contains only splits that do not conflict with any source tree, which results in SFP rate = 0 for all data sets. For the biological data sets the GSCM tree is less resolved than for the simulated data sets; in addition, resolution varies strongly between biological data sets, see figure 4. Consequently, we find that SuperFine trees are largely identical to MRP supertrees, and both methods show comparable performance. Again, BCD performs best when used in conjunction with GSCM and bootstrap values. BCD supertrees and CA-ML trees show higher SFN and SFP rates than SuperFine and MRP trees. The CA-MP tree of the legumes data set has lower SFP rate than the SuperFine, MRP and BCD trees, but the highest SFN rate of all estimated trees. For the OMM data set, the SuperFine GSCM calculation did not finish within 1 day, and the GSCM tree used by BCD did not contain a single clade; hence, no results are reported for these methods. Findings regarding the MRP-Score are qualitatively similar to those for SFN and SFP rates, see supplementary figure S10, Supplementary Material online.

Fig. 4.

Sum of false negative rates (SFN rate) of supertrees against source trees for the biological supertree data sets. Most of the supertree data sets contain neither bootstrap values nor branch lengths, prohibiting the use of BCD bootstrap and BCD branch length. CA-ML/-MP cannot be applied to the supertree instances.

Fig. 5.

Sum of false positive rates (SFP rate) of supertrees against source trees on the biological supertree data sets. Most of the supertree data sets contain neither bootstrap values nor branch lengths, prohibiting the use of BCD bootstrap and BCD branch length. CA-ML/-MP cannot be applied to the supertree instances.

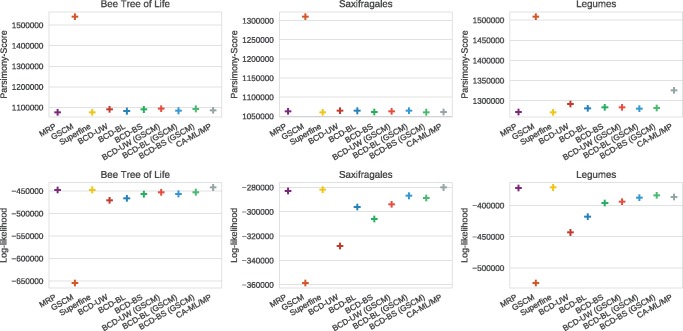
For the supermatrix data sets, we evaluated parsimony and log-likelihood scores, see figure 6. We find that MRP, SuperFine, and at least one variant of BCD have better parsimony scores than the CA-ML/-MP trees. This is despite the fact that for the legumes data set, the combined analysis tree has been computed using the parsimony optimization criterion. In all cases, SuperFine obtains the best parsimony scores. For the saxifragales data set, BCD Unit Weight (BCD-UW) and BCD-BS have better parsimony scores than MRP; on the other data sets, BCD produces slightly worse parsimony scores than MRP. For saxifragales and bees, CA-ML obtains the best log-likelihood scores, followed by SuperFine, MRP, and BCD. For legumes, SuperFine obtains the best log-likelihood score, followed by MRP, BCD-BS, and CA-MP.

Fig. 6.

Comparison of GSCM, MRP, SuperFine, BCD and the Combine Analysis (CA-ML/MP) with regards to parsimony scores (top) and log-likelihood scores (bottom) for the biological supermatrix data sets.

Running Time

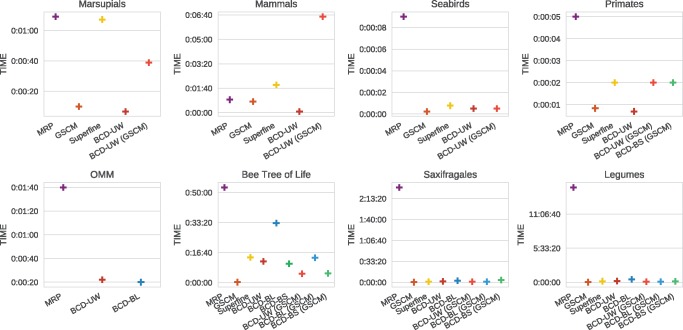
MRP is again the slowest supertree method by far (see fig. 7), where a variant of BCD is always the fastest. For data with many input trees compared with the number of taxa (primates, mammals, OMM, marsupials), using the GSCM tree does not speed up BCD and SuperFine.

Fig. 7.

Running times (in hh:mm:ss) of GSCM, MRP, SuperFine and BCD for all evaluated biological data sets. Running times of SuperFine and BCD-GSCM include the time of the GSCM preprocessing step.

Discussion

Our experiments with simulated data show that BCD can be an accurate and very fast supertree method. In particular, combining Bad Clade Deletion supertree computation with meta-information such as bootstrap values leads to excellent results, which are superior to the state-of-the-art supertree methods MRP and SuperFine. Unlike SuperFine and MRP, BCD has guaranteed polynomial worst-case running time. Among three proposed weightings, we find that BCD supertree accuracy is usually highest when using bootstrap values, followed by branch lengths and unit weights. Even with unit weights, BCD usually outperforms Matrix Representation with Parsimony for simulated data. Using the Greedy Strict Consensus Merger as a preprocessing step turned out to be both robust and effective. We also evaluated the undisputed sibling reduction as a preprocessing method (Brinkmeyer et al. 2013), but found that results of this combination were clearly dominated by BCD with GSCM. We also evaluated whether we can replace neighboring clades by a single joint clade during postprocessing (Bryant 1997; Pe’er et al. 2004; Jansson et al. 2012), but found that the effect on supertree accuracy are negligible. The 5,500 taxon data set demonstrates the advantage of a polynomial-time supertree method: MRP did not finish after 14 days on this data set, whereas BCD with branch lengths or bootstrap values never required more than a day of running time. Recall that SuperFine is identical to MRP when the GSCM tree is fully unresolved.

We also found that using an accurate supertree as starting tree for CA-ML can improve its accuracy and reduce the running time. Using CA-ML with a BCD starting tree produced the most accurate trees in our evaluation on simulated data, and also converges faster than CA-ML with the default starting tree. Hence, BCD supertrees can be a useful preprocessing tool for a combined analysis.

For the biological data sets, assessing accuracy is more intricate, as we lack an optimality criterion that is known to correlate reliably with the structural supertree accuracy. Using branch lengths and bootstrap values does not improve the accuracy of BCD as much as for the simulated data. This may be attributed to the fact that the source trees in the biological data sets have much weaker bootstrap support than those in the simulated data sets: For example, 40% of the clades in the saxifragales data set have bootstrap values <50%. The BCD supertrees contains only clades that are supported by at least one source tree; consequently, the BCD algorithm may have to choose from a set of clades which are all wrong. The performance of SuperFine is similar to MRP for these data sets; this comes as no surprise, since the GSCM tree is often largely unresolved, and SuperFine optimization is identical to the classical MRP optimization in these cases. Comparing the supertrees against the input trees (SFN and SFP rates), MRP and SuperFine show considerably better scores than BCD, but also than the CA-ML/MP, despite that the CA-ML trees may be assumed to be the most accurate trees. These results coincide with findings for simulated data evaluating SFN and SFP rates: There, MRP and Superfine also showed superior SFN and SFP rates compared with BCD and CA-ML, even when FN and FP rates compared to the model tree where significantly worse. Therefore, we cannot safely conclude which method performs best for biological data.

To the best of our knowledge, BCD is one of the most accurate supertree methods, and is by far the best of any supertree method with guaranteed polynomial running time (Brinkmeyer et al. 2011). But besides having a guaranteed polynomial running time, BCD is also very swift in practice: For example, BCD is always faster than SuperFine which, in turn, is one of the fastest supertree methods.

In current divide-and-conquer strategies, the decomposition step is computable in polynomial time, whereas the combination step (i.e., the supertree estimation) is not (Nelesen et al. 2012). Using BCD supertrees for this step, which has to be carried out for the complete set of taxa, can be highly beneficial. Further, a BCD supertree contains only clades that are supported by at least one of the source trees. Used as part of a divide-and-conquer approach, this leaves the estimation of clades to the sequence-based approach. To this end, we argue that BCD can be the “missing piece” for a powerful divide-and-conquer strategy, that allows an accurate ML analysis for large scale phylogeny reconstruction.

Materials and Methods

Preliminaries

Hereafter, we deal with three types of graph-theoretical objects: phylogenetic trees, graphs, and networks that we search for maximum flows. For readability, vertices of a tree will be called nodes, whereas directed edges of a network will be referred as arcs. Let N(V, E) be a network, with a set of vertices V and a set of arcs E. Each arc $e\in E$ has a nonnegative capacity$c:E\to {ℝ}_{\ge 0}$, which is the maximal amount of flow that e can take. Given source $s\in V$ and target $t\in V$, a flow is a function $f:E\to {ℝ}_{\ge 0}$ with $f(u,v)\le c(u,v)$ that maps a nonnegative flow value to each arc $e\in E$ in N. For each $v\in V\mathrm{\setminus }\{s,t\}$ the amount of flow entering v has to be equal to the amount of flow exiting it. The value of a flow is the amount of flow entering t; a maximum flow is a flow of maximum value.

Let $\mathcal{V}(T)$ be the node set of a rooted phylogenetic tree. Further, $\mathcal{L}(T)\subset \mathcal{V}(T)$ is the set of all leaves (nodes of out-degree zero) in T, corresponding to the set of taxa. All nodes $c\in \mathcal{V}(T)\mathrm{\setminus \ell }(T)$ are inner nodes. Each inner node v induces a clade $C=\mathcal{L}(T^v)\subseteq \mathcal{L}(T)$. Two clades C₁ and C₂ are compatible if $C_1\cap C_2\in \{C_1,C_2,\varnothing \}$. A set of trees compatible if all their clades are pairwise compatible. A clade C is supported by a tree T if $C\prime =C\cap \mathcal{L}(T)$ is a clade of T (Wilkinson, Pisani, et al. 2005). For a given set of input trees $\mathcal{T}=\{T_1,\dots ,T_l\}$, T is a supertree of $\mathcal{T}$ if $\mathcal{L}(T)=\underset{T_i\in \mathcal{T}}{\cup }\mathcal{L}(T_i)$. A supertree is called a consensus tree if for all pairs of input trees $T_i,T_j\in \mathcal{T},\hspace{0.17em}\mathcal{L}(T_i)=\mathcal{L}(T_j)$ holds. A strict consensus tree of $\mathcal{T}$ contains all clades present in all source trees $T_i\in \mathcal{T}$.

We use the Baum-Ragan (Baum 1992; Ragan 1992) encoding to transform a set of trees $\mathcal{T}$ into an incomplete binary matrix $M(\mathcal{T})$ with elements in $\{0,1,?\}$: Each row of the matrix corresponds to one taxon $1,\dots ,n$, and each clade C (except the root) in each tree is encoded in one column of the matrix. A “1” indicates that the corresponding taxon is part of C, whereas all other taxa of the tree are encoded “0”. The state of taxa that are not part of the tree is unknown, and represented by a question mark (“?”). A binary matrix (no “?”) has a perfect phylogeny if all matrix columns are pairwise compatible. Two matrix columns are compatible, if the corresponding clades are compatible. For a single tree T, the matrix $M(T):=M(\{T\})$ does not contain “?”-entries. According to the classical directed perfect phylogeny model (Wilson 1965), T is a (directed) perfect phylogeny of M(T). In the following, “perfect phylogeny” always refers to “directed perfect phylogeny”. An incomplete binary matrix allows for a perfect phylogeny if we can resolve all “?” to either “1” or “0” so that the resulting binary matrix has a perfect phylogeny. A tree T refines$T\prime$ if $T\prime$ can be reached from T by contracting internal edges. A supertree T of $T_1,\dots ,T_l$ is a parent tree if $T_{|\mathcal{L}(T_i)}$ refines T_i, for all $i=1,\dots ,l$. For trees $T,T\prime$ with identical taxa, T refines $T\prime$ if and only if $M(T\prime )$ can be obtained from M(T) by column deletion (Brinkmeyer et al. 2013). A collection of trees $\mathcal{T}$ has a parent tree if and only if $M(\mathcal{T})$ can be transformed into a perfect phylogeny by resolving each “?” entry to either “0” or “1” (Brinkmeyer et al. 2013).

Matrix $M(\mathcal{T})$ has size n × m where m is the total number of nonroot inner nodes in $T_1,\dots ,T_l$. The matrix can be computed in O(mn) time, using a tree traversal and lists of taxa. Pe’er et al. (2004) gave an $O(mn\hspace{0.17em}\text{polylog}(m,n))$-time algorithm to test whether an instance $M(\mathcal{T})$ allows for a perfect phylogeny by resolving all “?”-entries.

The Bad Clade Deletion Algorithm

Let $\mathcal{T}$ be the set of source trees. Assume that the matrix $M:=M(\mathcal{T})$ does not allow for a perfect phylogeny; how can we “correct” the matrix M accordingly? Brinkmeyer et al. (2013) introduced a top-down heuristic for the MRF problem, that uses minimum cuts in a graph representation of M. This algorithm, in turn, is based on the method of Pe’er et al. (2004) for deciding the incomplete perfect phylogeny problem.

Here, we consider a different way of “correcting” the matrix M: Namely, we remove a minimum number of characters (columns) from M, so that the resulting matrix allows for a perfect phylogeny. This formulation allows for an intuitive phylogenetic interpretation: Instead of removing columns from the matrix, an equivalent formulation of the problem is to remove clades from the source trees. The resulting Bad Clade Deletion supertree algorithm can be considered as the FlipCut algorithm with a particular choice of weights in the underlying graph (see below). Hence, all algorithmic results from Brinkmeyer et al. (2013) directly carry over to the BCD algorithm.

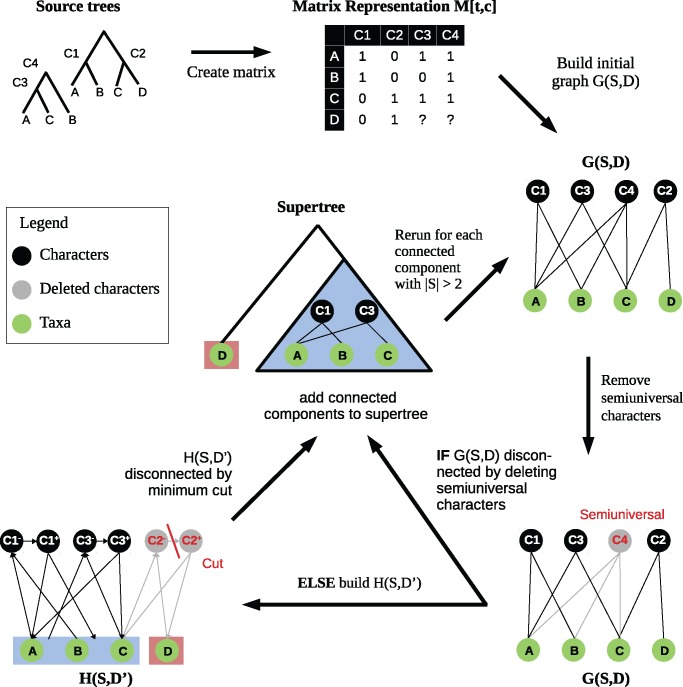
A high-level description of the algorithm is as follows: The algorithm proceeds in a recursive top-down fashion. In each recursive call, a subset of taxa and a subset of characters are provided; the subset of taxa is output as a clade of the supertree. A graph is constructed from the input matrix M and the two subsets, as proposed by Pe’er et al. (2004). If this graph is disconnected, the algorithm directly recurses on the connected components; otherwise, we search the graph for a minimum cut and remove the cut before recursing. If multiple optimal cuts exist, we choose one randomly. Recursion stops when the subset of taxa contains only a single taxon. For a Pseudo-code of this algorithm we refer to Brinkmeyer et al. (2013).

We now give the details of the BCD algorithm (an example is given in fig. 8), with reference to Brinkmeyer et al. (2013): For a subset $S\subseteq \{1,\dots ,n\}$ of taxa and a subset $D\subseteq \{1,\dots ,m\}$ of characters, G(S, D) is a bipartite graph with vertex sets S and D, and edges as follows: First, we build a graph such that an edge {t, c} is present if and only if $M[t,c]=1$, for $t\in S$ and $c\in D$. A character vertex $c\in D$ is semiuniversal (in S, D) if $M[t,c]\in \{1,?\}$ holds for all $t\in S$. We immediately remove all semiuniversal character vertices from the graph (Pe’er et al. 2004).

Fig. 8.

The BCD algorithm: For a subset S of taxa (green) and a subset D of characters (black), G(S, D) is a bipartite graph, where an edge {t, c} is present if and only if $M[t,c]=1$, for $t\in S$ and $c\in D$. A character vertex is semiuniversal if $M[t,c]\in \{1,?\}$ for all $t\in S$. For minimum cut computation, we transform G(S, D) into $H(S,D\prime )$. Supertree clades have the same colors (red or blue) as their corresponding connected components.

The BCD algorithm proceeds as follows: We start with $S\leftarrow \{1,\dots ,n\}$ and $D\leftarrow \{1,\dots ,m\}$. We then construct the graph G(S, D). If this graph is not connected, we recurse on each connected component $S\prime ,D\prime$ of the BCD graph with $|S\prime |>1$. The sets $S\prime$ of taxa computed during the course of the algorithm form a hierarchy which is transformed into the desired supertree.

If G(S, D) is connected at some point, the algorithm disconnects the graph by means of modifying the input matrix M. In contrast to the FlipCut algorithm, we do not allow edges to be removed, so all edges in G(S, D) get weight infinity. The only valid operation to split G(S, D) is deleting a subset of character nodes from D. For the moment, we assume all characters $c\in D$ in G(S, D) to have unit weight w(c):= 1. The weight of a bipartition of taxon vertices is the minimal cost of a set of character deletions, such that the two subsets of taxon vertices lie in separate components of the resulting graph. We search for a bipartition of minimal weight. To efficiently find a minimum bipartition, we fix one taxon vertex s, and for all other taxa vertices t we search for a minimum s-t-cut, allowing only character deletions. Among these cuts, the cut with minimal weight is the solution to the above problem. To find a minimum s-t-cut with character deletions, we transform G(S, D) into a directed network $H(S,D\prime )$ with capacities: Each taxon vertex t is also a vertex in the network, each character vertex c is transformed into two vertices c_– and c₊ plus an arc (c_–,c₊) in the network, and an edge {t, c} in G(S, D) is transformed to two arcs (t,c_–) and (c₊,t) in the network. Arcs (c_–,c₊) have capacity w(c), all other arcs have infinite capacity. By the generalized min-cut max-flow theorem (Elias et al. 1956; Ford and Fulkerson 1956), finding a minimum cut in G(S, D) is equivalent to computing a maximum flow in the network $H(S,D\prime )$ (Ford and Fulkerson 1962). Note that for all taxa s, t, the maximum s-t-flow in $H(S,D\prime )$ equals the maximum t-s-flow.

Given an input matrix M over $\{0,1,?\}$ for n taxa and m characters, the BCD algorithm computes a supertree in O(mn³) time, see Lemma 5 of Brinkmeyer et al. (2013). From the construction, we infer that each clade in the supertree is supported by at least one of the source trees: We only ever remove columns from the matrix; we never modify or add to the matrix. In particular, none of the clades in the supertree can be contradicted by all of the source trees. On the other hand, the reconstructed supertree does not necessarily minimize the number of inner nodes among all supertrees that are consistent with the same matrix columns: BCD supertrees may contain several clades where a single joint clade would be sufficient (Bryant 1997; Jansson et al. 2012). Our method inherited this property from the underlying algorithm of Pe’er et al. (2004), and shares it with supertree methods that build on the algorithm by Aho et al. (1981). BCD returns the perfect phylogeny for a given input matrix if one exists. This is not guaranteed for the supertree methods that use local search heuristics (e.g. MRP, MRF, MRL, MRC or SuperFine).

Weighting Strategies

By weighting G(S, D), we can incorporate information about the “reliability of clades” (characters). Here, we show how BCD uses branch lengths and bootstrap values:

• Unit weights (UW). All characters in the BCD graph have weight one. Using unit weights, a minimum cut is the removal of the smallest set of character vertices that disconnects the graph.

• Branch lengths (BL).Brinkmeyer et al. (2013) found that a clade that stems from a long branch is more stable (and, therefore, more likely to be correct) than a clade with a short branch. The weight of a character c is set to $w_{\text{BL}}(c):=\frac{l(e)}{l_{max}}$, where l(e) is the length of the branch e in the source tree that generated clade/character c, and l_max the longest branch of all source trees.

• Bootstrap values (BS). If available, we can use bootstrap values to weight the BCD graph. A bootstrap value tells us how sure we are about a clade. The weight of a character c is set to $w_{\text{BS}}(c):=\frac{b(v)}{100}$, where b(v) is the bootstrap value of the node v in the source tree corresponding to c.

• Tree weight. In addition to the weightings above, it is possible to modify the weights for source trees independently. For this, we multiply any of the above scores with a factor individually given for each source tree. This is not used in our evaluations.

GSCM Preprocessing

Since BCD is a greedy heuristic, restricting the search space in a sensible way will help to improve its accuracy. One way to do so, is to use a set of reliable clades, for which it is highly likely that they are part of the correct supertree. To use reliable clades for BCD, we add them to the matrix M, and give each corresponding character vertex infinite weight. Therefore, reliable character vertices cannot be deleted during minimum cut computations; they are only deleted from G(S, D) when they become semiuniversal, implying that they are already part of the supertree. Therefore, all taxon vertices $t_1\dots t_n$ in G(S, D) that are connected to the same reliable character vertex have to end up in the same connected component of G(S, D), and can be merged into a single taxon vertex. We then delete all trivial character vertices, each of which is connected to exactly one taxon vertex. This reduces the number of vertices in G(S, D) without changing its minimum cut, see figure 9.

Fig. 9.

Data reduction of G(S, D) using GSCM clades. Taxon vertices (S) displayed in green, character (D) vertices in black. Character vertices induced by the GSCM tree are blue.

We estimate the reliable clades by the Greedy Strict Consensus Merger (GSCM) supertree method. The GSCM supertree is conservative in the sense that it contains only clades that do not conflict with any of the source trees. The Strict Consensus Merger (SCM) generalizes the strict consensus tree problem for two trees to a supertree problem (Huson, Vawter, et al. 1999; Roshan et al. 2003). It restricts the two input trees to the subtrees of their common taxa, and calculates a strict consensus tree of these restricted input trees. Afterwards, it re-inserts previously removed taxa into this strict consensus tree. The GSCM algorithm is the generalization of SCM for more than two input trees. It combines the set of input trees by greedily applying the SCM algorithm to two of the remaining trees, until only one (super-)tree is left. The GSCM method is sensitive to the order in which the input and intermediate trees are merged. Therefore, the scoring for selecting the tree pairs has high influence on the supertree quality. The unrooted GSCM implementation of SuperFine uses overlap scoring (Swenson et al. 2012). The rooted GSCM implementation of BCD applies an improved scoring function: Namely, the unique clades lost scoring, which outperformed other known scorings but scales quadratically instead of linearly with the number of input trees (Fleischauer and Böcker 2016).

Merging Characters

The most time-consuming part of the BCD algorithm is searching for minimum cuts of G(S, D). Using the GSCM tree can strongly reduce running times of this step; here, we describe another algorithm engineering trick we use to further improve running times. To reduce the size of matrix M, it is common practice to merge identical matrix columns, summing up their weights. Identical matrix columns occur only rarely in the input matrix, as this requires input trees with identical taxon sets. (Recall that our method allows the user to define an individual weight for each input tree.) But when searching for minimum cuts in G(S, D), “0” and “?” entries in M are treated identical, which allows us to merge characters corresponding to trees with different taxon sets. Hence, we merge all character vertices in G(S, D) that are adjacent to the same set of taxon vertices, and sum up their weights. This can vastly reduce the number of vertices in G(S, D) without changing the minimum cut.

Software

The BCD command line tool and its source code are available at https://bio.informatik.uni-jena.de/software/bcd/ (last accessed July 7, 2017).

Data

All data sets are available online at https://bio.informatik.uni-jena.de/data/ (last accessed July 7, 2017).

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.