The Genotype–Phenotype Relationships in the Light of Natural Selection

Abstract

Although any genotype–phenotype relationships are a result of evolution, little is known about how natural selection and neutral drift, two distinct driving forces of evolution, operate to shape the relationships. By analyzing ∼500 yeast quantitative traits, we reveal a basic “supervisor–worker” gene architecture underlying a trait. Supervisors are often identified by “perturbational” approaches (such as gene deletion), whereas workers, which usually show small and statistically insignificant deletion effects, are tracked primarily by “observational” approaches that examine the correlation between gene activity and trait value across a number of conditions. Accordingly, supervisors provide most of the genetic understandings of the trait whereas workers provide rich mechanistic understandings. Further analyses suggest that most observed supervisor–worker interactions may evolve largely neutrally, resulting in pervasive between-worker epistasis that suppresses the tractability of workers. In contrast, a fraction of supervisors are recruited/maintained by natural selection to build worker co-expression, boosting the tractability of workers. Thus, by revealing a supervisor–worker gene architecture underlying complex traits, the opposite roles of natural selection versus neutral drift in shaping the gene architecture, and the complementary strengths of the perturbational and observational research strategies in characterizing the gene architecture, this study may lay a new conceptual foundation for understanding the molecular basis of complex traits.

Introduction

Characterization of genotype–phenotype relationships relies on two basic strategies (Parnas et al. 2015): The first one, which we here term “perturbational” strategy (P-strategy for short), relates a gene to a trait by considering the effect of a direct perturbation of the gene on the trait (e.g., knockout, knockdown, overexpression, or base-specific mutagenesis); with this strategy the causal relationships from genes to traits are clearly defined. The second one, which we here term “observational” strategy or O-strategy, relates a gene to a trait by considering the statistical correlation between the gene activity and the trait value across a number of different genetic or environmental backgrounds; because gene activity could affect trait and vice versa, the causality of the gene–trait associations defined by this strategy is not readily available. Despite the widespread usage of the two research strategies (Griffiths 1993; Chen et al. 2008; Emilsson et al. 2008; Visscher et al. 2012; Civelek and Lusis 2014; Mok et al. 2015; Ritchie et al. 2015), it is unclear under what circumstances they can be most successful and when they are doomed to fail.

Recent technical advances enabled the profiling of various types of gene activity (e.g., mRNA level, protein abundance, protein phosphorylation, protein location, protein–protein interactions [PPIs], and protein–DNA/RNA interactions; Ritchie et al. 2015), greatly facilitating O-strategy for inferring gene–trait relationships. As for P-strategy, it has been demonstrated that genome-wide association study, a forward genetic analysis, is powerful in associating DNA mutations/variants with a trait (Visscher et al. 2012). Meanwhile, genome-wide reverse genetic screenings based on homologous recombination (Giaever et al. 2002), RNAi (Kamath et al. 2003), or CRISPR-Cas9 (Shalem et al. 2014) have been applied to several model organisms to reveal the whole set of genes whose loss-of-function mutations alter specific traits. It is thus increasingly clear that data acquisition is no longer a major hurdle to understanding genotype–phenotype relationships. However, three key challenges to the field remain. First, the performance of O-strategy is often compromised by intergene epistasis, which appears to be pervasive (Costanzo et al. 2010). Second, because all genes within a cell are connected and work in conjunction to influence traits, mutating a random gene could, in principle, cause cellular-wide changes that affect every trait to some extent (Fisher 1999; Paaby and Rockman 2013). For example, mutating the gene encoding beta-actin would likely alter all cellular processes as well as all traits. Because no functional insights could be gained from claims of a gene affecting all traits or a trait affected by all genes, it is unclear what P-strategy could and could not provide. Third, and perhaps more importantly, there is no working framework to integrate genes revealed by O-strategy with genes revealed by P-strategy (Mackay et al. 2009; Ritchie et al. 2015).

These challenges partly reflect the limitation of the current framework of genetics that considers the relationships between variations in genes and variations in traits only (Schwartz 2000). Because genetic variants affect a trait through modulating the biochemical construction of the trait, understanding the making of a trait (Orgogozo et al. 2015), rather than just the variation of a trait, would help address the above challenges. A previous study analyzed the microscopic images of triple-stained cells of the yeast Saccharomyces cerevisiae and quantitatively characterized 501 morphological traits for each of 4,718 yeast mutants, each lacking a different nonessential genes (Ohya et al. 2005). Despite correlated traits, the 501 traits represent a comprehensive characterization of the yeast cell morphology, including cell size, cell roundness, nucleus position, bud neck position angle, bud growth direction, and so on. Additionally, whole transcriptomes have been measured for ∼1,300 out of the 4,718 yeast mutants (Kemmeren et al. 2014). The availability of both expression and trait information upon gene deletions at such a large scale provides a unique opportunity to study the gene–expression–trait relationships.

This study can be read as two parts. In Part I, we show that P-strategy and O-strategy tend to identify, respectively, two nonoverlapping gene sets (supervisors and workers) that are organized hierarchically in the gene regulatory network to control a trait. In Part II, we show the distinct roles natural selection and neutral drift could have played in shaping the supervisor–worker gene architecture, profoundly influencing the genotype–phenotype relationships as well as their tractability.

Results

O-Strategy and P-Strategy Reveal Two Nonoverlapping Gene Sets That Affect a Trait

For O-strategy we examined the correlation between all 6,123 yeast genes and the 501 morphological traits, using mRNA level as the representative gene activity (fig. 1A). Under a stringent statistical threshold we identified genes whose mRNA level is significantly correlated to a trait across the large number of yeast mutants with available expression profiles (see Materials and Methods). These genes were termed O-strategy identified genes or OIGs. The number of OIGs found for each trait ranged from 0 to ∼1,000, with the mean of 138 and the median of 12, and the proportion of trait variance explained by an OIG was 3.4 ± 2.1% (mean ± SD) (supplementary table S1, Supplementary Material online). A total of 2,541 nonredundant yeast genes were identified as OIGs of at least one trait.

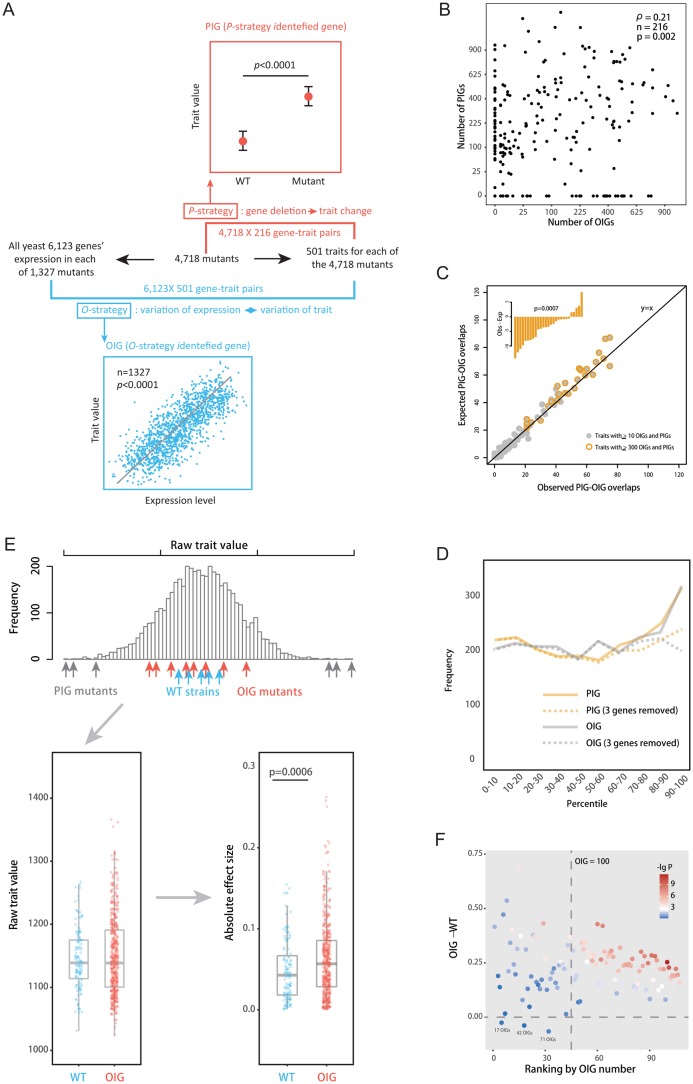
Fig. 1.

The P-strategy and O-strategy reveal two nonoverlapping gene sets. (A) A schematic explanation of the data structure and the P-strategy and O-strategy. (B) The PIG number of a trait does not predict the OIG number (Spearman’s ρ = 0.2, n = 216, P = 0.002). (C) The observed PIG–OIG overlaps are even slightly less than expected. A total of 108 traits each with ≥ 10 OIGs and ≥ 10 PIGs are examined. We reshuffle OIGs among the 108 traits and PIGs among the traits separately, while maintaining the OIG and PIG numbers of each trait. The average of 1,000 reshufflings is used to derive the expectation. Each dot represents a trait, with 27 highlighted in yellow. (D) The percentile of a PIG–OIG overlap among the PIGs (yellow lines) or OIGs (grey lines) of the focal trait in terms of the deletion effect or the explained trait variance. A total of 2,229 PIG–OIG overlaps found in the 108 traits are lumped to obtain the frequency distribution across the 10 percentile bins. (E) Comparison of the 123 wild-type clones and 853 OIG mutants for the trait C12_2_A1B. The difference between the two groups is significant when the absolute effects are considered (P = 0.0006; T test). (F) The summary of the analyses conducted as in Panel E for the 108 traits. The x-axis shows the ranking of a trait according to the OIG number, and the y-axis shows the difference of the mean absolute effect between OIG mutants and wild-types. Each dot represents a trait.

Gene deletion is a widely used P-strategy. Following the statistical threshold of a previous study (Ho and Zhang 2014), we defined the genes with significantly strong deletion effect on a trait as P-strategy identified genes (or PIGs) of the trait. Notably, only the 4,718 nonessential yeast genes and 216 morphological traits were examined (fig. 1A). This is because the deletion mutants of other yeast genes have not been available/characterized and because the intramutant error of a trait is not available for the rest morphological traits such that the statistical test of P-strategy cannot be done. The 4,718 × 216 gene–trait pairs tested by the P-strategy is a full subset of the 6,123 × 501 gene–trait pairs tested by the above O-strategy; this data heterogeneity has been carefully controlled in the following analyses to avoid bias. The number of PIGs found for each of the 216 traits ranged from 0 to ∼1,000, with the mean of 301 and the median of 212 (supplementary table S2, Supplementary Material online). A total of 4,554 nonredundant yeast genes were defined as PIGs of at least one trait.

Surprisingly, the OIG number of a trait was a poor predictor of its PIG number (Spearman’s ρ = 0.21, n = 216, P = 0.002; fig. 1B). For example, many traits had several hundred OIGs but no PIGs whereas many others had several hundred PIGs but no OIGs. The pattern held when exemplar traits that are less related with each other were considered (Spearman’s ρ = 0.30, n = 23, P = 0.16; , supplementary fig. S1, Supplementary Material online; see Materials and Methods). To further demonstrate this counterintuitive finding, we analyzed the overlaps between OIGs and PIGs for each of the 108 traits with ≥ 10 OIGs and ≥ 10 PIGs. The number of PIG–OIG overlaps was even slightly smaller than the expected number, which was derived by reshuffling the OIGs and PIGs, respectively, among the 108 traits (fig. 1C; see Materials and Methods). Because the overlapping rate expected by chance is very low (at the level of 1%), the lack of substantial overrepresentation of the overlaps means that the vast majority of OIGs were not recognized by P-strategy and the vast majority of PIGs were not recognized by O-strategy. A close examination of the sparse PIG–OIG overlaps in their deletion effect as PIG or their explained trait variance as OIG found a ∼1.5-fold overrepresentation of the overlaps as top PIGs and OIGs (fig. 1D). Strikingly, this overrepresentation was entirely due to three genes, YIL040W, YGR092W, and YNL148C, which are known for regulating nuclear envelope morphology, primary septum formation and cytokinesis, and the folding of alpha-tubulin, respectively. The three genes were among the strongest PIGs and OIGs in dozens of the traits. If the three “super-informative” genes were removed, the remaining overlaps showed regular deletion effect as other PIGs and explained similar trait variance as other OIGs (fig. 1D). This suggested that the depletion of PIG–OIG overlaps be insensitive to the statistical thresholds used for defining PIGs and OIGs. Gene Ontology (GO) analysis of the 200 most pleiotropic PIGs (∼5% of all nonredundant PIGs) found that up to 63.5% of them had the GO term of “Biological Regulator” (q < 1.2 × 10⁻¹⁶), whereas no such apparent GO enrichment was found for OIGs. Taken together, the OIGs and PIGs found for the same traits appear to be two distinct gene sets with little overlaps.

PIGs by definition can causally affect their traits; however, the causality of OIG–trait relationships is not readily clear. The trait difference of an OIG deletion mutant from wild-type is often small, unable to pass the given statistical threshold of P-strategy. This may represent a type II error of the statistical test if the mutant is truly different from the wild-type. Alternatively, the observed trait difference may represent measuring errors if the mutant and wild-type are actually identical in the focal trait. Under the former circumstance, we would expect a stronger signal by considering many OIG mutants collectively. Under the latter circumstance, however, there would be no such accumulated signals expected. We thus lumped the many OIGs of a trait together to test the causality. We explain the analysis using trait C12_2_A1B, which measures the circumference of the bud cell, as an example:

For this trait there are 909 OIGs, 56 of which were also defined as PIG of the trait and thus excluded from the analysis. In figure 1E, we plotted the raw trait values of the remaining 853 OIG mutants as well as 123 wild-type clones. Because deletion of a gene could either increase or decrease the trait, we considered the absolute trait difference from wild-type. Specifically, the absolute difference of a mutant or wild-type trait value (with log-transformation) from the median of the 123 wild-types was computed. The resulting absolute effect of the 853 OIG mutants was then compared with that of the 122 nonzero wild-types. Exclusion of the median of the 123 wild-types made the comparison fair. If deletions of the OIGs have absolutely no effects on the trait, no difference between the OIG mutants and the 122 wild-types would be expected. However, we found that the absolute effects were significantly larger for the 853 OIG mutants than the 122 wild-types (P = 0.0006, T test; fig. 1E). This result suggested that the OIGs can causally influence the trait, although their deletion effects, when tested separately, were all statistically insignificant.

We conducted a similar analysis for the other 107 traits each with at least 10 OIGs and PIGs. The difference of the absolute effects between OIG mutants and wild-types tended to be significant for traits with more OIGs (e.g., P < 0.05 for 63/69 = 91.3% of the traits with ≥ 100 OIGs but only 8/38 = 21% of the traits with < 100 OIGs), whereas the difference level was comparable between the two trait groups (fig. 1F). Importantly, OIG mutants had a larger mean absolute effect than wild-types for all but three traits (∼97%) (P < 10⁻¹⁶, Binomial test; fig. 1F). This dominant pattern can hardly be explained by the null hypothesis that OIGs mutants are same as wild-types in the focal traits. Thus, the statistically insignificant deletion effects observed for individual OIGs likely represent weak but true signals supported by insufficient samplings, rather than fake signals (see fig. 8 for further discussion of this issue).

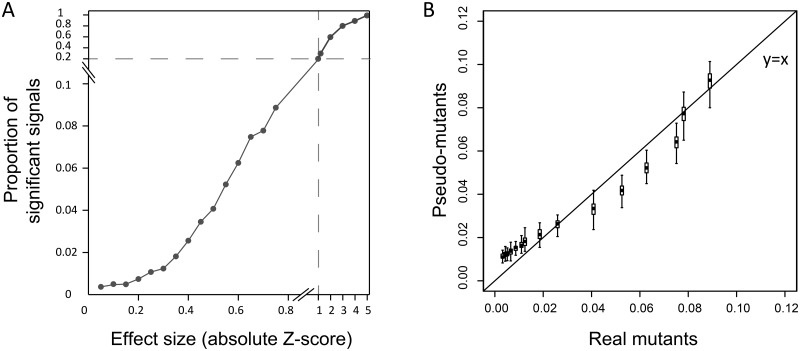
Fig. 8.

Statistically insignificant signals can be well explained by false negatives of P-strategy. (A) The proportion of observing significant differences between 50 mutant cells and 50 wild-type cells is a function of the effect sizes of mutants. (B) The proportion of significant signals of real gene deletion mutants is similar to that of the simulated pseudomutants that have genuine differences from the wild-type, suggesting that the remaining insignificant signals be well explained by false negatives of the P-strategy. We considered only the effect sizes of Z = 0–0.77, which cover 50% of the data with Z > 0 in a standard Gaussian distribution. The box and error bar encompass 50% and 90% of the data derived from 100 replicates, respectively.

PIGs and OIGs Form a Supervisor–Worker Hierarchical Architecture

How are the PIGs and OIGs found in a trait organized to affect the trait? According to the data structure, here an OIG was characterized because of its strong expression changes in mutants of deleting the PIGs, wherein the focal trait changed the most (fig. 2A). In other words, OIGs were generally under the control of PIGs of the same traits in the gene regulatory network. This is consistent with the above finding of PIGs as “Biological Regulator.” On average a PIG regulated 53 OIGs while the expected number was 20.4 ± 3.3 (P < 0.001; Permutation test); an OIG did not regulate more PIGs than expected by chance (15.3 vs. 17.8 ± 3.5; see Materials and Methods). Also, on average an OIG was regulated by 20.4 PIGs while the expected number is 9.2 ± 0.7 (P < 0.001; Permutation test); a PIG was not regulated by more OIGs than expected by chance (1.4 vs. 1.8 ± 0.3; see Materials and Methods). The relative position of the two causal gene sets in the gene regulatory network suggested a PIG–OIG hierarchical architecture, in which the effects of PIGs are mediated through the OIGs.

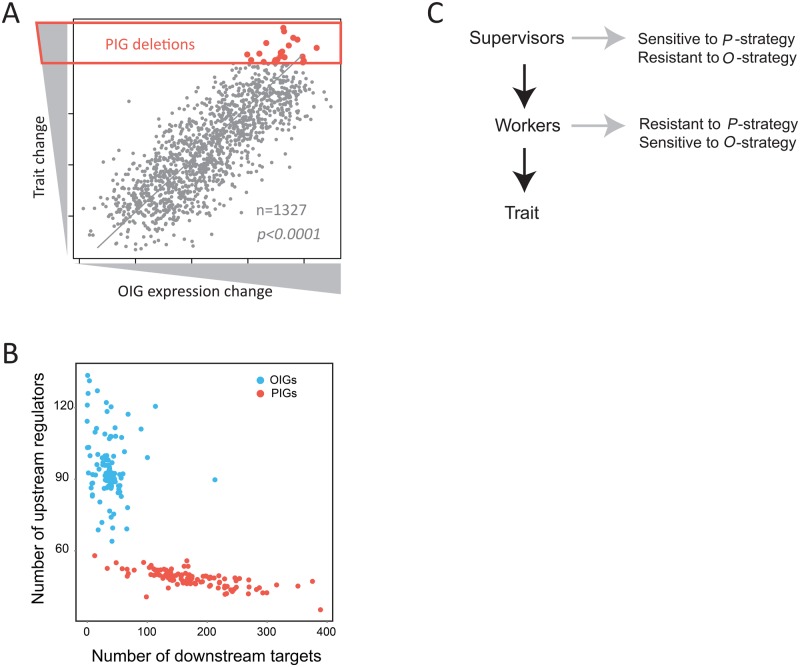
Fig. 2.

Characteristics of PIGs and OIGs suggest a supervisor–worker gene architecture. (A) A schematic diagram shows how OIGs are characterized because of their strong expression changes in mutants lacking a PIG, explaining why OIGs are overall regulated by PIGs of the same trait. (B) Distinct properties of PIGs and OIGs in the gene regulatory network. The numbers of downstream targets and upstream regulator per OIG (or PIG) are shown. Each dot represents a trait, and the average of all OIGs (or PIGs) of a trait is presented. The same 108 traits as in figure 1 are examined. Gene A is called the downstream target of gene B and B the upstream regulator of A if gene A shows a significant expression change (P < 0.0001) in the mutant lacking gene B. (C) The proposed supervisor–worker gene architecture.

The proposed architecture, if valid, should be useful for explaining why the identified PIGs were sensitive to P-strategy but resistance to O-strategy, and why the OIGs showed the opposite pattern. Analysis of the expression responses to the gene deletions showed that a PIG generally had a far larger number of downstream targets than an OIG (fig. 2B). A trait is presumably a function of the many OIGs, and the gene deletion effects are positively correlated to the number of OIGs with changed expression levels (supplementary fig. S2, Supplementary Material online). We thus expected more changed OIGs in a PIG deletion than an OIG deletion. This prediction was well-supported by the data (supplementary fig. S3, Supplementary Material online), explaining why PIGs tended to show larger deletion effects (hence sensitive to P-strategy) than OIGs. This is analogous to a manufacturing line run by workers who are managed by supervisors, wherein a major slowdown in productivity is often caused by removing a supervisor as opposed to removing a worker, despite that the workers are directly involved in the manufacturing. Meanwhile, we also examined the expression responses of PIGs and OIGs in all deletion mutants with available expression profiles. PIGs were found to have fewer upstream regulators, less responsive to the gene deletions than OIGs (fig. 2B); as a consequence, they were unable to account for a large proportion of the trait variance across the mutants. This explained why PIGs were insensitive to O-strategy despite their large mutational effects.

Collectively, these analyses suggest a roughly two-layer gene architecture underlying the formation of a trait (fig. 2C). It comprises many “worker” genes that are more directly responsible for the trait, and “supervisor” genes that control the expression/activity of the workers. In the current study, supervisors were identified primarily by deletion analysis, a P-strategy, as PIGs. For convenience, hereafter, PIGs will be referred to as observed supervisors. Workers were identified by O-strategy as OIGs. For convenience, hereafter, OIGs will be referred to as observed workers. The key difference of the supervisor–worker gene architecture from previously proposed models, such as QTL–QTT (Mackay et al. 2009), input–output genes (Davidson et al. 2002), and bow–tie structure (Friedlander et al. 2015), is that it explicitly specifies the research strategies by which the supervisors and workers are each identifiable and, even more importantly, unidentifiable.

Rich Mechanistic Understandings Provided by Workers

Identification of the genetic mutations/variants that alter a given trait is now rather straightforward, but understanding the mechanistic steps that bridge mutations/variants and trait is challenging (Civelek and Lusis 2014). The proposed architecture suggests that P-strategy and O-strategy would reveal complementary understandings of a trait. Specifically, supervisors would provide most of the genetic understandings of the trait because of their larger mutational effects; meanwhile, workers would provide rich mechanistic understandings that concern the bridging functional modules/pathways, as suggested by their more direct connection with trait as well as the better performance in explaining trait variance.

The capacity of supervisors in providing genetic understandings has been demonstrated. To assess how workers could provide mechanistic understandings, we dissected the 14 exemplar traits each with over 300 observed workers. We relied on PPIs to assemble the observed workers into PPI modules, which facilitates the characterization of the workers’ functions (see Materials and Methods). There were 1–9 modules found for each of the traits, resulting in 66 worker modules in total. Annotation of the modules was in general quite straightforward because of the strong enrichment of functionally similar proteins within each module (supplementary table S3, Supplementary Material online). For example, a worker module found for trait DCV14_2_C, which measures the area of nucleus region in daughter cell, comprised 22 proteins. Thirteen out of the 22 were involved in ATP synthesis related electron transportation, which is >100-fold higher than expected by chance. Notably, such a strong functional enrichment was just typical to the 66 worker modules (supplementary fig. S4, Supplementary Material online). Regrettably, the potential functional insights revealed for the yeast morphological traits cannot be compared with known understandings, because these traits have seldom been studied before.

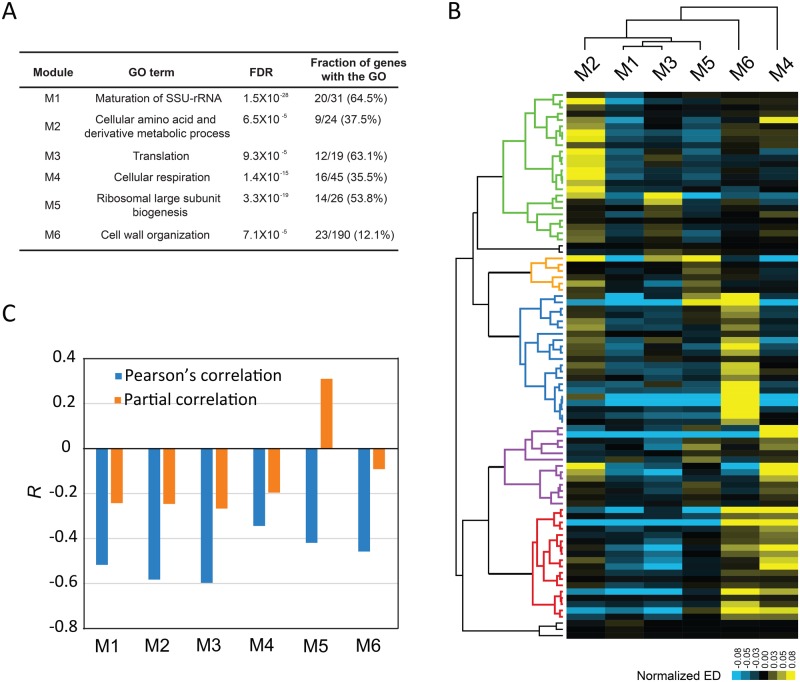
We thus conducted the same functional dissection for cell growth rate, a well-studied complex trait of the yeast. We identified ∼900 observed workers for cell growth rate and obtained six worker modules with clear functional annotations (supplementary table S4, Supplementary Material online; see Materials and Methods). The six modules (M1–M6) were all involved in critical biogenesis processes (fig. 3A). To check how the six modules could be used to understand cell growth reduction, we examined 87 slow-growth mutants each with a growth rate <80% of the wild-type and also with available expression profile. We computed the expression distance (ED) between mutant and wild-type for each of the six modules (see Materials and Methods). Although the functions of the deleted genes of the 87 mutants are highly diverged (supplementary table S5, Supplementary Material online), convergent understandings were obtained from the worker modules. With a few exceptions all mutants coalesced into five clusters each corresponding to a different expression pattern of the modules (fig. 3B). The diverse pattern cannot be explained by the expression responses to growth reduction, because such expression responses should lead to qualitatively the same pattern in the different mutants. Thus, there appeared to be five basic means of regulation for the yeast cell growth from the perspective of workers. The independence among the six major biogenesis modules explained a previous observation that the growth rate variation of different yeast strains found in nature was primarily related to amino acid biosynthesis genes (here M2) but not ribosomal genes (here M5), the latter were regarded as the general leading player of cell growth regulation according to studies on laboratory strains (Tamari et al. 2014). In addition, the cell growth rate was well explained by the ED of individual modules, with Pearson’s R ranging from about -0.4 to -0.6 (fig. 3C; see Materials and Methods). To test the effect of a single module independent from the other five modules we conducted partial correlation analysis. The Pearson’s R between cell growth rate and the ED of M5 changed from -0.4 to 0.3 after controlling for the other five modules. This seems intriguing. M5 represents ribosomal biogenesis, a process consuming up to 80% of the total cell energy (Schmidt 1999), and the ED of M5 for the mutants is primarily due to expression down-regulation. Thus, it is likely that the down-regulation of M5 could actually promote cell growth by saving energy as long as the alteration of the other modules has reduced the growth rate below a certain level. This notion may revise the conventional belief that down-regulation of ribosomal genes always suppresses cell growth (Airoldi et al. 2009).

Fig. 3.

Unique mechanistic insights provided by observed workers. (A) Details of the six worker modules underlying the yeast cell growth. (B) Five major types of cell growth reduction, marked by different colors in the dendrogram, are revealed by examining the activity of the worker modules. Each row represents a slow-growth mutant, and the expression distance (ED) of a module is normalized by subtracting the average ED of the six modules in the mutant. (C) The Pearson’s R between cell growth rate and the ED of each individual module, in comparison to that of the partial correlation that controls for the other five modules.

The results aimed to demonstrate the potential strengths of workers in providing mechanistic understandings. It should be pointed out that using such expression analysis (or O-strategy) to define genes to study biological phenomena/traits has been common; however, the expression analysis in previous studies was often auxiliary, suggesting candidate genes that await further tests by P-strategy (Aitman et al. 1999; Sandberg et al. 2000; Gagneur et al. 2013). Unfortunately, the finding that workers are generally insensitive to P-strategy compromises the rationales for this working practice, although occasional successes have been achieved in the field particularly when “super-informative” genes are involved. Instead of being auxiliary, O-strategy reveals essential understandings of a trait that are hardly accessible by P-strategy. Thus, the supervisor–worker gene architecture appears to form a new framework to integrate the two basic research strategies in molecular biology. Interestingly, a long-standing puzzle of the field, that genes up-regulated in a new environment often show negligible deletion effects in the environment (Giaever et al. 2002; Gibney et al. 2013), is readily understood with this framework.

Natural Selection by Building Worker Co-Expression Promotes Worker Tractability

The above analyses constitute the Part I of this study, offering a general demonstration of the supervisor–worker gene architecture. We next aim to know how natural selection and neutral drift would each be involved in shaping the gene architecture (Part II).

We start by asking why the same O-strategy revealed up to ∼1,000 observed workers for some traits but zero for many others. On the one hand, it is a bit unusual to observe for a single trait as many as ∼1,000 workers each accounting for ∼3.4% of the trait variance. Rules of statistics predict that, for an output determined by 1,000 input factors, the average output variance explained by an input factor will be 0.1% if the input factors are all independent from each other. If the 1,000 input factors form, say, 10 modules that are of equal size and have perfect intramodule coordination, the average output variance explained by a single factor will be same as that explained by a module, both being 10%. Thus, it is likely that the large number of observed workers are not independent; instead, they co-express. In support of this, we found strong co-expression among the observed workers of each trait (fig. 4A).

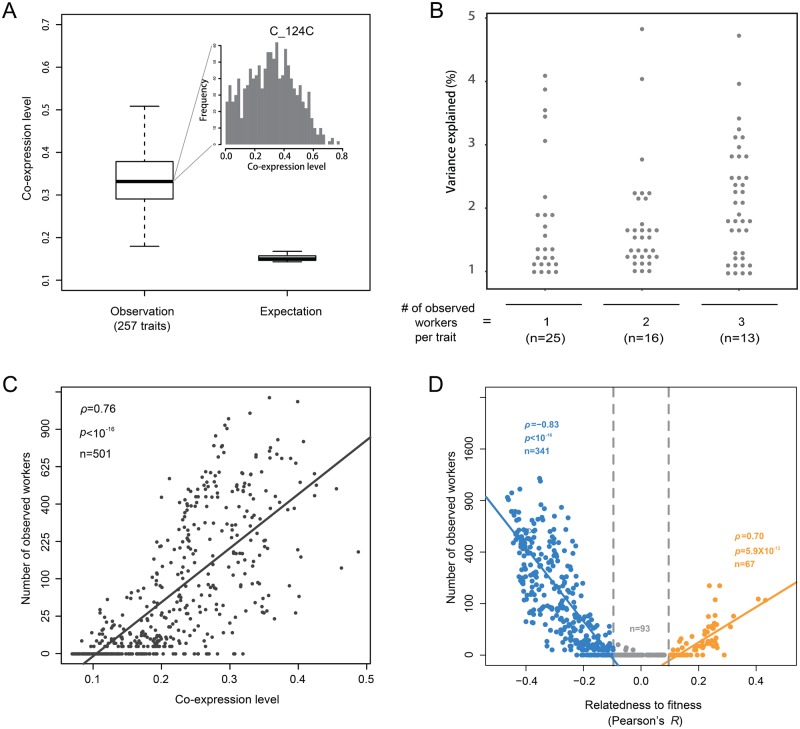
Fig. 4.

Natural selection builds worker co-expression to boost worker tractability. (A) The observed workers of a trait tend to co-express. The average absolute Pearson’s R of all worker pairs is shown for each of the 257 traits with at least 10 observed workers. The expectation is estimated by reshuffling the observed workers of all 257 traits while maintaining the worker number of each trait. Box-plots marking 50% of the data points near the median within the box and 90% of the data points near the median between the two horizontal lines are presented, with an inset showing the frequency distribution of the co-expression level of all worker pairs of the median trait C-124C. (B) The trait variance explained by each observed worker is small even for traits with only one, two, or three observed workers. (C) The number of observed workers is strongly correlated with the co-expression level of the 100 most probable workers (Spearman’s ρ = 0.76, n = 501, P < 10⁻¹⁶). (D) Fitness coupling underlies worker tractability. The relatedness to fitness of a trait is the Pearson’s R between trait value and cell growth rate. A larger absolute R means stronger fitness coupling, with -0.096 < R < 0.096 corresponding to a statistically insignificant range after controlling for multiple testing. Each dot represents a trait, and a total of 501 traits are included.

On the other hand, many traits had virtually no observed workers, although they had as many observed supervisors as the other traits (fig. 1B). If the worker number of the traits is indeed small, each worker should explain a large proportion of the trait variance and be readily observed. We examined 54 traits that each had 1–3 observed workers and found that the trait variance explained by the observed workers was invariably small, comparable to or even slightly lower than the average number 3.4% of all traits (fig. 4B). Thus, these traits should have many workers; our O-strategy failed to observe them because they did not co-express such that the trait variance explained by each individual worker is too small to be detected. The idea of no worker co-expression, however, cannot be directly tested for these traits because the workers were not observed. We reasoned that the workers of a trait should in general explain more trait variance than nonworkers. We thus, to make a fair comparison between traits, selected for every trait the top 100 genes with the strongest expression–trait correlations. We called these genes the “most probable” workers and calculated their pairwise co-expression levels (see Materials and Methods). In line with our prediction, the observed worker number of a trait was well explained by the co-expression level of the most probable workers found for the trait (Spearman’s ρ = 0.76, n = 501, P < 10⁻¹⁶; fig. 4C). The result was essentially the same when the top 50 or top 200 most probable workers were analyzed (supplementary fig. S5, Supplementary Material online).

Because gene co-expression is unlikely to evolve/remain without selective constraints, such worker co-expression can only be strong for traits that are subject to strong selection. If worker co-expression underlies worker tractability, the likelihood that workers are identifiable by O-strategy, we would expect more observed workers for traits more related to fitness. We used cell growth rate as a proxy for fitness, which is reasonable for the single-celled yeast (Giaever et al. 2002), and calculated the relatedness to fitness for each of the traits (supplementary table S6, Supplementary Material online; see Materials and Methods). Traits that are strongly coupled with fitness have a large absolute value of the calculated relatedness. Remarkably, the number of observed workers of a trait was largely explained by the trait’s relatedness to fitness (Spearman’s ρ = 0.89, n = 501, P < 10⁻¹⁶). There were typically several hundred observed workers for a trait tightly coupled to fitness but virtually zero for traits with no significant correlation to fitness (fig. 4D). This pattern remained when only exemplar traits were considered (supplementary fig. S6, Supplementary Material online). The result was not due to the different within-mutant variation (measuring noise) or across-mutant variation of the traits (supplementary figs. S7 and S8, Supplementary Material online). In addition, the nearly three orders of magnitude differences in the worker number cannot be explained by the potential false positives in the identification of workers, because the false positive rate is unlikely to be ∼100%. Again, one may argue that the observation might be simply due to the common expression responses to growth reduction, which affect fitness-coupled traits but not fitness-uncoupled traits. This is, however, not true because fitness-coupled traits have quite different observed workers (supplementary fig. S9A, Supplementary Material online). To avoid the potential effects of unknown common confounding factors, we excluded from the analysis all genes that are observed workers of more than one exemplar trait. This conservative analysis resulted in a qualitatively unchanged pattern (supplementary fig. S9B, Supplementary Material online). We noted that the large number of observed workers is somewhat expected for fitness-coupled traits since many genes are known for controlling the yeast fitness (Castrillo et al. 2007; Levy and Barkai 2009). Hence, the most striking signal here is the absence of observed workers for nearly all fitness-uncoupled traits. Although some traits may happen to have few workers because of unidentified factors, it is unlikely that such factors affect all fitness-uncoupled traits that represent a diverse profile of the yeast morphology (Ohya et al. 2005). Therefore, the selection-dependent co-expression hypothesis seems to be the most reasonable explanation. Specifically, for a trait with a large number of workers, the workers are tractable by O-strategy only when they are organized by natural selection into a small number of co-expression modules. The lack of selective constraints results in poor worker co-expression such that individual workers cannot account for a tractable proportion of the trait variance, leading to the failure of O-strategy. Note that for simplicity, throughout the manuscript, fitness-coupled or fitness-uncoupled traits refer to those that are strongly or weakly coupled with cell growth rate. We are fully aware that all traits are fitness-coupled to some extent.

Worker Co-Expression Is Managed by Coordinating Supervisors

Mechanistically, worker co-expression should be managed in trans by supervisors. For a given trait some of the supervisors may contribute to worker co-expression (coordinating supervisors), whereas the others do not (noncoordinating supervisors). To achieve worker co-expression, coordinating supervisors should have congruent regulation profiles to build an “expression linkage” for the workers; noncoordinating supervisors with incongruent regulation profiles would necessarily undermine the expression linkage (fig. 5A). Coordinating supervisors are supposed to be recruited/maintained by strong selection, because their congruent regulation profiles for managing worker co-expression are unlikely to evolve/remain without selective constraints. However, the interaction between noncoordinating supervisors and workers may evolve passively with little selective constraints (Wagner 2003; Lynch 2007), which is plausible considering the dense transcription factor binding sites on promoters (Harbison et al. 2004).

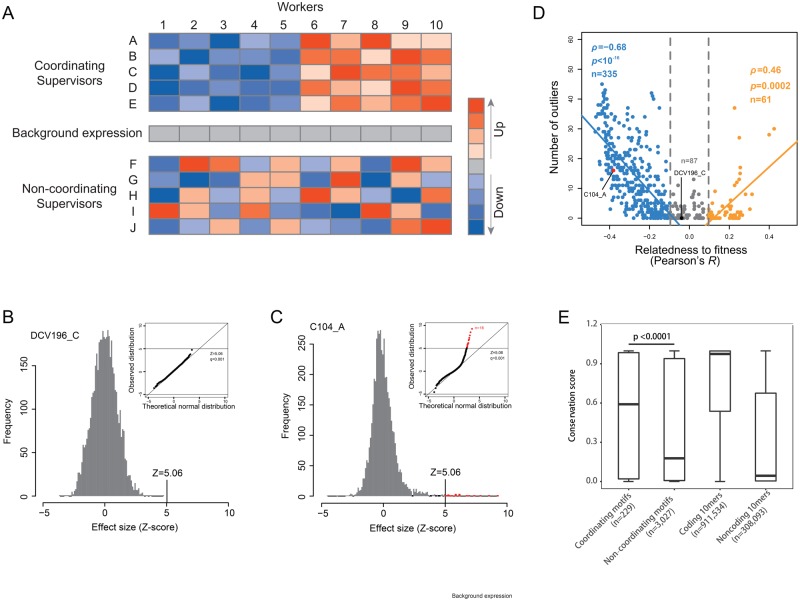
Fig. 5.

Genes showing outlier effects are found primarily for fitness-coupled traits. (A) A cartoon shows the proposed feature of coordinating versus noncoordinating supervisors. Coordinating supervisors with congruent regulation profiles are able to build an “expression linkage” of the workers to ensure worker co-expression, whereas noncoordinating supervisors with incongruent regulation profiles would break such expression linkage. (B) Frequency distribution of the effect sizes and a Q–Q plot comparing this distribution with the Gaussian approximation for trait DCV196_C. (C) The same parameters are shown as in Panel B, except for trait C104_A in which some outlier effects (highlighted in red) are found. (D) Fitness coupling determines outlier number. Each dot represents a trait, and a total of 483 trait are included. (E) Coordinating motifs are more conserved than noncoordinating motifs. Box plots of the conservation scores of coordinating motifs, noncoordinating motifs, 10-mer random sequences picked from coding regions of Saccharomyces cerevisiae, and 10-mer random sequences picked from noncoding regions of S. cerevisiae, respectively. Box-plots are presented with the horizontal bold line showing the median. Mann–Whitney U test was used to compute the P-value.

Because no worker co-expression was observed, no coordinating supervisors were expected for fitness-uncoupled traits. For a fitness-coupled trait, we expected some disproportionately large deletion effects from coordinating supervisors. This is because trait as a function of workers’ expression could be affected by the workers in two directions (increase or decrease). Selection may have shaped the regulation profile of coordinating supervisors such that, when a coordinating supervisor is perturbed, the affected workers would all push the focal trait coherently in the same direction to generate large effects. Such coherent effects from various workers would be unlikely when a noncoordinating supervisor is perturbed.

To search for such disproportionately large deletion effects, we modeled for each trait the density distribution of the effect sizes of the 4,718 gene deletions, using a Gaussian function that is commonly used to model quantitative traits (Turelli 1985; see Materials and Methods). We used quantile–quantile plots to compare the Gaussian approximation with the true distribution and found that the two distributions often fit each other reasonably well (fig. 5B). For some traits, however, disproportionately large effects far beyond the Gaussian approximation were observed (fig. 5C). For each trait, we defined outlier effects as those with an absolute Z-score > 5.06, which corresponds to P = 2.12 × 10⁻⁷ in the standard Gaussian distribution or q = 0.001 after Bonferroni correction for multiple testing (q = P × 4,718). The number of outliers found for each trait ranged from 0 to ∼50 (supplementary table S7, Supplementary Material online). Interestingly, outliers were found primarily for traits tightly coupled with fitness (Spearman’s ρ = 0.85, n = 483, P < 10⁻¹⁶; fig. 5D). The pattern remained when the Z-score cut-off used for defining outliers was changed to 4.56 (q < 0.005) or 4.06 (q < 0.01) (supplementary fig. S10, Supplementary Material online), and when only exemplar traits were analyzed (supplementary fig. S11, Supplementary Material online). Because this pattern could be possibly explained by a scenario that the presence of outliers caused strong fitness coupling, we recalculated each trait’s relatedness to fitness after excluding the outlier mutants (see Materials and Methods). The recalculated values were highly correlated to the original values (supplementary fig. S12, Supplementary Material online), a result in support of the opposite scenario that strong fitness coupling or selective constraint accounts for the presence of outliers. Thus, the genes with outlier deletion effects appeared to be good candidates for coordinating supervisors.

To further demonstrate the role of selection in maintaining the candidate coordinating supervisors/outliers we checked the sequence conservation of the binding motifs of some transcript factors (TFs) on the target genes (see Materials and Methods). We focused on the motifs where the TF is an observed supervisor of a trait assessed here and the target gene is an observed worker of the same trait. A motif was designated as “coordinating motif” if the TF is an observed supervisor with outlier deletion effect as defined above and the target gene is an observed worker of the same trait. Those that satisfied the criteria in none of the traits we assessed were designated as “noncoordinating motif.” A total of 229 nonredundant coordinating motifs and 3,027 nonredundant noncoordinating motifs were obtained (supplementary table S8, Supplementary Material online). We found that the coordinating motifs are overall much more conserved than the noncoordinating motifs as well as random noncoding sequences (fig. 5E and supplementary fig. S13, Supplementary Material online).

Because coordinating supervisors were defined by their congruent regulation profiles, we expected congruent expression responses upon deleting different candidate coordinating supervisors of a trait. Since only ∼30% of the yeast mutants have expression profiles available, for a trait the maximal number of candidate coordinating supervisors that can be analyzed here was 17. We thus selected for every trait 20 observed supervisors that have the largest deletion effects in one direction and also have corresponding expression profiles (see Materials and Methods). The proportions of candidate coordinating supervisors out of the 20 selected supervisors ranged from 0% to ∼90%, depending on the trait’s relatedness to fitness (fig. 6A). For each trait, we identified those genes with congruently changed expression across the deletion mutants of the 20 supervisors, with a statistical threshold under which the expected number of such genes is slightly smaller than one (0.6). We obtained typically dozens of congruently responsive genes when the 20 selected supervisors are mostly candidate coordinating supervisors, but very few for traits without candidate coordinating supervisors (Spearman’s ρ = 0.74, n = 129, P < 10⁻¹⁶; fig. 6B). The difference was unrelated to the overall expression changes in the mutants because for each trait the total number of responsive genes in the 20 selected mutants was similar (supplementary fig. S14, Supplementary Material online). As expected, ∼60% of the congruently responsive genes were also previously observed workers of the corresponding traits (P < 0.001; Permutation test; fig. 6C). Thus, the genes with outlier deletion effects are indeed enriched with coordinating supervisors that can regulate workers congruently.

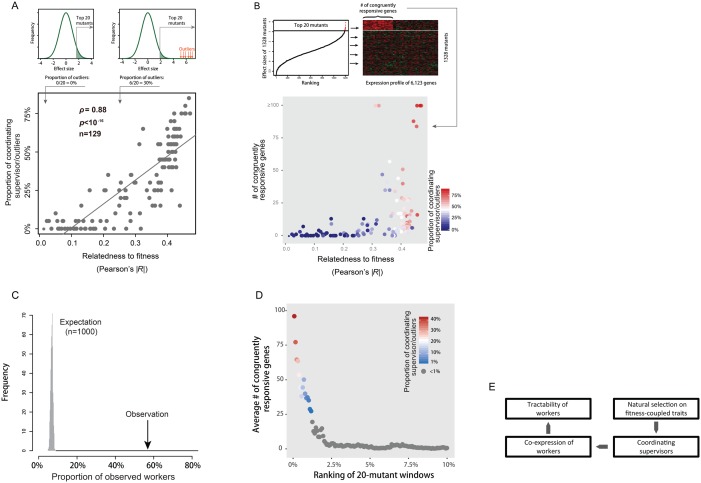
Fig. 6.

Identification of coordinating supervisors with congruent regulation profiles. (A) The proportion of candidate coordinating supervisors/outliers among the top 20 selected supervisors of a trait is a function of the trait’s relatedness to fitness. Each dot represents a trait. (B) The number of congruently responsive genes upon deleting the selected supervisors of a trait is positively correlated to the proportion of candidate coordinating supervisors/outliers among the 20 selected supervisors of the trait (Spearman’s ρ = 0.74, n = 129, P < 10⁻¹⁶) or the trait’s relatedness to fitness (Spearman’s ρ = 0.65, n = 129, P < 10⁻¹⁶). Each dot represents a trait. (C) The congruently responsive genes are enriched with observed workers of the same traits. The average overlapping rate of the 129 traits is shown at the x-axis, with the expectation derived from reshuffling the genes of interest across the different traits. (D) There is a rapid decay of the number of congruently responsive genes with the reduction of the proportion of coordinating supervisors/outliers. The y-axis shows the mean number of congruently responsive genes of the 17 traits, and the x-axis shows the ranking the first mutant of a 20-mutant window among all mutants with available expression profiles in terms of the deletion effects on the focal trait. (E) The logic chain of Part II analyses.

It is possible to find some coordinating supervisors with smaller deletion effects. We examined the 17 exemplar traits with the absolute relatedness to fitness >0.3. For each trait, we started from the mutants of the largest effects and used a sliding-window analysis to track the number of congruently responsive genes as a function of the proportion of candidate coordinating supervisors in each window (see Materials and Methods). There was a rapid decay of the number of congruently responsive genes with the reduction of the proportion of candidate coordinating supervisors, suggesting no apparent clustering of coordinating supervisors in the mutant windows of smaller deletion effects (fig. 6D).

A chain of logics helps summarize the Part II analyses (fig. 6E): For a typical complex trait controlled by many workers, the extent to which the workers are tractable by O-strategy is determined by worker co-expression, which is managed by coordinating supervisors that are recruited and/or maintained by natural selection, a process that is only effective when the trait is tightly coupled with fitness.

Discussion

This study suggests a selection-dependent supervisor–worker gene architecture underlying the “making” of a complex trait (fig. 7). Specifically, a trait is often controlled directly by a large number of workers, the expression of which is controlled by supervisors of two types: Coordinating supervisors help organize the large number of workers into a small number of co-expression modules such that each individual worker has a strong correlation with the trait (hence identifiable by O-strategy); in contrast, noncoordinating supervisors each with a unique regulation profile lead to no worker co-expression such that individual workers would show no tractable correlation with the trait (hence resistant to O-strategy). A critical issue here is that coordinating supervisors must be recruited and/or maintained by natural selection, whereas noncoordinating supervisors may evolve neutrally without selective constraints.

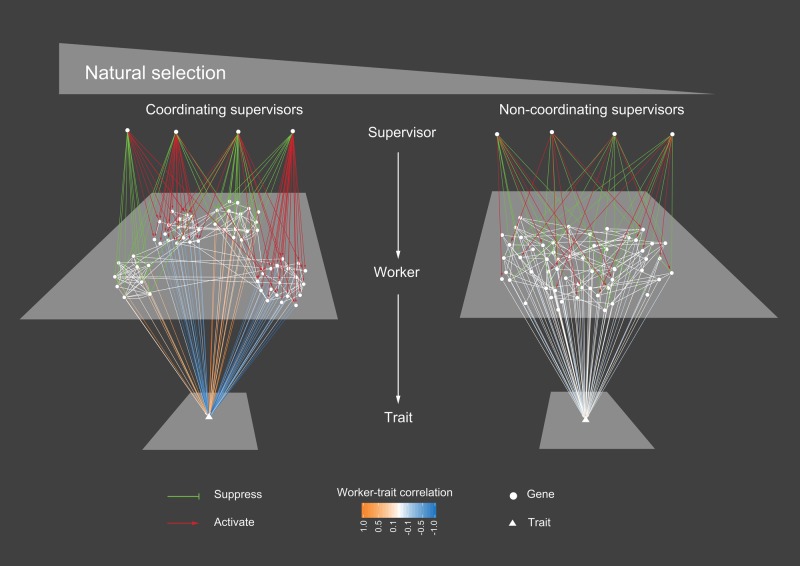
Fig. 7.

The selection-dependent supervisor–worker gene architecture underlying the making of a trait. With natural selection, coordinating supervisors are recruited/maintained to organize the ∼50 workers into four co-expression modules, such that each individual worker shows a strong correlation with the trait. When selection is absent, the ∼50 workers are controlled exclusively by noncoordinating supervisors and thus express independently. As a result, all workers show a weak correlation with the trait.

A few issues need to be clarified. First, because of data availability, we used mRNA level to represent gene activity and studied only morphological traits of the single-celled organism yeast. Further efforts are necessary to test the generality of our findings in other systems. In addition, although the gene architecture is for describing the making of a complex trait, it is not readily clear how it could be applied to natural populations affected by standing genetic variations. Second, the supervisor–worker gene architecture is an oversimplification of the regulatory structure underlying a complex trait: A supervisor regulates only some of the workers and a worker is regulated only by some of the supervisors; also, interactions among supervisors and among workers are ignored. In addition, we note that asking if an individual gene is supervisor or worker is not meaningful; supervisors and workers as two gene groups are most meaningful in the context of the P-strategy and O-strategy by which they each are identified. The dichotomy between the observed supervisors and workers in the current study relied on the stringent statistical thresholds used in both research strategies. Nevertheless, although the mutual exclusion of supervisors and workers is emphasized here, we do not deny the fact that some genes, like the three super-informative genes found in figure 1D, can be sensitive to both P-strategy and O-strategy. This also partly explains the occasional successes in studies without considering the proposed gene architecture. These being said, we draw two robust major conclusions: 1) for a trait controlled by a large number of workers, the individual workers are tractable via O-strategy only when they are organized into a limited number of co-expression modules; 2) the worker co-expression/coordination requires trans-factors (coordinating supervisors) that must be recruited and/or maintained by natural selection. The first conclusion, as we explained before, represents a rule of statistics. The second conclusion represents a rule of evolution, because, without selective constraints, any coordination in a living system would degenerate.

The supervisor–worker gene architecture for describing the making of a trait directly addresses the third challenge raised at the beginning of the article. For the remaining two challenges we start from the second one with two angles: The first angle is about the negative genes produced by P-strategy. P-strategy must rely on statistics to test the null hypothesis that the gene mutated/perturbed has absolutely no effects on the focal trait. This null hypothesis, however, doesn’t appear to be appropriate for a cellular system in which all genes are connected with each other to influence all traits (Fisher 1999). Consistently, the continuous and bell-shape distribution of the gene deletion effects, as in figure 5B and C, for the vast majority of the yeast traits suggests that the deletion effects are quantitatively rather than qualitatively different. Thus, the working practice of P-strategy is not to separate genes with effects from those without effects, but to separate genes of large effects from those of small effects. Whereas genes of large mutational effects could be of more practical value, genes of small mutational effects, like the workers, could explain more trait variance and provide direct mechanistic understandings. As the “gold standard” in genetic studies P-strategy reflects the classical reductionism view on a living system, with a belief that the whole is the sum of all broken parts. It is time to adopt a systems view by including all genes’ activity to understand the total variance.

To further demonstrate the false negatives of P-strategy we took advantage of the huge number of gene–trait relationships available in this study. As what a typical P-strategy would do, we compared a certain number (50) of individual cells of a given gene deletion mutant with the same number of wild-type cells. We detected a large number of both significant and insignificant deletion effects under the statistical cutoff of P < 0.001 (see Materials and Methods). As expected, with the increasing deletion effect size the frequency of significant signals increased substantially (fig. 8A). To gauge the extent to which the insignificant signals are false negatives we designed a simulation. Specifically, we modified the trait values of all wild-type cells (up to ∼16,000) by adding a given effect size to form pseudomutants, and then compared 50 randomly chosen pseudomutant cells with a set of 50 randomly chosen wild-type cells under the same statistical setting (see Materials and Methods). For the various traits examined we detected both significant and insignificant differences, which represent the variation of samplings from pseudomutants that by definition have true differences from the wild-types. In other words, the insignificant signals between the pseudomutants and wild-types represent false negatives of the P-strategy. Interestingly, the ratio of significant signals to insignificant signals observed for the pseudomutants was highly similar to that of the real gene deletion mutants (fig. 8B), suggesting that the insignificant signals of the real mutants be well explained by false negatives.

The other angle is about the positive genes produced by P-strategy. These genes tend to be supervisors of a trait. Whereas coordinating supervisors are recruited/maintained by selection, noncoordinating ones may often be of passive origin and evolve under little selective constraints. It is unclear how a noncoordinating supervisor revealed in laboratory would function in nature. The answer to this question would be critical for understanding why often a very limited number genes are used to drive the evolution of a given phenotype in nature even when the phenotype can be affected by a large number of genes (Stern and Orgogozo 2009). Thus, the field of molecular genetics, which has long been dominated by mechanistic perspectives, would make more sense in the light of evolution. This notion reminds us of a recently proposed idea that the genetic effects of a gene could be attributed to either the native functions that are built/maintained by natural selection or the “spurious” functions that are created by the given genetic manipulation (He 2016).

The last to-be-discussed challenge is about the O-strategy. As we have demonstrated, O-strategy will perform well only for fitness-coupled traits in which the workers are coordinated. In other words, for a trait determined by many workers, the effect of individual workers on the trait will appear stable only when the workers are coordinated to form functional modules/pathways. Suppose there is a trait controlled by ten workers that each have two functional statuses, on or off. The absence of coordination across the ten workers would lead to a total of 2¹⁰ = 1,024 different functional statuses underlying the trait, and the effect of an individual worker would be always epistatic to the other workers. Thus, context-dependent findings, a major confounding factor in current molecular cell biology (Freedman et al. 2015), appear to be an unavoidable outcome of the lack of selective constraints, which leads to the lack of coordination.

In summary, we studied the gene–expression–trait relationships from the perspective of trait making, and showed that the genes found for a trait are often decoupled from the expressions underlying the trait, and that the expressions underlying a trait are tractable only if they are coordinated by natural selection. The second issue reminds biologists of a simple fact: The order of a living system relies on natural selection and the lack of selection inevitably leads to disorder, and the internal order and disorder determine the success of the external research efforts. This notion has special implications to human biology because selection is inefficient in humans due to the small effective population size (Lynch and Conery 2003) and because aging-associated diseases or traits are often of little fitness relevance but of high interest to researchers (Finch 2010; Lopez-Otin et al. 2013). One may argue that the disorder is exactly the challenges we need to address, but the lack of selective constraints predicts that it might be ad hoc phenomena sensitive to genetic backgrounds (Mackay 2014). A robust discussion of both the necessity and the strategy for studying such phenomena is needed.

Materials and Methods

Data

A single-gene deletion stock of yeast S. cerevisiae with 4,718 mutant strains that each lacked a nonessential gene was generated by Giaever et al. (2002). To measure the cell growth rates of the 4,718 mutants in the rich medium YPD (yeast extract, peptone, and dextrose), Bar-seq-based data produced by Qian et al. (2012) were used. The 501 morphological traits of the mutants were characterized by Ohya et al. (2005) (SCMD). The PIGs were defined by Ho and Zhang (2014) under a stringent statistical cut-off for 220 out of the 501 traits; the remaining 281 traits contain no information necessary for statistics. We reproduced the analysis and obtained the same set of supervisors in 216 out of the 220 traits using the updated data in SCMD. Only these 216 traits were considered when defining PIGs. The microarray-based expression profiles of 1,484 of the single-gene deletion mutants were generated by Kemmeren et al. (2014).

Define OIGs

For nearly all of the examined morphological traits, a bell-shaped frequency distribution of the trait values among the 4,718 mutants was found, with the median trait value close to that of wild-type (supplementary fig. S15, Supplementary Material online). There was a total of 1,327 mutants, each with the expression profile generated by Kemmeren et al. (2014) as well as the information of cell growth rate. We randomly divided the 1,327 yeast mutants into two sets, placing two thirds of the mutants (884) in Set #1 and one third (443) in Set #2 (supplementary table S9, Supplementary Material online). There are 6,123 yeast genes on the microarray chip used by Kemmeren et al. (2014). We first generated 500 artificial data sets, each containing 443 strains picked randomly from the 884 Set #1 strains with replacements. We calculated Pearson’s R between the expression level and the trait value for each of the 6,123 genes in each of the 501 traits using each the 500 artificial data sets. The R-values were then transformed into P-values using a t-test, resulting in 500 P-values for each gene in a trait. We defined the correlation robustness (r-value) of a gene as the harmonic mean of its P-values after dropping both the highest and the lowest 5% of its 500 P-values, which was then multiplied by 6,123 for multiple testing correction. Genes with corrected r-values < 0.01 were considered putative O-strategy identified genes (pOIGs). To further reduce false positives, the pOIGs with a significant (P < 0.01) expression–trait correlation (Pearson’s R) in the independent Set #2 mutants were then defined as OIGs. The Pearson’s R in Set #2 mutants was used to derive the trait variance explained by an OIG (R²). The co-expression level between two OIGs or two the most probable OIGs (the absolute Pearson’s R) was also based on the 443 Set #2 mutants.

Morphological traits are not independent; for instance, the size and the diameter of a cell are correlated. To reduce correlated traits, we used an unsupervised affinity propagation strategy proposed by Frey and Dueck (2007) to cluster the 501 traits based on the r-values of the 6,123 yeast genes computed for a trait, resulting in a total of 57 clusters each with an exemplar trait. Twenty-three exemplars have both OIG and PIG information.

The frequency distribution of the cell growth rates of the yeast mutants was highly biased, with the majority close to the rate of wild-type. We thus computed the expression-growth rate correlation using a univariate Cox regression model that emphasizes differences between two categories, with growth rate serving as the parameter “time.” In this mode, strains with a growth rate <0.9 were weighted as “event = 1,” and all others were weighted as “event = 0.” Specifically, we performed Cox regression analysis using the 500 artificial data sets described above and obtained 500 P-values for every yeast gene. The corrected r-value was computed as described above. A total of 911 genes each with a corrected r-value < 0.001 were defined as OIGs of cell growth rate.

Define Gene Regulatory Relationships

Although there could be various definitions for gene regulatory relationships, we here considered a simple one based solely on the differential expression upon gene deletion. Specifically, gene A is called the downstream target of gene B and B the upstream regulator of A if gene A shows a significant expression change (P < 0.0001 as provided in the original data) in the mutant lacking gene B. The cutoff of P < 0.0001 holds throughout this study for assigning gene regulatory relationships. The average feature of a trait’s all PIGs (or OIGs) was used to represent the PIGs (or OIGs) of the trait.

To assess the PIG–OIG regulatory architecture we focused on the 108 traits with ≥ 10 OIGs and ≥ 10 PIGs. The 1,327 mutants with expression profiles were considered and the mean of the 108 traits were computed. On average a PIG regulated 53 OIGs and 36.8 PIGs, and an OIG regulated 17.7 OIGs and 15.3 PIGs; the expected numbers were 20.4 ± 2, 17.8 ± 1.3, 20.4 ± 3.3, and 17.8 ± 3.5 (mean ± SD of 1,000 simulations), respectively. On average an OIG was regulated by 20.4 PIGs and 3.0 OIGs, and a PIG was regulated by 10.3 PIGs and 1.4 OIGs; the expected numbers were 9.2 ± 0.7, 3.4 ± 0.6, 5.0 ± 0.3, and 1.8 ± 0.3 (mean ± SD of 1,000 simulations), respectively. The expected numbers were obtained by reshuffling the 1,327 mutants’ expression profiles while maintaining the identity of the deleted genes. The simulation was repeated one thousand times to obtain the mean and standard deviation.

Gain Mechanistic Understandings Using Worker Modules

Yeast PPIs were downloaded from BioGrid (http://thebiogrid.org/). For each trait, the PPIs among observed workers were examined, and protein modules were separated using an order statistics local optimization method (OSLOM) proposed by Lancichinetti et al. (2011) with default settings. To annotate the modules, we performed GO enrichment analysis using BinGO (Maere et al. 2005) and Cytoscape (Shannon et al. 2003).

A total of seven modules were identified for cell growth rate from the PPI network comprising the 911 observed workers. Six modules appeared to be highly enriched with functionally similar proteins under a false discovery rate of 0.001, all of which are related to a critical biogenesis process. The ED of a worker module between mutant and wild-type was defined as the normalized Euclidian distance:

$$\mathrm{E}\mathrm{D}=\frac{1}{n}{\left({\sum }_{i=1}^n{\left({\mathrm{l}\mathrm{o}\mathrm{g}}_2\frac{{MI}_i}{{WI}_i}\right)}^2\right)}^{1/2},$$

where MI_i is the expression level of gene i in the mutant, WI_i is the expression level of gene i in wild-type, and n is the number of genes in the module. The Pearson correlation analysis between cell growth rate and module activity (i.e., ED) was conducted using the 443 Set #2 mutants.

Calculate Trait’s Relatedness to Fitness

Because in this study all cellular traits were measured in YPD, we used cell growth rate in YPD as a proxy of fitness. Given the bell-shaped distribution of a morphological trait, where the wild-type trait value is almost always located in the middle, both an increase and a decrease of a trait value relative to wild-type could reduce fitness. Thus, for each trait, we divided the 4,718 mutants into two equal halves according to their trait values and calculated Pearson’s R between the trait value and the fitness of each half of the mutants separately, resulting in two Rs for each trait. The half showing the larger R (absolute value) was designated the fitness-more-coupled side of the trait, and the other half was designated the fitness-less-coupled side of the trait. We used the R of the fitness-more-coupled side to represent the relatedness of a trait to fitness. To exclude the potential effects of outlier trait values on the estimation of fitness coupling, for each trait, we also removed the top 50 trait values from each side and recalculated the trait’s relatedness to fitness.

Assess Data Noise in the 501 Traits As Well As Its Potential Consequences

To characterize yeast morphological traits, Ohya et al. examined an average of 400 individual cells for each mutant. The trait value of a given mutant is the mean trait value of all examined cells. Despite the generally large number of examined cells, for some traits, there were only a few tens of informative cells, which may have affected the reliability of the measurements. To address this issue, we randomly divided the examined cells for each mutant into two equal halves and computed the morphological traits of each mutant in each half separately. We then compared the trait values obtained from the two halves. The level of consistency between the two halves varied substantially among traits but was not dependent on a trait’s relatedness to fitness.

Characterize Coordinating and Noncoordinating Supervisors

We excluded 18 traits whose effect size distribution is not unimodal (P < 0.05, Hartigan’s Dip-test), leaving 483 traits for further analyses. We normalized the raw trait value X_ij of mutant j in trait i to Z-score effect size using:

$$Z_{i,j}=\frac{\left(X_{i,j}-M_i\right)}{{\sigma }_i}\mathrm{ }\mathrm{ }[i\in \left(1\dots 483\right),j\in \left(1\dots 4718\right)],$$

where M_i and σ_i are the mean and standard deviation of the raw trait values in trait i among the 4,718 mutants. The outlier effects are defined based on an absolute Z-score > 5.06, which corresponds to P < 0.001 × 1/4,718 or q < 0.001 according to a standard Gaussian distribution. Accordingly, the supervisors with an absolute Z-score > 5.06 are considered as outlier supervisors, and the remainder are considered as nonoutlier supervisors.

Congruent expression responses are expected upon deleting different outlier supervisors of the same traits if the outliers are coordinating supervisors. For the 216 traits with supervisor information, we excluded 20 traits that each had outlier supervisors in both the fitness-more-coupled and fitness-less-coupled sides, just to make the analysis simple (there is one outlier supervisor observed in the fitness-less-coupled side for all the 20 traits). For each trait, we selected the top 20 supervisors from the fitness-more-coupled side; they have the largest effect sizes and also available expression profiles. We excluded 67 traits that have <20 such supervisors, remaining 216 – 20 – 67 = 129 traits. For each trait, the genes with higher or lower expression level in the mutants of the 20 selected supervisors than the remaining 1,307 mutants were identified as congruently responsive genes of the trait under the statistical threshold P < 0.0001 (T test). A total of 1,060 nonredundant yeast genes were identified as congruently responsive genes in at least one of the 129 traits, with the mean and median numbers of traits for an involved gene being 2.97 and 2, respectively.

In the sliding window analysis, for each trait the 1,327 mutants were sorted decreasingly according the focal trait. The 20 mutants in the defined window were compared with all mutants with smaller trait values to obtain the congruently responsive genes under the same statistical threshold. A total of 133 windows were tested, so it was a 20 versus 1,307 comparison at the beginning but a 20 versus 1,175 comparison in the end. Although this treatment would cause bias, the bias should be small and unable to overturn the conclusion.

Analyze the Conservation of the DNA Motifs That Mediate Supervisor–Worker Interactions

The PFM files describing the typically 5–15 bp binding motif sequences of 256 S. cerevisiae proteins or protein complexes were downloaded from the Yeast Transcription Factor Specificity Compendium (YeTFaSCo; http://yetfasco.ccbr.utoronto.ca/). For each of the 6,123 yeast genes the 500 base pairs upstream of the transcription starting site of the gene were considered as promoter of the gene. Overlapping promoters were excluded from further analysis. TF binding motifs on each promoter were annotated according to the Track files of YeTFaSco and were used to define TF-target gene interactions. We excluded from further analysis the TF-target gene interactions if the target genes show no significant expression changes (P < 0.0001) in the TF deletion mutants.

We considered those TF-target gene interactions when the TF is an observed supervisor of a trait examined in the current study and the target gene is an observed worker of the same trait. A motif mediating the corresponding TF-target gene interaction was designated as coordinating motif if the TF is a coordinating supervisor (i.e., outlier) of a trait and the target gene is an observed worker of the same trait. The remaining motifs that were not designated as a coordinating motif are termed noncoordinating motifs, where the TFs act invariably as a noncoordinating supervisor of the target gene for all traits examined in the current study.

The conservation score of a motif is the mean conservation levels of all positions of the motif. The conservation level of a genomic position of the yeast is annotated in the multiple alignment tracks of the UCSC genome browser (https://genome.ucsc.edu/), and is the Adam S’s phylogenetic HMM score (Siepel and Haussler 2004) that can be extracted from the UCSC conservation track.

Evaluation of the False Negatives of P-Strategy

There are ∼400 individual cells for each mutant and a pool of ∼16,000 wild-type cells examined by Ohya et al. (2005), and the trait information of individual cells is available for 216 traits. The trait value of a mutant or the wild-type is the mean trait value of all individual cells of the strain. Because the trait value of wild-type is often slightly different from the mean trait value of the 4,718 mutants, all Z-score effect sizes of a trait were first added (or subtracted) a number to ensure that the wild-type’s Z = 0. For a mutant with a given adjusted effect size Z on a trait, we compared the raw trait values between its 50 randomly selected cells and 50 random wild-type cells, and used P < 0.001 (Mann–Whitney U test) to define statistically significant signals. This comparison was conducted for all 4,718 × 216 mutant-trait combinations, and the proportion of significant signals was calculated for all Zs within a given Z-score interval (for simplicity the absolute Z was used for assigning Z-score intervals: 0–0.05, 0.05–0.1, 0.1–0.15, 0.15–0.2, 0.2–0.25, 0.25–0.3, 0.3–0.35, 0.35–0.4, 0.4–0.45, 0.45–0.5, 0.5–0.55, 0.55–0.6, 0.6–0.65, 0.65–0.7, 0.7–0.77). To estimate the expected proportion of significant signals when the effect size is Z (= 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.77, respectively), for a given trait we compared the raw trait values between 50 random wild-type cells and another set of 50 random wild-type cells each being added an effect size of Zσ_i (i.e., pseudomutants), where Z is the focal effect size, and σ_i is the standard deviation of the 4,718 mutants of the focal trait. The same statistical cutoff was applied to define significant signals, and the proportion of significant signals was calculated based on all signals of the 216 traits. This simulation was repeated 100 times to get the confidence intervals for each Z. Because the variance was difficult to model for the pseudomutants with a given effect size, we assumed the same variance between the pseudomutants and the wild-type population, which may cause strong bias when the given effect size is large. Thus, we limited our analysis for Z = 0–0.77, which covers 50% of the data with Z > 0 in a standard Gaussian distribution.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.