Recombination Alters the Dynamics of Adaptation on Standing Variation in Laboratory Yeast Populations

Abstract

The rates and selective effects of beneficial mutations, together with population genetic factors such as population size and recombination rate, determine the outcomes of adaptation and the signatures this process leaves in patterns of genetic diversity. Previous experimental studies of microbial evolution have focused primarily on initially clonal populations, finding that adaptation is characterized by new strongly selected beneficial mutations that sweep rapidly to fixation. Here, we study evolution in diverse outcrossed yeast populations, tracking the rate and genetic basis of adaptation over time. We combine time-serial measurements of fitness and allele frequency changes in 18 populations of budding yeast evolved at different outcrossing rates to infer the drivers of adaptation on standing genetic variation. In contrast to initially clonal populations, we find that adaptation is driven by a large number of weakly selected, linked variants. Populations undergoing different rates of outcrossing make use of this selected variation differently: whereas asexual populations evolve via rapid, inefficient, and highly variable fixation of clones, sexual populations adapt continuously by gradually breaking down linkage disequilibrium between selected variants. Our results demonstrate how recombination can sustain adaptation over long timescales by inducing a transition from selection on genotypes to selection on individual alleles, and show how pervasive linked selection can affect evolutionary dynamics.

Introduction

Populations adapt to new environments by acquiring and amplifying adaptive variants, derived either from new mutations or from standing genetic variation. Sex can significantly alter the evolutionary dynamics of this process by reducing linkage disequilibrium through recombination, a phenomenon that has been appreciated for over a century (Weismann 1891; Fisher 1930; Muller 1932). In particular, recombination can improve the efficiency of selection by combining beneficial mutations onto a single genetic background (Fisher 1930; Muller 1932; Crow and Kimura 1965; Hill and Robertson 1966), by unlinking beneficial drivers from deleterious passengers (Peck 1994; Johnson and Barton 2002), or by uncovering fortuitous combinations of existing genetic variants (Neher and Shraiman 2009). The relative importance of these effects depends on the genetic architecture of fitness: that is, how common and how strongly selected mutations tend to be, along with their patterns of linkage and epistasis.

The effect of recombination on adaptation has been studied extensively, particularly in the context of the evolution of sex (Fisher 1930; Muller 1932; Bell 1982). Historically, theoretical studies in this area assumed that only a small number of selected sites were present in the population at a time (Crow and Kimura 1965; Hill and Robertson 1966; Eshel and Feldman 1970; Karlin 1975; Barton 1995; Green and Noakes 1995), or that the recombination rate was high enough for sites to be near linkage equilibrium (Kimura 1965; Neher and Shraiman 2011). Although important stepping stones, these constraints often poorly describe evolving populations, particularly when selection acts on complex traits or standing variation. In these cases, evidence suggests that beneficial alleles are generally neither rare nor fully independent, and instead typically consist of a large number of weakly selected, interacting loci (Barton and Keightley 2002; Moose et al. 2004; Carlborg et al. 2006; Falconer and Mackay 2009; Johansson et al. 2010; Huang et al. 2012).

Recently, a number of studies have analyzed the effect of recombination in populations with many selected sites in linkage disequilibrium (Rouzine and Coffin 2005; Neher and Shraiman 2009, 2011; Neher et al. 2010, 2013a,b; Weissman and Hallatschek 2014), focusing primarily on the rate of adaptation and patterns of genetic diversity. This work has predicted a strong adaptive advantage of rapid recombination (Rouzine and Coffin 2005; Neher et al. 2010; Weissman and Hallatschek 2014) and an increased efficiency of selection on weakly selected variation (Neher and Shraiman 2011), brought about in part by a transition between selection on entire genotypes at low recombination rates to selection on alleles at high ones (Neher and Shraiman 2009; Neher et al. 2013b). However, the relationship between sex, adaptation rate, and genetic diversity is not well-understood for genetic architectures with significant epistatic or other non-additive interactions (although some simple epistatic models have been explored, e.g., Neher and Shraiman 2009; Neher et al. 2013b). More fundamentally, the molecular dynamics of linked selected sites are not well characterized even without epistasis.

Experimental work in laboratory evolved populations has helped to bridge this gap by directly measuring the effect of sex on adaptation. These studies have confirmed that sex does increase the adaptation rate in both outcrossed and initially clonal populations (Zeyl and Bell 1997; Colegrave 2002; Goddard et al. 2005; Cooper 2007; Morran et al. 2009; Gray and Goddard 2012; McDonald et al. 2016; Noel et al. 2017). By investigating the dependence of this effect on different environmental conditions (Zeyl and Bell 1997; Goddard et al. 2005; Morran et al. 2009; Gray and Goddard 2012) and population genetic parameters such as mutation rate (Cooper 2007; Morran et al. 2009; Gray and Goddard 2012), these studies provided indirect evidence for different mechanisms by which recombination improves the efficiency of selection. More recent work has combined measurements of population fitness with time-serial genetic analysis to directly investigate the effect of recombination on evolutionary dynamics at the sequence level (McDonald et al. 2016). This study found that periodic rounds of recombination alleviated clonal interference and disrupted “cohorts” of linked neutral and deleterious passengers, demonstrating a few molecular mechanisms underlying the adaptive advantage of sex.

By initiating populations from single clones, prior investigations of molecular dynamics focused on adaptation driven by new mutations. However, many adaptations in eukaryotic populations arise from selection on standing variation (Barrett and Schluter 2008), especially in cases of environmental shifts, admixture or hybridization events, or colonization of new environmental niches (Rieseberg et al. 2003; Hancock et al. 2010b; Domingues et al. 2012). Such standing variants are predicted to exhibit a variety of systematic differences relative to new mutations. For example, adaptation from standing variation is expected to comprise a much larger number of mutations of smaller effects (Hermisson and Pennings 2005). Because of the larger number of variants involved, the evolutionary dynamics of standing variants are more likely to be constrained by patterns of epistasis and pleiotropy, which may shift as the genetic composition of the population changes. These effects have been studied in the context of “moving phenotypic optimum” models of adaptation (Chevin and Hospital 2008), which predict dynamics that are rarely, if ever, observed in evolution experiments initiated from clones. Furthermore, although these epistatic effects are likely to be sensitive to linkage disequilibrium between selected variants, the interaction between epistasis and recombination in this context is poorly understood.

In short, a complete characterization of molecular dynamics in sexual populations requires an investigation of both new mutations and standing genetic variation. While evolution from clones depends on the distribution of newly arising mutations, adaptation in diverse populations is often sensitive to the composition of the existing genetic background. For some genetic backgrounds, the effect of sex on adaptation from standing variation can be predicted explicitly, particularly in the absence of dominance or epistatic effects. When selected mutations are sufficiently rare, linkage disequilibrium between drivers will remain small over a broad range of recombination rates. In this case, the molecular signature of selection can be characterized by its effect on linked neutral variation over time, which includes a depletion in genetic diversity peaked at selected loci (Maynard Smith and Haigh 1974; Gillespie 2000, 2001), and specific patterns of linkage disequilibrium in regions flanking adaptive drivers (Sabeti et al. 2002; Kim and Nielsen 2004). Lower recombination rates would increase linkage disequilibrium, causing larger decreases in genetic diversity (Maynard Smith and Haigh 1974). However, so long as selected variants do not clonally interfere (and epistatic effects are minimal), lower recombination rates should not significantly affect the dynamics of drivers, nor substantially change fitness trajectories or outcomes of adaptation (Kimura 1965; Neher and Shraiman 2011).

At higher densities of selected sites, linkage between drivers is more likely to skew patterns of adaptation. In this regime, more frequent recombination will generate more haplotypes with rare or unique combinations of favored alleles, increasing the variance in fitness and, correspondingly, the rate of adaptation (Fisher 1930). Additionally, lower recombination rates are still expected to bring about a greater reduction of genetic diversity (Neher et al. 2013b; Good et al. 2014). However, selected haplotypes are more likely to be comprised of several linked beneficial variants, which may result in depletions in heterozygosity that are broader and less sharply peaked than those caused by isolated drivers. Additionally, the selective effect of any individual allele is determined both by its intrinsic effect on fitness and linkage disequilibrium with other selected sites in the population (Neher and Shraiman 2011; Neher 2013). Changing patterns of linkage will then result in fitness effects that appear to vary over time, resembling frequency dependence or certain types of epistatic interactions. Exactly how the dynamics of drivers and passengers will change in this regime, and how this depends on the recombination rate, is generally unknown.

Certain patterns of epistasis, pleiotropy, or dominance may alter some of the predictions above. For example, synergistic epistasis may result in faster adaptation at lower recombination rates, following a classic trade-off between removing deleterious hitchhikers from beneficial drivers and breaking apart fortuitous combinations of alleles (Crow and Kimura 1965; Eshel and Feldman 1970; Green and Noakes 1995; Neher and Shraiman 2009). Similarly, patterns of under- or overdominance may disfavor high recombination rates given specific distributions of genotype frequencies (Ewens 2004). Other well-studied non-additive models, such as diminishing returns epistasis and certain kinds of stabilizing selection, might not necessarily alter the qualitative relationship between genetic diversity and recombination rate. However, many of these non-additive genetic architectures predict fitness trajectories and molecular dynamics that stagnate or stabilize at intermediate frequencies, a phenomenon that is commonly observed in artificial selection experiments (Burke et al. 2010, 2014; Parts et al. 2011; Orozco-terWengel et al. 2012). The effect of linkage disequilibrium on such phenomena has not been studied.

In this work, we present the first experimental analysis of the effect of recombination on the molecular dynamics of adaptation on standing genetic variation. More specifically, we employ the tools of laboratory evolution to analyze how standing variation interacts with recombination to determine evolutionary dynamics at both genetic and phenotypic levels. To do so, we evolve outbred haploid and diploid populations of budding yeast at different recombination rates for 960 generations. Next, we sequence and measure the fitness of clones and whole-population metagenomic samples every 240 generations, which allows us to relate the evolutionary dynamics of allele frequencies and haplotypes to the changes in mean and variance in fitness over time. We also assay the relative contributions of new mutations versus standing variation through the experiment, which represents the largest number of generations analyzed in an outbred experimental eukaryotic population to date.

By combining time-serial measurements of fitness and allele frequencies with simulations of different genetic architectures, we infer that adaptation is driven by concurrent selection on hundreds of weakly selected, linked variants. Furthermore, the dynamics of adaptation on this variation depends sensitively on the recombination rate. In asexual populations, clones quickly fix and purge standing variation, causing adaptation to stall and introducing high variability between replicate lines. By contrast, even modest amounts of recombination lead to more deterministic evolution, in which populations continue adapting at a nearly constant pace for the entire duration of the experiment. Interestingly, this sustained adaptation is accompanied by genetic changes that appear to stagnate after several hundred generations. We infer that this pattern of sustained adaptation despite stagnating genetic change is due in part to a gradual decay in linkage disequilibrium between many weakly selected sites over time. We find that these observations are consistent across haploid and diploid populations. However, asexual haploid populations are more prone to chromosomal instability, following previous observations in yeast (Gerstein et al. 2006; Gerstein and Berman 2015).

Overall, our results demonstrate how recombination can induce a transition from selection on genotypes to selection on individual alleles. In this way, sex changes the numbers and targets of selection, altering the dynamics, outcomes, and efficiency of adaptation on standing genetic variation.

Results

Experimental System

We made use of the facultatively sexual life cycle of the budding yeast S. cerevisiae to evolve outbred populations to a permissive laboratory environment for 960 generations at three different recombination rates. Similar to previous laboratory evolution experiments in yeast (Zeyl and Bell 1997; Goddard et al. 2005; McDonald et al. 2016), we varied recombination rate by interspersing rounds of asexual mitotic growth in rich medium with periodic sexual cycles of mating followed by sporulation (for haploid lines) or sporulation followed by mating (for diploid lines). To implement these sexual cycles, we adapted a method recently developed by McDonald et al. (2016), which uses multiple haploid-specific and mating-type specific nutrient markers, along with drug resistance markers tightly linked to each mating locus, to effectively select for diploids, MATa, and MATα cells at the appropriate times in the evolution protocol, with very little leakage of cells of the wrong ploidy or mating type.

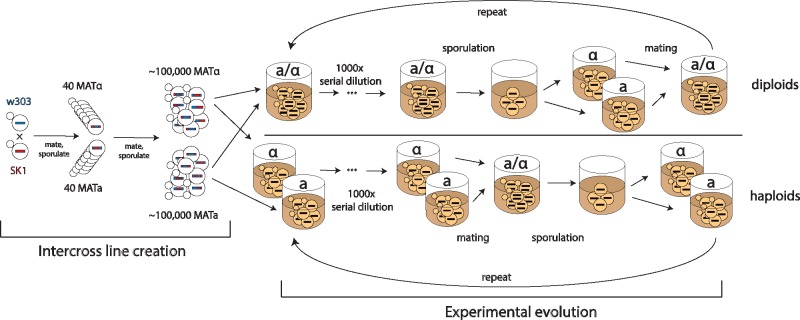
To found initially diverse outbred populations, we first mated W303 and SK1, two highly diverged strains of lab yeasts (Liti et al. 2009). We sporulated the resulting hybrid diploid in bulk, and screened the resulting pool of haploid F2 spores for the nutrient and drug resistance markers necessary for the sexual evolution protocol (see Materials and Methods). We randomly selected 40 mating type MATa and 40 mating type MATα spores and passaged these through another round of bulk mating and sporulation. We used the resulting diverse population to found 12 lines in each of six different treatments (72 populations in total, each with a unique collection of at least ∼10⁵ segregants generated from the 80 F2 haploid clones). We then evolved half of these populations primarily as haploids and half primarily as diploids, at three different recombination rates: “frequent sex” lines that outcrossed every 40 mitotic generations, “rare sex” lines that outcrossed every 120 mitotic generations, and asexual control lines. A summary of the intercross line creation and experimental evolution protocol is shown in figure 1, with a more detailed summary in supplementary figure S1, Supplementary Material online.

Fig. 1.

Schematic describing the line creation and experimental evolution protocol. We created a diverse pool of haploid segregants by two rounds of mating and sporulation. We used the resulting diverse outcrossed population to found 36 haploid and 36 diploid lines. We evolved these lines in batch culture for 960 generations, interspersing periods of asexual mitotic growth with rounds of mating followed by sporulation (for haploids) or sporulation followed by mating (diploids). We varied recombination rate by changing the duration of the asexual mitotic growth phase.

The Rate of Adaptation and Maintenance of Phenotypic Variation

After 960 generations of evolution, we measured adaptation to the laboratory environment in a subset of populations by measuring the mean fitness of each population through time (fig. 2A and Materials and Methods). Consistent with previous observations (Zeyl and Bell 1997; Colegrave 2002; Goddard et al. 2005; Cooper 2007; Morran et al. 2009; Gray and Goddard 2012; McDonald et al. 2016) and theoretical predictions (Muller 1932; Crow and Kimura 1965; Hill and Robertson 1966; Peck 1994; Neher and Shraiman 2009; Weissman and Hallatschek 2014), we found that populations undergoing any amount of recombination adapted more quickly than their asexual counterparts (P = 3.8 × 10⁻⁵, n = 12, haploids, P = 0.001, n = 9, diploids; unequal variances t-test). In both haploid and diploid asexual populations, fitness gains quickly plateau and adaptation largely stops, whereas the rate of adaptation in sexual populations declines only slightly over the course of the experiment. We did not observe a statistically significant benefit to more frequent outcrossing in either sexual haploids or diploids (P = 0.71, n = 6, haploids, P = 0.32, n = 6, diploids; unequal variances t-test). This observation could be due to a lack of statistical power, but may also result from a tradeoff between breaking apart well-adapted clones at high recombination rates and Hill–Robertson interference at lower ones (Crow and Kimura 1965; Eshel and Feldman 1970; Green and Noakes 1995; Neher and Shraiman 2009).

Fig. 2.

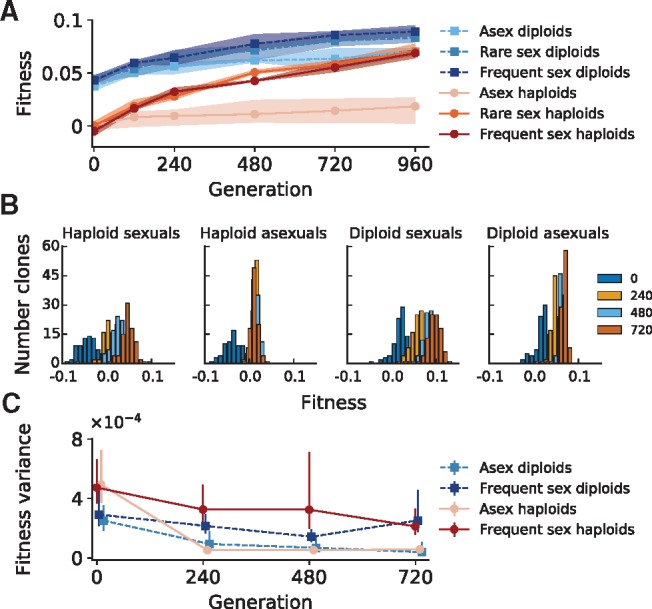
(A) Mean fitness through time of three replicate populations for each recombination rate and ploidy. Shading represents total range of fitnesses observed for each treatment and timepoint. Note that fitness measurements represent the average additional progeny per generation of the tested population when compared with the reference strain. (B) Distribution of fitness through time within an asexual haploid, sexual haploid, asexual diploid, and sexual diploid population. Legend denotes timepoint of sampling. (C) Within-population variance in fitness as a function of time in an asexual haploid, sexual haploid, asexual diploid and sexual diploid population, calculated from clone fitness data (96 clones per timepoint). Error bars are bootstrapped 95% confidence intervals.

Over the course of the experiment, we regularly assayed populations for incorrect ploidy and mating type. Although we found few such instances in diploids or in any sexual populations, 6 out of 12 asexual haploid lines underwent a whole genome duplication event at some point during evolution. This rare duplication event is highly beneficial in haploid asexuals, invariably causing a large increase in population fitness in those cases where it occurred (supplementary fig. S2, Supplementary Material online). This observation is consistent with previous work suggesting that chromosomal instability is a frequent outcome of experimental evolution in haploid and polyploid yeast (Gerstein et al. 2006; Yona et al. 2012; Gerstein and Berman 2015; Selmecki et al. 2015; Sunshine et al. 2015; Berman and Munro 2016). In particular, long-term experimental evolution in haploid yeast tends to result in genomic convergence to diploidy (Gerstein et al. 2006; Gerstein and Berman 2015), the historical ploidy level of S. cerevisiae. Other studies suggest that chromosomal duplications may be short term, effective responses to rapid environmental change (Yona et al. 2012; Sunshine et al. 2015; Berman and Munro 2016). Interestingly, the benefit of autodiploidization varied substantially between replicates, likely reflecting the variable benefit of autodiploidization in different haplotypes. Asexual populations undergoing spontaneous whole genome duplications were excluded from the primary analysis.

Surprisingly, the remaining asexual haploid populations adapted considerably less (∼1–2%) during the remaining 960 generations, a fitness increase that is much smaller than typically observed in laboratory evolution experiments in yeast (Lang et al. 2011, 2013; McDonald et al. 2016). This difference could be the result of a difference in fitness between our lines and similar experiments in asexuals: due largely to the rapid removal of a few strongly deleterious auxotrophic markers (trp1, ade2), the hybrid asexuals in our pool were significantly fitter than founder strains in previous experiments (e.g., the W303 ancestor of this experiment had a fitness of below −10% relative to our reference, and the SK1 founder of about −7%). A lower rate of adaptation may then be related to fitness-mediated diminishing returns epistasis (Barrick et al. 2009; Chou et al. 2011; Kryazhimskiy et al. 2014) or similar effects. Alternatively, asexual control conditions for the sexual evolution cycle results in a more variable laboratory evolution environment than is typical for laboratory evolution experiments in asexuals. Asexuals in this experiment were periodically exposed to nitrogen starvation in sporulation media, and other nutrient restrictions in synthetic dropout media (see supplementary fig. S1, Supplementary Material online). These conditions likely exclude a number of adaptive pathways frequently observed in laboratory evolution experiments, such as the RAS-cAMP pathway and associated IRA1 and IRA2 mutations (Kvitek et al. 2013; Venkataram et al. 2016).

Next, we measured the within-population distributions of fitness that underlie population-level adaptive changes in one population from each of four different treatments: a frequent-sex haploid, frequent-sex diploid, asexual haploid, and asexual diploid. To do so, we randomly selected 96 clones from each population from each of four timepoints (generation 0, 240, 480, and 720), and measured the fitness of the resulting 1,536 clones. We show the resulting fitness distributions in figure 2B. We also performed the same measurement for a single haploid asexual population that underwent a whole-genome duplication (supplementary fig. S3, Supplementary Material online), which confirmed the large adaptive advantage conferred by this event in this population (∼4%). We note that measurements of mean population fitnesses derived from clone data tended to be lower than those from population data by ∼1–2%, a consequence of population adaptation over the course of the fitness measurement (Materials and Methods).

In agreement with our population-level data, we found that fitness variation in asexual haploid and asexual diploid populations rapidly diminished over time, and at later timepoints was consistent with a single fitness value and potentially a single surviving genotype (given fitness measurement errors of 0.5% in haploids and 0.3% in diploids). On the other hand, fitness variation diminished slightly after the first timepoint in both sexual populations, but quickly plateaued to a steady state of 1.7% for haploid and 1.4% for diploid populations at later timepoints (fig. 2C). These differences in estimated variances between sexual and asexual populations were highly significant (P = 1.1 × 10⁻⁵, haploids; P = 1.7 × 10⁻⁸, diploids; Levene test, timepoint 720). Overall, sexual populations continued to adapt through the end of the experiment. However, we note that the rate of adaptation (4 × 10⁻⁵ in haploids and 7 × 10⁻⁵ in diploids) was substantially smaller than the population variance in fitness (3×10⁻⁴ in haploids and 2×10⁻⁴ in diploids), in contradiction with Fisher’s Theorem (Fisher 1930). This discrepancy may reflect interesting effects of epistatic interactions, genetic load, or linkage disequilibrium between selected sites (Bulmer 1980; Falconer and Mackay 2009), but it could also be a technical artifact arising from pleiotropic tradeoffs between fitness in different phases of the sexual selection protocol.

The Molecular Dynamics of Adaptation

To characterize the molecular basis of the phenotypic changes described previously, we focused on a subset of three populations from each ploidy and recombination rate (a total of nine diploid and nine haploid populations). We sequenced whole-population metagenomic samples from each of these populations at 240-generation intervals through the entire timecourse of the experiment (or until a single haplotype fixed, whichever was first). These sequence data allow us to track the frequency of each allele from the initial standing genetic variation over time. To do so, we first compiled a list of 56,648 high-quality segregating SNPs and indels from the initial founding population by cross-referencing permissive lists of mutations from the founding F3 hybrid populations with sequences of the 80 F2 clones and a high-coverage W303 genome (Materials and Methods). To minimize the effect of sampling noise on allele frequency measurements, we estimated frequencies over 15-kb sliding windows using kernel regression.

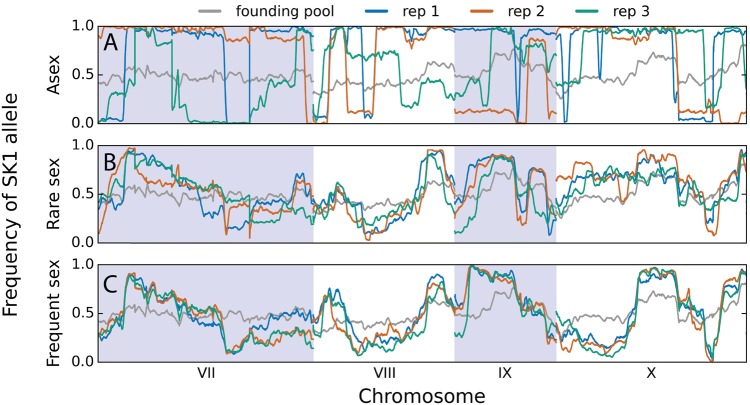
In figure 3, we show an example of how allele frequencies changed between generations 0 and 480 across chromosomes 7–10 in three replicate haploid populations at each of the three recombination rates. These regions exclude tracts of homozygosity intentionally introduced during the strain construction process (e.g., on chromosomes 3 and 5), but are otherwise representative of molecular dynamics genomewide. Full-genome data between generations 0 and 480 in all sequenced haploid populations are shown in supplementary figure S5, Supplementary Material online. Diploid populations display qualitatively similar behavior (supplementary figs. S4 and S6, Supplementary Material online).

Fig. 3.

SK1 allele frequencies across chromosomes 7–10 (averaged across 15-kb sliding windows) in the initial founding pool and at generation 480 in three replicate haploid populations from (A) asex, (B) rare sex and (C) frequent sex treatments.

In asexual populations, we find that standing genetic variation is rapidly purged by the fixation of one or a few clones (fig. 3A), consistent with the fitness data described previously. While intrapopulation diversity is quickly purged in these asexual populations (fig. 4A), there is substantial variation between populations with regards to which allele fixes at each genetic locus (fig. 4B), since each independent replicate population fixes a different initial clone. Because each replicate asexual population is seeded with a different set of haplotypes (Materials and Methods), it is not surprising that each population fixes a different clone. However, the genomic composition of each fixing haplotype is substantially different: only 37.6% of segregating genetic variation fixes for the same allele across each replicate (22522/59955, where fixation is taken to be >80% or <20% allele frequency) compared with 25% for purely random fixation. Note, however, that this difference is highly statistically significant (P = 0.0005; Materials and Methods).

Fig. 4.

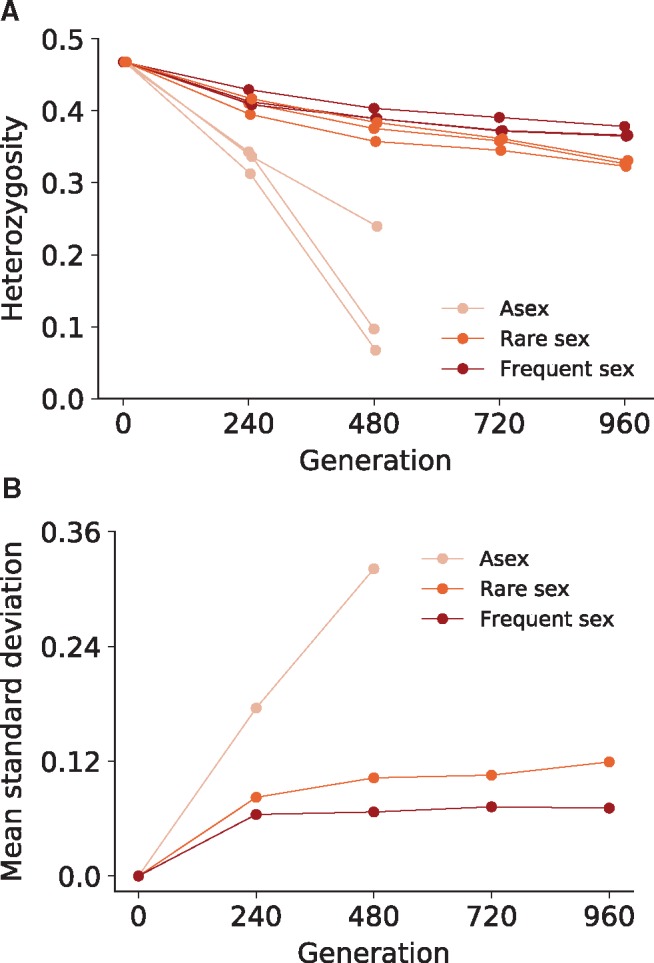
(A) Average within-population heterozygosity through time, computed from 15-kb sliding window frequencies every 100 bp across the genome, for each haploid population at each recombination rate. (B) Average between-population standard deviation of allele frequencies among replicate haploid populations at each recombination rate.

As the recombination rate increases, heterozygosity declines more slowly (P = 0.04, n = 3, asex vs. rare sex, timepoint 480; P = 0.003, n = 3, rare sex vs. frequent sex, timepoint 960; haploids, unequal variances t-test) and evolution proceeds more deterministically (P = 2 × 10⁻¹⁰, asex vs. rare sex, timepoint 480; P = 0.002, rare sex vs. frequent sex, timepoint 960; Materials and Methods), with each replicate population exhibiting very similar allele frequency dynamics (fig. 3B and C). More specifically, within-population heterozygosity is maintained throughout the full 960 generations of evolution in sexual populations (with marginally more variation maintained at higher recombination rate; fig. 4A), whereas at the same time between-population variation is dramatically reduced (fig. 4B). We find qualitatively similar effects of greater recombination increasing within-population heterozygosity while decreasing between-population variability in diploid populations (supplementary fig. S7, Supplementary Material online). However, only the difference in variance between asexual and sexual populations is significant (P = 10⁻⁸, asex vs. rare sex, timepoint 960; P = 0.25, rare sex vs. frequent sex, timepoint 960; Materials and Methods). Differences in average heterozygosity were also not significant in diploids, likely due to the fixation of heterozygous sites in diploid asexual populations (P = 0.17, n = 3, asex vs. rare sex; P = 0.42, n = 3, rare sex vs. frequent sex; timepoint 960, diploids, unequal variances t-test).

Another origin of the difference between diploids and haploids could be related to mitotic gene conversion, which effectively introduces a small, locus dependent recombination rate in diploid populations. Given previous mitotic conversion estimates of 10⁻⁷ to 10⁻⁶ per division per locus in yeast (Jinks-Robertson and Petes 1986; Lichten and Haber 1989; Steele et al. 1991; Lettier et al. 2006) and an effective population size of ∼10⁵ (Materials and Methods), we can expect roughly one to ten conversion events/locus every sexual cycle in diploid populations. Generally, rates of mitotic recombination events are estimated to be ∼10⁴ less common than meiotic ones (Esposito and Wagstaff 1981). These estimates are several orders of magnitude smaller than the number of recombination events experienced by the rare sex populations. However, it is likely that diploid clones continue to explore additional genotypic combinations at a low rate in asexual populations, sustaining competition between genotypes. This effect could help explain why heterozygosity is maintained in diploid asexual populations for longer than haploids (fig. 4B vs. supplementary fig. S7B, Supplementary Material online), and why diploid asexual populations adapted slightly more than haploid asexuals on average (3.2% vs. 1.8%).

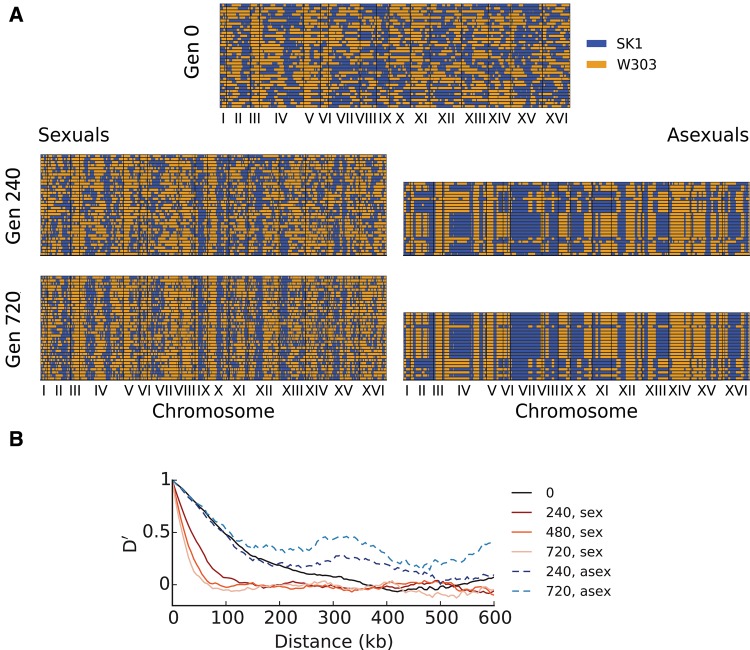
To investigate haplotype diversity in sexual versus asexual populations more directly, we sequenced and genotyped multiple clones from the initial haploid and diploid populations at generation 0, and from generations 240 and 720 in one high-recombination haploid population, one asexual haploid population, one high-recombination diploid population, and one asexual diploid population. Two highly fit clones quickly rise in frequency to dominate the asexual haploid population (fig. 5A). On the other hand, considerable haplotype diversity was maintained through the final timepoint sequenced in the sexual haploid population (fig. 5A), with linkage disequilibrium between sites decaying continuously over time (fig. 5B). We observe a similar pattern in the diploid populations, with a few haplotypes quickly dominating the asexual population while diversity is maintained and linkage disequilibrium decays over time in the sexual population (supplementary fig. S8, Supplementary Material online).

Fig. 5.

(A) Genotypes of sequenced haploid clones from the initial founder population at generation 0 (top) and at generations 240 and 720 from evolved sexual lines (left) and from evolved asexual lines (right). Each row denotes the genotype of a sequenced clone, with regions colored in blue denoting loci with the SK1 allele, and regions colored in orange denoting loci with the W303 allele. We sequenced 36 and 24 clones per timepoint for sexual and asexual populations, respectively. (B) Normalized, average linkage disequilibrium D′ (Lewontin 1964) calculated from clone sequences, as a function of distance from the focal site (Materials and Methods). Note that D′ declines over distance and time for sexual populations, whereas increasing over time for asexual populations, reflecting the fixation of individual clones.

In order to examine potential time-dependent effects of linkage disequilibrium, dominance, epistasis, and other multi-locus effects, we investigated how selective pressures on standing variants changed across the genome over time. In asexual populations, this information is not readily attainable, as one or a few clones rapidly dominate the population. However, in the high recombination populations, the repeatability between replicates allows us to calculate local selection pressures acting on each region of the genome through time from the average changes in allele frequencies across replicate populations. Specifically, we define an effective selection coefficient acting on a given locus between two timepoints t_i and t_f as:

$$s_{eff}=\frac{1}{t_f-t_i}\ln \left[\frac{x(t_f)(1-x(t_i))}{x(t_i)(1-x(t_f))}\right],$$ (1)

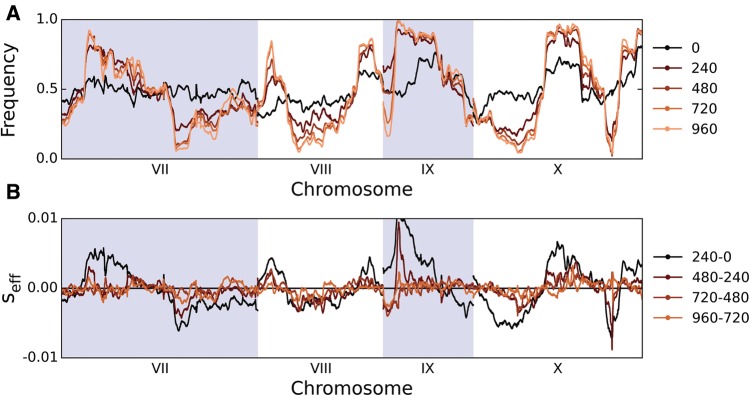
where x(t) denotes the frequency of the SK1 allele at that locus at time t. This parameter gives the average additional progeny per generation of an individual carrying an allele from the SK1 background relative to the W303 background in the period between t_i and t_f. Importantly, this parameter incorporates the effect of genetic draft from linked polymorphisms along with any selection acting on the allele itself. In figure 6, we show how the replicate-averaged allele frequencies and effective selection strengths change over time in our haploid high-recombination populations for a representative subset of the genome (whole genome data are shown in supplementary fig. S10, Supplementary Material online, and analogous results for diploids in supplementary figs. S9 and S11, Supplementary Material online).

Fig. 6.

(A) SK1 allele frequencies across chromosomes 7–10 (in 15-kb sliding windows), averaged among the three replicate haploid frequent-recombination populations, for each sequenced timepoint. (B) Corresponding average effective selection pressures s_eff through time.

A Gene Ontology analysis of the regions undergoing repeatable, rapid change in these populations reveals enrichments for a number of specific cellular processes, including nitrogen compound metabolism, cellular component biogenesis, and nucleic acid metabolism (Materials and Methods and supplementary file S2, Supplementary Material online). Interestingly, a few of the most strongly selected regions overlap detected copy number variants between SK1 and W303, including the rDNA encoding segment of chromosome 12 and a region encompassing the high-affinity hexose transporters HXT6 and HXT7 on chromosome 4 (Materials and Methods). However, due to the high degree of linkage disequilibrium between alleles (initially ranging over lengths of order 100 kb, declining to ∼20 kb by the end of the experiment—see fig. 5B), more work is required to confirm whether these associations are causal.

Although sexual populations increase steadily in fitness through time, figure 6 reveals that allele frequency changes generally stagnate by the end of the experiment. This is reflected in a decline in local effective selection pressures throughout the genome. Many of these changes cannot be explained by linkage to a site that fixed, since many loci that experience rapid early allele frequency changes do not ultimately fix for either allele, and the selection pressures at these loci often decline to very close to zero by the end of the experiment. Overall, out of 24 regions that we would expect to fix based on their initial changes in allele frequency (Materials and Methods), only 9 actually do fix through 960 generations. We note that this discrepancy is robust to the size of the sliding window used to infer allele frequencies, and cannot be an artifact of genetic drift, since the effective population size of these populations is of order 10⁵.

Finally, to analyze the potential impact of new mutations on the evolutionary dynamics, we used our metagenomic data in combination with clone sequences (where available) to identify new segregating mutations in all of our populations (Materials and Methods). Analysis of the clone sequences yielded a handful of mutations found at frequencies of ≥ 20% in three out of four populations analyzed (supplementary fig. S12, Supplementary Material online), including two different nonsynonymous substitutions in HSP104 in the two sexual populations. However, time-serial analysis suggested that these novel mutations were unlikely to substantially contribute to fitness variance or fitness increase in sexual populations (Materials and Methods). Furthermore, we searched for new mutations at frequencies >50% in the metagenomic sequence data sets in all populations where such data were available. Supporting our previous observations from clone data, we found no well-supported new mutations that were fixed in any population, and very few that were segregating at high frequencies by the end of the experiment (supplementary fig. S13, Supplementary Material online).

Simulations

A comparison between our fitness measurements and molecular data presents an interesting dichotomy for sexual populations. On the one hand, populations undergoing any amount of recombination adapted at a nearly linear pace and sustained variation in fitness throughout the duration of the experiment. On the other hand, these same populations experienced a clear stagnation in genetic change after 240 generations, as demonstrated by figure 6B. These molecular dynamics are consistent with many models of non-additive effects, including stabilizing selection, diminishing returns epistasis, frequency-dependent fitness effects, and certain models of pleiotropy. However, many of these models predict a plateau in fitness gains not observed in the data.

Conversely, sustained fitness increases may be explained by a highly polygenic, additive genetic architecture, or a steady influx of new mutations. Our molecular data reveal few, if any, new mutations driving adaptation. However, a large number of sites interacting additively could give rise to time-dependent, declining fitness effects if these sites are initially in strong linkage disequilibrium, as they were in our initial pool (we provide an in-depth explanation of this phenomenon in the Discussion). However, it is not clear whether this effect is strong enough to explain the genetic stagnation observed in our data.

To determine whether any simple model of genetic architecture could adequately explain both our fitness measurements and sequencing data, we implemented numerical simulations of our experiment, in which we varied the assumed genetic architecture underlying adaptation. We simulated our experiment by modifying SLiM (Messer 2013), a forward-time population genetic simulator for studying the effects of evolution under linked selection. Specifically, we simulated haploid populations of outbred individuals generated from a single hybrid diploid at a population size of N = 10⁵ for 960 generations of evolution, sampling a subset of the population every 240 generations. We did not perform simulations in diploids, because diploid and haploid populations exhibited few significant qualitative differences, and because diploid populations exhibit additional complexity in the form of dominance coefficients. To simulate sexual evolution, we allowed a small but constant probability of recombination of 8.3 × 10⁻⁸/bp each generation, consistent with the amount of outcrossing experienced by our high-recombination lines. For each simulation, we introduced standing variants with fitness effects drawn from an exponential distribution with an average effect $\overline{s}$, and a total number $n(\overline{s})\propto 1/{\overline{s}}^2$, chosen so that the initial standard deviation in fitness averaged ∼2.1%, matching the initial haploid fitness distribution in our experiment. We varied the number and strength of selected sites contributing to adaptation by varying $\overline{s}$, ranging from a model of rare, strong selection to dense, weak selection. For each parameter set, we tracked the distribution of fitnesses, allele frequencies, and average fitness over time. We assessed the fit of each simulation run to our empirical data by jointly comparing the average fitness and heterozygosity trajectories in a maximum likelihood framework (Materials and Methods).

In addition to these base simulations, we considered an additive model in which a few strongly selected mutations were interspersed among a large number of more weakly selected sites, motivated by the empirical observation of a small number of strongly selected loci which were nearly fixed by generation 240. Furthermore, this model probed the extent to which our results were sensitive to the specific shape of the distribution of fitness effects. Finally, we integrated a simple model of epistasis with the framework described previously. Motivated by empirical observations in other microbial evolution experiments (Wiser et al. 2013; Kryazhimskiy et al. 2014; Couce and Tenaillon 2015; Good and Desai 2015), we analyzed a model of macroscopic diminishing returns epistasis, in which the fitness effect of a selected site depends inversely on the total fitness of the genetic background on which it occurs. Our model is consistent with the existence of an additive trait Z that relates to fitness X as:

$$X(Z)=X_c(1-\hspace{0.17em}\text{exp}\hspace{0.17em}(-Z/X_c)),$$

where X_c is the theoretical fitness optimum. In this way, the model resembles a class of “phenotypic optimum” models of adaptation that have recently increased in popularity (Chevin and Hospital 2008). A closer look at typical allele frequency data, fitnesses, and heterozygosity trajectories for different values of $\overline{s}$ in these three models is shown in supplementary figures S14–S16, Supplementary Material online. A full list of simulated parameter sets is provided in supplementary file S3, Supplementary Material online.

In figure 7, we show the ten simulation runs with the highest likelihoods for each model. By comparing likelihood statistics, we find that our experimental data favors a model of diminishing returns epistasis (epistasis vs. additive model comparison, P < 10⁻¹⁵, likelihood-ratio test; epistasis vs. two-effect model, P < 10⁻¹¹, LOD score). Thus, we found that no model of purely additive effects adequately describes the heterozygosity and fitness trajectories observed in our experiment. However, our data are consistent with a model of many weakly selected sites (between 300 and 1,200, with average fitness effects between 0.075% and 0.15% per individual per generation; see Materials and Methods), constrained by fitness-mediated diminishing returns epistasis.

Fig. 7.

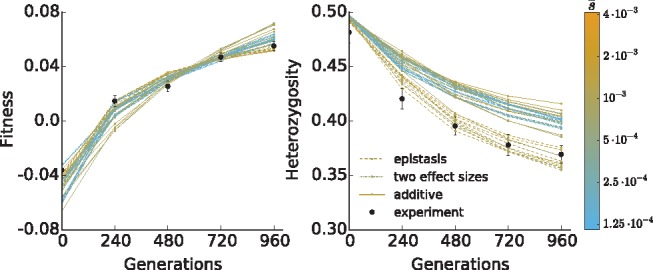
Comparison between experimental (black dots) and simulation (lines) fitness and heterozygosity data. Simulations shown are the ten runs with the highest log likelihood for each model among all measured parameters, with lines colored by the average selective effect of selected sites in the population. Because simulated populations are constrained to have the same starting variance in fitness, the total number of selected sites is inversely related to the average selective effect.

Because our model of diminishing returns fit reasonably well to our data, we did not simulate additional epistatic, pleiotropic, or other non-additive models of genetic architecture. Due to the vast number and flexibility of such models, we expect that our power to reject one model of epistasis in favor of another to be low. More fundamentally, it is unlikely that evolutionary dynamics in this experiment are distorted solely by a single pattern of epistasis. More likely, allele frequencies in this experiment are constrained by several kinds of interactions, which could include diminishing returns epistasis, pleiotropy, stabilizing selection, frequency dependence, linkage disequilibrium, and other non-additive effects. Thus, although we can reject the additive model of genetic architecture, we do not make the claim that diminishing returns epistasis is the only non-additive model that is consistent with our data.

In general, however, our simulations supported at least two factors underlying the observed evolutionary dynamics: a highly polygenic genetic architecture and some form of non-additive interaction between sites. We note that our inference of a polygenic architecture was robust to the specific model simulated.

Discussion

In this work, we track the rate, variance, and genetic basis of fitness increase over 960 generations of evolution in diverse, recombining populations, presenting the first analysis of the effects of recombination and ploidy on the molecular dynamics of adaptation on standing variation. By combining genetic data with time-serial phenotypic measurements, we reveal the dramatic impact of sex on selection on standing variation. In asexual populations, variance in fitness is quickly purged as clones sweep and stall future adaptation. In contrast, populations undergoing any amount of recombination sustain diversity in fitness and continue to adapt through 960 generations, despite an apparent stagnation in genetic change after 240 generations. Comparing adaptation in haploids and diploids, we observe similar dynamics in sexual populations, suggesting that dominance effects did not qualitatively alter patterns of adaptation. However, asexual populations exhibited a number of differences between haploids and diploids. In particular, haploid populations frequently experienced whole-genome duplication events, following previous observations that convergence to diploidy is a frequent outcome of asexual haploid evolution in yeast (Gerstein et al. 2006).

Relation to Previous Work

Focusing only on adaptation in sexual populations, our phenotypic measurements are consistent with typical observations from artificial selection experiments. These experiments, which track phenotypic changes in outbred populations under sustained selection, tend to observe long, continuous improvements to the selected phenotype over tens or hundreds of generations (Barton and Keightley 2002; Moose et al. 2004; Johansson et al. 2010). In a similar vein, our work also mirrors findings from “evolve-and-resequence” (E & R) experiments, which track the genetic response of outbred populations under artificial selection. These experiments typically find that adaptation is driven by polygenic selection on standing variation, to the exclusion of most novel mutations (Burke et al. 2010, 2014). For experiments in which time-serial genetic data are collected, allele frequency changes often stagnate and even stop at later phases of the experiment (Burke et al. 2010, 2014; Orozco-terWengel et al. 2012), in agreement with our observations.

Our work unifies observations from these two types of experiments by combining in-depth, time-serial measurements of both genetic composition and fitness, for both clones and populations. Our experiment demonstrates that sexual populations do not stop increasing in fitness, even though genetic changes appear to stagnate. This suggests that the disparate observations from these two classes of experiments—sustained phenotypic improvement in artificial selection experiments, and stagnating genetic change in E & R experiments—does not necessarily imply fundamentally different patterns of genetic architecture. Rather, our work suggests that sustained adaptation accompanied by genetic stagnation may be a relatively common attribute of adaptation on standing genetic variation in sexual populations, especially if linkage disequilibrium in the founding population is high.

Simulations of Genetic Architecture Suggest High Polygenicity

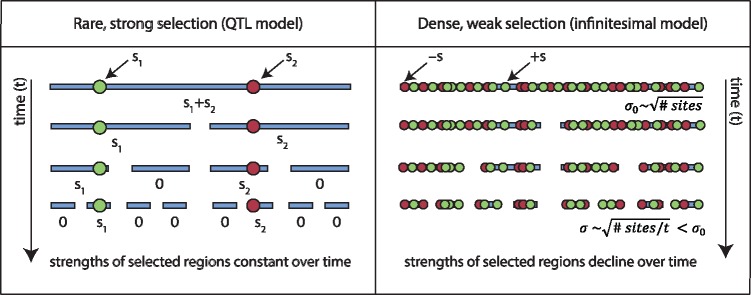
We can leverage the combination of our different data sources to understand the genetic architectures that could give rise to this observation- that is, sustained adaptation accompanied by genetic stagnation. A simple back-of-the-envelope calculation suggests a highly polygenic genetic basis for fitness: for most selected variants to be unfixed by 1,000 generations, typical fitness effects must be of order 0.1% per generation or smaller. The measured initial fitness variance of ∼2% then requires 800 or more selected sites to be present genomewide. These predictions are further corroborated by other features of the genetic data, including a lack of defined peaks in allele frequencies predicted by isolated drivers (Maynard Smith and Haigh 1974; Gillespie 2000, 2001) and a large, genome-wide decay in heterozygosity (Neher et al. 2013b; Good et al. 2014), suggesting ubiquitous selection pressure across the genome. Since linkage in our initial pool extended over regions of ∼100 kb (fig. 5B), selected sites at the densities inferred above must have been in linkage disequilibrium at the start of the experiment. Gradual alleviation of linkage disequilibrium over time contributes to the genetic stagnation observed in sexual populations (see below, fig. 8).

Fig. 8.

Schematic demonstrating the selective effects of individual haplotypes in the strong-selection and dense weak-selection regimes. In the strong-selection case, we show two mutations of selective effects s₁ and s₂ that are initially linked, but are quickly decoupled by recombination. Over time, the typical size of the haplotype on which each mutation is found gets shorter, but the fitness effect of the selected region stays constant. In contrast, in the dense weak-selection regime, an initial haplotype has many mutations with selective effects ±s. The central limit theorem implies that the typical fitness σ₀ of this haplotype is proportional to $\sqrt{n}$, where n is the number of mutations on the haplotype. Over time, haplotypes get smaller and n decreases, so the typical selection pressure σ of a haplotype declines. As a result, the rate of change in allele frequencies will decline over time.

To go beyond these rough estimates, our work introduces an advance in the interpretation of laboratory evolution experiments by integrating simulations with our genetic and phenotypic measurements. Although we do not attempt to use these simulations to reject any model of non-additive effects, they do provide additional support for the high polygenicity of fitness inferred above, suggesting contributions from between 300 and 1,200 sites of effects ∼10⁻³ or smaller (Materials and Methods). Furthermore, we are able to reject a purely additive model of adaptation. Our simulations support the conclusion that adaptation in this experiment was driven by highly polygenic selection, distorted both by changing patterns of linkage disequilibrium and non-additive genetic interactions between alleles.

Our simulations of non-additive genetic architectures focus on epistatic interactions between alleles. However, some other possible sources of nonadditivity are also worth exploring. For example, pleiotropy is likely to affect allele frequency dynamics to some extent, especially given the fact that there are known tradeoffs between growth and sporulation in yeast (Lang et al. 2009). In general, different selective effects across the sexual cycle will average out to a constant effective selection pressure, so long as the allele in question is common and allele frequency changes across a cycle are not too large (Gillespie 1991). However, this simple approximation breaks down when these conditions are not satisfied, giving rise to less predictable allele frequency changes (Cvijovic et al. 2015). Changing linkage disequilibrium, phenotypic optima, and interactions between alleles may also complicate these effects. More generally, it is likely that some amount of allele frequency dynamics are driven by selection for improved mating and sporulation. Although this effect helps resolve some discrepancies (e.g., fitness variance much larger than the adaptation rate), it cannot explain others (e.g., sustained improvements in growth rate despite the absence of new mutations).

Asexual Adaptation on Standing Variation Is Highly Inefficient

Regardless of the source of nonadditivity in our experiment, the inferences above allow us to investigate the effect of genetic architecture on evolution at different outcrossing rates and ploidies more closely. Although we observe broadly similar patterns of adaptation between haploids and diploids, we find that the speed, consistency, and repeatability of evolution is highly sensitive to recombination rate. In asexual populations, outcomes are highly variable, determined by the rapid and inefficient fixation of clones carrying a random subset of available variation. Although fixation of different clones is to be expected given the setup of the experiment, the genetic composition of fixing clones is substantially different, with a majority of variants exhibiting different fixation outcomes among replicates. Fixation of these clones purges standing variation, resulting in a plateau in fitness after 240 generations of evolution. Even a small amount of recombination alleviates this effect, as populations undergoing outcrossing events as rare as every 120 generations sustain genetic diversity and continue to improve in fitness. Superficially, these data corroborate earlier empirical and theoretical studies describing the evolutionary advantages of recombination: sexual populations adapt faster by maintaining a larger additive genetic variance in fitness (Weismann 1891; Fisher 1930; Noel et al. 2017), by alleviating Hill–Robertson inference between competing beneficial mutations (Muller 1932; Hill and Robertson 1966), and by decoupling beneficial drivers from deleterious passengers (Peck 1994).

Our insight into the genetic basis of fitness allows us to go beyond these observations to analyze the specific factors driving differences between sexual and asexual populations. More specifically, we inferred that fitness variation was likely driven by high polygenicity, non-additive genetic interactions, linkage disequilibrium, and few novel mutations—how do these factors contribute to the dramatic differences in evolutionary dynamics at different recombination rates?

First, we can see that a highly polygenic genetic architecture explains both the high variability and lower adaptability observed in asexual populations. Assuming totally random segregation of alleles and around 400 selected sites in total, the fittest individual in a population of size ∼10⁵ can only be expected to carry ∼60% of the available beneficial mutations. Linkage disequilibrium may either exacerbate or alleviate this effect, by making certain favored combinations of alleles more or less likely to arise. Regardless, this intuition explains why much of the standing variation is wasted in outcrossed asexuals, as adaptation in these populations proceeds by fixation of a small relative subset of beneficial mutations.

If all beneficial variants had approximately the same selective effect, the ∼60% of variants that fix would vary randomly from population to population. In reality, beneficial mutations vary in their effect size. As a result, fixations in each population are likely enriched for the most strongly selected variants in the initial pool, which helps to explain why fixation patterns between asexual replicates are more similar than random. On the other hand, the majority of weakly selected variation is fixed or purged stochastically, depending on its presence or absence in the genome of the fittest individual. Note once more that linkage disequilibrium can partially alleviate this stochasticity, by decreasing the number of likely combinations of selected alleles in the founding population.

In short, asexual populations adapt inefficiently on standing genetic variation because they can fix the fittest clone in the founding pool, and nothing more. The genotype of the fittest clone is dependent on the random set of haplotypes seeded into each founding population; thus, repeatability is low among asexuals, and the intrinsic effects of individual alleles are poorly reflected in their long-term evolutionary dynamics. By contrast, in sexual populations the genomes of the fittest clones are broken up by recombination before they have a chance to significantly amplify in frequency, allowing these populations to continue to adapt for nearly 1,000 generations by finding increasingly precise reshufflings of weakly selected variation. In sexual populations, each selected locus samples a large, constantly changing, continually improving set of genetic backgrounds on its way to fixation. The frequencies of these loci then change according to their average fitness effect sampled over all these backgrounds. The result is a transition from selection on entire genotypes at low recombination rates to selection on alleles at high ones, as we also see in the patterns of haplotype diversity through time (fig. 5). Although a transition from “genotype selection” to “allele selection” at higher recombination rates has been predicted by earlier theoretical work (Neher and Shraiman 2009; Neher et al. 2013b), our study presents the first experimental demonstration of this phenomenon.

Recombination Breaks Down Linkage Disequilibrium in Sexual Populations

The effects of linkage disequilibrium and a highly polygenic genetic architecture are dramatic in asexual populations. However, our work demonstrates that these factors also distort evolutionary dynamics at high recombination rates, causing deviations in allele frequency changes from simple population genetic predictions. This is exemplified by the earlier observation that sexual populations continue to improve in fitness, largely in the absence of newly arising mutations and despite the fact that selective pressures appear to decline genomewide over time (fig. 6). Our simulations suggest two factors that contribute to the apparent stagnation of genetic change at later phases of the experiment: some latent pattern of non-additive interactions between selected sites and a gradual alleviation of linkage disequilibrium over time.

The idea that a decrease in linkage disequilibrium can result in an apparent decline in selective effects is counterintuitive. However, we can demonstrate this effect with a simple idealized example. Consider a population generated by crossing two diverged lines with a polymorphism every 100 bp, where the selective effect of each polymorphism is distributed with mean 0 (i.e., alleles from each background are equally likely to be positively or negatively selected) and variance σ² = 10⁻⁸ (e.g., alleles with an effect of  ± 10⁻⁴). If mutations in this population are initially linked over 100 kb, then a given linkage block will typically consist of about 1,000 different mutations. On an average, these blocks all have the same fitness, but because of random fluctuations in the number of favored alleles in each block, the fitness effect of each block will be normally distributed with standard deviation ${\sigma }_n=\sqrt{n}\sigma \sim 0.3\%$. A genome of 10⁷ bp (approximately the size of the yeast genome) will contain about 100 such blocks. This implies that we expect ∼1 block with a fitness effect of >0.8% per generation, and about 10 blocks with effect size >0.5% per generation. Because many alleles start at high frequencies in an outbred population, these selective effects will cause large changes in frequency over timescales of hundreds of generations.

At later stages of the experiment, recombination unlinks distant loci, but many nearby sites are still in linkage disequilibrium. If, at these later stages, the correlation length is only ∼10 kb, then only about 100 mutations contribute to a given linkage block. A typical block then has σ_n ∼ 0.1%. Now, the likelihood of a given block having a selective effect >0.5% is <10⁻⁶, and, even though the genome now has about 1,200 blocks total, we can only expect 1–2 blocks with effect sizes >0.3% and none with effect sizes >0.35%. Thus, even though the population continues to adapt, allele frequencies are expected to change much more slowly. A schematic describing these dynamics is shown in figure 8.

As previously mentioned, the linkage disequilibrium effects described earlier are not strong enough to fully explain the deviations from additive, population genetic predictions observed in this experiment. Instead, our simulations suggest that allele trajectories are distorted both by linkage disequilibrium and a latent pattern of non-additive interactions between sites. However, our calculations above demonstrate how even a purely additive genetic architecture can generate apparently non-additive, time-dependent dynamics if linkage disequilibrium is high. Such effects may explain the frequent observation of stagnation and lack of fixation in some evolution experiments (Orozco-terWengel et al. 2012), although explanations involving epistasis, dominance, or pleiotropic effects are most likely better explanations in others (Burke et al. 2010, 2014; Parts et al. 2011). We also note that the strength of this effect in other E & R experiments should tend to increase with the number of founder haplotypes, the complexity of the selected phenotype, and the density of variants in the founding pool, since in these cases the population will be able to “discover” superior combinations of selected alleles at smaller lengthscales. Conversely, we expect that this effect will decrease with the number of crosses performed prior to the start of selection, as such populations will harbor less linkage disequilibrium in the initial pool.

Conclusion

In this work, we have demonstrated the substantial impact of recombination on adaptation to standing genetic variation. In sexual populations, sustained selection on standing variants can proceed for nearly 1,000 generations, as populations gradually break down linkage disequilibrium and uncover superior combinations of weakly selected variants. We find that this process leaves distinct genetic and phenotypic signatures, such as allele frequency changes that diminish over time, coupled with sustained and predictable gains in fitness. Conversely, in asexual populations, clones carrying a random assortment of alleles—consisting of both drivers and a typically much larger number of neutral or deleterious hitchhikers—eventually sweep and purge genetic variation. This finding has implications with respect to inference in asexual populations: instead of sustained and deterministic selection, long-term adaptation from standing genetic variation in these populations is characterized by high variability and low power. Inferences can still be made before clonal sweeps occur (Parts et al. 2011), but this time limit sets a lower bound on the size and resolution of inferred selective effects.

More broadly, our results demonstrate how rapid, time-dependent allele frequency dynamics can arise whenever two diverged genotypes intermix, as in the case of introgressions, hybridizations, or admixture between subdivided populations. In sexual populations, this process can generate genetic signals resembling strong selection even in the absence of single, strong QTLs. More generally, our work also suggests that sexual populations may harbor and sustain a large number of segregating sites that adopt some small fitness effect upon exposure to a new environment. These sites are capable of bringing about significant adaptive change, even though such adaptation is brought about by only modest short-term changes in allele frequencies. Although many existing linkage-based methods for detecting recent selection are based on models of hard sweeps driven by single, strongly selected beneficial mutations (Sabeti et al. 2002; Voight et al. 2006; Nielsen et al. 2007), some recent work has focused on developing alternative methods that are sensitive to signals of this type of polygenic selection (Hancock et al. 2008, 2010a,b; Turchin et al. 2012; Berg and Coop 2014; Field et al. 2016). Our findings underscore the need for further research in this area, and emphasize the importance of studying both new mutations and standing variation in order to gain a better understanding of recent evolution.

Materials and Methods

Strains

The strains used in this study were derived from the base strains MJM64, MJM36, and MDY493. MJM64 and MJM36 are haploid W303 yeast strains with genotypes MATa-KanMX, ho, Pr_STE5-URA3, ade2-1, his3:: 3xHA, leu2:: 3xHA, trp1-1, can1:: Pr_STE2-HIS3-Pr_STE3-LEU2 and MATα-HphMX, ho, Pr_STE5-URA3, ade2-1, his3Δ:: 3xHA, leu2Δ:: 3xHA, trp1-1, can1:: Pr_STE2-HIS3-Pr_STE3-LEU2, respectively (McDonald et al. 2016). These strains contain nutrient markers driven by promoters that are specific to mating type a (Pr_STE2—HIS3), mating type α (Pr_STE3—LEU2) or haploids (Pr_STE5—URA3). MDY493 is a haploid SK1 strain with genotype MATa, his3Δ200, leu2, trp1Δ1, ura3-52, lys2, a haploid derivative of MCY387 (Conrad et al. 1997). To generate a heterothallic SK1 haploid, we amplified the NatMX6 cassette from plasmid pJHK1912 (provided by John Koschwanez) using primers oKK1 and oKK2 (supplementary file S1, Supplementary Material online) and integrated it at the HO locus of MDY493, generating strain KK221. We used diagnostic PCR to verify the HO knockout (primers oKK3-8), along with the ploidy and mating type of this strain (primers oGW1068, oGW2004, oGW2018). The same plasmid was used to mating-type switch KK221 to generate a MATα heterothallic SK1 haploid, KK222.

Intercross Line Creation

We isolated an F1 hybrid diploid clone from a cross of MJM64 and KK222 and another F1 hybrid diploid from a cross of MJM36 and KK221. We grew two technical replicates for each hybrid clone overnight, inoculated into YEP + 2% KOAc for 1 day, and then transferred to a 2% KOAc solution for 1 week until all cultures exhibited sporulation efficiencies of at least 80%. We incubated the resulting spores overnight in a zymolyase solution (20 μg/ml) to kill unsporulated diploids. We then disrupted asci by mixing each culture with 100–200 μm diameter glass beads and inoculating on a roller drum for 1 h, then three alternating rounds of vortexing and sonication for 1 min each. We verified full disruption of asci by microscopy, and plated spores at low density onto YPD agar media (1% yeast extract, 2% peptone, 2% dextrose, 2% agar). We replica plated colonies on appropriate defined amino acid dropout media (CSM –uracil –histidine +G418 or CSM –uracil –leucine +hygromycin) to select for the mating-type specific can1:: Pr_STE2-HIS3-Pr_STE3-LEU2 locus, the haploid specific Pr_STE5-URA3 locus, and the MATa-KanMX or MATα-HphMX mating type loci, which were present in the original W303 but not the SK1 strains. We isolated 40 MATa and 40 MATα hybrid haploid spores with correct nutrient markers, and verified their phenotypes by a second round of growth in defined dropout media as appropriate (CSM –uracil, CSM –histidine, or CSM –leucine) and YPD supplemented with either G418 (200 μg/ml) or hygromycin (300 μg/ml).

To generate the final set of F3 haploids, we grew cultures of each haploid clone overnight and pooled them at a 33× dilution in YPD. We split the pooled culture into 12 replicate populations in a 96-well plate, with between 10⁵ and 10⁶ cells per well. We grew these cultures overnight and then diluted 1:10 in YPD supplemented with G418 and hygromycin to kill unmated haploids. We inoculated this diploid culture at a 1:10 dilution into spo ++ media (0.25% yeast extract, 1.5% KOAc, 0.05% glucose, 1× amino acid stock) and allowed it to sporulate on a 96-well plate shaker at 1,050 rpm at 30 °C for 2 days. After 2 days, we inspected cultures to verify the presence of tetrads, and digested asci by incubation in a solution of zymolyase (20 μg/ml) and glass beads on a 96-well plate shaker for 1 h. We diluted spores 1:10 into three 96-well plates with selective media for haploid MATa clones (CSM –uracil –histidine + G418) and three 96-well plates with selective media for MATα clones (CSM –uracil –leucine +hygromycin). We diluted saturated cultures 1:2¹⁰ into mating-type selective media (CSM –uracil –histidine for MATa and CSM –uracil –leucine for MATα). We assayed the final saturated cultures for leakage of the wrong ploidy or mating type using appropriate selective media, mixed with glycerol to a final concentration of 20%, and froze at −80 °C for long-term storage.

Laboratory Evolution

We founded 36 haploid and 36 diploid populations from the intercross lines described earlier. For both haploids and diploids, 12 populations underwent sexual cycles every 120 generations (the rare-outcrossing treatment), 12 underwent sexual cycles every 40 generations (the frequent-outcrossing treatment) and 12 populations never experienced additional outcrossing (the asexual treatment). The set of lines in each outcrossing treatment were founded by one of the three pairs of F3 MATa and MATα plates described earlier. We implemented sexual cycles by propagating each population asexually by serial dilution in batch culture for the appropriate number of days, followed by a round of obligate mating and sporulation (for haploids) or obligate sporulation and mating (for diploids). A summary of these experimental details is shown in supplementary figure S1, Supplementary Material online.

We founded haploid lines from a 1:2¹⁰ dilution of the F3 MATa and MATα lines. In haploid treatments, we propagated MATa and MATα subpopulations separately during the asexual phase. During sexual cycles, the corresponding population pairs were mixed, mated, sporulated and redivided into MATa and MATα subpopulations. For the asexual treatment, we substituted a second MATa line for the MATα subpopulation. The two MATa subpopulations in the asexual treatment were then mixed every 120 generations and maintained in similar conditions as the rare outcrossing treatment, where possible. We founded diploid lines by mixing and mating corresponding wells from the F3 MATa and MATα plates, selecting for diploids using G418 and hygromycin, and propagating the resulting diploid populations according to supplementary figure S1, Supplementary Material online.

For the asexual phase of each cycle, we propagated lines at 30 °C in unshaken, flat-bottomed 96-well plates containing 128 μl of YPD. Cultures were diluted daily by a factor of 1:2¹⁰. As described in previous work (Lang et al. 2011), this protocol results in approximately ten generations per day and an effective population size of $N_e\approx {10}^5$. Every 120 generations, plates were mixed with glycerol to a final concentration of 20%, and frozen at −80° for long-term storage. The mating step in each sexual cycle was implemented by mixing MATa and MATα cultures in a 1:10 dilution in YPD. After 6 h, we transferred cultures by a 1:10 dilution into YPD supplemented with G418 (200 μg/ml) and hygromycin (300 μg/ml) to kill unmated haploids. The sporulation step was performed identically to the bulk sporulation and mating type selection described in the intercross line creation. Briefly, we incubated diploid cultures in spo ++ media for 2 days, inspected cultures for tetrads, and digested asci in a zymolyase solution (20 μg/ml). We diluted spores 1:10 into two sets of plates filled with 117 μl selective media for each haploid mating type (CSM –uracil –histidine + G418 for MATa and CSM –uracil –leucine +hygromycin for MATα). Because of the high sporulation efficiency of the culture, the bottleneck size of this step was between 10⁴ and 10⁵ cells. After 18 h, saturated cultures were further diluted 1:2¹⁰ into mating-type selective media (CSM –uracil –histidine for MATa and CSM –uracil –leucine for MATα). All serial transfer, mating, and sporulation steps were carried out using a BioMek FX liquid handling robot (Beckman Coulter).

To verify that no leakage of the wrong ploidy or mating type occurred during the sexual cycle, we periodically spotted samples of each culture at a 1:1,000 dilution onto agar plates with selective media for $\text{MAT}\mathbf{a},\hspace{0.17em}\text{MAT}\alpha$ and diploid cells. We performed these leakage assays every four sexual cycles (every 160 generations) for frequent recombination treatments, every two sexual cycles (every 240 generations) for rare recombination treatments, and every two control cycles (every 240 generations) for asexual treatments. Assays were performed directly after the sexual or control cycles. Two additional assays were performed before the sexual cycle, to verify that cultures maintained the same mating type and ploidy over the entirety of the asexual phase. We found that rates of leakage of diploids in haploid MATa populations was <1%, and leakage of other ploidies or mating types in other treatments was <0.1%. These values are consistent with rates of leakage observed in previous work (McDonald et al. 2016). Diploid and mating type selection maintained the same efficiency in all populations throughout the experiment.

To test whether asexual populations maintained the correct ploidy for the entirety of the experiment, we fixed two replicate population samples from the final timepoint of the asexual haploid lines in ethanol, incubated samples in a solution of 2 mg/ml RNase A overnight and stained them using SYTOX Green nucleic acid stain (Invitrogen) to a final concentration of 240 nM. The fluorescence spectrum of each sample was measured using flow cytometry (Fortessa, BD Biosciences) on the FITC channel, counting ∼30,000 cells per sample, and cross-referenced with known haploid and diploid controls. We found that 6 of the 12 haploid asexual lines had become diploid by the end of the experiment. Since these populations maintained the drug and nutrient markers consistent with MATa haploids in this experiment, it is likely that these populations harbored MATa/MATa diploids generated by autodiploidization events.

The 12 populations per plate described here were part of a larger overall experiment in which all but eight blank wells in each 96-plate were filled with cell culture. To verify that no cross-contamination occurred between wells of 96-well plates during the sexual cycles, we inoculated every other well in nine pairs of MATa and MATα plates with strains MJM64 and MJM36 and propagated them through two rounds of mating and sporulation. Out of 864 blank wells, we observed one instance of cross-contamination, suggesting that cross-contamination induced by the sexual cycle occurred at rates of ∼0.2% or less. Finally, we cross-referenced new mutations detected in both metagenomic and clone sequencing between populations. Although some mutations matched between plates (suggesting some newly arising variation introduced in the founding F3 pool), there were no well-supported mutations confined to multiple populations of a single plate, suggesting no measurable cross-contamination occurred between the populations we study here and any other population.

Fitness Assays

Fitness assays were performed as previously described (Lang et al. 2011). Briefly, we measured fitness using competition assays between test populations or clones and a fluorescently labeled reference strain. The fluorescent reference used was a diploid strain created by mating MJM36 with DBY15084 (Lang et al. 2009), which has an mCitrine marker integrated at the HIS3 locus. To measure the relative fitness of the reference and test culture, we thawed 4 μl frozen stocks of each test culture into 128 μl of YPD and allowed this to saturate over 24 h. We then mixed test cultures in equal proportions with the fluorescent reference strain and propagated asexually for 3 days according to the standard transfer protocol described earlier. After 1 and 3 days, or ∼10 and 30 generations, respectively, we quantified the relative numbers of dark and fluorescent cells using flow cytometry (Fortessa, BD Biosciences), counting ∼30,000 cells per sample. Clustering of fluorescent and dark cells was done in batch using the SamSPECTRAL package (Zare et al. 2010) in R and manually inspected for correct clustering. We calculated the relative fitness s of the test and reference using the formula:

$$s=\frac{1}{\Delta t}\ln \left[\frac{x_f(1-x_i)}{x_i(1-x_f)}\right],$$ (2)

where x_i and x_f are the initial and final frequencies of the test cells and Δt is the number of generations between timepoints. Note that this quantity may be interpreted as the average additional progeny per generation of the test strain when compared with the reference. We performed three replicate measurements for each population. To infer the typical measurement error, we made 30 replicate measurements of a diploid clone (KK221×MJM36) and a haploid clone (KK221). We inferred the standard error of our measurements to be 0.5% for haploids and 0.3% for diploids.

To test for possible nontransitivity in fitness measurements, or biases associated with using a diploid rather than a haploid reference strain, we conducted fitness assays using the haploid DBY15084 as a reference for all of the haploid MATa and diploid F2 founder cells. We found very high correlation between the fitness measurements made using the two different references (Pearson’s r = 0.97).

We observed a systematic difference between estimates of mean fitness between clone and population data, resulting from continued adaptation in populations over the course of the fitness assay. The difference between clone and population measurements averaged 1.25%, and was larger in high variance populations (2.6% discrepancy at timepoint 0 vs. 0.5% discrepancy at timepoint 720). We note that this discrepancy is roughly consistent with the expected fitness increase of a population with standard deviation in fitness of 2% over the course of the fitness assay (∼40 generations, including thawing). As a result, we used estimates of mean fitness derived from clone measurements wherever possible.

Sequencing and Variant Calling

We thawed glycerol stocks of clones and populations to be sequenced, inoculated 4 μl of each into 128 μl YPD, and incubated without shaking for 16 h at 30 °C. In haploid populations, we sequenced only MATa subpopulations; since sequencing was performed immediately after each sexual cycle, we do not expect this to introduce any bias in inferred allele frequencies. We extracted genomic DNA in 96-well plates using a PureLink Pro 96 Genomic DNA Purification Kit, and prepared sequencing libraries as described by Baym et al. (2015). We sequenced metagenomic samples on an Illumina HiSeq 2500 to an approximate coverage depth of 15–20×, and clone samples on an Illumina NextSeq 500 to an approximate coverage depth of 10×.

We trimmed Nextera adapter sequences from reads using Trimmomatic and aligned to a high-quality SNP/indel-corrected W303 reference genome (Lang et al. 2013) using bowtie2 (Langmead and Salzberg 2012). Mitochondrial reads were removed and analyzed separately (below). To analyze frequencies of standing variants, we generated a high-quality list of SNPs and indels segregating in our sample. To do so, we first sequenced strain KK221 to 40× coverage, aligned the trimmed reads to our W303 reference genome, and generated a list of candidate SNPs and indels using breseq version 0.27.1 (Deatherage and Barrick 2014). This procedure generated 59,955 candidate SNPs and indels. To cross-reference this list with mutations detected in sequencing data, we constructed a complete list of SNPs and indels observed in sequenced F2 haploids using samtools version 0.1.19, using the commands “samtools mpileup -uBQ 10 -q -1 -o 0 -m 1 -F 0.00001 -f $REFERENCE $SAMPLE.bam— bcftools view -Avp 1.5 - > $OUTPUT.vcf” and “samtools mpileup -BQ 10 -q -1 -o 0 -f $REFERENCE $SAMPLE.bam— > $OUTPUT_coverage.vcf.” We cross-referenced these lists with the 59,955 candidate variants and removed all variants that were never found in any clone or fixed in all clones. At each candidate variant, we pooled allele frequencies in the F2 clones in 10-kb windows flanking the variant, and removed all variants whose frequency in the clone sample differed from the average window frequency by >3 σ, where $\sigma =\sqrt{x_w(1-x_w)/n}$, x_w is the sliding window frequency, and n is the number of clones with nonzero coverage at the variant locus. From this pruned candidate list, we genotyped the F2 clones at each locus by pooling allele frequencies in 4-kb windows, and calling the genetic background for SK1 if the pooled frequency was >75% and for W303 if the pooled frequency was <25%. Variants in regions with window frequencies in between these cutoffs usually occurred near crossovers and gene conversion tracts and were imputed by comparing their locations relative to inferred recombination breakpoints. Variants whose genetic background required imputation in >35% of cases were removed from the list of candidate variants. These rounds of filtering generated a final list of 56,648 high-quality variant SNPs and indels segregating within the F2 hybrid pool.

To infer frequencies of standing variants in the metagenomic sequencing data, we wrote custom MATLAB code to assign each paired-end sequencing read to a genetic background of SK1, W303, indeterminant, or recombinant. This was accomplished by cross-referencing our list of segregating standing variants with the location of each read listed in the sam file corresponding to that sample. The frequency of each genetic background in the population was then inferred every 100 bp across the genome using kernel regression with an exponential kernel with a scale parameter of 7.5 kb.

To infer which regions of the genome were predicted to fix based on their initial change in frequency, we inferred a threshold value of s_eff between generations 0 and 240 that would result in a final allele frequency of >98% or <2%, assuming that s_eff remained constant through time. We found 24 linked regions that cross this threshold, only 9 of which proceeded to eventually fix.

To genotype clone sequences, we constructed permissive lists of variants and coverage per site using the samtools commands described earlier, and cross-referenced the resulting lists with our set of segregating SNPs and indels. We genotyped each variant using LOWESS (locally weighted scatterplot smoothing) nonparametric regression on the variant frequencies in MATLAB with a span of 15 sites, weighted by distance from the focal variant and coverage at each site. Haploids were inferred to have the SK1 genetic background at the site if the smoothed allele frequency was >90% and the W303 background if the smoothed allele frequency was <10%. Diploids were inferred to be homozygous for the SK1 allele if their smoothed allele frequency was >90%, heterozygous if the smoothed allele frequency was <60% and >40%, and homozygous for the W303 allele if their frequency was <10%. Indeterminate variants were imputed in the manner described earlier.

To analyze the mitochondrial DNA, we compiled a high-confidence list of SK1 mitochondrial variants by trimming, aligning, and calling variants in a similar manner as that described earlier, and then applying depth, frequency, and q-score thresholds of 10, 0.95, and 10, respectively. We then manually reviewed the resulting list of SNPs and indels for mapping errors and inconsistencies, and removed any variants that occurred at frequency >5% at sites with a depth >10 in a corresponding set of 25 W303 short-read data sets (see Materials and Methods: Calling de novo mutations). This process resulted in a final list of 232 high-confidence SK1 mitochondrial mutations. This list of variants was cross-referenced with mitochondrial DNA from all 384 clone sequences and final timepoints of population sequences. For each data set, we recorded the number of fixed variants, the mean SK1 variant frequency, and the number of SK1 sites >50%. No data set was found with a mean SK1 variant frequency >5% or more than 3 out of 232 SK1 variant sites at frequency >50%. Furthermore, the typical number of alternate alleles with respect to the W303 reference mitochondrial sequence (median 7, max 16) was much smaller than that observed for the SK1 reference sequence. These observations suggest that either both diploid parental strains (MJM64×KK222, MJM36×KK221) were homoplasmic for the W303 mitochondria, or that the 80 F2 clones fixed the W303 mitochondrial sequence during or shortly after selection.

Statistical Analysis

Using the sliding window estimates of allele frequency, we computed the variance between replicate populations at each timepoint and treatment at each variant locus and averaged this quantity across all loci. To assess whether differences in estimated variances were significant between treatments, we employed the following strategy. A variant locus was selected randomly in 200-kb segments across each chromosome (52 variants in total; segments smaller than 200 kb were discarded). Segments of 200 kb were chosen following the estimate of linkage disequilibrium from figure 5B, so that selected sites were approximately in linkage equilibrium. We computed variance at each selected locus among replicate populations, and performed an unequal-variances t-test to assess significance between the means of each variance set between different treatments. This sampling and significance testing process was repeated 1,000 times. Reported P values are averages among all iterations.

To assess similarity between fixing clones in asexual populations, we performed the following simple statistical simulations of random fixation. A genome of 60,000 polymorphic loci was randomly segmented into pieces, with lengths of contiguous pieces following the geometric distribution with probability P = 76/60,000, following observed rates of crossovers in generation 0 clonal haplotypes. Alternating segments were assigned the SK1 or W303 genotypes. We segmented three individuals in this manner, and computed the fraction of sites that had concordant genotypes among all three individuals. This process was repeated 10,000 times. Statistical significance between observed and simulated clonal concordance was assessed by tabulating the fraction of times that the above procedure generated concordance rates greater than or equal to those measured experimentally.

We computed normalized linkage disequilibrium D′ from asexual and sexual clones at each sequenced timepoint. D′ for a pair of sites A and B, with frequencies p_A, p_B, and frequency of the 2-locus haplotype p_AB, is defined as $D^{\prime }=(p_{AB}-p_A{p}_B)/D_{max}$, where,

$$D_{max}=\{\begin{array}{cc}\min \{p_A{p}_B,(1-p_A)(1-p_B)\}\hfill & \text{if }{p}_{AB}-p_A{p}_B)<0\hfill \\ \min \{p_A(1-p_B),(1-p_A)p_B\}\hfill & \text{if }{p}_{AB}-p_A{p}_B)\ge 0\hfill \end{array}$$

We used in-house Python scripts to calculated the quantity above for each pair of variants on each chromosome, where p_A and p_B were calculated from all clones in a given timepoint and recombination treatment. Pairs of variants were binned by their distance in units of 1 kb. Plotted in figure 5B is the average of each bin for each population.

Gene Ontology Analysis

To investigate the biological processes underlying adaptation in frequently outcrossing populations, we performed a Gene Ontology (GO) analysis of the regions undergoing the most rapid change. First, the peakdetect algorithm (Bergman 2017) was used to detect all peaks in inferred selection coefficients between generation 0 and generation 960 in frequently outcrossing populations, using smoothed changes in allele frequencies averaged among all three replicates. Smoothing was performed using kernel regression in 15-kb sliding windows as previously described. Effective selection coefficients at each locus i, s_i were computed in sliding windows of 100 bp as described in the main text, using:

$$s_i=\frac{1}{960}\ln \left[\frac{x_i(960)(1-x_i(0))}{x_i(0)(1-x_i(960))}\right],$$

where x_i(t) denotes the frequency of the SK1 allele at locus i at generation t.

Peaks were thresholded at a minimum selective effect of 0.1% per generation and manually filtered for false positives. All genes within 5 kb of a peak region were collected and submitted to the GO Term Finder (Boyle et al. 2004) for significant enrichment of cellular process identifiers at a P < 0.01. This analysis yielded 66 peaks spanning 337 genes, which were significantly enriched for 30 GO categories (supplementary file S2, Supplementary Material online).

Calling De Novo Mutations

To call new mutations in clone sequence data, we compiled a more stringent list of mutations from the aligned sequences from each clone using the samtools command “samtools mpileup -uf $REFERENCE $SAMPLE—bcftools view -mv - > $OUTPUT.vcf.” This list was filtered to include only mutations at a 75% frequency in the sample and a coverage of at least 5-fold. Note that this threshold by default will discard most heterozygous mutations in diploids. To remove known standing variants and common mapping errors between the SK1 and W303 alignments, we filtered SNPs that were detected at a frequency of >50% or in at least six alternate reads in the KK221 high-coverage reference, and applied a more stringent threshold for indels (threshold frequency 25%, four alternate reads max).

We next compiled a large set of short-read data sets (25 sequence data sets at ∼20-fold coverage each) for the MJM64 strain, derived from an early sequencing timepoint from an alternate evolution experiment. We mapped these sequences to our W303 reference and filtered candidate variants of putative mutations that appeared frequently in the W303 alignments (i.e., exhibiting a net frequency of >50%, 30 reads across all samples, or presence in three or more independent populations). Since the presence of the same SNP or indel in different populations is rare, such mutations are likely to be the result of mapping errors or mistakes in the reference sequence. To remove standing variants that were present in the founding pool, and further eliminate possible mapping errors between the two founder strains, we next filtered any mutations detected at high frequency (>75% with at least 4-fold coverage) in any founder clone. Finally, we removed mutations with Q-scores <15, mutations within 15 bp of a known indel, and mutations segregating in more than one of the four sequenced populations. The remaining list of candidate de novo mutations was cross-referenced among all sequenced clones, and manually curated to remove remaining mapping errors and standing variants.

This procedure yielded a number of called mutations for each of the four populations analyzed, summarized in supplementary figure S12, Supplementary Material online. For the single haploid and diploid sexual populations where clone data were collected, we detected two different nonsynonymous substitutions in HSP104 segregating in the haploid and diploid populations at frequencies of ∼30% and 60% by generation 720, along with a handful of mutations segregating at lower frequencies. Similarly, we detected a few segregating mutations in the asexual haploid and diploid populations (e.g., three novel mutations accompanied the initial clonal sweep in the haploid population).

Next, we estimated our power to detect new mutations in haploid clones by computing:

$$P=\frac{\sum _i{n}_{i,new}}{\sum _i{n}_{i,cross}},$$

where $n_{i,new}$ is the total number of clones in which mutation i was detected using the algorithm described earlier, and $n_{i,cross}$ is the total number of clones in which mutation i was detected in at least 50% of reads at any coverage. For diploid clones, we first annotated each newly detected mutation as being heterozygous if its detected frequency was <1 and homozygous otherwise. To estimate our power to detect homozygous and heterozygous mutations, respectively, we computed:

$$P_{hom}=\frac{\sum _i{n}_{i,new,hom}}{\sum _i{n}_{i,cross,hom}}$$

and

$$P_{het}=\frac{\sum _i{n}_{i,new,het}}{\sum _i{n}_{i,cross,het}}.$$

Here, $n_{i,new,hom/het}$ is the total number of clones in which mutation i was detected de novo and annotated as homozygous/heterozygous, and $n_{i,cross,hom/het}$ is the total number of clones in which mutation i was detected at frequency 1 (for homozygotes) or at any nonzero frequency (for heterozygotes). Assuming each new mutation is detected with equal probability, P, P_hom, and P_het approximate the probability of detecting a mutation if it is found in only a single clone. This algorithm resulted in an estimate of $P\approx P_{hom}\approx 87\%$ for either mutations in haploids or homozygous in diploids, and $P_{het}\approx 3\%$ for heterozygous diploids. These estimates suggest that we detected most new mutations in haploids segregating at frequencies of ∼5% or higher, but likely missed many low-frequency new mutations in diploid populations.

We applied a similar algorithm to detect mutations in metagenomic sequencing data. Because of the relatively low coverage of these metagenomic sequences (15–20×), we restricted our search to mutations that reached frequencies of 50% or higher at a given timepoint. We generated lists of putative SNPs and indels, and filtered them of standing variants, mapping errors, and reference errors. Both of these steps were done in the same way as for the clone sequences described earlier. For a final round of filtering, we made use of our time serial data to only call mutations that were detected in at least two timepoints in a given population. The results of this analysis are shown in supplementary figure S13, Supplementary Material online.

This variant-calling pipeline was designed to detect substitutions and small insertions and deletions (∼3 bp or less). To detect longer de novo amplifications, deletions, or copy number variants (CNVs), we analyzed the distribution of coverage along the genome among sequenced clones using a method that resembles an algorithm described in previous work (McDonald et al. 2016). We first measured the average coverage in 100-bp windows along the genome for the 25 W303 sequence data sets described earlier. Coverage depth varies along the genome as a result of Poisson sampling noise, existing duplications, deletions, and CNVs, and biases or artifacts introduced by the PCR, library preparation, and alignment steps. Thus, for each window, we calculated the expected coverage relative to the median, by dividing the total number of reads for each window by the median total coverage among the pooled samples (∼500-fold). This gave us an expected baseline coverage in each 100-bp window for the clone data. For simpler statistical analysis, we modeled variance as a function of expected coverage m using the formula $v(m)\propto m+m^2/r$, where r is a parameter fit to the data. We then applied a variance-stabilizing Anscombe transformation $A(k)=\text{arcsinh}\left[\sqrt{\frac{k+3/8}{r-3/4}}\right]-\text{arcsinh}\left[\sqrt{\frac{m+3/8}{r-3/4}}\right]$ to these data, where k is the measured coverage in a window. This transformation results in approximately normally distributed data with mean 0 and constant variance. Finally, we transformed each data point by the standard deviation to scale our variance to 1. Large variations in coverage in this transformed data set will appear as long, spatially correlated signal above or below the expectation. To detect these signals in clone data, we applied a Hidden Markov Model using MATLAB’s hmmviterbi algorithm with three hidden states (0 = no change, 1 = amplification, 2 = deletion), with normally distributed emission probabilities (${\mathcal{N}}_0(\mu =0,\sigma =1),{\mathcal{N}}_1(\mu =4,\sigma =2),{\mathcal{N}}_2(\mu =-4,\sigma =2)$) and a transmission matrix:

$$T=\left(\begin{array}{ccc}0.9999& 5·{10}^{-5}& 5·{10}^{-5}\\ 5·{10}^{-3}& 0.99& 5·{10}^{-3}\\ 5·{10}^{-3}& 5·{10}^{-3}& 0.99\end{array}\right).$$ (3)

This analysis resulted in approximately 80 inferred duplications, deletions, and CNVs segregating between the SK1 and W303 founders, including a few (including the rDNA encoding segment of chromosome 12 and a region encompassing the high-affinity hexose transporters HXT6 and HXT7 on chromosome 4) that appeared to be in regions undergoing very strong selection in the early phase of the experiment. However, when applied to clones isolated from the frequent outcrossing treatment, this analysis did not find evidence of new CNVs segregating in these populations upon manual inspection of candidate regions.

Additive Genetic Variance Estimation for New Mutations

To estimate an upper bound on the potential contribution that new mutations have on fitness variation in the sexual haploid population for which clone data were collected, we estimated the fitness effects and origination times of new mutations using a maximum likelihood approach. A mutation originating at time τ with fitness effect s, assuming that it is not in linkage disequilibrium with other selected sites, will change in frequency x according to the logistic growth equation,

$$x(t)=\frac{e^{s(t-\tau )}}{N-e^{s(t-\tau )}},$$ (4)

provided that $s\ll 1$. Given a set of parameters $\Theta =(s,\tau )$ and number of clones sequenced per timepoint $\left\{n_t\right\}$, the likelihood of observed counts of mutant individuals $\left\{c_t\right\}$ is thus,

$$\mathit{L}(\{c_t\left\}\right|\Theta ,\left\{n_t\right\})=\prod _{t=1}^5(\begin{array}{c}{n}_t\\ c_t\end{array})x{(t,s,\tau )}^{c_t}{(1-x(t,s,\tau ))}^{n_t-c_t}.$$ (5)

Maximum likelihood estimates of parameters $\tilde{\Theta }=(\tilde{s},\tilde{\tau })$ can then be inferred by numerically solving:

$$\frac{\partial \ln L}{\partial s}{|}_{\tilde{\Theta }}=\frac{\partial \ln L}{\partial \tau }{|}_{\tilde{\Theta }}=0.$$ (6)

Uncertainties in these estimates are obtained from the covariance matrix ${\mathbf{\sigma }}^2$, given by ${\mathbf{\sigma }}^2=-{\mathbb{H}}^{-1}$, where $\mathbb{H}$ is the Hessian matrix ${\mathbb{H}}_{i,j}\equiv \frac{{\partial }^2\ln L}{didj}{|}_{\tilde{\Theta }}$.

In practice, new mutations are likely to be in linkage disequilibrium with many selected sites in these populations, and as such, neutral or slightly deleterious mutations could potentially hitchhike to high frequencies. Since this method does not take hitchhiking into account, it will tend to overestimate fitness effects, providing a conservative upper bound on the potential contribution of new mutations to fitness variation.

We wrote custom MATLAB code to apply this method to infer the fitness of mutations segregating at frequencies >20% in the sexual haploid population. Combining both clone and metagenomic data, we infer a maximum likelihood fitness effect of $\tilde{s}=0.3\%\pm 0.1\%$ for the only high-frequency mutation detected in this population. At its largest influence on fitness variance, this mutation could explain a maximum of $\frac{V_{mut}}{V_{A,total}}=\frac{2·{10}^{-6}}{6.7·{10}^{-5}}\approx 3\%$ fitness variation, where the additive genetic variance is estimated conservatively from the change in average fitness of clones between generations 240 and 720 ($V_{A,total}=v=\Delta s/480$).

Because of our lower power to detect new mutations in diploids, and because of the risk of overfitting arising from the extra dominance parameter, we did not estimate the contribution of new mutations to variance in the diploid sexual population. However, we do note that the mutation observed at high frequency in the diploid sexual population stopped significantly changing in frequency after generation 480 (supplementary fig. S12, Supplementary Material online), a trend that was corroborated by metagenomic data from this population at the end of the experiment (supplementary fig. S13, Supplementary Material online). Although we are unable to make conclusive inferences about the fitness effect of this novel mutation, these dynamics are consistent with either a neutral hitchhiker, or a selected mutation exhibiting some form of heterozygote advantage or epistasis. Regardless, it is unlikely that this mutation contributes a large proportion of additive genetic variation in this population, and could not explain the sustained increase in fitness observed through the end of the experiment.

Simulations

To quantify how we expect the genetic architecture of fitness and population genetic parameters to affect the phenotypic and sequence data we collected, we simulated our experiment by modifying SLiM (Messer 2013), a forward-time population genetic simulator for studying the effects of evolution under linked selection. First, we modified SLiM to simulate haploid rather than diploid evolution. We chose each child genome in every generation from two randomly selected haploid genomes, which we selected proportionally to each haploid genome’s fitness. The child genome was then assembled randomly from the chromosomes of the two parent genomes, with a small probability of cross-over between the two genomes. Next, we implemented an additive fitness model, in which the likelihood of haploid selection in each generation is proportional to $1+\sum _{i=1}^n{s}_i-\overline{s}$, where s_i is the fitness effect of the i-th mutation, n the total number of mutations carried by the individual, and $\overline{s}$ the average contribution of selected mutations among all individuals. This model prevents pathologies arising from dense and frequent selection in multiplicative fitness models, and allows for rescaling of fitness effects, recombination rates and population sizes. Finally, we included an additional, optional parameter X_c that could be passed to each simulation for a simple model of diminishing returns epistasis, where the realized fitness of a particular genotype, W, depends on the absolute fitness of the genotype, X, as:

$$W=\frac{X-{\overline{X}}_0}{\left[1+(X-{\overline{X}}_0)/X_c\right]},$$ (7)

where ${\overline{X}}_0$ is the starting mean absolute fitness of the population.

Using this modified version of SLiM, we simulated the laboratory evolution experiment while varying the number and strength of selected mutations as follows. First, we generated two diverged haploid individuals by evolving a population of size 2 at a very high mutation rate (0.0007 per individual per generation). Each haploid individual had a 9-Mb genome consisting of nine chromosomes, each with length 1 Mb. This size approximates the total size of the genome with standing variation in our experiment, once we exclude regions of very low diversity and regions purged of variation due to selection for the sexual system. A fraction of the introduced mutations were chosen to be selected (between 1 and 1/256, depending on the parameter set), with selective effects drawn from an exponential distribution with a mean effect that was passed as another parameter to the simulation (between ∼2×10⁻⁴ and 4×10⁻³). Next, to simulate the generation of the outcrossed lines, we applied a round of recombination to the two diverged haploids at a rate of about 30 crossovers per meiosis. This rate approximates the genome-wide recombination rate experienced by the frequent-outcrossing treatments, as inferred by both previous estimates of the recombination rate (yielding anywhere between 40 and 50 crossovers per individual per meiosis; Mancera et al. 2008), and by counting the observed number of crossovers in the sequenced founder clones (averaging 38 crossovers per spore per meiosis; fig. 5A). During the recombination step, we simulated our clone selection and intercross line generation procedure by introducing two demographic changes: a population expansion to 80 individuals following the first round of recombination, followed by an expansion to 2×10⁵ for the evolution. To improve computational efficiency, we rescaled population size $N\to N/10$, selection coefficients $s\to 10s$, recombination rate $r\to 10r$, and time $t\to t/10$ for this phase of the simulation. This transformation preserves stochastic and deterministic dynamics while yielding an $\mathcal{O}(100)$ increase in computational efficiency. We evolved each simulated population for 960 (rescaled 96) generations, and output every genotype in the population every 240 (24) generations. From these data, we measured the mean and variance in fitness, allele frequencies in 15-kb sliding windows, and the mean heterozygosity $2\overline{p(1-p)}$ calculated from sliding windows.

For computational efficiency, the numbers and strengths of selected sites were constrained so that the initial fitness variation in the simulated population matched the variation observed in the initial haploid clone pool, $\sigma \sim 2.1\%$. To accomplish this, we introduced an array of different selected mutation rates and selection effects, generated ten outcrossed populations for each parameter pair, and recorded their variances in fitness. Then, for every simulated number of selected sites n, we fit a linear model ${\sigma }_n=ms+b$, and inferred s(n) such that ${\sigma }_n=2.1\%$. We modified this procedure for two additional models of genetic architecture. First, we modeled populations undergoing fitness-mediated diminishing returns epistasis as described earlier, with $0.8<X_c<2.8$. This model decreases variance from the additive expectation, so for each diminishing returns parameter set we simulated a starting (additive) variance of 4%, which resulted in an actual starting fitness variance of ∼2%. Additionally, for the two-effect model of adaptation, we estimated from our experimental clone fitness data an initial fitness increase of ∼5.5% before generation 240, and a residual rate of adaptation of ∼1.2% every 240 generations thereafter. As a result, we introduced strong effect mutations with a total effect of 4% on fitness that were expected to be fixed or nearly fixed by generation 240, and a large number of small effect mutations whose combined contribution to the standard deviation was ∼0.7%, which would result in the rate of adaptation observed. The introduced “strong effect” mutations varied from 0.5% to 2%. Supplementary file S3, Supplementary Material online, provides the final set of parameters used for each simulated model. In total, nine sets of parameters were simulated for the additive model, 90 for the epistatic model, and 54 for the two-parameter model, with ten populations simulated per parameter set.

We compared our simulation results to experimentally measured fitness and heterozygosity trajectories. Although we could have employed a number of different statistics to analyze the simulated genomic data (e.g., number and shape of peaks, minor allele fraction, site frequency spectrum, average fitness effect), we chose to focus on an average heterozygosity for a number of reasons. First, average heterozygosity is not sensitive to variable read depth and sliding window effects (unlike a number of alternative statistics, including the site frequency spectrum and properties of allele frequency peaks). Furthermore, heterozygosity is commonly employed in the analysis of laboratory evolution experiments (Burke et al. 2010; Burke 2012; Long et al. 2015) and its relationship with selection and recombination is (comparatively) well-characterized theoretically (Maynard Smith and Haigh 1974; Gillespie 2000; Neher et al. 2013b). For a wide range of parameter regimes, this relationship is somewhat intuitive: an increase in selection density or a decrease in recombination rate will tend to result in a more rapid decline in heterozygosity (although this expectation breaks down at high selection densities).

Because the initial estimate of mean population fitness derived from the clone data more accurately includes the effect of low fitness genotypes, we used clone data to infer the fitness of one of our evolved populations over time, with the uncertainty in mean fitness estimated as ${\sigma }_t/\sqrt{n_t}$, where n_t and σ_t are the number of clones measured and the fitness deviation at timepoint t, respectively. For generation 960, we used the population estimate of mean fitness, normalized by the average difference between fitness measurements for generations 240, 480, and 720 between clones and populations. Uncertainty for this data point was calculated from the three replicate fitness measurements. Mean heterozygosity was estimated from 15-kb sliding windows generated from the metagenomic sequencing data, by measuring the inferred heterozygosity $2p(1-p)$ every 100 bp, and averaging this quantity across the genome. Regions of starting low genetic diversity were masked during this calculation. We estimated uncertainty in heterozygosity by calculating mean heterozygosity among all three sequenced populations, and computing ${\sigma }_{\pi }/2$, where ${\sigma }_{\pi }$ is the deviation in heterozygosity among the sequenced populations.

The likelihood of the data, given each parameter set $\Theta =(s,n,X_c)$ was estimated by:

$$L(\{{\pi }_{t,data},x_{t,data}\left\}\right|{\sigma }_{x,t},{\sigma }_{\pi ,t},\Theta )=\int L(\{{\pi }_{t,data},x_{t,data}\}|{\sigma }_{x,t},{\sigma }_{\pi ,t},x_{t,sim},{\pi }_{t,sim})P(x_{t,sim},{\pi }_{t,sim}|\Theta )d{x}_{t,sim}d{\pi }_{t,sim}\approx \frac{1}{n}\sum _{j=1}^{n}L(\{{\pi }_{t,data},x_{t,data}\}|{\sigma }_{x,t},{\sigma }_{\pi ,t},x_{t,sim,j},{\pi }_{t,sim,j})=\frac{1}{n}\sum _{j=1}^n\hspace{0.17em}\text{exp}\hspace{0.17em}\hspace{0.17em}\left(-\sum _{t=1}^5\left(\frac{{(x_{t,data}-x_{t,j,sim}-m_j)}^2}{2{\sigma }_{x,t}^2}+\frac{{({\pi }_{t,data}-{\pi }_{t,sim,j})}^2}{2{\sigma }_{\pi ,t}^2}\right)\right).$$ (8)

Here, $x_{t,data}$ and ${\pi }_{t,data}$ represent the measured fitness and heterozygosity; ${\sigma }_{x,t}$ and ${\sigma }_{\pi ,t}$ are uncertainties in measured fitness and heterozygosity; $x_{t,sim}$ and ${\pi }_{t,sim}$ are simulated fitnesses and heterozygosities; and

$$m_j=\frac{1}{\sum _t{\sigma }_{x,t}^{-1}}\sum _{t=1}^5\frac{x_{t,data}-x_{t,j,sim}}{{\sigma }_{x,t}}$$

is a parameter introduced to compare the relative fitnesses measured in the experiment and simulation, calculated to maximize the likelihood for each parameter set. We did not include fitness variance measurements in our log likelihood statistic, because our estimates of population fitness variance were likely inflated for a number of reasons (including deleterious load, an assay environment that did not include the sexual selection phase of the evolution protocol, or other nongenetic factors). In general, however, we found that simulated fitness variances were much smaller than those observed.

A comparison of likelihoods between the model of diminishing returns epistasis and the two-effect model rejected the two-effect model with P<10⁻¹¹. Applying a likelihood-ratio test between the most likely sets of parameters for the model of diminishing returns epistasis and the purely additive model rejects the additive model with P<1.1×10⁻¹⁶. We note, however, that other models of epistasis could potentially better describe the experimental data.

We employed two approaches to estimate the most likely density and strength of selected sites predicted by the epistatic model. First, we tabulated all simulation runs within 2 log likelihood units of the simulation run with the highest log likelihood, approximating a 95% confidence interval. Alternatively, we computed the mean likelihood for each pair of s, n (selection strength, number of sites), averaging among all simulation runs and epistasis parameters. We then tabulated the sets of s, n with mean log likelihood within two of the set of (s, n) with the highest likelihood. These two procedures yielded identical results; the most likely parameter set was ∼300 sites (i.e., selected site density of 3.3×10⁻⁵, with 9-Mb genome size) of fitness effect 0.13%. Parameter sets within 2 likelihood units of the maximum included ∼600 sites of 0.09% and ∼1,200 sites of 0.06%, suggesting roughly 300–1,200 selected sites genomewide.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.