Statistical Package for Growth Rates Made Easy

Abstract

Growth rates are an important tool in microbiology because they provide high throughput fitness measurements. The release of GrowthRates, a program that uses the output of plate reader files to automatically calculate growth rates, has facilitated experimental procedures in many areas. However, many sources of variation within replicate growth rate data exist and can decrease data reliability. We have developed a new statistical package, CompareGrowthRates (CGR), to enhance the program GrowthRates and accurately measure variation in growth rate data sets. We define a metric, Variability-score (V-score), that can help determine if variation within a data set might result in false interpretations. CGR also uses the bootstrap method to determine the fraction of bootstrap replicates in which a strain will grow the fastest. We illustrate the usage of CGR with growth rate data sets similar to those in Mira, Meza, et al. (Adaptive landscapes of resistance genes change as antibiotic concentrations change. Mol Biol Evol. 32(10): 2707–2715). These statistical methods are compatible with the analytic methods described in Growth Rates Made Easy and can be used with any set of growth rate output from GrowthRates.

Introduction

Growth rates have become increasingly useful in microbiology and are often used to quantify phenotypic properties in microorganisms (Mira, Meza, et al. 2015). Growth rates are used in a variety of areas; including proteomics (Klumpp and Hwa 2014), population dynamics (Santos et al. 2014), genomic mutation rates (Raynes and Sniegowski 2014), and mathematical modeling (Mira, Crona, et al. 2015). Studies in experimental evolution use growth rates as a measurement of fitness (Mira, Meza, et al. 2015) and measure the responses of microorganisms to various environmental factors (e.g., antibiotics) (Ross and McMeekin 1994).

Growth rates are calculated using the natural log of the optical density (O.D.) of a cell culture over time (Hall et al. 2014). Automatic plate readers that can measure the O.D. of up to 384 cultures simultaneously have made the collection of growth rate data very efficient. A software package, GrowthRates has allowed rapid high throughput analyses of growth rate data (Hall et al. 2014). GrowthRates has been used in diverse scientific areas, for example, to create antibiotic cycling strategies to combat antibiotic resistance (Mira, Crona, et al. 2015), to design programs for age phenotyping in yeast (Jung et al. 2015) and to develop smart food packaging that helps prevent spoilage (Cavallo et al. 2014) among others.

The power of modern growth rate experiments comes from the ability to have many replicate cultures in a plate reader, and the ability to measure growth under many conditions simultaneously. The conditions may be varied by the genotype of the organism or by environmental conditions (nutrient source, antibiotic, inhibitor concentrations, etc.) or both. The growth rates can then be used to assess fitness differences. However, a challenge presented by the use of a plate reader is that while their sensitivity makes it possible to identify both large and subtle differences, variance in replicate growth rates can make it difficult to determine the confidence of those comparisons. When growth rates are too similar it can be difficult to determine the fittest genotype.

In this study, we have focused on strains that have been cultured in sublethal concentrations of antibiotics because the resulting inhibition of growth creates a situation where variance is a source of concern. We have developed statistical methods for handling this variation and have automated the use of those statistics with a series of computer programs. Here, we present a statistical package for GrowthRates, CompareGrowthRates or CGR, that can measure the amount of variation within replicates. CGR is a solution to the problem of measuring variation and the effect of variation on reliability.

Methods and Results

The purpose of any statistical analysis is to evaluate the confidence we have in the data obtained and in the conclusions drawn from experiments. Confidence in the reliability of data is measured by the correlation coefficient, R, of the best fit line to the natural log of the optical density (ln(O.D.)) over time. Growth rates are calculated by taking the slope of that line. Confidence in the conclusions of an experiment depends upon the variability in the growth rates among members of a set of replicate cultures, which we will refer to hereafter as a set. Variability is measured by the V-score for a set, where the V-score is defined to be the ratio of the standard error of the mean to the mean growth rate for that set, $V\hspace{0.17em}=\hspace{0.17em}\frac{\mathrm{S}\mathrm{E}}{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}.}.$ The lower the V-score, the less variable were the growth rates within the given set.

GrowthRates reports the growth rate and the correlation coefficient (R) for each culture. R can be interpreted as a measure of the reliability of the growth rate. For each set of replicate cultures, CGR reports the mean growth rate, the mean R and the V-score.

CGR analysis of 45 experiments (supplementary data 2014, Supplementary Material online) where the culture conditions were various concentrations of antibiotics showed that when the mean growth rate was very low, the maximum O.D. and the mean R were also quite low (R < 0.9). In general, those low and unreliable growth rates were also highly variable, resulting in high V-scores. We concluded that the growth rates were unreliable in wells in which growth was very slow and maximum O.D.s were very low (supplementary table 1, Supplementary Material online).

Reliability of a Single Growth Rate Estimate

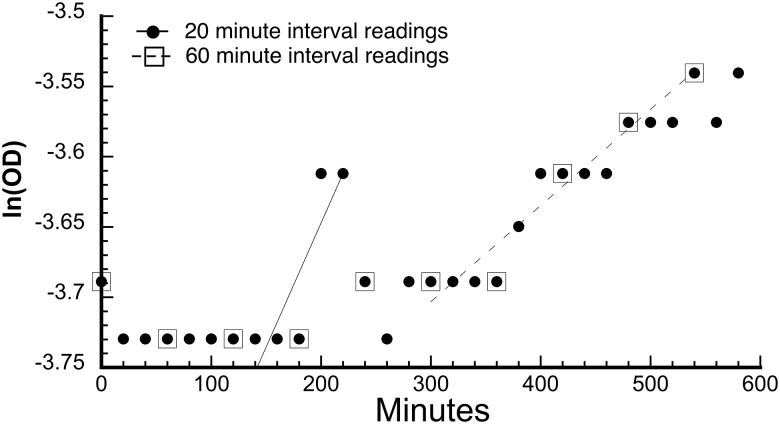
The GrowthRates program estimates growth rates by identifying the highest slope among all the slopes of five successive time points (Hall et al. 2014). For that set of points GrowthRates then, if possible, extends the number of points while the slope of the extended line remains above 95% of the slope of the initial highest slope. The reported growth rate is based on the slope of that extended line. Figure 1, based on data collected in 2017, illustrates when there is very little growth over those five points the scatter in the readings can result in low correlation coefficients.

Fig. 1.

Illustration of effects of O.D. readings at 20 versus 60-min intervals. This example is from a 2017 experiment in which genotype 1110 grew in the presence of 0.1 µg/ml ceftriaxone. See supplementary data 2017, Supplementary Material online, sheet CRO 0.1 rr1, cell L9 for the 60-min interval growth rate. Filled circles: Readings at 20-min intervals. Open squares: Subset of readings at 60-min intervals. Solid line: Line of best fit to the five consecutive 20-min interval points that give the highest growth rate. Growth rate = 0.00177 min⁻¹, and R = 0.866. Dashed line: Line of best fit to the five consecutive 60-min interval points that give the highest growth rate. Growth rate = 0.00068 min⁻¹, and R = 0.971.

Figure 1 shows many instances where O.D. did not change over several successive readings. That pattern is typical when the sampling interval is too frequent relative to the growth rate. The solid line shows the regression line through the points 140 through 220 min; the line that has the highest slope among all sequential 5-point lines at 20-min intervals. The slope of that line (growth rate) is 0.00177 min⁻¹, and the correlation coefficient R = 0.866.

Squares show the subset of those points at 60-min intervals, and the dashed line shows the regression line through those points 300 through 540 min; the line that had the highest slope among all sequential 60-min points. The slope of that line (growth rate) is 0.00068 min⁻¹, and the correlation coefficient R = 0.971.

The CGR program package includes a program, EditReadingIntervals, that facilitates easy editing of an input file for GrowthRates so that the input file only includes points at greater intervals than in the original input file.

To test the hypothesis that reading too frequently can decrease the reliability of growth rate estimates, we edited the GrowthRates input files of several experiments to delete readings so that the remaining readings were at 60-min intervals. We then compared the mean growth rates, mean R, and V-scores of readings at 20-min intervals with those of readings at 60-min intervals. Table 1 shows the result of modifying the reading intervals for one of those 2014 experiments in which the treatment was cefotetan (CTT) at 0.063 μg/ml.

Table 1.

Effects of Changing the Reading Interval from 20 to 60 min.

	20-Min Reading Interval			60-Min Reading Interval
Set ID	Mean Growth Rate (min−1)	V-score	Mean R	Mean Growth Rate (min−1)	V-Score	Mean R
0000	0.00673	0.0725	0.9768	0.00497	0.0250	0.9964
0000C	0.00931	0.3470	0.9566	0.00490	0.0458	0.9954
1000	0.01275	0.3392	0.9234	0.00505	0.0584	0.9960
1000C	0.01325	0.4109	0.9034	0.00603	0.1912	0.9795
0100	0.01023	0.4195	0.9327	0.00659	0.2496	0.9899
0100C	0.01933	0.3455	0.9197	0.00921	0.2582	0.9730
0010	0.01086	0.3918	0.9546	0.00693	0.2341	0.9900
0010C	0.02202	0.3163	0.8928	0.00745	0.2546	0.9707
0001	0.00378	0.0733	0.9888	0.00358	0.0547	0.9961
0001C	0.00336	0.0687	0.9922	0.00336	0.0493	0.9961
1100	0.00610	0.0853	0.9574	0.00487	0.0401	0.9975
1100C	0.01203	0.3644	0.9105	0.00782	0.2720	0.9757
1010	0.01500	0.2628	0.8896	0.00816	0.2207	0.9668
1010C	0.03121	0.2564	0.8877	0.01068	0.2216	0.9569
1001	0.00566	0.0537	0.9891	0.00470	0.0319	0.9959
1001C	0.00573	0.0928	0.9350	0.00453	0.0504	0.9969
0110	0.00433	0.0790	0.9910	0.00400	0.0444	0.9937
0110C	0.00458	0.0740	0.9878	0.00387	0.0642	0.9947
0101	0.00592	0.0744	0.9793	0.00477	0.0410	0.9973
0101C	0.00469	0.0621	0.9872	0.00437	0.0461	0.9977
0011	0.02788	0.2731	0.9082	0.01040	0.2074	0.9461
0011C	0.01552	0.3288	0.8756	0.00534	0.0456	0.9980
1110	0.02969	0.2085	0.8464	0.00944	0.2541	0.9802
1110C	0.02198	0.2901	0.8942	0.00826	0.2469	0.9821
1101	0.02528	0.2519	0.8675	0.01036	0.2266	0.9731
1101C	0.02032	0.3021	0.8467	0.00822	0.2234	0.9666
0111	0.02463	0.2781	0.8801	0.00779	0.2372	0.9705
0111C	0.00988	0.4363	0.9618	0.00584	0.1963	0.9802
1011	0.01212	0.2989	0.8830	0.00637	0.1738	0.9794
1011C	0.01014	0.3066	0.9103	0.00755	0.2471	0.9709
1111	0.00490	0.0688	0.9828	0.00383	0.0452	0.9966
1111C	0.00505	0.0465	0.9798	0.00383	0.0430	0.9973

Note.—Sets ending in “C” are controls. Those not ending in “C” include treatment with the antibiotic cefotetan (CTT) at a concentration of 0.063 µg/ml. Data are from CTT 0.063 in the supplementary data 2014, Supplementary Material online.

In each set, a reading interval of 60 min improved the correlation coefficient R by an average of 0.053 across all sets. In all but one set, a reading interval of 60 min improved the V-score, and the average improvement was 2-fold. We conclude that reading too frequently relative to the growth rate reduces the reliability of the growth rate estimates and increases the variability.

We applied CGR to the 45 experiments performed in 2014, one of which is referenced in table 1. One experiment consists of growth rates measured from 16 variant genotypes grown with and without an antibiotic treatment. For each genotype there were 12 experimental replicate growth rate measurements with one antibiotic at one concentration, and 12 control replicate growth rate measurements, without treatment. The 16 genotypes we used were TEM β-lactamase variants expressed in E. coli K12.

We performed 45 separate experiments in different antibiotic treatments. This design requires that we have confidence in the reliability of the mean growth rates of all 16 experimental and control sets in each experiment. We used a reading interval of 60 min and a minimum mean correlation coefficient of 0.95 for each set, as a standard for growth rate reliability. Fourteen of the 45 experiments were acceptable, meaning that none of the 16 genotypes in any of those 14 experiments had unreliable growth rates either in the presence or absence of antibiotics. Repetitions in 2017 (supplementary data 2017, Supplementary Material online) brought the number of acceptable experiments up to 29.

Measuring Variation within Growth Rate Replicates (V-Score)

The first source of variation we consider is variation among replicates within a single set. We measure that variation using a Variability-score, or V-score. The V-score is defined as $V\hspace{0.17em}=\hspace{0.17em}\frac{\mathrm{S}\mathrm{E}}{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ where SE is the standard error of the mean. For example, if the mean growth rate is 0.02 per minute, then a SE of 0.0001 (V = 0.005) is considered small and indicates that there is little variation among replicates. However, if the mean growth rate is 0.0005 per minute, then a SE of 0.0001 (V = 0.2) indicates that there is high variation among replicates. The SE alone is insufficient to give a clear picture of the extent of the variation. The lower V-score clearly implies less variation. Thus, the lower the V-score, the tighter the fit around the mean growth rate of each data set.

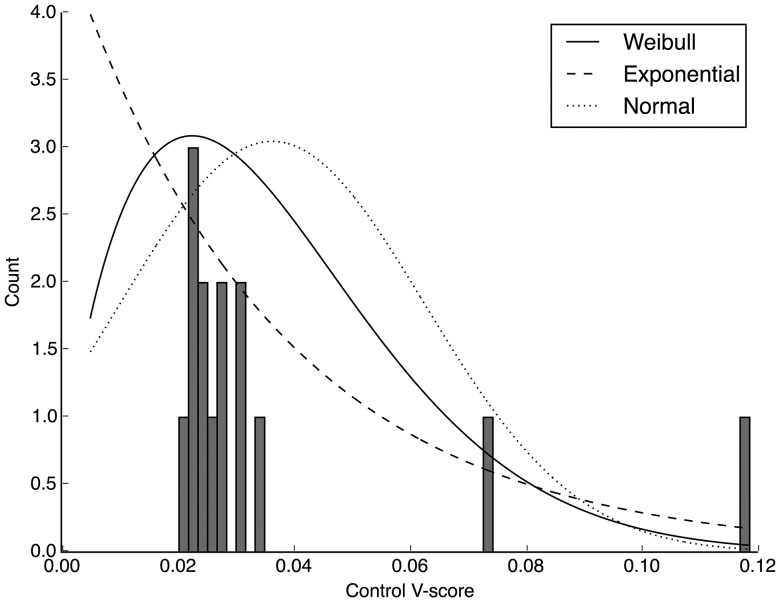
After determining the accepted experiments based on a minimum correlation coefficient of 0.95, we wanted to determine a threshold of variation within a group in which we can use to accept or reject an experiment. We plotted the frequency of control group V-scores from the 2014 experiments and determined the best fit distribution (fig. 2). Based on the Kolmogorov–Smirnov test, a statistical test that measures the fit of a data set to a distribution, the Weibull distribution was the most significant fit to our data. (It is important to note that one would need to calculate her own threshold of variation based on her data). Using the Weibull distribution, we calculated an upper 95% confidence limit (0.053) and determined that any experiments with V-scores above 0.053 should be repeated because of high variation within groups .

Fig. 2.

Distribution of mean V-scores of TEM-85 2014 data (supplementary data 2014, Supplementary Material online) that has been accepted based on the correlation coefficient thresholds (R > 0.95). Data were fit to three distributions; Exponential distribution in a dashed line (P value 0.007), Weibull distribution in a solid line (P value 9.1 × 10⁻⁵), and normal distribution in a dotted line (P value 0.0253).

Based on the V-score threshold from the Weibull distribution, two of the 14 acceptable experiments needed to be repeated (table 2).

Table 2.

V-Scores of Acceptable Experiments that Were Repeated because of High V-Scores.

	2014		2017Repeat 1		2017Repeat 2
Treatment (µg/ml)	Control	Experimental	Control	Experimental	Control	Experimental
CTT 0.125	0.0739	0.1433	0.0195	0.0296	0.0173	0.0249
CXM 3	0.1187	0.0818	0.0209	0.0167	0.0159	0.0166

Note.—CTT, cefotetan; CXM, cefuroxime.

Although the 2014 experiments in table 2 were acceptable by the criterion of having all correlation coefficients ≥ 0.95, they were repeated because the mean V-scores exceeded the threshold of 0.053. The experiments that were repeated in 2017 had V-scores below the 95% confidence limit threshold.

Based on our 29 reliable experiments, we found that for control data (no antibiotic present) the mean V-score was 0.0189 ±0.00099 with a range of 0.0121 to 0.0321. Since the control conditions involve no antibiotic, we judge that this level of variation reflects random variation in day-to-day conditions and variation in growth rates for each genotype.

The mean V-score for experimental data (antibiotic present) was 0.0293 ±0.00198 with a range of 0.0124–0.0502. The presence of an antibiotic (or other growth inhibitor) significantly increases variability, and hence increases V-scores.

The experiment shown in table 1 was among those rejected because of correlation coefficients <0.95. In that experiment the mean V-score (including control sets and experimental sets) was 0.1437. Table 1 shows that many of the experimental sets had V-scores between 0.2 and 0.25. Many of the other rejected experiments had mean V-scores > 0.1 as well, more than twice of what was seen for the accepted experiments. This is consistent with the earlier observation that low correlation coefficients are associated with high V-scores.

Of the thirty-one 2014 experiments that were rejected because of correlation coefficients < 0.95, 19 would also have been rejected on the basis of their V-scores.

Bootstrapping: Confidence Levels When Comparing Growth Rates

Variation within a set of growth rate replicates also contributes to uncertainty when sets of growth rates are compared, for example, when trying to determine the fittest strain or the optimum condition. When comparing two sets the objective is to determine which one grows faster. If the growth rates of all the members of set 1 are greater than the growth rates of all the members of set 2 (there is no overlap in growth rates) then we can assume that the cultures in set 1 will always grow faster than the cultures in set 2. But, if the distributions of growth rates overlap, we are less confident, and the more the distributions overlap the less confident we are. If we were to do another experiment, how likely is it that those cultures in set 1 will be favored? We could repeat the experiment many times and count the number of times that the mean growth rate of set 1 is greater than that of set 2, but that is time consuming and expensive. Alternatively, we can accomplish the same objective statistically by bootstrap sampling.

Let’s consider an example in which the two “conditions” are two different strains of the same species growing in identical media. Suppose that each set has ten replicate cultures. We randomly sample, with replacement, ten growth rates from set 1 to make up a new “bootstrap sample” (Efron 1979). We do the same for set 2. We do this thousands of times keeping track of how many times set 1 grows faster than set 2 and vice versa. Let’s assume that set 1 grows faster in 90% of the bootstrap samples and set 2 grows faster in 10% of the samples. We can now say with 90% confidence that set 1 cultures grow faster than set 2 cultures. If set 1 grows faster in only 50.01% of the samples then we might still say that set 1 grows faster than set 2, but our confidence is much lower (i.e., only 50.01% confident). It would be more accurate to say that the growth rates of the two strains are indistinguishable. In practice, we always use an odd number of bootstrap samples so that there can never be an exact tie between the two sets. Thus, we can determine which strain grows faster and the confidence that supports that statement.

This same approach can be extended to compare more than two sets. Using the bootstrap approach we can do all possible pairwise comparisons in each bootstrap replicate. We define a group as a group of sets that have some property in common. Often members of a group are to be compared in order to determine which set grows fastest. For instance, among a group of ten sets we might find that set 4 grows fastest in 45% of the bootstrap replicates, set 7 grows fastest in 35% of the replicates, set 2 grows fastest in 20% of the replicates, and none of the remaining sets ever grow fastest.

Using the “Comparison Score” to Determine the Number of Bootstrap Replicates to Use

Because of the stochastic element in bootstrap sampling, different bootstrap runs on the same data are not identical. CGR does pairwise comparisons of all of the bootstrap runs to assess their reproducibility. Each bootstrap run determines the fraction of bootstrap replicates in which each set grew fastest and saves that information in table 1 of a report file for that bootstrap run. The comparison score is the sum of the absolute value of the differences of the values in those tables of the runs being compared. For instance, if a set grew fastest in 0.9 of the replicates in one run, but grew fastest in only 0.83 of the replicates in the other run the absolute values of the differences is 0.07. The comparison score for that pair of runs is the sum of those differences over all sets. If the results of the different runs were identical the differences would be zero; because the values in each table sum to 1.0 the upper limit of the score is 2.0. Thus, the lower the comparison score the more similar are the two bootstrap runs being compared.

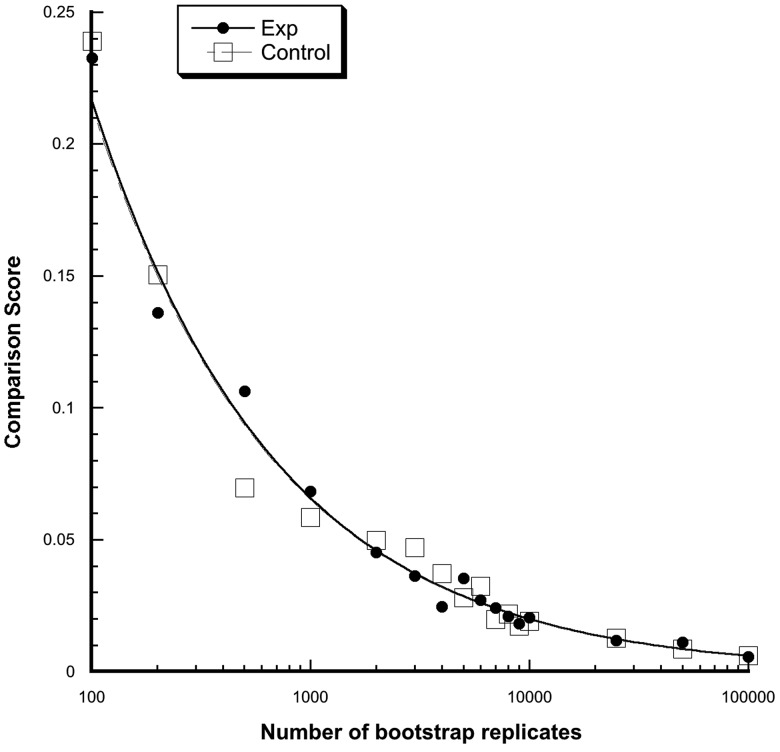
Because of stochastic variation, the more bootstrap replicates in a run, the more similar are the results of the runs. Figure 3 shows that as the number of bootstrap replicates per run increases the comparison score decreases (i.e., the runs become more similar), but increasing the number of bootstrap replicates beyond 10,001 results in very little improvement in comparison scores.

Fig. 3.

Comparison scores as the number of bootstrap replicates per run increase. Ten runs were done at each number of bootstrap replicates. Experimental data are depicted with filled circles and control data are depicted by squares. Bootstrap replicates above 10,001 shows little improvement in comparison score.

The default number of bootstrap replicates per bootstrap run is 10,001, but the user can increase or decrease that number on the command line. By default CGR includes ten independent bootstrap runs, but that number may be changed by the user as well.

Application of CGR to an Experimental Data Set

In our experimental design each experiment consists of two groups; an experimental group grown in the presence of an antibiotic and a control group grown in the absence of the antibiotic. For the 29 acceptable experiments among all experiments from 2014 to 2017, the control group V-scores ranged from 0.0121 to 0.031, with a mean of 0.0181 ±0.00087 and a median of 0.0159. For the experimental group, the V-scores ranged from 0.0124 to 0.0502 with a mean of 0.02936 ±0.00206 and a median of 0.0302.

To get a better understanding of how variance can affect our conclusions, we used the statistical method of bootstrapping as described above. Table 1 (60-min reading interval) shows that the genotypes 0101 and 1101 grow faster in the presence of the antibiotic than in its absence (genotypes ending in “C”). So, how confident are we that the antibiotic actually increases the growth rate in those genotypes? The results of ten independent bootstrap runs with 10,001 bootstrap samples per run, give us mixed levels of confidence. For genotype 0101, we are 92% confident that the antibiotic increases the growth rate relative to the control; for genotype1101 we are only 77% confident. Intuitively we expect to have greater confidence when the difference in growth rates is large, and less confidence when the difference is small. Genotype 0101 grows imperceptibly faster (4 × 10⁻⁴min⁻¹) than its control, yet we have 92% confidence that the faster growth is real. Genotype 1101 grows substantially faster (2.14 × 10⁻³min⁻¹) than its control, yet we only have 77% confidence that the faster growth is real. This illustrates the value of bootstrapping for assessing differences in growth rates.

We are also interested in the question of which experimental genotypes grew fastest. That information, the faster growing genotype, could be used to predict the outcomes of competition experiments among all the genotypes in the presence and absence of an antibiotic. For the experiment in table 1, in the presence of the antibiotic, genotype 0011 grows fastest with a mean growth rate of 0.0104 ±0.00216 per minute. However, when bootstrapping was used, genotype 0011 grew fastest only 33% of the time, whereas genotype 1101 grew fastest 34% of the time and genotype 1110 grew fastest 20% of the time.

Application of CGR to a Set of Experiments Involving Adaptive Landscapes

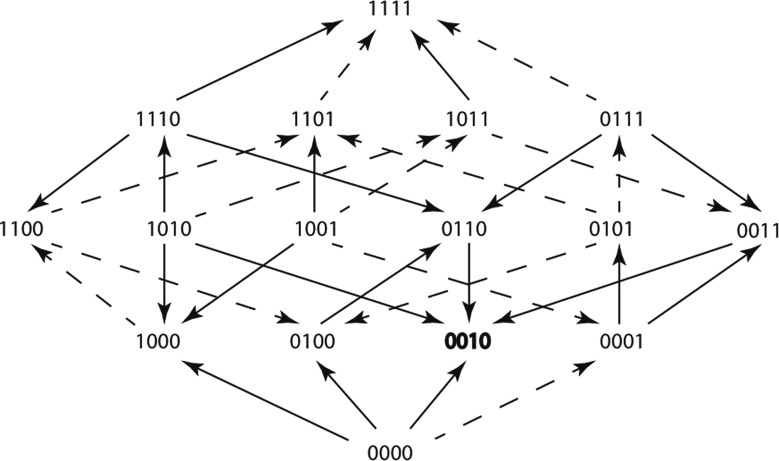
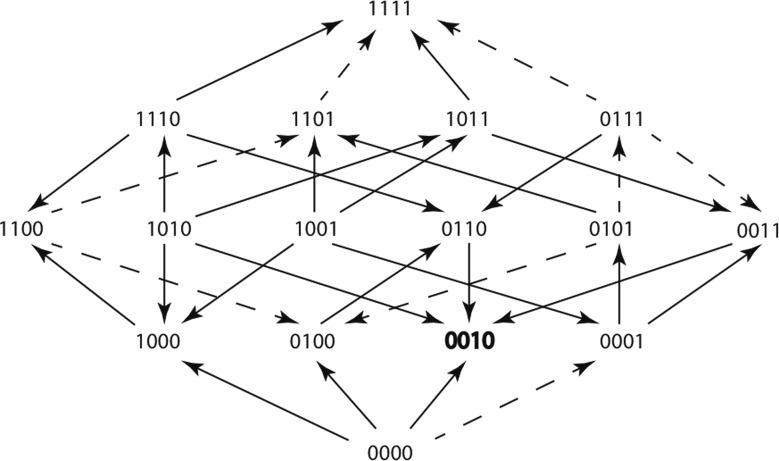
An adaptive landscape (fig. 4) is a visualization of the possible evolutionary trajectories that resistance genes can take in the presence of an antibiotic (Weinreich et al. 2006). It can also provide information about which trajectories are more likely to occur. Our adaptive landscapes consist of 16 nodes. Each node represents a different genotype, in comparison to the TEM allele TEM-1, and is depicted using binary allele code (0, 1) where 0 signifies the absence of an amino acid substitution and 1 signifies the presence of an amino acid substitution at a particular position. Genotype 0000 is TEM-1, genotype 1111 is TEM-85 (Baraniak et al. 2005) and see “β-Lactamase Classification and Amino Acid Sequences for TEM, SHV, and OXA Extended-Spectrum and Inhibitor Resistant Enzymes” http://www.lahey.org/Studies/? D=http://www.lahey.org/studies/webt.htm&C=404. The other genotypes are intermediates along the evolutionary path from TEM-1 to TEM-85. The edges are represented by arrows and the arrow direction points toward the node, or genotype, with the higher mean growth rate. Solid arrows represent significant differences between the two mean growth rates they connect, and dashed arrows represent nonsignificant differences using one-way ANOVA.

Fig. 4.

An adaptive landscape estimated from the growth rate means of 16 variant genotypes within TEM-85. The adaptive landscape was created using the treatment Cefotetan at the sublethal concentration of 0.063 µg/ml. Arrows point in the direction of the faster growing genotype, solid arrows represent significant differences between growth rates (using one-way ANOVA P value < 0.05), dashed arrows represent insignificant differences between growth rates (using one-way ANOVA P value > 0.05). The genotype that grew the fastest of all 16 genotypes is shown in bold font.

An adaptive landscape (fig. 4) can be estimated by comparing the mean growth rates of adjacent genotypes (Mira, Meza, et al. 2015). A pair of genotypes is adjacent if, and only if one can be transformed into the other by changing a single digit in the genotype. For example, 0000 and 0100 are adjacent genotypes, as are 1100 and 1101. However, 1001 and 1010 are not adjacent nor are 0101 and 1111.

An alternative method of estimating adaptive landscapes uses the statistical method of bootstrapping. After completing 10,001 replicates for each of ten runs, the results were combined to make a consensus bootstrap landscape (fig. 5).

Fig. 5.

Consensus bootstrap adaptive landscape for the treatment Cefotetan at 0.063 µg/ml. Solid arrows signify a probability > 0.90, dashed arrows represent probability < 0.90. The genotype that grew the fastest of all 16 genotypes in every bootstrap run is shown in bold font.

We then used three metrics to assess the reproducibility of adaptive landscapes: 1) similarity of arrow direction in landscapes based on mean growth rates, 2) similarity of arrow direction in bootstrap consensus landscapes, and 3) similarity of rank order of mean growth rates. For rank order, we ranked each of the 16 genotypes from each experiment 1–16 (1 as the fastest growing genotype, 16 as the slowest growing genotype). We then took the absolute difference in rank order in duplicate experiments divided by the number of genotypes (16) and calculated the percent similarity.

We considered four antibiotic treatments in which there were three acceptable replicate experiments (table 3). We were interested in the relationship, if any, between the mean V-scores of the experiments and reproducibility. Table 3 shows for each experiment the mean V-score for that experiment. Table 4 shows the reproducibility in pairwise comparisons of repeated experiments based on the three criteria of reproducibility described above.

Table 3.

Mean V-Scores of Accepted Experiments.

Treatment (µg/ml)	2014	2017 Repeat 1	2017 Repeat 2
CAZ 0.125	0.0260 ± 0.00113	0.0141 ± 0.00057	0.0172 ± 0.00236
CRO 0.5	0.0258 ± 0.00152	0.0169 ± 0.00189	0.0183 ± 0.00164
CRO 0.25	0.0308 ± 0.00236	0.0158 ± 0.00084	0.0148 ± 0.00090
ZOX 0.0156	0.0319 ± 0.00195	0.0147 ± 0.00076	0.0145 ± 0.00067

Note.—CAZ, ceftazidime; CRO, ceftriaxone; ZOX, ceftizoxime.

Table 4.

Reproducibility of Adaptive Landscapes for the Accepted Experiments Shown in Table 3.

	Arrow Direction Mean Growth Rate			Arrow DirectionBootstrap Consensus			Rank Order
Treatment (µg/ml)	Exp1 versus Exp2 (%)	Exp1 versus Exp3 (%)	Exp2 versus Exp3 (%)	Exp1 versus Exp2 (%)	Exp1 versus Exp3 (%)	Exp2 versus Exp3 (%)	Exp1 versus Exp2 (%)	Exp1 versus Exp3 (%)	Exp2 versus Exp3 (%)
CAZ 0.125	53.1	40.6	56.2	53.1	37.5	56.3	64.84	67.19	71.09
CRO 0.05	37.5	28.1	71.9	37.5	31.3	75	56.25	53.91	82.81
CRO 0.025	43.8	34.4	68.8	50	40.1	78.1	60.94	55.47	89.06
ZOX 0.0156	53.1	59.4	93.8	56.3	56.3	87.5	75.78	75.78	94.53

Note.—CAZ, ceftazidime; CRO, ceftriaxone; ZOX, ceftizoxime. Exp1 = 2014, Exp2 = 2017 repeat one, Exp3 = 2017 repeat two.

For all four treatments, experiment 1 was rejected because of one or more low correlation coefficients, and experiments 2 and 3 were repeated experiments in which the correlation coefficients were improved and the experiment was accepted. Experiments were consistently more similar when both experiments were accepted than when one of the two experiments was rejected (table 4). Rejecting experiments with unreliable data improves reproducibility.

Conclusions

Growth rates may vary for several reasons, including human error (such as pipetting error), random biological variation due to environmental or drug responses, contamination of controls caused by splashing or shaking of the plate and much more. A major function of CGR is to assist in judging what constitutes excessive variation in a data set.

We have developed a statistical package for the GrowthRates program called CompareGrowthRates (CGR), that allows users to evaluate the reliability of growth rates and to measure the amount of variation within their growth rate data sets. Even on a data set consisting of 384 individual growth rates, CGR requires <3 min to complete its analysis on a mid-2011 iMac with an Intel i7 processor and 16 GB of RAM.

The program CGR provides a broader view of the population dynamics of a set of coexisting and competing genotypes than does just examination of the mean growth rates of the individual sets. That broader view is likely to provide more realistic understanding of experimental outcomes.

CGR is freely available as a package for Mac OS X, Linux, and Windows at https://sourceforge.net/projects/growthrates/, last accessed September 2017, the same site that provides the GrowthRates program itself. The package includes the CGR executable for all three platforms, a detailed User Guide, the python source code, and an example folder.

The correlation coefficient is an effective way to measure the reliability of mean growth rates of a set. We used a minimum mean correlation coefficient of 0.95 to consider the mean growth rate of a set of replicate cultures to be reliable. Other investigators may well use different minimum correlation coefficients. Our experimental design required us to reject an experiment if any of the sets of replicates fell below that minimum of R < 0.95. That will certainly not always be the case. Many designs will permit rejection and replication of just those sets that are unreliable.

The V-score metric is an effective way to measure the amount of variation within a set of replicate growth rate data points. We find that even when the data are reliable, high mean V-scores reduce the reproducibility of experiments (table 4). High V-scores are often associated with low correlation coefficients, but that is not always the case. Excessive variation can also arise from other unknown factors. The V-score metric is a descriptive statistic, but it can also be used as a criterion for rejecting and repeating experiments that are acceptable on the basis of correlation coefficients.

In the laboratory, and in the real world, there is no way to completely account for random biological variation. By reading O.D.s at intervals appropriate to the slowest growth rates, we were able to increase correlation coefficients of slow-growing sets. By using CGR, and rejecting experiments with unreliable data or excessive variation, we were able to lower the variability in our results and as a consequence, increase the reliability of our interpretations. By using a bootstrap statistic, it becomes possible to compute the robustness of our interpretations of data.

We recommend that users of the GrowthRates program use this statistical package to assess the quality of their data and to assist in their interpretations.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.