Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2018 Mar 14.
Published in final edited form as: Magn Reson Med. 2014 Jan 16;73(1):44–50. doi: 10.1002/mrm.25094

Frequency and Phase Drift Correction of Magnetic Resonance Spectroscopy Data by Spectral Registration in the Time Domain

Jamie Near 1,*, Richard Edden 2, C John Evans 3, Raphael Paquin 4, Ashley Harris 2, Peter Jezzard 5
PMCID: PMC5851009  NIHMSID: NIHMS942582  PMID: 24436292

Abstract

Purpose

Frequency and phase drifts are a common problem in the acquisition of in vivo magnetic resonance spectroscopy (MRS) data. If not accounted for, frequency and phase drifts will result in artifactual broadening of spectral peaks, distortion of spectral lineshapes, and a reduction in signal-to-noise ratio (SNR). We present herein a new method for estimating and correcting frequency and phase drifts in in vivo MRS data.

Methods

We used a simple method of fitting each spectral average to a reference scan (often the first average in the series) in the time domain through adjustment of frequency and phase terms. Due to the similarity with image registration, this method is referred to as “spectral registration.” Using simulated data with known frequency and phase drifts, the performance of spectral registration was compared with two existing methods at various SNR levels.

Results

Spectral registration performed well in comparison with the other methods tested in terms of both frequency and phase drift estimation.

Conclusions

Spectral registration provides an effective method for frequency and phase drift correction. It does not involve the collection of navigator echoes, and does not rely on any specific resonances, such as residual water or creatine, making it highly versatile.

Keywords: magnetic resonance spectroscopy, frequency drift, B0 drift, phase drift, motion correction

INTRODUCTION

In vivo magnetic resonance spectroscopy (MRS) generally involves summation of multiple averages to build up the signal-to-noise ratio (SNR) of low-concentration metabolite signals. Perfect summation requires temporal stability of the acquired averages, which is difficult or impossible to achieve in practice. Specifically, temporal drift in the main (B0) magnetic field results in frequency errors, whereas subject motion (both physiological and bulk) results in both frequency and phase errors in the acquired signals. If not accounted for, these frequency and phase errors (or drifts) give rise to incoherent signal averaging, which leads to artifactual line broadening, lineshape distortion, and reduced SNR. Fortunately, these artifacts can be largely avoided by measuring and correcting the scan-to-scan frequency and phase errors prior to signal averaging.

Several methods of frequency and phase drift estimation and correction have been proposed previously. Many of these methods use an unsuppressed or partially suppressed (residual) water resonance to estimate the frequency and phase error of each scan (1–5). The main drawback of using unsuppressed water for frequency and phase drift correction is that a large unsuppressed water signal can give rise to artifacts such as baseline distortions and sideband peaks induced by mechanical vibration. Furthermore, the use of a residual water peak is not possible in certain applications of MRS (e.g., MRS of X-nuclei). Given an unsuppressed or partially suppressed water peak, the frequency can be estimated in a number of ways. The simplest method is to identify the frequency at which the modulus of the water peak is a maximum (2). Alternatively, the frequency can be estimated by measuring the slope of the phase function in the time domain (3) or by deconvolution with a high SNR reference scan (6). The spectral phase can be estimated simply by measuring the phase of the first point in the time domain (2), or instead, by deconvolution with a high SNR reference scan (6). To maintain a residual water peak in individual averages while avoiding a large residual water signal in the final spectrum, it is possible to phase-cycle the water resonance such that the residual water signal is cancelled upon signal averaging (4). Alternatively, frequency and phase errors can be estimated via a separately acquired navigator echo (3,6), however, such navigator echoes do not account for very short time-scale temporal instabilities such as physiological motion or rapid bulk motion, since they are not acquired simultaneously with the data itself.

Because the majority of clinical MRS acquisitions require good water suppression and do not involve the collection of navigator echoes, there is a need for simple frequency and phase drift correction methods that perform well in the absence of residual water signals or separately acquired navigator echoes. One such method has been presented previously, and is based on fitting the creatine peak to a Lorentzian function, from which the frequency and phase are estimated (7). Although this and similar methods have been used successfully (8,9), such methods rely on the presence of a known resonance peak with sufficient SNR and are therefore not applicable across different types of MRS without some modification.

In this paper, we describe a simple method for estimating frequency and phase drift errors in MRS data. The proposed method, which we term “spectral registration,” involves fitting (or registering) each spectral average to a reference scan (usually the first average in the series) in the time domain through adjustment of frequency and phase terms. The proposed method does not require the collection of any navigator echoes, and it does not rely on the presence of any specific resonances such as residual water or creatine. Using simulated MRS data with known frequency and phase drifts, the performance of spectral registration is compared against two commonly used frequency and phase drift correction methods, revealing that spectral registration performs comparably to these other methods while providing advantages in terms of versatility and breadth of applicability. An example of spectral registration applied to in vivo data is also given.

METHODS

Spectral Registration

Spectral registration uses nonlinear least squares minimization to fit each signal average, S(t), to a reference scan, R(t), by adjustment of the frequency, f (in Hz), and phase, φ (in degrees), of the signal S(t). In this case, we have chosen the reference signal R(t) to be the first average in the series. This minimization operation can be expressed as

minimizef,φ∈R‖R(t)-G(t,f,φ)‖. [1]

where

G(t,f,φ)=S(t)·e2π(ft+φ360). [2]

To limit the contribution of noise, which dominates in the later part of the Fourier induction decay (FID), or time domain signal, only the first 200 ms of each FID is considered in the fitting. The above minimization for spectral registration was implemented in MATLAB (MathWorks, Natick, Massachusetts, USA) using the “nlinfit” function, a nonlinear least squares regression algorithm and a member of the MATLAB statistics tool-box. To enable fitting of complex data while avoiding complex (nonphysical) parameter estimates, the vectors R and G were modified prior to minimization by concatenating their real and imaginary parts into a single real-valued vector. No other restrictions were placed on either of the parameter values (frequency or phase).

Spectral Registration Over a Limited Frequency Range

In some cases, the signal may contain frequency components that are not stable from scan to scan. For example, the shape and amplitude of the residual water peak may vary, as scanner drift causes the frequency of the water suppression pulse to drift relative to the spectrum. Alternately, in the case of phase-cycled data with incomplete localization, certain regions of the spectrum may exhibit instabilities across steps of the phase cycle. Such unstable frequency components may introduce errors in the spectral registration method described above, since the FID contains all frequency components at all time points. To avoid this problem, it is possible to perform the time-domain spectral registration over a limited frequency range simply by defining S(t) and R(t) as the inverse Fourier transforms of the desired stable frequency range (i.e., excluding the unstable frequencies) of the frequency domain spectra.

Evaluation and Comparison of Frequency Drift Correction Methods

Simulated brain proton MRS data were generated with known frequency and phase drift errors to evaluate the performance of the proposed method and compare it with previously described methods. First, simulated point resolved spectroscopy pulse sequence (PRESS) model spectra (echo time [TE] = 80 ms; 2048 points; spectral width = 2000 Hz; B0 = 3T) were generated for 22 metabolites, six macromolecule resonances, and a water resonance using an in-house MATLAB-based implementation of the density matrix formalism as described previously (10). The model spectra were then exponentially line-broadened to a linewidth of 6 Hz and combined in approximately physiological concentrations to produce a simulated, noise-free MR spectrum. The amplitude of the simulated residual water resonance was chosen to be approximately twice the height of the N-acetyl aspartate (NAA) resonance. The spectrum was then replicated 128 times to simulate 128 acquired averages, and frequency and phase drifts were applied to each average. The frequency error, f, of each average, N, was chosen as a linear slope superposed with noise, εf, according to:f (N) = (5/128)N + εf Hz, and the phase error, φ, of each average was chosen as a flat slope superposed with noise, εφ, according to: φ(N) − (0)N + εφ degrees. The added noise terms, εf and εφ, involved the addition of a random value at each point N with mean values of zero and standard deviations of 0.2 Hz and 2 degrees, respectively. These terms were used to roughly approximate the effects of physiological and bulk noise. Finally, a normally distributed random noise seed was added to the each of the simulated averages to achieve the desired SNR. To approximate a range of SNR conditions, spectra were generated using per-average SNR values (measured as the peak NAA amplitude divided by the standard deviation of the added noise) of 20, 10, 5, and 2.5. For each SNR value, 10 simulated datasets (each with 128 averages) were generated as described above, and a frequency and phase drift correction was performed on each dataset using the spectral registration method, as well as two existing correction methods; the creatine fitting method (7), and the residual water method (2), as described below. To evaluate the various correction methods, the frequency estimation error and phase estimation error were quantified for each of the correction methods. Specifically, the estimation error was obtained by taking the difference between the measured drift and the actual drift and calculating the standard deviation of this residual difference across all 128 averages.

Implementation of Previously Described Correction Schemes

Two previously described methods—the creatine fitting method (7) and the residual water method (2)—were implemented for comparison against the method of spectral registration. In the creatine fitting method, the spectrum was zero-filled to 8192 points and apodized using a 2-Hz exponential filter, and the creatine peak was fit in the frequency domain to a Lorentzian function with five free parameters: frequency, phase, amplitude, baseline offset, and baseline slope. To ensure only the creatine peak was included in the fit, the spectrum was windowed from 2.72 to 3.12 ppm. The fitted frequency and phase parameters were used for frequency and phase error estimation and drift correction. In the residual water method, the spectrum was zero-filled to 8192 points and apodized using a 2-Hz exponential filter. The frequency was then estimated as the frequency at which the water modulus peak is at a maximum, and the phase was estimated using the phase of the first point in the FID.

Demonstration of Spectral Registration over a Limited Frequency Range

To illustrate a situation in which spectral registration over a limited frequency range is preferred, a simulated dataset was generated to approximate highly unstable water suppression due to drifting of the water suppression pulse. To achieve this, a simulated dataset was generated as described above, with 128 averages, but with a total frequency drift of 20 Hz and a residual water peak (approximately equal in amplitude to the NAA peak) that varies linearly in intensity as a function of frequency drift such that its final intensity is equal and opposite in sign to its initial intensity. A drift correction was performed on this “water-unstable” dataset using both the normal spectral registration and spectral registration over a limited frequency range (from 0 to 3.5 ppm). The performance of the two drift correction methods was evaluated again using the aforementioned performance metrics.

Demonstration of Frequency and Phase Drift Correction In Vivo Using Spectral Registration

In vivo MRS data were acquired in single healthy human volunteers using a 3T MAGNETOM Trio system (Siemens, Erlangen, Germany) with a body coil transmitter and a 32-channel head receiver array coil. Data were acquired from a region of interest in the medial prefrontal cortex (15 × 30 × 15 mm3) using the SPECIAL sequence (11) (repetition time [TR]/TE = 3200/8.5 ms; spectral width = 4000 Hz; 4096 points; 256 averages; 16 phase cycle steps). Six outer volume suppression slabs were applied (one on each side of the cubic voxel) to suppress outer volume signals due to imperfect localization and to minimize ISIS subtraction artifacts. Following data acquisition, the interleaved inversion-on and inversion-off scans were subtracted, resulting in 128 fully localized spectra. Spectral registration was then performed using a frequency range of −2 ppm to 4.2 ppm, to include only the part of the spectrum upfield of water. Because the true frequency and phase drift of this in vivo dataset are not known, the performance of the registration was assessed simply by inspection of the estimated frequency and phase drift curves, and by visual assessment of the alignment of the averages before and after correction.

RESULTS

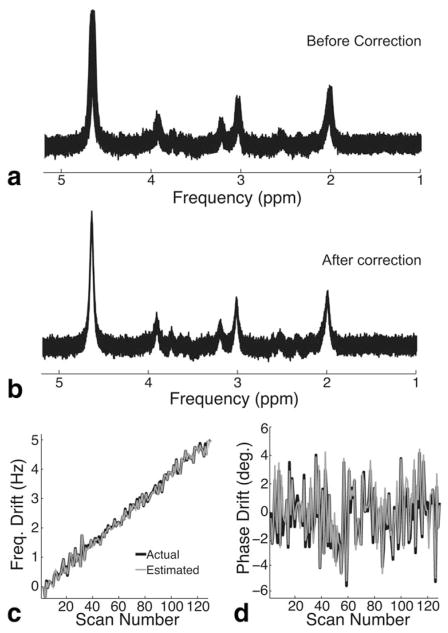
An example of a simulated spectrum with frequency and phase drift and an SNR of 20 is shown in Figure 1a. Figure 1b shows the same spectrum, following frequency and phase drift correction using spectral registration. Figure 1c and 1d show the actual frequency and phase errors (solid black lines), respectively, of the simulated dataset, as well as the estimated frequency and phase errors (solid gray lines), respectively, as determined by the spectral registration algorithm.

FIG. 1.

FIG. 1

Open in a new tab

Frequency and phase drift correction using spectral registration. a: Simulated PRESS MRS data (TE = 80 ms) consisting of 128 averages with a total frequency drift of 5 Hz, a random phase error, and a per-average SNR of 20. b: The same spectrum following frequency and phase drift correction using spectral registration. c: Actual (black line) and estimated (gray line) frequency drift as a function of scan number. d: Actual (black line) and estimated (gray line) phase drift as a function of scan number.

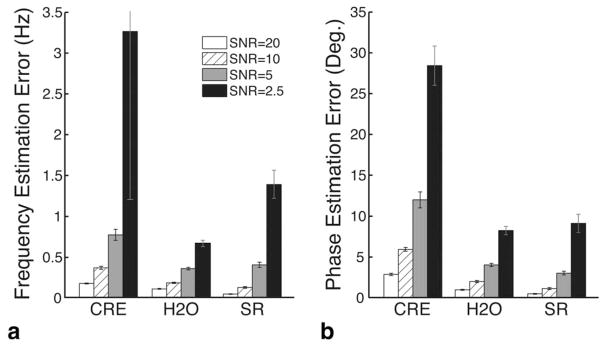
Figure 2a and 2b show the frequency and phase estimation errors, respectively, of the three methods tested at four SNR levels. Each bar represents the average across 10 simulated datasets. For simulated datasets with SNRs of 20, 10, 5, and 2.5, respectively, the frequency estimation errors were 0.17, 0.36, 0.77, and 3.27 Hz for the creatine fitting method; 0.10, 0.18, 0.35, and 0.66 Hz for the residual water method; and 0.04, 0.12, 0.40, and 1.38 Hz for the spectral registration method. The corresponding phase estimation errors were 2.82, 5.90, 11.97, and 28.39 degrees for the creatine fitting method; 0.95, 1.96, 4.00, and 8.21 degrees for the residual water method; and 0.44, 1.09, 2.97, and 9.09 degrees for the spectral registration method.

FIG. 2.

FIG. 2

Open in a new tab

Comparison of spectral registration with existing drift correction methods. a: Bar graph showing the standard deviation of the residual frequency estimation error (in Hz) of the creatine fitting method (CRE), the residual water method (H2O), and the spectral registration method (SR). b: Bar graph showing the standard deviation of the residual phase estimation error (in degrees) of the same three methods. The four bars in each group represent the four different SNR levels tested. Bar heights and error bars represent the average and standard deviation, respectively, across 10 simulated datasets.

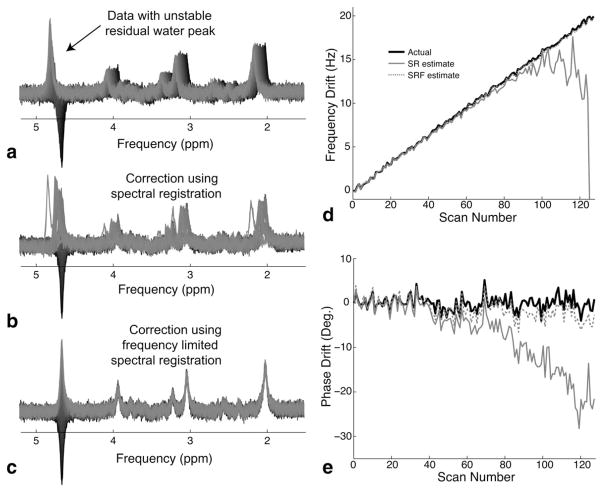
Figure 3a shows the water-unstable dataset that was generated by varying the intensity of the residual water peak across averages. Figure 3b and 3c show the results of frequency drift correction on the water-unstable data-set using spectral registration and spectral registration over a limited frequency range, respectively. The frequency and phase drift correction were noticeably improved when using spectral registration over a limited frequency range. Figure 3d and 3e show the actual frequency and phase errors, respectively, of the simulated dataset as well as the corresponding frequency and phase error estimates from the spectral registration method and the method of spectral registration over a limited frequency range. Spectral registration over a limited frequency range provided improved estimates of both frequency and phase when the residual water resonance was highly unstable. The frequency and phase estimation errors for the spectral registration method were 5.62 Hz and 8.93 degrees, respectively, whereas the frequency and phase estimation errors for the method of spectral registration over a limited frequency range were greatly improved (0.14 Hz and 1.72 degrees, respectively).

FIG. 3.

FIG. 3

Open in a new tab

Illustration of spectral registration over a limited frequency range. a: Simulated PRESS MRS data (TE = 80 ms) consisting of 128 averages, with a large unstable residual water peak and a total frequency drift of 20 Hz and random phase error. b: The same spectrum following frequency and phase drift correction using spectral registration. Note the visibly poor alignment of the averages. c: The same spectrum following frequency and phase drift correction using spectral registration over a limited frequency range (0–3.5 ppm). Note the improved alignment of the averages. d: The actual frequency drift (solid black line) is shown with the drift estimates using spectral registration (SR, solid gray line), and spectral registration over a limited frequency range (SRF, dotted gray line). e: The actual phase drift (solid black line) is shown with the drift estimates using SR (solid gray line), and SRF (dotted gray line).

Figure 4a shows the in vivo short echo-time MRS data that were collected from the medial prefrontal cortex of a healthy human volunteer following the subtraction of partial ISIS inversion-on/inversion-off scans but prior to signal averaging. The SNR of each localized volume (2 averages per volume due to partial ISIS localization) was ~40. Figure 4b shows the same spectrum following frequency drift correction using spectral registration over a limited frequency range. On visual inspection, the alignment of the averages was greatly improved following spectral registration. Figure 4c and 4d show the frequency and phase drifts, respectively, as estimated by the spectral registration method. The total frequency drift over the duration of the scan was approximately 6 Hz, whereas the phase drift was approximately flat with a standard deviation of 2.8 degrees. Figure 4e shows the final averaged spectrum both before and after drift correction. The use of drift correction resulted in a reduction in the full width at half-maximum of the residual water peak from 8.2 Hz (before drift correction) to 5.6 Hz (after drift correction).

FIG. 4.

FIG. 4

Open in a new tab

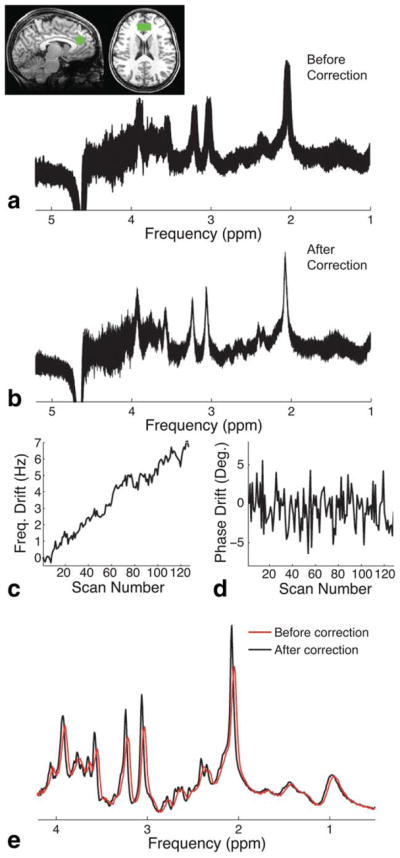
Frequency and phase drift correction on in vivo data. a: In vivo SPECIAL MRS data (TR/TE = 3200/8.5 ms) acquired from the medial prefrontal cortex of a healthy volunteer. Data are shown following subtraction of the partial ISIS inversion-on/inversion-off scans. The voxel position is shown in the top left. b: Same spectrum as above, following frequency and phase drift correction using spectral registration over a limited frequency range (from −2 to 4.2 ppm). Note the improved alignment of the averages. c: The measured frequency drift. d: The measured phase drift. e: The final averaged spectrum before (red line) and after (black line) drift correction. Note that both peak intensity and lineshape are improved following drift correction.

DISCUSSION

Our results suggest that spectral registration accurately estimates and corrects frequency and phase drift in MRS data acquired over multiple signal averages.

We compared spectral registration against two existing methods: the creatine fitting method and the residual water method. Specifically, we assessed the ability of each of these methods to accurately estimate frequency and phase drift in simulated MRS datasets in which the drifts are known, and at various SNR levels. Spectral registration outperformed the creatine fitting method by a factor of >2 at all SNR levels tested. At high SNR levels (≥10 per average), spectral registration also outperformed the residual water method. At low SNR levels (≤5 per average), the performance of spectral registration was comparable to that of the residual water method, except in the lowest SNR case (SNR = 2.5), in which the residual water method outperformed the spectral registration method by a factor of two in terms of frequency drift estimation only.

Based on these results, spectral registration performs comparably to both of the other methods tested. The performance of spectral registration (and other methods) is limited when the per-average SNR is reduced to ≤2.5. This is not surprising, because no method can accurately estimate frequency and phase errors in data that are dominated by noise. In cases where the SNR is too low for frequency and phase to be estimated from the data itself, the previously described navigator-based methods (3,5,6,12) are preferable.

Performance notwithstanding, spectral registration provides a distinct advantage in terms of versatility. Spectral registration uses the initial part of the time domain signal, which is almost guaranteed to have useful information with which to estimate frequency and phase, regardless of the type of MRS data in question. Therefore, the spectral registration method can be applied exactly as presented here with little or no modification, to almost any kind of MRS data, provided that SNR is sufficient and that the averages can be stored separately. On the other hand, the use of the creatine fitting method is limited to spectra containing a creatine peak, such as proton MR spectra of the brain, and use of the residual water method is limited to spectra containing a residual water peak.

The creatine fitting method is versatile enough to be applied to other resonances, but this requires modification of the initial fit parameters, and it assumes prior knowledge of an isolated resonance besides creatine that can be used for frequency and phase estimation. Furthermore, the results of this study show that the creatine fitting method performs relatively poorly compared with the other two methods.

Use of the residual water method requires the presence of a residual water peak. This automatically excludes all types of X-nuclei spectroscopy. Furthermore, it is not applicable to MRS data in which the water suppression is very good, as is the case in many types of clinical MR spectroscopy. It should also be noted that it is not possible to estimate the spectral phase using the first point in the FID if the signal at the first point in the FID is close to zero, or equivalently, if the net area in the frequency domain is close to zero. This situation can arise if there are both upright and inverted peaks in the spectrum, such as a normal spectrum with an oversuppressed water peak, or a Mescher-Garwood spectral editing method–PRESS (13) edited gamma-aminobutyric acid spectrum, which consists of a large inverted NAA peak and several smaller upright peaks. In such a situation where the net area in the frequency domain is close to zero, the first point in the FID is primarily noise, and does not contain useful phase information. To avoid this problem, one could estimate phase using the time domain signal point with the maximum complex magnitude or by taking the average phase across multiple time domain points.

It was shown that spectral registration may fail to correctly estimate the spectral frequency and phase if there are unstable frequency components in the spectrum. This was illustrated using a spectrum with a large residual water peak that varies in intensity across averages. In this case, the registration method fails because the FIDs being registered are intrinsically unalike, and cannot be made alike using frequency and phase adjustment. However, by restricting the frequency range of the spectral registration to between 0 ppm and 3.5 ppm, the region where the signals are stable across averages, the performance of the method was restored.

In addition to the demonstration of spectral registration on simulated data, the method was also demonstrated to substantially reduce frequency and phase errors in in vivo MRS data acquired from the medial pre-frontal cortex of a healthy human volunteer. For brevity, only one example of in vivo registration has been given here; however, this method has been tested extensively and has been used to successfully remove frequency and phase drift from hundreds of datasets of various types of MRS data (10,14–17).

Although we presented spectral registration in the time domain, it may also be possible to perform spectral registration in the frequency domain. We expect that spectral registration in the frequency domain may improve frequency (not phase) estimation in spectra consisting of primarily broad, short T2 signals, since these signals have limited extent in the time domain. However, performing the method in the frequency domain may require the use of weighted registrations to minimize the influence of noisy parts of the spectrum.

In this paper, we have only described the use of spectral registration for retrospective drift correction. However, spectral registration may also prove to be a useful method for prospective frequency drift correction. This would provide the additional benefit of enabling the real-time adjustment of transmitter frequencies, thus preventing the degradation of water suppression or editing pulse efficiency, for example. Currently, most prospective frequency drift correction methods require either a separately acquired navigator echo or intentionally weak water suppression (3,4). Spectral registration may be an attractive alternative for prospective frequency correction, as it can provide rapid estimation of frequency offsets using the normally acquired data by itself, with no requirement for navigator echoes or weak water suppression.

CONCLUSIONS

Spectral registration provides an effective and versatile means of estimating and correcting frequency and phase drifts in MRS data.

Acknowledgments

Grant sponsor: Medical Research Council; Grant number: G0701421.

References

  • 1.Star-Lack JM, Adalsteinsson E, Gold GE, Ikeda DM, Spielman DM. Motion correction and lipid suppression for 1H magnetic resonance spectroscopy. Magn Reson Med. 2000;43:325–330. doi: 10.1002/(sici)1522-2594(200003)43:3<325::aid-mrm1>3.0.co;2-8. [DOI] [PubMed] [Google Scholar]
  • 2.Helms G, Piringer A. Restoration of motion-related signal loss and line-shape deterioration of proton MR spectra using the residual water as intrinsic reference. Magn Reson Med. 2001;46:395–400. doi: 10.1002/mrm.1203. [DOI] [PubMed] [Google Scholar]
  • 3.Henry PG, van de Moortele PF, Giacomini E, Nauerth A, Bloch G. Field-frequency locked in vivo proton MRS on a whole-body spectrometer. Magn Reson Med. 1999;42:636–642. doi: 10.1002/(sici)1522-2594(199910)42:4<636::aid-mrm4>3.0.co;2-i. [DOI] [PubMed] [Google Scholar]
  • 4.Keating B, Deng W, Roddey JC, White N, Dale A, Stenger VA, Ernst T. Prospective motion correction for single-voxel 1H MR spectroscopy. Magn Reson Med. 2010;64:672–679. doi: 10.1002/mrm.22448. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Zaitsev M, Speck O, Hennig J, Buchert M. Single-voxel MRS with prospective motion correction and retrospective frequency correction. NMR Biomed. 2010;23:325–332. doi: 10.1002/nbm.1469. [DOI] [PubMed] [Google Scholar]
  • 6.Thiel T, Czisch M, Elbel GK, Hennig J. Phase coherent averaging in magnetic resonance spectroscopy using interleaved navigator scans: compensation of motion artifacts and magnetic field instabilities. Magn Reson Med. 2002;47:1077–1082. doi: 10.1002/mrm.10174. [DOI] [PubMed] [Google Scholar]
  • 7.Waddell KW, Avison MJ, Joers JM, Gore JC. A practical guide to robust detection of GABA in human brain by J-difference spectroscopy at 3 T using a standard volume coil. Magn Reson Imaging. 2007;25:1032–1038. doi: 10.1016/j.mri.2006.11.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Donahue MJ, Near J, Blicher JU, Jezzard P. Baseline GABA concentration and fMRI response. Neuroimage. 2010;53:392–398. doi: 10.1016/j.neuroimage.2010.07.017. [DOI] [PubMed] [Google Scholar]
  • 9.Evans CJ, Puts NA, Robson SE, Boy F, McGonigle DJ, Sumner P, Singh KD, Edden RA. Subtraction artifacts and frequency (Mis-)alignment in J-difference GABA editing. J Magn Reson Imaging. 2013;38:970–975. doi: 10.1002/jmri.23923. [DOI] [PubMed] [Google Scholar]
  • 10.Near J, Andersson J, Maron E, Mekle R, Gruetter R, Cowen P, Jezzard P. Unedited in-vivo detection and quantification of GABA in the occipital cortex using short-TE magnetic resonance spectroscopy at 3 Tesla. NMR Biomed. 2013;26:1353–1362. doi: 10.1002/nbm.2960. [DOI] [PubMed] [Google Scholar]
  • 11.Mekle R, Mlynarik V, Gambarota G, Hergt M, Krueger G, Gruetter R. MR spectroscopy of the human brain with enhanced signal intensity at ultrashort echo times on a clinical platform at 3T and 7T. Magn Reson Med. 2009;61:1279–1285. doi: 10.1002/mrm.21961. [DOI] [PubMed] [Google Scholar]
  • 12.Hess AT, Tisdall MD, Andronesi OC, Meintjes EM, van der Kouwe AJ. Real-time motion and B0 corrected single voxel spectroscopy using volumetric navigators. Magn Reson Med. 2011;66:314–323. doi: 10.1002/mrm.22805. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Mescher M, Merkle H, Kirsch J, Garwood M, Gruetter R. Simultaneous in vivo spectral editing and water suppression. NMR Biomed. 1998;11:266–272. doi: 10.1002/(sici)1099-1492(199810)11:6<266::aid-nbm530>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
  • 14.Godlewska BR, Yip SW, Near J, Goodwin GM, Cowen PJ. Cortical glutathione levels in young people with bipolar disorder: a pilot study using magnetic resonance spectroscopy. Psychopharmacology (Berl) 2014;231:327–332. doi: 10.1007/s00213-013-3244-0. [DOI] [PubMed] [Google Scholar]
  • 15.Taylor MJ, Godlewska B, Near J, Christmas D, Potokar J, Collier J, Klenerman P, Barnes E, Cowen PJ. Effect of interferon-alpha on cortical glutamate in patients with hepatitis C: a proton magnetic resonance spectroscopy study. Psychol Med. 2013:1–7. doi: 10.1017/S0033291713001062. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Jocham G, Hunt LT, Near J, Behrens TE. A mechanism for value-guided choice based on the excitation-inhibition balance in prefrontal cortex. Nat Neurosci. 2012;15:960–961. doi: 10.1038/nn.3140. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Stagg CJ, Bestmann S, Constantinescu AO, Moreno LM, Allman C, Mekle R, Woolrich M, Near J, Johansen-Berg H, Rothwell JC. Relationship between physiological measures of excitability and levels of glutamate and GABA in the human motor cortex. J Physiol. 2011;589:5845–5855. doi: 10.1113/jphysiol.2011.216978. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES