Automatic Adaptation of Basal Insulin Using Sensor-Augmented Pump Therapy

Abstract

Background:

People with insulin-dependent diabetes rely on an intensified insulin regimen. Despite several guidelines, they are usually impractical and fall short in achieving optimal glycemic outcomes. In this work, a novel technique for automatic adaptation of the basal insulin profile of people with diabetes on sensor-augmented pump therapy is presented.

Methods:

The presented technique is based on a run-to-run control law that overcomes some of the limitations of previously proposed methods. To prove its validity, an in silico validation was performed. Finally, the artificial intelligence technique of case-based reasoning is proposed as a potential solution to deal with variability in basal insulin requirements.

Results:

Over a period of 4 months, the proposed run-to-run control law successfully adapts the basal insulin profile of a virtual population (10 adults, 10 adolescents, and 10 children). In particular, average percentage time in target [70, 180] mg/dl was significantly improved over the evaluated period (first week versus last week): 70.9 ± 11.8 versus 91.1 ± 4.4 (adults), 46.5 ± 11.9 versus 80.1 ± 10.9 (adolescents), 49.4 ± 12.9 versus 73.7 ± 4.1 (children). Average percentage time in hypoglycemia (<70 mg/dl) was also significantly reduced: 9.7 ± 6.6 versus 0.9 ± 1.2 (adults), 10.5 ± 8.3 versus 0.83 ± 1.0 (adolescents), 10.9 ± 6.1 versus 3.2 ± 3.5 (children). When compared against an existing technique over the whole evaluated period, the presented approach achieved superior results on percentage of time in hypoglycemia: 3.9 ± 2.6 versus 2.6 ± 2.2 (adults), 2.9 ± 1.9 versus 2.0 ± 1.5 (adolescents), 4.6 ± 2.8 versus 3.5 ± 2.0 (children), without increasing the percentage time in hyperglycemia.

Conclusion:

The present study shows the potential of a novel technique to effectively adjust the basal insulin profile of a type 1 diabetes population on sensor-augmented insulin pump therapy.

Type 1 diabetes mellitus (T1DM) is an autoimmune condition characterized by elevated blood glucose levels due to the lack of endogenous insulin production.¹ People with T1DM require exogenous insulin delivery to regulate glucose. Current therapies for T1DM management include the administration of multiple daily injections (MDI) or continuous subcutaneous insulin infusion (CSII) with pumps.

A basal-bolus insulin regimen involves taking a longer acting form of insulin to keep blood glucose levels stable through periods of fasting and separate injections of shorter acting insulin to prevent rises in blood glucose levels resulting from meals. Such a regimen attempts to roughly emulate how the body of a person without diabetes delivers insulin. People with T1DM using insulin pumps are able to preprogram different infusion rates along the day, hence they are able to achieve finer control.² Figure 1 shows an example of the insulin profile of a typical CSII basal-bolus regimen.

Figure 1.

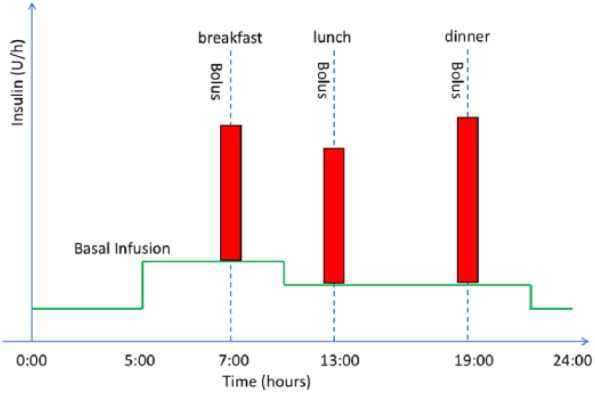
Plasma insulin profile of a typical basal-bolus regimen using CSII. Red vertical bars correspond to meal bolus; solid green horizontal lines represent the basal insulin profile.

Several guidelines exist for adjusting insulin doses in a basal-bolus regime;^3-5 these often require a cumbersome process of trial and error supported by an expert clinician.

Total basal insulin can be estimated based on the total daily dose (TDD) (eg, basal = 0.5 TDD), but requirements are rarely constant during the day and tend to be higher in the early morning (eg, dawn phenomenon). In addition, insulin requirements may significantly change due to perturbations such as, physical exercise, psychological stress, hormonal cycles and recurrent illness,¹ which makes adjusting insulin therapy a challenging task. In CSII therapy, different guidelines have been proposed to adjust the basal insulin profiles along the day, which usually consist of assigning different basal rate over different time windows.³

Since it is difficult to adjust basal insulin during the postprandial period, people with T1DM are asked to skip one meal per day and with the help of a continuous glucose monitor (CGM) or regular capillary self-monitoring are able to adjust the corresponding basal profiles. However, this process is inconvenient and impractical in many cases.

Meal bolus insulin is usually computed by means of the so-called bolus calculator, a simple mathematical formula that accounts for the amount of ingested carbohydrates, the premeal glucose levels, and the remaining active insulin from previous boluses (ie, insulin-on-board).⁶ Such formula is described by

$$B=\frac{CHO}{ICR}+\frac{\left(G-G_T\right)}{ISF}-IOB,$$

where B (U) is the total calculated bolus, CHO (g) is the estimated amount of ingested carbohydrates, ICR (g/U) is the insulin-to-carbohydrate-ratio, G (mg/dl) is the measured glucose at meal time, G_T (mg/dl) is the glucose target, ISF (mg/dl/U) is the insulin sensitivity factor, and IOB (U) is the insulin on board, which represents an estimation of the remaining active insulin in the body and which can be calculated using a linear decay expressed as

$$IOB=B_p\left(1-\frac{T_{int}}{T_{act}}\right),$$

where B_p the previously administered insulin bolus, T_int is the elapsed time since the last administered insulin bolus, and T_act is the insulin action time, which is subject dependent.

Note that equation (2) is just a particular way to estimate IOB using a linear decay. Other methods to estimate IOB have been proposed by different authors (eg, curvilinear decay),^7-9 with some of them taking into account time-varying characteristics such as intraday variability.¹⁰ The parameters ICR and ISF are also scenario-dependent, and guidelines exist to calculate them.¹¹

Seeing the complexity of insulin dosing, there is a need for more automated and efficient strategies to adapt such regimens, removing self-management burden and improving outcomes. Different authors have previously proposed methods to automatically adjust the bolus-basal insulin therapy. The concept of adaptive bolus calculator was first proposed by Owens et al by means of the utilization of run-to-run (R2R) control,¹² and later clinically tested by Palerm et al.¹³ Although showing some promising preliminary clinical results, this approach has the limitation of being very sensitive to meal composition and does not account for hyperglycemia. Tuo et al¹⁴ proposed a similar technique based on a high order R2R control scheme. Similarly to the approach by Owens et al, the employed control law by Tuo et al does not account for hypoglycemia. Finally, Herrero and colleagues proposed a new R2R control law combined with case-based reasoning that overcomes some of the previous limitations.^15-17

Regarding the adaptation of the basal insulin profile, Palerm et al¹⁸ proposed an R2R algorithm which is used to adjust four basal rates throughout the day using capillary measurements taken at the extremes of the selected time intervals. One limitation of this method is that it does not account for hypoglycemic and hyperglycemic events within the time intervals.

Toffanin and colleagues recently introduces an R2R algorithm for adaptation a 24-hour basal insulin injection. Such technique is based on the well-stablished glycemic metrics of percentage time in euglycemia and hypoglycemia computed from continuous glucose sensor data.¹⁹

In the context of an artificial pancreas (ie, hybrid closed-loop control), different solutions have been proposed to adjust the basal insulin and the meal bolus. A method to adapt basal therapy based on the value and rate of change of blood glucose was proposed by Wang et al.²⁰ Herrero et al proposed an R2R technique to automatically adjust the insulin-to-carbohydrate ratio of the bolus calculator within a hybrid artificial pancreas that uses information from the closed-loop controller.²¹ Dassau et al clinically evaluated an adaptive artificial pancreas where basal insulin delivery settings were adapted weekly, and carbohydrate ratios were adapted every 4 weeks.²² Finally, an R2R approach that adapts the basal insulin delivery during the night and the carbohydrate-to-insulin ratio during the day, based on glycemic metrics calculated from subcutaneous continuous glucose sensor data, was proposed by Toffanin et al²³ and was later clinically evaluated.²⁴

In this work, we present a novel technique to automatically adjust the 24-hour basal insulin regimen of a person with diabetes on sensor-augmented insulin pump therapy. The introduced technique uses an enhanced version of the R2R algorithm by Palerm et al¹⁸ by taking advantage of CGM technology. It also improves on the work proposed by Toffanin et al¹⁹ by allowing different basal insulin rates along the day, as required by insulin pump users.

It is important to remark that previously proposed techniques for automatically adapting the basal-insulin therapy do not consider temporary events such as physical exercise, illness, and hormone cycle. For this purpose, and following the same approach as the work proposed by Herrero et al for adapting meal-insulin boluses,^15-17 the artificial intelligence technique of case-based reasoning²⁵ is proposed as a potential solution to account for variability on basal insulin requirements due to such temporary events.

Methods

Run-to-Run Control

R2R is a control methodology designed to exploit repetitiveness in the process that is being controlled.²⁶ Its purpose is to enhance performance, using a mechanism of trial and error. The simplest formulation of R2R may be,

$$u_{k+1}=u_k+K.error,$$

where u is the control action, K is a tuning gain, and error is the tracking error defined as the difference between a measurement from the process and a set-point.

Insulin dosing has a repetitive nature. Therefore, R2R control can be used to exploit such characteristic. As previously discussed, R2R control has been extensively used for adapting the meal-bolus insulin regimen^13,14,16 and single-dose injection basal-insulin¹⁹ and overnight basal-insulin,^22,23 but to less of an extent for adapting the 24-hour basal regimen in pump therapy.¹⁸

Proposed R2R Algorithm

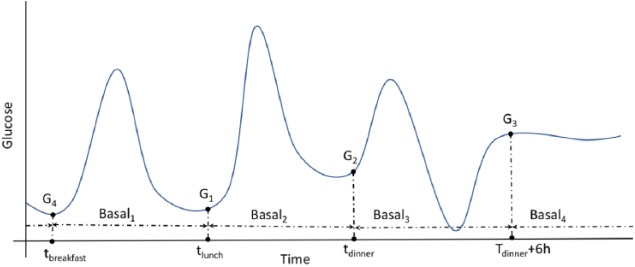
The proposed R2R algorithm for adapting the 24-hour basal-insulin regimen of a person with T1DM is based on the hypothesis that four time intervals are enough to account for the changes in basal insulin requirements due to circadian variations. In addition, it assumes that the time of the day-time when a person is closest to the fasting conditions is just before the meals and during the night time (eg, 6 hours after dinner). Therefore, the meal-time glucose measurements and a nighttime measurement are considered to adjust the basal-insulin rates between such times (t_breakfast, t_lunch, t_dinner, t_dinner + 6 h). Note that such time intervals might slightly change from day to day. Figure 2 shows a graphical representation of the four time intervals defining the basal profile (Basal₁, Basal₂, Basal₃, Basal₄).

Figure 2.

Graphical representation of the four time intervals defining the basal profile (Basal₁, Basal₂, Basal₃, Basal₄). Time points t_breakfast, t_lunch, t_dinner correspond to the meal intake times and G₁, G₂, and G₄ to their corresponding glucose levels.

The proposed R2R algorithm is based on the control law introduced by Palerm et al,¹⁸ which is described as

$$\begin{array}{c}Basa{l}_i\left(k+1\right)=Basa{l}_i\left(k\right)+k_1.\left(\frac{\left(G_{start}+G_{end}\right)}{2}-G_T\right)\\ +k_2.\left(G_{start}-G_{end}\right),\end{array}$$

where subindex i indicates the time interval (i = [1,2,3,4]), index k indicates the iteration (ie, run), k₁ and k₂ are tuning gains, G_start is the glucose value at the beginning of the interval, G_end is the glucose value at the end of the interval, and G_T is the glucose target.

This control law was designed to be used with capillary measurements and has the limitation of not taking into account if hypoglycemic and hyperglycemia events occur between measurements. In this work, a new control law that takes advantage of CGM technology by accounting for hypoglycemia and hyperglycemia within the considered time intervals is proposed. Current CGM technology has been approved by the FDA as a nonadjunctive technology, which makes it much more user-friendly by significantly reducing the number of required capillary measurements (ie, calibration). In addition to considering variability due to the circadian cycle, the proposed control law allows taking into account the type of day (eg, sickness day). The control law is described as

$$Basa{l}_i^j\left(k\right)=\{\begin{array}{l}Basa{l}_i^j\left(k-1\right)+k_1.\left(\frac{\left(G_{start}+G_{min}+G_{end}\right)}{3}-G_T\right)\\ +k_2.dG,if{G}_{min}<70(\mathrm{mg}/\mathrm{dL})\\ Basa{l}_i^k\left(k-1\right)+k_1.\left(\frac{\left(G_{start}+G_{min}+G_{end}\right)}{3}-G_T\right)\\ +k_2.dG+k_3.\left(G_{avg}-G_T\right),otherwise\end{array}$$

where subindex i indicates the time interval, the super-index j represents the type of day (eg, sickness day), k indicates the iteration (ie, run), k₁, k₂ and k₃ are tuning gains, G_start is the glucose value at the beginning of the interval, G_min is the postprandial minimum glucose value calculated over a postprandial glucose window from 2 hours postmeal to the next meal or 6 hours if the meal does not occur before, G_end is the glucose value at the end of the interval, G_T is the glucose target, and dG is the slope of a linear regression of the glucose values G_start, G_min, and G_end and their corresponding time instants, and G_avg is the glucose average over a postprandial glucose window from 3 hours postmeal to the next meal or 6 hours if the meal does not occur before. For the overnight time interval (Basal₄), G_avg is computed over the whole period.

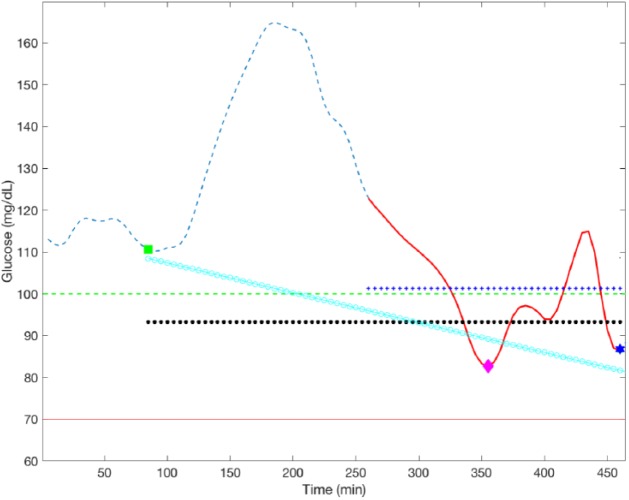
The reason for excluding the initial meal-time glucose measurement, and the following 2 hours, in the computation of G_min is because these glucose measurements are not the consequence of the basal rate being adapted, but the result of the previous basal-insulin rate. Finally, the first 3 hours are excluded in the calculation of G_avg within Basal₁, Basal₂, and Basal₃ intervals to eliminate the postprandial excursion due to the meal intake. Figure 3 shows a graphical representation of the variables involved in the proposed R2R control law.

Figure 3.

Graphical representation of the proposed R2R control law over a postprandial excursion. Dashed blue line represent the CGM measurement; green square, pink diamond, and blue star markers correspond to G_start, G_min, and G_end, respectively. Solid red line corresponds to the postprandial window [G_start+3h, G_start+6h]; horizontal black circled line is the average of G_start, G_min, and G_end; horizontal crossed blue line is G_avg and inclined circled cyan line is the linear regression of G_start, G_min, and G_end.

It is worth noting that the proposed R2R controller shares some similarities with the one proposed by Toffanin and colleagues,¹⁹ since both define two different laws based on the CGM performance and both put particular emphasis on hypoglycemia minimization. However, unlike Toffanin’s work, the proposed controller allows one to adapt different basal-insulin rates along the day, as required by insulin pump users.

To make the proposed control law more robust in front of uncertainty and sensor errors, the applied basal rate is obtained by computing the average of three consecutive adaptations corresponding to same basal rate segment (i) of the same day type (j). This is expressed by

$$avgBasa{l}_i^j=\frac{Basa{l}_i^j\left(k\right)+Basa{l}_i^j\left(k-1\right)+Basa{l}_i^j\left(k-2\right)}{3},$$

where k represents the run within the same basal rate segment (i) of the same day type ( j).

Safety constraint are put in place to avoid excessive adaptations. A relative constraint to limit the adaptation by ± 30% and a global constraint to limit the maximum and minimum rates to three times and a third of the original rate, respectively, are implemented.

Stability Analysis

Stability of the control law expressed by equation (5) is investigated next. Remark that, for each time interval $i\in \left\{1,\dots ,4\right\}$, G_min, G_end, G_avg, and dG in (5) are indeed functions of the starting glucose value for that interval, G_start, and the applied basal value, $Basa{l}_i$. Thus, the system (5) can be expressed as

$$Basa{l}_i^{k+1}=\{\begin{array}{l}Basa{l}_i^k+k_1.\left(h\left(Basa{l}_i^k,G_{start}\right)-G_T\right)\\ +k_2.dG\left(Basa{l}_i^k,G_{start}\right),\\ if.G_{min}\left(Basa{l}_i^k,G_{start}\right)<70\\ Basa{l}_i^k+k_1.\left(h\left(Basa{l}_i^k,G_{start}\right)-G_T\right)\\ +k_2.dG\left(Basa{l}_i^k,G_{start}\right)\\ +k_3.\left(G_{avg}\left(Basa{l}_i^k,G_{start}\right)-G_T\right),otherwise\end{array}$$

where

$$h\left(Basa{l}_i^k,G_{start}\right):=\frac{\left(\begin{array}{l}{G}_{start}+G_{min}\left(Basa{l}_i^k,G_{start}\right)\\ +G_{end}\left(Basa{l}_i^k,G_{start}\right)\end{array}\right)}{3}.$$

Analogously to Toffanin and colleagues,¹⁹ a simulation study was conducted to identify functions in (7) for a set of starting glucose and basal values, fixing all other parameters in the simulation, for a postprandial ($i\in \left\{1,2,3\right\})$ and a night period $(i=4)$. As a result, a set of quadratic functions for each period was obtained:

$$\begin{array}{l}h\left(Basa{l}_i^k,G_{start}\right)={\alpha }_h\left(G_{start}\right){\left(Basa{l}_i^k\right)}^2\\ +{\beta }_h\left(G_{start}\right)Basa{l}_i^k+{\gamma }_h\left(G_{start}\right)\end{array}$$

$$\begin{array}{l}dG\left(Basa{l}_i^k,G_{start}\right)={\alpha }_{dG}\left(G_{start}\right){\left(Basa{l}_i^k\right)}^2\\ +{\beta }_{dG}\left(G_{start}\right)Basa{l}_i^k+{\gamma }_{dG}\left(G_{start}\right)\end{array}$$

$$\begin{array}{l}{G}_{min}\left(Basa{l}_i^k,G_{start}\right)={\alpha }_{Gmin}\left(G_{start}\right){\left(Basa{l}_i^k\right)}^2\\ +{\beta }_{Gmin}\left(G_{start}\right)Basa{l}_i^k+{\gamma }_{Gmin}\left(G_{start}\right)\end{array}$$

$$\begin{array}{l}{G}_{avg}\left(Basa{l}_i^k,G_{start}\right)={\alpha }_{Gavg}\left(G_{start}\right){\left(Basa{l}_i^k\right)}^2\\ +{\beta }_{Gavg}\left(G_{start}\right)Basa{l}_i^k+{\gamma }_{Gavg}\left(G_{start}\right)\end{array}$$

$$\begin{array}{l}{G}_{end}\left(Basa{l}_i^k,G_{start}\right)={\alpha }_{end}\left(G_{start}\right){\left(Basa{l}_i^k\right)}^2\\ +{\beta }_{Gend}\left(G_{start}\right)Basa{l}_i^k+{\gamma }_{Gend}\left(G_{start}\right)\end{array}$$

The following monotonicity properties hold:

• $h$, $G_{min}$, $G_{avg}$, and $G_{end}$ are monotonically increasing with respect to $G_{start}$.

• $dG$ is monotonically decreasing with respect to $G_{start}$.

• $h$, $G_{min}$, $G_{avg}$, $G_{end}$, and $dG$ are monotonically decreasing with respect to $Basa{l}_i^k$.

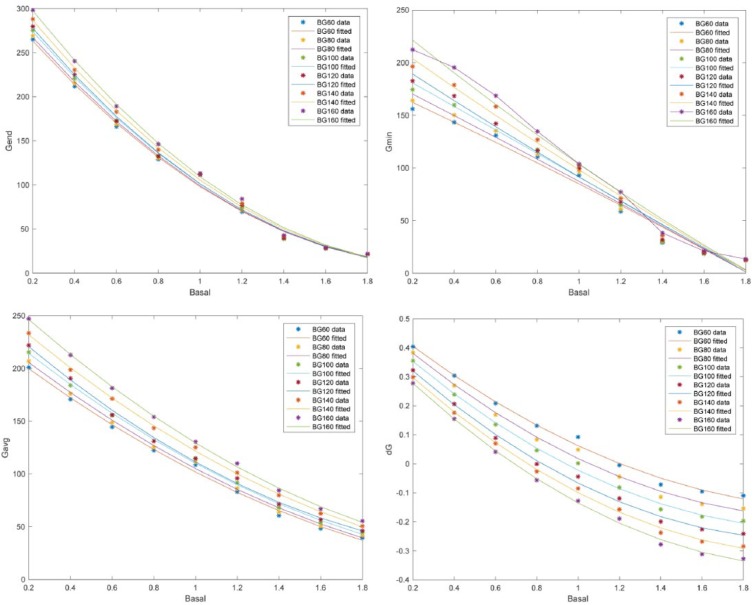
Figure 4 shows, as an illustration, the fitted functions for a starting glucose ranging from 60 to 160 mg/dL in the case of the postprandial period.

Figure 4.

Fitted quadratic functions for $G_{end}$, $G_{min}$, $G_{avg}$, and $dG$ for a postprandial period and a sweep in starting glucose values in the range 60 to 160 mg/dL.

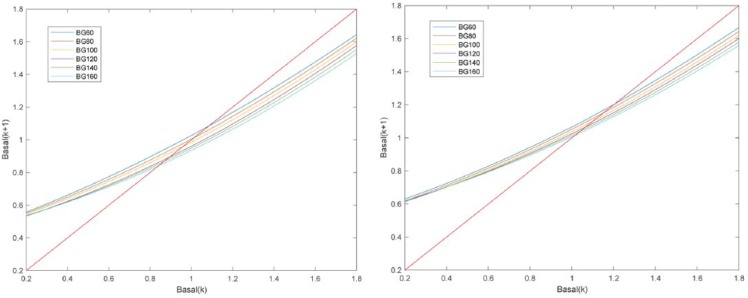
Since (7) is a first-order system, its stability can be derived from the phase plot, which depicts $Basa{l}_i^{k+1}$ versus $Basa{l}_i^k$ (curve corresponding to the right-hand side of (7)). Figure 5 shows the phase plot for a postprandial and night period, and a sweep in $G_{start},$. Denoting as $Basa{l}^{*}$ the crossing of the curve, for a given $G_{start},$ with the line $Basa{l}_i^{k+1}=Basa{l}_i^k$ (unit slope line), $\left|Basa{l}_i^{k+1}-Basa{l}^{*}\right|<\left|Basa{l}_i^k-Basa{l}^{*}\right|$ must hold for $Basa{l}^{*}$ to be an equilibrium point, that is, the curve must lie inside the ±45 degrees sector with origin $Basa{l}^{*},$ as it is in our case. For any $G_{start}$, if $Basa{l}_i^k>Basa{l}^{*},$then the basal will be decreasing toward $Basa{l}^{*}$ until convergence. If $Basa{l}_i^k<Basa{l}^{*}$, then the basal will be increased toward $Basa{l}^{*}$ until convergence. At each time step, $G_{start}$ will be the value of $G_{end}$ for the previously evaluated time interval (eg, $G_{start}$ at lunch is $G_{end}$ at breakfast), meaning that a curve switching in the phase plot will happen. However, these are monotonically decreasing with respect to $G_{start}$ and $G_{end}$ is monotonically decreasing with respect to basal, which means that the switching will happen in a monotonic way according to the direction of basal changes in the previous time interval.

Figure 5.

Phase plots of (6) for a postprandial period (left) and night period (right), and a sweep in starting glucose values in the range 60 to 160 mg/dL.

Case-Based Reasoning

The proposed R2R algorithm is able to deal with intraday variability in insulin requirements due circadian variations by separating the 24-h basal insulin profile into four time intervals. It is also able to deal with some degree of interday variability due to temporary events such as physical exercise, recurrent illness, psychological stress, and menstrual cycle. However, when the number of temporary events increases (eg, different intensities of exercise or stress) the problem might become untreatable. Similar to the work proposed by Herrero et al for recommending meal insulin boluses,¹⁵ the utilization of case-based reasoning is proposed as a potential solution to overcome this limitation.

Case-based reasoning (CBR) is an artificial intelligence problem solving framework that solves a newly encountered problem, based on the information obtained from previously solved problems and stored as cases in a case base.²⁵ A clinician who diagnoses a patient’s disease by recalling another patient who exhibited similar symptoms is using CBR.

CBR is usually described in four steps: Retrieve the most similar cases to the problem to be solved from the case base; Reuse the solutions of retrieved cases; Revise the outcome of the applied solution to the new problem; and Retain the new problem if its solution is considered useful for solving future problems. Figure 6 show the four steps of the CBR cycle (Retrieve, Reuse, Revise, Retain).

Figure 6.

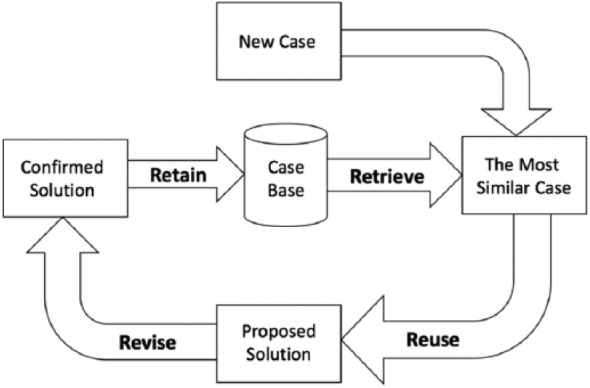
CBR cycle (Retrieve, Reuse, Revise, Retain).

In this work, CBR is used to recall previous scenarios where basal insulin requirements were similar to the current scenario (eg, dinner after moderate aerobic exercise) and then reuse such information to calculate the current basal insulin. Due to the significant intersubject variability in type 1 diabetes, cases are stored in a subject-specific case base.

Changes in insulin requirements along the day due to circadian variations are defined as a context within the case base. Cases of the different contexts are not compared against each other since they are considered to be too different. Table 1 shows a context and parameters, together with their potential values, considered in this work. Note that these parameters are just a subset of the parameter affecting insulin requirements. Other parameters that are known to affect insulin sensitivity, or affect blood glucose levels, and which could be considered in a real-life application of the proposed algorithm are alcohol consumption, hours and quality of sleep, traveling across time zones, and meal absorption.

Table 1.

Context and Parameters With Their Corresponding Values.

Parameter (P)/context (C)	Values
Time of day (C)	Postbreakfast, postlunch, postdinner, night
Aerobic exercise (P)	None, moderate, intense
Psychological stress (P)	None, mild, severe
Menstrual cycle (P)	Menstrual, follicular, ovulation, luteal
Illness (P)	None, mild, severe

Cases are retrieved from the case base (Retrieve step) by means of a k-nearest neighbors (KNN) algorithm, that is, computing the distance (eg, Euclidian) between the current case and all the cases in the case base and by selecting the case(s) with the shorter distance.²⁷ In particular the Euclidian distance is employed, which is described by

$$Distanc{e}_k=\sqrt{{\displaystyle \sum }_{j=1}^n{w}_j{\left(V_j^C-V_j^k\right)}^2},$$

where k indicates the distance between the current case and the case k in the case base, n is the number of parameters defining a case, $V_j^C$is the value of parameter j for the current case, $V_j^k$ is the value of parameter j for a case k in the case base, and w_j is the weight associated to parameter j. To calculate such distance, the distance between parameters, that is $V_j^C-V_j^k$), is defined as 0 if the values are equal, 1 if the value are adjacent (eg, none versus moderate), or 2 if the values are nonadjacent (eg, none versus intense). In this work, parameters are weighted equally (ie, w₁… w_n = 1), but these can be tunable in a real-life application.

If the retrieved case k is different from the current case (ie, $Distanc{e}_k\ne 0$), its solution (basal rate) needs to be adjusted by a percentage before applying it to the current scenario (Reuse step). Such percentage ($P_T)$ is defined as follows,

$$P_T=100{\displaystyle \prod }_{j=1}^n\frac{P_j^c}{P_j^R},$$

where $P_j^c$ and $P_j^R$ represent the percentages corresponding to parameter j for the current case and the retrieved case, respectively. Table 2 shows the applied percentages for each one of the values of the selected parameters. Note that in a clinical scenario, these values need to be individualized by the clinician to fit the needs of a particular person with T1DM.

Table 2.

Applied Percentages on the Basal-Insulin Rate for Each One of the Values of the Selected Parameters.

Parameter	Value (percentage)
Aerobic exercise	None (100%), moderate (50%), intense (20%)
Psychological stress	None (100%), mild (140%), severe (170%)
Menstrual cycle	None (100%), follicular (150%), luteal (170%)
Illness	None (100%), mild (130%), severe (180%)

If the retrieved case is different from the current case (ie, $Distanc{e}_k\ne 0$), then, a new case is created with the new adapted solution, and it is stored in the case base (Retain step). Once the solution of a case has been applied, a retrospective revision of the resulting glycemic outcome is carried out (Revision step) by means of the proposed R2R control law (equation (5)). Note that the solution of a case in the case base is only updated after being revised three times (equation (6)).

Unlike the traditional CBR approach²⁵ where the solutions of the cases in the case base are static, in this work the solutions (ie, basal rate) can be adapted if they are found to be suboptimal. This strategy partially solves the so-called problem of cold start in CBR (ie, insufficient initial cases in the case base) by initializing the case base with a small set of safe cases (most likely suboptimal) and letting the system converge toward an optimal solution while adapting solutions of existing cases and adding new cases to the case base.

When compared to a lookup table-based approach, where all the cases resulting from all combinations of parameters are independently adapted with the R2R control law, the proposed CBR algorithm is expected to converge swifter to an optimal basal-insulin therapy thanks to reusing information from similar cases.

Finally, a very important issue which must be accounted for in a CBR application is the case-based maintenance. Case-based maintenance is used to control the size of the case base and removes cases that have lost their validity (eg, too old).

It is important to remark that, due to the limited number of cases available in the employed simulator, the evaluation of the proposed CBR algorithm has not been possible. It is important to note that the feasibility of CBR in a clinical setting has already been proven¹⁷ in the context of meal-bolus adaptation.

In Silico Evaluation Under Intraday and Interday Variability

The UVa-Padova T1DM simulator (v3.2)²⁸ was used to evaluate the proposed R2R technique against the R2R control law proposed by Palerm and colleagues.¹⁸

Intraday variability and uncertainty on meal type, meal time, carbohydrate estimation, meal absorption, insulin absorption, and insulin sensitivity were introduced in the simulator as described by Herrero and colleagues.²¹ In addition, interday variability was represented by three types of days, which were generated multiplying by 1.1 (day 1), 0.5 (day 2), and 1 (day 3) the insulin sensitivity parameters (V_mx and K_p3) in the simulator model.²⁹ Note that the selected insulin sensitivity changes are not necessarily physiological and their sole purpose is to test the algorithm. In addition, two days had an of exercise 60 min at 50% V02 max at 5 pm (day 1 and day 2) and one did not (day 3). For this purpose, the model of exercise proposed by Schiavon et al³⁰ was included in the simulator. In total, 12 different scenarios composed by 4 contexts per day (postbreakfast, postlunch, postdinner, night) and 3 types of days were generated. Hence, the two R2R control laws were applied on each one of the 12 different scenarios.

The 10 adult, 10 adolescent, and 10 child subjects available in the simulator were used for evaluating purposes. The initial basal insulin infusion rate for the virtual subjects was the one provided by the default insulin therapy of the simulator. The selected CGM to perform the simulations was the Dexcom G4 platinum. A virtual pump with no error was selected to deliver the insulin. A 17-week scenario was employed, with the first week having no adaptation. The selected daily pattern of carbohydrate dose intake was 7 am (40 g), 1 pm (80 g), and 7 pm (60 g).

The following glycemic metrics, which are widely accepted by the diabetes technology community to evaluate glucose controllers,³¹ were selected for comparison purposes: mean blood glucose (BG) in mg/dl; percentage time in glucose target range [70,180] mg/dl (% in target); percentage time below target (ie, hypoglycemia) (% < target); percentage time above target (ie, hyperglycemia) (% > target); risk index (RI); low blood glucose index (LBGI); and high blood glucose index (HBGI).

Controllers Tuning

Tables 3 and 4 shows the tuning parameters employed for the in silico evaluation of the control law proposed by Palerm et al¹⁸ and the proposed control law, respectively. Note that the tuning of the R2R by Palerm et al is significantly different from the tuning proposed in the original work (ie, an order of magnitude). This might be explained by the difference between the employed simulators, as the UVa-Padova T1DM simulator is a validated software tool accepted by the FDA as a substitute to animal trials.

Table 3.

Tuning Parameters for the Control Law Proposed by Palerm et al¹⁸.

	Adults	Adolescents	Children
k1	0.001	0.001	0.0005
k2	0.001	0.001	0.0005

Table 4.

Tuning Parameters for the Proposed Control Law.

	Adults	Adolescents	Children
k1	0.001	0.001	0.0005
k2	0.7	0.7	0.35
k3	0.0001	0.0001	0.00005

Results

Tables 5-7 show the average results corresponding to the 10 adults, 10 adolescents, and 10 children at week 1 (no adaptation) and at week 17 after 16 weeks of basal adaptations. Note that all the calculated glycemic metrics for the three cohorts significantly improve over the 17 weeks.

Table 5.

Average Glycemic Outcomes Corresponding to Week 1 (No Adaptation) and Week 17 for the 10 Adult Subjects.

Week	BG	% in T	% < T	% > T	RI	LBGI	HBGI	TDD
1	138.8 ± 12.9	70.9 ± 11.8	9.7 ± 6.6	19.3 ± 8.6	7.2 ± 3.7	2.7 ± 2.2	4.5 ± 2.3	42.1 ± 9.9
17	128.5 ± 5.3	91.1 ± 4.4	0.9 ± 1.2	7.9 ± 4.5	2.4 ± 0.8	0.4 ± 0.3	2.0 ± 0.7	43.8 ± 9.2
P value	P < .05	P < .01	P < .01	P < .01	P < .01	P < .01	P < .01	P < .05

Table 6.

Average Glycemic Outcomes Corresponding to Week 1 (No Adaptation) and Week 17 for the 10 Adolescent Subjects.

Week	BG	% in T	% < T	% > T	RI	LBGI	HBGI	TDD
1	175.0 ± 24.9	46.5 ± 11.9	10.5 ± 8.3	42.9 ± 9.8	15.8 ± 6.8	4.5 ± 4.3	11.3 ± 4.6	31.9 ± 8.1
17	140.4 ± 12.4	80.1 ± 10.9	0.83 ± 1.0	19.0 ± 10.9	4.4 ± 2.1	0.4 ± 0.2	3.9 ± 2.0	35.4 ± 8.5
P value	P < .01	P < .01	P < .01	P < .01	P < .01	P < .05	P < .01	P < .01

Table 7.

Average Glycemic Outcomes Corresponding to Week 1 (No Adaptation) and Week 17 for the 10 Child Subjects.

Week	BG	% in T	% < T	% > T	RI	LBGI	HBGI	TDD
1	169.6 ± 16.9	49.4 ± 12.9	10.9 ± 6.1	39.7 ± 9.3	14.9 ± 6.0	4.6 ± 3.6	10.3 ± 3.6	16.7 ± 3.6
17	144.6 ± 10.3	73.7 ± 4.1	3.2 ± 3.5	23.1 ± 6.3	6.1 ± 1.0	1.2 ± 1.2	5.0 ± 1.4	18.2 ± 3.8
P value	P < .01	P < .01	P < .01	P < .01	P < .01	P < .01	P < .01	P < .01

Tables 8-10 show the comparison of the glycemic outcomes achieved with the R2R control law by Palerm and colleagues¹⁸ and by the one the proposed in the current work computed over the whole simulation period (17 weeks). Note that the proposed approach achieves a superior performance over the three cohorts regarding the percentage time in hypoglycemia, without increasing the percentage time in hyperglycemia.

Table 8.

Comparison Between Average Glycemic Control Achieved With the R2R Control Law by Palerm et al Against the Control Law Proposed in the Current Work.

	BG	% in T	% < T	% > T	RI	LBGI	HBGI	TDD
Palerm et al	129.0 ± 6.5	84.6 ± 5.1	3.9 ± 2.6	11.5 ± 4.8	3.8 ± 1.2	1.2 ± 0.7	2.6 ± 0.9	40.9 ± 8.9
Proposed	131.6 ± 6.0	85.9 ± 5.3	2.6 ± 2.2	11.5 ± 4.7	3.4 ± 1.2	0.8 ± 0.7	2.6 ± 0.8	40.7 ± 8.9
P	P < .01	P < .01	P < .01	P = .9	P < .01	P < .01	P = .3	P = .06

Results correspond to the 10 adult subjects in the simulator.

Table 9.

Comparison Between Glycemic Control Achieved With the R2R Control Law by Palerm et al Against the Control Law Proposed in the Current Work.

	BG	% in T	% < T	% > T	RI	LBGI	HBGI	TDD
Palerm et al	149.3 ± 15.5	70.8 ± 10.1	2.9 ± 1.9	26.4 ± 9.9	7.1 ± 2.8	1.1 ± 0.7	5.9 ± 2.8	32.2 ± 7.8
Proposed	150.5 ± 15.1	72.1 ± 9.9	2.0 ± 1.5	25.9 ± 10.0	6.6 ± 2.6	0.8 ± 0.6	5.7 ± 2.6	32.4 ± 7.8
P	P < .05	P < .01	P < .01	P = .1	P < .01	P < .01	P < .05	P < .05

Results correspond to the 10 adult subjects in the simulator.

Table 10.

Comparison Between Glycemic Control Achieved With the R2R Control Law by Palerm et al Against the Control Law Proposed in the Current Work.

	BG	% in T	% < T	% > T	RI	LBGI	HBGI	TDD
Palerm et al	151.3 ± 12.2	67.5 ± 6.2	4.6 ± 2.8	27.9 ± 7.3	8.1 ± 2.1	1.6 ± 0.9	6.5 ± 2.0	16.8 ± 3.4
Proposed	153.5 ± 10.7	68.6 ± 6.3	3.5 ± 2.0	27.9 ± 6.9	7.7 ± 1.9	1.2 ± 0.7	6.4 ± 1.8	16.8 ± 3.5
P	P < .05	P < .01	P < .01	P = .8	P < .01	P < .01	P = .3	P = .9

Results correspond to the 10 adult subjects in the simulator.

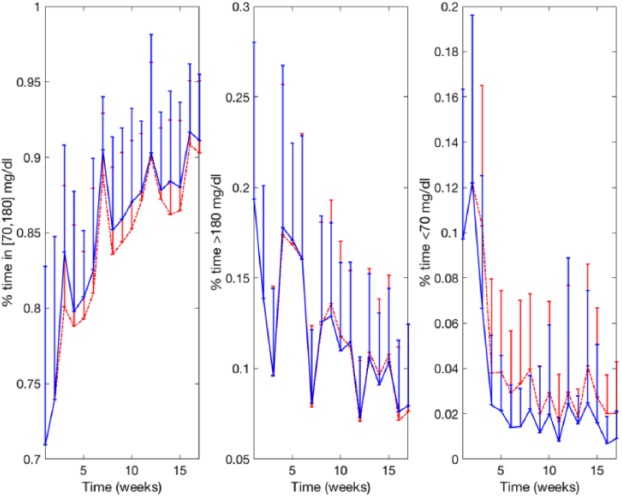
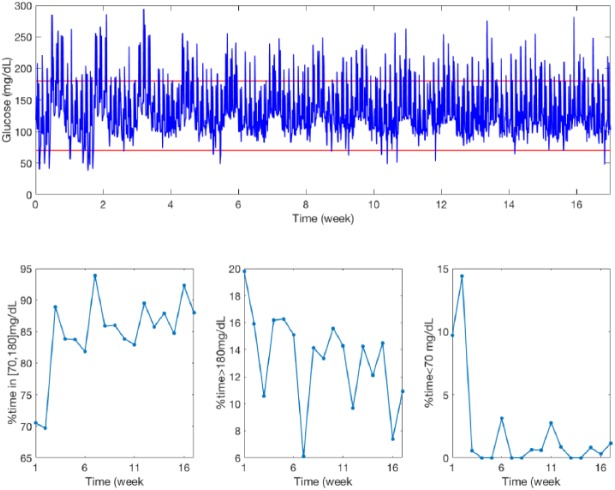
Figure 7 shows a comparison between Palerm et al R2R and the new R2R of the weekly evolution for three of the evaluated glycemic metrics (% in T, % < T, and % > T) for the adult cohort. Note that despite oscillations due to the interday variability, the algorithm converges after approximately 10 weeks. Figure 8 shows the glucose profile of adult 1 over the 17-week simulation together with the corresponding glycemic metrics (% in T, % < T, and % > T). Figure 9 displays the evolution of the 12 basal rates over time corresponding to Figure 8. Note that basal levels for different days differ up to 100%.

Figure 7.

Weekly evolution of the average percentage time in target (% in T), percentage time below target (% < T), and percentage time above target (% > T) corresponding to the adult cohort corresponding the original R2R controller (dashed red line) and the new R2R controller (solid blue line). Error bars represent the standard deviation.

Figure 8.

Glucose profile for adult 1 over the 17-week simulation (upper graph) together with the corresponding glycemic metrics (lower graphs).

Figure 9.

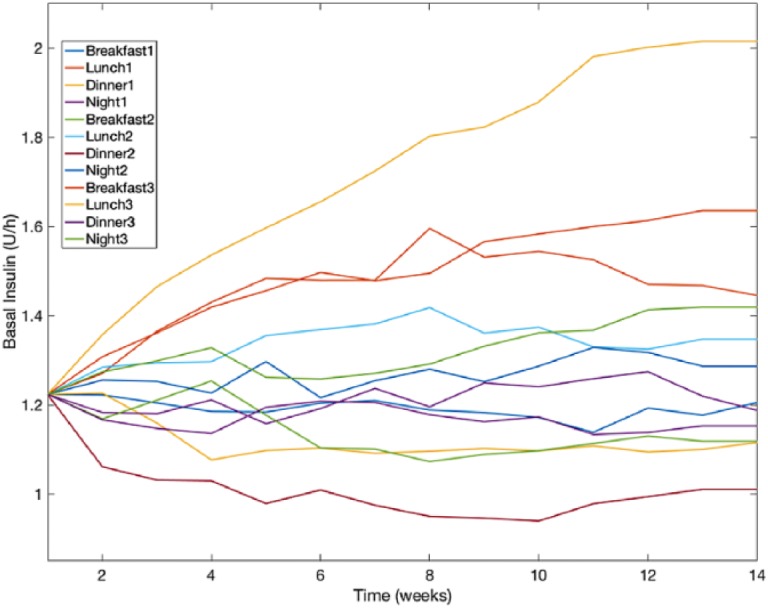
Temporal evolution of the 12 basal rates corresponding to Figure 8. Breakfast, lunch, dinner, and night indicate the context and the accompanying number represents the day type.

Discussion

In a virtual T1DM population (10 adults, 10 adolescents, 10 children) over a 17-week scenario with intraday and interday variability, the presented basal insulin adaptation technique based on R2R control significantly improves all the evaluated glycemic metrics. When compared against an existing technique by Palerm et al¹⁸ the proposed algorithm outperforms the former in the three studied cohorts by reducing the time in hypoglycemia, increasing the time in target while not increasing the time in hyperglycemia. A marginal increase in mean glucose (ie, <2 mg/dL) is observed.

When analyzing the weekly evolution of the evaluated glycemic metrics, it can be observed that glycemic metrics take about 10 weeks to converge to a relatively steady state. This convergence rate could be increased by using a less conservative strategy when saturating/filtering the adaptations, but at the expenses of losing robustness.

Although the robustness of the proposed algorithm has been tested to some degree by introducing significant intrasubject and intersubject variability in the in silico study, which might be not too far from a real-life scenario, a systematic robustness analysis is still desirable. This can be considered a limitation of the current work, and a complete robustness evaluation is planned as future work. Such analysis should evaluate the ability of the algorithm to adjust basal insulin rates in case of systematic variations in bolus calculator parameters. In addition, it would be interesting to evaluate possible compensations between bolus calculator parameters and basal insulin infusion, as could appear in real life. An additional challenge that could be added to further test the robustness of the algorithm would be the misclassification of the type of day.

One important aspect that has not been considered in this work, and which it is essential in a real-life scenario, is the need to take into account hypo-treatments and/or insulin correction boluses since they can have a significant input on the glycemic outcomes. One solution to this problem is to discard these scenarios from the adaptations when such information is available. This was the approach followed by Reddy and colleagues in the evaluation of an adaptive meal bolus calculator.¹⁷

It is important to remark that the effectiveness of the CBR algorithm could not be evaluated due to the limitations of the employed simulator. To prove the efficacy of the CBR algorithm, a clinical trial is required. Note that the clinical feasibility of CBR in the context of meal bolus calculations has been proved by Reddy et al.¹⁷

Once the technology has been validated in a pivotal study and has gone through the corresponding regulatory approvals, this could be implemented on a sensor-augmented insulin pump with Internet connectivity (eg, Cellnovo System, Pencoed, UK), which would allow remote adaptation and supervision by expert clinicians. Future work also includes the evaluation of the presented technique in combination with a meal bolus adaptation technique such as the one proposed by Herrero and colleagues.¹⁶

Conclusion

Based on the presented in silico study, the proposed basal insulin adaptation technique has the potential to effectively adjust the 24-hour basal insulin profile of a type 1 diabetes population on sensor-augmented insulin pump therapy. Further clinical studies are required to evaluate its effectiveness in a real scenario.