A Framework for Executive Function in the Late Elementary Years

Abstract

Objective

Executive Function (EF) is a commonly used but difficult to operationalize construct. In this study, we considered EF and related components as they are commonly presented in the neuropsychological literature, as well as those of developmental, educational, and cognitive psychology. These components have not previously been examined simultaneously, particularly with this level of comprehensiveness, and/or at this age range or with this sample size. We expected that the EF components would be separate but related, and that a bifactor model would best represent the data relative to alternative models.

Method

We assessed EF with 27 measures in a large sample (N = 846) of late elementary school aged children, many of whom were struggling in reading, and who were demographically diverse. We tested structural models of EF, from unitary models to methodological models, utilizing model-comparison factor analytic techniques. We examined both a common factor as well as a bifactor structure.

Results

Initial models showed strong overlap among several EF latent variables. The final model was a bifactor model with a common EF, and five specific EF factors (Working Memory-Span/Manipulation and Planning; Working Memory-Updating; Generative Fluency, Self-Regulated Learning; Metacognition).

Conclusions

Results speak to the commonality and potential separability of EF. These results are discussed in light of prevailing models of EF, and how EF might be used for structure/description, prediction, and for identifying its mechanism for relevant outcomes.

Executive function (EF) is a domain-general control process important for managing goal-directed behavior. However, any straightforward definition belies the variability in the way EF is conceptualized within and across literatures. One approach addresses functions that are disrupted with damage to the frontal lobes (e.g., Stuss, 2011), and includes group or individual studies of brain injury (e.g., Tranel, Anderson, & Benton, 1994; Welsh, Pennington, & Grossier, 1991), and/or structural and/or functional imaging to evaluate these associations (e.g., Alvarez & Emory, 2006; Jonides et al., 1993). A second approach delineates a collection of separate but related cognitive functions (e.g., shifting, inhibition, working memory, planning, fluency), through theory (e.g., working memory and inhibition, Roberts & Pennington, 1996) or empirical study (e.g., factor analysis; e.g., Miyake et al., 2000; Wiebe, Espy, & Charak, 2008), that have in common the management or facilitation of goal-directed behaviors. A third approach identifies problem solving stages of representation and preparation, generating and implementing solutions, performance monitoring, and reflection. These stages have been considered from the perspective of development (e.g., Zelazo, Carter, Reznick, & Frye, 1997), from neuropsychology and rehabilitation (e.g., Levine et al., 2000; 2011; Ylvisaker & Feeney, 2002), or from education (e.g., Zimmerman, 1989; 2000; Pintrich, 2000; 2004). Terms used to reflect this process include self-regulation (and in particular, self-regulated learning), metacognition, executive/attentional control, executive attention, and executive function, among others.

The goal of the present study was to provide a framework for EF, mainly relying on the second and third approaches noted above, and utilizing factor analytic methodology. While imaging or lesion data was not emphasized, the measurement structure identified could provide impetus for studies that do. We considered EF to be an umbrella term with both cognitive and self-regulatory aspects (Hofmann, Schmeichel, & Baddeley, 2012; Ilkowska & Engle, 2010).

We evaluated students in grades 3 through 5 (ages 8 to 11) for three interrelated reasons. First, developmentally sensitive change occurs cognitively and biologically across this age span, with the development of EF following a nonlinear trajectory corresponding with the physical maturity of the frontal lobes (Anderson, Anderson, Northam, Jacobs, & Catroppa, 2001; Best, Miller, & Jones, 2009; Garon, Bryson, & Smith, 2008; Jurado & Roselli, 2007; Luciana & Nelson, 2002; Yakovlev & Lecours, 1967). Second, most existing structural studies of EF focus on preschool or adult age ranges; in contrast, a key question the present study is well equipped to address is whether EF components reflect a more unitary versus segregated group of processes at this intermediate age range. Third, students in this age range are expected to have “mastered” basic academic skills, and greater independence, initiative, and planning is required as curricula shift towards developing and applying generalized learning skills to new contexts (Speece, Ritchey, Silverman, Schatschneider, Walker, & Andrusik, 2010). EF becomes a key support as students integrate and regulate academic learning and understanding within and across domains.

The present study emphasizes a large and diverse urban public school sample. Many of these participants are of minority status, are raised in lower SES households, and some may speak languages in addition to English, which is representative of most large urban school districts (National Center for Education Statistics, 2016). These characteristics are associated with lower levels of achievement and/or EF (Hackman & Farah, 2009; Hackman, Gallop, Evans, & Farah, 2015; Raver, Blair, Willoughby, & The Family Life Project Key Investigators, 2013). We oversampled students in grade 4 with reading difficulty because this work overlapped with a large-scale intervention study (though the data reported preceded rather than followed intervention; see Methods below). Doing so was necessary to improve feasibility (and efficiency) for both studies, but evaluating the structure of EF in this context is also relevant to a population where supports for EF are likely to be appropriate.

Executive Function Components

We identified eight EF components across neuropsychological, cognitive, developmental, and educational literatures: (1) working memory; (2) inhibition; (3) shifting; (4) planning; (5) generative fluency; (6) self-regulated learning; (7) metacognition; and (8) behavioral regulation. The first three of these were encapsulated in the work of Miyake et al. (2000), but the other five are distributed across the literatures noted above. No single work has considered all of the above simultaneously. It is possible to argue for the inclusion versus exclusion of any of these individual components, or to separate them by complexity, or even as “outcomes” of EF. We took an inclusionary approach because different literatures use different terminology and different measures. If each of the domains examined here are equally representative of EF, than they should relate to one another to some degree, but also share commonality. To the extent that a particular EF component “does not fit” then it should separate from the others, and the results of this study will be well-positioned to understand whether and along what lines such distinctions might occur.

Baddeley, Allen and Hitch (2011) describe the overlap of working memory (WM) with EF. Theorists such as Cowan (2008) and Engle (2002) emphasize WM as the active portion of long-term memory, such that it can be proffered as a substitution for EF itself – that is, EF theories become theories about how working memory operates. For this study, we chose working memory tasks that required: (a) recall with manipulation; or (b) simultaneous processing and storage; or (c) ongoing maintenance/updating of information in active memory. Inhibition is also featured in many studies of EF, though inhibition can be difficult to separate from a common EF factor (e.g., Miyake & Friedman, 2012). A key requirement is that a prepotent response is inhibited, and this was featured in the measurement of this domain for this study. Shifting as considered here requires a move from one cognitive set of rules, sequences, or patterns, to another, as similarly defined in other studies (Miyake et al., 2000). Planning has often been assessed as a clinical task (Delis, Kaplan, & Kramer, 2001), and may be considered a “higher-level” EF (Miyake et al., 2000). Solving a problem within a set of rules/parameters most closely resembles the process function of EF because strategies must be selected, implemented, and monitored. Tests of Generative Fluency have a lengthy history in neuropsychology (Milner & Petrides, 1984), with the key component being efficient and accurate retrieval from semantic memory within a set of parameters.

Models of Self-Regulated Learning (SRL) (e.g., Pintrich, 2000; 2004; Zimmerman & Schunk, 2011) focus on how individuals control their own learning processes. Zimmerman’s (2000) model includes phases of forethought, performance, and self-reflection; Pintrich (2004) emphasized planning, monitoring, control, and reflection. These phases are similar to the frameworks of EF described by Zelazo et al. (1997) and Ylvisaker & Feeney (2002). SRL is multifaceted, but here we focused on strategy use and self-efficacy, as well as perceived skill and preference for reading (as a proxy for motivational stance), as these imply knowledge of one’s own abilities. An important methodological difference in comparing the literatures of SRL with EF is that SRL is often assessed via self-report, whereas EF is usually assessed via cognitive performance measures (particularly the “cool” variety; e.g., Welsh & Peterson, 2014).

Metacognition and EF are both often described as superordinate processes – those that monitor, manipulate, or control/regulate other cognitive processes, and metacognitive processes are featured in some models alongside EF (e.g., Stuss, 2011). Metacognition has also been perceived as a “bridge” function, for example, between EF and motivation (Borkowski, Chan, & Muthukrishna, 2000); Barkley’s model (1997; 2014) considered metacognition as a component of EF (reconstitution). The Behavioral Rating Inventory of Executive Function (BRIEF; Gioia, Isquith, Guy, Kenworthy, 2000) considers Metacognition as one of its primary scales.

In contrast to SRL, Behavioral Regulation models are often concerned with the ability of individuals to control their behavioral actions and/or emotions (Blair, 2002; Barkley, 1997; 2014; Posner & Rothbart, 2000; Raver, 2004). In some ways, this is similar to the idea of “hot” executive functions, where the situation is in some way emotionally valanced (Allan & Lonigan, 2011; Zelazo & Carlson, 2012; Welsh & Peterson, 2014). Although decision-based cognitive tasks are available, most often behavioral regulation is assessed through self- or other-ratings, especially beyond the preschool age. Few studies evaluate the relationship of neuropsychological measures of EF to behavioral self-regulation measures beyond the earliest elementary ages, though where examined, relationships are generally small (e.g., Duckworth & Kern, 2011).

Prior Factor-Analytic Studies in School-Aged Children

The literature on EF is vast, and many factor analytic studies have been conducted. However, none have matched the scope (e.g., number of measures, across different literature perspectives) and sample size evaluated here, particularly in this sensitive age range (middle to late elementary students). Several recent studies have focused on preschool children using careful measurement approaches, identifying a unitary EF factor (Wiebe et al., 2008; Willoughby, Blair, Wirth, & Greenberg, 2010). On the other hand, latent variable studies in adults show that EF components are notably fractionated though not independent (e.g., Miyake, 2000; Hull, Martin, Beier, Lane & Hamilton, 2008; Kane, et al., 2004). Structural results in school-aged samples vary, often finding factors associated with WM or updating, inhibition, and shifting/flexibility, though not always together. For example, sometimes a combination of shifting and inhibition is included, as a latent factor (Brydges, Fox, Reid, & Anderson, 2014; Lee, Bull, and Ho, 2013). Only a few studies have considered factors other than working memory, inhibition or shifting (Floyd, Bergeron, Hamilton, & Parra; 2010; Gioia, Isquith, Retzlaff, & Espy, 2002), making it unclear how additional domains such as fluency, planning, or self-regulated learning may or may not fit. The study by Huizinga et al. (2006) utilized a sophisticated modeling approach and covered the age range from 7 to 21, with a relatively large sample size (~400). All tasks were computerized and involved speeded choice reaction times. Controlling for processing speed, factors of working memory and shifting were obtained, though not inhibition. Most prior studies captured only performance-based (e.g., paper-and-pencil, computerized, and/or experimental) measures of EF – none included self-report measures, with the exception of Gioia et al. (2002) where the structure of EF was examined using the BRIEF.

EF Factor Models: Common versus Bifactor?

There is debate about how EF components aggregate with or disaggregate from one another. For example, Willoughby, Pek, and Blair (2013) noted the typically weak interrelationships of factor indicators of EF. Factor analytic choices typically include a common factor model, a hierarchical factor model, and a bifactor model (Canivez, 2014). Common factor models comprise the vast majority of prior work, specifying which latent factors cause which indicators. Hierarchical factor models posit factors that have direct effects on indicators, but go on to posit second-order factors that have only indirect effects on indicators (through the specific factors); the second order factor also is presumed to account for all the relationships of the specific factors with one another. Bifactor models also posit general and specific factors, but in these models, indicators have two direct effects – one from the general factor, and another from the specific factor to which it is assigned. Specific factors are typically uncorrelated with both the general factor, and with one another; correlations among measures from the same latent variable arise from the general and specific factors, whereas correlations among measures from different factors arise from the general (EF) factor only (Holzinger & Swineford, 1937; Reise, 2012). In this study, we compare the common factor model to the bifactor case, given its consistency with the Miyake and Friedman models (Friedman, Miyake, Robinson, & Hewitt, 2011; Friedman et al., 2008; Miyake et al., 2000) in adults, and with a more general conceptualization of EF as “separate but related” function(s).

Summary and Hypotheses

The present study extends prior work in at least three ways. First, we address the need for a clearer understanding of the structure of EF in the school-age range. Second, measures from different literatures are simultaneously evaluated. Third, the large sample in a relevant context is novel, and we employed advanced modeling techniques to examine EF comprehensively. An overarching goal was to align the way that EF is conceptualized across literatures while also reflecting the myriad ways it is operationalized.

Our primary hypothesis was that we could model together numerous observed indicators at the confirmatory factor analytic (CFA) and bifactor level. To the extent that different literatures describe similar conceptualizations of domain-general control processes important for managing goal-directed behavior (sometimes calling it EF, other times working memory or executive attention, other times self-regulation), then measurement of each should bear relation to one another. However, to the extent that these measurements differ either methodologically (e.g., ratings versus laboratory tasks), or as lower versus higher level (e.g., “predictors” versus “outcomes”), then latent factors of these should be clearly separable from the others. These issues reflect a key debate regarding EF – whether it is unitary versus fractionated. Because both are likely true to some degree true, a bifactor model should fit the data better than a common factor model (8 correlated domains), and better than a single-factor model. We also specifically compared unitary, common, and bifactor models against those driven by methodological factors (e.g., type of measure – rating scales or performance measures; type of content – visual or verbal); these should fit the data more poorly than our hypothesized bifactor model.

Second, we expected predictable relationships with demographic factors including age, sex, economic disadvantage, sex, and English proficiency status. We expected that any common EF factor (resulting from a bifactor model) would relate positively with age (older students having stronger performances). Age was examined rather than grade, as EF domains are not typically part of school curricula. We did not have a priori expectations for sex differences in EF. We expected that a common EF factor would correlate negatively with economic disadvantage and English proficiency (disadvantaged students or those with of limited English proficiency having weaker EF), which may in part be due to the language demands of many of the tasks.

Methods

Participants

Participants were 846 students in grades 3 to 5 (age range 8 to 12 years). Table S1 (see Supplementary Files) presents demographic characteristics (N, sex, age, site, ethnicity, economic disadvantage, special education status, and limited English proficiency status), by grade and for the overall sample. The sample was diverse ethnically, and a majority were economically disadvantaged. Students were drawn from 147 classrooms 19 schools. However, we chose not to fit multilevel models because the study was not designed to address multilevel questions about between-classroom level interrelations of EF factors. EF is not instructed the way core academic skills are, making it ambiguous to hypothesize about classroom effects.

Measures

Descriptive information for all measures by EF factor is provided in Table 1. For space considerations, additional information about task requirements, administration details, and psychometric properties can be found in Supplement 2. Raw scores instead of norm-referenced standard scores were utilized in analyses for consistency and because relations with age were examined directly.

Table 1.

Descriptive statistics and data patterns.

								Data Patterns
Variable	N	%N	Mean	SD	Skew	Kurt	Rel	1	2	3	4	5	6
Shifting							0.80
D-KEFSa: Design Switch (max = 9)	420	50	3.98	1.79	0.32	0.16			x		x		x
D-KEFSa: Verbal Switch (max = 14)	419	50	5.02	2.95	0.09	−0.43		x			x	x
D-KEFSb: Inhibit Switch (max = 177)	408	48	91.55	24.97	1.31	1.99				x		x	x
D-KEFSb: Trails Switch (max = 240)	410	48	159.26	58.96	0.05	−1.35		x	x	x
WM-S/M and Plan							0.79
Working Memorya (max = 22)	434	51	11.37	3.70	−0.09	−0.02		x	x	x
Corsi Blocksa (max = 47)	422	50	19.29	9.45	0.10	−0.13				x		x	x
Tower of Londona (max = 78)	832	98	51.04	15.11	−1.17	1.61		x	x	x	x	x	x
Tower of Londona (exmov) (max = 4.5)	832	98	1.71	1.05	0.04	−0.78		x	x	x	x	x	x
WJ-III Planningc (max = 504)	807	95	500.05	1.76	−0.98	2.66		x	x	x	x	x	x
WMU							0.82
N-Backd: 1 Letter (max = 4.10)	210	25	1.68	1.14	0.26	−0.19			x		x		x
N-Backd: 2 Letters (max = 4.10)	210	25	0.80	1.06	1.01	2.01			x		x		x
N-Backd: 1 Shape (max = 4.10)	408	48	0.98	0.97	0.49	0.71		x			x	x
N-Backd: 2 Shapes (max = 2.52)	408	48	0.27	0.68	0.50	0.95		x			x	x
Inhibition							0.54
Cued Go No-God (max = 4.30)	556	66	3.29	0.65	−0.69	0.49		x	x		x	x
Stop Signal Testb (max = 773)	524	62	319.82	109.24	0.68	0.61		x	x	x	x		x
Fluency							0.77
D-KEFSa: Filled/Empty Dots (max = 26)	827	98	11.22	4.17	0.52	−0.07		x	x	x	x	x	x
D-KEFSa: Category Fluency (max = 48)	832	98	24.52	6.78	0.37	0.15		x	x	x	x	x	x
D-KEFSa: Letter Fluency (max = 47)	832	98	18.22	7.13	0.48	0.27		x	x	x	x	x	x
Self-Regulation Learning							0.88
Effort/Self-Efficacya (max = 42)	826	98	30.86	7.85	−0.99	0.86		x	x	x	x	x	x
Skill/Preferencea (max = 15)	826	98	8.33	3.67	−0.25	−0.62		x	x	x	x	x	x
Learning Strategiesa (max = 54)	827	98	30.88	11.30	−0.06	−0.66		x	x	x	x	x	x
Metacognition							0.97
BRIEFa: Initiate (max = 21)	534	63	12.49	4.33	0.33	−0.99		x	x	x	x	x	x
BRIEFa: Monitor (max = 30)	534	63	17.46	5.98	0.50	−0.81		x	x	x	x	x	x
BRIEFa: Planning/Organizing (max = 30)	534	63	17.46	5.81	0.41	−0.89		x	x	x	x	x	x
BRIEFa: Organization (max = 21)	533	63	11.16	4.43	0.80	−0.68		x	x	x	x	x	x
BRIEFa: Working Memory (max = 30)	535	63	16.92	6.09	0.55	−0.82		x	x	x	x	x	x
SWANa: Inattention (max = 27)	750	89	0.83	12.70	−0.21	−0.38		x	x	x	x	x	x

Note. D-KEFS = Delis-Kaplan Executive Function System; BRIEF = Behavior Rating Inventory of Executive Function; WJ-III = Woodcock Johnson III; SWAN = Strengths and Weaknesses of Attention-Deficit/Hyperactivity Disorder Symptoms and Normal Behavior; Skew = skewness; Kurt = kurtosis; Rel = maximal reliability for the latent factors from Model 2.

^aRaw accuracy score;

^bResponse time (in milliseconds for Stop Signal Test median reaction time, and in seconds for D- KEFS Color Word Interference Inhibition Switching and Trailmaking Letter-Number Switching);

^cW-score;

^dd-prime;

Working Memory was assessed with: (a) Working Memory Test Battery for Children (WMTB-C; Pickering & Gathercole, 2001) Listening Recall subtest; (b) Inquisit Corsi Blocks (Inquisit 3, 2003) was included as a measure of span; and (c-f) four n-back measures were used, from the same platform (Inquisit 3, 2003); two that utilized letters versus complex (un-nameable) shapes, and each had a 1-back and 2-back version. Inhibition used: (a) Inquisit Cued Go-No-Go task (Inquisit 3, 2003); and (b) Stop Signal task (Inquisit 3, 2003). Shifting used specific components of four tests of the Delis-Kaplan Executive Function System (D-KEFS; Delis et al., 2001) that required alternation: (a) Design Fluency; (b) Verbal Fluency; (c) Color-Word Identification Test; and (d) Trail Making Test. Planning was assessed with: (a) Tower of London (Inquisit 3, 2003); and Woodcock-Johnson-III Planning subtest (Woodcock, McGrew & Mather, 2001). Generative Fluency used three D-KEFS (Delis et al., 2001) fluency measures (Letter Fluency, Category Fluency, Design Fluency) that did not require alternation. Self-Regulated Learning was assessed with three subscales (self-efficacy and effort, strategies, and perceived skill and preference for reading) derived from a prior factor analytic study of the Contextual Learning Scale (Author, 2012), a self-report measure derived from previously used and novel items. Metacognition was assessed with teacher-reported subscales (Initiate, Monitor, Planning/Organization, and Working Memory) of the Metacognition Index from the Behavioral Rating Inventory of Executive Function (BRIEF; Gioia et al., 2000), and with teacher ratings of the Inattention subscale of the Strengths as Weaknesses of Attention-deficit hyperactivity disorder symptoms and Normal behavior (SWAN, Swanson et al., 2006). Behavioral Regulation was also assessed with the BRIEF (Gioia et al., 2000) and the SWAN (Swanson et al., 2012), using alternate subscales (Inhibit, Shift, and Emotional Control from the BRIEF, and Hyperactivity/Impulsivity from the SWAN).

Planned Missing Data

The current study reports on 27 different measures, and it was not feasible to administer all measures to all students. Rather than restrict the number of measures (and reduce construct coverage), we opted to decrease some covariance coverage (the number of students that had data for any pair of measures to establish their relationships). Missing data are problematic if they are not missing completely at random (MCAR) or missing at random (MAR) (Rhemtulla & Little, 2012; Rubin, 1976). We empirically tested the tenability of the MCAR assumption using Little’s MCAR test (Little, 1988), and the results suggested that the data were not MCAR (χ² (1927) = 2105.27, χ²/df = 1.09p = 0.03). However, MCAR is a stringent assumption which may not be tenable in practice (Muthén, Kaplan & Hollis, 1987; Rhemtulla & Hancock, 2016). Modern methods for handling missing data, such as full information maximum likelihood (FIML), allow MCAR assumptions to be relaxed to allow for data to be MAR such that the likelihood of missingness on a given variable is conditional on other variables in the data (Enders & Bandalos, 2001). The primary issue is power, which is ameliorated with FIML (Little, Jorgensen, Lang, & Moore, 2013), so that all observations, measures, and available data points are utilized. Therefore, we followed these techniques in the present study. The specific method we used was a variant of the multiform approach (Rhemtulla & Little, 2012). Students were randomly assigned within grade to receive a “pattern” of tests. In practical terms, 9 of the 19 different tests were included in all patterns (though some missingness within pattern was also randomly assigned for three measures). There were six patterns (see Table 1) that produced covariance coverage of 15% to 98% for any pair of variables, and the proportion of students who received each pattern was similar, (e.g., overall and within grade p = .981 and p = .990, respectively). A proportion of students in grade 4 were designated as limited English proficiency, though each pattern also included similar proportions with and without this status, p = .938.

Procedures

Performance data were collected in schools by well-trained examiners with on-site supervision, primarily in Fall; teacher-rated measures were collected in late Spring. All performance based measures were collected individually; group-administration was used for student rating scales and for the screening measure of reading. Total assessment time was approximately 4 hours, distributed across 4 or 5 sessions typically distributed across a week. Test orders within the randomly assigned patterns were not fixed. All research procedures were approved by participating Institutional Review Boards.

Analytic Approach

Variable distributions and outliers were specifically evaluated. Where issues with test administration or scoring were flagged, source documents and observations were examined for serious concerns regarding data appropriateness. This resulted in 84 data points being trimmed (set to missing). Also, if performance was well outside typical bounds (+/− 3 SD and ~ 0.5 SD from the next nearest score) then data were Winsorized (placed just beyond the next nearest value and so maintaining rank ordering) similar to criteria used elsewhere (Willcutt, Pennington, Olson, Chhabildas, & Hulslander, 2005); this was true for 46 additional data points. It should be noted that these 130 data points comprised only 0.83% of the total number of points available for analyses. The Stop Signal Test was an exception; here, 161 data points were excluded due to aberrant performance; cutoffs (Schachar, Mota, Logan, Tannock, & Klim, 2000) were less than 67% correct on go trials (n=116), and/or less than 12.5% correctly inhibited stop trials (n = 21); 24 students met both cutoffs. There were no differences between students whose Stop Signal score was versus was not included, in terms of pattern received, grade, age, sex, race, economic disadvantage, or limited English proficiency status (all p > .05), although those who were excluded had lower vocabulary scores than those whose scores remained, p = .008, d = .24).

For all analyses, a “weight” was assigned to each observation. Because of oversampling for reading difficulty in grade 4, reading scores in this grade (and presumably, correlates of reading skill) would be systematically lower than expectation. Weighting applied during analyses has the effect of decreasing the impact of the oversampled group on the overall mean, which in turn becomes more representative of the population from which they were drawn (in our case, the 19 schools across three school districts with whom we worked). Weighting has its largest effects on means, which was less relevant for the purposes of the present study, but it can also impact covariances. However, it should be noted that we also ran our final models with and without weighting and results were highly similar. Specific details regarding weighting appear in Supplement 3.

The primary analytic technique was factor analyses. Our proposed framework was designed to consider the eight domains in a confirmatory factor analytic (CFA) measurement model as well as its counterpart bifactor model. We ran models in MPlus v 7.1 (Muthén & Muthén, 2012) with robust full-information maximum-likelihood estimation to establish model fit. These models revealed several obvious sources of misfit, the details of which are presented in Supplement 3; for brevity, the final model is emphasized below. We evaluated the fit of all models at both the global and local level. For global fit, we used common measures, and accepted cut-offs (Hu & Bentler, 1999; Kline, 2011): Comparative Fit Index (CFI) and Tucker-Lewis Index (TLI) > .90 to .95; χ²; root mean squared error of approximation (RMSEA < .06), and squared root mean residual (SRMR < .08). For local fit, we examined parameters such as loadings, standard errors and residuals. In all models, indicators were scaled so that higher scores were associated with better performance. For comparison to methodological models and other model comparisons, we used χ² differences, and changes in global measures such as Akaike Information Criteria (AIC), Bayesian Information Criteria (BIC) and Adjusted BIC (of ~ 10; Burnham & Anderson, 2004). Once all models has been evaluated, we correlated age, sex, economic disadvantage, and English proficiency status with the factors to evaluate their relations.

Results

Table 1 presents the means, standard deviation, skewness and kurtosis values for each measure. Table S2 presents the correlations among measures.

Common Factor Models

Model specifications and fit statistics for four common factor models are reported in Table 2. The first model (Model 1a) evaluated the eight proposed latent variables, and was a poor fit to the data due to latent variables that were too strongly correlated. The revised model (Model 1b) fit the data much better, but the Working Memory (WM) correlated strongly with several others, and factor loadings suggested a distinction among measures of span and manipulation, versus updating. This is in line with recent debate about the extent to which these two types of tasks are more similar versus different (Schmiedek, Hildebrandt, Lovden, Wilhelm, & Lindenberger, 2009; Redick & Lindsey, 2013; Schmiedek, Lovden, & Lindenberger, 2014). Therefore, we separated the original WM factor into separable components of Span/Manipulation (WM-S/M) versus Update (WM-U). This model (Model 2a) did not converge, as the span and manipulation WM factor was strongly correlated with Shifting, and so were combined, resulting in a final common factor model (Model 2b) with seven factors: (1) WM-S/M with Planning; (2) WM-U; (3) Inhibition; (4) Shifting; (5) Generative Fluency; (6) Self-Regulated Learning; and (7) Metacognition (MCOG). Further details regarding model revisions are in Supplement 3. Table 1 provides maximal reliabilities (ρ*, Raykov & Hancock, 2005) from Model 2b; as expected, factor reliabilities were better than the reliability of any separate indicator. It was also the case that factors with more reliable indicators had higher maximal reliability; the only noticeably low value was for Inhibition (ρinhibition= 0.54). Table 3 contains common factor intercorrelations.

Table 2.

Model fit indices.

Model	AIC	BIC	ABIC	χ2	df	RMSEA [CI]	CFI	TLI	SRMR	χ2 diffa	χ2 diffb
Preliminary Hypothesized CFA Models
Model 1a - 8 factors	45582.57	46170.39	45776.60	2203.37	436	0.069 [.066, .072]	0.80	0.77	0.08
Model 1b - 7 factors	42251.91	42735.44	42411.52	851.56	303	0.046 [.043, .050]	0.90	0.89	0.08
Correlated Hypothesized CFA Factors
Model 2a - 8 factors	42133.71	42650.43	42304.28	742.42	296	0.042 [.038, .046]	0.92	0.91	0.06
Model 2b - 7 factors	39423.83	39907.36	39583.44	748.57	303	0.042 [.038, .045]	0.92	0.91	0.06	6.46c
Contrastive CFA Models
Model 3a - 1 factor	43954.46	44338.44	44081.21	2279.01	324	0.080 [.081, .088]	0.66	0.63	0.13	1526.31**	1530.44**
Model 3b - 2 factors (P,R)	43060.74	43454.21	43190.62	1536.48	322	0.067 [.063, 070]	0.79	0.77	0.09	897.14**	955.36**
Model 3c - 3 factors (P,S,T)	42382.97	42785.92	42515.98	980.42	320	0.049 [.046, .053]	0.89	0.87	0.08	239.98**	237.28**
Model 3d - 3 factors (PC,PP,R)	42992.36	43390.56	43123.80	1488.85	321	0.066 [.062, .069]	0.80	0.78	0.09	663.44**	631.51**
Model 3e - 4 factors (PC,PP,S,T)	42312.60	42725.03	42448.74	925.23	318	0.048 [.044, .051]	0.89	0.88	0.08	157.84**	140.32**
Model 3f - 3 factors (PVe, Pvi, R)	43013.03	43411.24	43144.48	1502.02	321	0.066 [.063, .069]	0.79	0.78	0.09	737.13**	728.72**
Model 3g - 4 factors (PVe, PVi, S, T)	42329.95	42742.38	42466.09	937.55	318	0.048 [.044, .052]	0.89	0.88	0.09	176.96**	162.55**
Bifactor Model
Model 4 - 5 specific factors	39301.57	39785.11	39461.19	649.31	303	0.037 [.033, .041]	0.94	0.93	0.07	−62.13**	n/ad

Note. AIC = Akaike’s Information Criterion; ABIC = Adjusted Bayesian Information Criterion; BIC = Bayesian Information Criterion; CFI = Comparative Fit Index; Chi sq. = Chi square; RMSEA = Root Mean Square Error of Approximation; SRMR = Standardized Root Mean Square Residual. TLI = Tucker Lewis Index. P = any performance measure; PC = computer performance; PP = paper performance; R = any report rating; S = self-report; T = teacher report; PVe = verbal performance; PVi = visual performance.

^**p < 0.001;

^aSatorra-Bentler scaled chi-square difference test versus Model 2a; Model 2a produced a non-positive definite covariance matrix and fit details are provided only for completeness.

^bSatorra-Bentler scaled chi-square difference test versus Model 2b

^cSatorra-Bentler scaled chi-square difference test for Model 2a vs. Model 2b

^dThe Satorra-Bentler scaled chi-square difference test could not be computed for Model 4 versus Model 2b because both models estimated the same number of parameters (df = 303).

Table 3.

Correlations among factors for the CFA models with 8 factors (Model 2a; below diagonal) and 7 factors (Model 2b; above diagonal).

	WM-S/M	WMU	INHIBIT	SHIFT	PLANa	FLUENCY	SRL	MCOG
WMU	0.17	–	0.63	0.25	0.26	0.07	−0.03	0.23
INHIBIT	0.71	0.65	–	0.62	0.55	0.25	0.03	0.30
SHIFT	0.92	0.25	0.63	–	0.87	0.80	−0.06	0.37
PLANa	0.96	0.29	0.46	0.81	–	0.64	−0.19	0.43
FLUENCY	0.66	0.06	0.25	0.80	0.61	–	−0.10	0.17
SRL	−0.22	−0.03	0.03	−0.07	−0.17	−0.10	–	0.12
MCOG	0.42	0.23	0.31	0.37	0.43	0.17	0.12	–

Note. Factor names: WM-S/M = Working Memory as Span/Manipulate; WMU= Working Memory as Updating; INHIBIT = Inhibition; SHIFT = Shifting; PLAN = Planning; SRL = Self-Regulated Learning; MCOG = Metacognition.

^aAs column header, PLAN represents the Working Memory as Span/Manipulate and Planning factor for Model 2b; as a row header, PLAN represents only the original Planning indicators. r’s < |.16| not significant; r’s > |.16| significant at 0.05.

With Model 2b finalized, we compared this to alternative models, including a bifactor analogue. A unitary model (Model 3a) was considered, one that is nested within Model 2b (using the same 27 indicators of Table 1). The unitary model was a substantially worse fit relative to Model 2b. A variety of methodological models were also evaluated and each also produced a significantly worse fit to the data than Model 2b (see Table 2).

Bifactor Model

We had hypothesized that a bifactor model (Model 4) would fit the data better than its common factor analogue (Model 2b). The initial bifactor model did not converge because the Shifting and Inhibition specific factors did not identify their respective indicators (i.e., specific loadings were very low) in the context of a common EF factor. Therefore, these two specific factors were dropped leaving their indicators to load only on common EF. The final bifactor model (see Figure 1) had five specific factors (WM-S/M and Planning, WM-U, Generative Fluency, Self-Regulated Learning, and MCOG), and was clearly a better fit to the data than Model 2b by most criteria (e.g., χ² difference, change in CFI, AIC, and BIC).

Figure 1. Bifactor model with 5 specific and one general factors (model 4).

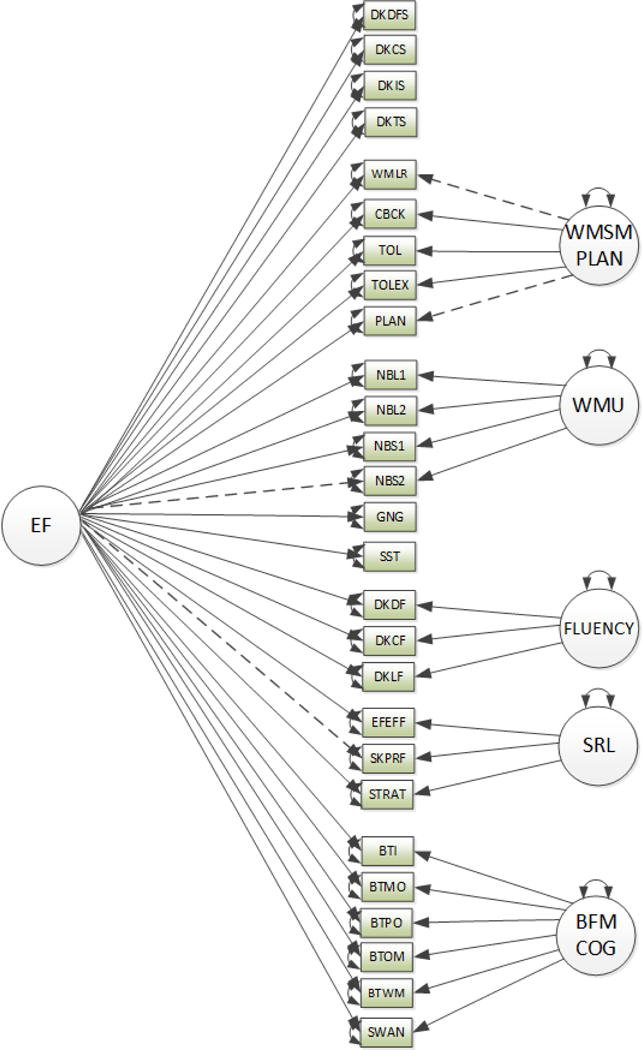
Note. DKDFS = D-KEFS Design Fluency Switching; DKCS = D-KEFS Verbal Fluency Category Switching; DKIS = D-KEFS Color Word Interference Inhibition Switching; DKTS = D-KEFS Trailmaking Test Letter-Number Switching; WMLR = WMTB-C Listening Recall; CBCK = Corsi Blocks Backwards Recall; TOL = Tower of London Accuracy; TOLEX = Tower of London Extra Moves; PLAN = WJ-III Planning; NBL1 = n-back 1 Letter; NBL2 = n-back 2 Letter; NBS1 = n-back 1Shape; NBS2 = n-back 2 Shape; GNG = Go No-Go; SST = Stop Signal Task; DKDF = D-KEFS Design Fluency Filled+Empty Dots; DKCF = D-KEFS Verbal Fluency Categories; DKLF = D-KEFS Verbal Fluency Letters; EFEFF = CLS Effort/Self-Efficacy; SKPRF = CLS Skill/Preference; STRAT = CLS Learning Strategies; BTI = BRIEF Initiate; BTMO = BRIEF Monitor; BTPO = BRIEF Planning/Organization; BTOM = BRIEF Organization of Materials; BTWM = BRIEF Working Memory; SWAN = SWAN Inattention.

WM-S/M = Working Memory as Span/Manipulate; WMU= Working Memory as Updating; SRL = Self-Regulated Learning; MCOG = Metacognition.

Solid lines = statistically significant at the p < 0.05 level; dashed lines = not statistically significant; rectangles = measured variables; circles = latent variables; double-headed arrows = variances; single-headed arrows = loadings

Table 4 shows the pattern of loadings for common EF and specific factors of Model 4. Loadings were stronger for the indicators of three specific factors (WM-U, Self-Regulated Learning, and MCOG) relative to the common EF factor. Conversely, loadings were higher for the specific WM-S/M and Planning factor. Fluency factor loadings were intermediate but generally larger for common EF. Indicators of Shifting and Inhibition loaded only on the common EF factor, though these were larger and more consistent for Shifting relative to Inhibition. Maximal reliabilities were also computed for the specific factors and the general EF factor from Model 4. From Model 2b to Model 4, reliability was highest for the EF factor (ρ_EF=0.97), and was also high for three of the specific factors from Model 4 (ρ_WMU= 0.82, ρ_self-regulation=0.84, and ρ_meta-cognition= 0.97). Reliability was moderate for two specific factors (ρ_WMSMρ_WM/planning = 0.66, and ρ_fluency= 0.79). The average intercorrelation among all 27 indicator variables (see Table S2) was r = .17 (median r = .15), though the intercorrelations within each of the specific factors that remained in the bifactor model were appreciably higher (WM/SM and Planning, median r = .28; WMU = .41; SRL = .52; Generative Fluency = .32; MCOG = .77).

Table 4.

Standardized solution for Models 2a, 2b and 4.

	CFA (8 factors) Model 2a	CFA (7 factors) Model 2b	Bifactor (with 5 specific factors) Model 4
	Loading (SE)	Loading (SE)	Loadings (SE)	EF Loadings (SE)
Shifting
DKDFS	0.49 (0.06)	0.52 (0.05)		0.45 (0.06)
DKCS	0.52 (0.05)	0.55 (0.05)		0.54 (0.05)
DKIS	0.73 (0.05)	0.48 (0.06)		0.71 (0.04)
DKTS	0.55 (0.05)	0.73 (0.05)		0.58 (0.05)
WM-S/M + Plan
WMLR	0.60 (0.10)	0.61 (0.05)	0.02 (0.10)	0.60 (0.04)
CBCK	0.60 (0.10)	0.61 (0.05)	0.27 (0.11)	0.49 (0.06)
TOLa	0.45 (0.05)	0.43 (0.04)	0.54 (0.15)	0.34 (0.04)
TOLEXa	0.52 (0.05)	0.49 (0.04)	0.34 (0.10)	0.41 (0.04)
PLANa	0.51 (0.04)	0.51 (0.04)	0.09 (0.08)	0.48 (0.04)
WMU
NBL1	0.78 (0.07)	0.78 (0.08)	0.73 (0.09)	0.22 (0.08)
NBL2	0.58 (0.08)	0.58 (0.08)	0.57 (0.09)	0.19 (0.07)
NBS1	0.63 (0.08)	0.64 (0.09)	0.57 (0.12)	0.15 (0.06)
NBS2	0.52 (0.09)	0.51 (0.09)	0.57 (0.12)	0.05 (0.06)
Inhibition
GNG	0.53 (0.09)	0.36 (0.08)		0.18 (0.06)
SST	0.53 (0.09)	0.55 (0.09)		0.34 (0.04)
Fluency
DKDF	0.51 (0.04)	0.51 (0.04)	0.14 (0.05)	0.48 (0.04)
DKCF	0.69 (0.03)	0.69 (0.03)	0.72 (0.21)	0.46 (0.04)
DKLF	0.69 (0.04)	0.69 (0.04)	0.38 (0.12)	0.53 (0.04)
Self-Regulated Learning
EFEFF	0.71 (0.04)	0.71 (0.04)	0.75 (0.03)	0.18 (0.05)
SKPRF	0.58 (0.04)	0.59 (0.04)	0.72 (0.21)	−0.06 (0.05)
STRAT	0.90 (0.04)	0.90 (0.04)	0.38 (0.12)	−0.18 (0.04)
Metacognition
BTI	0.93 (0.01)	0.93 (0.01)	0.84 (0.02)	0.42 (0.05)
BTMO	0.88 (0.01)	0.88 (0.01)	0.84 (0.02)	0.28 (0.05)
BTPO	0.96 (0.01)	0.96 (0.01)	0.89 (0.02)	0.37 (0.05)
BTOM	0.80 (0.02)	0.80 (0.02)	0.77 (0.02)	0.23 (0.05)
BTWM	0.95 (0.01)	0.95 (0.01)	0.88 (0.02)	0.36 (0.05)
SWAN	0.81 (0.02)	0.81 (0.01)	0.71 (0.03)	0.40 (0.04)

Note. DKDFS = D-KEFS Design Fluency Switching; DKCS = D-KEFS Verbal Fluency Category Switching; DKIS = D-KEFS Color Word Interference Inhibition Switching; DKTS = D-KEFS Trailmaking Test Letter-Number Switching; WMLR = WMTB-C Listening Recall; CBCK = Corsi Blocks Backwards Recall; TOL = Tower of London Accuracy; TOLEX = Tower of London Extra Moves; PLAN = WJ-III Planning; NBL1 = n-back 1 Letter; NBL2 = n-back 2 Letter; NBS1 = n-back 1Shape; NBS2 = n-back 2 Shape; GNG = Go No-Go; SST = Stop Signal Task; DKDF = D-KEFS Design Fluency Filled+Empty Dots; DKCF = D-KEFS Verbal Fluency Categories; DKLF = D-KEFS Verbal Fluency Letters; EFEFF = CLS Effort/Self-Efficacy; SKPRF = CLS Skill/Preference; STRAT = CLS Learning Strategies; BTI = BRIEF Initiate; BTMO = BRIEF Monitor; BTPO = BRIEF Planning/Organization; BTOM = BRIEF Organization of Materials; BTWM = BRIEF Working Memory; SWIN = SWAN Inattention. WM-S/M = Working Memory as Span/Manipulate; WMU = Working Memory as Updating.

^aThese variables were indicators of the planning factor in Model 1.

Individual and Group Differences

With the finalized structural model, we related the resultant general and specific EF factors to demographic factors of age, economic disadvantage, sex, and language proficiency status. The model converged but the robust chi-square was not computable, though SRMR = .063, and parameter estimates were provided, which were of primary interest.

Age was positively correlated with general EF, r = .38, p < 0.001, and negatively correlated with specific Metacognition, r = −.19, p < 0.001 factors. All other age correlations were smaller in magnitude (range r = |.03 to .09|) and non-significant. Economic disadvantage correlated negatively with EF, r = −.20, p = 0.003, such that receipt of free lunch was associated with lower EF performances; there were no significant relations with other factors. Sex was positively correlated with WM-U, r = .15, p = 0.017; with SRL, r = .14, p = 0.001; and with Metacognition, r = .27, p < 0.001. These correlations were modest and conferred a slight advantage for girls; for WM-S/M and Plan, and for Fluency, advantages for boys were of similar magnitude (r = −.13 and r = −.14, respectively), though neither were significant. Finally, for students designated as having limited English proficiency, their performances were lower on EF, r = −.26, p < 0.001, and Fluency, r = −.25, p = 0.009, but higher on WMU, r = .22, p < 0.001, with no significant differences on other specific factors. The correlational pattern was strongly similar when computed within the structural framework versus when factor scores were exported and correlations were computed externally, except that the relations of fluency with age and sex, while directionally the same as those above and similar in value, were now significant.

Discussion

The goal of this study was to evaluate a framework for EF. A unique contribution of this study is the comprehensiveness with which EFs were measured to encompass different conceptualizations across different academic literatures, in latent variable fashion, in a large sample in a key school-age range. The best-fitting model included a common EF factor in addition to five distinguishable factors: Working Memory as Span/Manipulate with Planning (WM-S/M and Planning); Working Memory as Updating (WM-U); Generative Fluency; Self-Regulated Learning (SRL); and Metacognition (MCOG).

Results supported the hypothesized framework in that: (a) most indicators had adequate loadings on their hypothesized factor; (b) the bifactor model showed a better fit than a correlated factors model; (c) the SRL and MCOG factors showed higher loadings on their specific factor than that of common EF; (d) relations with demographic variables were generally predictable, particularly with regard to the common EF factor. However, on a number of other points, the originally hypothesized framework was not supported: (a) the indicators chosen did not allow for the separate measurement of MCOG and Behavioral Self-Regulation; (b) correlations among factors in Models 1a, 1b, and 2a were too strongly correlated; (c) indicators of WM-U showed unexpectedly strong specific loadings in the bifactor context; (d) latent factors of both Shifting and Inhibition were not identifiable outside of the common EF factor; and (e) relationships of the final specific factors with covariates were more sparse, and weaker, than anticipated.

The structural pattern of this study is partially consistent with a number of other factor analytic studies, though the number and range of EF-related constructs considered here is larger than prior work. We were unable to replicate either the preschool structure of EF as a unitary factor, nor the well-known triumvirate of Shifting, Updating, and Inhibition (Miyake et al., 2000). Prior attempts to reproduce this three-factor structure, even when expressly attempted, often show some inconsistency. For example, in van der Sluis, de Jong, and van der Leij (2007), an inhibition factor was not identified; in van der Ven, Kriesbergen, Boom, and Leseman (2012) with younger children, an inhibition and shifting factor were combined. In twin studies, Friedman et al. (2008) found that inhibition correlated robustly (r = .73) with both shifting and updating; in their hierarchical genetic analysis, inhibition had a perfect correlation with Common EF, and in nested (bifactor) analyses, their indicators of inhibition were subsumed in Common EF. Lee et al. (2013) also found that factors of shifting and inhibition were generally combined from ages 6 to 15 (when the three factors were separable). Finally, where studies have clearly considered working memory from the perspective of both updating (e.g., n-back) and storage/maintenance (e.g., listening recall) (Engelhardt et al., 2015), these are found to be separable, at least in children. This issue has been previously considered in meta-analyses that show quite weak correspondence between these two types of measures (Redick & Lindsey, 2013) whereas latent variable models show more overlap (Schmiedek et al., 2009; 2014); although unlike Engelhardt et al. (2015), these studies were with adults. The present results are intriguing but there is a strong need for more work regarding the separation of these factors theoretically and empirically, as well as their relation to outcomes.

How Unitary is EF?

The present study is unable to conclude that indicators of EF are interchangeable and each contributes similarly to a unitary factor; it is also unable to conclude that hypothesized factors are separable and non-overlapping. That neither is clearly true supports the “separate but related” perspective on EF (Miyake et al., 2000). However, the pattern of structural relations in this study helps to clarify which posited EFs are more “separable” and which are more “related”.

Separable EFs

There was a clear distinction among latent variables of: (a) SRL; (b) MCOG; and of (c) several performance measures of EF. That these types of measures arise from more or less different literatures is interesting. Because evaluation of the relationships among these different kinds of variables is somewhat confounded by measurement, it is unclear what drives their differentiation – their method of ascertainment or a fundamental difference in constructs. Where all indicators share a common platform (e.g., all computerized, or all timed, or all experimental, or all from the same co-normed battery), separation may be easier, but combining methods is very common in clinical settings. In single-group predictive or causal-comparative studies, different types of measures contribute differentially and in complementary fashion (e.g., Richardson, Abraham, & Bond, 2012; Gerst, Cirino, Fletcher, & Yoshida, 2017). This issue of methodological variance may have played a role in other studies as well. For example, in Lee et al. (2013), one of their factors (working memory) consisted of accuracy scores, whereas the other factor (combining switch/inhibit) was predominantly assessed with response-time measures. However, a critical finding in the present study was that a contrastive model that only considered mode of administration was a substantially worse fit to the data than the hypothesized model (see Table 2), suggesting that the potential viability of the specific EF constructs identified here is not solely due to measurement. More directed structural studies, along with future validity studies, are warranted to sort out the relative utility of this EF disaggregation by measurement type versus construct.

Common EF

However separable EF factors may be, the results of this study suggest there is also some value in considering EF from a more general perspective. A common EF has potential to (literally) unite different and sometimes competing theoretical conceptualizations of EF. To the extent that a common EF can be reliably and robustly measured, it may be possible to choose indicators that most closely tap into it. For example, in the present study, measures of Shifting, Working Memory (as span/manipulation), Planning, and Generative Fluency had robust loadings on the primary EF factor. Even at the specific level, the combination of WM(S/M) with Planning also makes sense conceptually since the act of planning requires simultaneous representation and manipulation of potential action sequences, along with a judgement as to their relative success. Future studies may attempt to ascertain how minimally the common EF factor can be assessed without losing structural identification or predictive power.

The relatively weak interrelationships among the indicator variables (median r = .15, see Table S2) were initially unexpected, and prompted a secondary review of prior factor analytic studies. For example, the ten tasks in Wiebe et al. (2008) had a median intercorrelation of r = .28; for the nine tasks in Miyake et al. (2000), r = .13; for the nine tasks in Lee et al. (2013), r = .33 (without partialling their control tasks); and for the 14 tasks in Lehto et al. (2003), r = .23. This range is especially noteworthy as those studies span the age range, utilize different combinations of measures, and come to somewhat different conclusions regarding the structure of EF.

Capitalizing on Knowledge Related to EF

The purpose of EF is to manage goal-directed behavior. Data that speak to the way in which EF can be used for this purpose come from at least three types of studies: (a) structure; (b) relations to other variables; and (c) mechanism and intervention.

Structure

The framework of the present study is fundamentally about how the structure of EF broadly construed can be aggregated versus disaggregated in this age/grade range. Thus structure describes EF; other forms of description include the identification of brain regions implicated in EF performance, or how groups of patients or other subgroups of individuals differ from one another on one or more aspects of EF. Description is key for complex or difficult-to-grasp constructs, which is clearly apt for EF (it is difficult to discuss “the EF, the whole EF, and nothing but the EF”). In the present study we chose to focus the impact on synthesizing diverse ways of referencing this construct. What remains less clear is whether the pattern of loadings found in this study holds up in other populations, particularly in neurodevelopmental disorders or acquired neurological disorders – given that some of these are explicitly associated with or defined by changes in the brain. It is also unclear whether different sets of measures would produce the same set of broad and specific factors. A firmer understanding of the structure of EF is relevant to its practical utility, and can be quite useful in enhancing communication within or across fields, much as the study of Miyake et al. (2000) focused discussion of EF around their three core components of Shifting, Inhibition, and Updating. We view the present study as expanding discussion beyond these three factors in the context of one another.

Relations to Other Variables

In the present study, we focused on demographic characteristics. We found a predictable, positive relationship of the common EF factor with age (r = .38) which is robust, even though the age range, albeit important, was not large. This is consistent with prior studies that show relation of EF with age (Engelhardt et al., 2015; Wiebe et al., 2008). The common EF factor also showed predictable (negative) relationships with economic disadvantage (Raver, 2004; Raver et al., 2013), and with limited English proficiency (Abedi, 2002). It is not particularly surprising that girls were rated as having stronger MCOG than boys, given the well-known elevated rates of attentional and related difficulties for boys relative to girls (DuPaul, et al., 1997; Gershon & Gershon, 2002). Although there is little data with which to compare current results, given the need for English proficiency on an (English) verbal fluency task, it is also not particularly surprising that a negative correlation of performance and limited English proficiency was noted (r = −.26).

It is less clear why there was a significant negative relation of age and MCOG (r = −.19), implying that older students have less developed skills in this area, since the expectation would be that an increase in age produces an increase in meta-cognition. It should be noted that the absolute value of this relationship was not strong, and that the raw indicator scores showed no significant relation with age; also the relation with age was reduced in absolute size when the sample was not weighted. Notably, the MCOG factor is derived to be uncorrelated with all other latent variables, both specific and common, and therefore, its relationship is closer to a beta weight then a zero-order correlation, since any shared variance is attributed to the common EF factor. A second less expected (directionally opposite) relation was found between Working Memory (as updating) for students with limited English proficiency (r = .22), where such students exhibited stronger performance. The raw scores produced somewhat similar patterns. It is possible to interpret this albeit small effect in light of the “bilingual advantage” literature, where it has been suggested that bilingual individuals have improved EF performances (Bialystock, 1999; see Morton & Harper, 2007, and Paap & Greenberg, 2013), but two caveats may be in order. First, the bilingual advantage is typically associated with individuals who excel at both languages, whereas the students in the present study by definition do not; some of the students are bilingual in the sense that they have skills in both languages, but they are still in the process of learning English, even though their instruction occurs in English. Second, all the students with limited English proficiency were in the fourth grade and all were struggling readers.

Mechanism and Intervention

Beyond structure/description and relation to other variables, it is critical to understand how and/or why EF operates to manage goal-directed behavior. Descriptive studies, even those with large sample sizes and theoretically driven and comprehensive measures, cannot provide information relevant to mechanism and causal direction. In contrast, experimental studies, including intervention studies, allows for a recognition of key ingredients and how they might be implemented and for whom, particularly within populations where EF is compromised, or where it is more strongly related to outcomes – for example, academic achievement (Best, Miller, & Naglieri, 2011; Biederman et al., 2004). In their review, Jacob and Parkinson (2015) found clear and consistent relationships between EF and academic achievement, but interventions designed to improve EF had little generalizability for improving achievement. Although the structural framework of EF and how it relates to other variables can set the parameters for other types of studies, an understanding of this mechanism is needed for (and is testable by) interventions designed to affect that mechanism (see for example, recent work by Fuchs, Fuchs, & Malone, 2016).

Limitations and Conclusions

One potential limitation is how the nature of the sampling plan impacts generalizability. Students with reading difficulty were oversampled (purposefully). Weights were applied to individuals’ data so that the overall contributions from the oversampled students were in proportion to their distribution in the schools as a whole. However, there is no rationale to hypothesize a different pattern of relationships based on level of performance. In addition, weighting is common in large scale national samples to increase verisimilitude to the population. A second limitation is that while it would have been ideal to administer all measures to all students, this was not practicable. Indeed, it would also be ideal to administer more measures (e.g., wider coverage of working memory). Similarly, including both performance and rating measures of metacognition would have been interesting, particularly in light of the weak correlations between these kinds of measures with regard to EF generally (e.g., Gerst et al., 2017; Toplak, West, and Stanovich, 2013). In this study, we opted to increase construct coverage at the cost of covariance coverage. However, the missingness was planned (by design) via randomization and so did not bias structural loadings (Rhemtulla & Little, 2012). Finally, EF structure was not evaluated in a multilevel context; however, accounting for nesting effects would be important to address where EF is used to predict outcomes, particularly those that are instructed (e.g., reading).

In spite of these limitations, the present study benefitted from a large, diverse sample, and the statistical approach was inclusive and confirmatory, examining both correlated factors and bifactor models. The best-fitting model was a bifactor model with a common EF factor, and specific factors of (a) Working Memory (as storage/maintenance) combined with Planning; (b) Working Memory (as updating); (c) Generative Fluency; (d) Self-Regulated Learning; and (e) Metacognition. This model speaks to both the robustness of a general factor of EF, but also to the potential separable impact of specific EF factors.

Public Significance.

Terms such as executive function (EF) are used in many different ways by different scientists as well as different professional and commercial interests. The present study brings together many of the ways that EF is operationalized across these literatures and other arenas. There is more commonality, but also some separability, across these different operationalizations, which has implications for its conceptualization and use.