A novel metric that quantifies risk stratification for evaluating diagnostic tests: The example of evaluating cervical-cancer screening tests across populations

Abstract

Our work involves assessing whether new biomarkers might be useful for cervical-cancer screening across populations with different disease prevalences and biomarker distributions. When comparing across populations, we show that standard diagnostic accuracy statistics (predictive values, risk-differences, Youden’s index and Area Under the Curve (AUC)) can easily be misinterpreted. We introduce an intuitively simple statistic for a 2×2 table, Mean Risk Stratification (MRS): the average change in risk (pre-test vs. post-test) revealed for tested individuals. High MRS implies better risk separation achieved by testing. MRS has 3 key advantages for comparing test performance across populations with different disease prevalences and biomarker distributions. First, MRS demonstrates that conventional predictive values and the risk-difference do not measure risk-stratification because they do not account for test-positivity rates. Second, Youden’s index and AUC measure only multiplicative relative gains in risk-stratification: AUC=0.6 achieves only 20% of maximum risk-stratification (AUC=0.9 achieves 80%). Third, large relative gains in risk-stratification might not imply large absolute gains if disease is rare, demonstrating a “high-bar” to justify population-based screening for rare diseases such as cancer. We illustrate MRS by our experience comparing the performance of cervical-cancer screening tests in China vs. the USA. The test with the worst AUC=0.72 in China (visual inspection with acetic acid) provides twice the risk-stratification (i.e. MRS) of the test with best AUC=0.83 in the USA (human papillomavirus and Pap cotesting) because China has three times more cervical precancer/cancer. MRS could be routinely calculated to better understand the clinical/public-health implications of standard diagnostic accuracy statistics.

Introduction

After a new biomarker is convincingly associated with disease, a next question is to assess preliminarily, without enumerating costs/benefits/harms, whether the new biomarker is predictive enough to justify formal cost-effectiveness analyses that determine clinical/public-health use. For example, our work involves assessing whether new biomarkers might be useful for cervical-cancer screening in low/middle/high-resource populations, across which both disease prevalence and biomarker distributions vary substantially¹.

Unfortunately, standard metrics reported for binary biomarkers provide at best indirect information about predictiveness for clinical/public-health use. The odds-ratio is a well-known poor measure of predictiveness². When comparing two tests, it is uncommon for one test to have both higher sensitivity and specificity, or both higher positive predictive value (PPV) and negative predictive value (NPV). Two summary statistics, Youden’s Index ³ and the Area Under the Curve (AUC) statistic⁴, have been correctly criticized for not taking predictive values (i.e. absolute risks) into account, and for not permitting differential weighting of false-positives versus false-negatives⁵. AUC is the probability that someone with disease has higher risk than someone without disease, which requires only the risk ranks, not the absolute risks ⁴. Although AUC is used for continuous biomarkers, because the AUC for a binary test is a function of only Youden’s Index⁶, criticisms of Youden’s index also apply to AUC.

To better understand the implications of standard diagnostic accuracy metrics for clinical/public-health utility, we reinterpret standard metrics in light of a novel framework for quantifying risk-stratification. Although “risk-stratification” is a broadly used term, we define it as the ability of a test to separate those at high risk of disease from those at low risk⁷, allowing clinicians to intervene only for those that testing indicates are more likely to develop disease. We introduce two new broadly applicable, linked statistics that have proven useful in our epidemiologic work. We define mean risk-stratification (MRS) as the average change in risk of disease revealed by a test (post-test minus pre-test). We also define a complementary statistic, the Number Needed to Test (NNtest), which quantifies how many people require testing to identify one more disease case than would be identified by randomly selecting people for testing. All statistical details, including comparison to other statistics such as Decision Curves⁸, are in a preprint⁹. We have also used MRS to assess agreement between occupational exposure experts¹⁰.

MRS/NNtest have 3 advantages for comparing test performance across populations with different disease prevalences and biomarker distributions. First, PPV, NPV, and the risk-difference do not measure risk-stratification because they do not account for test-positivity rates, unlike MRS. That is, biomarkers that are rarely positive cannot provide much risk-stratification, regardless of how large the risk-difference is. Second, Youden’s index and AUC measure multiplicative relative gains in risk-stratification. However, large relative gains in risk-stratification might not imply large absolute gains if disease is rare. Third, the maximum MRS is limited by disease prevalence. Thus, little risk-stratification is possible for rare diseases such as cancer, demonstrating a “high-bar” to justify population-based screening. MRS/NNtest reinterpret the risk-difference, Youden’s index, and AUC, in the context of disease prevalence and biomarker distributions, which is crucial when considering test performance across populations. AUC cannot be used to rank tests between populations with different disease prevalence, and we show examples from our experience. Our webtool calculates MRS/NNtest (https://analysistools.nci.nih.gov/biomarkerTools/).

Background: Cervical-cancer screening tests

Human papillomavirus (HPV) causes almost all cervical cancer¹. HPV-based screening is replacing cervical cytology (“Pap smears”), but many new tests are available or being developed^11–12. For low/middle-income countries, a low-cost, but unreliable and inaccurate, test is visual inspection with acetic acid (VIA)^13,14. Screen-positive women by any test are referred for definitive disease ascertainment by colposcopy. To expedite screening guidelines development^15,16, we propose using MRS/NNtest to better identify potentially useful biomarkers.

To illustrate MRS/NNtest, we present data from 2 collaborations. Colleagues in China evaluated 3 tests (HPV testing, cervical cytology, and VIA) in an unscreened population of 30,371 women, to select a test as the basis for future nationwide screening¹⁷. Second, in support of US screening guidelines, we previously analyzed data on 331,818 women screened at Kaiser Permanente Northern California (KPNC) with cervical cytology, HPV testing, or both concurrently (“cotesting”)¹⁸.

Table 1 shows standard metrics for each test in China and KPNC. When comparing two tests in the same population, there is usually a tradeoff of sensitivity vs. specificity, or PPV vs. cNPV. This dilemma makes it hard to draw firm conclusions on the basis of any single statistic.

Table 1.

Characteristics of cervical screening tests in two populations: an unscreened population in China (1.6% precancer/cancer prevalence)¹⁷ and a previously heavily screened population in the USA at Kaiser Permanente Northern California (0.55% precancer/cancer prevalence)¹⁸. Acronyms: HPV (human papillomavirus), Pap (Papanicolaou Test), KPNC (Kaiser Permanente Northern California), VIA (visual inspection with acetic acid), PPV (positive predictive value), cNPV (complement of negative predictive value), Sens (Sensitivity), Spec (Specificity), LR+ (Likelihood Ratio positive), LR− (Likelihood Ratio negative), AUC (Area under the receiver operating characteristic curve), MRS (Mean Risk Stratification), NNtest (Number Needed to Test). Note that the odds ratio equals LR+/LR−.

(I moved VIA to the bottom of the China rows to make an easier eye comparison to Cotesting the USA. This also has the advantage of ordering the rows by MRS and NNtest. I didn’t put it in track changes because track changes marked up the whole page uselessly.)

Population	Cervical screening testing modality	Odds ratio	Test positivity	PPV	cNPV	Sens	Spec	LR+	LR−	Youden’s Index	AUC	MRS	NNtest
Unscreened population in China	HPV	206	17.3%	9.1%	0.05%	98%	84.0%	6	0.03	82%	91%	2.60%	77
	Pap	108	16.7%	9.4%	0.10%	95%	84.6%	6	0.06	80%	90%	2.60%	77
	VIA	11	10.7%	8.3%	0.83%	55%	90.1%	5	0.50	45%	72%	1.43%	140
Screened population KPNC (USA)	HPV/Pap Cotesting	37	7.5%	5.4%	0.16%	74%	92.9%	10	0.28	67%	83%	0.73%	275
	HPV	47	5.1%	7.6%	0.17%	70%	95.3%	15	0.31	65%	83%	0.71%	280
	Pap	13	3.8%	4.7%	0.36%	34%	96.3%	9	0.69	30%	65%	0.32%	633

Methods: Mean Risk Stratification (MRS) and Number Needed to Test (NNtest)

In the absence of test results or other pre-test information, each individual can only be assigned as a best guess the same population-average risk π=P(D+). After taking a test, people learn how their predicted individual risks differ from population-average. Two outcomes are possible:

1. With probability p=P(M+), the test is positive. The person’s risk increases from π=P(D+) to Positive Predictive Value (PPV=P(D+|M+)), an increase of PPV − π.

2. With probability P(M−)=1− p, the test is negative. The person’s risk decreases from π=P(D+) to complement of Negative Predictive Value: cNPV=1−NPV=P(D+|M−). The person’s risk decreases by π − cNPV.

Mean Risk Stratification (MRS) is a weighted average of the increase in risk among those who test positive and the decrease in risk among those who test negative:

$$\mathit{MRS}=\{\mathit{PPV}-\pi \}p+\{\pi -\mathit{cNP}V\}(1-p).$$ (1)

MRS is the average difference between predicted post-test individual risk and population-average (pre-test) risk. Simply, MRS is the average change in risk revealed by the test. Useful tests reveal that post-test risk is far enough from pre-test risk to justify changing management.

MRS also measures association of disease and marker. Denoting P(D+,M+) as a joint probability, and because the two terms on the right-hand side of MRS (1) are equal⁹, thus

$$\mathit{MRS}=2\{P(D+,M+)-P(D+)P(M+)\}.$$ (2)

MRS measures association as twice the covariance of disease and marker. MRS is zero if and only if disease and marker are not associated. MRS is between −0.5 and +0.5.⁹

An inverse expression of MRS is also useful. A test is only useful if it is substantially better than randomly identifying cases by sheer luck, for which the joint probability P(D+,M+) would equal P(D+)P(M+). The Number Needed to Test (NNtest), to identify 1 more disease case than by randomly selecting individuals for definitive disease ascertainment is

$$\mathit{NNtest}={\{P(D+,M+)-P(D+)P(M+)\}}^{-1}.$$

Thus, NNtest=2/MRS. Although MRS and NNtest convey the same information, they are on different scales. MRS is on the scale of absolute risk, allowing comparison to absolute risks of other diseases. NNtest presents test performance in terms of numbers of people tested, which helps with considering the benefits, harms, and costs associated with the test and interventions. NNtest is not the Number Needed to Treat (NNT), which is the reciprocal of the risk-difference: NNT=(PPV−cNPV)⁻¹. NNT conditions on test results, which is useful when exposures can be assigned, as in clinical trials. For deciding whether to screen a population, NNT is less relevant because test results cannot be assigned and the number testing positive is initially unknown.

For example, HPV testing in an unscreened population in China¹⁷ changed the risk of cervical precancer/cancer on average by MRS=2.6% (Table 1), which seems important because that is greater than precancer/cancer prevalence of 1.6%. In contrast, at KPNC, a heavily screened USA population, HPV testing had MRS=0.71%. A KPNC woman’s risk changed by only 0.71% on average by taking an HPV test, because cervical precancer/cancer prevalence is only 0.55% at KPNC. Similarly, only NNtest=140 Chinese women are required for VIA to identify 1 more precancer/cancer than would referring random women to colposcopy, versus the much higher NNtest=280 for HPV testing at KPNC, because disease is much more prevalent in China than at KPNC.

MRS/NNtest convey that cervical screening is less informative and efficient in the KPNC USA vs. China populations, due to previous screening and treatment reducing disease prevalence in the USA. Broadly, MRS/NNtest demonstrate inherent limits of screening for rare diseases like cancer¹⁹: although the few individuals testing positive may have large change in risk, the average change in risk following testing all individuals (the big majority of whom test negative) is modest. Hundreds may require screening to identify only one more disease case.

MRS has a simple formula for the standard cross-sectional population 2×2 table (n.b. not sampled case-control counts). For cell frequencies a=P(D+,M+), b=P(D+,M−), c=P(D−,M+), d=P(D−,M−), and inserting P(D+)=a+b and P(M+)=a+c into MRS equation (2):

$$\mathit{MRS}=2(\mathit{ad}-\mathit{bc})\text{and}\mathit{NNtest}={(\mathit{ad}-\mathit{bc})}^{-1}.$$ (3)

MRS is easy to remember as twice the cross-product difference of the frequencies in the interior of the 2×2 table for a cross-sectional population or unstratified random sample. In contrast, the odds-ratio is the cross-product ratio ad/bc. The odds-ratio is dimensionless, but MRS is on the scale of risk, and NNtest represents a number of people. In particular, if a,b,c,d represent cell-counts (not frequencies), with n being their sum, then (see Table 2):

$$\mathit{MRS}=2(\mathit{ad}-\mathit{bc})/n^2\text{and}\mathit{NNtest}=n^2/(\mathit{ad}-\mathit{bc}).$$

n² does not cancel in MRS/NNtest as it does in the odds ratio (i.e. (ad/n²) / (bc/n²) = ad/bc).

Table 2.

Calculating Mean Risk Stratification (MRS) and Number Needed to Test (NNtest) from cell counts in a cross-sectional population 2×2 table. While the odds ratio is the cross-product ratio (ad/bc), MRS and NNtest are functions of the cross-product difference (ad−bc).

	Test Result
	Positive	Negative	Total
Diseased	a	b	a+b
Not Diseased	c	d	c+d
Total	a+c	b+d	n=a+b+c+d
Odds Ratio:		OR = ad/bc
Mean Risk Stratification:		MRS = 2(ad−bc)/n2
Number Needed to Test:		NNtest = n2/(ad−bc)

MRS is also the numerators of Pearson’s correlation, the Mantel-Haenszel test²⁰, and Kappa¹⁰ (see eAppendix for relation to other statistics). Our preprint⁹ provides all statistical details, including variances, confidence intervals, and hypothesis testing.

Results: Implications of MRS and NNtest for evaluating diagnostic tests

1. Rarely positive tests with good PPV and cNPV provide little risk-stratification

Intuitively, but incorrectly, risk-stratification seems to depend only on how far the absolute risks, the PPV and cNPV, spread apart: the risk-difference RD=PPV − cNPV. Substitute into the MRS equation (1) P(D+) = PPV×P(M+) + cNPV×P(M−), and denoting p=P(M+), yields:

$$\mathit{MRS}=2p(1-p)\times \mathit{RD}$$

Risk-stratification depends on not only the spread between absolute risks (risk-difference RD), but crucially, also on test-positivity p. Thus, a rarely positive test, no matter how big the risk-difference, provides little risk-stratification.

For example, consider the hypothetical use of cervical cytology (contrary to usual practice to make a point), dichotomized simply as a cytologic result of cancer or not cancer (“not cancer” includes all precancerous and negative cytology results). At KPNC, the 5-year PPV for finding a precancer or cancer, following a cytology result of cancer, is 84%, the cNPV is 0.519%, and the overall precancer/cancer prevalence is 0.524%²¹. The risk-difference (RD) of 84%–0.519% = 83.5% is enormous, suggesting high risk-stratification. However, the probability of having a cytology result of cancer is only 0.006%. Consequently, only with probability 0.006% does a woman get the dramatic risk increase PPV−P(D+) = 84%−0.524% = 83.5%. Almost all the time (99.994%), she has a trivial risk decrease P(D+) −cNPV = 0.524%−0.519% = 0.005%. The MRS is 0.01%: only 1 extra precancer/cancer on average will be found over 5 years per 10,000 women using this test versus random selection. The NNtest=20,086 is an enormous number of women to screen to improve upon randomly selecting women to screen. Thus, good risk-stratification requires both a large risk-difference and a test that is positive sufficiently often.

Figure 1 plots the relationship of MRS/NNtest to the risk-difference for 3 test positivity rates. When risk-difference is 1, the maximum MRS and minimum NNtest are achieved. The importance of test positivity is illustrated by noting that, the MRS/NNtest achieved for risk-difference of 1 is also obtained for a risk-difference of approximately only 0.1 when the test is 10 times as positive (dashed line). Thus, a perfect marker for a rarely positive test provides the same risk-stratification as a much weaker-associated marker that is 10 times as positive.

Figure 1.

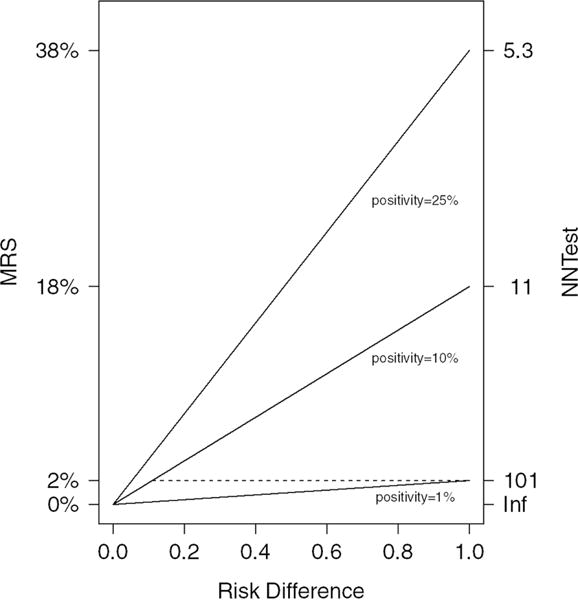
Risk-difference vs. MRS and NNtest for 3 test positivities (1%, 10%, and 25%). Acronyms: MRS (Mean Risk Stratification), NNtest (Number Needed to Test)

2. AUC and Youden’s index do not fully measure risk-stratification, because risk-stratification depends strongly on disease prevalence

MRS/NNtest can be calculated by combining disease prevalence with Youden’s index (J=Sens+Spec−1) or AUC for a binary marker. Writing each joint probability in the MRS equation (3) as a function of sensitivity (Sens) and specificity (Spec), their respective complements cSens=1−Sens and cSpec=1−Spec, and disease prevalence π =P(D+):

$$\mathit{MRS}=2(\mathit{ad}-\mathit{bc})=2\{(\mathit{Sens}\times \pi )(\mathit{Spec}\times (1-\pi ))-(\mathit{cSens}\times \pi )(\mathit{cSpec}\times (1-\pi ))\}=2\pi (1-\pi )\times J.$$

Although AUC is mostly used for continuous markers, for binary tests, the AUC is the average of sensitivity and specificity⁶, which relates AUC to Youden’s index as J = 2×AUC − 1. Thus MRS, in terms of binary AUC, is MRS=4π(1− π)×(AUC− 0.5).

The key point is that MRS and NNtest are functions of AUC/Youden’s index and disease prevalence. This leads to 4 key conclusions:

1. The risk-stratification implied by Youden’s index, AUC, or diagnostic likelihood ratios depends on disease prevalence. Good values of Youden’s index, AUC, or diagnostic likelihood ratios do not imply good risk-stratification if the disease is too rare

A test with good values of Youden’s index, AUC, or diagnostic likelihood ratios in a population with low disease prevalence may provide less risk-stratification than a test with worse Youden’s index, AUC, or diagnostic likelihood ratios in a population with higher disease prevalence.

In Table 1, cotesting at KPNC in the USA has a greater AUC than VIA in China (83% in KPNC vs. 72% in China) and also better diagnostic likelihood ratios (LR+=10 vs. 5 & LR−=0.28 vs. 0.50). However, VIA in China has twice the MRS (0.7% vs. 1.4%), and half the NNtest (275 vs. 140), of cotesting at KPNC. Cotesting is incontestably more accurate than VIA¹⁴, but VIA stratifies risk better in an easier setting (unscreened population) than cotesting stratifies risk in a more challenging setting (heavily screened population). Thus, conducting even VIA in China could identify more treatable precancer (and hence prevent more cervical-cancer) than cotesting at KPNC. This point is obscured by the AUC and diagnostic likelihood ratios, but revealed by MRS.

For fixed AUC, MRS and NNtest are dramatically better as disease becomes more prevalent (Figure 2). In contrast, increasing AUC only slowly increases MRS. Thus, a screening test considered infeasible for general-population screening, may be feasible for screening higher-risk subpopulations¹⁹.

Figure 2.

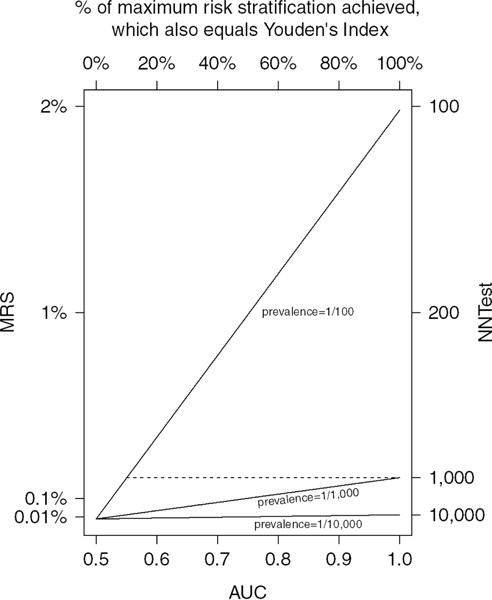
AUC vs. MRS and NNtest for 3 disease prevalences (1/100, 1/1,000, and 1/10,000). Acronyms: AUC (Area under the receiver operating characteristic curve), MRS (Mean Risk Stratification), NNtest (Number Needed to Test)

2. Disease prevalence defines the maximal amount of risk-stratification that a test can provide. Rare diseases inherently have limited risk-stratification

Since J=1 is a perfect biomarker, the maximum MRS for a disease is 2π(1− π); minimum NNtest is {π(1− π)}⁻¹. Maximal MRS is solely determined by disease prevalence π=P(D+). The rarer the disease, the less risk-stratification is possible. If the maximum risk-stratification is small, every test must inevitably have low risk-stratification This is a reality of general-population cancer screening: on average, screening tests for uncommon diseases such as cancer do not reveal much risk information to tested individuals, and thus, hundreds require screening to identify one more disease case than would be found by randomly selecting people to screen.

In Table 1, the same tests have greater MRS (and lower NNtest) in an unscreened higher-risk population (China; 1.6% disease prevalence) than a screened low-risk population (USA KPNC; 0.55% disease prevalence). The maximum possible MRS is 3 times greater in China vs. KPNC (MRS: 3.2% vs. 1.1%; minimum NNtest: 64 vs. 183, respectively). A test with a fixed Youden’s index (or AUC) should stratify risk better in populations with more disease, such as previously unscreened populations or populations enriched for high-risk people (such as referral populations), because the maximum possible risk-stratification is greater.

Figure 2 plots the relationship of MRS and NNtest to AUC for 3 uncommon disease prevalences. The importance of disease prevalence is illustrated by noting that, the maximum MRS/NNtest (achieved for AUC=1) is also obtained if AUC=0.55 when disease is 10 times as prevalent (dashed line); AUC=0.6 is required if disease is 5 times as prevalent. Thus, a perfect marker for a rare disease provides the same risk-stratification as a weakly associated marker for a disease that is 5 or 10 times as prevalent.

3. Youden’s index is the percent of maximum risk-stratification actually achieved by the test. This interprets the meaning of increases in AUC in terms of risk-stratification

Because MRS = 2π(1− π)×J, and maximum MRS is 2π(1− π), thus the ratio of MRS to the maximum MRS is Youden’s index (J). Therefore, Youden’s index, instead of measuring risk-stratification, measures the percent of maximum risk-stratification actually achieved.

This expression helps interpret the sometimes obscure meaning of increases in AUC. Since J = 2×AUC − 1, each 1% increase in AUC implies a 2% increase in MRS (or decrease in NNtest). Thus, MRS doubles from AUC=0.6 to 0.7. An AUC=0.6 is widely considered to be “modest”, and indeed, only 20% of the maximum MRS is achieved. An AUC=0.7 is widely considered “good”, but only 40% of the maximum MRS is achieved. An AUC=0.9 is required to achieve 80% of the maximum MRS.

Although a high Youden’s index and AUC imply that a high percentage of the maximum risk-stratification has been achieved, they may conceal that there is little risk-stratification if disease is rare. The top axis of Figure 2 shows how the percent of maximum MRS increases linearly with AUC. As disease becomes rarer, such as for prevalence of 1/10,000, there is little discernible increase in MRS as AUC increases.

Similarly, we can interpret the risk-stratification implied by an odds-ratio. The minimum odds-ratio required to achieve a Youden’s index has sensitivity equal to specificity. Table 3 shows the minimum odds-ratio required to achieve each fraction of the maximum MRS (the maximum odds-ratio is always infinity, when sensitivity or specificity are 100%). For example, a marker with odds-ratio of 3.4 can attain no higher than 30% of the maximum MRS. If specificity must be high (say 95%), as is often the case for screening for rare diseases such as cancer, then OR=3.4 attains no higher than 10% of the maximum MRS. Seemingly large odds-ratios do not suffice to imply large risk-stratification. At KPNC, the 3 tests with the lowest and similar MRS of about 0.3% have odds-ratios varying widely (13-36) (Table 1). Similarly, the 4 best tests in China have similar MRS (2.6%-2.8%), but odds-ratios vary widely (108-206). Odds-ratios can reveal little about risk-stratification.

Table 3.

The minimum odds-ratios required for a marker to account for each fraction of the maximum possible risk-stratification. The right column provides the minimum odds-ratio if specificity must be high (set at 95%).

% of maximum risk-stratification achieved	minimum odds-ratio required
	overall	fix specificity=95%
0%	1.0	1.0
10%	1.5	3.4
20%	2.3	6.3
30%	3.4	10.2
40%	5.4	15.5
50%	9.0	23.2
60%	16.0	35.3
70%	32.1	57.0
80%	81.0	107.7
90%	361.0	361.0
100%	Infinity	Infinity

4. It is important to distinguish rankings of different tests referring to the same population or between populations. Either can be useful depending on the objective

MRS/NNtest and J/AUC will rank the risk-stratification capability of tests in the same order in the same population, because disease prevalence is fixed (see Table 1). In Figure 1, the MRS increases monotonically with AUC. Thus comparing the MRS/NNtest for 2 tests in the same population is equivalent to comparing their J/AUCs, which is useful for hypothesis testing⁹. However, when prevalence varies across populations, J/AUC do not necessarily even rank test risk-stratification correctly according to MRS/NNtest. For example, a test with AUC=1 has less risk-stratification than any test with AUC>0.55 for a disease 10 times as prevalent (Figure 2, dashed line). VIA in China (AUC=0.72) provided twice the risk-stratification (i.e. MRS) of cotesting in the USA (AUC=0.83) in the USA. Thus, it is important to supplement AUC with MRS/NNtest to compare the risk-stratification of a test across populations with different disease prevalences.

Discussion and Conclusions

To enhance our work on assessing whether new biomarkers might be useful for cervical-cancer screening in low-, middle- and high-resource populations, we introduced two linked metrics, MRS and NNtest, that quantify risk-stratification from diagnostic tests. MRS and NNtest have 3 key advantages for comparing test performance across populations with different disease prevalences and biomarker distributions.

First, MRS and NNtest demonstrate that there is little risk-stratification possible for rarely positive tests, regardless of how high the risk-difference is. Second, MRS and NNtest demonstrate that tests with high AUC or Youden’s index do not necessarily imply high risk-stratification for rare diseases. Justifying screening for rare diseases, such as cancer, requires a strong justification that includes both sufficient prevalence and test positivity. China has 3 times the precancer/cancer prevalence of KPNC in the USA, and all tests, including VIA, the weakest cervical-screening test, provide far more risk-stratification in China than at KPNC. As expected, prior effective secondary-prevention screening reduces the value of more screening.

Third, MRS and NNtest demonstrate that Youden’s index and AUC measure multiplicative relative gains in risk-stratification, which might not imply large absolute gains if disease is too rare. An AUC=0.6 achieves only 20% of maximum risk-stratification; AUC=0.9 is required to achieve 80%. This is in accord with findings that AUC appropriately casts ‘pessimism’ on the power of risk prediction^22,23. Within a population, Youden’s index and AUC will rank tests for risk-stratification in the same order as MRS and NNtest, although rankings may well differ across populations with differing disease prevalence.

This paper introduces MRS and NNtest to epidemiology. For diseases like cancer, the MRS is small and NNtest is large, and more experience is necessary to develop an intuitive sense of sufficient MRS and NNtest in various settings. Research on estimating MRS/NNtest from different study designs and statistical models is necessary. We have extended MRS to continuous markers and risk-prediction models, have compared MRS to new statistics, such as decision curves⁸, and calculated MRS at different risk-thresholds to identify “optimally informative” thresholds⁹. We have also used MRS to assess agreement between occupational exposure experts¹⁰. MRS should be considered alongside metrics of test accuracy, such as likelihood ratios and AUC, to reveal their risk stratification implications.

Standard diagnostic accuracy statistics are easy to misinterpret when comparing test performance across populations with differing disease prevalence or biomarker distributions. The STARD guidelines²⁴ require reporting sensitivity/specificity, predictive values, or AUC, but these are hard to compare across populations and none directly informs about risk-stratification. MRS and NNtest might be worth adding to studies of test performance to quantify risk-stratification, improve cross-population comparisons, and better understand the meaning of standard statistics. For example, it is immediately clear from MRS and NNtest why BRCA1/2 testing of all women, justified on the basis of high PPV and risk-difference²⁵, would have little public-health value because of low mutation-prevalence (0.25%). However, MRS and NNtest would also immediately clarify that restricting testing to populations with higher mutation-prevalence, such as Ashkenazi Jews (2.5%), is more likely to have public-health value⁹. MRS and NNtest can help temper premature claims of clinical/public-health utility and also help justify future definitive studies that account for benefits/harms/costs to decide clinical/public-health usefulness. Our risk-stratification webtool is publicly available: https://analysistools.nci.nih.gov/biomarkerTools/.

Highlights.

• We propose new diagnostic accuracy metrics for comparing tests across populations

• Rare diseases inherently permit limited risk-stratification

• Tests that are rarely positive do not provide much risk-stratification

• High AUC does not imply good risk-stratification if the disease is too rare

• Our new metrics support a “high-bar” to justify population screening for cancer