On the number of non-equivalent ancestral configurations for matching gene trees and species trees

Abstract

An ancestral configuration is one of the combinatorially distinct sets of gene lineages that, for a given gene tree, can reach a given node of a specified species tree. Ancestral configurations have appeared in recursive algebraic computations of the conditional probability that a gene tree topology is produced under the multispecies coalescent model for a given species tree. For matching gene trees and species trees, we study the number of ancestral configurations, considered up to an equivalence relation introduced by Wu (2012) to reduce the complexity of the recursive probability computation. We examine the largest number of non-equivalent ancestral configurations possible for a given tree size n. Whereas the smallest number of non-equivalent ancestral configurations increases polynomially with n, we show that the largest number increases with kⁿ, where k is a constant that satisfies $\sqrt[3]{3}\le k<1.503$. Under a uniform distribution on the set of binary labeled trees with a given size n, the mean number of non-equivalent ancestral configurations grows exponentially with n. The results refine an earlier analysis of the number of ancestral configurations considered without applying the equivalence relation, showing that use of the equivalence relation does not alter the exponential nature of the increase with tree size.

1 Introduction

Under the multispecies coalescent model for the evolution of gene trees conditional on species trees, symmetries and identities among gene tree probabilities and algebraic perspectives for examining the probability computations have contributed to advances in understanding the properties of evolutionary descent in closely related species (Allman et al., 2011). Calculations of the probabilities of gene tree topologies can proceed by one of two computational approaches: nonrecursive (Degnan and Salter, 2005) or recursive (Wu, 2012). Both methods involve combinatorial and probabilistic components, in which probabilities are evaluated for each element of a set of objects that can be defined purely in mathematical terms. Computational complexity is affected both by the size of the underlying set of objects and by the complexity of the probability calculation.

In the recursive approach, the relevant combinatorial set consists of ancestral configurations, each of which represents a set of gene lineages that can be extant at a given node of the species tree (Wu, 2012). We have previously studied the set of ancestral configurations possible for a given gene tree and matching species tree, showing that the largest number of ancestral configurations across labeled tree topologies of a fixed tree size n increases exponentially with n (Disanto and Rosenberg, 2017).

To lower the computation time of the recursive evaluation of gene tree probabilities, Wu (2012) introduced an equivalence relation that, taking into account symmetries in tree shapes, reduces the set of ancestral configurations to a potentially much smaller set of non-equivalent ancestral configurations. The computation of gene tree probabilities can then make use of intermediate steps calculated for the elements of this smaller set, rather than for the full set of ancestral configurations.

Here, for gene trees and species trees with a matching labeled topology t, we study the number of non-equivalent ancestral configurations that can appear at the nodes of a species tree t. We determine the number of non-equivalent ancestral configurations when t belongs to special families of trees characterized by balanced and unbalanced patterns. We study the largest number of non-equivalent ancestral configurations possible for a given tree size n, showing that this number grows exponentially with kⁿ, where k is a constant that satisfies $\sqrt[3]{3}\le k<1.503$. Although tree families exist for which the number of non-equivalent ancestral configurations grows polynomially in n (Wu, 2012), we show that under a uniform distribution on the set of labeled trees of size n, the mean number of non-equivalent ancestral configurations of a random labeled tree shape also grows exponentially in n. Finally, we compare our results on the number of non-equivalent ancestral configurations with corresponding results for the full set of ancestral configurations (Disanto and Rosenberg, 2017). Although by definition, the non-equivalent ancestral configurations are no more numerous than ancestral configurations that do not take into account the equivalence relation—and indeed, are intended to be less numerous—the base k for the maximal number of non-equivalent ancestral configurations kⁿ across trees of size n is bounded below by a constant only slightly smaller than the corresponding base for the maximal number of ancestral configurations.

2 Preliminaries

We study the number of non-equivalent ancestral configurations of rooted binary labeled trees. We start by giving definitions and preliminary results. In Section 2.1, we recall some properties of rooted binary labeled trees. In Section 2.2, we discuss properties of the exponential growth of sequences of non-negative numbers. Following Wu (2012), Section 2.3 defines ancestral configurations for a gene tree and a species trees with a matching labeled topology t. In Section 2.4, we recall related enumerative results of Disanto and Rosenberg (2017).

2.1 Labeled topologies

A labeled topology t of size |t| = n is a bifurcating rooted tree with n labeled leaves, also termed “taxa” (Fig. 1A). We sometimes refer to labeled topologies simply as “trees.” We define a total order a ≺ b ≺ c ≺ … for the set {a, b, c, …} of labels of the leaves of a tree, proceeding alphabetically. That is, without loss of generality, we assume that a tree of size n has its taxa labeled using the first n symbols that appear in the order ≺.

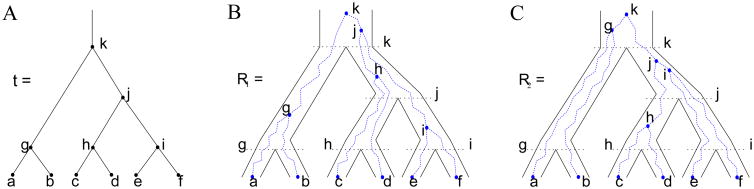
Figure 1.

A matching gene tree and species tree with labeled topology t. (A) A tree t of size 6 isomorphic to the gene tree and species tree in (B) and (C). Tree t is uniquely determined by the labeling of its leaves and by its unlabeled shape. It is convenient to assign arbitrary labels to the internal nodes of t as well. We use letters g, h, i, j, k in this case. Each lineage (edge) of t is identified by the lowest node it intersects; for example, lineages h and i descend from lineage j. (B) A possible realization R₁ of a gene tree (dotted lines) in a species tree (solid lines). The gene tree and the species tree have a matching topology that follows (A). At species tree node j, the ancestral configuration is {c, d, i}. At node k, the configuration is {g, h, i}. (C) A non-equivalent realization R₂ of the gene tree in (A) in the matching species tree. At species tree nodes j and k, the configurations are {h, e, f} and {a, b, j}, respectively.

We represent labeled topologies in Newick notation (Felsenstein, 2004), in which t = (t₁, t₂) is the tree obtained by appending trees t₁ and t₂ to a common root node. For example, ((a, b), ((c, d), (e, f))) gives the Newick notation for the tree depicted in Fig. 1A. We term non-leaf nodes of a tree “internal” nodes. By “subtree” of a tree t, we mean a node of t together with all its descendants; a “root subtree” of t is a subtree—one of two possible—immediately descended from the root of t.

For two trees t₁, t₂, we say that t₁ is isomorphic to t₂ and write t₁ ≅ t₂ when, after their leaf labels are removed, t₁ and t₂ have the same unlabeled topology. Moreover, given trees t₁ and t₂ with |t₁| ≥ |t₂|, we say that a subtree t of t₁ is equal to t₂ up to “rescaling” labels when, respecting the order ≺, we can replace the labels of t to obtain t₂. For instance, the largest root subtree ((c, d), (e, f)) of the tree depicted in Fig. 1A is equal to ((a, b), (c, d)) up to rescaling, as we can replace the labels c → a, d → b, e → c, f → d. Note that alphabetical order is preserved in this replacement.

We denote by T_n the set of trees of size n, and by $T={\cup }_{n=1}^{\infty }{T}_n$ the set of all trees of any size. The number of trees of size n ≥ 2 is given by

$$|T_n|=(2n-3)!!=1\times 3\times 5\times \cdots \times (2n-3)$$ (1)

(Felsenstein, 1978), which assuming n ≥ 1 can be rewritten

$$|T_n|=\frac{(2n-2)!}{2^{n-1}(n-1)!}=\frac{(2n)!}{2^n(2n-1)n!}.$$ (2)

We will have occasion to employ a uniform probability distribution over the set of trees of fixed size. In this distribution, each tree of size n has probability 1/|T_n|.

2.2 Exponential growth of a sequence

As in Flajolet and Sedgewick (2009), we say that a sequence of positive numbers a_n is of exponential order k or, equivalently, has exponential growth kⁿ, when

$$\underset{n\to \infty }{limsup}[{(a_n)}^{1/n}]=\underset{n\to \infty }{lim}[\underset{m\ge n}{sup}[{(a_m)}^{1/m}]]=k.$$

This relation holds when a_n = kⁿs(n), where s is a subexponential factor, so that limsup_n→∞[s(n)^1/n] = 1. According to these definitions, a sequence a_n grows exponentially in n if its exponential order strictly exceeds 1.

The exponential order of a sequence describes its asymptotic growth. It follows from the definition that if (a_n) has exponential order k_a and (b_n) has exponential order k_b > k_a, then a_n/b_n converges to 0 exponentially fast as (k_a/k_b)ⁿ for n → ∞. When two sequences (a_n) and (b_n) have the same exponential order, we write a_n ⋈ b_n. If a_n ⋈ b_n and lim_n→∞(a_n/b_n) = 1, we write a_n ∼ b_n.

2.3 Ancestral configurations

This section defines the set of ancestral configurations of a gene tree G in a species tree S. In our setting, exactly one gene lineage is selected from each species. We assume a matching labeled topology t for G and S.

Consider a realization R of a gene tree G in a species tree S, with G = S = t (Fig. 1). Equivalently, R is one of the possible evolutionary scenarios for gene tree G on species tree S. Given a node κ of t, we denote by C(κ, R) the set of gene lineages, i.e. edges of G, that are present in S at the point right before node κ looking backward in time. Following Wu (2012), we call the set C(κ, R) the ancestral configuration of G at node κ of S.

For the tree t in Fig. 1A, if we consider the realization R₁ of the gene tree G = t in the species tree S = t depicted in Fig. 1B, then we see that C(k, R₁) = {g, h, i} is the ancestral configuration of the gene tree at node k of the species tree. The gene lineages g, h, and i are those present in the species tree at the point right before the root node k. Similarly, the ancestral configuration of the gene tree at node j of the species tree is given by the set of gene lineages C(j, R₁) = {c, d, i}. In Fig. 1C, a different realization R₂ of the same gene tree is described. The ancestral configuration at the root k of the species tree is in this case C(k, R₂) = {a, b, j}, whereas the ancestral configuration at node j is C(j, R₂) = {h, e, f}.

We denote the set of all possible realizations of the gene tree G = t in the species tree S = t by ℜ(G, S). By considering all elements R ∈ ℜ(G, S), for a given node κ of t we define the set of all possible ancestral configurations at node κ,

$$C(\kappa )=\{C(\kappa ,R):R\in \Re (G,S)\},$$ (3)

and the number of such configurations,

$$c(\kappa )=|C(\kappa )|.$$ (4)

In particular, c(κ) counts the number of ways the gene lineages of G can reach the point right below node κ in S, when all possible realizations of G in S are taken into account. For example, if we set t as in Fig. 1A, then we have C(g) = {{a, b}} and C(j) = {{c, d, e, f}, {h, e, f}, {c, d, i}, {h, i}}. At the root node k, the set of all possible ancestral configurations is

$$C(k)=\{\{g,j\},\{a,b,j\},\{g,c,d,e,f\},\{a,b,c,d,e,f\},\{g,h,e,f\},\{a,b,h,e,f\},\{g,c,d,i\},\{a,b,c,d,i\},\{g,h,i\},\{a,b,h,i\}\}.$$

Note that two different realizations R₁, R₂ ∈ ℜ(G, S) can generate the same ancestral configuration C(κ, R₁) = C(κ, R₂) at an internal node κ.

Following Disanto and Rosenberg (2017), for each internal node κ, our definition of ancestral configuration excludes the case {κ} ∈ C(κ). This choice accords with the fact that each configuration at node κ is considered at the point right below node κ in the species tree, with no time for the gene lineages from the left and right subtrees of κ to coalesce together. With the exception that we say that a leaf or 1-taxon tree has 0 ancestral configurations, our definition is identical to that of Wu (2012), which assigns these cases 1 ancestral configuration.

Under our assumption of a matching gene tree and species tree G = S = t, the set C(κ) defined in (3) and its cardinality c(κ) (4) depend only on node κ and tree t. When we refer to an element of C(κ), we use the term configuration at node κ of t. When κ is the root node, we use the term root configuration to describe an element of C(κ). Also, considering the union of all the sets C(κ) of configurations across all internal nodes κ of t, we can count the total number of configurations.

2.4 The number of configurations

We recall some of the results of Disanto and Rosenberg (2017) on the number of configurations possessed by a tree. These results are used to measure the decrease in the number of configurations when, as in Wu (2012), an equivalence relation is introduced in Section 3 to merge topologically equivalent configurations.

1. If A, B are two sets of sets, define A ⊗ B = {a ∪ b : a ∈ A, b ∈ B}. For a given tree t with |t| > 1, the set C(r) of configurations at the root r of t satisfies the following decomposition

   $$C(r)=\{\{r_{\ell },r_r\}\}\cup [C(r_{\ell })\otimes \{\{r_r\}\}]\cup [\{\{r_{\ell }\}\}\otimes C(r_r)]\cup [C(r_{\ell })\otimes C(r_r)],$$

   where r_ℓ and r_r respectively denote the left and right children of r.

2. For a given tree t with |t| > 1, the number c(r) of possible configurations at the root node r of t can be recursively computed as

   $$c(r)=[c(r_{\ell })+1][c(r_r)+1]=1+c(r_{\ell })+c(r_r)+c(r_{\ell })c(r_r),$$ (5)

   where we set c(r) = 0 when |t| = 1. At each node κ of t, the number of configurations c(κ) is bounded as c(κ) ≤ c(r). Thus, the total number of configurations c = Σ_κc(κ) satisfies c(r) ≤ c ≤ (2|t| − 1)c(r). In particular, the quantities c and c(r) are equal up to a factor that is at most polynomial in |t|, and they have the same exponential order when measured across families of trees of increasing size.

3. Denote by M_n(r) and M_n, respectively, the largest number of root configurations and the largest total number of configurations that a tree of size n can have. The exponential growth of the sequences M_n(r) and M_n is $M_n(r)\bowtie M_n\bowtie k_0^n$, where k₀ is a constant, k₀ ≈ 1.5028.

4. A completely balanced tree of size n = 2^h has $\lfloor k_0^n\rfloor -1$ root configurations. A caterpillar tree of size n has n − 1 root configurations.

5. For a tree of given size n leaves selected uniformly at random, the mean number of root configurations c(r) and the mean total number of configurations c have exponential growth 𝔼_n[c(r)] ⋈ 𝔼_n[c] ⋈ (4/3)ⁿ with n.

3 Equivalent and non-equivalent configurations

Wu (2012) introduced an equivalence relation over the set of configurations at a given node of a species tree, using this equivalence relation to evaluate the probability of a gene tree topology by performing computations over the sets of non-equivalent configurations of the gene tree at species tree nodes (e.g. eq. (7) of Wu (2012)). Following the definition of Wu (2012), in this section, we introduce the notion of equivalent configurations for gene trees and species trees with matching topology t. Under certain assumptions on t, in Section 3.3, we provide a recursion analogous to the one in (5) for counting non-equivalent configurations at the root of t.

3.1 An equivalence relation

We begin with some notation. If κ is a node of a tree t, denote by t_κ the subtree of t generated by κ (i.e., κ and all nodes below it). If X is a set of nodes of a subtree t_κ, the restriction t_κ(X) of t_κ to X is the tree shape obtained by removing from t_κ all nodes that remain strictly below the nodes belonging to X. For instance, if t_j is the subtree generated by node j in the tree t in Fig. 1A and X = {h, e, f}, then t_j(X) is obtained by removing nodes c and d from t_j, and thus is the caterpillar tree shape of size 3. Similarly, if X = {a, b, h, i}, then t_k(X) is the balanced tree shape of size 4.

The definition of equivalent configurations given by Wu (2012) reduces to the following one when gene trees and species trees are matching. Given a tree t and a node κ, two configurations γ₁, γ₂ at node κ, γ₁, γ₂ ∈ C(κ), are equivalent at κ—with the equivalence denoted by γ₁ ∼_κ γ₂—when the tree shape t_κ(γ₁) is isomorphic to the tree shape t_κ(γ₂). For instance, in Fig. 1A, we have {h, e, f} ∼_j {c, d, i} and {a, b, j} ∼_k {g, h, i}. The set of non-equivalent configurations at a given node κ is denoted by C*(κ), and its cardinality is c*(κ) = |C*(κ)|

The notion of equivalent configurations groups together at a given node configurations for which exactly the same topological constraints apply in ordering the coalescent events of their gene lineages. In other words, gene lineages of equivalent configurations at a node κ of a species tree have completely topologically equivalent transitions when they move from node κ backward in time (upward in the species tree).

For instance, consider the tree in Fig. 1A, where the configurations {a, b, j} and {g, h, i} at node k satisfy {a, b, j} ∼_k {g, h, i}. Consider the mapping ϕ(a) = h, ϕ(b) = i, ϕ(j) = g, ϕ(g) = j, ϕ(k) = k. The transition in Fig. 1C that along the root branch of the species tree transforms the set of gene lineages {a, b, j} into the single lineage k corresponds topologically to the transition in Fig. 1B that transforms {g, h, i} into k. Indeed, the two trees t_k({a, b, j}) with nodes {a, b, j, g, k}, and t_k({g, h, i}) with nodes {g, h, i, j, k} are isomorphic through ϕ.

As described in Fig. 2, for a given tree t, the effective computation of non-equivalent configurations can be performed recursively as in the algorithm STELLS (Wu, 2012) by scanning t from bottom to top with a postorder traversal. At each visited node κ, we first compute the set

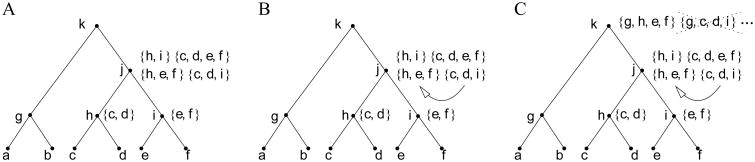
Figure 2.

Merging of equivalent configurations at node κ = j. (A) At node j, the set C̃(j) = {{h, i}, {h, e, f}, {c, d, i}, {c, d, e, f}} of configurations is computed from the non-equivalent configurations at the child nodes h and i by using (6). (B) Two equivalent configurations appear in C̃(j), namely {h, e, f} ∼_j {c, d, i}. Configuration {c, d, i} is merged into {h, e, f} (or vice versa). (C) The configurations in C*(j) = {{h, e, f}, {h, i}, {c, d, e, f}} are used to determine configurations at node k. In particular, {g, h, e, f} ∈ C̃(k) and {g, c, d, i} ∉ C̃(k), as {c, d, i} has been merged into {h, e, f}. Configuration {g, c, d, i}, which is not present in C̃(k), is represented by the equivalent configuration {g, h, e, f} ∼_k {g, c, d, i}. Similarly, {a, b, c, d, i} ∉ C̃(k), and it is represented by {a, b, h, e, f} ∼_k {a, b, c, d, i}.

$$\stackrel{\sim }{C}(\kappa )=\{\{{\kappa }_{\ell },{\kappa }_r\}\}\cup [C^{\ast }({\kappa }_{\ell })\otimes \{\{{\kappa }_r\}\}]\cup [\{\{{\kappa }_{\ell }\}\}\otimes C^{\ast }({\kappa }_r)]\cup [C^{\ast }({\kappa }_{\ell })\otimes C^{\ast }({\kappa }_r)]$$ (6)

from the sets of non-equivalent configurations of the two child nodes κ_ℓ, κ_r (Fig. 2A with κ = j). Next, we merge all the equivalent configurations present in C̃(κ) into a single representative, one for each class of equivalence of the relation ∼_κ, to determine the set C*(κ) of non-equivalent configurations at κ (Fig. 2B). Only the configurations in C*(κ) are used to determine configurations at the parent node of κ (Fig. 2C). Note that from (6), the cardinality of the set C̃(κ) ⊇ C*(κ) satisfies

$$c^{\ast }(\kappa )\le |\stackrel{\sim }{C}(\kappa )|=1+c^{\ast }({\kappa }_{\ell })+c^{\ast }({\kappa }_r)+c^{\ast }({\kappa }_{\ell })c^{\ast }({\kappa }_r).$$ (7)

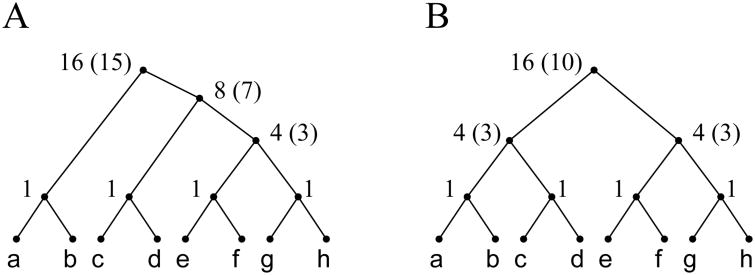
Following this procedure in Fig. 3, we report the quantities |C̃(κ)| and c*(κ) at each internal node κ of two trees of size 8. When |C̃(κ)| > c*(κ), the latter value is given in parentheses. The same trees are considered in the enumerations provided in Table A1 (Fig. 3A) and Table 1 (Fig. 3B) by Wu (2012).

Figure 3.

Computing the number of non-equivalent configurations in two trees of size 8. By using (7), at each internal node κ, |C̃(κ)| is computed from the number of non-equivalent configurations at the nodes descending from κ. When |C̃(κ)| > c*(κ), c*(κ) appears in parentheses. (A) A tree considered in Table A1 by Wu (2012). Adding |t| = 8 to the value Σ_κ |C̃(κ)| = 32 to take into account the fact that Wu (2012) counts a configuration for each leaf whereas our definition does not do so, we produce entry 40 of the table of Wu (2012). (B) The completely balanced tree of size 8 considered in Table 1 by Wu (2012). Adding |t| = 8 to Σ_κ |C̃(κ)| = 28, we produce entry 36. The numbers c*(κ) satisfy recursion (10).

In the next sections, we study the number c*(κ) = |C*(κ)| of pairwise non-equivalent configurations at a given node κ of a fixed or random tree t ∈ T_n selected uniformly as well as the total number of non-equivalent configurations c* = Σ_κ c*(κ) in t. To measure the strength of the equivalence relation ∼_κ, we focus on c*(r), the number of non-equivalent configurations at the root κ = r of t, comparing our results with those in Section 2.4.

When there is no need to distinguish between the number of non-equivalent root configurations and the total number of non-equivalent configurations, we simply write “number of non-equivalent configurations”. It is then understood that a statement applies to both root and total non-equivalent configurations. Similarly, “number of configurations” stands for both “number of root configurations” and “total number of configurations.”

3.2 Non-equivalent root configurations in small trees

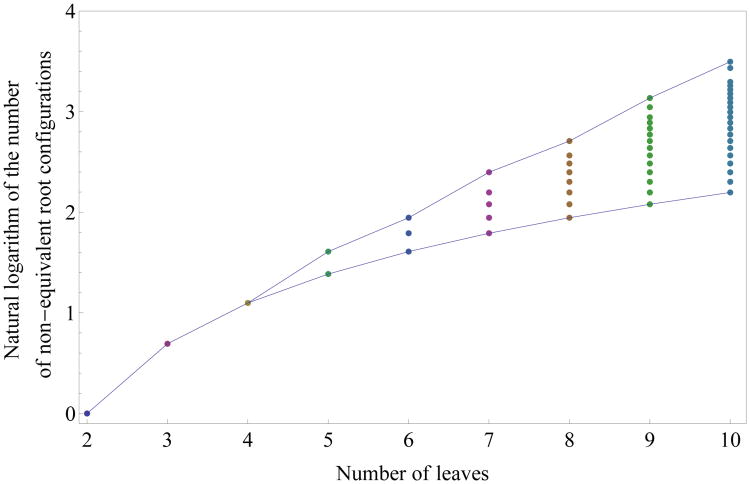
For small values of n, it is possible to exhaustively compute the number of non-equivalent root configurations c*(r) for representative labelings of each of the unlabeled topologies of size n. In Fig. 4, each dot corresponds to the logarithm of the number of non-equivalent root configurations for a certain tree shape of size determined by its x-coordinate. The points associated with the largest values of c*(r) are connected by the top line, whose growth appears to be linear in n. Indeed, as we show in Section 4, tree families exist for which the growth of the number of non-equivalent root configurations is exponential in the tree size.

Figure 4.

Natural logarithm of the number of non-equivalent root configurations for all possible tree shapes of size 2 ≤ n ≤ 10. The value for n = 1, log(0), is omitted. Points corresponding to the largest and smallest numbers of root configurations for each n are connected by the top and bottom lines, respectively.

The tree shapes whose labeled topologies possess the largest number of non-equivalent root configurations among trees of fixed size n ≤ 20 appear in Fig. 5. For 12 ≤ n ≤ 20, each shape in the sequence is produced by connecting the tree with three taxa and the tree of size n − 3 already in the sequence to a shared root. This pattern is used in Section 4.3 to determine a lower bound for the exponential growth of the sequence $M_n^{\ast }(r)$ describing the largest number of non-equivalent root configurations among trees at fixed n.

Figure 5.

Tree shapes of size 5 ≤ n ≤ 20 with the largest number of non-equivalent root configurations. For n = 4, both unlabeled topologies have c*(r) = 3. For 12 ≤ n ≤ 20, the tree with the largest value of c*(r) is obtained by appending a caterpillar of size 3 and the tree of size n – 3 with the largest value of c*(r) to a common root node. From n = 2 to n = 20, the largest values of c*(r) follow the sequence 1, 2, 3, 5, 7, 11, 15, 23, 33, 47, 69, 99, 141, 207, 297, 423, 621, 891, 1269.

For values of n ≤ 20, the tree shape that minimizes the number of non-equivalent root configurations is the caterpillar topology. The number of non-equivalent root configurations in the caterpillar of size n is n − 1 (Wu, 2012). The bottom line in Fig. 4, which connects points corresponding to the smallest number of non-equivalent root configurations for a tree with n taxa, grows with log(n − 1).

These observations show that tree topology can have a considerable impact on the number of non-equivalent configurations possible at a given tree size. Indeed, Section 4 investigates the effect of symmetries in a tree on its number of non-equivalent configurations. In Section 5, we show that although tree families (e.g. caterpillars) exist for which the growth of the number of non-equivalent configurations is polynomial in the tree size n, the expected number of non-equivalent configurations in a labeled topology selected uniformly at random in T_n grows exponentially in n.

3.3 A recursion for the number of non-equivalent root configurations

In this section, we provide a recursive procedure for computing the number of non-equivalent root configurations in trees satisfying certain topological constraints. We later use this recursion to study the number of non-equivalent root configurations for several families of trees.

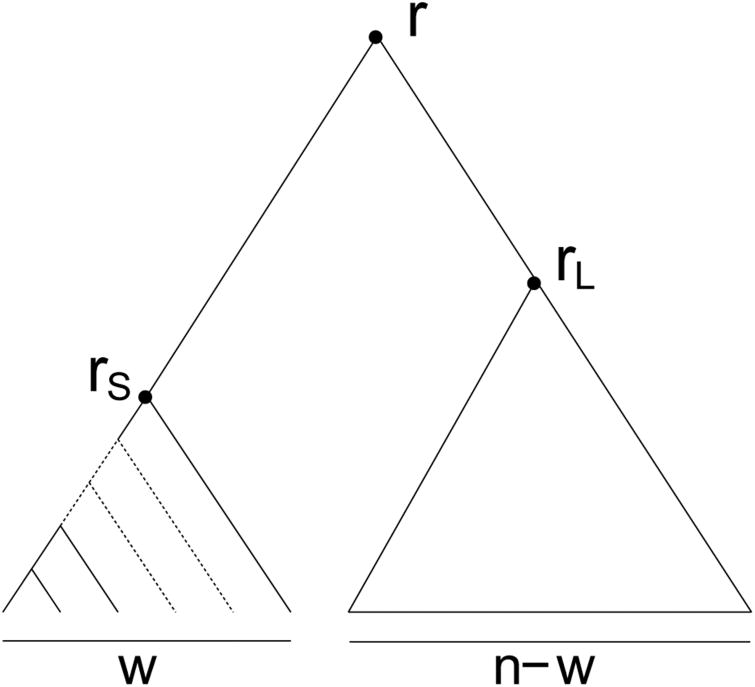
Let r be the root of a tree t. We denote by r_S and r_L the nodes descending from r that generate the smaller, t_rS, and the larger, t_rL, root subtrees of t (we will soon see that if the root subtrees of t have equal size, then we can choose either labeling). As depicted in Fig. 6, suppose subtree t_rS can be displayed inside subtree t_rL by a configuration at node r_L; that is, assume there is a configuration γ at node r_L such that

Figure 6.

A tree t in which the smaller root subtree t_rS can be displayed as t_rS ≅ t_rL (γ) in the larger root subtree t_rL through a configuration γ at node r_L. The configuration γ is determined by the black squares.

$$t_{r_S}\cong t_{r_L}(\gamma ).$$ (8)

Note that it immediately follows that when (8) is satisfied, if t_rS and t_rL have the same size, then they must have the same unlabeled shape, and it does not matter which is assigned the label t_rS and which is assigned t_rL. It is trivial that (8) is satisfied when t_rS ≅ t_rL, by the configuration γ that simply consists of all leaves of t_rL.

When condition (8) is satisfied, as shown in Appendix 1, the number of non-equivalent configurations c*(r) at the root r of a tree t with |t| > 1 can be directly computed from the corresponding numbers at the children r_S and r_L:

$$c^{\ast }(r)=[c^{\ast }(r_S)+1][c^{\ast }(r_L)+1]-\frac{c^{\ast }(r_S)}{2}[c^{\ast }(r_S)+1]=1+\frac{c^{\ast }(r_S)}{2}+c^{\ast }(r_L)+c^{\ast }(r_S)c^{\ast }(r_L)-\frac{{[c^{\ast }(r_S)]}^2}{2},$$ (9)

where c*(r) = 0 if |t| = 1. Note that if the smaller root subtree has size |t_rS| = 1, then condition (8) is technically not satisfied, as each configuration at node r_L has at least 2 elements (unless |t| = 2). However, in this case as well, with |t_rS| = 1 and c*(r_S) = 0, formula (9) holds, yielding c*(r) = 1 + c*(r_L).

4 Non-equivalent configurations for special tree families

In this section, we study the number of non-equivalent configurations for special families of trees. We consider completely unbalanced caterpillar trees in Section 4.1 and completely balanced trees in Section 4.2. The number of non-equivalent configurations in the caterpillar family has been investigated by Wu (2012). For the completely balanced family, we show that the number of non-equivalent configurations grows exponentially in the tree size, though in a manner slower than the exponential growth of the number of configurations (see point (iv) in Section 2.4). By considering a particular family of unbalanced trees, in Section 4.3, we bound the exponential growth of the sequence $M_n^{\ast }(r)$ of the largest number of non-equivalent root configurations for a given tree size n.

4.1 Completely unbalanced trees

Consider the family of caterpillar trees. Recursive application of (9) shows that, as was already observed by Wu (2012), the number of non-equivalent root configurations in the caterpillar with n taxa is n − 1. In particular, for caterpillar trees, t_rS has only one leaf, and c*(r) = 1 + c*(r_L). For a caterpillar tree of size n, subtree r_L is simply a caterpillar tree of size n − 1. Noting that c*(r) = 1 for a two-taxon caterpillar tree, we can iterate to obtain c*(r) = n − 1 for an n-taxon caterpillar tree. Considering all internal nodes of an n-taxon caterpillar, each of which has one fewer non-equivalent configuration than the number of leaves it subtends, the total number of non-equivalent configurations in the caterpillar of size n is ${\sum }_{k=2}^n(k-1)=n(n-1)/2$.

We have thus found a family of trees for which the growth of the number of non-equivalent configurations is polynomial in the tree size. This result suggests that 𝔼_n[c*(r)]—the expected number of non-equivalent root configurations in a random tree selected uniformly among those of size n—could, in theory, grow as a subexponential function of n. We study the growth of this expectation in Section 5, showing that 𝔼_n[c*(r)] in fact grows exponentially in n.

4.2 Completely balanced trees

Now consider the family of completely balanced trees b₀, b₁, b₂, …, where b_h is the completely balanced tree of size n = 2^h (Fig. 3B). Each tree b_h satisfies condition (8), as t_rS ≅ t_rL. Because of this equivalence of unlabeled shapes, c*(r_S) = c*(r_L). Therefore, denoting by γ_h the number of non-equivalent root configurations in b_h, from (9) we have the recursion

$${\gamma }_{h+1}=\frac{{\gamma }_h^2}{2}+\frac{3{\gamma }_h}{2}+1,$$ (10)

where γ₀ = 0. Setting x_h = (γ_h + 1)/2, this recursion can be written

$$x_{h+1}=x_h^2+\frac{x_h+1}{2},$$ (11)

with x₀ = 1/2. The sequence (x_h) can be studied as in Appendix 2. A constant $k_0^{\ast }$ exists for which

$$x_h~{(k_0^{\ast })}^{(2^h)}.$$ (12)

The constant $k_0^{\ast }$ can be approximated using the recursive definition of x_h, summing terms in a series

$$k_0^{\ast }=\left(\frac{1}{2}\right)exp[\sum _{i=0}^{\infty }{2}^{-i-1}log(1+\frac{1}{2x_i}+\frac{1}{2x_i^2}\left)\right]\approx 1.2460.$$ (13)

Switching back to γ_h, we obtain

$${\gamma }_h=2x_h-1~2{(k_0^{\ast })}^{(2^h)}=2{(k_0^{\ast })}^n,$$

where n = 2^h = |b_h|.

The following proposition summarizes our result.

Proposition 1 Consider the family of completely balanced trees (b_h), with n = 2^h = |b_h|. Its sequence of the number of non-equivalent root configurations, c*(r), grows asymptotically as $c^{\ast }(r)~2{(k_0^{\ast })}^n$, where $k_0^{\ast }\approx 1.2460$ (13). In particular, c*(r) and the sequence of the total number of non-equivalent configurations, c*, both have exponential growth ${(k_0^{\ast })}^n$.

Proof. It remains to show that for tree family (b_h), the exponential growth of the total number of non-equivalent configurations equals the exponential growth of the number of non-equivalent root configurations. Because the sequence γ_h (10) is increasing, in the completely balanced tree b_h, the maximum number of non-equivalent configurations across all internal nodes is reached at the root of the tree, equaling c*(r). The total number of nodes (including the leaves) in b_h is 2n − 1. We therefore have the inequality c*(r) ≤ c* ≤ (2n − 1)c*(r). In particular, the quantities c* and c*(r) are equal up to a factor that is at most polynomial in the size n. It follows that the exponential growth of c* equals the exponential growth of c*(r).

Comparing the constant $k_0^{\ast }$ with the value of k₀ ≈ 1.5028 that describes the exponential growth of the number of configurations for the completely balanced family of trees (Disanto and Rosenberg, 2017), the proposition shows that in this family, the sequence of the number of non-equivalent configurations grows exponentially slower than the sequence of the number of configurations. However, the growth is still exponential in the tree size, and it is not true that non-equivalent configurations always grow polynomially—as they do for caterpillar trees.

4.3 Bounds for the largest number of non-equivalent configurations for a given tree size

We now seek to bound the value of $M_n^{\ast }(r)={max}_{\{t:|t|=n\}}{c}_t^{\ast }(r)$, the largest number of non-equivalent root configurations among trees of size n.

Proposition 2 Let k₀ ≈ 1.5028 be the exponential order of the sequence (M_n(r)) describing the largest number of root configurations in trees of size n (point (iii) of Section 2.4). Then $M_n^{\ast }(r)\bowtie {(k_1^{\ast })}^n$, where $\sqrt[3]{3}\le k_1^{\ast }\le k_0$.

Proof. For the upper bound, because non-equivalent configurations are no more numerous than configurations, $M_n^{\ast }(r)\le M_n(r)$, and the upper bound follows.

For the lower bound, it suffices to exhibit a tree family in which the number of non-equivalent root configurations has exponential order $\sqrt[3]{3}$. For n ≥ 9, we define the family of unlabeled topologies (u_n) by taking u_n as the tree shape of size n depicted in Fig. 5 if n ∈ {9, 10, 11} and u_n = (u_n−3, c₃)—where c₃ is the caterpillar with 3 taxa—when n ≥ 12. Note that for n ≥ 12, the tree t = u_n satisfies condition (8) with t_rS = c₃ (Fig. 6).

Let γ_n be the number of non-equivalent root configurations in u_n. For n ≥ 12, (9) yields the recursion

$${\gamma }_n=3{\gamma }_{n-3},$$ (14)

with γ₉ = 23, γ₁₀ = 33, and γ₁₁ = 47. We set x_n = [2(n − 3⌊n/3⌋)² + 8(n − 3⌊n/3⌋) + 23]/27 to produce a function that cycles through the values 23/27, 33/27, and 47/27 as n is incremented. From (14), we have

$${\gamma }_n=3^{\lfloor \frac{n}{3}\rfloor }{x}_n$$ (15)

when n ≥ 9. In particular, using (15), we see that (γ_n) has exponential growth ${\gamma }_n\bowtie {\sqrt[3]{3}}^n$ as desired.

The recursive definition u_n = (u_n−3, c₃) of the tree family (u_n) matches the pattern found by exhaustive computation for the unlabeled topologies of trees of size 12 ≤ n ≤ 20 with the largest number of non-equivalent root configurations (Fig. 5). Applying the floor function to the expression in (15), we obtain

$$\lfloor 3^{\lfloor \frac{n}{3}\rfloor }\frac{2{(n-3\lfloor \frac{n}{3}\rfloor )}^2+8(n-3\lfloor \frac{n}{3}\rfloor )+23}{27}\rfloor .$$ (16)

This formula, which equals (15) for n ≥ 9, computes the correct values of $M_n^{\ast }(r)$ from Figure 5 for 2 ≤ n ≤ 20. Based on this result, it is a plausible conjecture that (16) gives the exact value for the maximum number of non-equivalent root configurations at a given n ≥ 2.

Note that the constant $k_1^{\ast }$ bounds from below the exponential order of the sequence $M_n^{\ast }$ of the largest total number of non-equivalent configurations among trees of given size, as total non-equivalent configurations are at least as numerous as non-equivalent root configurations. Further, because k₀ is the exponential order of the sequence M_n of the largest total number of configurations in trees of fixed size (see point (iii) of Section 2.4), k₀ bounds from above the exponential order of the sequence $M_n^{\ast }$.

Because $\sqrt[3]{3}\approx 1.4422$, another consequence of Propositions 1 and 2 is that sequences $M_n^{\ast }(r)$ and $M_n^{\ast }$ grow exponentially faster than the sequence of the number of non-equivalent configurations in the family of completely balanced trees. This property illustrates a remarkable effect of merging equivalent configurations. From points (iii) and (iv) of Section 2.4, the number of configurations for completely balanced trees follows the sequence of the largest number of configurations for trees of size n. When equivalent configurations are merged together, however, other tree families, such as the unbalanced family (u_n), possess a number of non-equivalent configurations that grows faster than the corresponding number for completely balanced trees.

5 Mean number of non-equivalent root configurations

We denote by 𝔼_n[c*(r)] the expected number of non-equivalent root configurations in a random tree of size n drawn under a uniform distribution. This section shows that 𝔼_n[c*(r)] grows as an exponential function of n. We first present a lower bound for 𝔼_n[c*(r)]. Next, we show that this lower bound is itself bounded below by a quantity that increases exponentially with n.

For the first step, we bound the expectation 𝔼_n[c*(r)] by considering a certain set $T_n^{\prime }\subseteq T_n$ in which each tree satisfies formula (9). For n ≥ 2, define the quantity x = x(n) as the solution of 2^x−2 + x = n − 1, and consider the function w′(n) given by w′(2) = 1 and for n ≥ 3,

$$w^{\prime }(n)=\lfloor x\rfloor .$$ (17)

In Appendix 3, it is shown that w′(n) satisfies w′(n) ≤ n/2, and that w′(n) = n/2 holds only when n = 2, 4, or 6. For 2 ≤ n ≤ 10, the values of (n, w′(n)) are (2, 1), (3, 1), (4, 2), (5, 2), (6, 3), (7, 3), (8, 3), (9, 4), and (10, 4).

The growth of w′(n) is logarithmic. Indeed, for increasing values of n, the ratio x/n becomes small, so that x − 2 = log₂[n(1 − (x + 1)/n)] ≈ (log₂n) − (x + 1)/(n log 2), where the Taylor approximation log(1 − u) ≈ −u for u near 0 is used. We then obtain x(n) ≈ [n log(4n) − 1]/(n log 2 + 1) ∼ (log n)/(log 2).

For a given n ≥ 2 and a given w ∈ [1, w′(n)], we denote by T_n,w the set of trees of size n such that t_rS, the smaller root subtree, is a caterpillar of size w, and t_rL, the larger root subtree, has an unconstrained labeled topology of size n − w (Fig. 7). For a given n ≥ 2, we define the set of trees

Figure 7.

Schematic representation of the unlabeled topology of a tree in set T_n,w. The smaller root subtree, t_rS, is a caterpillar of size w ∈ [1, w′(n)]. The larger t_rL, has an unconstrained labeled topology of size n – w. The largest possible value of w, or w′(n), is small enough for t_rS to be displayed in t_rL, as in (8). Note that T_n,w1 ⋂ T_n,w2 = ø if w₁ ≠ w₂.

$$T_n^{\prime }=\underset{w=1}{\overset{w^{\prime }(n)}{\cup }}{T}_{n,w}.$$

Four properties can be demonstrated for trees in T_n,w. (i) If w ≥ 2, then each tree t ∈ T_n,w satisfies (8) (Appendix 4), and thus, the number of non-equivalent root configurations in t satisfies (9). Furthermore, note that as was observed in Section 3.3, if t ∈ T_n,1, we have c*(r_S) = 0, and (9) holds even though (8) does not.

(ii) For any fixed n ≥ 2 and w ∈ [1, w′(n)], with w ≠ n/2, the probability of observing a given tree t̄ ∈ T_n−w as the rescaled larger root subtree of a tree t ∈ T_n,w selected uniformly at random is, as shown in Appendix 5,

$$\mathbb{P}[t_{r_L}=\overline{t}|t\in T_{n,w}]=\frac{1}{|T_{n-w}|}.$$ (18)

(iii) Because γ_w = w!/(2 − δ_w,1) is the number of caterpillar trees of size w ≥ 1 given a set of w labels, the probability p_n,w = ℙ[t ∈ T_n,w] for a random tree of size n drawn under a uniform distribution to be in T_n,w can be computed as p_n,w = |T_n,w|/|T_n|, or

$$p_{n,w}=\left(\begin{array}{c}n\\ w\end{array}\right)[(1-{\delta }_{n,2w}){\gamma }_w|T_{n-w}|+{\delta }_{n,2w}({\gamma }_w(|T_w|-{\gamma }_w)+\frac{1}{2}{\gamma }_w^2\left)\right]/|T_n|=\frac{w!(\begin{array}{c}n\\ w\end{array})[2(2-{\delta }_{w,1})(2n-2w-3)!!(1-{\delta }_{n,2w})-{\delta }_{n,2w}(w!+2(2w-3)!!{\delta }_{w,1}-4(2w-3)!!)]}{2(2n-3)!!{(2-{\delta }_{w,1})}^2}.$$ (19)

Here, $(\begin{array}{c}n\\ w\end{array})$ counts the number of ways of choosing the w taxa for the caterpillar subtree, and we have used (1) to expand |T_n|, |T_w|, and |T_n−w|.

(iv) If w₁ ≠ w₂, then the sets T_n,w1 and T_n,w2 are disjoint, with T_n,w1 ⋂ T_n,w2 = ∅. Indeed, if t ∈ T_n,w1 ⋂ T_n,w2, then we would have w₁ + w₂ = n, as t must have a caterpillar of size w₁ and a caterpillar of size w₂ as root subtrees. However, w₁ + w₂ cannot equal n, as either w₁ < w₂ ≤ n/2 or w₂ < w₁ ≤ n/2.

For a tree t of size n ≥ 2 selected uniformly at random, the mean number 𝔼_n[c*(r)] of non-equivalent root configurations can be written by conditioning on $t\in T_n^{\prime }$, that is,

$${\mathbb{E}}_n[c^{\ast }(r)]=(\sum _{w=1}^{w^{\prime }(n)}{p}_{n,w}{\mathbb{E}}_n[c_t^{\ast }(r)|t\in T_{n,w}])+(1-\sum _{w=1}^{w\prime (n)}{p}_{n,w}){\mathbb{E}}_n[c_t^{\ast }(r)|t\notin T_n^{\prime }].$$ (20)

Here, the probability $\mathbb{P}[t\in T_n^{\prime }]$ has been calculated as the sum $\mathbb{P}[t\in T_n^{\prime }]={\sum }_{w=1}^{w^{\prime }(n)}\mathbb{P}[t\in T_{n,w}]$ because $T_n^{\prime }={\cup }_{w=1}^{w^{\prime }(n)}{T}_{n,w}$ is a disjoint union.

The expression ${\mathbb{E}}_n[c_t^{\ast }(r)|t\in T_{n,w}]$ in (20) can be replaced by

$${\mathbb{E}}_n[c_t^{\ast }(r)|t\in T_{n,w}]=1+\frac{w-1}{2}+{\mathbb{E}}_{n-w}[c^{\ast }(r)]+(w-1){\mathbb{E}}_{n-w}[c^{\ast }(r)]-\frac{{(w-1)}^2}{2}=1+\frac{(w-1)(2-w)}{2}+w{\mathbb{E}}_{n-w}[c^{\ast }(r)],$$ (21)

because for a random tree t ∈ T_n,w selected under a uniform distribution, (9) applies with c*(r_S) = w − 1 and c*(r_L) = 𝔼_n−w[c*(r)]. In particular, c*(r_S) = w − 1, as a caterpillar of size w has w − 1 non-equivalent root configurations (Section 4.2), and c*(r_L) = E_n−w[c*(r)], as the larger root subtree t_rL of a random t ∈ T_n,w selected uniformly has a uniform distribution over T_n−w if w ≠ n/2 (18). If w = n/2—which can happen only for n = 2, 4, or 6—(21) holds because ${\mathbb{E}}_n[c_t^{\ast }(r)|t\in T_{2,1}]=1$, ${\mathbb{E}}_n[c_t^{\ast }(r)|t\in T_{4,2}]=3$, and ${\mathbb{E}}_n[c_t^{\ast }(r)|t\in T_{6,3}]=6$, while 𝔼₁[c*(r)] = 0, 𝔼₂[c*(r)] = 1, and 𝔼₃[c*(r)] = 2.

Using (21) and ignoring the second term in (20) yields the inequality

$${\mathbb{E}}_n[c^{\ast }(r)]\ge \sum _{w=1}^{w^{\prime }(n)}{p}_{n,w}[1+\frac{(w-1)(2-w)}{2}+w{\mathbb{E}}_{n-w}[c^{\ast }(r)]].$$

This inequality can be iterated if n − w ≥ 2 by applying the same procedure to 𝔼_n−w[c*(r)]. It follows that for each n ≥ 1, the integer e_n defined recursively for n ≥ 2 by

$$e_n=\sum _{w-1}^{w^{\prime }(n)}{p}_{n,w}[1+\frac{(w-1)(2-w)}{2}+w{e}_{n-w}],$$ (22)

where e₁ = 0, bounds from below the expectation 𝔼_n[c*(r)]. The first values of e_n and 𝔼_n[c*(r)] are reported in Table 1. The values of e_n match the values of 𝔼_n[c*(r)] for n ≤ 7, that is, as long as $T_n^{\prime }=T_n$ and the second term in (20) is 0. We also have the following result.

Table 1.

The sequences e_n, 𝔼_n[c*(r)] and 𝔼_n[c(r)] for small values of n.

n	en	𝔼n[c*(r)]	𝔼n[c(r)]
1	0	0	0
2	1	1	1
3	2	2	2
4	3	3	$\frac{16}{5}$
5	$\frac{30}{7}$	$\frac{30}{7}$	$\frac{33}{7}$
6	$\frac{121}{21}$	$\frac{121}{21}$	$\frac{20}{3}$
7	$\frac{254}{33}$	$\frac{254}{33}$	$\frac{304}{33}$
8	$\frac{1356}{143}$	$\frac{334}{33}$	$\frac{1795}{143}$
9	$\frac{8961}{715}$	$\frac{729}{55}$	$\frac{1102}{65}$
10	$\frac{37549}{2431}$	$\frac{42039}{2431}$	$\frac{296}{13}$
11	$\frac{4613}{247}$	$\frac{94667}{4199}$	$\frac{9841}{323}$
12	$\frac{654726}{29393}$	$\frac{863372}{29393}$	$\frac{4840}{119}$
13	$\frac{195593}{7429}$	$\frac{1990481}{52003}$	$\frac{402752}{7429}$
14	$\frac{6033381}{185725}$	$\frac{9266561}{185725}$	$\frac{788741}{10925}$
15	$\frac{4299031}{111435}$	$\frac{21753971}{334305}$	$\frac{99454}{1035}$
16	$\frac{88030888}{1938969}$	$\frac{164642378}{1938969}$	$\frac{3837632}{30015}$
17	$\frac{9891227}{186093}$	$\frac{1959845063}{17678835}$	$\frac{52758677}{310155}$
18	$\frac{4014691853}{64822395}$	$\frac{3128723951}{21607465}$	$\frac{1157564}{5115}$
19	$\frac{1715903641}{23881935}$	$\frac{22592912099}{119409675}$	$\frac{1563215792}{5191725}$
20	$\frac{24415042314}{294543865}$	$\frac{72844824142}{294543865}$	$\frac{39979649}{99789}$

Values of en were computed by using (22). Values of 𝔼_n[c*(r)] were computed by generating all possible unlabeled topologies of size n and then using STELLS (Wu, 2012) to obtain the number $c_t^{\ast }(r)$ of non-equivalent root configurations for each unlabeled topology t. The probability of t under a uniform distribution over labeled topologies of size n was obtained by noting that its number of labelings L(t) follows the recursion in Eq. 5.1 of Harding (1971); nonrecursively, the number of labelings is n!/2^s(t), where s(t) is the number of internal nodes of t, including cherries and possibly the root, whose two descendant subtrees are isomorphic (this result is obtained by taking the quotient of the results of Theorems 3.5 and 3.3 of Rosenberg (2006)). To compute $c_t^{\ast }(r)$, we ran STELLS on tree (t, •) in which the two root subtrees were t and the one-taxon tree •. According to (7), the number of root configurations computed by STELLS is $c_t^{\ast }(r)+1$, from which the desired $c_t^{\ast }(r)$ is obtained. Values of 𝔼_n[c(r)] were computed by the method of Disanto and Rosenberg (2017, Fig. 7).

Proposition 3 The expected number 𝔼_n[c*(r)] of non-equivalent root configurations in a random tree of size n ≥ 1 selected under a uniform distribution can be bounded

$$e_n\le {\mathbb{E}}_n[c^{\ast }(r)]\le {\mathbb{E}}_n[c(r)],$$ (23)

where e_n is defined in (22) and 𝔼_n[c(r)] is the expected number of root configurations. Furthermore, the sequence 𝔼_n[c*(r)] grows exponentially in n, with exponential order at most 4/3.

Proof. The upper bound follows from the fact that for any tree, c*(r) ≤ c(r), and by point (v) in Section 2.4, 𝔼_n[c(r)] has exponential order 4/3. All that remains is to show that 𝔼_n[c*(r)] grows exponentially in n. To achieve this goal, we prove that the exponential order of the lower bound sequence e_n strictly exceeds one.

Truncating the sum (22) after the first four terms, for n ≥ 9, we have

$$e_n\ge p_{n,1}{e}_{n-1}+2p_{n,2}{e}_{n-2}+3p_{n,3}{e}_{n-3}+4p_{n,4}{e}_{n-4}+(p_{n,1}+p_{n,2}-2p_{n,4})\ge p_{n,1}{e}_{n-1}+2p_{n,2}{e}_{n-2}+3p_{n,3}{e}_{n-3}+4p_{n,4}{e}_{n-4}.$$ (24)

The last step follows because according to (19), when n ≥ 9, p_n,1 = n/(2n−3), p_n,2 = n(n−1)/[2(2n−3)(2n−5)], p_n,4 = n(n − 1)(n − 2)(n − 3)/[2(2n − 3)(2n − 5)(2n − 7)(2n − 9)], and

$$p_{n,1}+p_{n,2}-2p_{n,4}=\frac{n(2n-11)!!(18n^3-192n^2+645n-681)}{2(2n-3)!!}\ge 0.$$

Define the sequence a_n by a_n = e_n for 1 ≤ n ≤ 8, and a_n = p_n,1a_n−1 + 2p_n,2a_n−2 + 3p_n,3a_n−3 + 4p_n,4a_n−4 for n ≥ 9. From (24), we have, for each n ≥ 1,

$$e_n\ge a_n.$$ (25)

When n ≥ 9 and 1 ≤ w ≤ 4, because w ≠ n/2 and δ_n,w/2 = 0, the probability p_n,w in (19) can be written

$$p_{n,w}=\frac{(2n-2w-3)!!}{(2n-3)!!}\frac{n!}{(n-w)!}\frac{1}{2-{\delta }_{w,1}}.$$

The recursion for a_n then becomes

$$a_n=\frac{n(2n-5)!!}{(2n-3)!!}{a}_{n-1}+\frac{n(n-1)(2n-7)!!}{(2n-3)!!}{a}_{n-2}+\frac{3n(n-1)(n-2)(2n-9)!!}{2(2n-3)!!}{a}_{n-3}+\frac{2n(n-1)(n-2)(n-3)(2n-11)!!}{(2n-3)!!}{a}_{n-4}.$$ (26)

Setting q_n = a_n(2n − 3)!!/n!, we obtain from (26)

$$q_n=q_{n-1}+q_{n-2}+\frac{3q_{n-3}}{2}+2q_{n-4}.$$ (27)

Recursion (27) is homogeneous and linear with constant coefficients, and therefore (Sedgewick and Flajolet, 1996, Theorems 3.3 and 4.1), the exponential order of the sequence q_n is the inverse of the unique positive solution z₀ of the characteristic equation 1 = z + z² + 3z³/2 + 2z⁴.

Solving the equation numerically, we find q_n ⋈ (1/z₀)ⁿ, where z₀ ≈ 0.4845. In particular, the exponential order 1/z₀ of the sequence q_n strictly exceeds 2. Using (2) to rewrite (2n − 3)!!, and observing by Stirling's formula $n!~{(n/e)}^n\sqrt{2\pi n}$ that $(\begin{array}{c}2n\\ n\end{array})\bowtie 4^n$, it follows that sequence a_n = q_nn!/(2n − 3)!! has exponential growth

$$a_n\bowtie q_n\frac{n!}{\frac{(2n)!}{2^{n}n!}}=q_n\frac{2^n}{\left(\begin{array}{c}2n\\ n\end{array}\right)}\bowtie {\left(\frac{1/z_0}{2}\right)}^n.$$

Therefore, the exponential order of the sequence a_n is 1/(2z₀) ≈ 1.0320 > 1. By inequality (25), the sequence e_n grows exponentially in n.

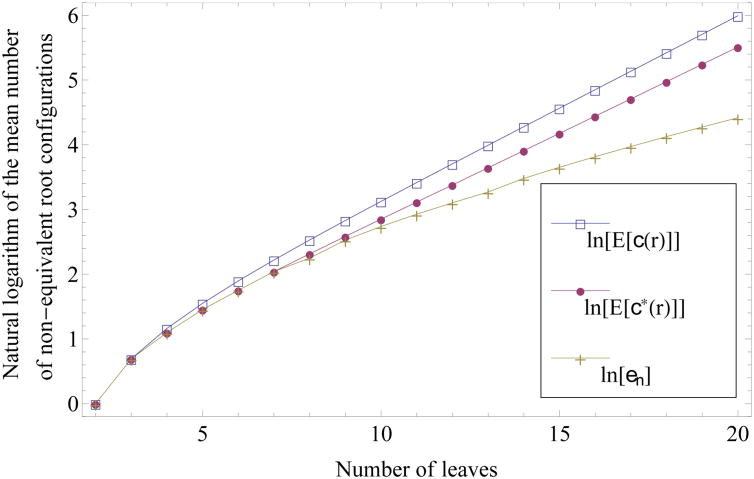
For n ≤ 20, the exact values of e_n, 𝔼_n[c*(r)], and 𝔼_n[c(r)] are reported in Table 1 and plotted in Fig. 8. The figure illustrates that the numerical values of log 𝔼_n[c*(r)], though initially coincident with the values of log e_n, are already closer to the values of log 𝔼_n[c(r)] by n = 20. This observation suggests that in bounding 𝔼_n[c*(r)] from below to demonstrate its exponential growth, the steps we have taken have led to a bound that is quite loose; the exponential growth of 𝔼_n[c*(r)] is likely to have a comparable magnitude to that of 𝔼_n[c(r)], or 4/3.

Figure 8.

Natural logarithm of the mean number 𝔼_n[c*(r)] of non-equivalent root configurations for labeled topologies of size 2 ≤ n ≤ 20. The value for n = 1, log(0), is omitted. The natural logarithms of the bounds e_n and 𝔼_n[c(r)] (23) determine the lower and upper lines. Exact values for the three quantities are reported in Table 1.

6 Discussion

For labeled gene tree topologies t that match the labeled species tree topology, we have extended the enumerative study of ancestral configurations, considering non-equivalent configurations specified by an equivalence relation that groups ancestral configurations according to symmetries in t. We have focused on the exponential growth in the tree size |t| = n of the number of non-equivalent configurations present at the root of t.

We have shown that when t satisfies certain constraints, its number of non-equivalent root configurations can be recursively computed from corresponding quantities for its root subtrees. The recursion (9), which shares three of its five terms with an analogous recursion for root configurations (Disanto and Rosenberg, 2017, Proposition 1), enables the study of the number of non-equivalent root configurations for special tree families. For the family of completely balanced trees, the number of non-equivalent root configurations and the total number of non-equivalent configurations grow exponentially with order $k_0^{\ast }\approx 1.2460$ in n (Proposition 1). Comparing this constant with the exponential orders of the numbers of root configurations and total configurations in the family, both of which equal k₀ ≈ 1.5028 (Disanto and Rosenberg, 2017), we see that for the completely balanced trees, the number of configurations grows exponentially faster than the number of non-equivalent configurations. Their symmetric structure collapses the set of configurations into fewer non-equivalent configurations.

A different recursively defined tree family (u_n), however, has asymptotically more non-equivalent configurations than the balanced trees, its number of root configurations growing with exponential order $\sqrt[3]{3}\approx 1.4422$ (Proposition 2). This value is close to the upper bound of k₀ ≈ 1.5028 on the exponential order of the maximal number of configurations across all labeled topologies of size n (Disanto and Rosenberg, 2017, Corollary 1). Although the unlabeled shapes that give rise to the largest numbers of non-equivalent root configurations (Figure 5) and root configurations (Disanto and Rosenberg, 2017, Figure 3) are not in general the same, the maximal numbers of non-equivalent configurations and configurations have comparable exponential order.

As was found by Wu (2012), the growth of the number of non-equivalent configurations for some tree families (e.g. caterpillars) can be polynomial in n. Assuming a uniform distribution over the labeled topologies with size n, however, we have shown that the expected number of non-equivalent configurations for a random labeled topology of size n grows exponentially (Proposition 3). The exponential order of this growth is bounded below by 1/(2z₀) ≈ 1.0320; numerical exploration suggests that it is closer to the upper bound of 4/3 that describes the exponential order of the mean number of configurations (Disanto and Rosenberg, 2017, Proposition 5).

We focused on the situation in which the gene tree and species tree have a matching topology. In the non-matching case, in parallel to a similar result for configurations (Disanto and Rosenberg, 2017), it is possible that the number of non-equivalent root configurations and the total number of non-equivalent configurations exceed the corresponding values for matching gene trees and species trees. This claim can be verified in a simple example. Let χ_n = ((… ((a₁, a₂), a₃), …), a_n) be a caterpillar species tree, and label the unique internal node with k descendants by b_k for 2 ≤ k ≤ n. For a matching caterpillar gene tree, all configurations are non-equivalent, the number of non-equivalent configurations at node b_k is c*(b_k) = k − 1, the number of root configurations is c*(b_n) = n − 1, and the total number of configurations is $c^{\ast }={\sum }_{k=2}^n{c}^{\ast }(b_k)=n(n-1)/2$.

Continuing with χ_n as the species tree topology, consider a gene tree topology

$${\xi }_n=((\dots ((((a_1,a_2),a_3),(a_4,a_5)),a_6),\dots ),a_n)$$

with n ≥ 6. The gene trees (ξ_n) represent a caterpillar family (Disanto and Rosenberg, 2016) with seed tree (((a₁, a₂), a₃), (a₄, a₅)). We label the node of ξ_n ancestral to a₁ and a₂ by d₂, the node ancestral to a₁, a₂, and a₃ by d₃, the node ancestral to a₄ and a₅ by $d_2^{\ast }$, and the unique node ancestral to k taxa, 5 ≤ k ≤ n, by d_k. Following Wu (2012), the definition of equivalent configurations in the non-matching case generalizes the definition in Section 3.1. Consider a gene tree G, a species tree S, a node κ of S, and two configurations γ₁, γ₂ at node κ—two possible sets of gene lineages that could be present in S at κ under different realizations of G in S. Let κ′ be the most recent common ancestor of the lineages of G collected in the set γ₁, and note that κ′ is also the most recent common ancestor of the lineages collected in γ₂. Following the terminology of Section 3.1, we say that γ₁, γ₂ are equivalent at κ when the unlabeled tree shape G_κ′(γ₁) is isomorphic to the unlabeled tree shape G_κ′(γ₂). We denote by C*(κ) and c*(κ) the set of non-equivalent configurations at κ and its cardinality, respectively.

Proceeding sequentially through the internal nodes of χ_n, the non-equivalent configurations are C*(b₂) = {{a₁, a₂}}, C*(b₃) = {{a₁, a₂, a₃}, {d₂, a₃}}, C*(b₄) = {{a₁, a₂, a₃, a₄}, {d₂, a₃, a₄}, {d₃, a₄}}, and C*(b₅) = {{a₁, a₂, a₃, a₄, a₅}, {d₂, a₃, a₄, a₅}, {d₃, a₄, a₅}}, with c*(b₂) = 1, c*(b₃) = 2, c*(b₄) = 3, and c*(b₅) = 3. At node b₆ of χ_n, the non-equivalent configurations are C*(b₆) = {{a₁, a₂, a₃, a₄, a₅, a₆}, {d₂, a₃, a₄, a₅, a₆}, {d₃, a₄, a₅, a₆}, {a₁, a₂, a₃, $d_2^{\ast }$, a₆}, {d₃, $d_2^{\ast }$, a₆}, {d₅, a₆}}, and configuration {d₂, a₃, $d_2^{\ast }$, a₆} is not included owing to equivalence with {d₃, a₄, a₅, a₆}.

For 7 ≤ k ≤ n, C*(b_k) is obtained by augmenting configuration {d_k−1, a_k} to the set of all configurations formed by adding taxon a_k to the non-equivalent configurations in C*(b_k−1); none of the resulting configurations are equivalent, and c*(b_k) = c*(b_k−1) + 1. The number of non-equivalent root configurations of ξ_n for n ≥ 6 is c*(b_n) = n, and the number of total configurations is $c=1+2+3+3+{\sum }_{k=6}^n{c}^{\ast }(b_k)=n(n+1)/2-6$. Because n > n − 1 and n(n + 1)/2 − 6 > n(n − 1)/2 for n ≥ 7, non-equivalent root configurations and total non-equivalent configurations are more numerous for the non-matching ξ_n than for the matching caterpillar.

Our enumerative results on ancestral configurations can help to compare the cost of procedures for calculating gene tree probabilities recursively using ancestral configurations (Wu, 2012) to those that proceed nonrecursively using a different data structure, the “coalescent histories” (Degnan and Salter, 2005; Rosenberg, 2007; Than et al., 2007; Rosenberg and Degnan, 2010; Rosenberg, 2013; Disanto and Rosenberg, 2015, 2016). In this context, it is noteworthy that the trees u_n, which have many non-equivalent root configurations, have a similar recursive structure to the lodgepole trees, which have large numbers of coalescent histories (Disanto and Rosenberg, 2015).

Note that unlike for root configurations, we did not prove a general result describing the unlabeled shapes of trees that give rise to the most non-equivalent root configurations, merely evaluating the number of non-equivalent root configurations for trees u_n and noting by exhaustive computation that this value is near the maximum for small trees. We also did not produce a general relationship between non-equivalent root configurations and total non-equivalent configurations. For the family of completely balanced trees, the number of non-equivalent root configurations and the total number of non-equivalent configurations have the same exponential growth, as the maximal number of non-equivalent configurations across all internal nodes of a balanced tree is reached at its root (Proposition 1). However, we did not provide a generalization that such a maximum is applicable for arbitrary trees. Because it is the non-equivalent configurations that are employed by Wu (2012) in gene tree probability computations, their further exploration will be important for understanding the relative computational complexity of gene tree probability computations with different species trees.

Appendix 1

Proof of (9)

Let C*(r_S) = {γ_S,1, …, γ_S,q} with c*(r_S) = q, and let C*(r_L) = {γ_L,1, …, γ_L,Q}, with c*(r_L) = Q. Because condition (8) is satisfied, the entire tree t_rS can be displayed in t_rL, each configuration γ_S,i ∈ C*(r_S) has exactly one corresponding configuration γ_L,i ∈ C*(r_L) such that t_rS(γ_S,i) ≅ t_rL(γ_L,i), and Q ≥ q.

From (6), we obtain

$$\stackrel{\sim }{C}\left(r\right)=\left\{\right\{r_S,r_L\left\}\right\}\cup \left[C^{\ast }\right(r_S)\otimes \{\left\{r_L\right\}\left\}\right]\cup \left[\right\{\left\{r_S\right\}\}\otimes C^{\ast }(r_L\left)\right]\cup \left[C^{\ast }\right(r_S)\otimes C^{\ast }(r_L\left)\right],$$

which can be further decomposed as

$$\begin{gathered} \stackrel{\sim }{C}\left(r\right)=\left\{\right\{r_S,r_L\left\}\right\}\cup \left[\right\{{\gamma }_{S,1},\dots ,{\gamma }_{S,q}\}\otimes \{\left\{r_L\right\}\left\}\right]\cup \left[\right\{\left\{r_S\right\}\}\otimes [\{{\gamma }_{L,1},\dots ,{\gamma }_{L,q}\}\cup \{{\gamma }_{L,q+1},\dots ,{\gamma }_{L,Q}\}\left]\right]\cup \left[\right\{{\gamma }_{S,1},\dots ,{\gamma }_{S,q}\} \\ \otimes [\{{\gamma }_{L,1},\dots ,{\gamma }_{L,q}\}\cup \{{\gamma }_{L,q+1},\dots ,{\gamma }_{L,Q}\}\left]\right] \end{gathered}$$

$$=\left\{\right\{r_S,r_L\left\}\right\}$$ (28)

$$\cup \left[\right\{{\gamma }_{S,1},\dots ,{\gamma }_{S,q}\}\otimes \{\left\{r_L\right\}\left\}\right]\cup \left[\right\{\left\{r_S\right\}\}\otimes \{{\gamma }_{L,1},\dots {\gamma }_{L,q}\left\}\right]$$ (29)

$$\cup \left[\right\{\left\{r_S\right\}\}\otimes \{{\gamma }_{L,q+1},\dots ,{\gamma }_{L,Q}\left\}\right]$$ (30)

$$\cup \left[\right\{{\gamma }_{S,1},\dots ,{\gamma }_{S,q}\}\otimes \{{\gamma }_{L,1},\dots ,{\gamma }_{L,q}\left\}\right]$$ (31)

$$\cup \left[\right\{{\gamma }_{S,1},\dots ,{\gamma }_{S,q}\}\otimes \{{\gamma }_{L,q+1},\dots ,{\gamma }_{L,Q}\left\}\right].$$ (32)

We merge equivalent configurations to obtain C*(r) from C̃(r). From (29), we remove those in {γ_S,1, …, γ_S,q} ⊗ {{r_L}}, as they are equivalent to those in {{r_S}} ⊗ {γ_L,1, …, γ_L,q}. Thus, we take only q among the 2q configurations in (29). Moreover, due to the equivalence γ_S,i⋃γ_L,j ∼_r γ_S,j ⋃ γ_L,i, we take only those configurations of the form γ_S,i ⋃ γ_L,j with i ≤ j among those in {γ_S,1, …, γ_S,q} ⊗ {γ_L,1, …, γ_L,q}. Thus, among the q² configurations in (31)—those with 1 ≤ i, j ≤ q—we take only q(q + 1)/2 non-equivalent ones. No equivalences are possible among configurations in (28), (30), and (32), and all are retained in C*(r). From (28)-(32), we then have

$$c^{\ast }(r)=|C^{\ast }(r)|=1+q+(Q-q)+\frac{q(q+1)}{2}+q(Q-q)=1+q+Q+qQ-\frac{q(q+1)}{2}.$$

Replacing q by c*(r_S) and Q by c*(r_L) gives (9).

Appendix 2

Proof of (12)

The proof follows the approach of Aho and Sloane (1973, Section 3) for solving certain recurrences. From (11), we have $x_{h+1}=x_h^2[1+1/(2x_h)+1/(2x_h^2)]$. Taking the logarithm y_h = log x_h yields y_h+1 = 2y_h + α_h, where ${\alpha }_h=log[1+1/(2x_h)+1/(2x_h^2)]$. Following Aho and Sloane (1973), y_h has solution

$$y_h=2^h{y}_0+\sum _{i=0}^{\infty }{2}^{h-i-1}{\alpha }_i-\sum _{i=h}^{\infty }{2}^{h-i-1}{\alpha }_i=2^h(y_0+\sum _{i=0}^{\infty }{2}^{-i-1}{\alpha }_i)-\sum _{i=h}^{\infty }{2}^{h-i-1}{\alpha }_i.$$ (33)

Converting back to x_h = exp(y_h), from (33) we have

$$x_h={[x_{0}exp(\sum _{i=0}^{\infty }{2}^{-i-1}{\alpha }_i\left)\right]}^{(2^h)}exp(-\sum _{i=h}^{\infty }{2}^{h-i-1}{\alpha }_i)={(k_0^{\ast })}^{(2^h)}exp(-\sum _{i=h}^{\infty }{2}^{h-i-1}{\alpha }_i),$$

where the last step uses the fact that x₀ = 1/2.

We then have

$$\frac{x_h}{{\left(k_0^{\ast }\right)}^{(2^h)}}=exp(-\sum _{i=h}^{\infty }{2}^{h-i-1}{\alpha }_i).$$

When h → ∞, the sum ${\sum }_{i=h}^{\infty }{2}^{h-i-1}{\alpha }_i$converges to zero because it can be bounded $0\le {\sum }_{i=h}^{\infty }{2}^{h-i-1}{\alpha }_i\le {\alpha }_h{\sum }_{i=h}^{\infty }{2}^{h-i-1}={\alpha }_h$, where, because x_h → ∞ as h → ∞, α_h → 0 as h → ∞. It follows that $x_h/{\left(k_0^{\ast }\right)}^{(2^h)}$converges to 1, producing (12).

Appendix 3

Properties of w′(n)

We prove that for each n ≥ 2, w′(n) ≤ n/2, with equality only for n = 2, 4, or 6. The result is verified by direct computation of w′(n) for 2 ≤ n ≤ 7. For n ≥ 8, by definition, w′(n) = ⌊x⌋, where x satisfies 2^x–2 + x = n – 1. Seeking a contradiction, suppose ⌊x⌋ = w′(n) ≥ n/2. Because x ≥ ⌊x⌋, we would have x ≥ n/2, and therefore n – 1 = 2^x–2 + x ≥ 2^n/2–2 + n/2 ≥ 2(n/2 – 2) + n/2 = 3n/2 – 4, noting that 2^u ≥ 2u for u ≥ 2. The inequality n – 1 ≥ 3n/2 – 4 cannot hold if n ≥ 8. Therefore, when n ≥ 8, we must have w′(n) < n/2.

Appendix 4

Proof that trees in T_n,w satisfy (8) for w ≥ 2

We first prove that given any w ≥ 2, a caterpillar tree t₁ of size |t₁| = w can be displayed in any tree t₂ of size |t₂| ≥ 2^w–2 + 1 through a root configuration γ of t₂, that is, t₁ ≅ t₂(γ). The proof is by induction on w.

For w = 2, we have |t₂| ≥ 2 and the result follows by taking the root configuration γ determined by the left and right descendants of the root in t₂. For the inductive step, because |t₂| ≥ 2^w–2 + 1, the larger root subtree of t₂ has size at least ⌈|t₂|/2⌉ ≥ ⌈2^w–3 + 1/2⌉ = 2^w–3 + 1. By the inductive hypothesis, the larger root subtree of t₂ can display a caterpillar of size w – 1 through a root configuration γ′. Taking the root configuration γ of t₂ obtained as γ = γ′ ⋃ {ρ}, where ρ is the root of the smaller root subtree of t₂, we have t₁ ≅ t₂(γ) as desired.

Now suppose we are given a tree t ∈ T_n,w, with 2 ≤ w ≤ w′(n). The smaller root subtree t_rS of t is by definition a caterpillar of size w ≥ 2, and the larger root subtree t_rL has size |t_rL| = n – w. By definition, w ≤ w′(n) = ⌊x⌋ ≤ x, where x = n – 2^x–2 – 1, and therefore, w ≤ n – 2^w–2 – 1. In particular, |t_rL| = n – w ≥ 2^w–2 + 1. From what we have shown above, a root configuration γ of t_rL exists such that t_rS ≅ t_rL(γ).

Appendix 5

Proof of (18)

Recall that for each tree t ∈ T_n,w, the smaller root subtree t_rS is a caterpillar of size w ∈ [1,w′] and the larger root subtree t_rL has size n – w. Because we assume w < n/2, t_rS and t_rL have different sizes and different unlabeled topologies. Given a tree t̄ ∈ T_n–w, the number of trees in T_n,w such that t_rL = t̄ (after rescaling labels for the taxa) is $\left(\begin{array}{c}n\\ w\end{array}\right){\gamma }_w$, where γ_w is the number of caterpillar labeled topologies of size w. Dividing by $\left|T_{n,w}\right|=\left(\begin{array}{c}n\\ w\end{array}\right){\gamma }_w\left|T_{n-w}\right|$yields the probability ℙ[t_rL = t̄|t ∈ T_n,w] = 1/|T_n–w| as desired.