Abstract
Metabolic pathways reflect an organism's chemical repertoire and hence their elucidation and design have been a primary goal in metabolic engineering. Various computational methods have been developed to design novel metabolic pathways while taking into account several prerequisites such as pathway stoichiometry, thermodynamics, host compatibility, and enzyme availability. The choice of the method is often determined by the nature of the metabolites of interest and preferred host organism, along with computational complexity and availability of software tools. In this paper, we review different computational approaches used to design metabolic pathways based on the reaction network representation of the database (i.e., graph or stoichiometric matrix) and the search algorithm (i.e., graph search, flux balance analysis, or retrosynthetic search). We also put forth a systematic workflow that can be implemented in projects requiring pathway design and highlight current limitations and obstacles in computational pathway design.
1. Introduction
Nature has endowed specific biochemical capabilities to many organisms spanning diverse metabolic pathways ranging from carbon dioxide fixation by Clostridium ljungdahlii using Wood-Ljungdahl pathway [1] to ammonia assimilation by cyanobacteria using the glutamine synthase cycle (GS-GOGAT) [2]. Advancements in metabolic engineering have enabled us to engineer and express enzymes and construct novel pathways for various applications including drug discovery [3], [4] and value-added biochemical production [5]. Notably, Galanie et al. recently engineered the complete opioids biosynthesis pathways constituting of 21 and 23 native and heterologous enzymes to produce thebaine and hydrocodone, respectively in yeast [4]. In addition, multi-enzymatic steps can nowadays be engineered in a cell-free system for in vitro synthesis [6], [7]. The pathway search involves finding the right combination of enzymes to form the pathway connecting a given source molecule (e.g., carbon substrate or any native metabolites in a cell) to a target molecule. Computational pathway design algorithms enumerate potential routes linking the two molecules, while often taking into consideration a multitude of criteria such as shortest route, minimal number of heterologous reactions, thermodynamic feasibility, and enzyme availability. While most methods capitalize on the large number of enzymatic reactions available in nature, there is also an increasing number of tools that employ biotransformation rules derived from the existing reactions to design de novo pathways [8], [9]. The latter relies on the remarkable malleability of enzymes [10], [11], [12] to accept a broad range of substrates as well as the potential of protein engineering [13], [14] and de novo enzyme design [15]. As an example, Savile et al. carried out in vitro synthesis of enantiopure anti-diabetic sitagliptin by combining computational protein engineering and directed evolution to broaden the substrate range of transaminase enzyme [7].
Pathway discovery tools have successfully guided several metabolic engineering efforts. In particular, Yim et al. [5] demonstrated the production of up to 18 g/L of 1,4-butanediol (BDO) in E. coli by engineering the best pathways after surveying over 10,000 computationally designed pathways. The BDO titer was increased to 110 g/L with improved downstream enzymes [16]. Their success highlights the potential application of pathway design algorithms to a variety of projects [6]. Pathway design tools are not only applicable to pathway prospecting for biosynthesis of commodity chemicals, biofuels, or pharmaceuticals, but have also been applied to develop biosensing pathways for target molecules. For example, Libis et al. used the retrosynthetic approach (XTMS) to identify pathways from undetectable target molecules such as drugs, pollutants, and biomarkers to known inducer molecules, which could then activate transcription factors [17]. The activated transcription factors can be used to regulate an easily detectable metabolite, antibiotic marker or fluorescence protein, which can be subsequently used to screen for strains producing target molecules [17].
As a large number of pathway design tools have been published, identifying the best method depending on the overarching project goal and available computational tools is a non-trivial task. Although a number of review articles have been published to complete the task, they generally focus on specific aspects such as existing de novo pathway design tools [8], [9], [18], reconstructing metabolic pathways in organisms of interest [19], or identifying/refactoring parts and circuit designs beyond pathway prediction [20]. In this review, we discuss in detail all the steps involved in implementing pathway design algorithms (e.g., database construction, pathway ranking, enzyme selection, etc.). There exist several classifications of pathway design tools based on different aspects of the implementation procedures. For example, Koreta et al. classified these tools into reference-based, reaction-filling, and compound-filling frameworks [19]; Nakamura et al. classified them as fingerprint-based, maximum common substructure-based, and rule-based method [21]; Cho et al. classified them as chemical structural changes-based, enzymatic information-based, and reaction mechanism-based methods [22]. In this review, we choose to classify the tools based on their algorithmic choices such as graph theory, integer optimization, and retrosynthetic organic synthesis. In particular, the algorithms are classified into graph-based [23] (i.e., reactions and metabolites represented as a graph), stoichiometric-based [24] (i.e., reactions and metabolites represented using a stoichiometric matrix) and retrosynthesis-based [8] (i.e., iteratively identify reaction rules that can transform a reactant molecule) approaches. We also compare the pathway design algorithms based on their database curation, reaction network representation and its pruning, search algorithm, and pathway ranking methods used to prioritize the often-expansive list of possible pathways. As the next step for pathway design, we discuss the possibilities to apply protein engineering and de novo enzyme design tools to aid in protein design and discovery for the designed pathways. Finally, we highlight current limitations and explore potential applications of these tools.
2. Generalized in silico pathway design workflow
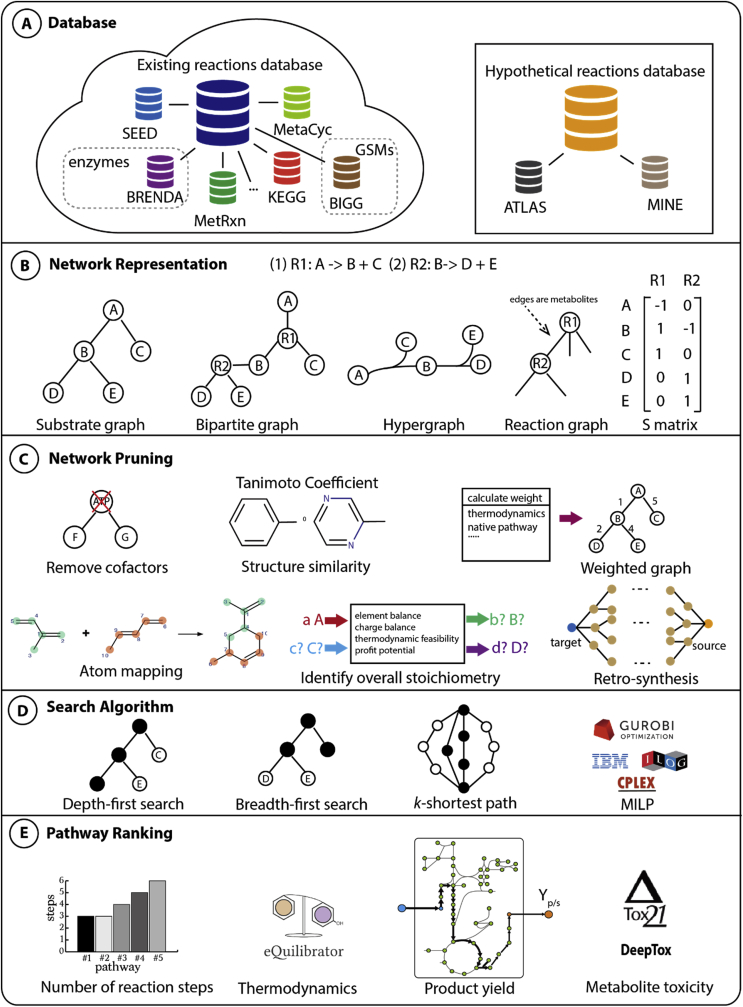
A generalized pathway design workflow highlighting the five steps is presented in Fig. 1: (1) database construction, (2) metabolic network representation, (3) network pruning, (4) search algorithm implementation, and (5) pathway ranking to select the best pathways of interest. In the following section, we discuss a number of pathway design algorithms that follow this design workflow (see Table 1) and highlight the challenges that potential new tools can be developed to tackle.
Fig. 1.
A conceptualized pathway design workflow.
Table 1.
Graph-based, Stoichiometry-based, and retrosynthesis-based pathway design tools and their characteristics.
| Category | Name | Database | Network representation | Network pruning | Search algorithm | Pathway ranking | Reference |
|---|---|---|---|---|---|---|---|
| Graph-based | ReTrace | KEGG | Bipartite graph | Atom mapping | Heuristic search | Atom conservation and pathway length | [23] |
| PathComp | KEGG | Substrate graph | – | Depth-first search (DFS) | – | [26] | |
| MetaRoute | KEGG | Reaction graph | Weighted graph and atom mapping | Eppstein's k-shortest path | Atom conservation and metabolite connectivity | [51] | |
| Pathway Hunter Tool | KEGG | Substrate graph | – | Breadth-first search (BFS) with (Higher-order horn logic) HOHL | Structure similarity and pathway length | [63] | |
| FMM | KEGG | Substrate graph | Manual cofactor removal | BFS | Compare pathway across organisms | [64] | |
| RouteSearch | MetaCyc | Substrate graph | Atom mapping | Branch and Bound | Atom conservation and pathway length | [65] | |
| MRE | KEGG | Substrate graph | Weighted graph | Yen's loopless k-shortest path | Thermodynamics and genes from host organism | [66] | |
| CMPF | KEGG, RPAIR | Bipartite graph | Weighted graph | Bounded depth path enumeration | Metabolite connectivity, reaction occurrence frequency, and pathway switching | [67] | |
| NeAT | MetaCyc | Bipartite graph | Weighted graph | Takahashi–Matsuyama, Pairwise K-shortest paths, and kWalks | Metabolite connectivity | [68] | |
| LPAT/BPAT | KEGG | Bipartite graph | Atom mapping | BPAT-M Search | Atom conservation and pathway length | [69], [139] | |
| Rahnuma | KEGG | Hypergraph | Phylogeny or sub-network | DFS | – | [70] | |
| Metabolic Tinker | CHEBI, Rhea | Hypergraph | Weighted graph | Heuristic search | Pathway length, structure similarity, and thermodynamics | [71] | |
| FogLight | KEGG, MetaCyc | Hypergraph | And/Or graph | Brute-force search | Pathway length | [73] | |
| MRSD | KEGG | substrate graph | Weighted graph | Eppstein's k-shortest path | Reaction occurrence frequency | [78] | |
| DESHARKY | KEGG | – | Phylogeny | Monte Carlo | Metabolic burden | [88] | |
| Stoichiometry-based | optStoic | KEGG, MetRxn | S matrix | Design overall stoichiometry | MILP | Pathway length or total metabolic flux | [24] |
| PathTracer | BIGG, iJO1366 | Substrate graph, S matrix | Atom mapping (MapMaker) | MILP | Pathway length or most active path | [50] | |
| CFP | BIGG | Substrate graph, S matrix | Atom mapping (carbon exchange network) | MILP | Pathway length | [75] | |
| METATOOL 5.0/k-shortest EFM | BIGG, iAF1260 | S matrix | – | MILP | Pathway length | [76], [89] | |
| OptStrain | KEGG | S matrix | – | MILP | Number of heterologous reactions | [99] | |
| Retrosynthesis-based | Simpheny | BIGG | Substrate graph | molecule sizes | Retrosynthetic enumeration | Pathway length, thermodynamics, product yield, number of known metabolites/enzymes, and existence of reaction operators | [5] |
| GEM-Path | BIGG, iJO1366 | Substrate graph | Third level EC number and substrate similarity | Retrosynthetic enumeration | Thermodynamics and product yield | [57] | |
| XTMS/RetroPath/RetroPath 2.0 | MetaCyc, BioCyc | S matrix | Molecular signature with predetermined distance | Retrosynthetic enumeration and MILP | Thermodynamics, gene prediction, pathway length, number of putative steps, and product yield | [52], [82], [84] | |
| BNICE | KEGG, ATLAS | Substrate graph | Qualitative/Quantitative pruning | Retrosynthetic enumeration | Pruning criteria assessment (thermodynamics, pathway length, etc.) | [8], [53] | |
| UM-PPS | UM-BBD | Substrate graph | Rule priority | Retrosynthetic enumeration | – | [56] | |
| PathPred | KEGG, RPAIR | Substrate graph | Structure similarity | Retrosynthetic enumeration | Compound similarity and pathway score | [54] | |
| Route Designer | MOS, Beilste Crossfile | Substrate graph | Heuristics and user defined limits | Retrosynthetic enumeration | Weighted function (wastage, example counts, and balanced disconnections.) | [55] | |
| SimIndex/SimZyme | BRENDA | Substrate graph | Structure similarity | Byers–Waterman type pathway search | Pathway length | [83] | |
| Method by Cho et al. | KEGG | Substrate graph | – | Retrosynthetic enumeration | Combination of five priority factors | [22] |
2.1. Databases
All pathway search tools rely on a database from which biochemical reactions and molecules can be recruited to constitute the pathway of interest. Currently, a number of databases have been constructed for known biochemical reactions and pathways (i.e., BIGG [25], KEGG [26], MetaCyc [27], BRENDA [28], ModelSEED [29], MetRxn [30], Rhea [31], UM-BBD [32], MOS [33], and Beilste Crossfile [34]), as well as hypothetical metabolites and reactions (such as ATLAS of Biochemistry [35], and MINE [36]) (see Fig. 1A). The current version of BIGG database consists of 80 manually curated organism-specific genome-scale metabolic models (GSMs) [25], while KEGG and MetaCyc catalog a more comprehensive array of organisms and their metabolic pathways [37]. KEGG contains 4102 more metabolites than MetaCyc while MetaCyc contains 3695 more reactions (as of August 20, 2017) [37]. BRENDA includes detailed enzyme information such as measured kinetic parameters [28], whereas ModelSEED provides the reaction mapping between KEGG and curated GSMs [29]. Existing databases sometimes have incorrect stoichiometries, imbalanced charges, redundancies due to molecule and reaction synonyms, as well as the lack of chemical structures. Since these databases are ultimately used for pathway design and hypothetical reaction rules construction, manual curation is often a necessary step in order to unify the metabolite and reaction names (to ensure network connectivity) and remove stoichiometrically imbalanced and redundant reactions [38], [39]. Attempts to standardize reaction and metabolite name (e.g., MetRxn [30] and Rhea [31]) were previously made, however, automation of the process remains elusive and is further compounded by the continued discovery of new reactions and metabolites [40]. In a recent effort, MetaNetX [41] employed a reconciliation algorithm MNXref [42] to resolve the discrepancies in reaction and metabolite naming between GSMs. BKM-react matched metabolites and reactions by comparing InChI structures and compound synonyms [43]. RxnFinder used PubChem database to unify compound synonyms and added more than 50,000 reactions curated from literature to its in-house database [44]. Alternatively, the Chemical Translation Service [45] and UniChem [46] provide a simple web application that can interconvert metabolite IDs across different databases. Organism-specific GSMs or knowledge-bases (e.g., EcoCyc [47], AraCyc [48], and HumanCyc [49]) are often constructed or extracted from the larger databases, to ensure the design or identification of alternative pathways within an organism's native network. While certain tools limit the search space to only reactions within a particular organism (e.g., PathTracer [50] uses the E. coli GSM iJO1366), the search for a heterologous pathway would entail the use of a more comprehensive database encompassing multiple organisms, thereby ensuring that a desirable biotransformation (i.e., gene/enzyme) can be found (e.g., optStoic [24] and MetaRoute [51] use the curated KEGG database; XTMS [52] uses MetaCyc).
The potential of broad-substrate enzymes or synthetic enzymes to catalyze previously unknown or de novo reactions have also garnered the interest in using de novo pathway involving various non-natural molecules (e.g., pharmaceutical drugs). Such de novo pathways can be designed by exploiting the generalized reaction rules (e.g., ATLAS of Biochemistry [35]) which could act upon structurally similar metabolites in the databases (e.g., MINE [36]). Although hypothetical reactions have been generated for the implementation of most de novo pathway design algorithms, only two databases, namely ATLAS of Biochemistry and MINE, are currently available for public access. The database of hypothetical reactions can be developed using (but not limited to) five different reaction operators which encode chemical transformation mechanisms in a different manner as described here: (i) BNICE uses bond-electron matrix (BEM) to define non-bonded valence electrons and bond orders [53]; (ii) XTMS uses a molecular signature to generate reaction rules based on substructure of adjacent atoms [52]; (iii) PathPred uses the RDM pattern (developed by KEGG researchers) consisting of reaction center atom (R), atoms of different region (D), and atoms of the matched region (M) [54]; (iv) Route Designer applies a similar rule to that of RDM, by defining reaction core and extended reaction core with primary and secondary bonds and non-reacting neighborhood atoms [55]; (v) UM-PPS [56] and GEM-path [57] use SMIRKS and SMARTS, which exploit a feature string encoding the chemical properties of each atom. Reactions operators generally loose information while converting a known reaction to a rule due to the inherent assumptions in their method to encode chemical transformation mechanisms [58]. In particular, stereochemical changes are often overlooked, including BEM (in BNICE) and molecular signatures (in XTMS), as they do not contain chiral center information [58]. As a result, the predicted pathway would use stereoisomers (such as l-alanine and d-alanine) interchangeably. This would increase the number of potential pathways with several biologically incorrect predictions (i.e., subsequent reaction steps may use different stereoisomers). However, stereochemical changes have already been captured by many computational tools such as EC-Blast [59] and Reaction Decoder Tool [60], which use the Chemistry Development Kit (CDK) [61], and CLCA [62] to model stereochemical changes by appending stereochemical descriptors to the canonical labeling of each atom. It is therefore timely for reaction rule-based methods to incorporate such advanced descriptors to generate descriptions that are more detailed.
2.2. Representation of the database (metabolic network)
The curated reaction and metabolite database used for pathway search are henceforth denoted as a metabolic network in the text. Metabolic network (with and without hypothetical reactions) can be represented by a graph (i.e., substrate graph, bipartite graph, hypergraph, or reaction graph) or a stoichiometric matrix (S matrix) (see Fig. 1B). The vertices of substrate graph are metabolites and edges represent reactions, while the bipartite graph uses both metabolites and reactions as vertices with the edges connecting either a substrate to a reaction or a reaction to a product. Most of the pathway design tools are based on substrate graphs, namely Pathway Hunter Tools [63], FMM [64], RouteSearch [65], and MRE [66]. In contrast to the substrate graph, bipartite graph accounts for enzyme information in the vertices of reactions. Bipartite graph-based tools (such as CMPF [67] and NeAT [68]) enable tracking of reactions identified during pathway search thereby avoiding any post-processing step to link the identified edges to reactions as implemented in substrate graphs [23], [67], [68], [69]. On the other hand, a hypergraph is a more direct representation of biochemical reaction wherein a hyper-edge (representing the reaction) connects all of its participating metabolites (represented as vertices). However, due to the dearth of sophisticated algorithms which can be applied to search hypergraphs, only three methods, namely Rahnuma [70], Metabolic Tinker [71] and the method developed by Carbonell et al. [72], use hypergraph directly, whereas another tool, Foglight simplifies the hypergraph into matrices before performing pathway search [73].
Although bipartite graph and hypergraph can be interconverted, it has been shown that bipartite graphs fail to ensure co-reactant availability while predicting a pathway feasibility unlike hypergraphs [74]. In addition, stoichiometry matrix representation of a metabolic network is equivalent to hypergraphs. The stoichiometry matrix and hypergraph representations have also been shown to be superior to the substrate or bipartite graphs as they retain (co)metabolite information from the original network [74]. Graph-based methods require an additional post-processing step to balance (co)metabolites of the identified pathway due to missing stoichiometry information, which was resolved in CFP [75] and PathTracer [50] by combining graph search with additional stoichiometry constraints to ensure the steady state of the identified pathways. Thus, with careful addition of co-reactant/co-products availability and their stoichiometry information, graph-based methods can make prediction with similar accuracy as stoichiometry-based methods. Moreover, stoichiometry-based pathway search methods can operate on the S matrix alone (such as METATOOL 5.0 [76], optStoic [24], and XTMS [52]) to identify cofactor-balanced pathways. However, the reversibility of a reaction has to be defined as constraints alongside the S matrix while a directed graph inherently contains the information.
2.3. Network pruning
Graph-based methods search for pathways from a given source metabolite to a target metabolite by looking for adjacent reactions which share metabolites as done in PathComp [26]. However, this procedure often arrives at irrelevant biological transitions due to the overwhelming participation of cofactors in metabolic networks as highlighted by Rahman et al. [63]. These procedures rely on substrate graph based metabolic network representation which maps all reactants to all products of a reaction in the graph. However, this representation also connects metabolites that do not exchange any carbon atoms but are participants of the same reaction (e.g., ADP to pyruvate). A simple resolution to this problem is the exclusion of cofactors and other highly connected metabolites (hub metabolites) from the search space (see Fig. 1C), but this option could miss pathways such as nucleotide biosynthesis which involve hub metabolites such as ADP as major intermediates [51]. A more systematic approach involves incorporation of structural similarity between the intermediate metabolites to guide pathway search by using a 1-D chemical fingerprint of the metabolites [63]. Alternatively, this can be achieved by using weighted edges where the network hub metabolites (such as ATP, NAD, etc. that have high participation) can be penalized [77]. The pathway searches can also be made biologically relevant by weighing the reactions edges in the graphs with more information. This was achieved in MRSD using reaction occurrence frequency across multiple organisms as reaction weights to account for biochemical transformations which are conserved across multiple species [78]. Similarly, reaction with more negative Gibbs-free energy can be assigned larger weight according to the thermodynamic favorability-based weighting scheme used in MRE [66]. However, all these approaches do not track the atoms from the substrate which are lost during the transformation to the target metabolites. By including the atom conservation criteria, Route Search [65] enables us to measure the fraction of the carbon atoms from substrates which are lost by the pathway while producing the target metabolite, thus capturing the efficiency of the discovered pathway. The network pruning steps can also take advantage of more systematic information of chemical structure such as atom mapping and KEGG RPAIR database [79]. Atom mapping methods map the transfer of C, O, N, P, S atoms between metabolites in a given reaction. Thus, atom-mapping rules for reactions can also be incorporated to ensure the chemical feasibility of the identified pathways as done by MetaRoute [51], CFP [75], PathTracer [50], AGPathFinder [80], and RouteSearch [65]. KEGG RPAIR data offers a manually curated catalog of main and side metabolites thus avoiding irrelevant biological transitions [79].
Stoichiometry-based methods employ flux balance analysis (FBA) during pathway search which only identifies mass balanced pathways [23]. However, the mass balance restrictions can be relaxed by allowing for cofactors, co-reactants or co-products to be exchanged with the environment which reflects biological reality where pathways do not exist in isolation and exchange metabolites with their surrounding or other pathways. Moreover, the stoichiometry can also be predefined as employed in the first step of the optStoic algorithm [24] to establish an overall stoichiometry design goal that is necessary for the selection of cofactors and co-reactants (see Fig. 1C). Upon identifying the overall stoichiometry equation, the stoichiometric coefficients of the reactants and products are fixed as “uptake” and “secretion” flux of the network. The mixed-integer linear programming (MILP)-based minFlux [24] (i.e., minimize total flux through the network) or minRxn [24] (i.e., minimize the total number of reactions) formulation can then be used to identify an internal network of reactions that could convert the reactants to the products in a mass-balanced manner. Unlike the CFP [75] or the PathTracer [50] approach which generates carbon exchange networks a priori, the minFlux/minRxn [24] formulation uses a metabolic network identical to that of a typical FBA analysis and can be easily extended to any currently available GSMs. Moreover, CFP-related approaches might predict pathways with biologically irrelevant carbon (or other elemental) exchanges [75], [81] due to inaccuracies in the carbon exchange network, which can be resolved using more sophisticated atom-mapping algorithms [81].
In addition to the network pruning steps of existing metabolic networks, retrosynthesis-based approaches for designing de novo pathway require the generation of a metabolic network based on all the hypothetical reaction rules derived using reaction operators (see section 2.1 and Fig. 1C). This hypothetical network can be appended to the network of known reactions, thereby allowing the search of both putative and verified reactions. However, the extended metabolic network is often too large for exhaustive pathway exploration. For example, the initial BNICE computational framework generates an exponentially growing range of hypothetical molecules [53]. In order to reduce the search space, XTMS/RetroPath uses a diameter which defines graph distance of atoms within the radius to control the network size [52], [82]. UM-PPS applies reactions rules based on an ‘absolute aerobic likelihood’ to prune unlikely biotransformation thus avoiding exploration of redundant reaction network [56]. The number of reaction rules that can act upon a metabolite can also be culled based on the availability of (broad-substrate or promiscuous) reactions/enzymes (e.g., GEM-Path uses third level EC number [57]; SimZyme/SimIndex quantifies a molecule's similarity to the typical substrate of an enzyme [83]; RetroPath 2.0 uses enzyme score [84]), molecule sizes (e.g. SimPheny), and expert knowledge such as THERESA [85].
2.4. Search algorithms
The selection of pathway search algorithm is inherently dependent on the underlying representation of the metabolic network (see Fig. 1D). Breadth-first search (BFS) is a widely used algorithm to find the k-shortest paths in a loopless unweighted graph as applied in the Pathway Hunter Tool [63]. As many preprocessing steps assign weights to a graph based on thermodynamics or other criteria, the search requires algorithms such as Yen's k-shortest path algorithm [86] that works on loopless graphs, and Eppstein's k-shortest path algorithm and its modifications [87] that do not require the graph to be loopless. In addition to the weighted graph with a fixed cost at each edge, RouteSearch defined an additional criterion at each edge for non-static atom lost and applied branch-and-bound search to find the best paths to minimize the loss [65]. On the other hand, DESHARKY [88] applied Monte Carlo method to search for reaction combinations. To find the shortest path by S matrix representation, stoichiometry-based pathway design algorithms that use MILP is the common approach (e.g., k-shortest Elementary Flux Modes (k-shortest EFMs) [89] and optStoic [24]). k-shortest EFM has been shown to provide more accurate pathway designs from fatty-acids to glucose than graph-based methods such as Pathway Hunter Tools [90], [91], [92], [93]. Stoichiometry-based methods are better than graph-based methods as they account for mass balance constraints by directly incorporating the stoichiometry information. Currently, MILP can be solved by many open-source solvers (e.g., SCIP [94]) and commercial solvers (e.g., CPLEX [95] and GUROBI [96]), which employ algorithms such as Branch-and-Bound and Branch-and-Cut along with customized heuristic searches. Alternative pathways can be also identified by adding integer cut constraints.
The selection of search algorithms also relies on the desired type of pathways, namely linear or branching pathways. The abovementioned graph-based algorithms only search for linear pathways with one source molecule and one target molecule. In order to identify branching pathways, ReTrace [23] combines shortest paths into branched pathways to reach a higher fraction of atom transfer from source to target metabolite. LPAT [69] developed another linear pathway merging algorithm BPAT-M using atom tracking information. In addition, graph-based algorithms that can efficiently find paths from two nodes (e.g. A*) can be adapted to recursively search the relevant branched sub-paths without atom mapping information. In contrast to graph-based algorithms, MILP algorithms can find branched or even cyclic pathways [24].
2.5. Pathway ranking
Pathway design tools often identify multiple pathways for a given substrate and metabolite pair which can be distinguished based on several factors such as host compatibility, availability of natural enzymes (or protein engineering), and protein solubility (see Fig. 1E). The most common method used to rank pathways is by the number of reaction steps, as this can be easily translated into an objective function in a number of methods (e.g., optStoic [24], CFP [75], and k-shortest EFM [89], FindPath [97]) to find the shortest pathway or pathway with the least total flux. The shortest pathway also implies fewest reaction steps or minimal enzyme requirement, thereby reducing the metabolic/genetic burden on the host cells. This is based on the assumption that each reaction is catalyzed by a single gene, which however is not always true [98]. Reduced number of genetic modifications also enables a faster and simpler experimental implementation. Alternately, one could directly aim for the minimal number of genes as the objective (e.g., SimOptStrain [98] identifies the minimal number of genetic interventions). Likewise, if the host organism is predefined, then it is also possible to minimize the number of heterologous reactions that need to be added (e.g., in OptStrain [99] and MRE [66]). This is a plausible objective as dealing with heterologous enzymes in metabolic engineering project often poses a different set of challenges including that of enzyme activity, protein solubility, codon optimization, and foreign cofactor utilization. In particular, for rule-based approaches, if an existing enzyme that can perform the biotransformation is not known, then it is often required to search for a natural promiscuous enzyme for the substrate of interest or even design a de novo protein [100]. Despite various successful cases (e.g., Merck & Co.'s in vitro sitagliptin synthesis [7] and deep learning to rank the most suitable reaction rules [101]), protein engineering to confer a novel enzyme activity is a time-consuming effort with an uncertain outcome. Therefore, when using a rule-based pathway design approach, it is common to rank pathways based on the number of known enzymes [5].
Thermodynamic feasibility is another commonly used method for pathway ranking. Similar to the preprocessing step that assigns weight to a graph to prune infeasible pathways and select pathway with more negative ΔG, the designed pathways can be sorted based on their most negative overall ΔG, which sums up the ΔG of each reaction step. Group Contribution Method [102], and a recently developed and publicly available Component Contributions Method [103] or eQuilibrator [104] can be used to estimate the standard transformed Gibbs free energy of reaction under the host cell environment (e.g., cellular compartment pH, growth temperature). Knowledge of the intracellular metabolite concentrations can be used to further refine the estimation of the actual Gibbs free energy of reaction, but it is generally not used due to the lack of metabolome data. Instead, the Max-min Driving Force [105] approach can be used to optimize the concentrations of metabolites within a pathway given the physiological concentration ranges and quantify the thermodynamic feasibility of the pathway. Although the availability of intracellular metabolite concentrations is often limited, this could be overcome by an approach that uses the support vector machine (SVM) model to infer the theoretical intracellular metabolite concentration [106].
In order to rank pathway based on product yield, a designed pathway can be introduced into the GSM of the host strain and FBA can be performed to identify the maximum achievable yield from the pathway [3], [57], [107]. This is particularly important as many pathway design tools often only target a short pathway from any precursor metabolite that can be produced by a host cell to the target product. However, in addition to simulating whether a carbon source (e.g., glucose) could drive flux towards the target product, FBA also ensures all cofactors/co-substrates and biomass of the cell could be produced and every reaction (native or heterologous) used in the identified pathway must carry non-zero flux [50], [108]. Another possible method is by constructing kinetic models of the designed pathway and calculating the flux through the pathway. This method is used recently to evaluate a large number of trunk glycolytic pathways [109]. However, the paucity of kinetic parameters could hamper such an approach. Alternately, an ensemble of kinetic parameters can be sampled and used to determine the stability of the pathway (EMRA) [110]. These approaches are however more computationally demanding and may not be suitable for initial filtering of a large number of the designed pathways [111], [112]. A simpler more tractable approach based on modular kinetic rate law [113], [114], [115] can be applied to evaluate the protein cost of a pathway as an alternate pathway ranking criteria.
Other possible approaches include a scoring system based on assessing the toxicity of intermediate metabolites of a pathway in a host cell [116], [117]. For example, a database like Tox21 [118] and a deep learning based algorithm (DeepTox) [119] have been applied to identify potentially toxic effects of chemical compounds. The selection of pathway ranking method(s) depends on the design goal. For example, in order to design a pathway for the production of a certain biomolecule, one may consider thermodynamics, theoretical yield from FBA simulation, the minimal number of reactions, and toxicity of intermediate metabolite on host cell as primary ranking criteria. Often, a combination of these filtering, ranking or scoring systems can be used as demonstrated by Yim et al. [5].
3. DNA sequence selection, protein engineering, and de novo enzyme design
The selection and design of DNA sequence still remain elusive for pathway designs. Most of the pathway design tools identify the list of reactions that are needed to fill the gap between source and target metabolites. However, there is currently a large natural catalog of enzyme sequences from which the user has to select to express the pathway. A number of pathway design tools prioritize the selection based on binding site covalence, chemical similarity, and organism specificity [22]. Additional screening criteria such as protein solubility in the host system can also be employed to refine the sequence selection. Generally, the host organism is known a priori, and native enzymes are assigned higher priority and the minimal number of heterologous reactions are selected from closely related species. However, in certain projects where the target metabolite is not common (e.g., xenobiotics), it is necessary to select a host organism based on the pathways that are identified. In addition, promiscuous enzymes are required to perform the biotransformation in the reactions without natural enzymes. The in vivo discovery of such enzymes is a daunting task and requires the assistance of computational prediction tools. For example, Carbonell et al. [120] performed a machine learning-based promiscuity analysis to predict if a reaction rule can be catalyzed by a natural enzyme. However, the prediction relies on manually defined promiscuity instead of actual in vivo data. Supervised machine learning algorithms can give better predictions with more correctly labeled “big data”. Hence, a database of DNA sequences and the corresponding enzyme substrate and enzyme activity (such as BRENDA [28] and SABIO-RK [121]) should be included in machine learning workflow to predict enzyme-substrate pairs with high likelihood for interaction.
When natural enzymes fail to perform the predicted reaction steps, protein engineering fills the void by altering existing enzyme activity and specificity [100] and ultimately designing de novo enzymes. Computational protein engineering tools can guide rational protein design and facilitate the efforts involving random mutagenesis-based directed evolution. Two widely applied strategies are used to predict protein designs: (i) statistical methods to compare modified sequences with sequence database (e.g. GenBank [122]), and (ii) molecular modeling methods to take advantage of the atom-level structural information to predict its biochemical properties. Taking advantage of both these methods, Pantazes et al. [123], [124], [125] developed an Iterative Protein Redesign and Optimization (IPRO) suite which applies the workflow of alternating protein backbone perturbations and amino acid sequence mutations to design proteins with desired catalytic activity. In addition, a number of computational tools (e.g. DEZYMER [126], [127], ORBIT [128], ROSETTA [129], CCBuilder [130], [131], and Protein WISDOM [132]) are aimed at de novo enzyme design by exploiting the underlying protein biochemistry and biophysics. However certain enzyme properties such as configurational entropy changes are beyond the scope of computational tools [15], thus in practice, the computational predictions are often complemented with directed evolution methods to provide a starting design for in vitro improvement. For example, Rothlisberger et al. [15] used directed evolution after the molecular modeling method to further improve the enzyme's catalytic efficiencies. In spite of the numerous successes in engineering and designing new proteins, protein engineering and design tools have not been integrated with traditional pathway design tools as the latter focus on naturally occurring enzymes. However, retrosynthesis-based pathway design tools often propose novel biotransformation by natural enzymes based on the structural similarities between the enzyme's native substrate and the new substrate (e.g. SimZyme [83]). The identified enzyme can serve as a starting point for the protein engineering and design tools to further its catalytic activity towards the novel biotransformation. For detailed tools and applications of protein engineering for pathways, we refer the reader to the following resources [133], [134], [135], [136].
4. Perspective
In this paper, we have compared different computational approaches used to design metabolic pathways in terms of the database used, its representation and pruning, search algorithm and pathway ranking. The graph-based methods often need additional post-processing steps to balance co-metabolites of predicted pathways that may be unbalanced. Stoichiometry-based methods avoid the preprocessing steps to remove no-carbon transfer connections because the S matrix representation accounts for all participating metabolites of a reaction similar to hypergraph representation. In addition, stoichiometry-based methods can incorporate pathway ranking criteria, such as thermodynamics, relative cost, and pathway length into the MILP optimization framework as an objective function thus homing at first at the most desirable designs avoiding exhaustive enumeration of pathways and ranking them a posteriori. Retrosynthesis-based methods employ similar search methods as used by graph-based or stoichiometry-based methods to design pathways by searching through an extended graph or stoichiometric network. Out of the reviewed retrosynthesis-based pathway design tools, only XTMS uses stoichiometry-based EFM tools to search for pathways while other methods rely on graph-based tools [52]. The performance of de novo pathway tools can be improved by switching to stoichiometry-based tools in order to circumvent unbalanced pathways and pathway post-processing that are inherent in graph-based methods. Although XTMS [52] enumerates pathways based on EFMs, it does not directly consider the stoichiometry of the source and target metabolites. A retrosynthetic tool that can design stoichiometry a priori based on the first step of optStoic [24] and identify cofactor balanced pathways by design while limiting the number of novel reaction steps would be an important advancement for de novo pathway design.
Nevertheless, it is worth mentioning that stoichiometry-based methods are not without their challenges such as longer computational time and the possible presence of thermodynamically infeasible cycles within designed pathways. The computational time depends highly on the objective function and constraints (or integer cuts) that are imposed. For example, the minRxn formulation of optStoic requires significantly higher computational cost than the minFlux formulation [24]. Furthermore, the computational time also scales with the search space, which can be resolved by first removing blocked reactions (i.e., reaction that could not carry any flux under a specific condition) from the S matrix. Alongside formulating the strongest MILP problem, a number of heuristics based on branch-and-bound and branch-and-cut methods are available and are under-development in open-source, academic, and commercial software packages to improve the solving time [137]. Stoichiometry-based methods sometimes identify futile cycles to balance cofactors. In CFP [75] and PathTracer [50], this is remedied by preventing flux from re-visiting a metabolite (node), whereas an updated version of optStoic is currently in development to resolve this issue in a systematic manner (Ng, Chowdhury, Maranas, manuscript in preparation).
Despite the success of current computational design tools to identify pathways, challenges still remain on the selection of genes, discovery of promiscuous enzymes, engineering proteins, and designing de novo enzymes to catalyze putative reactions. Overall, a completely automated pipeline that goes from selection of source and target molecule to the final output of DNA sequences of a pathway would significantly facilitate the discovery of new metabolic pathways for various applications. Experimental validation of multiple pathway designs has already been accelerated through an automated digital-to-biological DNA manufacturing system [138]. Although there remain several limitations that need to be addressed, exemplary efforts such as RetroPath 2.0 [84] and ATLAS [35] provide a benchmark that can be improved upon to realize the ultimate goal.
Acknowledgment
The authors gratefully acknowledge funding from the DOE (http://www.energy.gov/) grant no. DE-SC0008091 and NSF (http://www.nsf.gov/) award no. EEC-0813570 and no. NSF/MCB-1546840.
Footnotes
Peer review under responsibility of KeAi Communications Co., Ltd.
References
- 1.Wood H.G. Life with Co or Co2 and H2 as a source of carbon and energy. Faseb J. 1991;5(2):156–163. doi: 10.1096/fasebj.5.2.1900793. [DOI] [PubMed] [Google Scholar]
- 2.Chavez S. The presence of glutamate dehydrogenase is a selective advantage for the Cyanobacterium synechocystis sp. strain PCC 6803 under nonexponential growth conditions. J Bacteriol. 1999;181(3):808–813. doi: 10.1128/jb.181.3.808-813.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Moura M. Evaluating enzymatic synthesis of small molecule drugs. Metab Eng. 2016;33:138–147. doi: 10.1016/j.ymben.2015.11.006. [DOI] [PubMed] [Google Scholar]
- 4.Galanie S. Complete biosynthesis of opioids in yeast. Science. 2015;349(6252):1095–1100. doi: 10.1126/science.aac9373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Yim H. Metabolic engineering of Escherichia coli for direct production of 1,4-butanediol. Nat Chem Biol. 2011;7(7):445–452. doi: 10.1038/nchembio.580. [DOI] [PubMed] [Google Scholar]
- 6.Blass L.K., Weyler C., Heinzle E. Network design and analysis for multi-enzyme biocatalysis. BMC Bioinforma. 2017;18(1):366. doi: 10.1186/s12859-017-1773-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Savile C.K. Biocatalytic asymmetric synthesis of chiral amines from ketones applied to sitagliptin manufacture. Science. 2010;329(5989):305–309. doi: 10.1126/science.1188934. [DOI] [PubMed] [Google Scholar]
- 8.Hadadi N., Hatzimanikatis V. Design of computational retrobiosynthesis tools for the design of de novo synthetic pathways. Curr Opin Chem Biol. 2015;28:99–104. doi: 10.1016/j.cbpa.2015.06.025. [DOI] [PubMed] [Google Scholar]
- 9.Prather K.L., Martin C.H. De novo biosynthetic pathways: rational design of microbial chemical factories. Curr Opin Biotechnol. 2008;19(5):468–474. doi: 10.1016/j.copbio.2008.07.009. [DOI] [PubMed] [Google Scholar]
- 10.Nam H. Network context and selection in the evolution to enzyme specificity. Science. 2012;337(6098):1101–1104. doi: 10.1126/science.1216861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Khare S.D. Computational redesign of a mononuclear zinc metalloenzyme for organophosphate hydrolysis. Nat Chem Biol. 2012;8(3):294–300. doi: 10.1038/nchembio.777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ekroos M., Sjogren T. Structural basis for ligand promiscuity in cytochrome P450 3A4. Proc Natl Acad Sci U. S. A. 2006;103(37):13682–13687. doi: 10.1073/pnas.0603236103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Coelho P.S. Olefin cyclopropanation via carbene transfer catalyzed by engineered cytochrome P450 enzymes. Science. 2013;339(6117):307–310. doi: 10.1126/science.1231434. [DOI] [PubMed] [Google Scholar]
- 14.Young E.M. Rewiring yeast sugar transporter preference through modifying a conserved protein motif. Proc Natl Acad Sci U. S. A. 2014;111(1):131–136. doi: 10.1073/pnas.1311970111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rothlisberger D. Kemp elimination catalysts by computational enzyme design. Nature. 2008;453(7192):190–195. doi: 10.1038/nature06879. [DOI] [PubMed] [Google Scholar]
- 16.Burgard A. Development of a commercial scale process for production of 1,4-butanediol from sugar. Curr Opin Biotechnol. 2016;42:118–125. doi: 10.1016/j.copbio.2016.04.016. [DOI] [PubMed] [Google Scholar]
- 17.Libis V., Delepine B., Faulon J.L. Expanding biosensing abilities through computer-aided design of metabolic pathways. ACS Synth Biol. 2016;5(10):1076–1085. doi: 10.1021/acssynbio.5b00225. [DOI] [PubMed] [Google Scholar]
- 18.Fernandez-Castane A. Computer-aided design for metabolic engineering. J Biotechnol. 2014:302–313. doi: 10.1016/j.jbiotec.2014.03.029. 192 Pt B. [DOI] [PubMed] [Google Scholar]
- 19.Kotera M., Goto S. Metabolic pathway reconstruction strategies for central metabolism and natural product biosynthesis. Biophys Physicobiol. 2016;13:195–205. doi: 10.2142/biophysico.13.0_195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Medema M.H. Computational tools for the synthetic design of biochemical pathways. Nat Rev Microbiol. 2012;10(3):191–202. doi: 10.1038/nrmicro2717. [DOI] [PubMed] [Google Scholar]
- 21.Nakamura M. An efficient algorithm for de novo predictions of biochemical pathways between chemical compounds. Bmc Bioinforma. 2012;13 doi: 10.1186/1471-2105-13-S17-S8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Cho A. Prediction of novel synthetic pathways for the production of desired chemicals. BMC Syst Biol. 2010;4:35. doi: 10.1186/1752-0509-4-35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Pitkanen E., Jouhten P., Rousu J. Inferring branching pathways in genome-scale metabolic networks. BMC Syst Biol. 2009;3:103. doi: 10.1186/1752-0509-3-103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chowdhury A., Maranas C.D. Designing overall stoichiometric conversions and intervening metabolic reactions. Sci Rep. 2015:5. doi: 10.1038/srep16009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.King Z.A. BiGG Models: a platform for integrating, standardizing and sharing genome-scale models. Nucleic Acids Res. 2016;44(D1):D515–D522. doi: 10.1093/nar/gkv1049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Goto S. Organizing and computing metabolic pathway data in terms of binary relations. Pac Symp Biocomput. 1997:175–186. [PubMed] [Google Scholar]
- 27.Caspi R. The MetaCyc database of metabolic pathways and enzymes and the BioCyc collection of pathway/genome databases. Nucleic Acids Res. 2016;44(D1):D471–D480. doi: 10.1093/nar/gkv1164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Scheer M. BRENDA, the enzyme information system in 2011. Nucleic Acids Res. 2011;39:D670–D676. doi: 10.1093/nar/gkq1089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Henry C.S. High-throughput generation, optimization and analysis of genome-scale metabolic models. Nat Biotechnol. 2010;28(9) doi: 10.1038/nbt.1672. 977-U22. [DOI] [PubMed] [Google Scholar]
- 30.Kumar A., Suthers P.F., Maranas C.D. MetRxn: a knowledgebase of metabolites and reactions spanning metabolic models and databases. BMC Bioinforma. 2012;13:6. doi: 10.1186/1471-2105-13-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Alcantara R. Rhea-a manually curated resource of biochemical reactions. Nucleic Acids Res. 2012;40(D1):D754–D760. doi: 10.1093/nar/gkr1126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gao J., Ellis L.B., Wackett L.P. The University of Minnesota Biocatalysis/Biodegradation Database: improving public access. Nucleic Acids Res. 2010;38(Database issue):D488–D491. doi: 10.1093/nar/gkp771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sutter J. New features that improve the pharmacophore tools from Accelrys. Curr Comput Aided Drug Des. 2011;7(3):173–180. doi: 10.2174/157340911796504305. [DOI] [PubMed] [Google Scholar]
- 34.Vanco J. The beilstein CrossFire information system and its use in pharmaceutical chemistry. Ceska Slov Farm. 2003;52(2):68–72. [PubMed] [Google Scholar]
- 35.Hadadi N. ATLAS of biochemistry: a repository of all possible biochemical reactions for synthetic biology and metabolic engineering studies. Acs Synth Biol. 2016;5(10):1155–1166. doi: 10.1021/acssynbio.6b00054. [DOI] [PubMed] [Google Scholar]
- 36.Jeffryes J.G. MINEs: open access databases of computationally predicted enzyme promiscuity products for untargeted metabolomics. J Cheminformatics. 2015;7 doi: 10.1186/s13321-015-0087-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Altman T. A systematic comparison of the MetaCyc and KEGG pathway databases. Bmc Bioinforma. 2013;14 doi: 10.1186/1471-2105-14-112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Chan, S.H., et al., Standardizing biomass reactions and ensuring complete mass balance in genome-scale metabolic models. Bioinformatics. [DOI] [PubMed]
- 39.Dash S., Ng C.Y., Maranas C.D. Metabolic modeling of clostridia: current developments and applications. FEMS Microbiol Lett. 2016;363(4) doi: 10.1093/femsle/fnw004. [DOI] [PubMed] [Google Scholar]
- 40.Mukherjee S. 1,003 reference genomes of bacterial and archaeal isolates expand coverage of the tree of life. Nat Biotechnol. 2017;35(7):676–683. doi: 10.1038/nbt.3886. [DOI] [PubMed] [Google Scholar]
- 41.Moretti S. MetaNetX/MNXref–reconciliation of metabolites and biochemical reactions to bring together genome-scale metabolic networks. Nucleic Acids Res. 2016;44(D1):D523–D526. doi: 10.1093/nar/gkv1117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bernard T. Reconciliation of metabolites and biochemical reactions for metabolic networks. Brief Bioinform. 2014;15(1):123–135. doi: 10.1093/bib/bbs058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lang M., Stelzer M., Schomburg D. BKM-react, an integrated biochemical reaction database. BMC Biochem. 2011;12:42. doi: 10.1186/1471-2091-12-42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hu Q.N. RxnFinder: biochemical reaction search engines using molecular structures, molecular fragments and reaction similarity. Bioinformatics. 2011;27(17):2465–2467. doi: 10.1093/bioinformatics/btr413. [DOI] [PubMed] [Google Scholar]
- 45.Wohlgemuth G. The Chemical Translation Service–a web-based tool to improve standardization of metabolomic reports. Bioinformatics. 2010;26(20):2647–2648. doi: 10.1093/bioinformatics/btq476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Chambers J. UniChem: a unified chemical structure cross-referencing and identifier tracking system. J Cheminform. 2013;5(1):3. doi: 10.1186/1758-2946-5-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Keseler I.M. The EcoCyc database: reflecting new knowledge about Escherichia coli K-12. Nucleic Acids Res. 2017;45(D1):D543–D550. doi: 10.1093/nar/gkw1003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Mueller L.A., Zhang P., Rhee S.Y. AraCyc: a biochemical pathway database for Arabidopsis. Plant Physiol. 2003;132(2):453–460. doi: 10.1104/pp.102.017236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Romero P. Computational prediction of human metabolic pathways from the complete human genome. Genome Biol. 2005;6(1):R2. doi: 10.1186/gb-2004-6-1-r2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Tervo C.J., Reed J.L. MapMaker and PathTracer for tracking carbon in genome-scale metabolic models. Biotechnol J. 2016;11(5):648–661. doi: 10.1002/biot.201500267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Blum T., Kohlbacher O. MetaRoute: fast search for relevant metabolic routes for interactive network navigation and visualization. Bioinformatics. 2008;24(18):2108–2109. doi: 10.1093/bioinformatics/btn360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Carbonell P. XTMS: pathway design in an eXTended metabolic space. Nucleic Acids Res. 2014;42(Web Server issue):W389–W394. doi: 10.1093/nar/gku362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Hatzimanikatis V. Exploring the diversity of complex metabolic networks. Bioinformatics. 2005;21(8):1603–1609. doi: 10.1093/bioinformatics/bti213. [DOI] [PubMed] [Google Scholar]
- 54.Moriya Y. PathPred: an enzyme-catalyzed metabolic pathway prediction server. Nucleic Acids Res. 2010;38(Web Server issue):W138–W143. doi: 10.1093/nar/gkq318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Law J. Route Designer: a retrosynthetic analysis tool utilizing automated retrosynthetic rule generation. J Chem Inf Model. 2009;49(3):593–602. doi: 10.1021/ci800228y. [DOI] [PubMed] [Google Scholar]
- 56.Gao J., Ellis L.B., Wackett L.P. The university of Minnesota pathway prediction system: multi-level prediction and visualization. Nucleic Acids Res. 2011;39(Web Server issue):W406–W411. doi: 10.1093/nar/gkr200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Campodonico M.A. Generation of an atlas for commodity chemical production in Escherichia coli and a novel pathway prediction algorithm, GEM-Path. Metab Eng. 2014;25:140–158. doi: 10.1016/j.ymben.2014.07.009. [DOI] [PubMed] [Google Scholar]
- 58.Shin J.H. Production of bulk chemicals via novel metabolic pathways in microorganisms. Biotechnol Adv. 2013;31(6):925–935. doi: 10.1016/j.biotechadv.2012.12.008. [DOI] [PubMed] [Google Scholar]
- 59.Rahman S.A. EC-BLAST: a tool to automatically search and compare enzyme reactions. Nat Methods. 2014;11(2):171–174. doi: 10.1038/nmeth.2803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Rahman S.A. Reaction Decoder Tool (RDT): extracting features from chemical reactions. Bioinformatics. 2016;32(13):2065–2066. doi: 10.1093/bioinformatics/btw096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Steinbeck C. The chemistry development Kit (CDK): an open-source java library for chemo- and bioinformatics. J Chem Inf Comput Sci. 2003;43(2):493–500. doi: 10.1021/ci025584y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Kumar A., Maranas C.D. CLCA: maximum common molecular substructure queries within the MetRxn database. J Chem Inf Model. 2014;54(12):3417–3438. doi: 10.1021/ci5003922. [DOI] [PubMed] [Google Scholar]
- 63.Rahman S.A. Metabolic pathway analysis web service (Pathway Hunter Tool at CUBIC) Bioinformatics. 2005;21(7):1189–1193. doi: 10.1093/bioinformatics/bti116. [DOI] [PubMed] [Google Scholar]
- 64.Chou C.H. FMM: a web server for metabolic pathway reconstruction and comparative analysis. Nucleic Acids Res. 2009;37(Web Server issue):W129–W134. doi: 10.1093/nar/gkp264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Latendresse M., Krummenacker M., Karp P.D. Optimal metabolic route search based on atom mappings. Bioinformatics. 2014;30(14):2043–2050. doi: 10.1093/bioinformatics/btu150. [DOI] [PubMed] [Google Scholar]
- 66.Kuwahara H. MRE: a web tool to suggest foreign enzymes for the biosynthesis pathway design with competing endogenous reactions in mind. Nucleic Acids Res. 2016;44(W1):W217–W225. doi: 10.1093/nar/gkw342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Lim K., Wong L. CMPF: class-switching minimized pathfinding in metabolic networks. BMC Bioinforma. 2012;13(Suppl 17):S17. doi: 10.1186/1471-2105-13-S17-S17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Faust K. Pathway discovery in metabolic networks by subgraph extraction. Bioinformatics. 2010;26(9):1211–1218. doi: 10.1093/bioinformatics/btq105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Heath A.P., Bennett G.N., Kavraki L.E. An algorithm for efficient identification of branched metabolic pathways. J Comput Biol. 2011;18(11):1575–1597. doi: 10.1089/cmb.2011.0165. [DOI] [PubMed] [Google Scholar]
- 70.Mithani A., Preston G.M., Hein J. Rahnuma: hypergraph-based tool for metabolic pathway prediction and network comparison. Bioinformatics. 2009;25(14):1831–1832. doi: 10.1093/bioinformatics/btp269. [DOI] [PubMed] [Google Scholar]
- 71.McClymont K., Soyer O.S. Metabolic tinker: an online tool for guiding the design of synthetic metabolic pathways. Nucleic Acids Res. 2013;41(11):e113. doi: 10.1093/nar/gkt234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Carbonell P. Enumerating metabolic pathways for the production of heterologous target chemicals in chassis organisms. BMC Syst Biol. 2012;6:10. doi: 10.1186/1752-0509-6-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Khosraviani M., Saheb Zamani M., Bidkhori G. FogLight: an efficient matrix-based approach to construct metabolic pathways by search space reduction. Bioinformatics. 2016;32(3):398–408. doi: 10.1093/bioinformatics/btv578. [DOI] [PubMed] [Google Scholar]
- 74.Klamt S., Haus U.U., Theis F. Hypergraphs and cellular networks. PLoS Comput Biol. 2009;5(5) doi: 10.1371/journal.pcbi.1000385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Pey J. Path finding methods accounting for stoichiometry in metabolic networks. Genome Biol. 2011;12(5):R49. doi: 10.1186/gb-2011-12-5-r49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.von Kamp A., Schuster S. Metatool 5.0: fast and flexible elementary modes analysis. Bioinformatics. 2006;22(15):1930–1931. doi: 10.1093/bioinformatics/btl267. [DOI] [PubMed] [Google Scholar]
- 77.Croes D. Metabolic PathFinding: inferring relevant pathways in biochemical networks. Nucleic Acids Res. 2005;33(Web Server issue):W326–W330. doi: 10.1093/nar/gki437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Xia D. MRSD: a web server for metabolic route search and design. Bioinformatics. 2011;27(11):1581–1582. doi: 10.1093/bioinformatics/btr160. [DOI] [PubMed] [Google Scholar]
- 79.Faust K., Croes D., van Helden J. Metabolic pathfinding using RPAIR annotation. J Mol Biol. 2009;388(2):390–414. doi: 10.1016/j.jmb.2009.03.006. [DOI] [PubMed] [Google Scholar]
- 80.Huang Y.R. A method for finding metabolic pathways using atomic group tracking. Plos One. 2017;12(1) doi: 10.1371/journal.pone.0168725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Pey J., Planes F.J., Beasley J.E. Refining carbon flux paths using atomic trace data. Bioinformatics. 2014;30(7):975–980. doi: 10.1093/bioinformatics/btt653. [DOI] [PubMed] [Google Scholar]
- 82.Carbonell P. A retrosynthetic biology approach to metabolic pathway design for therapeutic production. BMC Syst Biol. 2011;5:122. doi: 10.1186/1752-0509-5-122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Pertusi D.A. Efficient searching and annotation of metabolic networks using chemical similarity. Bioinformatics. 2015;31(7):1016–1024. doi: 10.1093/bioinformatics/btu760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Delépine B. bioRxiv; 2017. RetroPath2.0: a retrosynthesis workflow for metabolic engineers; p. 141721. [DOI] [PubMed] [Google Scholar]
- 85.Liu M. Combining chemoinformatics with bioinformatics: in silico prediction of bacterial flavor-forming pathways by a chemical systems biology approach “reverse pathway engineering”. PLoS One. 2014;9(1):e84769. doi: 10.1371/journal.pone.0084769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Yen J.Y. Finding K shortest loopless paths in a network. Manag Sci Ser a-Theory. 1971;17(11):712–716. [Google Scholar]
- 87.Eppstein D. Finding the k shortest paths. Siam J Comput. 1998;28(2):652–673. [Google Scholar]
- 88.Rodrigo G. DESHARKY: automatic design of metabolic pathways for optimal cell growth. Bioinformatics. 2008;24(21):2554–2556. doi: 10.1093/bioinformatics/btn471. [DOI] [PubMed] [Google Scholar]
- 89.de Figueiredo L.F. Computing the shortest elementary flux modes in genome-scale metabolic networks. Bioinformatics. 2009;25(23):3158–3165. doi: 10.1093/bioinformatics/btp564. [DOI] [PubMed] [Google Scholar]
- 90.de Figueiredo L.F. Response to comment on 'Can sugars be produced from fatty acids? A test case for pathway analysis tools'. Bioinformatics. 2009;25(24):3330–3331. doi: 10.1093/bioinformatics/btp591. [DOI] [PubMed] [Google Scholar]
- 91.Faust K., Croes D., van Helden J. In response to 'Can sugars be produced from fatty acids? A test case for pathway analysis tools'. Bioinformatics. 2009;25(23):3202–3205. doi: 10.1093/bioinformatics/btp557. [DOI] [PubMed] [Google Scholar]
- 92.de Figueiredo L.F. Can sugars be produced from fatty acids? A test case for pathway analysis tools. Bioinformatics. 2009;25(1):152–158. doi: 10.1093/bioinformatics/btn621. [DOI] [PubMed] [Google Scholar]
- 93.de Figueiredo L.F. Can sugars be produced from fatty acids? A test case for pathway analysis tools. Bioinformatics. 2008;24(22):2615–2621. doi: 10.1093/bioinformatics/btn500. [DOI] [PubMed] [Google Scholar]
- 94.Maher S.J. 2017. The SCIP optimization suite 4.0. [Google Scholar]
- 95.Optimizer I.I.C. 2015. 12.6. 2. IBM ILOG. [Google Scholar]
- 96.Gurobi Optimization I. 2016. Gurobi optimizer reference manual. [Google Scholar]
- 97.Vieira G. FindPath: a Matlab solution for in silico design of synthetic metabolic pathways. Bioinformatics. 2014;30(20):2986–2988. doi: 10.1093/bioinformatics/btu422. [DOI] [PubMed] [Google Scholar]
- 98.Kim J., Reed J.L., Maravelias C.T. Large-scale bi-level strain design approaches and mixed-integer programming solution techniques. PLoS One. 2011;6(9):e24162. doi: 10.1371/journal.pone.0024162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Pharkya P., Burgard A.P., Maranas C.D. OptStrain: a computational framework for redesign of microbial production systems. Genome Res. 2004;14(11):2367–2376. doi: 10.1101/gr.2872004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Siegel J.B. Computational protein design enables a novel one-carbon assimilation pathway. Proc Natl Acad Sci U. S. A. 2015;112(12):3704–3709. doi: 10.1073/pnas.1500545112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Segler M.H.S., Waller M.P. Neural-symbolic machine learning for retrosynthesis and reaction prediction. Chemistry. 2017;23(25):5966–5971. doi: 10.1002/chem.201605499. [DOI] [PubMed] [Google Scholar]
- 102.Jankowski M.D. Group contribution method for thermodynamic analysis of complex metabolic networks. Biophys J. 2008;95(3):1487–1499. doi: 10.1529/biophysj.107.124784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Noor E. Consistent estimation of Gibbs energy using component contributions. PLoS Comput Biol. 2013;9(7):e1003098. doi: 10.1371/journal.pcbi.1003098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Flamholz A. eQuilibrator–the biochemical thermodynamics calculator. Nucleic Acids Res. 2012;40(Database issue):D770–D775. doi: 10.1093/nar/gkr874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Noor E. Pathway thermodynamics highlights kinetic obstacles in central metabolism. PLoS Comput Biol. 2014;10(2):e1003483. doi: 10.1371/journal.pcbi.1003483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Yang H.F. Theoretical studies of intracellular concentration of micro-organisms' metabolites. Sci Rep. 2017;7(1):9048. doi: 10.1038/s41598-017-08793-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Wu D. A computational approach to design and evaluate enzymatic reaction pathways: application to 1-butanol production from pyruvate. J Chem Inf Model. 2011;51(7):1634–1647. doi: 10.1021/ci2000659. [DOI] [PubMed] [Google Scholar]
- 108.Zhang X.L., Tervo C.J., Reed J.L. Metabolic assessment of E. coli as a Biofactory for commercial products. Metab Eng. 2016;35:64–74. doi: 10.1016/j.ymben.2016.01.007. [DOI] [PubMed] [Google Scholar]
- 109.Court S.J., Waclaw B., Allen R.J. Lower glycolysis carries a higher flux than any biochemically possible alternative. Nat Commun. 2015;6:8427. doi: 10.1038/ncomms9427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Lee Y., Lafontaine Rivera J.G., Liao J.C. Ensemble Modeling for Robustness Analysis in engineering non-native metabolic pathways. Metab Eng. 2014;25:63–71. doi: 10.1016/j.ymben.2014.06.006. [DOI] [PubMed] [Google Scholar]
- 111.Khodayari A. A kinetic model of Escherichia coli core metabolism satisfying multiple sets of mutant flux data. Metab Eng. 2014;25:50–62. doi: 10.1016/j.ymben.2014.05.014. [DOI] [PubMed] [Google Scholar]
- 112.Khodayari A., Maranas C.D. A genome-scale Escherichia coli kinetic metabolic model k-ecoli457 satisfying flux data for multiple mutant strains. Nat Commun. 2016;7:13806. doi: 10.1038/ncomms13806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Liebermeister W., Uhlendorf J., Klipp E. Modular rate laws for enzymatic reactions: thermodynamics, elasticities and implementation. Bioinformatics. 2010;26(12):1528–1534. doi: 10.1093/bioinformatics/btq141. [DOI] [PubMed] [Google Scholar]
- 114.Flamholz A. Glycolytic strategy as a tradeoff between energy yield and protein cost. Proc Natl Acad Sci U. S. A. 2013;110(24):10039–10044. doi: 10.1073/pnas.1215283110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Noor E. The protein cost of metabolic fluxes: prediction from enzymatic rate laws and cost minimization. Plos Comput Biol. 2016;12(11) doi: 10.1371/journal.pcbi.1005167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Planson A.G. Compound toxicity screening and structure-activity relationship modeling in Escherichia coli. Biotechnol Bioeng. 2012;109(3):846–850. doi: 10.1002/bit.24356. [DOI] [PubMed] [Google Scholar]
- 117.Planson A.G. A retrosynthetic biology approach to therapeutics: from conception to delivery. Curr Opin Biotechnol. 2012;23(6):948–956. doi: 10.1016/j.copbio.2012.03.009. [DOI] [PubMed] [Google Scholar]
- 118.Tice R.R. Improving the human hazard characterization of chemicals: a Tox21 update. Environ Health Perspect. 2013;121(7):756–765. doi: 10.1289/ehp.1205784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Mayr A. DeepTox: toxicity prediction using deep learning. Front Environ Sci. 2016;3:80. [Google Scholar]
- 120.Carbonell P., Faulon J.L. Molecular signatures-based prediction of enzyme promiscuity. Bioinformatics. 2010;26(16):2012–2019. doi: 10.1093/bioinformatics/btq317. [DOI] [PubMed] [Google Scholar]
- 121.Wittig U. SABIO-RK–database for biochemical reaction kinetics. Nucleic Acids Res. 2012;40(Database issue):D790–D796. doi: 10.1093/nar/gkr1046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Benson D.A. GenBank. Nucleic Acids Res. 2017;45(D1):D37–D42. doi: 10.1093/nar/gkw1070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Pantazes R.J. The iterative protein redesign and optimization (IPRO) suite of programs. J Comput Chem. 2015;36(4):251–263. doi: 10.1002/jcc.23796. [DOI] [PubMed] [Google Scholar]
- 124.Fazelinia H., Cirino P.C., Maranas C.D. Extending Iterative Protein Redesign and Optimization (IPRO) in protein library design for ligand specificity. Biophys J. 2007;92(6):2120–2130. doi: 10.1529/biophysj.106.096016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Saraf M.C. IPRO: an iterative computational protein library redesign and optimization procedure. Biophys J. 2006;90(11):4167–4180. doi: 10.1529/biophysj.105.079277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Hellinga H.W., Richards F.M. Construction of new ligand binding sites in proteins of known structure. I. Computer-aided modeling of sites with pre-defined geometry. J Mol Biol. 1991;222(3):763–785. doi: 10.1016/0022-2836(91)90510-d. [DOI] [PubMed] [Google Scholar]
- 127.Hellinga H.W., Caradonna J.P., Richards F.M. Construction of new ligand binding sites in proteins of known structure. II. Grafting of a buried transition metal binding site into Escherichia coli thioredoxin. J Mol Biol. 1991;222(3):787–803. doi: 10.1016/0022-2836(91)90511-4. [DOI] [PubMed] [Google Scholar]
- 128.Dahiyat B.I., Mayo S.L. Protein design automation. Protein Sci. 1996;5(5):895–903. doi: 10.1002/pro.5560050511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Zanghellini A. New algorithms and an in silico benchmark for computational enzyme design. Protein Sci. 2006;15(12):2785–2794. doi: 10.1110/ps.062353106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Wood C.W., Woolfson D.N. CCBuilder 2.0: powerful and accessible coiled-coil modeling. Protein Sci. 2017;00 doi: 10.1002/pro.3279. 00–00. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Wood C.W. CCBuilder: an interactive web-based tool for building, designing and assessing coiled-coil protein assemblies. Bioinformatics. 2014;30(21):3029–3035. doi: 10.1093/bioinformatics/btu502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Smadbeck J. Protein WISDOM: a workbench for in silico de novo design of biomolecules. J Vis Exp. 2013;77:50476. doi: 10.3791/50476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Huang P.S., Boyken S.E., Baker D. The coming of age of de novo protein design. Nature. 2016;537(7620):320–327. doi: 10.1038/nature19946. [DOI] [PubMed] [Google Scholar]
- 134.Pleiss J. Protein design in metabolic engineering and synthetic biology. Curr Opin Biotechnol. 2011;22(5):611–617. doi: 10.1016/j.copbio.2011.03.004. [DOI] [PubMed] [Google Scholar]
- 135.Damborsky J., Brezovsky J. Computational tools for designing and engineering biocatalysts. Curr Opin Chem Biol. 2009;13(1):26–34. doi: 10.1016/j.cbpa.2009.02.021. [DOI] [PubMed] [Google Scholar]
- 136.Eriksen D.T., Lian J., Zhao H. Protein design for pathway engineering. J Struct Biol. 2014;185(2):234–242. doi: 10.1016/j.jsb.2013.03.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Klotz E., Newman A.M. Practical guidelines for solving difficult mixed integer linear programs. Surv Operat. Res Manag Sci. 2013;18(1):18–32. [Google Scholar]
- 138.Boles K.S. Digital-to-biological converter for on-demand production of biologics. Nat Biotechnol. 2017;35(7):672–675. doi: 10.1038/nbt.3859. [DOI] [PubMed] [Google Scholar]
- 139.Heath A.P., Bennett G.N., Kavraki L.E. Finding metabolic pathways using atom tracking. Bioinformatics. 2010;26(12):1548–1555. doi: 10.1093/bioinformatics/btq223. [DOI] [PMC free article] [PubMed] [Google Scholar]