Multiwavelength anomalous diffraction analysis at the M absorption edges of uranium

Abstract

The multiwavelength anomalous diffraction (MAD) method for phase evaluation is now widely used in macromolecular crystallography. Successful MAD structure determinations have been carried out at the K or L absorption edges of a variety of elements. In this study, we investigate the anomalous scattering properties of uranium at its M_IV (3.326 Å) and M_V (3.490 Å) edge. Fluorescence spectra showed remarkably strong anomalous scattering at these edges (f′ = −70e, f′′ = 80e at the M_IV edge and f′ = −90e, f′′ = 105e at the M_V edge), many times higher than from any anomalous scatterers used previously for MAD phasing. However, the large scattering angles and high absorption at the low energies of these edges present some difficulties not found in typical crystallographic studies. We conducted test experiments at the M_IV edge with crystals of porcine elastase derivatized with uranyl nitrate. A four-wavelength MAD data set complete to 3.2-Å Bragg spacings was collected from a single small frozen crystal. Analysis of the data yielded satisfactory phase information (average difference of ⁰ϕ_T − ⁰ϕ_A for replicated determinations is 32°) and produced an interpretable electron-density map. Our results demonstrate that it is practical to measure macromolecular diffraction data at these edges with current instrumentation and that phase information of good accuracy can be extracted from such experiments. We show that such experiments have potential for the phasing of very large macromolecular assemblages.

X-ray absorption increases sharply as the energy of incident x-rays meets the transition energy needed to excite an electron from an atomic orbital into the continuum. A prominent peak of absorption, known as a “white line,” can also appear at an absorption edge. These features enhance the intrinsic atomic absorption to produce a very rapid change with respect to wavelength in the vicinity of the absorption edge. White line features result from the stimulated resonant transition of an electron from a bound atomic state to an unoccupied molecular orbital. A resonant modulation of x-ray scattering accompanies the dispersion of x-ray absorption; these anomalous scattering increments to the normal scattering include an imaginary part, f′′, that is proportional to the x-ray absorption spectrum and a real part, f′, that is related to f′′ by the Kramers-Kronig dispersion integral. The method of multiwavelength anomalous diffraction (MAD) takes advantage of such anomalous dispersion of x-ray scattering to accomplish de novo phasing of macromolecular crystal structures (1). In a MAD experiment, diffraction data are measured at several different wavelengths chosen in the vicinity of the absorption edge of a certain anomalous scatterer present in the crystal. This approach contrasts with the more conventional multiple isomorphous replacement (MIR) method, in which data sets are collected at the same single wavelength from native and different heavy-atom derivatives of the crystal. Anomalous scatterers have different atomic scattering factors at the different wavelengths, which gives rise to variation in diffraction intensity. In effect, MAD thus achieves in situ MIR with the guarantee of perfect isomorphism.

MAD is now widely used for structural analysis of biological macromolecules as appropriate synchrotron beamlines have become broadly available. Successful MAD experiments have been carried out with many different anomalous scatterers over a wide energy range from 7.1 keV (Fe K edge) to 17.2 keV (U L_III edge) (refs. 1–3). They include two types of absorption edges, the L_III or L_II edges of heavier elements (e.g., Hg, Pt, and Yb), many of which are also commonly used for MIR derivatives, and the K edges of lighter elements (e.g., Se and Fe). K-edge scatterers are often intrinsic to the macromolecule (e.g., iron in a heme protein), or they can be engineered to become an integral part of the macromolecule (e.g., in selenomethioninyl proteins and brominated oligonucleotides); thus, full occupancy can be guaranteed. L_III-edge scatterers have the advantage of producing significantly greater anomalous scattering and sometimes a much stronger white-line structure. This enhancement can be rationalized rather simply. Whereas the K absorption edge results from the excitation of a 1s electron to p states, the L_III edge couples a 2p_3/2 electron to d states. Therefore, there simply are more electrons to participate in the transition and more unoccupied molecular obits into which these core electrons can be transferred when comparing L_III with K edges (4). A direct extension of this reasoning is that we can expect even stronger anomalous scattering from M_IV and M_V absorption edges, which couple 3d_3/2 and 3d_5/2 electrons, respectively, to 5f states. Because the M absorption edge energies are much lower than those of L edges but increase with atomic number, uranium, the heaviest stable element, stands as the natural candidate to study. Indeed, there is both experimental and theoretical evidence for very strong anomalous scattering at the M_IV and M_V edges of uranium (5–8).

We report here our investigation of the anomalous scattering property of uranium at its M_IV and M_V edges. Results from our experiments show that the anomalous scattering power at these edges is indeed quite remarkable (extreme values of f′ = −70e, f′′ = 80e at the M_IV edge and f′ = −90e, f′′ = 105e at the M_V edge). The possibility of phasing very large macromolecules by MAD experiments at these edges is particularly interesting to us. However, these edges are located in an energy range much lower than that typically used for crystallographic study and bring about some particular experimental difficulties, the principal one being the much stronger x-ray absorption in this energy range because absorption increases with the cube of wavelength. Although previous attempts have been made to study anomalous diffraction at the K absorption edges of sulfur and phosphorus (9, 10), there have not to our knowledge been any complete structural studies at atomic resolution in this low energy range. To assess the feasibility of such an experiment, we conducted test MAD experiments at the M_IV edge by using a porcine elastase crystal derivatized with uranyl nitrate. Apart from some modifications on the beamline and the image-plate cassette, the data collection was carried out by essentially standard oscillation methods. Complete MAD data sets were collected to 3.2-Å Bragg spacings at four different wavelengths, and subsequent analysis shows that the phase information extracted from this data set is as accurate as the more standard MAD experiments.

Methods

Beamline Setup.

Experiments were carried out on beamline X4A of the National Synchrotron Light Source (11). The beamline optics include a fixed-exit, double-crystal Si(111) monochromator with sagittal focusing in the horizontal direction. The energy resolution ΔE/E is estimated to be about 2 × 10⁻⁴. A fused silica mirror is used at lower energies to concentrate the beam in the vertical direction while filtering out higher order harmonic wavelengths, particularly the (333) reflection from the monochromator. The main experimental difficulty is the much stronger x-ray absorption in this energy range. Table 1 gives the absorption lengths for 1/e reduction in x-ray intensity at the M_IV and M_V edge energies for some of the absorbing materials present along the beam path. Under the standard configuration of the X4A beamline, the x-ray flight path inside the radiation hutch consists of various instruments such as the filter wheel, the attenuator wheel, the shutter wheel, and two 5-cm-long N₂ ion chambers for intensity monitoring. Segments between these elements are covered with evacuated beam pipes, and each segment is sealed on both ends by 25-μm-thick Kapton film (total number 10), with substantial gaps exposed to air. It is estimated that the absorption from the Kapton films and the air path would reduce the intensity of x-ray at the M_IV edge by two orders of magnitude. To minimize the intensity losses in these experiments, all beampath segments inside the hutch including the associated instruments were removed and replaced with a single evacuated beam pipe that extended all the way to the exit end of the collimator, which is only a few millimeters from the sample. These modifications effectively eliminated the above mentioned absorption. An electromagnet-driven mechanism inside this beam pipe served as the x-ray shutter.

Table 1.

X-ray absorption length at U M-edges

	Air	Kapton film	Protein crystal*
MIV edge	87 mm	110 μm	110 μm
MV edge	75 mm	90 μm	100 μm

^*Calculated with parameters of the elastase crystal. 

Spectrum Measurements.

Fluorescence absorption spectra were measured from a UF₄-coated mylar film, a single RbUO₂(NO₃)₂ crystal, and uranyl-derivatized elastase crystals by scanning x-ray energy. A Li drifted silicon detector cooled at liquid nitrogen temperature was used to collect the fluorescence scattering. The detection surface was placed perpendicular to the polarization vector of the x-ray beam to minimize the detection of scattered photons. Pulse signals from the detector were routed to a multichannel analyzer. The energy resolution of this system is calibrated to about 180 ev @ 5.9 keV and is sufficient to distinguish direct scattering photon and fluorescence emission photon energy wise. We were, therefore, able to exclude the majority of direct scattering background by setting the proper upper and lower cutoff limits on pulse signal height. Typical final count rates were 5000 counts/s at the M_IV edge and 1500 counts/s at the M_V edge, and we were able to obtain relatively clean absorption spectra. The background discrimination provided by this scheme was critical because we were unable to detect the absorption edge in previous experiments by using a scintillation counter, which has poor energy resolution.

Diffraction Data Collection.

Although anomalous scattering is stronger at the M_V edge than at the M_IV edge, we chose to conduct the test experiment at the M_IV edge because of the higher x-ray intensity available (about three times that at the M_V edge). A very large detection area was required for data collection to a reasonable resolution limit as a result of the unusually long x-ray wavelength used in this experiment as dictated by the Bragg relation, 2d sin θ = λ. Two 20-cm × 40-cm Fuji imaging plates were put together in a specially designed cassette holder to provide a 40-cm × 40-cm detection area, and they were placed at a distance of 90 mm from the crystal to cover diffraction out to about 3.2-Å Bragg spacings for M_IV-edge x-rays. No black paper was used to shield the image plates from room light, as is usually done, to eliminate x-ray absorption by the paper. All data collection was therefore done with lights off inside the radiation hutch, and care was taken to minimize the stray lights when opening the hutch to retrieve the imaging plates. A helium cone was specially built to fit between the crystal and the imaging plates. Use of a helium path proved to be absolutely necessary even though the detector was very close by usual standards. This is so not only because absorption through 90 mm of air is itself significant (Table 1), but more importantly because the distance from the crystal to the edge of the plate is about three times longer than to the center, which would drastically reduce the diffraction intensity.

Porcine pancreatic elastase (Sigma) was chosen for this test experiment because it produces crystals of excellent diffraction quality that are well known to have a good uranyl derivative (12). Orthorhombic crystals were grown and derivatized by soaking in 2 mM uranyl nitrate as described earlier (13). A relatively small single crystal with dimensions ≈70 μm × 70 μm × 200 μm was chosen for MAD data collection to reduce x-ray absorption in the crystal (Table 1). The crystal was cryoprotected by soaking for several hours in a stabilizing solution containing 20% ethylene glycol and was then flash frozen in the cold stream of an Oxford cryosystem. Lattice parameters for this frozen, derivatized crystal (a = 50.2 Å, b = 58.0 Å, c = 75.4 Å° in space group P2₁2₁2₁) were significantly different from those reported before. Care was taken to minimize the solvent frozen around the crystal to reduce needless absorption. MAD data were collected at four wavelengths chosen to maximize both dispersive and Bijvoet signals: λ₁ (3728 eV, ascending inflection point of absorption and minimum of f′), λ₂ (3730.5 eV, peak of absorption and f′′), λ₃ (3733 eV, descending inflection point of absorption and peak of f′), and λ₄ (3770 eV, remote point). Although the beamline is equipped with a four-circle Huber diffractometer, only the phi motion was possible in our setup because of the closeness of the imaging plate cassette and the helium cone. To avoid the missing-cone problem in data collection, the crystal was aligned such that the (101) axis was approximately parallel to the phi axis. Friedel mates were collected by using the inverse-beam method. Oscillation steps of 2.5–3.5° were used with 0.5° overlap, and the typical exposure time was 6–10 min. On finishing the four-wavelength MAD data collection, the x-ray energy was shifted to 11.3 keV (1.097 Å) to collect an additional “normal” data set from the same crystal. These data were used subsequently for an independent refinement of the frozen uranyl elastase crystal structure. Although no significant radiation damage was seen and the crystal still diffracted at least to 1.8-Å spacings, data collection was completed only to 2.3 Å because of limited beamtime.

Results

Spectrum.

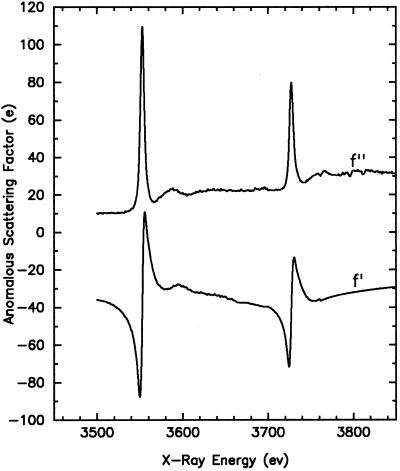
Atomic anomalous scattering factors were derived from fluorescence absorption spectrum data by previously described procedures (2). The imaginary component, f′′, is directly proportional to the atomic absorption coefficient. The relatively flat parts of the spectrum away from absorption edge were fitted to standard values of the absorption coefficient (14) to determine the proper scale factor, and f′′ values were then calculated over the entire energy range. The real component, f′, was in turn derived from f′′ by the Kramers-Kronig transformation. The anomalous scattering factors f′ and f′′ at the M_IV and M_V edges calculated from a fluorescence absorption spectrum measured from a UF₄-coated film are shown in Fig. 1. Absorption spectra taken from a RbUO₂(NO₃)₂ crystal or uranyl derivatized elastase crystals produced very similar results.

Figure 1.

Atomic anomalous scattering factors of uranium for the M_IV and M_V edge derived from fluorescence absorption spectrum of a UF₄-coated film. The imaginary components, f′′, are shown in the upper curve and the real components, f′, are in the lower curve.

MAD Analysis.

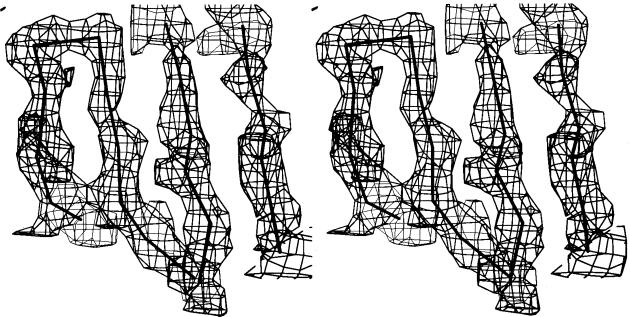
Image-plate data were processed with denzo and scaled together with scalepack (15). Subsequent analysis was performed by using the madsys programs developed in our laboratory. Reflections measured exactly the same way except wavelength are grouped together, and redundant or symmetry-related measurements of the same reflection are kept separate. The data from different wavelengths were placed on the same scale with the local scaling program wvlscl. Then, least squares analysis as described in ref. 1 was performed by the program madlsq to extract the amplitudes of F_A and F_T and the phase-angle differences between them. Redundant determinations of these parameters from symmetry-related reflections were merged together with the program mergit to provide a measure of self consistency in the madlsq results. Relevant statistics from the analyses are shown in Tables 2, 3, and 4. A Fourier synthesis based on these derived phases and the extracted |F_T| values was of interpretable quality (Fig. 2).

Table 2.

Statistics from data measurements

	Wavelength, Å	dmin, Å	Reflections*	Completeness, %	〈I/σ(I)〉	Rsym†, %
λ1 (asc. inflection)	3.3281	3.2	28,821 (6,484)	93.5	9.5	12.1
λ2 (peak)	3.3256	3.2	28,889 (6,499)	93.7	9.1	12.3
λ3 (desc. inflection)	3.3239	3.2	29,022 (6,559)	94.6	9.6	12.1
λ4 (remote)	3.2886	3.2	29,231 (6,550)	94.5	9.7	11.8
λ5 (high energy)	1.0970	2.3	145,528 (18,756)	97.6	38.6	6.0

^*Value in parentheses is the number of unique reflections. Bijvoet mates are considered independent in all cases. 

^† R_sym = 100 × Σ_hΣ_i|I_i(h) − 〈I(h)〉|/Σ_hΣ_iI_i(h). 

Table 3.

Anomalous diffraction ratios

	20.0 < d < 4.0 Å				4.0 < d < 3.2 Å				Scattering factors (e)
	λ1	λ2	λ3	λ4	λ1	λ2	λ3	λ4	f′	f"
λ1	0.248 (0.101)	0.145	0.168	0.144	0.253 (0.127)	0.159	0.187	0.165	−77.9	45.3
λ2		0.329 (0.096)	0.115	0.133		0.323 (0.121)	0.140	0.162	−43.7	72.2
λ3			0.229 (0.093)	0.102			0.247 (0.121)	0.140	−15.4	53.9
λ4				0.165 (0.092)				0.195 (0.120)	−31.0	32.0

Table values represent rms(Δ|F|)/rms(|F|), where Δ|F| is the Bijvoet difference at one wavelength (diagonal elements) or of the dispersive difference between two wavelengths (off-diagonal elements). The values in parentheses are the ratios for centric Bijvoet reflections, which would be equal to zero for perfect data; these serve as an estimate of the noise in the anomalous signals. 

Table 4.

Statistics from MAD phasing

R(|0FT|) = 0.152	〈Δ(Δφ)〉 = 31.89°	〈m〉 = 0.97
R(|0FA|) = 0.343	〈σ(Δφ)〉 = 10.84°

Values shown are for data between 15.0 and 3.2 Å. R = Σ_hΣ_i∥F_i(h)| − 〈|F(h)|〉|/Σ_h|F(h)|. ⁰F_T(h) is the structure factor due to normal scattering from all the atoms. ⁰F_A(h) is the structure factor due to normal scattering from the anomalous scatterers only, and Δφ(h) is the phase difference between ⁰F_T(h) and ⁰F_A(h). Δ(Δφ) is the difference between independent determinations of Δφ(h) = ⁰ϕ_T − ⁰ϕ_A. 

Figure 2.

Stereodrawing of a portion of the electron-density distribution in porcine elastase calculated at 3.2 Å resolution with the MAD phases. The Cα-backbone from the independently refined elastase model is superimposed.

Phase Comparison.

For an objective assessment of the accuracy of the MAD phases determined in this experiment, we compared the MAD phase with the phase calculated directly from the refined structure model. The cell dimensions of our frozen crystal have changed significantly from that of the unfrozen ones reported earlier. We proceeded with the refinement against the 2.3 Å data collected at higher energy (λ5, 1.097 Å) from the same crystal. The PDB entry 3EST (16) was used as the starting model, which was refined initially as a rigid body and then in several rounds of individual-atom conjugate-gradient minimization, followed by temperature factor refinement and water building. The refined model had good geometry and a final R value of 20.1%. Model phases calculated from this final refined structure were compared with the MAD experimental phases, and the results are shown in Table 5. To place these results into perspective, Table 6 also lists the same difference between the experimental and refined-model phases as reported for several other protein structures determined by MAD (2, 3, 17, 18). It can be seen that the overall accuracy of the MAD phases obtained in our experiment based on the uranium M_IV edge is comparable to that from more conventional MAD analyses.

Table 5.

Statistics of phase comparison

Bragg spacings, Å	No. of reflections	Average phase difference
15.00–5.44	699	51.1°
5.44–4.33	703	40.1°
4.33–3.79	639	46.0°
3.79–3.45	630	47.1°
3.45–3.20	560	50.7°
Overall	3,231	46.8°

Comparison between MAD determined structure factors and model calculated structure factors. 

Table 6.

Comparison of experimental refined model phases for some published MAD experiments

Structure	dmin, Å	Average phase difference	Ref.
N-cadherin	1.9	43.0°	3
BamHI	2.5	46.6°	18
Lamprey hemoglobin	3.0	50.5°	2
hCG	2.8	53.1°	17
Porcine elastase	3.2	46.8°	This work

Discussion

The signal strengths in a MAD experiment are customarily measured by the average Bijvoet difference, |ΔF|_±h, and dispersive difference, |ΔF|_Δλ, relative to the average structure factors, and these can be conveniently estimated with the following formulae (19): for the expected Bijvoet-difference ratio,

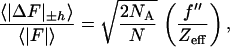1

and for the expected dispersive-difference ratio,

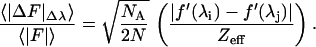2

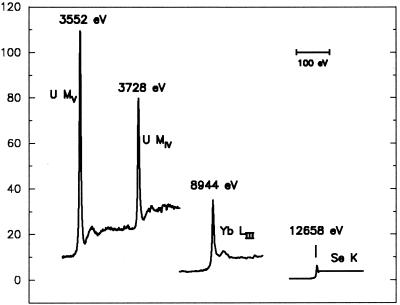
Here, N_A is the number of anomalous scattering atoms and N is the number of all non-hydrogen atoms, which on average have an effective atomic scattering factor Z_eff (6.7 for typical proteins). It can be seen from the above formulae that, whereas the relative MAD signal is directly proportional to the anomalous scattering factors, it is affected only by the square root of the number of atoms. Therefore, to obtain a certain level of MAD signal for a larger structure, one can either increase the number of anomalous scatterers of a given strength or use a stronger anomalous scatterer. The former approach has been effective with mega-site selenium structures (20), but the latter approach also has great potential. The relative strength of the uranium M edges is striking when compared directly with that from a lanthanide L edge and from the selenium K edge (Fig. 3). Thus, the extraordinary anomalous scattering exhibited by uranium at its M_IV and M_V edges presents itself as a powerful phasing vehicle for very large systems.

Figure 3.

Anomalous scattering factors f". Comparison of the imaginary components of anomalous scattering. The U M_IV and U M_V edges are from this work, the Yb L_III edge is from an ytterbium-derivatized crystal of N-cadherin (3), and the Se K edge is from a crystal of selenomethionyl human choriogonadotropin (17).

The exciting potential of uranium M edges can be illustrated by a thought experiment, taking the example of the 50S ribosomal subunit, one of the largest and most interesting biological complexes yet crystallized. Crystals of the 1.6 million-Dalton 50S subunit from the halobacteria Haloarcula marismortui diffract well (21, 22) and have now been analyzed at 2.4 Å resolution to define the positions of nearly 90,000 atoms (22). Initial phase information derived from electron-microscopic images at low resolution was used to define the sites of many heavy atoms and extend the phasing to high resolution. One can contemplate an alternative approach based on a MAD experiment at the uranium M_V edge. Maximal dispersive and Bijvoet difference can be achieved with three wavelengths associated with the dramatic M_V absorption edge: λ₁ (ascending inflection point), λ₂ (absorption peak), and λ₃ (descending inflection point). From data presented in Fig. 1, these give f′′(λ₂) = 105e and f′(λ₃) − f′(λ₁) = 10e − (−90e) = 100e. Then, assuming only one uranyl ion for each complex, the maximum Bijvoet and dispersive signals would be 6.7% and 3.2%, respectively, appreciably higher than that obtained for many published MAD structure determinations. Such an experiment could provide phase information out to spacings approaching 3 Å as in our elastase experiment, but, in less favorable circumstances, the phase information corresponding to lower resolution and poorer quality could still serve as an important phasing foothold for a very large complex. Data measured at more convenient wavelengths, nearer to 1 Å as with our λ₅ and perhaps at the K or L_III edge of another element, could then be used to complete the structure analysis.

Several issues would need attention when planning a MAD experiment at the uranium M_IV or M_V edges. The integrated diffraction intensity measured in an oscillation experiment is given by the expression (12):

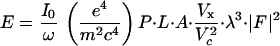3

where I₀ is the beam intensity; ω the oscillation speed; P, L, and A are polarization, Lorentz, and absorption correction factors, respectively; V_x is the volume of the crystal immersed in the beam and V_c is the unit-cell volume. Absorption for x-rays at the energy of uranium M_IV and M_V edges imposes a fundamental limitation on the dimension of crystals that can be used in such diffraction experiments. The potential increase in diffraction with crystal volume is diminished and ultimately offset by absorption inside the crystal. The optimal x-ray path length equals the absorption length (12), which at these energies is ≈100 μm in the dimensions that x-rays will transverse (Table 1). Therefore, the diffracting volume is essentially fixed independent of molecular size. For larger macromolecular complexes, the unit-cell volume V_c is expected to increase accordingly. Because |F|² will also increase proportional to the unit-cell content, the integrated intensity will be effectively proportional to the inverse of V_c. Therefore, the diffraction intensity for a large macromolecular assemblage such as the ribosome will be approximately two orders of magnitude weaker than that from smaller protein crystals such as elastase. Moreover, reflections are necessarily close together in diffraction patterns from large unit cells. Consequently, MAD experiments on large complexes at the uranium M edges will require a bright x-ray source that can deliver a high flux of highly parallel x-rays focused into a small spot.

Fortunately, undulator beamlines at third generation synchrotron facilities can provide dramatically improved brilliance as compared with that from bending-magnet beamlines, such as X4A. Obviously, a first requirement for any beamline that can accommodate experiments at the uranium M_V edge is a monochromator that can reach energies down to nearly 3.5 keV, and it needs to do so with an absolute minimum of absorbing materials in the beam path. It is also highly desirable, if not essential, in such a MAD experiment to reduce the effect of systematic errors, such as those from radiation damage and absorption, by collecting all data needed to define the phase of a given reflection (different wavelengths and Bijvoet mates) under similar circumstances. Thus, an appropriate beamline should have the capability to switch rapidly among the several wavelengths and to rotate quickly by 180° for inverse-beam measurements. Although it is possible to tune the spectrum from an undulator by changing the magnet gap width, it may be impractical to do so on an image-to-image basis. In the case of uranium M_IV or M_V edges, however, an optimal experiment can be conducted within the 5-ev energy span between the ascending and descending inflection points of the white-line feature. Therefore, uranium M-edge experiments could readily be performed on an undulator beamline at a single gap setting.

In conclusion, we believe our work demonstrates that it is practical to conduct MAD experiments at the uranium M_IV and M_V edges with the current instrumentation and that the strength of anomalous scattering at these edges provides new options for attacking very large macromolecular assemblages.

Abbreviation

MAD

multiwavelength anomalous diffraction

MIR

multiple isomorphous replacement