Mesoscopic neuron population modeling of normal/epileptic brain dynamics

Abstract

Simulations of EEG data provide the understanding of how the limbic system exhibits normal and abnormal states of the electrical activity of the brain. While brain activity exhibits a type of homeostasis of excitatory and inhibitory mesoscopic neuron behavior, abnormal neural firings found in the seizure state exhibits brain instability due to runaway oscillatory entrained neural behavior. We utilize a model of mesoscopic brain activity, the KIV model, where each network represents the areas of the limbic system, i.e., hippocampus, sensory cortex, and the amygdala. Our model initially demonstrates oscillatory entrained neural behavior as the epileptogenesis, and then by increasing the external weights that join the three networks that represent the areas of the limbic system, seizure activity entrains the entire system. By introducing an external signal into the model, simulating external electrical titration therapy, the modeled seizure behavior can be ‘rebalanced’ back to its normal state.

Introduction

Quantitative studies of the brain’s electrical activity based on EEG analysis have provided methods to differentiate among various cognitive states, i.e., sleep, awake, normal, or seizure (Freeman et al. 2006). Models of relatively large groups of interacting excitatory and inhibitory neural populations have been developed to exhibit abnormal/normal brain states and the effects of imbalanced excitatory and inhibitory neurons (Takeshita et al. 2007). Tsakalis and Chakravarthy (Tsakalis et al. 2005; Chakravarthy et al. 2007) developed a neural mass model, with an internal feedback mechanism to maintain synchronous behavior within normal levels despite elevated coupling. Normal internal feedback quickly regulates an abnormally high coupling between the neural populations, whereas pathological internal feedback can lead to hyper-synchronization and the appearance of seizure-like high amplitude oscillations. Feedback decoupling was introduced (Chakravarthy et al. 2007) as a robust seizure control strategy. An external feedback decoupling controller was also introduced to maintain normal level of synchronous behavior. Other internal feedback models featured closed-loop feedback control systems in epileptic seizures combining methods from seizure prediction and deep brain stimulation (Good et al. 2009). Periodic stimulation was also performed, with a reduction of seizure frequency in 33% of six rat modeling instances.

External open-loop stimulation epilepsy experiments have been accomplished in order to understand the effects of electrical stimulation modulation of the brain. The effects of open-loop stimulation are divided into ON effects, and OFF effects. The distinction between ON and OFF effects is made when the stimulation is intermittent (e.g., repeated patterns of 5 min on, 5 min off): the ON effects occur during a functional stimulation “unit” such as a pulse train, and the OFF effects are observed transiently after each ON functional unit ends.

In hyperexcitable tissue, brain slice studies have indicated whether DC fields suppress or aggravate seizures depends on neuronal geometry relative to the sign and direction of the applied fields (Sunderam et al. 2010). Richardson et al. (2003) demonstrated that a cylindrical electrode placed axially in the hippocampus, similar to the placement of a standard clinical hippocampal depth electrode, creates a radially expanding field that is aligned with the CA3 pyramidal cell neurons and can be used to polarize them and thereby modulate their activity. Though this study was performed on animals, the finding has a direct clinical translation path. Very-low frequency stimulation through CNS-implanted electrodes has not been applied to humans, in part due to electrochemical safety concerns (Sunderam et al. 2010).

Vagus nerve stimulation (VNS) devices result in a significant reduction of seizure frequency in many patients when antiepileptic drugs (AED) or resection of the seizure focus localized to one mesial temporal lobe cannot avail the effects of the seizure state (Karceski 2007). Titration parameters, such as frequency, intensity, pulse width, and duration are used as external input into the KIV simulated limbic system in order to model the interaction of external stimulation into the cortex. The following VNS attributes were found in the literature. Low intensity trains of VNS (100 μA, 30 Hz, 500 μs, 20 s periods) have been found to hyperpolarize pyramidal neurons of rat parietal association cortex (Zagon and Kemeny 2000). A range of values were utilized starting with the parameters: 1.5–5 V; pulse width 90–200 μs, stimulation frequency, 5–10 cps (Kerrigan et al. 2004). In another study, five patients treated with the VNS system using the parameters: output current 1 mA, signal frequency 30 Hz, signal pulse width 500 μs, signal on for 30 s, showed increased cortical inhibition associated with stimulation without any evidence of cortical excitability (Marrosu et al. 2003). Additional experimental results suggested that the sensitivity of epileptic brain to VNS was different during the epileptic process, such that the inhibiting effect of VNS to seizure decreased as the development of seizures occurs over time (Yang et al. 2007).

An ideal form of electrical seizure control might be a single precisely tuned pulse that resets or annihilates a developing or ongoing seizure. Entrainment of interictal-like bursts with low frequency (1–5 Hz) pulse trains in hippocampal slices was shown to interrupt the development of full electrographic seizures causing short-term synaptic depression of excitatory neurotransmission. But clinical tests of low-frequency pulse trains have had mixed results. It is well known that even a single pulse can trigger an electrographic discharge in hyper-excitable tissue (Lesser et al. 2008). It has also been proposed that high-frequency (50–100 Hz) stimulation can suppress, or at least shorten, an ongoing electrographic seizure. Specific high-frequency stimulation waveforms can trigger seizures. Notable is the classic and popular kindling seizure model elicited from high-frequency trains (Bertram 2007). It is clear from the preceding discussion that it may not be possible to define a unique stimulation protocol that is optimal for every situation, and therefore a patient-tailored stimulation protocol is needed (Sunderam et al. 2010; Osorio et al. 2005).

In this work, an in-depth analysis of quantifiable temporal shifts in the electrical activity of the brain, as well as ictal synchronization of mesoscopic neuron populations is studied. As normal EEG is enormously varied, a method is developed to quantify brain states using EEG features. Additionally, the distinctive features of normal and abnormal states of the brain are considered. Ictal behavior is distinguished from non-ictal behavior, and captured in the EEG simulator. Finally, the capability of the KIV based EEG simulator to incorporate electrical stimulation therapies that can re-instate the simulated brain back from the effects of the seizure state is demonstrated.

Methods

Four neurosurgical patients were selected for this study with medically intractable epilepsy. Dense-array EEG was collected from 256 Hydrocel electrodes at a 1000 Hz sampling rate and amplified with a commercial EEG system (ElectroGeodesics Inc.). Subjects were monitored in a clinical setting during EEG recording sessions. Electrode contact impedance was maintained < 5 kΩ. Raw EEG signals from Net station acquisition software was preprocessed in order to remove myogenic noise such as blink artifacts (± 50 μV) and filtered (0.1–100 Hz band-pass with 60 Hz Notch) using MATLAB (The MathWorks Inc., v.R2009a).

Features of normal/abnormal brain activity have been monitored for 60–90 min. The data for this study was provided from Dr. J.W. Wheless, Pediatric Neurology, University of Tennessee Health Science Center, using Electrical Geodesics (EGI) high density EEG system. Experiments were conducted in accordance to The University of Memphis IRB regulations, IRB reference protocol: E06-80.

The KIV model

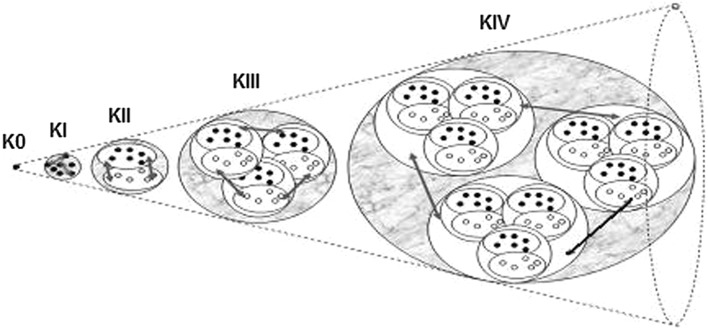
The K-set family includes a hierarchy of K models, including K0, KI, KII, KIII, and KIV, see Fig. 1. K-sets represent a family of models with increasing complexity. They represent different aspects of the vertebrate brain. K0 consists of a single node with input and output and a nonlinear transfer function. K-sets represent a family of models with increasing complexity. They represent different aspects of the vertebrate brain. K0 consists of a single node with input and output and a nonlinear transfer function. Anatomically, the existence of neural populations is manifested in the micro-column structure of cortical tissues. The granulation level of K0 sets can include approx. 104 neurons, i.e., it represents an intermediate level between microscopic neurons and the whole brain. The intermediate level is often referred to as mesoscopic level, and the corresponding processes manifest mesoscopic brain dynamics. Traditionally, individual neurons are typically modeled using Hodgkin–Huxley equations (Hodgkin and Huxley 1952).

Fig. 1.

Illustration of K0, KI, KII, KIII, and KIV sets. Solid and open cycles signify excitatory and inhibitory populations, respectively (Kozma et al. 2007)

The Hodgkin–Huxley equations employ a system of first order ordinary differential equations (ODEs) to describe the physical properties of the cell membrane and the concentrations of different ions in the proximity of the membrane. In these models, the state variables are the membrane potentials of the individual neurons and the action potentials (also called pulses or spikes) are determined by solving first-order differential equations with respect to the membrane potentials. The first order approximation used in these ODEs produces a very efficient way of describing the dynamics of neural pulses using exponential decay in time. In some cases, however, a higher-order approximation may be beneficial, which would allow a dynamical characterization which is more refined than a sequence of pure exponential decays. In the field of physics, the use of second order equations is a common practice, starting from Newton’s basic equation of motion.

A description of the K-model hierarchy

The dynamics of the K0 set is governed by a point attractor. This means that, over time, a non interacting population of neurons will converge to the point zero. The K0 set is the basic unit of the K models, upon which the rest of the hierarchy is based on. The dynamics of the K0 set are given by the following second order ODE (ordinary differential equation).

$$\frac{1}{\mathit{ab}}\left[\frac{d^{2}p(t)}{d{t}^2}+(a+b)\frac{dp(t)}{\mathit{dt}}+abp(t)\right]=X(t)+I(t)$$ 1

where ‘a’ and ‘b’ are rate constants determined based on physiological experiments, p(t) is the pulse density at time t and X(t) is the internal input, and I(t) is the external input at time t. Dendrites convert the axonal pulse they receive into a wave, which is later converted back into a pulse by the axon. This pulse-wave and wave-pulse is an essential function of the neurons and neuron populations. The pulse to wave transfer function is assumed to be linear, and the wave-pulse transfer function is nonlinear and is given by the following equation (Freeman 1975):

$$p=Q(v)=q_{m}1-\left(exp\frac{1-expv}{q_m}\right)$$ 2

where v is the average wave density, p is the average pulse density and q_m is a constant whose value is between 1 and 14. The asymetric nature of Eq. (2) changes for different values of q_m.

The KI is a coupling of either exhibitory or inhibitory K0 units. A simple case of two interacting excitatory K0 sets are shown in Fig. 2.

Fig. 2.

a Excitatory KI population and inhibitory KI population are made up of two interacting neuron populations. b Simple excitatory KI_e set with two K0 units. KIe has a single parameter w_ee which represents the level of mutual excitation within the neural population

We assume that the pulse density of the first K0 set is transformed into the wave density by the nonlinear function Q(v) [Eqs. (3, 4)] and again into the pulse density by the linear function, represented by the weight w_ee. The same holds for the second K0 set. The dynamics is given by the following two second order ODEs:

$${\ddot{y}}_1+\mathrm{\alpha }{\dot{y}}_1+\mathrm{\beta }{\text{y}}_1=\mathrm{\beta }{\text{w}}_{\text{ee}}\text{Q}({\text{y}}_2),$$ 3

$${\ddot{y}}_2+\mathrm{\alpha }{\dot{y}}_2+\mathrm{\beta }{\text{y}}_2=\mathrm{\beta }{\text{w}}_{\text{ee}}\text{Q}({\text{y}}_1),$$ 4

Here α = a + b, and β = ab. The equilibrium can be found by setting the derivatives to zero, which gives the following equations for the equilibrium values of y₁ and y₂:

$$y_1^{\ast }={\text{w}}_{\text{ee}}\text{Q}\left(y_2^{\ast }\right),$$ 5

$$y_2^{\ast }={\text{w}}_{\text{ee}}\text{Q}\left(y_1^{\ast }\right).$$ 6

We characterize the equilibria of Eqs. (5, 6) depending on gain parameter w_ee. For small values of w_ee, there is a unique stable zero equilibrium. Increasing w_ee, the value w_LP is reached when a limit point (LP) appears. The zero equilibrium is stable until a threshold value of w_ee = w_BP, which is a bifurcation point (transcritical bifurcation). Above w_BP, the zero equilibrium becomes unstable (Ilin and Kozma 2006).

KII is a double layer of both exhibitory and inhibitory KI units. The feedback between the excitatory and inhibitory components produces periodic oscillations which are governed by a limit cycle attractor (Freeman 2000; Kozma et al. 2007) (Fig. 3). There are four types of interactions (connections) that are possible in KII sets, namely excitatory–excitatory, excitatory–inhibitory, inhibitory–excitatory and inhibitory–inhibitory. Each connection is assigned a weight.

Fig. 3.

KII sets contain both excitatory and inhibitory feedback, which produces oscillatory behavior

KIII is three-layer architecture with one or more KIIs connected by feed forward and delayed feedback neural network, seen in Fig. 4. The KIII model is a working example of the chaotic principles.

Fig. 4.

Simplified KIII system and its relationship with the anatomy of the olfactory system. Top layer: Inputs from the receptors via the glomeruli. Additional layers: olfactory bulb (OB), anterior olfactory nucleus (AON), prepyriform cortex (PC). Downward arrows are feedback connections, upward arrows are delayed feedback connections. Black and white circles: inhibitory and excitatory populations, respectively (Freeman 1986)

The KIV model is a biologically inspired neural network (Kozma et al. 2003). The KIV model architecture is represented by three major parts; the KIII cortex, KIII hippocampus and the KII amygdala. Hippocampus models include navigation functions. The cortex models sensory processing and pattern recognition in various sensory modalities. The amygdala is the unit where the activations from the cortex and hippo-campus are projected and decision is made concerning the next action, based on the fusion of the signals from other brain areas.

With proper weight selection between the networks of KIV, the entire network can maintain non-convergent chaotic oscillations. The internal and external weights between these chaotic networks, WA, WB, and WC, provide the manner in which mesoscopic neuron activity can be modeled. Internal weighting within the KIIIs and KII, can influence the behavior of the entire KIV network. The activations from hippocampus and sensory cortical KIII’s are transferred between the networks through connection weight matrix WA. The activations between hippocampus and amygdala are passed through weighted matrix WB. Finally, the activations between sensory cortex and amygdala are passed through weight matrix WC, as seen in Fig. 5. Weight settings of the KIV are described in Table 1 which includes, excitatory and inhibitory weighting of all three networks, feedforward and feedback connections and external connection values.

Fig. 5.

The KIV model of the limbic system, consisting of two KIII’s and one KII (Myers et al. 2008). Feedforward (Wff1, Wff2, Wff3) and Feedback (Wfb1, Wfb2, Wfb3) weights can be adjusted within each network of the KIV. External weights (WA, WB, WC) and can be adjusted to determine the level of influence the independent networks have on the entire system

Table 1.

KIV parameters

WA = WB = WC	KIII parameters (hippocampus)	KIII parameters (sensory cortex)	KII parameters (amygdala)	KIII feed-forward weights (wff1, wff2, wff3)	KIII delayed feed-back weights (wfb1, wfb2, wfb3)
0.325	kii 1 = [0.50, 2.20, 2.20, 2.50]	kii 4 = [0.05, 2.20, 2.20, 2.50]	kii = [2.00, 1.50, 2.00, 1.00]	[0.30, 0.50, 0.50]	[0.60, − 0.50, 0.50]
	kii 2 = [0.06, 2.25, 2.23, 2.40]	kii 5 = [0.06, 2.25, 2.23, 2.50]
	kii 3 = [0.30, 2.30, 2.00, 2.36]	kii 6 = [0.30, 2.00, 2.10, 2.25]

Epileptogenesis

Freeman’s analysis of electrical stimulation of the lateral olfactory tract (LOT) has been found to induce an epileptiform seizure in the prepyriform cortex (PC) of the cat, rat and rabbit models (Freeman 1962, 1972). As the complex sensory dynamics has been observed first in the olfactory bulb, early KIII sets mimic the architecture of the olfactory system (Chang et al. 1998; Kozma and Freeman 2001). Each layer is a distributed KII set, which consists of interacting neural populations. The simplified KIII set shown here consists of 3 parts of distributed KII sets corresponding to different anatomical parts of the brain: the OB, AON, and PC. Input signals enter OB through the glomeruli layer (top layer in Fig. 4). Excitatory elements of the OB layer correspond to the populations of the secondary dendrites of the mitral cells. The inhibitory populations are the granule cells. The mutual excitation between the mitral cells and mutual inhibition between the granule cells (Freeman 1975; Linster and Gervais 1996) is also modeled. AON consists of excitatory pyramidal and inhibitory stellate cells. OB sends projections to AON and PC, as shown as downward arrows. They, in turn, send feedback projections, as shown by the upward arrows in Fig. 4. The delays in the feedback tract are greater than in other parts of the olfactory system, due to the length of the tract. Therefore, feedback links are modeled by delayed connections as in Fig. 4 (Freeman et al. 1997).

In each KII set, the strength of mutual inhibition must exceed that of mutual excitation (kii > kee). Coupling of the KII_OB set with the KII_AON set results in multi–frequency oscillation that repeats a complex pattern about every 0.3 s. Introduction of the KII_PC set to attain the KIII level deregularizes the 3/s activity (Freeman 1972).

The seizure parameterized KIII will be incorporated into the KIV model, as described in Table 2, under the ‘Seizure’ state, with increased weighting between KII_OB set with the KII_AON set and reduced weighting between the KII_AON set with the KII_PC set. The feedback changes within the KIII will reduce the activity of excitatory elements and increase inhibitory elements in order to simulate the epileptogenesis. The external weights between the KIII and KII networks provide the manner in which the model can demonstrate local ictal activity propagation throughout the network. As the connection weight matrices increase, a tighter coupling of the oscillators occurs thereby causing an entrainment of all the nodes within each oscillator. The increase in weights between values of the connection matrices enable the entrainment of the neurons throughout the KIV to behave in a semi-periodic manner caused by the epileptogenesis. This type of signal entrainment behavior is seen in the EEG of seizure patients that exhibit the same attributes of mesoscopic clusters of neurons.

Table 2.

KIV transitional parameters

State	WA = WB = WC	KIII feed-forward weights (wff1, wff2, wff3)	KIII delayed feed-back weights (wfb1, wfb2, wfb3)	External Input into KIV via I(t)
Normal	0.325	[0.30, 0.50, 0.50]	[0.60, − 0.50, 0.50]
Seizure	5.000	[0.30, 0.20, 0.20]	[10.0, − 0.50, 0.30]
Restore	5.000	[0.30, 0.20, 0.20]	[10.0, − 0.50, 0.30]	[2.00, 1.50, 2.00, 1.00]

We apply the following spatio-temporal dynamic methods to demonstrate the similarities between EEG data behavior and the KIV model.

Power spectral density analysis

Power spectral density (PSD), or energy spectral density, is a general concept applied to a signal which may have physical dimensions such as power per Hz, or energy per Hz, etc. It is often called simply the spectrum of the signal. Due to the identified spatio-temporal dynamics of EEG signals, the PSD often exhibits a linearly decreasing behavior over log10 coordinates considering frequency and amplitude of PSD or spectral power. This is called in the literature “power law” or scale-free behavior (1/f^α), where cognitive processing states varied by the slope, − α. Power law behavior is attributed to the brain structural connectivity and dynamical properties.

The power spectral density (PSD) may often conform to a power-law distribution, by taking the linear regression of the PSD in coordinates of log power versus log frequency. These findings are explained with a model of the neural source of the background activity in mutual excitation among pyramidal cells. The dendritic response of a population of interactive excitatory neurons to an impulse input is a rapid exponential rise and a slow exponential decay, which can be fitted with the sum of two exponential terms. When that function is convolved as the kernel with pulses from a Poisson process and summed, the resulting “brown” (1/f²) or “black“(1/f³) noise conforms to the EEG time series and the PSD in rest and sleep states (Freeman and Zhai 2009). Linear regression ranges are selected within self-stabilized neural beta–gamma range (20–50 Hz) based on analysis of human EEG normal/abnormal states.

Variations in the observed slope are attributed to changes in the level of the background activity that is homeostatically regulated by the refractory periods of the excitatory neurons. Departures in behavior from rest and sleep to action are accompanied by local peaks in the PSD, which manifest emergent nonrandom structure in the EEG. Awake and sleep states will have slope values within 2 and 3 in the beta-gamma range (Freeman and Zhai 2009). The stability of the normal background activity is governed by a non-zero point attractor, by which the level is homeostatically regulated. The PSD values involve a range of values where PSD values are initially flat, then decay rapidly throughout the rest of the PSD display. The location of the inflection frequency in PSD of EEG between 1 and 10 Hz, or delta-theta-alpha ranges, indicates typical values between 0.1 and 10/s for prevailing steady state input levels (Freeman and Zhai 2009). This is verified by simulating the PSD of the signal which shows the inflection point as located above 10 Hz.

The PSD of the states of sleep, awake, seizure, and VNS dampened seizure conform to the power law relation, 1/f^−α, where α = − 3 when the patient is at rest, α = − 3 to − 2 during the awake state, α = − 2 during cognitive tasks, whereas when α = − 2, that referred to as brown noise, 1/f², which is found to the PSD of the EEG in animals engaged in intentional behaviors (Freeman 2006). This change also appears in pre-ictal EEG, so it might offer a clue to understanding the mechanisms of complex partial seizures and predicting their onsets (Freeman et al. 2006). Alpha values of human EEGs during awake and sleep states have been found to be within − 2 to − 3 (Freeman et al. 2006). The calculated PSD linear regression values during the seizure state approaches the theoretical limit of − 4 (Freeman and Zhai 2009).

Phase space analysis

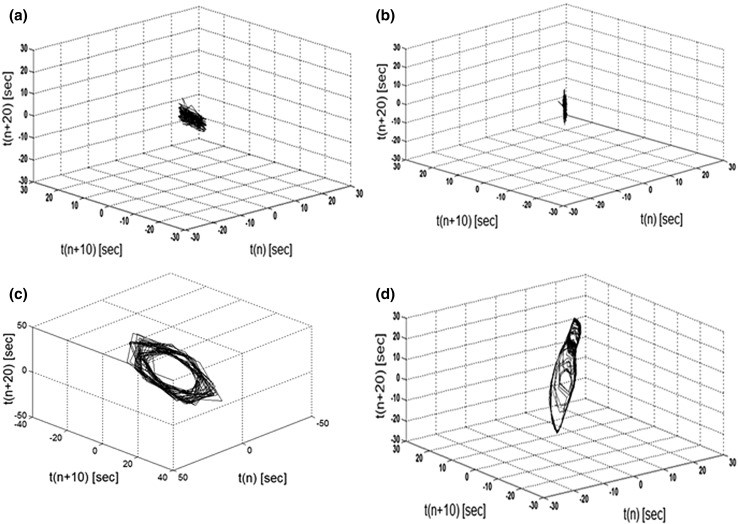
Phase space representations of the normal and abnormal states of seizure patient’s EEGs were taken in order to demonstrate limit cycle and chaotic behavior. Nonlinear analyses have suggested that the seizure state may represent a transition from the normal EEG state to one of increased synchronous activity and that a more orderly state characterizes an epileptic seizure (Velazquez et al. 2003). Phase diagrams will demonstrate normal/abnormal brain states in order to demonstrate the normal EEG in the form of a chaotic attractor versus the abnormal seizure EEG in the form of a limit cycle. Plots of the EEG time series against by a fixed time offset reveal the dynamics of the EEG signal as the time series may converge, diverge or move in a period motion (Freeman 1986). Time series offset values (n) were plotted for normal and seizure states, where the x, y, and z axis where plotted with the x-axis = T(n), y-axis = T(n + 10), and the z-axis = T(n + 20) for EEG and simulated EEG analysis. The selected offsets enable a clearer depiction of the chaotic attractors found in the normal EEG time series versus the semi-periodic behavior found in the EEG of the seizure state.

Autocorrelation analysis

The autocorrelation function is used to measure ‘rhythmicity’ or periodic areas found in the signal (Liu et al. 1992). Autocorrelation, the cross-correlation of a signal with a delayed version of itself, is useful for finding repeating patterns in a signal, such as determining the presence of periodic signals in complex signals. In the case of a repeating pattern, such as seizure spikes, the autocorrelation results in regularly spaced peaks and troughs. During non-seizure times when the signal is not rhythmic, the autocorrelation results in irregular peaks and troughs (Faul and Boylan 2005). Regularity in peaks is the same as having a dominant frequency. In theory, the entropy of the autocorrelation function should be able to quantify how regular the peaks are and therefore the level of rhythmicity in the original signal. Regularity in peaks is the same as having a dominant frequency. Autocorrelation is performed on 1 min windows of EEG data and 16 s windows of simulated EEGs. Low-pass filtering using the Remez filter for filtering 6-12 Hz of the EEG and simulated EEG was performed in order to locate semi-periodic behavior in the signals.

Results

The KIV model is used as an EEG simulator to exhibit the attributes found in human EEGs. In order to exhibit the ‘normal’ chaotic state of human EEGs, the KIV model was adjusted to exhibit the same ‘noisy’ attributes through the input of randomized values throughout the network. Low coupling between the networks enabled low feedback to occur and therefore diminish the influence of the three networks onto each other.

Figure 6 shows normal and seizure EEG behavior (left), and simulated normal and seizure behavior using KIV model (right). These sites will be used for comparative analysis. In Fig. 6 (bottom row) it is observed that the seizure behavior changes from a broad-band dynamic behavior to a state with narrow-band semi-periodic oscillations. The seizure state is performed through the KIV network through the adjustment of internal nodes of one the KIII networks that correlate to the sensory cortex of the limbic system. Reduction of excitatory nodes within the KIII, as described above, enables runaway inhibitory behavior of the signal, with a frequency of 3/s.

Fig. 6.

a EEG figures featuring EEG time series and c seizure event. b Simulated EEG of normal and d seizure state

PSD analysis found in Fig. 7, features PSD displays of EEG and simulated EEG time series, where linear regression was performed in order to find the slope of the PSD values. The slope corresponds to the alpha value in 1/f^α. Simulated EEG PSD alpha values are in the same range of normal EEGs (2–3) and seizure state EEGs (< 4).

Fig. 7.

a EEG figures featuring PSD values for EEG data where alpha = − 2.16 and c seizure event, where alpha = − 3.68. b Simulated EEG of normal, where alpha = − 2.73 and d seizure state, where alpha = − 3.88

Five simulated patients are constructed through the KIV by varying the levels of noise throughout the KIV by 5%, whereas patient A1 is a KIV with full input noise, and patient A5 has 20% less noise than A1. These simulated ‘patient’ EEGs illustrate how noise effects the alpha values collected from their respective EEGs.

The PSDs of four human patients EEGs were analyzed to confirm the differing alpha values found between the normal and seizure states, as seen in Tables 3 and 4.

Table 3.

PSD–EEG-normal state

	Patient 1 (25)	Patient 2 (25)	Patient 3 (25)	Patient 4 (25)
$\overline{\propto }$	2.38	2.53	2.46	2.51
${\mathit{\sigma }}_{\mathit{\alpha }}$	0.24	0.29	0.25	0.24
Min (− α)	2.02	2.01	2.04	2.15
Max (− α)	2.91	2.93	2.86	2.89

Table 4.

PSD–EEG-seizure state

	Patient 1 (25)	Patient 2 (25)	Patient 3 (25)	Patient 4 (25)
$\overline{\propto }$	3.65	3.68	3.72	3.64
${\mathit{\sigma }}_{\mathit{\alpha }}$	0.16	0.14	0.11	0.10
Min (− α)	3.41	3.39	3.54	3.42
Max (− α)	3.89	3.91	3.88	3.81

Alpha values collected from the slope of the log10 values confirmed the ranges for normal/seizure states, where $\overline{\propto }$ and ${\mathit{\sigma }}_{\mathit{\alpha }}$ denote the average and standard deviation of α, respectively.

The PSD values found during seizure activity exhibited high power in both the low and high theta ranges, corresponding to the 3/s wave that dominated the EEG (Freeman et al. 2006). Additionally, the KIV normal and seizure state exhibited the same alpha value range in Tables 5 and 6.

Table 5.

PSD–KIV-normal state

	A1 (25)	A2 (25)	A3 (25)	A4 (25)	A5 (25)
$\overline{\propto }$	2.40	2.40	2.50	2.67	2.70
${\mathit{\sigma }}_{\mathit{\alpha }}$	0.28	0.26	0.24	0.22	0.16
Min (− α)	2.04	2.06	2.12	2.32	2.41
Max (− α)	2.86	2.88	2.92	2.95	2.96

Table 6.

PSD–KIV-seziure state

	A1 (25)	A2 (25)	A3 (25)	A4 (25)	A5 (25)
$\overline{\propto }$	3.61	3.65	3.74	3.77	3.77
${\mathit{\sigma }}_{\mathit{\alpha }}$	0.18	0.17	0.13	0.11	0.11
Min (− α)	3.31	3.33	3.44	3.57	3.60
Max (− α)	3.96	3.91	3.95	3.97	3.98

Autocorrelation diagrams depicted in Fig. 8 show the same periodic and non-periodic behavior between seizure and non-seizure states of the simulated EEG. Phase diagrams displayed in Fig. 9 depict the chaotic attractors found in normal ureEEG and simulated EEG as well as limit cycles found in the EEG and simulated EEGs of the seizure state.

Fig. 8.

a EEG figures featuring autocorrelation diagrams where the normal chaotic state is exhibited in the diagram and c seizure event depicts periodic activity. b Simulated EEG of normal chaotic values is depicted and d the simulated EEG shows periodic activity

Fig. 9.

a EEG figures featuring phase diagram values where the normal chaotic state is exhibited in the diagram and c a seizure event depicts a limit cycle. b Simulated EEG of normal chaotic values are depicted and d seizure state, exhibits the same limit cycle attributes

Restoration of the KIV seizure state back to the initial chaotic state is accomplished through the introduction of an external signal I(t) from Eq. (1) into the KIV network. This external signal is a modified KII object with slightly increased values (1%) of the original KII object values, which altogether comprises of the external Brain Stimulator Interface (BSI) signal. The parameters of the BSI external input object and the entire KIV network is listed in the ‘restore’ state in Table 2. The BSI signal is applied to the top node of the amygdala KII object, where the input of this signal is updated throughout the combined KIII hippocampus and cortex objects, as well as the KII amygdala. The KIV model is re-executed with an external input to simulate electrical pacing therapy at the same time segment as the simulated seizure state. The BSI signal to the KIV model is a 42 Hz signal, with a 21 ms pulse width applied over the seizure state time series. The external BSI signal is applied to the KII (amygdala) matrix before the next output KII signal is calculated through the 2nd order ODE. The BSI signal restores the signal back to its normal state. Our model supports the idea that a patient-tailored protocol may be the best approach to reducing the seizure effect (Osorio et al. 2005; Sunderam et al. 2010).

When this signal is applied to the KIV as the time series is calculated, the output of the KIV displays the restored normal state, as seen in Fig. 10.

Fig. 10.

a Simulated EEG featuring the restored simulated EEG state where the normal chaotic state is exhibited in the diagram and c the phase diagram depicts chaotic behavior as a chaotic attractor, b the restored state PSD has an alpha value = 2.33, and d the autocorrelation display has non-periodic attributes

Conclusions and discussion

Within the KIV model, our simulation of EEG activity involves near-white noise embedded in the signal; which is based on the premise of immense numbers of interacting pyramidal cells, whose activity episodically undergoes transient increases in spatial coherence (Freeman 2006). The role of noise in the KIV is illustrated in Table 6, whereas the lessening of noise from patient A1 to A5 seems to increase the PSD alpha values from the normal to abnormal KIV time series. The rise of PSD values found in the theta frequency bands of 3-8 Hz causes the slope of the PSD to rise sharply, causing the higher frequency bands to diminish due to the reduction of noise in the system (Kozma 2003).

PSD values found during the EEG time series and the simulated EEG time series exhibit low standard deviation during the seizure states per patient. This activity may be due to the entrainment of large scale neural population whose power per frequency is limited to the theta range. High theta activity causes the slope of the PSD to rise sharply, and diminishes any other brain activity state, i.e., the carrier wave in the rest state, active state and sleep state which seems to be diminished or lost during the seizure (Freeman et al. 2006). Noteworthy are the steepened slope − α of 1/f^α PSD in the seizure state compared with the normal state (Fig. 7c) which is simulated in the KIV model (Fig. 7d).

The PSD in the normal state of human and simulated EEG conforms roughly to 1/f^−α having a slope near − 2 (Fig. 7a, b). We propose that the normal neural activity manifests a process of self-organized criticality (Jensen 1998), in which the mean firing rates of neurons are held at a critical value throughout the cortex, homeostatically stabilized locally by their thresholds and refractory periods (Freeman 2004).

The onset of seizures is characterized by high amplitude slow waves and a shift in the PSD nearer to 1/f^−α with a slope less than ‘− 4’ and loss of the peaks in PSD in the classical ranges (beta–gamma frequency ranges). The seizures were characterized by high amplitude waves at 3/s showing that the normal shared waveform (the carrier wave in the normal state (beta–gamma ranges) was diminished or lost during the seizure. The PSD during seizure likewise often differed sharply from the 1/f^−α form of the PSD in the normal states with high power in both the low and high theta ranges, corresponding to the 3/s wave that dominated the EEG (Freeman et al. 2006). We attribute these properties to sustained loss of large-scale synaptic integration (Varela et al. 2001) that normally smoothes by cooperative interactions the local spatial variations in activity that arise through competitive inhibition and prevents breakdown of large-scale organization of the neocortex (Chavez et al. 2003). When interactions among inhibitory neurons rose to a high intensity with a deficit of excitation, an instability emerged in which some neurons increased their activity, inhibiting their neighbors, and thus producing a more excited regenerative feedback that produced a self-limited explosive discharge of half the population and an inhibitory post-synaptic potential in the excitatory neurons to which they projected (Freeman et al. 2006). The seizure states are departures from this sequence into diminished global integration by sustained loss of long-range correlated activity, initially with loss of spectral peaks in the PSD, followed by explosive growth of local activity (Freeman et al. 2006).

The restoration state is the simulated EEG restored back to its chaotic signal generating state due to the implementation of an external signal. The external signal exhibits the same type of treatment found in VNS treatment that may restore the seizure state through a rebalancing of excitatory and inhibitory neural activity. This object is a modified KII object which enables the restoration of the KIV seizure state back to its normal chaotic attractor output. In this manner, we are adding a KII network to the KIV network to overcome the semi-periodic firings of the network due to runaway inhibitory neuron activity. The introduction of an additional KII network to the KIV model may act in a similar manner as described previously as a de-regularizer of the 3/s activity throughout the network.

Figure 10 shows the restored simulated EEG after an external input has been added to the system. Phase diagrams display chaotic attractor behavior as found in the normal and simulated EEG as well as autocorrelation displays depicts the restored signal back to its original non-periodic state.

PSD analysis of the KIV model restoration state also exhibits small standard deviation across the simulated patient EEGs, while maintaining the alpha range of 2–3, as seen in Table 7.

Table 7.

PSD–KIV restored state

	A1 (25)	A2 (25)	A3 (25)	A4 (25)	A5 (25)
$\overline{\propto }$	2.47	2.52	2.61	2.69	2.77
${\mathit{\sigma }}_{\mathit{\alpha }}$	0.18	0.17	0.17	0.17	0.16
Min (− α)	2.13	2.17	2.28	2.36	2.44
Max (− α)	2.65	2.70	2.78	2.89	2.95

The external signal that restores the KIV model back to its initial state causes the runaway inhibitory signal to become ‘rebalanced’, since the external signal may provide the excitatory signal needed to restore the signal. Through the EEG simulator, electrical titration methodologies can be tested, and researched in order to provide an insight to the manner VNS treatment reduces the effects of the seizure state.