Compaction of single DNA molecules induced by binding of integration host factor (IHF)

Abstract

We studied the interaction between the integration host factor (IHF), a major nucleoid-associated protein in bacteria, and single DNA molecules. Force–extension measurements of λ DNA and an analysis of the Brownian motion of small beads tethered to a surface by single short DNA molecules, in equilibrium with an IHF solution, indicate that: (i) the DNA–IHF complex retains a random, although more compact, coiled configuration for zero or small values of the tension, (ii) IHF induces DNA compaction by binding to multiple DNA sites with low specificity, and (iii) with increasing tension on the DNA, the elastic properties of bare DNA are recovered. This behavior is consistent with the predictions of a statistical mechanical model describing how proteins bending DNA are driven off by an applied tension on the DNA molecule. Estimates of the amount of bound IHF in DNA–IHF complexes obtained from the model agree very well with independent measurements of this quantity obtained from the analysis of DNA–IHF crosslinking. Our findings support the long-held view that IHF and other histone-like proteins play an important role in shaping the long-scale structure of the bacterial nucleoid.

The genetic material in bacterial cells is organized in a structure called the nucleoid (1–3). In Escherichia coli, this nucleoprotein complex consists of a single circular DNA molecule 4.7 million bp long, RNA, and a large variety of bound proteins. Among these, about 10 so-called histone-like proteins, including HU, integration host factor (IHF), and H-NS (1–3), shape the short-scale structure of the nucleoid by bending DNA locally on binding. These proteins therefore play an important role in compacting the DNA molecule, in addition to other factors such as supercoiling (4), macromolecular crowding (5), and osmotic effects (6).

The level of nucleoid-associated proteins changes as a function of bacterial growth. For example, the level of IHF was shown to increase on entry to the stationary phase of growth, becoming one of the major histone-like proteins in the cell (7–10). By binding to specific DNA sites, IHF participates in forming higher-order DNA structures required for replication, site-specific recombination, phage packaging, and regulation of transcription initiation (8). IHF can also bind to DNA nonspecifically and can be substituted by HU. In fact, IHF and HU possess similar overall structures and share several regions of conserved homologies (11, 12).

Very little is known about the structural modifications on DNA induced by histone-like proteins in nucleoid formation. In particular, the degree of compaction induced by each of these proteins has not been quantified, and information about the large-scale structure of nucleoprotein complexes is scarce. This deficiency stems in part from the fact that classical techniques used in molecular biology are designed for studying relatively strong DNA-binding sites and cannot appropriately assess the contribution of nonspecific low-affinity interactions. Furthermore, analyses based on electron microscopy may alter the structure under study.

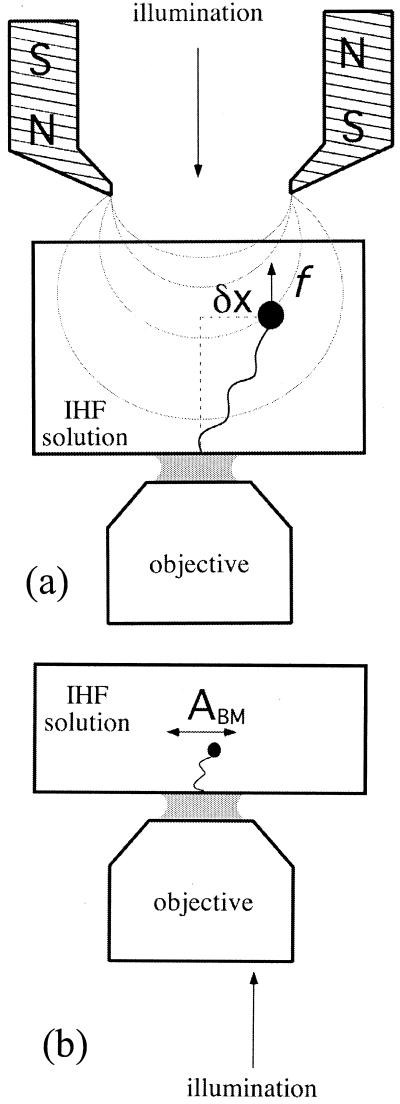
In this work, we describe the results of a new experimental approach designed to shed light on these issues by studying the elasticity of single DNA molecules interacting with IHF molecules in solution. A DNA molecule, anchored on one end to a glass substrate and on the other to a small magnetic bead, is stretched with a pair of magnets (Fig. 1a). By moving the magnets up or down, the force on the bead can be changed, force–extension curves can be measured (13, 14), and the degree of compaction for different forces and IHF concentrations assayed. These measurements allow us to quantify the compaction of a DNA macromolecule (λ-phage DNA) by a histone-like protein and obtain information about the large-scale structure of the resulting nucleoprotein complex.

Figure 1.

(a) Experimental setup for force–extension measurements of λ-phage DNA–IHF complexes. A force is exerted on the DNA-tethered paramagnetic bead by a pair of magnets, whose height can be controlled to change the force's magnitude. (b) Experimental setup for measurements of the amplitude of transversal Brownian motion A_BM of small beads tethered by short DNA molecules to a glass slide in the presence of IHF.

Materials and Methods

IHF Protein.

Wild-type and mutant proteins were purified from overexpressing bacteria, as described previously (15, 16).

DNA Bead Constructs.

λ-Phage DNA-bead constructs were prepared by mixing 2.8 μm magnetic tosyl-activated beads [Dynal (Oslo) M280] coated with antidigoxigenin (anti-DIG) and passivated with α-casein, with λ-phage DNA labeled at the right and left ends with biotin and DIG, respectively. Labeling was achieved by hybridizing and ligating bare λ-phage DNA with labeled complementary DNA oligomers. λ-Phage DNA was obtained from Roche Molecular Biochemicals.

Experiments with short DNA fragments were carried out by using 1,288-bp DNA molecules having a specific IHF-binding site or 850-bp molecules without a binding site. The DNA fragments were labeled at the ends by cleaving first with SalI and filling the 3′-recessed ends with DNA polymerase (Klenow) and biotinylated dUTP, followed by cleavage with AflII and filling with DIG-labeled dUTP. The DNA molecules, labeled at the ends with DIG and biotin, were bound to a glass slide in a sample well and incubated with streptavidin-coated beads at room temperature for 1 h. A fragment containing an IHF site (GATCCACCATCTAAGTAGTTGATTCATAGTGACTGCATAGGTGAGGATTCTCTAGGTTCTCTACATGCTA), when present, was located 481 bp away from a biotin-labeled end. The beads [Interfacial Dynamics (Portland, OR) surfactant-free aldehyde beads 290 nm in diameter] were prepared by coating them first with streptavidin and then passivating them with α casein.

Sample Cells.

Cells for DNA elasticity measurements were similar to those used by Strick et al. (14). In brief, samples were prepared in capillaries of square cross section (Vitro Dynamics, Rockaway, NY), which were washed first in a NH₄/H₂O₂/H₂O solution (1:1:5), rinsed in H₂O for 10 min and dried. The inner surface of each capillary was then made hydrophobic by soaking in Sigmacote (Sigma) and rinsed in both ethanol and H₂O. Next, the capillary was coated with BSA–biotin (incubation for 2 h at 37°C), followed by incubation with streptavidin for 2 h at 37°C. DNA–bead constructs in casein buffer (10 mM Tris⋅HCl/200 mM KCl/5% DMSO/0.1 mM EDTA/0.2 mg/ml of α casein, pH 8.0) were then introduced and incubated at room temperature to allow for enough constructs to bind to the lower inner side of the capillary.

Sample wells for experiments with short DNA molecules were constructed by sticking a 1.0-mm-thick plastic disk with a concentric hole of 6-mm diameter to a hydrophobic cover glass with a parafilm layer. A cover glass was then used to seal the well from the top, leaving a sample volume of about 45 μl. Two syringe needles through the plastic disk allowed for buffer exchange and the introduction of IHF into the well. All cover glasses were washed and made hydrophobic by following the above procedures for the capillaries. A typical sample was prepared within a well by first coating the hydrophobic surface with a polyclonal antibody to DIG, followed by passivation with α-casein to eliminate nonspecific binding of the DNA to the surface. DNA–bead constructs in casein buffer were dispensed into the well before sealing the latter from the top and were in incubation for 2 h at room temperature. This incubation allowed for enough DIG-labeled constructs to bind to the anti-DIG-covered surface (Fig. 1b).

Experiments with both λ DNA and short DNA were carried out in IHF solutions of various concentrations in casein buffer.

Force Measurements and Optical Setup.

Samples containing λ-DNA-tethered magnetic beads were observed by bright-field illumination by using a home-built inverted microscope (Fig. 1a). Extension–force measurements were made by using the magnetic force technique of Strick et al. (14). In brief, a vertical magnetic force stretching the tethering DNA molecule was applied on a bead by means of a pair of magnets, whose height could be controlled accurately. The vertical force F was obtained from measurements of the bead's Brownian motion transverse to the direction of the force, by using the equipartition theorem:

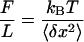1

Here, L is the extension of the tether, 〈δx²〉 represents an average over the square of the bead transverse displacements in the x direction (Fig. 1a), T is the temperature, and k_B is Boltzmann's constant. In practice, the measurement of force–extension curves was carried out in two steps. First, the force corresponding to each magnet height was determined. This was done by evaluating 〈δx²〉 as a function of the magnets' height, in the absence of IHF. Next, the extension L was measured by accumulating images for 12 seconds and then correlating each of these images with a library of images taken of the same bead–DNA construct, when stretched by a large force (>10 pN), to prevent large fluctuation in the longitudinal z direction. The images in the library were obtained at different foci separated by a known amount over a range of 20 μm. The procedure just outlined determined the force for each magnet height. To measure the force–distance relationship of a nucleoprotein complex, only the extension of the complex was measured for each calibrated magnet position. The reproducibility of force–extension curves was checked by making measurements on 10 different λ-DNA molecules for each IHF concentration.

The motion of small beads attached to short DNA tethers was tracked by using a dark-field light-scattering illumination method (unpublished work). This method allowed us to observe the 290-nm beads with high contrast. Ten-minute movies of the transversal x,y motion of the tethered beads were recorded and later analyzed to determine the effect of the IHF, as explained below.

Data Processing and Analysis.

The extension of λ-DNA molecules was measured by the following procedure: the center of the first bead image in an experimental run and the center of all of the bead images in the library were initially determined. The radial intensity profiles of the bead image and those in the library were then calculated. Next, the radial intensity profile of the bead image was correlated with the profiles corresponding to each image in the library. Bead height was determined by performing a parabolic fit around the maximum of the correlation, as a function of the height corresponding to each library image. The height value corresponding to the maximum of the fit was then defined as the bead height. This procedure was repeated for each image in an experimental run after the first, calculating the correlation only with images in the library corresponding to small differences in height relative to the previous image in the experimental run. We estimate the error in our measurements at about 1% of the total length, or about 150 nm.

Video recordings of experiments with short DNA molecules tethering small beads to a glass slide were processed to determine the amplitude of the beads' Brownian motion parallel to the slide. Images taken at 0.1-sec intervals were downloaded into a computer, after which even lines were removed and odd lines interpolated to eliminate the blurring caused by interlacing. The contrast of each image was then enhanced by filtering with a Gaussian mask (17). The x,y coordinates of the center of mass of the filtered images were then determined. After subtracting from each coordinate its average throughout the recording, the x and y coordinates were plotted against each other. The number of events at a given distance from the origin was counted, and this value was divided by that distance to obtain a radial density distribution function. The amplitude of the transversal Brownian motion was then defined as the width at half height of the radial distribution function.

Density Gradient Centrifugation of IHF–DNA Complexes.

[³²P]-labeled λ-DNA was incubated with IHF (1 μM) in 20 μl of 10 mM Tris⋅HCl, pH 7.5/100 mM KCl/2.5% glycerol for 20 min at 20°C. In control reactions, IHF was omitted or poly(dI-dC) was added as competitor at 0.2 mg/ml. Two hundred microliters of an ice-cold solution of 4% formaldehyde in 50 mM sodium phosphate, pH 7.0, was added, followed by incubation for 2 h on ice. Then 5 μl of 10% sarcosyl and 5 μg of unlabeled λ-DNA were added, and the solution was layered over 11 ml of CsCl solution (50% wt/wt in 10 mM Na-phosphate, pH 7.0/2% formaldehyde, refractive index = 1.3915) in a polyallomer ultracentrifuge tube. The samples were then centrifuged for 60 h at 24,000 rpm in a SW41 rotor (Beckman Coulter). Fractions of 0.3 ml were collected from the bottom of the tube; aliquots of each fraction were analyzed for radioactivity by scintillation counting, presence of unlabeled DNA by agarose gel electrophoresis, and density by refractometry. The protein/DNA ratio in the complexes was estimated on the basis of a simplified model (18).

Results

Elasticity of λ-Phage DNA–IHF Complexes.

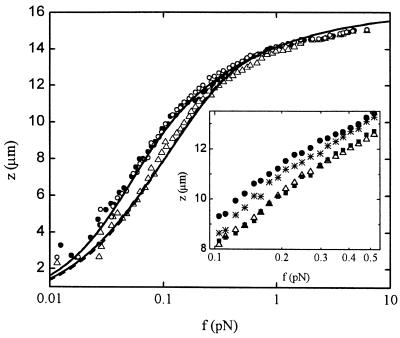
The effects of IHF on a λ-DNA molecule tethering a magnetic bead are illustrated in Fig. 2, where we plot the extension z of the DNA molecule as a function of the force f applied to it for 0 nM and 1,250 nM IHF. Measurements spanning the range of concentrations between these two values (as illustrated in Fig. 2 Inset for 250 nM IHF) indicate that for IHF concentrations below ≈500 nM, the strength of the effects increases with IHF concentration, whereas above this value, the effects level off. For example, data at 500 nM are indistinguishable within experimental error from the data at 1,250 nM shown in Fig. 2. The effects of IHF are markedly stronger for small forces and decrease as the molecule becomes tauter. For IHF concentrations at and above ≈500 nM, the change in the linear extent of the molecule can reach around 30% relative to bare DNA. We note that no hysteresis is observed during repeated cycles of extension and retraction, as illustrated for the case of 1,250 nM (Fig. 2 Inset). We accumulated images for 12 sec at each value of the force. Given that the typical residence time of a protein on a specific site is of the order of 1 sec (19), and that the residence time on a low-affinity site is expected to be much smaller, the DNA–IHF complex can be regarded as in equilibrium with the IHF solution during force–extension measurements.

Figure 2.

Extension z versus force f curves for a λ-phage DNA molecule in protein solutions of different concentration: 0 nM IHF (full circles), 1,250 nM IHF (empty triangles), and 1,250 nM of mutant βR46C (empty circles). The data for 0 nM data were fitted with Eq. 2 (full line), assuming fixed persistence and molecular lengths A₀ and L₀, respectively. The 1,250 nM data were fitted with the full model (see text and ref. 22), assuming either IHF sliding along the DNA molecule (full line) or fixed IHF positions (dashed line). (Inset) Magnification of the region of maximal difference between experimental force–distance curves for different IHF concentrations, showing behavior at an intermediate concentration, 250 nM IHF (stars), as well as the absence of hysteresis at a typical large concentration, 1,250 nM. Extension (empty triangles) of the nucleoprotein complex is followed by retraction (full squares).

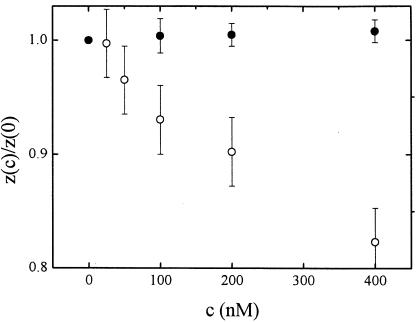
The compaction could in principle be caused both by specific and low-affinity binding of the protein. However, the range of IHF concentration over which effects are observed (hundreds of nanomolars), the small number of known high-affinity specific sites on the λ-phage genome and their highly clustered distribution make it rather unlikely that high-affinity specific binding alone can account for the degree of compaction we observe. To provide further support for this contention, we have conducted similar measurements in the presence of 0.02 mg/ml poly(dI-dC), which competes with nonspecific binding but not with the binding of IHF to high-affinity sites. We plot in Fig. 3 the height of a magnetic bead tethered by a λ-DNA molecule subjected to a constant force of 150 fN as a function of IHF concentration. This value of the force falls well within the range where IHF effects are observed to be the largest. Poly(dI-dC) indeed inhibits DNA compaction, competing effectively for IHF with the DNA molecules. Hence we conclude that low-affinity binding of IHF to DNA is the dominant mechanism responsible for compaction. This conclusion is consistent with the fact that we observe no hysteresis on extension and subsequent retraction of the DNA molecule.

Figure 3.

Height z(c) of a 2.8-μm bead tethered by a λ-phage DNA molecule as a function of IHF concentration c, normalized by the height at c = 0 in the presence of 0.02 mg/ml poly(dI-dC) (full circles) and in its absence (empty circles). The molecule is stretched with a constant force of 150 fN.

Effects of IHF on Short DNA Molecules.

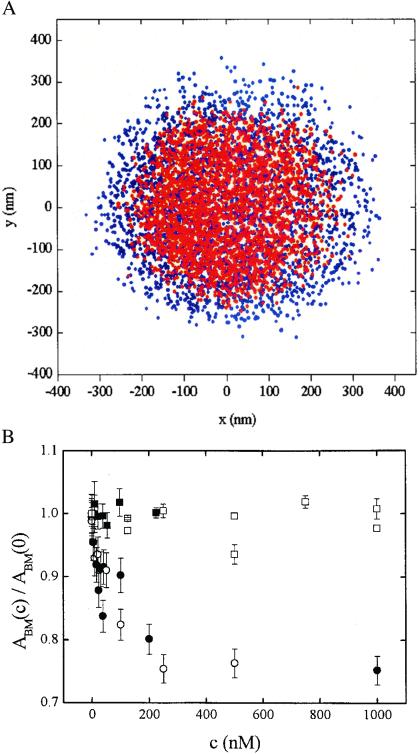
The contribution of specific binding to compaction can also be assayed by studying the Brownian motion of small beads tethered by short DNA molecules with and without a specific binding site and with no external force applied on the beads. For this purpose, DNA molecules 1,288 bp long with a single high-affinity IHF binding site and DNA molecules 850 bp long without a specific site were studied. The beads' transversal Brownian motion was followed, and the decrease in the amplitude of the latter was determined as a function of IHF concentration. Typical data out of which the amplitude of Brownian motion at [IHF]c A_BM(c) was calculated are illustrated in Fig. 4A, where the x,y coordinates of a tethered bead are plotted, both without and with IHF.

Figure 4.

Brownian motion of beads tethered by short DNA fragments. (A) x,y coordinates of a bead undergoing Brownian motion without IHF (blue) and with 1.0 μM IHF (red). The bead was tethered by a 1,288-bp DNA molecule with a specific IHF site. (B) Normalized amplitude of Brownian motion A_BM(c)/A_BM(0) of tethered beads as a function of wild-type IHF concentration c: 1,288-bp DNA with a specific IHF site (full circles), 850-bp DNA without a specific site (empty circles), 1,288-bp DNA with a specific site in the presence of 0.02 mg/ml of poly(dI-dC) (full squares). A_BM(c)/A_BM(0) as a function of mutant βR46C concentration c in the case of a bead tethered by a 1,200-bp DNA molecule (empty squares).

An increasing IHF concentration led to a decrease of the same magnitude, irrespective of whether a specific site was present or absent, as shown in Fig. 4B. The amplitude of Brownian motion A_BM(c), normalized by the amplitude at zero IHF concentration decreased monotonously by ≈25%, which is close in magnitude to the effect observed with λ-phage DNA. Leveling off of the effects on further addition of IHF is observed at concentrations above 400 nM, consistent with elasticity measurements. The addition of 0.02 mg/ml of poly(dI-dC) resulted in the inhibition of DNA compaction by IHF, as shown also in Fig. 4B. These findings provide further support for the hypothesis that DNA compaction by IHF is because of low-affinity binding of IHF to DNA.

IHF Mutant βR46C Does Not Induce Compaction.

We have also studied the effects of a mutant IHF protein on compaction. The mutant differs from native IHF in just one amino acid substitution (βR46C). The arginine at this position in the native protein is believed to play an important role in specific binding, by making a direct contact with the edge of a DNA base (20). As shown in Figs. 2 and 4B, this mutant has no appreciable effect on the elasticity or on DNA conformation, in stark contrast with the native protein. This result correlates well with the reduced activity of this mutant in vivo, where it retains only about 1% of the native IHF activity (15), and shows that this mutation affects considerably low-affinity binding as well. This finding is also consistent with previous studies that showed that the identical mutant protein failed to bind to DNA fragments containing a specific IHF site (21).

Number of Bound IHF Molecules in a λ-DNA–IHF Complex.

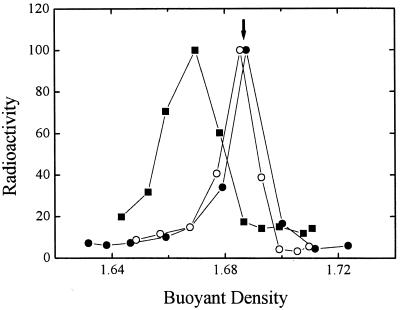
To estimate the number of IHF molecules bound to a λ-DNA molecule under conditions at which further addition of IHF does not induce further compaction, we measured the shift in buoyant density of the complexes relative to unbound DNA. λ-DNA was incubated with IHF, crosslinked with formaldehyde to prevent dissociation, and resolved by equilibrium density centrifugation on CsCl gradients. Binding of IHF causes a decrease in the buoyant density of λ-DNA, yielding a broader distribution (Fig. 5). This decrease was not seen when competitor DNA [poly(dI-dC)] was added, or when IHF was replaced by the βR46C mutant. In additional control experiments (not shown), preincubation of IHF with formaldehyde before addition of λ-DNA for as little as 2 min abolished the density shift. The extent of the density shift did not measurably depend on the length of incubation with formaldehyde or on the presence of formaldehyde in the density gradient and was the same when glutaraldehyde was used as crosslinker. From the buoyant densities, we estimate that the protein constitutes 4–14% of the weight of the complexes, corresponding to 60–150 IHF molecules per λ DNA.

Figure 5.

Buoyant densities of DNA–IHF complexes. Radioactive λ DNA alone (full circles) incubated with native IHF (full squares) or with mutant IHF (empty circles) was fixed with formaldehyde and fractionated by equilibrium density gradient centrifugation in CsCl. The radioactivity in each fraction is shown as a function of the density, as calculated from the refractive index. Unlabeled λ DNA added to all gradients as an internal standard banded at the position marked by the arrow.

Discussion

IHF Induces Compaction by Binding to Low-Affinity Sites.

Our results indicate that DNA molecules retain a random, although more compact, coiled structure in the presence of IHF. The extent of compaction increases with IHF concentration for concentrations below ≈500 nM. Above this concentration, further addition of IHF shows no effect on the DNA molecule. Several pieces of evidence suggest that the behavior we observe is caused by binding of IHF to low-affinity sites on the DNA molecule: (i) the large IHF concentrations over which the effects we report are observed, (ii) experiments with short DNA molecules show that within experimental error, the same degree of compaction is achieved whether the DNA molecules include a specific site or not, and (iii) no compaction is observed when poly(dI-dC), a nonspecific substrate for IHF, is added.

Analysis of Force–Extension Curves.

We observe the largest effects at small extensions, for which DNA molecules are relaxed. With increasing force, DNA molecules become tauter, the degree of compaction induced by IHF decreases, and the elastic behavior of bare DNA is recovered. These findings suggest that tension makes it more unfavorable for IHF molecules to bind, and bound molecules can be driven off, in line with recent theoretical ideas (22).

Previous bare DNA elasticity experiments (13, 14) have demonstrated that the conformation of DNA molecules in solution can be adequately described by the worm-like chain model (23), according to which a DNA molecule is described as an intermediate between a rigid rod and a flexible coil. This description accounts on the one hand for the short-range stiffness, as measured by the bare persistence length A₀, and on the other for long-range flexibility. A₀ is defined as the distance over which the orientation of two segments along the DNA contour is still correlated and under physiological conditions is of the order of 55 nm. Recently, Marko and Siggia (22) have extended these ideas to model the elasticity of a nucleoprotein complex. Although they considered explicitly the case of chromatin in which DNA wraps around histone octamers, their ideas apply equally well to our experiments. Following this model, we describe the IHF–DNA complex as a coil with effective contour and persistence lengths (L and A, respectively) shorter than the contour and persistence lengths of bare DNA (L₀ and A₀), because of the presence of a concentration-dependent number of bends or kinks induced by low-affinity IHF binding. L and A depend on the length of the stretch of DNA λ associated with an IHF molecule, as well as on the IHF concentration c through the chemical potential μ ≡ k_BT log(c/K_a).

Within the model, the force f for a given extension z is given by the same formula as for bare DNA.

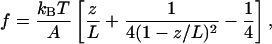2

where A and L are given by:

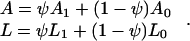3

Here, ψ is the fraction of DNA length occupied by bound protein, whereas L₁ and A₁ are the contour and persistence lengths of the portion of the DNA molecule associated with IHF. Note that Eq. 2 alone cannot be fitted directly to the data, because both A and L are tension-dependent. Marko and Siggia (22) considered two possible extreme cases: while bound, IHF molecules can either be fixed in position, or alternatively, IHF molecules can slide freely along the DNA contour. These two cases correspond to different free energies, F_fixed (z,ψ), F_slide (z,ψ), respectively (22). Fitting involves minimization of either of the free energies with respect to ψ for given values of all of the parameters (μ, L₀, A₀, L₁ and A₁, and ℓ) and z (22).

The fits to the data in the case of 1,250 nM IHF for both fixed and sliding are shown in Fig. 2, together with a fit to bare DNA. For the latter, we obtained A₀ = 62 ± 4 nm and L₀ = 16.2 ± 0.2 μm, in agreement with accepted values. The fits to the data corresponding to 1,250 nM IHF yielded the fractional compaction L₁/L₀, the length of the segment associated with an IHF molecule ℓ, and an effective dissociation constant K_dis, which we display in Table 1. The values of K_dis for both fixed and slide cases are higher by ≈3 orders of magnitude than the nanomolar scale characteristic specific binding and are in reasonable agreement with the accepted value (≈1.5 μM) for nonspecific binding (24–26). We note, however, that the values of K_dis deduced from our measurements comprise a weighted average over all binding sites on the λ-DNA molecule, with all their spectrum of affinities, and therefore cannot be faithfully compared with measurements carried out on small oligomers with binding sites of well-characterized affinity.

Table 1.

Parameters of λ-DNA-IHF interaction from best fit of force–extension measurements, for two cases: sliding and fixed IHF positions

	Slide	Fixed
L1/L0	0.35  ± 0.09	0.33  ± 0.13
ℓ (bp)	240  ± 40	233  ± 38
Kdis (nM)	600  ± 110	2,300  ± 440

Because ψ approaches a constant value for low tensions, we can calculate the number of IHF molecules associated with a λ-DNA molecule under conditions at which further addition of IHF does not induce further compaction as L₀ψ/ℓ, where L₀ = 48,502 is the number of base pairs in a λ-DNA molecule. We obtained 69 ± 17 IHF molecules for sliding, and 78 ± 22 IHF molecules for fixed IHF molecules. These numbers are in very good agreement with our independent estimates of bound IHF molecules obtained from the CsCl gradient experiments. Interestingly, our estimates indicate that the number of bound IHF molecules, irrespective of the model, is much smaller than ≈1,400, the number that one would expect for full coverage, given that specific binding sites are about 35 bp long (27, 28).

We point out that the elastic behavior of single DNA molecules under the influence of IHF is very different from the behavior observed in solutions of simple polyvalent ions such as spermidine or hexaamine cobalt III (29). Force–extension curves in such solutions, at high enough concentration, show the existence of a plateau of the force for sufficiently small contour extensions, a signature that is rather different from the one we see. Thus, simple polyvalent salts induce the collapse of the DNA molecule, instead of compaction. Collapse is brought about by salt-induced intersegmental attraction, instead of the local bending induced by IHF. Thus the microscopic effects of simple polyvalent salts and IHF are completely different.

Implications for the Compaction of the Bacterial Nucleoid.

The compact yet dynamic structure of the E. coli nucleoid is maintained through the association of the bacterial genome with about 10 different DNA-binding proteins. Although most studies of IHF, a prominent member of this group, have focused on its specific activity in site-specific recombination, λ-phage DNA encapsidation and, in the control of gene expression, the nonspecific activity of this protein have also been documented. The importance of nonspecific binding is highlighted by recent estimates (7) of the number of IHF molecules in a cell: steady-state exponential-phase cultures contain about 8,500 to 17,000 IHF molecules per cell. The numbers are even higher in stationary phase, the concentration increasing 5- to 6-fold. This high concentration of IHF, for a protein having a limited number of high-affinity sites, suggests that nonspecific binding has an important biological role (30). Recent in vivo measurements suggest that the vast majority of IHF molecules, about 10 μM in growing cells, are found bound to DNA (26, 30). It is interesting to note that the ratio of the number of base pairs in an E. coli genome (4.7 × 10⁶ bp), to the number of IHF molecules in a cell in exponential phase is about the same as in our experiments, at IHF concentrations at which further addition of IHF does not bring forth further compaction. The binding of IHF to λ-DNA becomes nearly concentration-independent above 500 nM, but the number of bound molecules is much lower than that required for full coverage of the DNA. Thus, although this binding displays some selectivity, the simple polymer poly(dI-dC) competes with it. The binding affinity of IHF to selected sites can vary by two orders of magnitude (27). It is conceivable that the binding affinity of IHF to random DNA sequences varies over a larger range, from nanomolar affinity to canonical sites, through 10⁻⁷–10⁻⁶ M affinity to sites we observe in this study, and finally to very low affinity to other DNA sequences. The different binding affinities can be because of differences in local DNA flexibility. Similar effects are thought to influence the binding preferences of histone octamers to DNA (31).

Our studies addressed directly and, to our knowledge, for the first time, the issue of the extent of DNA compaction by a histone-like protein. Single-molecule techniques allowed us to tackle this question in quantitative terms by using a DNA macromolecule and shed light on the contribution of IHF to the large-scale structure of the bacterial nucleoid. Our conclusions underscore the importance of IHF low-affinity binding, in agreement with other studies (25, 30). Similar studies of other histone-like proteins, being carried out now, may allow for a comparison of the relative contribution of these proteins in shaping the bacterial nucleoid.

Abbreviations

IHF

integration host factor

poly(dI-dC)

polydeoxyinosinic-deoxycytylic acid

DIG

digoxigenin