The Pennsylvania Trauma Outcomes Study Risk-Adjusted Mortality Model: Results of a Statewide Benchmarking Program

Abstract

Trauma centers need objective feedback on performance to inform quality improvement efforts. The Trauma Quality Improvement Program recently published recommended methodology for case mix adjustment and benchmarking performance. We tested the feasibility of applying this methodology to develop risk-adjusted mortality models for a statewide trauma system. We performed a retrospective cohort study of patients ≥16 years old at Pennsylvania trauma centers from 2011 to 2013 (n = 100,278). Our main outcome measure was observed-to-expected mortality ratios (overall and within blunt, penetrating, multisystem, isolated head, and geriatric subgroups). Patient demographic variables, physiology, mechanism of injury, transfer status, injury severity, and pre-existing conditions were included as predictor variables. The statistical model had excellent discrimination (area under the curve = 0.94). Funnel plots of observed-to-expected identified five centers with lower than expected mortality and two centers with higher than expected mortality. No centers were outliers for management of penetrating trauma, but five centers had lower and three had higher than expected mortality for blunt trauma. It is feasible to use Trauma Quality Improvement Program methodology to develop risk-adjusted models for statewide trauma systems. Even with smaller numbers of trauma centers that are available in national datasets, it is possible to identify high and low outliers in performance.

Quality improvement is an important component of trauma care. Organized efforts in the form of institutional trauma registries have been in place for nearly 50 years in the United States,¹ but more recent efforts have placed emphasis on the comparative performance of trauma centers as a means to explore variation and improve outcomes. This emphasis has been underscored by the most recent version of the American College of Surgeons (ACS) Committee on Trauma Resources for Optimal Care of the Injured Patient 2014,² which stipulates that all ACS-verified trauma centers must participate in a risk-adjusted benchmarking system to measure the performance and outcomes (Clarification Document 15-5) to maintain ACS verification.

Although the ACS Committee on Trauma is the largest entity responsible for the verification of trauma centers in the United States, in Pennsylvania, all trauma centers must be accredited by the Pennsylvania Trauma Systems Foundation (PTSF), which is charged by the state law with ensuring the quality of trauma care within Pennsylvania. Through this mission, the PTSF oversees the Pennsylvania Trauma Outcomes Study (PTOS), a registry to which all centers must contribute data to maintain accreditation. Because of the rigorous standards for data collection and relative paucity of missing elements, this dataset has enjoyed widespread usage in trauma outcomes research.^3–7 Until recently, however, no formal risk-adjusted benchmarking effort has been pursued using this dataset. In an effort to improve the quality of trauma care in Pennsylvania, in 2013, the PTSF set out to develop a program to report benchmarked risk-adjusted outcomes back to trauma centers in the state.

The largest and most successful trauma center benchmarking program in existence is the ACS Trauma Quality Improvement Program (ACS-TQIP), which seeks to improve the quality of trauma care through outcomes based, risk-adjusted benchmarking of trauma centers, and feedback reports.^{8, 9} The methodology, data processing, data quality, statistical analysis, and analytic rationale for the methods used by TQIP to develop risk-adjusted models for comparisons of trauma center performance have been recently published by Newgard et al.¹⁰ Our group replicated these methods as closely as possible using data elements available in the PTOS database to develop the analysis and results reported here. This manuscript reports the results of the analysis that developed a risk-adjusted mortality model for the (PTSF-RAM). First, we present the overall model that was applied to the entire patient sample. Subsequently, we present the application of the model to patients in sub-categories of interest: blunt, penetrating, multisystem, isolated head injury, and geriatric.

Methods

Data Source and Case Definition

This analysis was conducted using data from the PTOS and including all records for patient’s age 16 years and older with blunt or penetrating trauma treated at trauma centers in Pennsylvania during 2011 to 2013. Inclusion criteria for the PTOS are all patients treated for a diagnosis of trauma (ICD-9-CM injury codes 800–995, excluding 930–939.9) and any patients meeting the following criteria; intensive care unit admission, step-down unit admissions, death on arrival, all trauma deaths, all patients remaining at centers for >48 hours, and all admitted transfers in. Further details of the PTOS registry inclusion/exclusion criteria are online at www.ptsf.org/upload/2014_PTOS_PATIENT_INCLUSION_CRITERIA.pdf. This study included a total of 100,278 patients treated at 27 trauma centers over the study period.

Simple statistics were used to describe the demographic, physiologic, and injury characteristics of the overall cohort. Inspection of the data set revealed that the rate of missing data was less than 8 per cent for any given variable. However, given the concern that casewise deletion through multiple regression could induce bias in our modeling,¹¹ we used multiple imputation to impute missing values before imputation, continuous variables that were not normally distributed were log transformed to approximate a normal distribution, imputed, and then exponentiated to retain their original distribution. A total of 10 new datasets in which missing values were replaced with imputed values were generated. Those 10 datasets were modeled simultaneously using logistic regression that pooled the effect estimates and adjusted the standard errors accordingly.

We then mapped variables in the PTOS dataset as closely as possible to the 16 variables used to generate the original TQIP model. To allow for nonlinear relationships between predictors and mortality, continuous variables were considered in their original format as well as categorical septiles of value. For each model considered, conventional diagnostics including bivariate correlations, variance inflation factors to identify multicollinearity, and plots of deviance versus leverage values to identify outlier observations were conducted. Model calibration was tested using receiver operator characteristic curves while fit was tested using Hosmer-Lemeshow goodness of fit test and plots.¹² Performance of candidate model was compared using Akaike¹³ and Bayesian¹⁴ information criteria and the final risk-adjusted model was selected based on discrimination, calibration, and goodness of fit statistics.

This model was used to generate the risk-adjusted predicted probability of death for each patient in the original sample of 100,278 patients. These probabilities were summed by center to generate the expected mortality at each center. This was compared with the observed mortality to generate observed-to-expected (O:E) ratios for each center, whereas the 95 per cent confidence intervals (CIs) for these ratios were estimated using the method of Breslow and Day.¹⁵ A caterpillar plot was then generated by plotting O:E ratios by center, and those centers with O:E 95 per cent CIs that did not include one were identified as significant outliers for mortality.

Funnel plots were then created as an alternative method to evaluate the impact of center volume on outlier status. Unlike a caterpillar plot, where CIs indicate uncertainty for each observed hospital O:E ratio, in a funnel plot a single envelope of uncertainty is drawn from the expected line. This line can be thought of as a threshold for “alert” and hospitals that lie outside the expected line (e.g., 95% CI for the entire sample of hospitals) can be considered further for characteristics that may be associated with their disproportionately above- or below-expected mortality.^{16, 17}

In addition examining overall risk-adjusted mortality at trauma centers in Pennsylvania, analyses were conducted to examine risk-adjusted mortality at trauma centers within subgroups for blunt trauma, penetrating trauma, multisystem trauma, isolated head injury, and geriatric patients. All statistical analyses were conducted using Stata 13.1 (College Station, TX).

Results

Characteristics of the overall cohort and missingness of included variables are reported in Table 1. The amount of missing data were minimal and ranged from 0 per cent missing on age, sex, discharge status (died, survived), and transfer status to 7.8 per cent missing on injury mechanism. Characteristics of patients treated at the 27 trauma centers can be seen in Supplemental Table 1. Number of patients treated per center ranged from a low of 1,756 to a high of 12,823 patients, although deaths per center ranged from 42 to 527 over the study period. Center level mortality ranged from 2.2 to 9.5 per cent. The proportion of transfer patients varied between 0 and 63 per cent across the 27 trauma centers and the proportion of transfer patients was correlated with trauma center volume (correlation coefficient = 0.74).

Table 1.

Characteristics of 100,278 Patients Treated at 27 Trauma Centers in Pennsylvania, 2011 to 2013

Characteristic	Mean (SD) or Per Cent	Per Cent Missing
Age (years), mean (SD)	55.5 (23.2)	0
Female (%)	40.6	0
Died (%)	4.9	0
Mechanism		7.8
Pedestrian/pedal (%)	4.6
Motor vehicle occupant (%)	23.5
Motorcyclist (%)	5.2
Fall (%)	54.0
Struck by/against (%)	2.8
Firearm (%)	4.8
Cut/pierce (%)	2.6
Other (%)	2.4
Transfer patient (%)	30.6	0
SBP, admission, mean (SD)	139.7 (31.1)	0.49
GCS motor, mean (SD)	5.62 (1.24)	5.75
Pulse, mean (SD)	86.8 (21.0)	0.32
SWI, mean (SD)	0.06 (0.16)
ISS, mean (SD)	10.3 (8.6)	0.95
AIS, head, mean (SD)*	2.5 (1.3)	0
Lowest AIS, mean (SD)	0 (0.0)	0
Heart disease (%)	18.5	2.33
Cancer (%)	1.6	2.33
Liver disease (%)	1.1	2.33
Hypertension (%)	42.9	2.33
Diabetes (%)	16.1	2.33
Bleeding disorder (%)	14.5	2.33
Arrest SBP (%)	1.2	0.49
Shock (%)	3.3	0.49
Multisystem (%)	7.2	0
Isolated head (%)	17.4	0
Admitted to intensive care unit (%)	38.0	0

^*Calculated among patients with head AIS ≥1.

SWI, single worst injury; SBP, systolic blood pressure.

Arrest SBP: systolic blood pressure in ED ≤40 mm Hg.

Shock SBP: systolic blood pressure in ED <90 mm Hg.

Multisystem: AIS ≥3 on 2 or more AIS body regions.

Isolated head injury: AIS head ≥3 and AIS <3 on other AIS body regions.

A total of 16 variables based on TQIP parameters were modeled as exposure variables on the outcome of mortality. The variables were selected to match the variables used by Newgard et al. in the final TQIP statistical model. One variable used in TQIP models [lowest Abbreviated Injury Scale (AIS)] did not contribute statistically to our prediction models and was therefore excluded. Age, mechanism of injury, transfer status, systolic blood pressure, Glasgow Coma Score (GCS), head AIS, heart disease, cancer, liver disease, hypertension, diabetes, bleeding disorder, and cardiac arrest were all found to be independently associated with mortality and were included in the final multi-variable model (Table 2). The area under the curve for the final model was 0.94 (95% CI 0.94–0.95), indicating excellent discrimination. In comparison, the c-statistic reported recently by Newgard et al. in their model to demonstrate the TQIP method of risk adjustment was 0.90. Although formal statistical comparison of the two models is not possible given the differing data sets, the PTSF-RAM model appears to discriminate as well or better than the model used by the TQIP that computed risk-adjusted outcomes for demonstration purposes. Model calibration was assessed using the Hosmer-Lemeshow χ² statistic (final model was 55.43 (df = 10, P < 0.0001). Although this could indicate poor calibration, large sample sizes often result in significant Hosmer-Lemeshow tests. The Akaike information criterion of our final model was 20,084. A plot of the observed versus predicted mortality by decile of predicted risk demonstrated excellent fit across all deciles and can be seen in Fig. 1. Plotting the median residuals between trauma centers demonstrated no evidence of systematic errors in specification as a function of trauma center characteristics.

Table 2.

Results of the Final PTOS-RAM Model to Estimate the Risk of Death Based on Patient Demographic and Clinical Characteristics (n = 100,278)

	Odds Ratio	SE	t	P Value	95% CI
Age group (years, mean)
(20.2) 1 (youngest)	Ref
(30.5) 2	1.04	0.10	0.77	0.629	0.898	1.280
(44.5) 3	1.34	0.12	2.95	0.003	1.098	1.590
(55.4) 4	2.16	0.21	8.11	<0.001	1.805	2.631
(66.3) 5	4.35	0.41	15.01	<0.001	3.521	5.140
(78.5) 6	7.75	0.76	20.98	<0.001	6.420	9.419
(88.8) 7 (oldest)	10.98	1.13	24.17	<0.001	9.237	13.676
Mechanism
Pedestrian/pedal	Ref
MV occupant	0.79	0.05	−3.68	<0.001	0.696	0.895
Motorcyclist	0.91	0.09	−1.05	0.321	0.745	1.093
Fall	0.69	0.04	−5.76	<0.001	0.618	0.789
Struck by/against	0.39	0.07	−5.31	<0.001	0.267	0.544
Firearm	4.26	0.34	17.96	<0.001	3.598	4.923
Cut/pierce	0.81	0.12	−1.32	0.186	0.606	1.102
Other	0.69	0.09	−2.81	0.005	0.560	0.902
Transfer patient	0.83	0.04	−4.30	<0.001	0.749	0.898
SBP (admission, mean)
(91.3) 1 (lowest)	Ref
(119.7) 2	0.39	0.03	−12.55	<0.001	0.332	0.447
(130.1) 3	0.40	0.03	−12.17	<0.001	0.341	0.460
(138.8) 4	0.34	0.03	−14.03	<0.001	0.294	0.396
(148.8) 5	0.35	0.03	−14.41	<0.001	0.303	0.403
(160.2) 6	0.32	0.02	−15.84	<0.001	0.273	0.364
(186.7) 7 (highest)	0.38	0.02	−15.11	<0.001	0.336	0.432
GCS, motor score
1 (lowest)	Ref
2	3.36	0.48	8.49	<0.001	2.539	4.442
3	1.48	0.20	2.94	0.003	1.139	1.915
4	0.67	0.06	−4.54	<0.001	0.562	0.795
5	0.31	0.02	−15.90	<0.001	0.272	0.362
6 (highest)	0.07	0.00	−51.98	<0.001	0.063	0.077
Pulse rate (mean)
(56.0) 1 (lowest)	Ref
(71.7) 2	0.76	0.06	−3.64	<0.001	0.656	0.881
(78.5) 3	0.67	0.05	−4.95	<0.001	0.572	0.786
(85.1) 4	0.82	0.06	−2.62	0.008	0.711	0.952
(91.9) 5	0.77	0.06	−3.29	<0.001	0.652	0.897
(100.4) 6	0.87	0.07	−1.83	0.040	0.753	1.009
(119.9) 7 (highest)	1.33	0.09	4.32	<0.001	1.168	1.510
Single worst AIS
1 (lowest)	Ref
2	1.65	0.27	3.11	0.001	1.204	2.306
3	2.06	0.31	4.39	<0.001	1.454	2.678
4	2.37	0.32	5.92	<0.001	1.736	2.996
5	2.90	0.43	7.54	<0.001	2.235	3.953
6	3.69	0.52	9.26	<0.001	2.799	4.886
7 (highest)	7.13	0.99	14.15	<0.001	5.421	9.379
Head AIS
No head injury	Ref
1 (lowest)	1.04	0.08	0.57	0.529	0.899	1.213
2	0.81	0.08	−2.27	0.022	0.674	0.971
3	1.42	0.08	5.86	<0.001	1.261	1.592
4	1.34	0.11	3.69	<0.001	1.147	1.565
5	5.99	0.37	29.08	<0.001	5.306	6.754
6 (highest)	36.67	21.965	6.110	<0.001	11.640	118.382
Comorbidities
Heart disease	1.46	0.08	7.14	<0.001	1.317	1.623
Cancer	1.74	0.19	4.91	<0.001	1.383	2.129
Liver disease	4.00	0.51	10.71	<0.001	3.094	5.132
Hypertension	0.93	0.05	−1.61	0.107	0.833	1.018
Diabetes	1.08	0.06	1.96	0.051	1.000	1.240
Bleeding disorder	1.51	0.08	7.52	<0.001	1.346	1.660
Arrest SBP	46.13	6.67	26.21	<0.001	34.376	60.899
Constant	0.05	0.01	−18.46	<0.001	0.034	0.065

SE, standard error; SBP, systolic blood pressure.

Fig. 1.

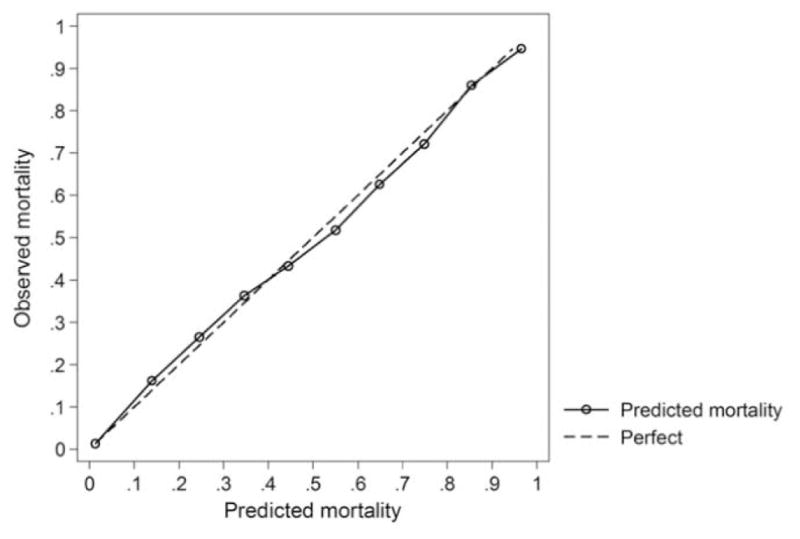
Graph observed versus predicted mortality plotted in 10 groups of risk equally spaced from 0 to 100 per cent predicted risk as a measure of calibration of the PTSF-RAM model in 100,278 patients.

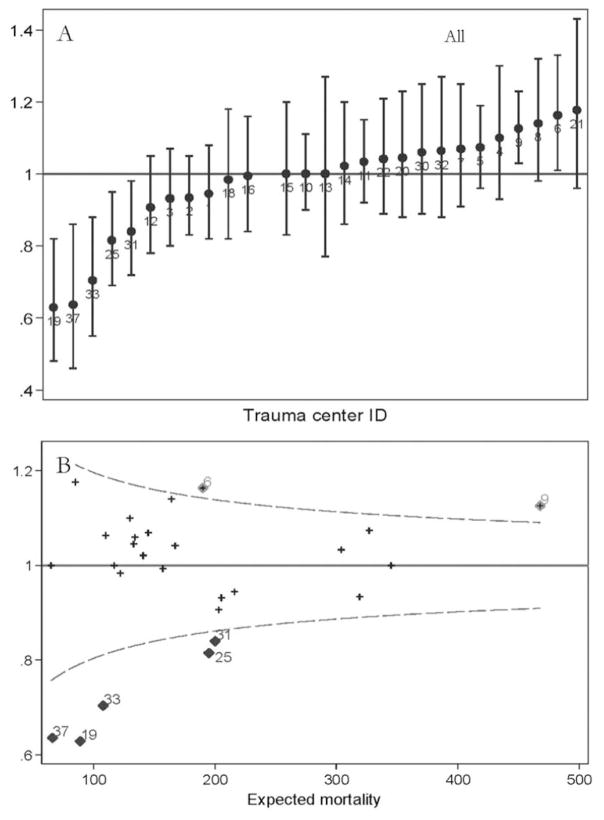
Caterpillar and funnel plots of O:E mortality for the 27 trauma centers in Pennsylvania based on the PTSF-RAM analysis of all 100,278 patients is shown in Fig. 2. In total, five centers that were low outliers for mortality (centers 19, 25, 33, 31, and 37) and two centers that were high outliers for mortality (centers 6 and 9) were identified using this approach. When the same data are examined using funnel plots, the same outlying centers are identified.

Fig. 2.

(A) Caterpillar plot and (B) funnel plot of risk-adjusted O:E mortality ratios for 27 trauma centers in Pennsylvania. (Top) rank (caterpillar) plot and (bottom) funnel plot. Dashed lines denote 95 per cent confidence limits.

In addition to the overall cohort, we also examined the performance of the PTSF-RAM model within the subgroups of blunt mechanism, penetrating mechanism, multisystem trauma, isolated head trauma, and geriatric patients. The c-statistic values for these subgroups ranged from 0.879 to 0.980 patients (Supplemental Table 2), indicating G/E discrimination. Caterpillar and funnel plots displaying the results of the risk-adjusted mortality analyses with the subgroups of blunt trauma, penetrating trauma, multisystem trauma, isolated head trauma, and geriatric are available in Supplemental Figures 1 to 5. In the funnel plots, O:E ratios are not plotted in a number of instances for specific trauma centers when the O:E ratio could not be calculated due to a zero denominator.

In the funnel plots provided, it was not possible to list each trauma center by number given the large number of trauma centers and instances where points fell on top of one another. Table 3 therefore, summarizes the results reported in the funnel plots by listing the trauma centers that had an O:E mortality ratio that fell above or below the limit of expected threshold (i.e., 95% CI) for all patients and for the subgroups of interest (blunt mechanism, penetrating mechanism, multisystem trauma, isolated head injury, and geriatric).

Table 3.

Trauma Centers with Mortality O:E Ratio Outside the 95 per cent CI in Funnel Plot Analysis

	Trauma centers with O:E ratio outside 95% CI
	Above	Below
All patients	6, 9	19, 25, 31, 33, 37
Blunt	6, 8, 9	19, 25, 31, 33, 37
Penetrating	None	None
Multisystem	9, 15, 18, 21	None
Isolated head	9	19, 25, 37
Geriatric	8, 9	19, 25, 31, 33, 37

Discussion

The use of O/E outcome rates to identify clinically significant variability in care is not new, having been described over 50 years ago by Moses and Mosteller.¹⁸ With the growth of registries, specifically designed for use in outcomes research, advances in data science, and increased computing power over the past decade, several large-scale efforts to explore variation in outcomes in surgical disease states have been successfully implemented. The largest of these is the ACS National Surgical Quality Improvement Program, which uses a sample surgical cases at over 680 centers in the United States and provides benchmarked risk-adjusted outcome reports back to participating centers.¹⁹ This program was soon followed by the development of the ACS-TQIP,⁸ which functions in much the same fashion but is dedicated to improving outcomes after injury. Although this program has led to critical insights into both quality improvement efforts and injury outcomes research and clearly represents the gold standard in risk-adjusted injury outcomes research, the PTSF-RAM benchmarking program may offer several benefits to trauma centers in Pennsylvania relative to ACS-TQIP participation. First, because participation ACS-TQIP is strictly voluntary, reports derived from ACS-TQIP can only reflect the relative performance of those centers that choose to participate. Centers that choose to participate may be fundamentally different than those that do not. In contrast, reporting of data to PTOS is mandatory to maintain trauma center accreditation in Pennsylvania, which eliminates the possibility of bias associated with voluntary reporting. Second, the PTSF-RAM benchmarking program operates at a regional level. While Pennsylvania is a large state, the localized nature of the PTSF-RAM makes it possible for stakeholders to communicate and collaborate much more easily than is possible on a national level. Regional collaborations have been used to improve the quality of care across a variety of surgical disease states,^{20, 21} including trauma.²² Finally, because the PTSF-RAM uses data that is already being collected for the PTOS dataset by trained registrars as mandated by the state law, there are no additional participation or personnel costs associated with the program.

The end goal of generating risk-adjusted O:E ratios using the PTOS data is to provide readily interpretable and informative comparisons of the performance of trauma centers in Pennsylvania. A rank plot (also called caterpillar plots) is a familiar format used traditionally to enable comparative “ranking” of hospitals.” As Newgard et al. point out, these plots have important limitations. In particular, a rank ordering is not necessarily meaningful given that two trauma centers may be ranked far apart but yet may not be statistically different in how they performed. Also, caterpillar plots do not indicate trauma center volume and thus, cannot be used to compare outcomes among centers with similar volumes. For these and other reasons, TQIP recommends using funnel plots to report on trauma center performance. Funnel plots allow trauma center volume to be directly assessed, and enable improved visual assessment of outlier hospitals (high and low), elimination of nonmeaningful hospital rankings, and easier identification of hospitals close to outlier status (e.g., early recognition of quality issues that can prompt behavior change, even if not yet statistically significant).

Although the c-statistic (i.e., the area under the receiver operator characteristic curve) for the final model was very high, it is possible that a different regression modeling approach could have provided an even better fit to the data. For example, using a mixed-effects logistic regression model with random effects to represent patient subgroups would have allowed for instances where the relationships between fixed effects covariates and the outcome may have varied.²³ Despite this potential benefit, the basic approach to logistic regression modeling performs adequately and in addition is a widely understood technique that can be readily adopted.¹⁰ This facilitates a common modeling approach that allows for more direct comparisons between the results of different groups that develop risk-adjusted models.

While the TQIP guidance for risk-adjusted modeling lists steps for developing a model for a patient population overall, we took the additional step of developing O:E ratios for patient population subgroups. This step was not detailed in previous methodological descriptions, and it is possible that use of a mixed-effects model for these subgroups could improve the accuracy of subgroup-specific O:E ratios. We chose not to explore this option based on our desire to be consistent with TQIP guidelines and on evidence that our final model was well calibrated in the subgroups of interest. Results of these subgroup analyses revealed that no trauma centers had higher than expected mortality and no trauma centers had lower than expected mortality in terms of the management of penetrating trauma. In contrast, no trauma centers had lower than expected mortality in the management of multisystem trauma, but four trauma centers had higher than expected mortality in the management of multisystem trauma. One possible interpretation of these results is that training and protocols for the management of penetrating trauma are uniformly robust, but best practices for the management of multisystem trauma may need further elucidation. Alternatively, the volume of penetrating trauma seen at many centers may have been too small to result in statistically significant variation between centers.

As with any effort of this nature, there are important limitations that must be considered. As this project includes only in-hospital mortality as an endpoint, it does not by definition speak to variations in longer term mortality that may occur between centers. Although longer term mortality after trauma is known to be increased,²⁴ the majority of deaths occur early after trauma,²⁵ and so these late deaths are unlikely to significantly influence our findings. Second, because these data are derived from a single state, the variables predictive of mortality in our model may vary somewhat from states with differing demographic and injury mechanism characteristics. Risk-adjusted mortality models are expected to have best performance in the population from which they are derived. Finally, the factors which contribute to center-level variations in risk-adjusted mortality demonstrated here remain unknown. It is possible that future investigations will be unable to pinpoint what these factors are, or, if discovered, that they may not be subject to modification. Despite these possibilities, there is a growing body of literature that suggests participation in quality improvement efforts based on clinical registries can and do lead to improvements in outcomes²⁶ and we believe that the PTSF-RAM sets the stage for these improvements in the Pennsylvania state trauma system.

In conclusion, it is feasible to apply the methodology of the ACS-TQIP to statewide registries to benchmark trauma center performance. We believe the results of this effort will be useful as a cornerstone of a statewide regional quality improvement collaborative that will lead to measurable improvements in patient outcomes. The results of the risk-adjusted mortality analysis that are presented in this report should be used as a guide to help explore characteristics of trauma centers, patients, and other factors including geography that may influence trauma center performance.