Mimicking the cardiac cycle in intact cardiomyocytes using diastolic and systolic force clamps; measuring power output

Abstract

Aims

A single isolated cardiomyocyte is the smallest functional unit of the heart. Yet, all single isolated cardiomyocyte experiments have been limited by the lack of proper methods that could reproduce a physiological cardiac cycle. We aimed to investigate the contractile properties of a single cardiomyocyte that correctly mimic the cardiac cycle.

Methods and results

By adjusting the parameters of the feedback loop, using a suitably engineered feedback system and recording the developed force and the length of a single rat cardiomyocyte during contraction and relaxation, we were able to construct force–length (FL) relations analogous to the pressure–volume (PV) relations at the whole heart level. From the cardiac loop graphs, we obtained, for the first time, the power generated by one single cardiomyocyte.

Conclusion

Here, we introduce a new approach that by combining mechanics, electronics, and a new type optical force transducer can measure the FL relationship of a single isolated cardiomyocyte undergoing a mechanical loop that mimics the PV cycle of a beating heart.

1. Introduction

The functional properties of a beating heart are typically captured by analysing how the pressure–volume (PV) relationship evolves during a cardiac cycle.^1–3 This approach is widely recognized as an invaluable tool in cardiovascular (patho)physiology and pharmaceutical research.^4–8 To study the effects of various haemodynamic conditions and disease states at the tissue level, researchers often rely on direct measurements of the force–length (FL) loop of multicellular cardiac muscle strips.^9,10 The interpretation of multicellular muscle strip experiments is complicated by the presence of the extracellular matrix, which makes it difficult to disentangle the properties of the cardiac muscle cells from those of the milieu.¹¹ Moreover, multicellular muscle strip experiments suffer from diffusion constraints that limit oxygenation and metabolic work. This can be overcome with the use of ultra-thin trabeculae,^12,13 however that is a skill few laboratories possess. Both problems can be solved by replacing the multicellular strip with a single isolated cardiomyocyte.^14,15 However, the forces generated by a single intact cardiomyocyte under physiological conditions are 3 orders of magnitude smaller than those recorded in multicellular muscle preparations.¹⁶ It is thus not surprising to find that none of the force transducers presented in the literature has been able to achieve the required sensitivity and responsiveness (i.e. reaction speed) to establish FL cycles in a single isolated cardiomyocyte experiment that could correctly mimic the behaviour of cells in the heart. To perform such measurements, a feedback control system would be needed that could accurately measure the force developed by the cell and, in real time, change its length to control force development. Here, we solve this longstanding problem by introducing a sensor that improves sensitivity and responsiveness by an order of magnitude over the current state-of-the-art. We demonstrate that, by anchoring a single cardiomyocyte to our force transducer, it is indeed possible to drive a feedback control loop that adapts the length of the cell to control the force it exerts. We show that this approach can be used to functionally approximate the cardiac PV relationship at the cellular level by imposing a ‘pre-load’ and ‘after-load’ by modulating cardiomyocyte length using feedback based on force level. This allows measuring the external work performed and the power generated by a single intact cardiomyocyte under physiological conditions.

2. Methods

The animal experiments were performed in accordance with the guidelines from Directive 2010/63/EU of the European Parliament on the protection of animals used for scientific purposes.

2.1. Force transducer design

Intact isolated cardiomyocytes at 37°C produce 10–20% of the maximum forces measured in membrane-permeabilized cardiomyocytes at equivalent sarcomere lengths (SLs) at room temperature.¹⁵ To measure the force generated by a single intact cardiomyocyte with sufficient sensitivity, responsiveness, and stability to allow force control, a new type of force transducer was developed. For any force control to be meaningful, the baseline drift has to be low, which was targeted at constant temperature <0.1 μN/min. As most of the baseline drift arises from the air–water interface (buoyance, surface tension), the only practical solution was to design a force probe that could be fully submersed.

In addition to having to function submerged in an aqueous solution, the force transducer was required to sense forces on the scale of micronewton with a resolution of nanonewton and with a resonance frequency >1 kHz to enable feedback control of force. To match these requirements, we designed an optical force transducer where we use the traditional deflection of a cantilever as an indicator of force, although bending of the cantilever was measured via laser interferometry (Fabry–Perot type interferometer) as already used for applications in other research fields (Figure 1A and B).^13,17 Briefly, laser light is delivered to the cantilever through a standard 125 µm diameter optical fibre (Figure 1B). The light reflected from the fibre-to-liquid interface and from the cantilever travels back through the same optical fibre towards its distal end, creating an interference signal whose amplitude depends on the position of the cantilever end relative to the fibre. Before the start of the experiment, the wavelength of the laser is adjusted to put the interferometer in quadrature condition, i.e. at the point where the sine that describes the amplitude of the interference signal has maximum derivative.¹⁷ Under this condition, the linear range of the signal (i.e. <5% error) extends over a range of at least 100 nm in either direction, with a resolution of 1 nm (over 20 kHz bandwidth). Stiffness of the manufactured probes can easily be varied between 5 and 100 N/m, which will affect the force resolution accordingly. Because the spring constant of the cantilever used for these experiments was equal to 37 N/m, the force had a force resolution of 37 nN on a 3.7 µN range in either direction with a noise band of 1.5 nm which equals 56 nN. Baseline drift was <0.1 µN/min at constant temperature. None of the traces shown in this paper are filtered; they all show the raw output of the read-out. As the cantilever is just a very small rectangular sheet of gold-coated glass (1200 µm × 400 µm × 40 µm), it has a high resonance frequency of ∼7 kHz. This provides sufficient responsiveness to allow force control. For details on the manufacture and calibration of the probe, see the Supplementary material online.

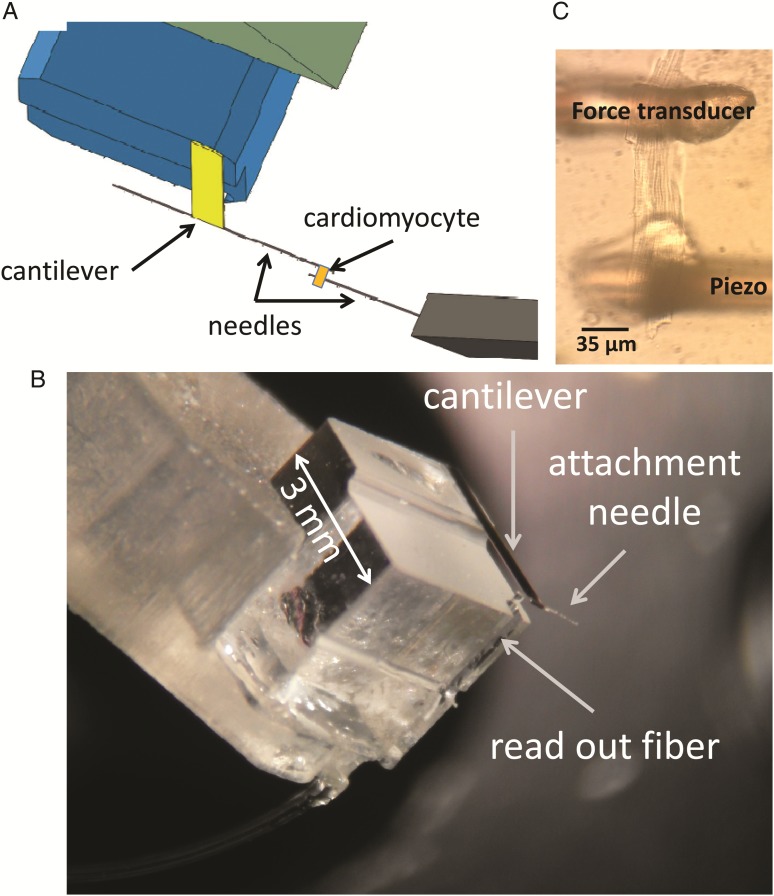
Figure 1.

The experimental approach. (A) Schematic view of the experimental set-up. (B) Microscope image of an intact, live cardiomyocyte glued in between the two anchoring needles; one of the two needles is anchored to the free hanging end of the cantilever, the other to a piezoelectric translator that allows one to modulate the length of the cell. (C) Microscope image of the force sensor.

2.2. System set-up

The workloop data collected for this paper were generated with a system built around a standard Ionoptix set-up designed for calcium and contractility measurements in cardiac myocytes. To be able to attach cardiomyocytes, two 3D micro-manipulators were attached on the back of the microscope. To each of the micro-manipulators, an arm was attached to which a force probe or a piezo-translator (Mad City Labs) was mounted. From both the force probe and the piezo-translator, a 35 µm diameter glass needle protruded (Fiberoptics Technologies, Pomfret, CT, USA) that was used to pick up the myocyte.

The interface box of the Ionoptix system contains a Field Programmable Gate Array (FPGA, Cyclone III, Altera, San Jose, CA, USA) that was re-programmed to apply the workloop algorithm. The feedback parameters of the force clamp (frequency of the iteration loop and the multiplier of the proportional correction) could be modified via a newly designed module that was added to the Ionoptix software and could be adjusted interactively during the experiment.

Excitable cardiomyocytes are normally between 100 and 140 μm in length and 15 and 30 μm in width. Under experimental conditions at 37°C, unloaded cardiomyocytes, excited with electrical stimulation, can shorten up to 15 μm with the fastest rates of shortening in the order of 500 μm/s (10 μm within a 20 ms time period). To follow this contraction, our set-up relies on a closed-loop direct drive piezo-translator that has 50 μm range and that can complete a 1 μm step in <1 ms (Mad City Labs, Madison, WI, USA). To determine the SL, the sarcomere length acquisition module from Ionoptix (Milton, MA, USA) in combination with a high-speed camera (Myocam-S, Ionoptix) was used to acquire SL at a rate of 250 Hz. The algorithm does a frequency analysis of the region of interest (FFT) from which the SL is determined.

2.3. Attachment of single cardiomyocyte

Cardiomyocytes were glued to 35 μm glass needles that were attached to the cantilever of the force transducer and to the piezo-translator (Figure 1C). The needles were between 0.5 and 1.5 mm long, and were sufficiently stiff to prevent bending during the contractions. The gluing procedure is similar to the method described by Prosser et al.¹⁸ The tips were coated with an aluminium silicate suspension (Ionoptix pre-coat). The pre-coat was air-dried after which they were dipped in MyoTak (Ionoptix). In a well-attached cell, we could do force measurements for up to an hour in a temperature-controlled chamber (see Supplementary material online, FigureS1) at 37°C without significant run-down of the preparation.

2.4. Workloop algorithm

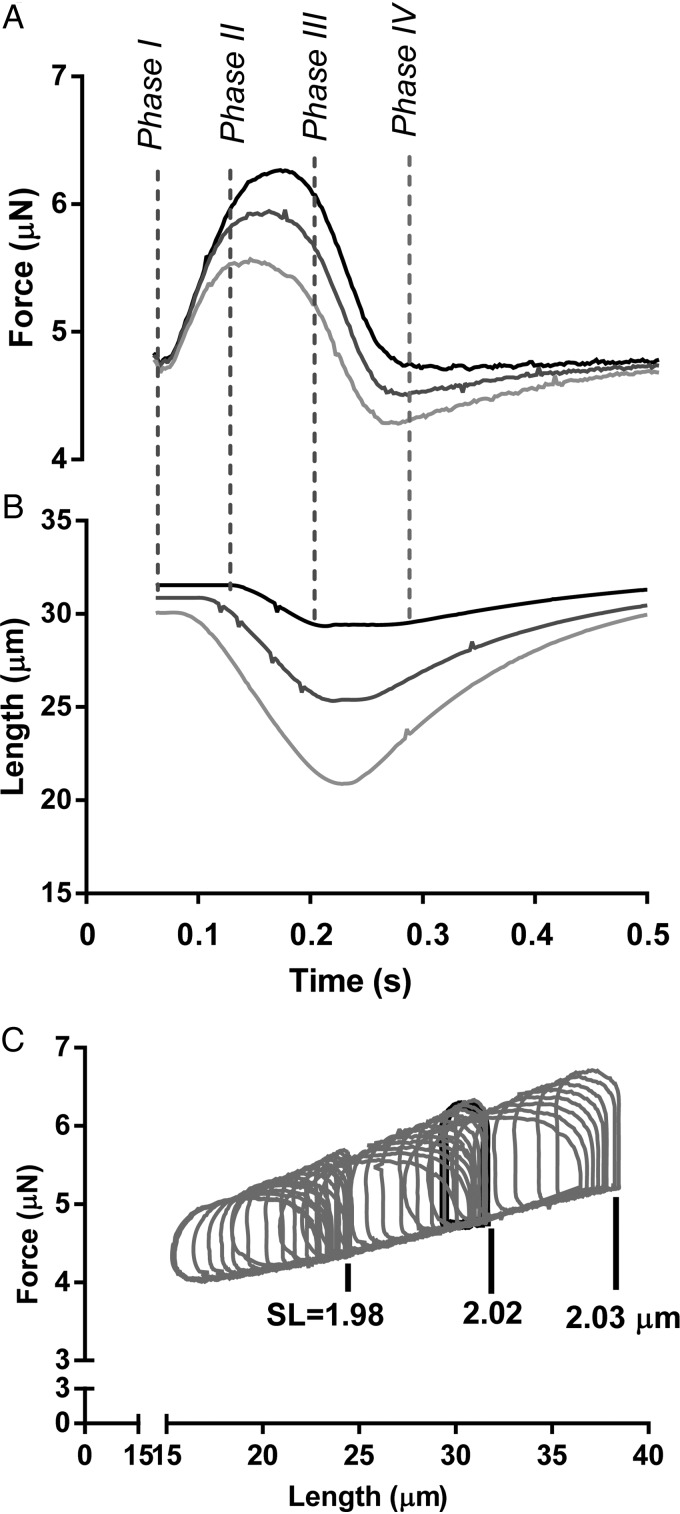
To mimic the cardiac PV relationship at the cellular level with an analogous FL relationship, we implemented a feedback control system that, by modulating the cardiomyocyte length, controls the force generated by the cardiomyocyte between a predefined pre-load and after-load. Pre-load and after-load when used in this paper refer to the target force levels of the feedback control during the diastolic and systolic phase of the myocyte contraction, respectively. In our method, the four phases of the cardiac cycle are defined as follows (Figure 2A and B); Phase I, which is analogous to the isovolumic contraction of a ventricle, starts immediately after electrical stimulation and encompasses a brief period of time during which the cell generates a force without substantially changing its length. Phase II, which is analogous to the ejection phase of the ventricle after the aortic valve opens, refers to the period of time when the pre-programmed after-load force is maintained constant by shortening the cell via the feed-back loop. This phase ends when the force measured by the transducer drops below the after-load value. The reversal of the piezo-translator from shortening to stretching, when it tries to maintain the force level, triggers the exit of Phase II. Phase III, which is analogous to the isovolumic relaxation, is characterized by a natural decrease in force at constant length. Phase IV starts as soon as the force decreases below the pre-programmed pre-load force. In this last phase, which simulates the filling of the heart in diastole, the feedback loop stretches the cell to maintain the pre-load force value until the start of the next cycle with the next electrical stimulus. For the implementation of the algorithm, we used FPGA, which digitizes in real time the force signal and the prescribed pre-load and after-load values (programmed and communicated via the software). The output from the FPGA drives the piezoelectric translator in Phase II and Phase IV to maintain the force exerted by the cell constantly equal to the prescribed values.

Figure 2.

The four phases of the cardiac cycle. (A and B) Force and length tracings of a myocyte contracting at 4 Hz (240 bpm) subjected to pre- and after-load force control. The three depicted contractions have the same pre-load but different after-load. Phase I through IV correspond to the cardiac cycle (see text for details). (C) Force vs. length workloops; the area within a loop represents the mechanical work performed by the cardiomyocyte.

The precision of the force control can be tweaked with two parameters, the frequency of the iteration loop and multiplier of the proportional correction when a mismatch between the set-point and the actual is measured. We set the frequency of the iteration loop as close as possible to the update frequency of the force transducer (20 kHz). During test runs, the multiplier was increased to the point where oscillations started to occur and then we used half that value for the remainder of the experiments. This resulted in an overall response frequency of the feedback system in the order of 100 Hz. At room temperature, this was fast enough to achieve practically square loops (see Supplementary material online, FigureS2). At 37°C, however this still left significant overshoot of the set-points. This can probably be solved with more sophisticated feedback algorithms, but that was beyond the scope of this study. Figure 2A and B shows exemplary force and length signals acquired during one of these cycles. Figure 2C further shows, by way of example, the FL curves obtained for different pre-load and after-load values in a series of mechanical loops with the myocyte beating at 4 Hz. As expected from whole heart experiments, the slope of the loop curve at the end-systolic point is relatively constant throughout the entire manoeuvre.

2.5. Experimental protocol

To set the feedback control parameters, a rat ventricular myocyte was electrically stimulated and stretched until a minimum force development of 0.3–0.5 μN was recorded. The forces at 10 and 30% of the developed force (i.e. of the difference between the maximum and minimum forces registered from isometric contractions) were used to designate the initial pre-load and after-load values, respectively. With these initial pre-load and after-load values set, we engaged the force clamping algorithm. When control of the cardiac cycle appeared stable, the actual protocol was started (see Supplementary material online, FigureS3, for an example of a stable recording). At each pre-load condition, the after-load was varied using a ramp function that would rise over several electrical stimulations by 0.75 µN and then decline back by 0.45 µN. The pre-load was then raised by 0.3 µN and, thereafter, by another 0.3 µN (see Supplementary material online, FigureS4). This protocol was repeated for 1, 2, 4, 6, and 8 Hz pacing frequencies in the presence of Tyrode or Tyrode with 100 nmol/L isoprenaline (ISO, Sigma Aldrich). More than 90% of the attempts to attach a cell was successful. Because of the elaborate protocol, the full protocol could be completed in 3–5 cells per experimental day.

2.6. Data presentation and analysis

For data analysis, we imported the force- and length-data into the PV loop module from LabChart 7.0 (AD instruments, Australia). The analysis calculated the external work value and the end-systolic and end-diastolic force values for each loop. Further analysis of these loop data was done in a Microsoft Excel spreadsheet and Prism version 6.0 (Graphpad Software, Inc., La Jolla, CA, USA). All the force and length measurements were differential, i.e. initial force was not set to zero, which explains why the forces do not go to zero as would be expected in some of the graphs. Length always refers to movement of the piezo motor, not to cell length.

3. Results

3.1. Optimal cardiomyocyte isolation

Stretching intact myocytes has been possible for a long time using carbon fibres,¹⁵ but the force-bearing capacity was limited. The development of a glue specific for intact myocytes¹⁸ greatly improved the ability to stretch intact cardiomyocytes. In rat cardiomyocytes, we can now measure forces of up to 3–4 µN, which is a 5- to 10-fold improvement over the carbon fibre method.¹⁵ To achieve these relatively high levels of force, cell isolation had to be optimized for mechanical experiments. We attempted two different digestive enzymes, Liberase TM (0.16 mg/mL; Roche) and Worthington type II. While cardiomyocyte yield was highest with Liberase digestion, the Worthington type II digested cells were more sticky and would bear forces that were 2–3 times higher before cells detached. We also found that we could not add protease to the digestion procedure.¹⁹ Protease is used to make cardiomyocytes more accessible for patch clamping. We found however that adding protease led to cells that were very prone to arrhythmias when stretched.

3.2. Workloops

We were able to control force development by the myocyte by modulating cell length in a real-time feedback loop. See Supplementary material online, FigureS3 shows an example of a stable recording where the data show that force can be successfully modulated. See Supplementary material online, FigureS3 also shows over- and under-shoot of the targeted pre- and after-load at 37°C. Feedback is often set up using proportional-, integral-, and derivative response. Our algorithm only has a proportional response. This works well for the slow changes at room temperature, but proved to be inadequate at 37°C; the rapid rate of force development in early systole and early diastole could easily be controlled at the set-point by setting the multiplier of the P (Proportional) very high, but this resulted in oscillations when the relaxation later in diastole slowed down. The lesser of two evils was accepting an over- and undershoot. The relative over/undershoot will vary with the rate of force development; the higher the pre-load and the closer the after-load is to the pre-load, the more over- and undershoot. This does not materially affect the experiments as the end-systolic and end-diastolic values are still controlled and correct. To remove the over- and undershoot, the feedback response has to be differentiated with respect to the rate of force change. To do this properly however, it should probably also include a time-varying after-load to better mimic the cardiac cycle. The electronics infrastructure allows for this and will be the subject of a next study.

Signal generators built into the software allowed us to pre-program changes in the pre- and after-load. Figure 2C shows the results of a typical protocol. The data traces show that both pre- and after-load can indeed be varied in a controlled manner. The end-diastolic and end-systolic force relation are well described with a linear line in the region studied.

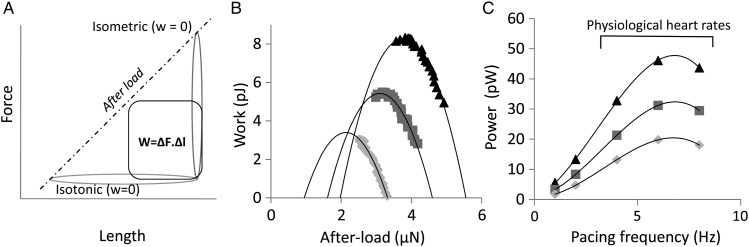
Furthermore, calculating the area within an FL cycle (or, in other words, by integrating the force loop as a function of length over a cardiac cycle), we can obtain the total mechanical work produced by the cardiomyocyte during the contraction-relengthening process (Figure 3A). This method allows us to study how the mechanical work may vary as a function of pre-load, after-load, and stimulation frequency. It is expected that, for very low or very high after-load values, the cycle would be predominantly isotonic or isometric, respectively, producing virtually no external mechanical work (Figure 3A). Therefore, for each value of pre-load force, there must exist an after-load force value for which the external mechanical work produced is maximal. To find the peak work, the work vs. after-load relation was fitted with a second-order polynomial. Figure 3B proves that our method is indeed capable to capture this feature (for more examples, see Supplementary material online, FigureS2). Knowing the pacing frequency, we can then quantify the power generated by a single cardiomyocyte, as shown in Figure 3C. The average peak power was 55.2 ± 20.5 pW (n = 10). Maximum work per loop was achieved at 4 Hz for 8 out of 10 cardiomyocytes; peak power was achieved at 6 Hz for 7 out of 10 cells. The maximal power generated by a single cardiomyocyte is thus achieved at physiological heart rates.

Figure 3.

The power generation of a single cardiomyocyte. (A) Diagram to illustrate that the expected power generated by a single cardiomyocyte will be maximal at intermediate values of after-load; (B) work performed by a single isolated cardiomyocyte (paced at 4 Hz) plotted as a function of after-load for three different values of pre-load (0.2, 0.5, and 0.8 μN). Data were fitted with a parabola to find the highest value of performed work; (C) peak power generated by a single isolated cardiomyocyte as a function of pacing frequency. The maximum peak power is generated at physiological rates, where pre-load is the main determinant of power generation.

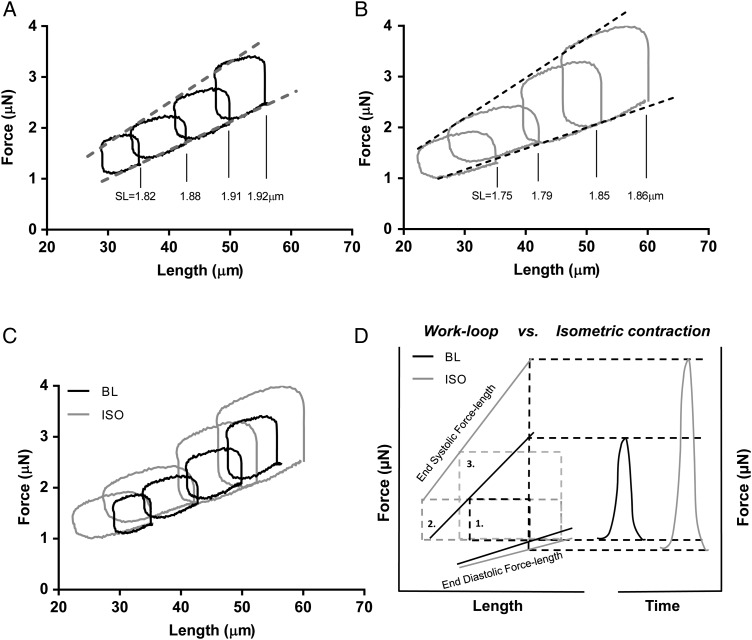
We tested our approach by exposing a single cardiomyocyte to a β-adrenergic receptor stimulus by measuring the FL relation before (Figure 4A) and after steady-state exposure to 100 nmol/L ISO (Figure 4B). The ISO increased the developed force as expected, and lowered the slope of the end-diastolic force–length (EDFL) relation (Figure 4A and B). The combination of increased force development, illustrated by the higher end-systolic force–length (ESFL) relation, and reduced EDFL led, in this example, to a four-fold increase in the work performed per cycle (Figure 4C).

Figure 4.

The power generation of a single cardiomyocyte upon isoproteronol (ISO) treatment. (A) Force-Length relation of a single cardiomyocyte. Loops where maximum work was performed are plotted for four different pre-load levels. (B) After the baseline (BL) measurements, the cell was exposed to 100 nmol/L of ISO and subsequently, the workloop protocol was repeated. The EDFL and ESFL values can be determined for both BL- and ISO-treated cardiomyocytes. (C) For every pre-load step, the generated work (i.e. the area of a single loop) is higher after ISO treatment. (D) Schematic presentation of the effect of ISO on workloops and its effect on both the EDFL and the ESFL. The loop marked with (1) is at baseline, (2) is the loop after ISO with the same pre- and after-load as (1), and (3) is the loop where the after-load is adjusted to measure the maximum amount of work. On the right, a sketch of the equivalent isometric contractions. With the isometric contraction, the ISO effect is heavily weighted towards increases in systolic force development, with only a small change in diastolic force. This is due to the EDFL being much shallower than the ESFL. Using workloops, the functional effects on both diastole and systole are given equal weight. The difference between BL and ISO is further enhanced when looking at the maximum work that can be performed for a given pre-load. The maximum work shows an approximate four-fold increase compared with a 50–75% increase in isometrically developed force upon ISO treatment. The figure is based on the loops collected in (C).

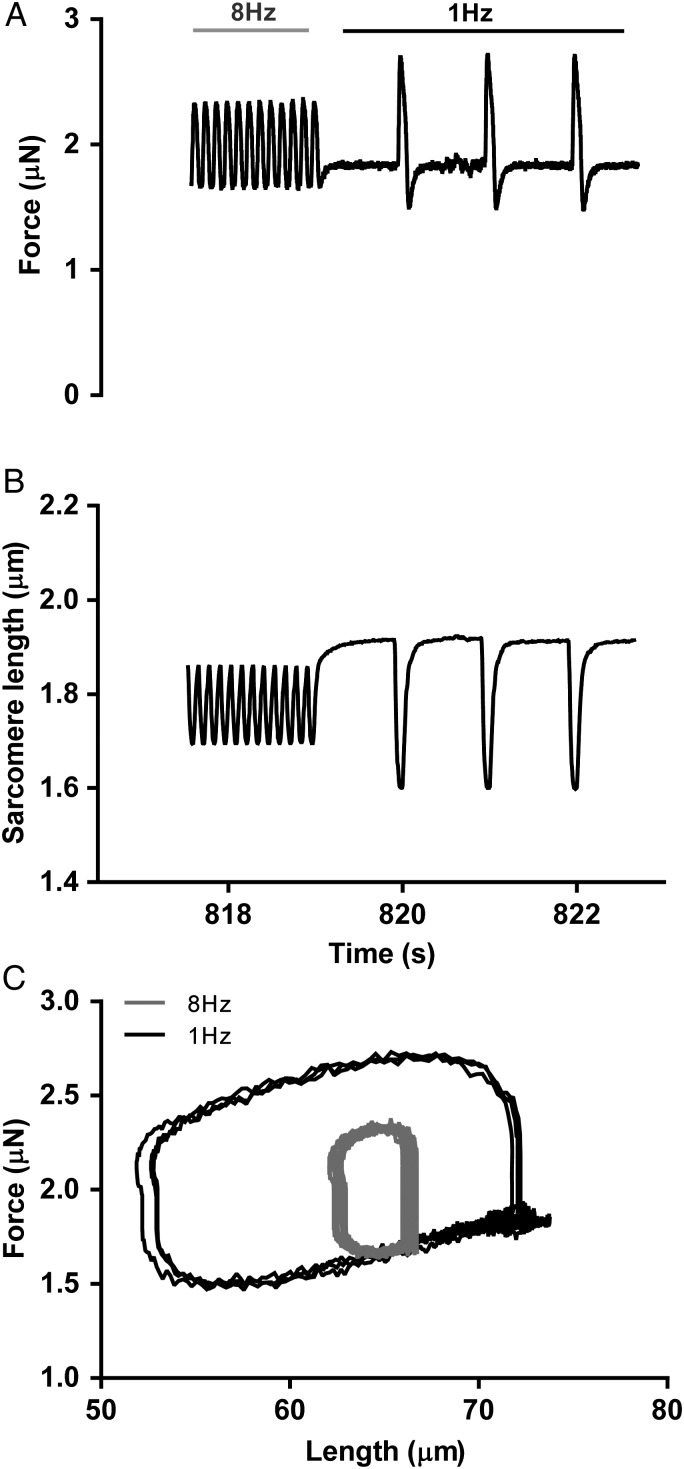
Another example is shown in Figure 5 and Supplementary material online, Video S2, where pacing frequency is switched abruptly from 8 to 1 Hz. In the build-up of frequency from 1 Hz (not shown) to 8 Hz, there is little difference in the maximum amount of work per loop; the increase in peak systolic force at 8 Hz due to higher systolic calcium is cancelled out by impaired relaxation. The post-rest potentiation effect due to the systolic effect of high sarcoplasmic reticulum calcium load after 8 Hz pacing and the improved relaxation in diastole leads to a five-fold increase in the work performed per loop (Figure 5C).

Figure 5.

The post-rest potentiation effect. Switching the frequency from 8 to 1 Hz resulted in an increase in force development (A), sarcomere shortening (B), and approximately a five-fold increase in single-cell work generation within the first contractions (C).

The method is repeatable. In a number of cells (n = 8), we repeated the 4 Hz pacing frequency after completing the protocol from 1 to 8 Hz pacing frequencies (see Supplementary material online, FigureS6A). Returning to a lower frequency after pacing at 6 and 8 Hz leads to a small reduction in the maximum work vs. end-diastolic SL relation, which may be indicative of some run down (see Supplementary material online, FigureS6B–I), but a Bland–Altman plot shows that the repeated runs at the 4 Hz pacing frequency are well in agreement with each other (see Supplementary material online, FigureS7A and B; n = 8). This indicates that the method presented in this paper is suitable for repeated measures, for example, to test pharmaceutical compounds.

3.3. SL range

In the experiments described in the present study, the ceiling of the end-diastolic SL at the highest pre-load level was frequently between 2.0 and 2.1 μm, but almost never exceeded 2.1 μm (Supplementary material online, Figure S5A demonstrates the SL range of each experiment vs. the generated work). It is important to note that these SLs were commonly achieved at low pacing frequencies (1 and 2 Hz). At higher pacing frequencies, the end-diastolic SL decreases slightly. End-systolic SLs were always between 1.6 and 1.7 μm SL.

4. Discussion

Using a force transducer based on laser interferometry in combination with a micro-machined probe, we were able to measure the force development of a single cardiomyocyte with unprecedented sensitivity, signal quality, and responsiveness. Its sensitivity bridges the gap between atomic force microscopy, which excels in the piconewton range and the classic force transducers used for muscle physiology, where the effective sensitivity ends in the micronewton range. The ability to fully submerse the force transducer also gives it very good baseline stability. The combination of nN-sensitivity, stability, and a 7 kHz resonance frequency for the first time opens up the possibility to control the force development at the level of a single intact myocyte using true feedback.

4.1. Workloops and power generation

We have used the ability to control force to mimic the cardiac cycle at the single myocyte level. Our method provides reproducible linear EDFL as well as ESFL relations. Changes in the inotropic state of the cardiomyocyte by increasing the pacing rate or β-adrenergic receptor stimulation changes the ESFL and EDFL in a predictable manner. We are also able to measure the changes in cardiomyocyte generated work in response to changes in pre- and after-load. In particular, the ability to do repeated measures will be useful in studying pharmaceutical interventions.

The focus of the experiments in the present study was to establish the relation between levels of pre-load, after-load, and pacing frequency with the external work the myocyte produces. The amount of external work is what ultimately determines the capacity of the heart to pump blood. The amount of work per loop increases with pacing frequency up to 4 Hz. At 6 and 8 Hz, the work per loop decreases slightly, mostly due to an elevated EDFL. The power generation peaks at 6 Hz. This is consistent with studies on ultra-thin rat trabeculae²⁰ that can be paced at high rates, where isometric force peaks at 6 Hz. In cardiomyocytes, the pacing frequency has a limited effect on power generation between 4 and 8 Hz (Figure 3C), while the major determinant of power generation is the pre-load level (Figure 3B). Rat ventricular myocytes appear to be adapted to produce most power over the physiological range of heart rates.²¹ Output per cardiomyocyte is further increased by β-adrenergic receptor stimulation.

The effects of β-adrenergic stimulation have been studied extensively in linear preparations such as permeabilized myocytes, unloaded intact myocytes, or muscle strips like trabeculae or papillary muscle.^22–24 Experiments on permeabilized myocytes are suitable to measure the effects of PKA-mediated phosphorylation on calcium-sensitivity and passive force of the myofilaments.^25,26 Unloaded, intact myocytes are ideal for studying the effects on excitation–contraction coupling because of the ease with which calcium kinetics can be measured in combination with myocyte shortening. The current work-loop experiments on intact cardiomyocytes illustrate the contribution of both changes in sarcomere properties and in calcium handling. The combined effects of myofilament calcium desensitization, reduced passive force, and enhanced calcium re-uptake during β-adrenergic receptor stimulation led to a small decrease in the slope of the EDFL relation. The reduced slope of the EDFL relation, while the pre-load stays constant, results in increased stretch of the cardiomyocyte at end-diastole. This extra stretch further enhances the force development in systole by length-dependent activation, on top of the increased force development caused by higher end-systolic cytosolic calcium levels. The increase in stretch during diastole and greater force development in systole both augment the area encompassed by the work-loop. It leads to an approximate four-fold increase in the work generated by the cardiomyocyte (Figure 4C) upon β-adrenergic receptor stimulation.

4.2. Limitations of the used methods

Measuring workloops in isolated myocytes by controlling the force in parts of the cycle gives results similar to those achieved in PV-loop measurements of the whole heart. This is illustrated by the suitability of existing PV-loop analysis software to analyse the data. But it would go too far to consider these FL loops as one-dimensional PV loops. For example, we have no dynamic force control in systole to mimic the changing impedance in the ejection phase. Better models have been made in the past using trabeculae.^27–29 The use of a real-time programmable machine, such as the FPGA, will allow future modifications of the algorithm that do take these complexities into account. The data shown here do however properly represent some of the key aspects of the whole heart measurements, most importantly a consistent end-diastolic and end-systolic pressure (i.e. force)–volume (i.e. length) relation. This had been shown before by Iribe et al.;¹⁵ however, those graphs had to be painstakingly constructed by manually adjusting the feed-forward parameters with each change in pre- and after-load. The current method greatly simplifies the process. The data for Figure 2C where three pre-load levels were tested for a full range of after-loads took <13 s to collect. As it is feed-back and not feed-forward, it is also sufficiently robust to cope with beat-to-beat changes in contractility. An example is shown in Figure 5C where pacing is abruptly changed from 8 to 1 Hz, resulting in an acute five-fold increase in the amount of work performed per stroke.

The workloops in Figure 3B and the power calculated in Figure 3C are based on the length change of the piezo-translator as force × length change determines the external work performed by the myocyte. Looking at Figure 5B, however, and this is exemplary for all our data, there is a lot of internal shortening of the sarcomeres. The sarcomeres display no distinct isometric activation and isometric relaxation phase. With the current gluing procedure, this cannot be avoided and it probably can never be completely avoided, even with better attachment methods. In the past, using the carbon fibre technique that has less compliance in the attachment we experienced the same.¹⁵ The classic study by ter Keurs et al.,¹⁶ where length-dependent activation in rat trabeculae is described, shows internal shortening where end-systolic SL does not increase till the trabecula is stretched beyond 1.95 µm end-diastolic SL.¹⁶ At that point, the majority of length-dependent force increase has already taken place. It appears as if in rats, the end-systolic SL is of limited relevance for the force development, which for a given inotropic state is dominated by the end-diastolic SL.

The upper limit of the end-diastolic SLs in our experiments was found to be ∼2.1 µm, but usually ended between 1.95 and 2.00 µm SL after which further increases in pre-load did not further stretch the cells. The experiments here were done at relatively high extracellular calcium levels (∼1.8 mmol/L). We hypothesize that the intracellular calcium levels were such that the diastolic force levels had an active component (as previously shown in King et al.³⁰) that was further enhanced by length-dependent activation upon stretch, effectively leading to a very non-linear relation between pre-load and SL increase. We do think that we cover the majority of the physiological range with maximal end-diastolic SLs of up to 2.1 µm. X-ray studies on intact mouse hearts and measurements on skinned mouse hearts come up with a range of 1.9–2.1 and 1.8–2.1 µm, respectively.^31,32 Older studies on fixed rat hearts showed SLs of 2.0–2.1 µm at diastolic filling pressures.³³ The physiological range likely increases with the size of the animal, but even in canine hearts fixed at end-diastolic pressure, the SLs were below 2.1 µm.³⁴ Rat cardiomyocytes have a compliance similar to mouse myocytes and we thus expect a comparable physiological SL range as in mice.

4.3. Advantages of work-loop measurements at the single cell level

Work-loops offer a specific advantage over isometric contractions which have been the norm over the past decades, and that is the sensitivity to changes in diastolic properties. As the slope of the EDFL is shallow, a small change in the slope will result in a significant change in end-diastolic SL, while other parameters remain equal. As our data show, a 0.1 µm increase in end-diastolic SL results in a ∼100% change of the maximum work that can be produced at that pre-load. This is illustrated in the schematic drawing of Figure 4D. The figure also shows the contrast with equivalent isometric contractions, where a small change in the slope will result in a small change in the measured end-diastolic force that, although important, may sometimes not even be noticed.³⁵ It could be argued that the bias towards systolic changes with studies using isometric contractions has led to a research bias towards treatments that affect systolic function. We therefore think that the ability to measure work-loops at the single cell level adds an important tool to study the functional consequences of disease and treatment options in animal models, notably with respect to diastolic dysfunction. This paper describes for the first time a method that can be used practically in testing the effect of drugs or disease models that affect diastolic function by measuring its effect on the work that the myocyte can perform.

Supplementary material

Supplementary material is available at Cardiovascular Research online.

Funding

D.I. acknowledges the support of the European Research Council (grant agreement n. 615170) and of the Stichting voor Fundamenteel Onderzoek der Materie (FOM). J.V. is financially supported by the Netherlands organization for scientific research (NWO, VIDI grant 91711344) and CVON-consortium grant (ARENA). We also acknowledge support from the 7th Framework Program of the European Union (‘BIG-HEART’, grant agreement 241577) and from ICIN-Netherlands Heart Institute.