Extreme sensitive metasensor for targeted biomarkers identification using colloidal nanoparticles-integrated plasmonic unit cells

Abstract

Engineered terahertz (THz) plasmonic metamaterials have emerged as promising platforms for quick infection diagnosis, cost-effective and real-time pharmacology applications owing to their non-destructive and harmless interaction with biological tissues in both in vivo and in vitro assays. As a recent member of THz metamaterials family, toroidal metamaterials have been demonstrated to be supporting high-quality sharp resonance modes. Here we introduce a THz metasensor based on a plasmonic surface consisting of metamolecules that support ultra-narrow toroidal resonances excited by the incident radiation and demonstrate detection of an ultralow concertation targeted biomarker. The toroidal plasmonic metasurface was designed and optimized through extensive numerical studies and fabricated by standard microfabrication techniques. The surface then functionalized by immobilizing the antibody for virus-envelope proteins (ZIKV-EPs) for selective sensing. We sensed and quantified the ZIKV-EP in the assays by measuring the spectral shifts of the toroidal resonances while varying the concentration. In an improved protocol, we introduced gold nanoparticles (GNPs) decorated with the same antibodies onto the metamolecules and monitored the resonance shifts for the same concentrations. Our studies verified that the presence of GNPs enhances capturing of biomarker molecules in the surrounding medium of the metamaterial. By measuring the shift of the toroidal dipolar momentum (up to Δω~0.35 cm⁻¹) for different concentrations of the biomarker proteins, we analyzed the sensitivity, repeatability, and limit of detection (LoD) of the proposed toroidal THz metasensor. The results show that up to 100-fold sensitivity enhancement can be obtained by utilizing plasmonic nanoparticles-integrated toroidal metamolecules in comparison to analogous devices. This approach allows for detection of low molecular-weight biomolecules (≈13 kDa) in diluted solutions using toroidal THz plasmonic unit cells.

1. Introduction

Plasmonic metamaterials are compositional periodic arrays of artificially engineered subwavelength building blocks with exotic spectral properties beyond natural materials [1]. As powerful photonic tools, they have been extensively employed for numerous applications including but not limited to light harvesters [2,3], label-free molecular detection [4–6], light velocity reducers [7–9], modulation [10–12], cloaking [13–15], nonlinear spectroscopy [16–18], and optoelectronics [19–22]. Such broad applications of plasmonic metamaterials have triggered researchers to design metamolecules to sustain highly localized, tunable and pronounced resonant moments in a wide range of spectrum. Recent studies have shown that plasmonic metamaterials can be tailored to support classical electromagnetic multipoles [23,24], as well as strong asymmetric lineshapes via an interference between optically driven eigenmodes (i.e. Fano resonances [25,26], electromagnetically induced transparency (EIT) [27,28], etc.). On the other hand, a new family of multipole resonances far from conventional electromagnetic multipoles, known as toroidal resonances, have been observed in both all-dielectric and plasmonic metamaterials [29–31]. In the toroidal multipole zoo [32], toroidal dipole has received growing attention as a strategic momentum, recognizable as a circular head-to-tail configuration of magnetic dipoles [33]. Due to concealing the far-field radiation signature of toroidal resonances by conventional and strong electromagnetic multipoles, hence, detection of this type of resonant modes is quite challenging [29–34]. To address this difficulty, in recent years, well-designed 3D and planar patterns have been introduced to improve the toroidal response of metamaterials [35,36]. The unique behavior of toroidal metamaterials have newly been utilized for designing photonic devices such as terahertz (THz) switches [37]. However, the studies of these masked or hidden resonances are majorly limited to investigating the physics behind the formation of them in different structures and practical devices have not been reported yet.

Being promising platforms for sustaining pronounced classical resonances, THz plasmonic metamaterials can be efficiently utilized for biomolecule identification [6,38] and detection of specific targeted bio-agents [39]. This is achieved by strong and steady binding of biological substances to the plasmonic metamolecules [40]. Possessing low photon energies around a few meV, THz waves are non-ionizing and harmless for organic tissues and hence have become very attractive for biomedical applications [41]. Such exquisite features of THz technology have led to development of pharmaceutical applications in imaging tools [42] and enzyme reaction analysis [43]. Although, there have been significant progress in THz plasmonic technology, the sensitivity, accuracy, and reliability of these platforms are limited, especially at low molecular-weight bio-substances [44]. To address these shortcomings and also to enhance the spectral features of plasmonic THz metamaterials, in this work, we excited ultrasharp toroidal dipole resonances across the sub-THz domain; 0.1 THz ≤ f ≤ 1 THz (3.35 cm⁻¹ ≤ ω ≤ 33.35 cm⁻¹) by using a metasurface consisting of planar metallic unit cells. The experimental characterizations followed by numerical analysis, helped to understand the physical mechanism of the narrow linewidth toroidal dipolar momentum. By introducing GNPs to the microsystem, we investigated the influence of metallic nanoparticles on the spectral response. We showed that such an integration of metamolecules and colloidal nanoparticles can be exploited for tailoring ultrasensitive THz biosensors to detect targeted infectious proteins with high accuracy and sensitivity. To demonstrate and quantify the biosensing capability of the proposed toroidal metamaterial, Zika virus-envelope proteins (ZIKV-EPs, NS1) were selected as targeted biomarkers in the presence of its respective antibody (ZIKV-AB) and measured the sensitivity and limit of detection (LoD) of the studied system. We also qualitatively analyzed the binding quality and influence of the low-concentration, low molecular-weight (≈13 kDa) proteins on the toroidal response originating from the refractive index variations in the surrounding environment of the unit cells via capturing of proteins by GNPs. To provide a comparative study, the sensitivity of the developed metasensor was analyzed in the presence and absence of the gold nanoparticles, when the ZIKV-EPs are attached to the system. This comparison would help us to compare the binding properties and capturing of biomarker proteins in two different regimes to investigate the immunosensing and fingerprinting capabilities of the developed metasensor.

2. The toroidal response of the proposed plasmonic metamolecule

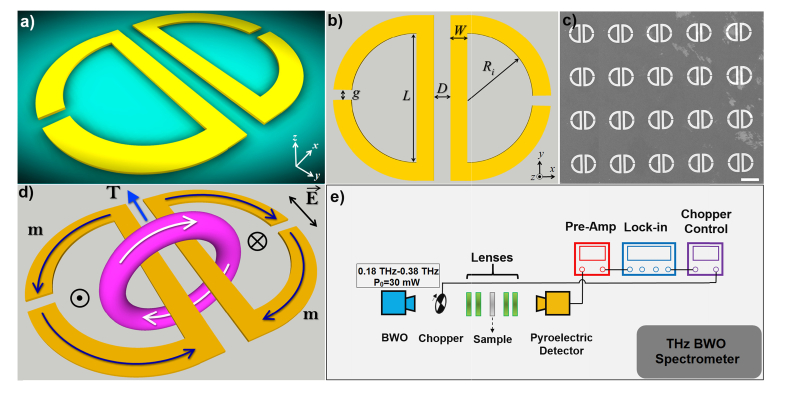
Figure 1(a) demonstrates an artistic 3D rendering of the investigated planar toroidal gold unit cell composed of two symmetric proximal resonators with an offset capacitive gap in the curved arms. The important geometrical parameters of the plasmonic structure are given in Fig. 1(b). As a critical component in the formation of toroidal momentum, we focused our electromagnetic and experimental analysis on the capacitive gaps (g) variations by providing constant values for the other geometrical parameters as follows: R_i/W/L/D = 60/15/105/15 μm. The scanning electron microscope (SEM) image of the fabricated metamolecule arrays with the gap of g = 5 μm is depicted in Fig. 1(c). The schematic image of toroidal dipole (T) formation is shown in Fig. 1(d), which is originated due to near-field interference of antiparallel magnetic moments arising from proximal resonators. The circulation of magnetic field around the parallel arms of the unit cell blocks is plotted with the direction of magnetic field (m) across the unit cell, verifying the formation of head-to-tail and closed-loop configuration of toroidal dipole that will be discussed later. It should be noted that the proposed unit cells are strongly polarization-dependent and the toroidal resonance can be excited only under y-polarized beam excitation, while for the x-polarized illumination the toroidal mode does not form. Figure 1(e) exhibits the utilized THz backward wave oscillator (BWO) setup, used for excitation and characterization of toroidal moments (Methods). In the Methods section we also present the fabrication steps and numerical approaches that were employed to predict and verify the spectral features of the plasmonic unit cell arrays.

Fig. 1.

(a) Artistic rendering of the toroidal unit cell. (b) Geometrical parameters of the unit cell. (c) SEM image of the fabricated metasurface. (d) Schematics of the formation of head-to-tail arrangement correlating with the toroidal momentum between the proximal resonators with the direction of magnetic momenta. (e) A schematic representation of the BWO setup used to characterize the spectral response of the metasensor.

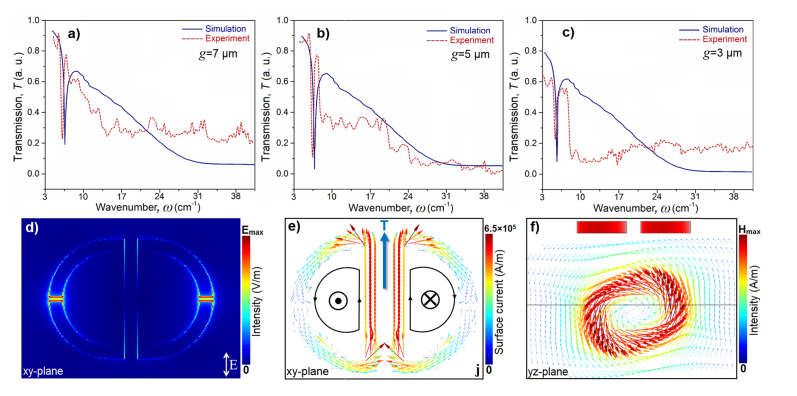
The proposed structure is gold with the dielectric function experimentally obtained by Ordal et al. [45] and Yasuda et al. [46] for submillimeter wavelengths. By assuming the electric component (E) of the incident beam is parallel with the adjacent arms of unit cell (y-polarized wave), and interacting with the planar metamolecules in the z-direction, we calculated and measured the transmission (T) amplitude spectra in Figs. 2(a)-2(c). These profiles show the projected toroidal dipole momentum normal to the z-axis (${\mathbf{T}}_{xy}^{\parallel }=T_x\overrightarrow{x}+T_y\overrightarrow{y}$) for varying capacitive gap sizes (3 μm ≤ g ≤ 7 μm) as a function of wavenumber, ω (cm⁻¹). The toroidal resonance slightly red-shifted by decreasing the capacitive gap distance (g) fromω≈8 cm⁻¹ to ω≈5 cm⁻¹. In all three regimes distinct and pronounced toroidal dipoles are excited in the transmission (T) spectra, while the deepest and the most significant enhancement of toroidal dipole resonance is observed for g = 5 μm around ω≈7 cm⁻¹. There is an excellent agreement between the numerical analysis and the experimental measurements of the metasurface due to high resolution fabrication of the metamaterial. Theoretically, formation of coplanar loops of magnetic dipoles (m) in proximal planar resonators that are oscillating oppositely leading to creating a platform for formation of toroidal multipoles (with the dominancy of strong toroidal dipole). The local electric-field (E-field) map for the plasmonic unit cell in the xy-plane at the toroidal dipole momentum is shown in Fig. 2(d), demonstrating the strong electric field intensity and localization at the capacitive openings. Formation of a magnetic circular head-to-tail current in the proposed structure is substantiated by plotting the surface current density (j) plane, shown in Fig. 2(e). In this profile, we plotted the antiparallel current distribution in the proximal resonators, which have significant role in formation of strong toroidal dipole excitation. The perfect antiparallel oscillation of surface currents and magnetic fields are taken place in two sides of a single plasmonic metamolecule gives rise to formation of toroidal spectral feature. Besides, the vectorial profile for the yz-plane magnetic-field (H-field) intensity provides complete verification for the creation of closed-loop magnetic field around the central arms of a unit cell (Fig. 2(f)).

Fig. 2.

(a), (b), and (c) Normalized transmission amplitude for the toroidal metamaterials with three different gap distances g=7 μm, 5 μm, and 3 μm, respectively.(d) Local near-field map of the E-field enhancement at the gaps at the toroidal mode frequency. (e) Surface current plot for the current across the structure and formation of toroidal mode. (f) A cross-sectional yz-plane of the resonators, showing the head-to-tail magnetic moments forming the toroidal moment in a vectorial map.

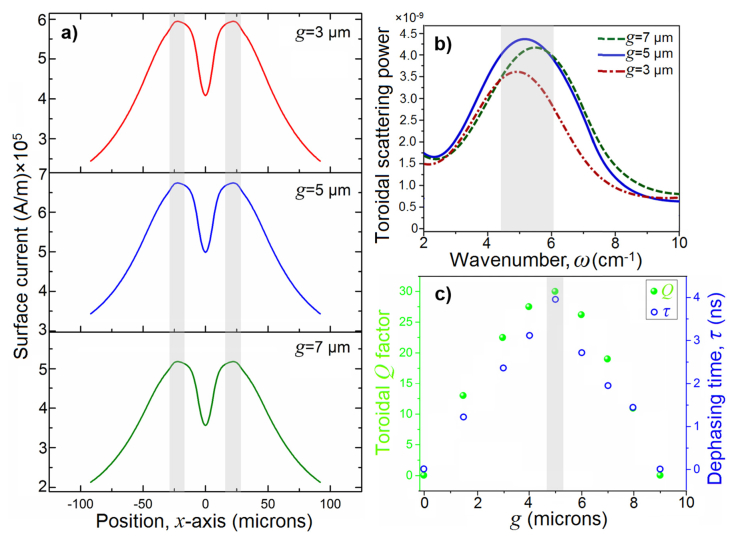
The effect of the gap distance on the plasmonic response of the toroidal antenna can be further analyzed by comparing the surface current density for three different gap distances. Figure 3(a) illustrates these variations in an yz-plane, showing the highest current density for g = 5 μm at the toroidal dipole resonant mode, reaching up to ~6.5 × 10⁵ A/m. This plot implies that stronger surface currents leads to formation of intense shared inductance between neighboring resonators and resulting in substantial confinement of magnetic power in the metamolecules arrays.^37,47 We also quantified the far-field (FF) scattered toroidal power or intensity for varying capacitive gap distances as shown in Fig. 3(b) using [47]:$I_{\text{T}}^{FF}=2{\omega }^6{\left|{\mathbf{T}}_{xy}^{\parallel }\right|}^2/3c^5$. The arisen distinct extremes are correlated with the targeted magnetic toroidal dipole resonant mode with dominant scattering power for the projected toroidal normal to the incident beam direction (z-axis). The electromagnetic computations demonstrate the highest scattered intensity for the gap of 5 μm. Finally, the quality factor (Q) of the induced toroidal momentum in the system for several gap sizes is plotted in Fig. 3(c), using the following equation: $Q=\left(\text{FWHM}/{\omega }_{\mathbf{T}}\right)-\left({\omega }_{\mathbf{T}}/4{(\text{FWHM})}^2\right)$, where FWHM = |ω₁-ω₂|, and ω_T is the center frequency of toroidal resonance. Here, for the absence of capacitive opening (g = 0 μm), the toroidal moment does not exist. A homogenous increase in the capacitive opening of the curved part of resonators leads to the substantial enhancement in the toroidal Q factor and reaches the highest value ~30 for g = 5 μm. Increasing the gap spacing causes drastic reduction in the Q factor due to perturbations in the antiparallel surface currents flowing in proximal resonators, which prevents formation of pronounced toroidal dipole. As a crucial parameter for surface plasmon-enhanced sensing systems [48], this profile also contains the quantified resonance dephasing time (τ), calculated using Fourier transformation approach. To model the damped harmonic oscillator, we utilized the Cauchy-Lorentz distribution [49], with the dephasing time of toroidal dipole given by [50]: $\tau =2\hslash /\Delta \omega$, in which $\hslash$ is the reduced Planck’s constant. As shown in Fig. 3(c), the dephasing time of toroidal lineshape increases up to ~3.9 ns for the resonators with capacitive opening of 5 μm. The presented optimizations for the proposed plasmonic unit cell should enable stronger interactions with the dielectric biological substances, leading to more precise and accurate sensing via shifting the position of the toroidal lineshape [51].

Fig. 3.

(a) Surface current as a function of x-axis for three different gap spacing. (b) The toroidal scattering intensity as a function of frequency for three different gap spacing. (c) The Q factor of the toroidal lineshape and dephasing time (τ) as a function of three different gap spacing.

3. Detection of ZIKV-EPs by toroidal metamaterial

In the past years, significant progresses have been accomplished to develop culture-based infectious biomarkers and bio-agents detection devices such as antibody-based methods (e.g. ELISA) [52,53], reverse transcriptase-polymerase chain reaction (PCR) approach [54], point-of-care (POC) molecular detection [55], electrochemical biosensing [56], and fluorescence-based microbial detection systems [57]. Although all these methods are promising for biodetection purposes, they dramatically suffer from long sample preparation and processing time, high-cost, need for trained personnel and lack of sensitivity. To address these limitations, plasmonic metamaterials in both micro- and nanoscale dimensions have been introduced as reliable, fast, label-free, quantitative, sensitive, and cost-effective platforms for biosensing and immunosensing purposes [58–60]. Fundamentally, plasmonic biosensing systems operate based on excitation of charge density oscillations (propagation of plasmons) and confinement of photoinduced electrons in subwavelength spots (localization of plasmons) that are highly sensitive to the refractive index variations in the ambience [60,61]. Much of the current interest in plasmonic subwavelength on-chip sensors stems from the high sensitivity of asymmetric Fano resonance lineshapes [25,62]. The exquisite sensitivity of Fano-resonant structures to the environmental perturbations led to tailoring of advanced biochemical and biological sensors [62–64]. Despite of the high sensitivity of Fano-resonant nanoscale platforms to the presence of biological nano-objects in direct contact with them, Fano-based THz plasmonic sensors suffer from low accuracy due to the transparency, low scattering cross-section and non-responsivity of nanoscale bio-agents (with the geometry of on the order of ~λ/100) and proteins to the incident THz wave [65]. On the other hand, THz spectroscopy based biosensing attracts attention due to the advantages like simpler fabrication techniques, low-costs, and high signal to noise ratio [66]. Therefore, THz plasmonic metasurfaces with the ability to recognize the presence of a specific nanosize biomarkers would be an excellent device for practical biomedical applications. To realize this feature, we integrated the studied plasmonic metasurface and colloidal GNPs with each other to enhance the sensitivity of the metasurface. Using functionalized and conjugated colloidal GNPs with the average diameter of 40 nm (see Methods), we investigated the change in the toroidal response to detect the presence of a specific biomarker. Here, we used the metasurface with the highest quality toroidal dipole to achieve the maximum sensitivity and accuracy to the environmental perturbations. As it was studied in the earlier section, the proposed multipixel unit cell shows the narrowest toroidal resonance for the gap distance of g = 5 μm in the broken areas of the curved resonators. Hence, we designed the metasensor based on the following geometrical parameters: R_i/W/L/D/g = 60/15/105/15/5 μm.

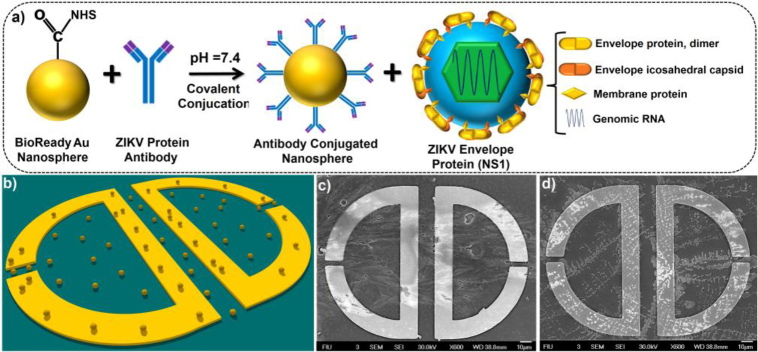
We used ZIKV-EP (NS1) with the molecular-weight of ≈13 kDa as a biological target in the presence of respective ZIKV-AB, as shown schematically in Fig. 4(a) with the subsequent components of ZIKV protein and illustration of ZIKV-AB and ZIKV-EPs conjugation. The GNPs here are used to trap the proteins (see the schematic picture and SEM image in Fig. 4(b) and 4(c), respectively) and change the refractive index of the medium to facilitate substantial shift in the position of toroidal dipole. For simplicity, we used fixed concentration of nanoparticles (10 μg/mL or ~77 picomolar (pM)), while the injected envelope protein concentration was varied between 1 fg/mL and 1 μg/mL. Figure 4(d) illustrates the SEM image of the toroidal unit cell with the presence of ZIKV-EP, captured by functionalized nanoparticles. To show the binding quality of ZIKV-AB and ZIKV-EPs to the GNPs, we illustrated the corresponding transmission electron microscopy (TEM) pictures in Fig. 5(a)-5(c) to show the uniform and strong binding of the bio-molecules to the nanoparticles, which enhances the sensitivity of the metasensor.

Fig. 4.

(a) Schematic flowchart of functionalized gold nanoparticle conjugation with the ZIKV-AB and ZIKV-EPs NS1 with the explanation for different parts. (b) Schematic representation of gold nanoparticles-integrated toroidal unit cells. (c) and (d) The SEM images of plasmonic metamolecule in the presence of GNPs with AB and ZIKV-EPs, respectively.

Fig. 5.

(a), (b) TEM images of functionalized GNPs binding with AB in two different scales. (c) The TEM image of ZIKV-EPs captured by AB-conjugated GNPs.

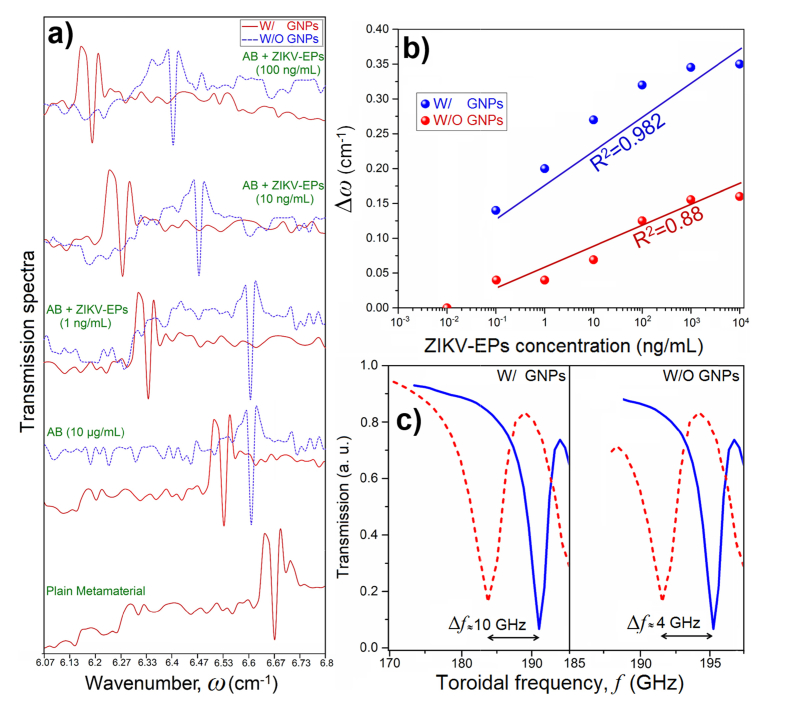
The experimentally obtained THz transmission spectra with distinct toroidal responses for different concentrations of ZIKV-EPs are presented in Fig. 6(a). For the absence of colloidal GNPs and biological agents and in the ambient atmosphere, the magnetic toroidal moment appears at 6.67 cm⁻¹. By introducing the ZIKV-AB-conjugated GNPs to themetasurface chips, the toroidal mode red-shifts to 6.53 cm⁻¹, while for the absence of nanoparticles and direct binding of ZIKV-AB to the metamolecule, the resonant mode slightly shifts to 6.6 cm⁻¹. Adding ZIKV-EPs with increasing concentration from 1 fg/mL to 100 pg/mL did not cause any shift in the toroidal moment and it stayed at the initial position of the presence of ZIKV-AB in both cases. The major toroidal shift in the position of toroidal resonance was observed for 1 ng/mL concentration of biomarker proteins for the presence of GNPs-conjugated system (red-shifts to 6.33 cm⁻¹), while the toroidal lineshape did not shift for the bare metamolecule with the presence of the same amount of envelope proteins. Further increase in the concentration of biomarker proteins leads to further shift in the position of toroidal dipole, while for the presence of 100 ng/mL of proteins, the toroidal mode appears at 6.13 cm⁻¹. On the other hand, the bare unit cell starts to show reaction to the presence of ZIKV-EPs at the concentration of 10 ng/mL (red-shifts to 6.47 cm⁻¹). Moreover, for the concentration of 100 ng/mL of proteins, the toroidal dipole red-shifts slightly to 6.4 cm⁻¹. It should be underlined that the position of toroidal moment shows trivial shift for the concentrations of proteins more than ≥ 1 μg/mL. The toroidal dipole shifts (Δω) as a function of concentration is plotted in a semi-logarithmic graph in Fig. 6(b) for the presence and absence of GNPs attached to the system. It should be underlined that the measurements here are linear and the logarithmic scale in Fig. 6(b) is utilized to clearly demonstrate how the toroidal dipole moment shifts for exponentially increasing concentrations of targeted proteins. This profile clearly shows how the presence of GNPs improved the sensitivity of the toroidal metasurface significantly. A large red-shift was obtained for GNPs-introduced system around Δω~0.35 cm⁻¹ (Δf ~10 GHz, Fig. 6(c)) for the biomarker concentration of 100 ng/mL (~77 pM) with the coefficient of determination R² = 0.982. For the system without plasmonic nanoparticles, the largest shift was around Δω~0.14 cm⁻¹ (Δf ~4 GHz, Fig. 6(c)), with determination coefficient of R² = 0.88.

Fig. 6.

(a) The transmission amplitude spectra for the fabricated metasurfaces in both W/ and W/O GNPs regimes in the presence of ZIKV-AB and ZIKV-EPs with different concentrations. (b) The toroidal resonance shift as a function of ZIKV-EPs concentration W/ and W/O GNPs with the corresponding determination coefficient. (c) The magnified transmission spectra as a function of frequency, showing the maximum shift of the toroidal moment in the presence and absence of GNPs attached to the system.

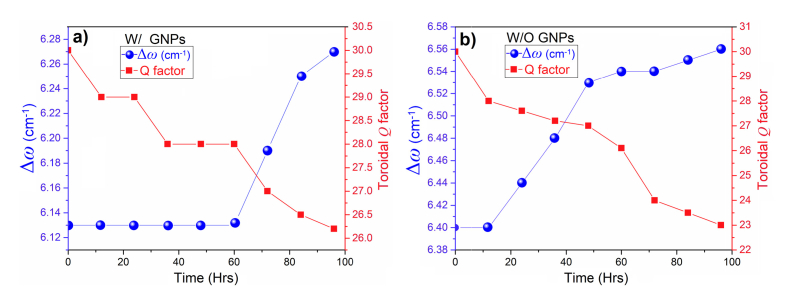
In continue, we studied the repeatability and stability of the THz toroidal response by time as demonstrated in Figs. 7(a) and 7(b) for nanoparticle integrated and bare metasurfaces, respectively. These experiments were done at the presence of 100 ng/mL of ZIKV-EPs bound to the system. We compared the toroidal shifts and the corresponding Q factors as a function of time. For the GNPs-integrated metasurface, the resonance shift remains fixed for approximately 60 hours, while a gradual blue-shift in the position of is monitored afterwards. However, the blue-shift and deterioration of the toroidal mode are drastic in bare metamolecules in the absence of GNPs (Figs. 7(b)). The same behavior observed for the Q factor, where the Q factor of the bare unit cells monotonically declined. This deterioration also included a significant blue-shift in the position of magnetic resonant mode to the higher energies. As a final comparison between two types of studied samples, we accurately quantified the limit of detection (LoD) and sensitivity of the metasensors as (see Methods for calculations): ~560 pg/mL and 5.81 GHz/log(pg/mL) for the GNP-integrated metasurface and 12 ng/mL and 2.25 GHz/log(pg/mL) for the bare metasurface.

Fig. 7.

(a) and (b) The toroidal resonance shift (Δω) and Q factor as a function to time in hours for the presence and absence of GNPs, respectively.

Recently, THz based biosensors with noteworthy sensitivities for detection of bio-molecules with larger molecular weights such as Avidin (~68 kDa) [6], and Rat IgG (~150 kDa) [67] have been reported. Demonstration of high-sensitivity detection of ZIKV-EPs with much lower molecular weight (~13 kDa) shows the superiority of the proposed toroidal plasmonic THz metasensor over the previously reported THz based biosensors. Use of plasmonic GNPs enabled strong binding of proteins and further improved the sensitivity and responsivity. It should be underlined that although the utilized infectious protein for the targeted ZIKV infection shows the similar behavior to the actual virus and provides much safer experiments, the direct contact of the targeted biomarker to the system can also be employed as an alternative method depending on the laboratory conditions that has been reported in Ref. [68]. The proposed method in this work is a proof of concept for sensing of the targeted biomarkers and also it is based on using nontoxic biomarker’s proteins in typical optics lab environment.

4. Conclusions

To conclude, we have analyzed the plasmonic response of a multipixel metamolecule with the ability to support high-Q factor toroidal dipole moment along the THz domain. By introducing gold nanospheres to the system, we have shown that the toroidal resonance can be tuned effectively. To show the exotic dependency of the induced resonant mode to the surrounding variations, by using infectious proteins to the system, we investigated the resonant mode behavior for different concentrations of biomarker proteins. To show the influence of the presence of plasmonic GNPs, we provided the experimental data for the presence and absence of gold particles. The results verified that in the presence of gold nanoparticles the sensitivity of the metasensor can be enhanced and large resonance shift can be achieved. In addition, due to strong binding of nanoparticles and biomarker nano-objects, a significant repeatability was observed for the chip integrated with GNPs for more than 75 h. We believe that this study paves new methods to provide highly sensitive, efficient, and promising THz metamaterials for detection of biomarker agents.

Methods

Fabrication of plasmonic metasurface. For the fabrication of the proposed planar metasensors conventional single-level lithography based microfabrication process was developed. An undoped and high-resistivity silicon (Si) wafer (>10 kΩ.cm) with the crystal orientation of <100> and thickness of 500 µm was used as substrate to provide the required transparency in the THz spectrum [69]. It was sonicated in acetone for 10 min, and rinsed with isopropyl alcohol (IPA), deionized (DI) water, and dried by Nitrogen prior to the fabrication process. In continue, we deposited negative photoresists (NLOF 2020) with the thickness of 2.2 μm and patterned intently in two different steps. Employing e-beam evaporation, we then deposited 50 nm of titanium (Ti) and 300 nm of gold (Au) layers separately with the rate of 1 Å/s (99.99% purity for Ti and 99.9995% purity for Au, vacuum pressure ~3.2 × 10⁻⁴ mTorr). The Ti sublayer was used to enhance the adherence of gold layer to the surface of the Si wafer. The lift-off process was performed for 15 min by immersing the samples in acetone for 20 min at room-temperature using a sonication device, followed by IPA and DI water rinse. The SEM images shown in the manuscript were obtained using JEOL 7000 tool.

Preparation of GNPs and conjugation of AB. Surface functionalized gold colloids (with the diameter of 42 nm, and with an optical density (OD) of 20.09, BioReady NHS dried, NanoComposix) were used with robust covalent conjugation to primary amines (-NH₂) of proteins. For the conjugation of ZIKV-AB with the GNPs, a reconstitution buffer was prepared by combining 1 mL of reaction buffer was with 35 μL of purified ZIKV-AB. Then the prepared buffer was added to the NHS dried gold colloid, sonicated for 30 seconds. The solution is incubated while rotating at room temperature for 60 minutes. Next, we added 10 μL of quencher to deactivate the possible remaining active NHS-esters. The solution centrifuged at 3600 RCF for 10 min, then the supernatant removed cautiously and resuspended with 1 mL of reaction buffer including a sonication until fully resuspension. By repeating the previous protocol from centrifuging process with the same protocol, finally, we added 50 μL of conjugate diluent by sonication. The conjugated samples were stored at 4 °C. To conjugate the prepared GNPs with the fabricated toroidal unit cells, we dropped 10 μL (1 mg/mL) of colloidal solution to the chips and wait till dried. Then, the prepared targeted ZIKV biomarker proteins were added to the prepared plasmonic metamolecules and stored at 4 °C. The corresponding TEM pictures were taken by PHILIPS CM200 machine.

Preparation of the samples for biological assay. Firstly, we used both lyophilized 99% bovine serum albumin (BSA) purchased from Sigma-Aldrich, and pH~7.4 phosphate buffer solution (PBS) to dissolve the immunoreagents. For preparing the samples for real-time characterization, after washing the chips with PBS, ZIKV-AB-modified structures were incubated in PBS containing 0.1 wt. % BSA for 15 min, and then, in a solution of a recombinant Zika diluted in PBS for at least 20 min (The ZIKV-EPs concentration was ranged from 1 fg/mL to 1 µg/mL). Once prepared, antibody-functionalized microstructures were rinsed and stored at 4 °C until used. The mouse monoclonal antibody and the envelope proteins purchased from Aalto Bio Reagents and Sino Biological Inc., respectively.

Calculation of LoD and sensitivity. In this context, the LoD can be defined by [70]: LoD = 3(SD)/S, where “SD” is the standard deviation of the frequency shift and “S” is the slope of the fitting line (shown by the fitting lines in Fig. 7(a)). By defining the slope of the toroidal position shift as a function of ZIKV-EPs concentration, we qualitatively estimated the sensitivity of the structures.

Characterization of plasmonic unit cells. To characterize samples and extract the plasmon response of arrays with and without biological targets, a millimetre wave backward wave oscillator (BWO) setup combined with frequency multiplier (Microtech Instruments, Inc.) and broadband pyroelectric detector (Gentec Electro Optics Inc.) was operated at room-temperature. The spectral range of the incident radiation is between 100 GHz and 1.5 THz. The spectral resolution of the system is 10 MHz.

Electromagnetic simulations. Numerical analysis were performed using three-dimensional (3D) finite-difference time-domain (FDTD) method (Lumerical 2017) [71]. The toroidal metamolecules on top of a semi-infinite high-resistive silicon substrate were simulated using the refractive index of 3.9 for Si at THz domain. To achieve accurate results, the spatial grid sizes in all three axes were set to 25 nm. Moreover, the induced current module was employed to estimate the surface current density in the unit cell.

Theoretical analysis. In terms of condensed matters and nuclear physics, the toroidization concept operates based on both time-reversal ($t\to -t$) and space inversion ($r\to -r$) symmetry [30,32,72,73]. In the toroidal multipole family, the dipolar toroidal mode ($\overrightarrow{\mathbf{T}}=\overrightarrow{\mathbf{p}}\times \overrightarrow{\mathbf{m}}={\displaystyle {\sum }_j{q}_j{\overrightarrow{r}}_j}\times ({\overrightarrow{r}}_j\times d{\overrightarrow{r}}_j/dt)$) has received growing interest to employ for nano- and microscale devices. For the proposed planar metamolecule, the projected multipolar toroidal momentum can be explained using the far-field signature of the emitted electric field from the metamolecule arrays can be explained using the proposed description by Savinov et al.⁷⁴ for far-field component as follows: ${\overrightarrow{\mathbf{E}}}_s^{FF}=(-{\mu }_0{c}^2{k}^2{\overrightarrow{\mathbf{T}}}_{xy}^{\parallel }/2A^2)\exp (-ikr)$, the reflected electric field from the metamaterial for toroidal dipolar momentum as dominant component can be written as [29,74–76]:

$${\overrightarrow{\mathbf{E}}}_{\mathbf{s}}=\left(\frac{{\mu }_{0}k{c}^2}{2A^2}\right)\left[i\left\{\hat{\mathbf{r}}\left({\overrightarrow{\mathbf{m}}}^{\parallel }-k^2{\overrightarrow{\mathbf{m}}}_{(1)}^{\parallel }/10\right)-{\overrightarrow{\mathbf{p}}}^{\parallel }\right\}-k\left({\overrightarrow{\mathbf{T}}}_{xy}^{\parallel }-\raisebox{1ex}{$k^2{\mathbf{T}}_{(1)}^{\parallel }$}\!\left/ \!\raisebox{-1ex}{$10$}\right.\right)\right]\exp (-ikr)$$ (1)

where k is the wavenumber, μ₀ is the magnetic permeability, A² is the area of the unit cell, r is the perpendicular distance of the monitor from the metasurface, $\hat{\mathbf{r}}$ is the unit vector perpendicular to the metasurface. In addition, m₍₁₎ and T₍₁₎ signify the mean-square radii of magnetic and toroidal dipoles, respectively, which are considered for the metamolecules with finite geometries. The analysis in the manuscript was simplified by ignoring the influence of the high order toroidal multipoles.

Funding

Army Research Laboratory (ARL) Multiscale Multidisciplinary Modelling of Electronic Materials (MSME) Collaborative Research Alliance (CRA) (Grant No. W911NF-12-2-0023, Program Manager: Dr. Meredith L. Reed). The authors have acknowledge grants R01-DA027049, R01-DA034547, R01-DA037838, R01-DA040537, and R01-DA042706 awarded by National Institutes of Health (NIH).

Disclosures

The authors declare that there are no conflicts of interest related to this article.