Holographic line field en-face OCT with digital adaptive optics in the retina in vivo

Abstract

We demonstrate a high-resolution line field en-face time domain optical coherence tomography (OCT) system using an off-axis holography configuration. Line field en-face OCT produces high speed en-face images at rates of up to 100 Hz. The high frame rate favors good phase stability across the lateral field-of-view which is indispensable for digital adaptive optics (DAO). Human retinal structures are acquired in-vivo with a broadband light source at 840 nm, and line rates of 10 kHz to 100 kHz. Structures of different retinal layers, such as photoreceptors, capillaries, and nerve fibers are visualized with high resolution of 2.8 µm and 5.5 µm in lateral directions. Subaperture based DAO is successfully applied to increase the visibility of cone-photoreceptors and nerve fibers. Furthermore, en-face Doppler OCT maps are generated based on calculating the differential phase shifts between recorded lines.

1. Introduction

OCT has become a standard technique in ophthalmic imaging, showing the different layers of the human retina and their alteration in the progression of various diseases, such as age related macular degeneration (AMD), glaucoma, etc. in-vivo. The introduction of OCT has brought a huge improvement in the understanding of diseases and their development. Throughout all the advantages of OCT, high resolution investigation on a cellular level has always been a technological challenge. High lateral resolution is achieved by an increase of the pupil diameter, finally limited by the human pupil size (7-8 mm) [1]. In the ideal case, increasing the beam diameter should results in a sharper focus at the retina ultimately allowing to resolve cellular details. Unfortunately the human eye is not perfect, which prevents diffraction limited resolution of the imaging system.

Hardware based adaptive optics, similar to systems used in astronomy has been introduced to compensate for these aberrations achieving cellular resolution in the eye [2,3]. These systems require a wavefront sensor and a hardware based wavefront manipulator, which increase the complexity and cost of such systems. Digital aberration correction (DAC) or digital adaptive optics (DAO) instead manipulates the wavefront in post processing, with no need for wavefront sensors or additional hardware. Although DAO cannot compensate for the reduced sensitivity due to the aberrated illumination beam, it is possible to correct aberration for backscattered light. The overall sensitivity will reduce but can be recovered to a certain extent by the avoiding using a wavefront sensor and deformable mirrors which are reducing the sensitive of hardware based AO systems. The main limitation to DAO is the need of proper phase correlation across an acquired en-face image or volume. Involuntary movement of the eye and the heart beat call for fast acquisition in order to decrease the adverse effect of movement to the phase correlation [4–6]. Full field Fourier domain OCT does not suffer from such lateral phase decorrelation but yields only weak structural contrast in scattering tissue due to the missing confocal gating [7]. For scanning OCT systems it has been shown, that high tomogram rates are required for stable performance of DAO. This has been first achieved with en-face OCT in a single plane and for point scanning swept source OCT across a limited field of view [8]. En-face OCT is a variant of time domain (TD) OCT, with fast lateral scanning to achieve high en-face image rates [9,10]. En face OCT has the advantage of achieving high frame rates, which guarantees phase correlation along the acquired frame. In previous realizations a fast local oscillator was used in the reference arm to extract the complex OCT signal from the DC background [11]. In our present work, we apply holographic signal reconstruction using line-field illumination together with an off-axis reference arm at the detection plane [12]. Such passive signal modulation together with parallel detection allows to achieve en-face rates up to 100 Hz with a commercially available line-scan sensor. Parallel or line illumination has the advantage to reduce the scanning dimension to only one, which enables high tomogram rates without sophisticated synchronization of resonant scanners. Furthermore, line field configurations maintain still half the confocal gating, with a better rejection of out of focus light, which results in higher contrast and signal to noise ratio (SNR) as compared to full field OCT [13–17].

Retinal blood flow is an important indicator for alterations of the retina, induced by diseases such as glaucoma or diabetic retinopathy [18,19]. Retinal blood flow can be calculated with Doppler OCT (DOCT) by evaluating the differential phase shift induced by moving red blood cells in the direction of the illumination beam [20]. Although first realizations of DOCT were already based on TD OCT [21], the intrinsic slower detection speed and sensitivity hindered its stable application in retinal perfusion imaging. This changed with the introduction of Fourier domain DOCT, as a large range of vessels in the retina could be assessed due to the higher speed [22,23]. En-face OCT on the other hand, although still a variant of TD OCT, provides actually fast en-face line rates of several tens of kHz. The present line field en-face OCT system achieves up to 100 kHz en-face line rates, which covers well the necessary range for assessing blood flow in human retinal vessels.

2. Methods

A line field scanning laser ophthalmoscope (SLO) was built in an off-axis holography configuration in order to achieve time domain en-face OCT signal reconstruction. Depth information is obtained by tuning the reference arm length over time. The off-axis angle between reference and sample arm at the sensor was introduced by using a holographic grating in the reference arm. The angle introduces a spatial modulation of the interference signal between reference and sample arm across the line sensor. Fourier filtering in the spatial domain enables then in post-processing to separate the structure carrying cross correlation signal form the DC and autocorrelation signal as described in [12]. The used light source is a superluminescence diode (Superlum BLM S-840) with a bandwidth of 50 nm and a central wavelength of 840 nm. It has a coherence length of 6.2 µm in air, and 4.5 µm in tissue.

The camera in use is a complementary metal-oxide-semiconductor (CMOS) line camera (Basler sprint spl4096) operated at 10 kHz to 100 kHz line rate, reading out 2048 pixel. The illumination power at the sample was set to 4.5 mW which is well below the maximum permissible exposure, according to the European laser safety standards [13,24]. This configuration permits en-face rates from 10 up to 100 Hz at 10 kHz to 100 kHz lines rate, with a field of view of 4° x 2°, sampled by 2048 x 1000 pixels respectively. The 2048 pixels are acquired in parallel defining the coordinate x along the line sensor and 1000 pixel along the scanning direction define y. Changing the reference arm delay enables to choose different retinal layer structures of interest. At such high frame rates the influence of head movement on the lateral phase correlation becomes negligible. The lateral resolution measured with a reduced eye model using a focal length of 30 mm and a resolution test target at the focal plane is 2.8 µm in y and 5.5 µm in x direction (see Fig. 4). As we have a holographic setup the interference between sample and reference arm provides access to the complex valued backscattered sample field. Availability of signal field information enables digital wavefront manipulation [25,26]. Figure 1 shows a schematic of the setup, which is designed for high resolution retinal imaging supporting a beam diameter of 4.5 mm at the cornea. The transmission grating (G1) introduces the off-axis angle. Along the x direction the structure is sampled by the camera in parallel and the y direction is sampled by employing a galvo-scanner. Using a transmission grating has the advantage to create the off axis angle for the reference beam with a constant group delay across the detector plane. Only the phase delay changes, which results in high contrast spatial interference fringes of constant frequency along the parallel direction and avoids an axial shift of the coherence gate [27,28].

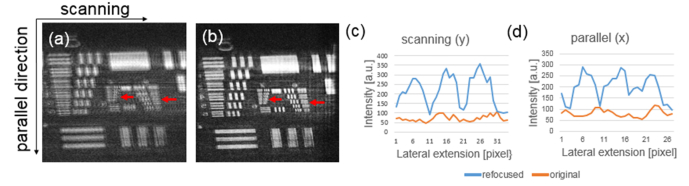
Fig. 4.

(a) shows the OCT en-face image of a resolution test target acquired with defocus. (b) is the OCT en-face image after digital refocusing, as can be seen the visibility of single bars clearly increases (c, d) are the intensity plot along the bars indicated by the red arrows in scanning and parallel direction. A clear differentiation can be seen between the 3 bars in the refocused image as in comparison to the original.

Fig. 1.

(a), schematic of the holographic line field time domain OCT system, CL1 and CL2 being the cylindrical lenses to create a line focus; the Galvo-scanner scans along the y dimension and L1 to L5 being achromatic lenses. G1 is a holographic grating introducing the off axis angle for the first diffraction order, which is filter using iris IS1. The angle remains constant during reference arm length tuning LS is the light source and EL the eye length. The illumination and detection beams are marked in black and green dotted lines, for both x and y dimensions. The orange dotted line is the reference path. The ray diagram of the detection can be seen in (b) showing in green the sagittal plane (y, z) and in black the orthogonal tangential plane (x, z) with z being the direction of propagation.

The off axis angle between reference arm and sample arm α introduces the spatial frequency modulation of the interference signal [12,29–31]

$$S(x,k)\propto \cos \left\{2k\Delta z+kx\sin (\alpha )\right\}$$ (1)

where S is the interference signal between reference and sample arm, Δz the path length difference between reference and sample arm and k is the wavenumber. The modulation frequency produces an offset of the structure carrying signal in the spatial frequency domain corresponding to the parallel direction x. The angle α is adjusted such that the shifted signal is well set apart from the DC term, typically at about three quarters of the Nyquist range. In the current setup it is set to 1.2°. Figure 2 shows schematically the result after Fourier transform along the parallel direction. The shifted interference term can be filtered out (blue dotted box). After inverse Fourier transform, the OCT structural information is retrieved. The un-shifted signal at zero spatial frequency (DC term) corresponds to a line-field SLO image. A similar approach has been recently shown by Sudkamp et al. with a full field approach having a two-dimensional array camera instead of a line camera [32].

Fig. 2.

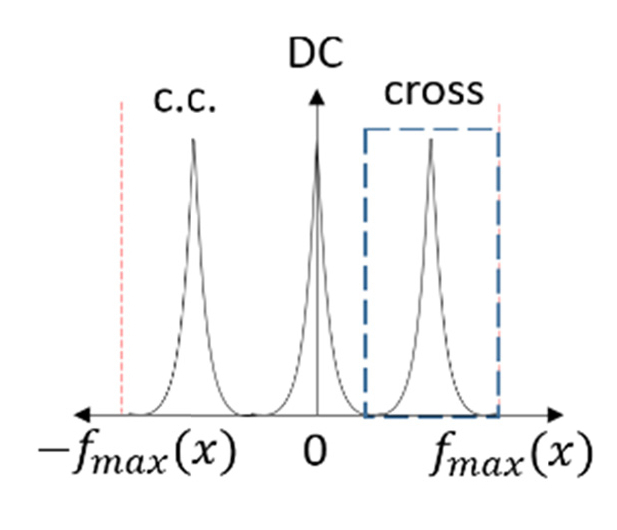
Shows the Fourier transform in the lateral direction x, the cross correlation term (blue dotted box) is shifted with the corresponding modulation frequency, the not interfering part (DC) remains in the center. The red dotted line is the maximum frequency which is provided by the pixel pitch.

With the reconstructed OCT image, computational aberration correction can be applied. In particular we apply the non-iterative split aperture based wavefront sensing and correction method by Kumar et al. [33]. This method operates on complex valued en-face image data. As mentioned above for DAO, we need proper phase correlation along the acquired frame. Further we need to compensate for axial bulk motion, during the measurement. This is done by calculating the phase different between successive lines along the scanned en-face plane.

$$\begin{array}{c}\Delta \phi (x,y_n)=\arg \left\{\left[A(x,y_n)e^{i\phi (x,y_n)}\right]\times \left[A(x,y_{n+1})e^{i\phi (x,y_{n+1})}\right]\right\},\\ n=\mathrm{1......}N-1\end{array}$$ (2)

with, x being the parallel direction and y the scanning direction, N being the number of recorded en-face lines, A the amplitude of the OCT signal and $\phi$ the phase. We further calculate the average phase difference along the parallel direction using phasor representation. As all pixels along the sensor line x are acquired parallel they are affected by the same bulk motion, which can therefore be calculated as average phase shift:

$$\begin{array}{c}\Delta {\phi }_{avg}(y_n)=\arg {\displaystyle \sum _{j=1}^{N_x}\left[e^{i\Delta \phi (x_j,y_n)}\right]}\\ n=\mathrm{1.....}N-1\end{array}$$ (3)

with $N_x$ being the number of parallel pixels along the line. This average phase shift is used to compensate for bulk motion during acquisition and therefore multiplied successively [6] as:

$$\begin{array}{c}{I}_{corr}(x,y_n)=A(x,y_n)e^{i\phi (x,y_n)}{\displaystyle \prod _{i=1}^{i=n-1}{e}^{i\Delta {\phi }_{avg}(y_i)}}\\ n=\mathrm{2....}N-1\end{array}$$ (4)

with $I_{corr}(x,y_1)=A(x,y_1)e^{i\phi (x,y_1)}$ being the unchanged first line. As a next step a Fourier transform is performed on the complex en-face image to get to the pupil or Fourier plane of the image. The pupil plane is subsequently split into 5x5 equally sized quadratic sub-apertures and the inverse Fourier transform is calculated for each of the sub-images. The result are 5x5 low resolution copies of the original image, which are shifted from the respective central sub aperture image by an amount proportional to the local slope of the wavefront. The overall wavefront can then be reconstructed by polynomial fitting based on the available local slope data. As such, the method acts as a scene based wavefront sensor as opposed to a Hartman-Shack sensor. The aberration correction is then performed in a single step by applying the conjugate of the wavefront phase to the original image. The number M of subapertures chosen results in M-1 Zernike coefficients which can be calculated [6].

For Doppler OCT evaluation the phase difference between successive en-face lines are calculated, following Eq. (2), but using $I_{corr}(x,y)$ instead, after bulk motion correction (Eq. (3)-(4)). Knowing the line rate $\frac{1}{\tau }$ and the wavelength λ enables to calculate the axial flow velocity in direction of the illuminating beam z,

$$v_z=\frac{\lambda \Delta \phi }{n4\pi \tau }$$ (5)

with n being the refractive index [34,35]. The maximum axial velocity that can be unambiguously resolved is given as$v_{\max }=\frac{\lambda }{4\tau }$ . The sign is determined by the direction of the flow with respect to the detection direction. The minimal axial velocity is determined by the phase noise of the system as$v_{\min }=\frac{\lambda \Delta \phi }{4\pi \tau }$ [22].

The sensitivity was calculated by measuring the reflex from a mirror in the sample arm with a neutral density filter of given attenuation D. The coherence gate was aligned with the confocal gate and placed at the position of the sample mirror. In a second step the reference path was changed and the signal at an axial position after the mirror recorded. This allows to assess the noise level, which is quantified by calculating the standard deviation of the noise over time. The SNR is then calculated by the peak mirror signal squared divided by the noise variance. The sensitivity is given as the SNR in dB added to the attenuation offset of 20*D resulting in 86 dB. The noise level is dependent on the spatial Fourier filter bandwidth and the sampling. Hence to be comparable, always the same Fourier filter bandwidth was applied for the measurements. Calculating the theoretical sensitivity with: $SNR=10*\log (\frac{g\eta \tau }{\hslash \nu }{\eta }_{sample}{P}_0)$, including the correction factor g for the central pixel at peak intensity due to the Gaussian weighting of the line field illumination, η the quantum efficiency of the detector, τ the exposure time, υ the central frequency of the used light source, η_sample includes the losses in the detection part (beam splitter, surface reflections and mismatch between pixel size and focal spot size) and P₀ the sample power. We end up with an expected sensitivity 88 dB, which is in close agreement to the measured value. The effect of the Fourier filtering on the SNR is explained by Yasuno et al [36].

3. Experimental results

3.1 Ex-vivo results

To validate the performance of the system a resolution test target was imaged with a line rate of 10 kHz resulting in 10 Hz en-face frame rate. Figure 3 displays the results of the signal processing steps. Figure 3(a) shows the original en-face sample image, exhibiting spatial modulation as seen from the zoom-in of Fig. 3(b). The modulation frequency shifts the terms, due to interference between reference and sample field, in the spatial frequency domain away from the DC location, where the non-interfering or DC terms remain (Fig. 3(c)). The spatial spectrum plot is obtained by performing the Fourier transform of the original image along the parallel (x) direction. The OCT en-face image can be reconstructed by performing Fourier filtering of the interference terms for all parallel recorded lines resulting in Fig. 3(d).

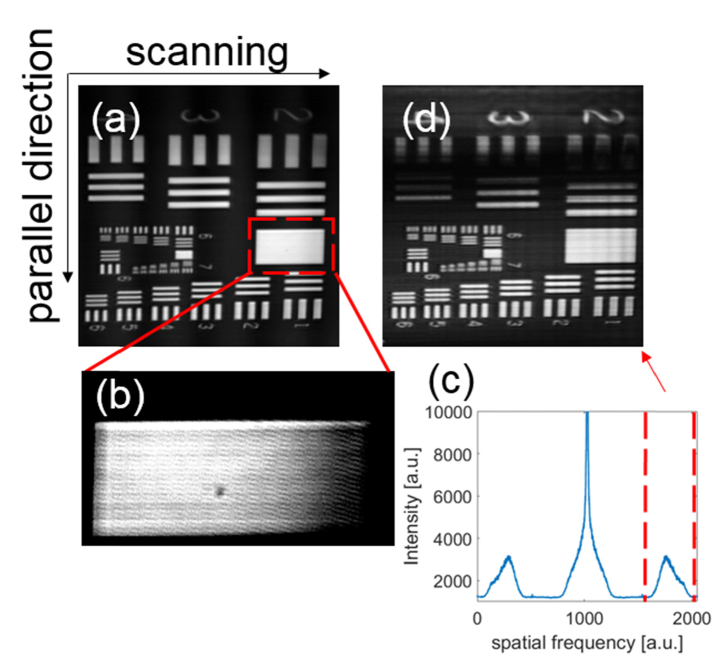
Fig. 3.

(a), shows the SLO image of a resolution test target. (b) is the zoom-in of (a), the modulation frequency due to the off axis approach can be seen, this shifts the interference as can be seen in the red dotted lines of the Fourier transform along the parallel dimension of (a) in (c). (d) is the reconstructed en-face OCT image by inverse Fourier transform of the filtered interference terms.

As a next step digital refocusing was performed on the OCT en-face image after the digital holographic reconstruction. Figure 4(a) shows the OCT en-face image of a defocused resolution test target. The signal profile in Fig. 4(b) is extracted from across the group 7-2 of the resolution test target indicated by the red line in Fig. 4(a). Due to the defocus, it is impossible to distinguish different lines. After applying DAC bases on a forward model [37,38] the actual structure is recovered as shown in Fig. 4(c) with the root-mean-square (RMS) of the used defocus phase of 2.08 µm. Again the red line indicates the position of the extracted intensity profile shown in Fig. 4(d). The bars of group 7-4 can now be distinguished in scanning direction y and the actual resolution of 2.8 µm is recovered. In parallel direction x the group 6-4 is resolved, resulting in 5.5 µm resolution. As we have an anamorphic line field system, the illumination properties are different for each lateral dimension, corresponding to confocal illumination in the scanning and unfocused line illumination in the parallel direction [39]. It has been shown, that the lateral resolution of coherent illumination is degraded by a factor of 2 as compared to spatially uncorrelated illumination, as in the case of scanning [14,40].

3.2 In-vivo validation

In vivo measurements were performed with three healthy volunteers. All measurements were approved by the ethics committee of the Medical University of Vienna and informed consent was obtained from all volunteers. A region at an eccentricity of approximately 7° from the fovea was imaged with a field of view of 4x2°. The line rate settings for the acquisition were 10 kHz line rate. The coherence gate was set subsequently to the nerve fiber layer, the outer plexiform layer and to the photoreceptor layer resulting in Fig. 5(a)-5(f), where Fig. 5(a), 5(c) and 5(e) are the original en-face frames, whereas Figure (b), (d) and (f) are the OCT en-face images after Fourier filtering. In Fig. 5(d) micro vascular details of the outer plexiform layer are visible in the OCT image that are not seen in the SLO image due to the different axial setting of the coherence gate for OCT and the confocal gate in SLO. For the photoreceptor image both images exhibit similar structural information. Note, that in the en-face OCT image only information within the axial coherence gate is retrieved. Since the coherence gate of 4.5µm is much smaller than the confocal gate of 90 µm it is possible to select retinal structures of distinct layers with much higher precision than with line field SLO. In general, the finer axial gating in OCT results in a smaller image SNR of the OCT image. We applied therefore 10 fold averaging for the displayed images. The validation that we indeed realized coherence gating for the OCT en-face images is to perform axial scanning of the reference arm and to record a full B-scan. The tomogram obtained with a line rate of 10 kHz is shown in Fig. 5(g). Note that the confocal gate has been kept at constant position during reference arm scanning and no dynamic focusing has been applied [41]. Hence the system allows for flexible imaging by using the tomogram view on-line for proper adjustment of the subject with subsequent en-face view at 10 Hz up to 100 Hz frame rate.

Fig. 5.

(a) is an SLO image average of 10 frames at the nerve fiber layer, (b) shows the en-face OCT image of the nerve fiber layer. In (c) the photoreceptor layer is clearly visible, whereas in the OCT en-face image (d) only microvasculature can be seen. (e) is the SLO image of the photoreceptors and (f) the OCT en-face image. (g) is a single B-scan acquired close to the fovea, the color bars give the different axial areas of the OCT en-face images. The white scale bar indicates 200 µm.

Having access to the complex valued OCT image information enables numerical wavefront manipulation. As outlined in 2, we employ the split aperture method to determine the wavefront error and correct for it by numerical phase conjugation. Figure 6(a) shows the holographic SLO image from the photoreceptor layer with present defocus and higher order aberrations. In the corresponding filtered OCT en-face image barely any photoreceptor structures are recognized (Fig. 6(b)). After digital adaptive optics using 5x5 sub-apertures resulting in 24 calculated Zernike values, the contrast and visibility of photoreceptors can be recovered (Fig. 6(c)). This becomes also evident from the visibility of Yellot’s rings in the respective Fourier planes (Fig. 6(d), 6(e), and 6(f)). In Fig. 6(d) the shifted interference terms are visible due to the off-axis reference arm configuration. The used correction phase map is displayed aside Fig. 6(c), together with the corresponding Zernike coefficients. As can be seen the major aberrations are defocus and astigmatism, with a RMS value for the correction phase of 0.36 µm. Note that this is 6 times higher than the Maréchal criterion for diffraction limited performance.

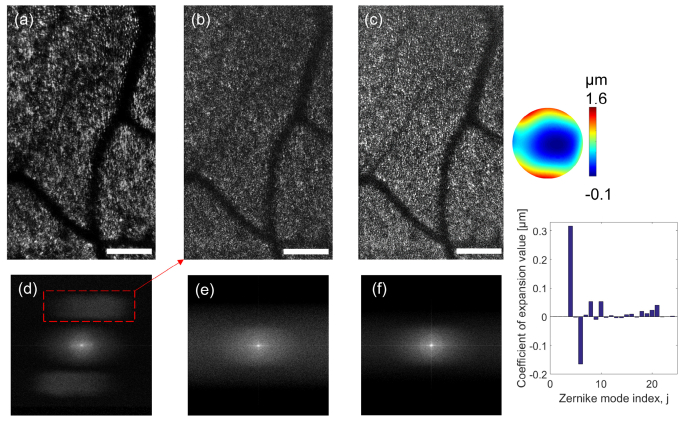
Fig. 6.

(a), shows an aberrated image of the photoreceptor acquired 7° from the fovea, (a) is the original en-face image average over 5 frames (b) the OCT en-face image over the same frames and (c) the corrected images after DAO. (d, e, f) show the respective Fourier planes with Yellot’s rings well visible in (f). On the right side is the correction phase map and the corresponding Zernike coefficient plot of the phase map. The white scale bar indicates 200 µm.

The difference between confocal and coherence gating becomes even better visible in the following results. In Fig. 7, the focus is set close to the photoreceptor layer. DAO allows then bringing the nerve fiber structure originally outside the confocal range again into focus. Figure 7(a) is the original SLO image where hardly any details from the nerve fiber layer are visible. In Fig. 7(b) the OCT en-face image is shown with the coherence gate set to the nerve fiber layer but outside the confocal range. In Fig. 7(c) the DAO image of the never fibers is displayed, retrieving the fiber structure, similar to nerve fibers shown by Barry et al. [42].

Fig. 7.

(a) the original image shows that the focus was set at the photoreceptor layer, (b) is the OCT en-face image with the coherence gate at the nerve fiber layer. (c) is the refocused image of the nerve fiber layer. The white scale bar indicates 200 µm.

All images in the section above were acquired with 10 kHz line rate. In order to test the system for high speed, the frame rate of the sensor was set to 100 kHz line rate. The high speed allows for en-face image rates of 100 Hz. Figure 8(a) shows an average of 20 SLO frames at the photoreceptor layer, with (b) the corresponding en-face OCT image averaged over the same number of frames. Figure 8(c) shows the nerve fiber layer and (d) the corresponding en-face OCT image. Visualization 1 ^{(4.6MB, gif)} shows even with 100 Hz en-face rate axial motion brings different depth structures into the small axial coherence gate. Still the high frame rate enables to select retrospectively frames taken at the same axial position. Averaging over those frames enhances the contrast and image SNR. Figure 8(e) and 8(f) are OCT en-face images from a sequence of 100 measurements. Each image is obtained by averaging over 20 en-face frames after retrospective selection. The visualization displays the pulsatile axial motion due to the heart beat. Furthermore the fast frame rate allows to determine the blood flow direction (red arrows in Fig. 8(e)), as the erythrocyte movement can be seen (see Visualization 1 ^{(4.6MB, gif)} ).

Fig. 8.

Acquisition with 100 kHz line rate and 100 Hz frame rate, (a, c) being the original images and (b, d) the OCT en-face images, either focused on the photoreceptor layer (b) or the nerve fiber layer (d). (e, f) are OCT en-face images extracted from a time series (Visualization 1 ^{(4.6MB, gif)} ). The white scale bar indicates 200 µm.

3.3 Line field en-face Doppler OCT

Having the complex data of the structures of interest acquired at fast line rates, enables for en-face DOCT flow calculations within retinal blood vessels. This is in fact hard to realize with full field configurations due to the in general lower frame rates of 2D sensors [32]. In case of 10 kHz line rate the maximum axial velocity that can be unambiguously determined is ± 1.6 mm/s with n = 1.34. In a first step we determined the phase noise of the system. With $\Delta {\phi }_{noise}$ = 0.042 rad as measured from a glass surface reflex we obtain a minimal detectable axial velocity of $v_{min}$ = 56 µm/s. Figure 9 shows the differential phase shift due to blood movement along the axial dimension. Figure 9(a) is the OCT intensity image; in (b) the OCT image is overlaid with a color-coded axial velocity direction image of the Doppler flow, with red being positive flow and green negative flow velocity with respect to the detection direction. The direction map shows well the axial tortuosity of the vessel. Bulk phase correction is performed before calculating the difference phase as described in section 2. Figure 9(c) is the averaged phase difference over 20 frames. Figure 9(d) shows the OCT intensity image of micro capillaries; Fig. 9(e) is again the DOCT image with color coded velocity direction (red positive and green negative Doppler phase shift) to show the axial vessel tortuosity. Figure 9(f) is the quantitative color DOCT map, showing velocity values according to the color bars to the right. Note, that due to the low phase noise axial velocities within micro capillaries, which are around 10 µm in diameter are quantifiable in vivo.

Fig. 9.

Shows an en-face Doppler calculation of the vascular flow. (a) is the OCT image with a red green map marking positive or negative flow direction in (b). (c) is the averaged Doppler shift over 20 frames. (d) is the OCT image of the microvasculature, (e) the red green map of either positive or negative flow direction and (f) the averaged Doppler shift with the velocity according to the color bar. The white scale bar indicated 200 µm.

4. Discussion and conclusion

We introduce line field en-face OCT system in a holographic off-axis configuration with high frame rates, which enables DAO based correction in post-processing, as well as the realization of DOCT. Although the sensitivity of the system itself is rather low (86 dB at 10 kHz line rate), as it is a time domain OCT system, we can still clearly visualize relevant retinal structures such as nerve fibers, micro capillaries or photoreceptors. The high en-face frame rates guarantee phase correlation across the en-face plane, which is essential for DAO. The system itself is flexible to be used for en-face recording or for single B-scan recording. Still a challenge is the rather short coherence length of 4.5 µm and therefore a strong axial movement dependency of the system. This becomes particularly critical for recording full volumes. Also, in combination with the natural curvature of the retina it is challenging to obtain large field of views over single retinal layers. We compensate this effect by averaging of several frames recorded over time, which compresses the information from different layers into a single en-face view. For faster frame rate gated frame visualization as demonstrated in Fig. 8 also helps to keep a defined axial position over a longer period of time until general axial drifts occur. In particular we are able to enhance image contrast and SNR by retrospective selection of en-face frames with the same morphologic details and averaging. Overall, the system is best suited for en-face OCT. A solution for stable axial positioning and 3D imaging would be axial tracking as shown by Pircher et al [43]. Another solution is to use a source with a smaller optical bandwidth resulting in a longer axial coherence window. This would however degrade the axial resolution performance of the OCT tomogram. TD OCT has been shown in combination with dynamic focusing [41] where the coherence gate has been adjusted to the actual confocal gate. Digital refocusing alleviates the need of axially aligning the confocal and coherence gate. Although, strong axial displacement will cause degradation of SNR. The dynamic range of digital wavefront sensing has been compared to a Shack-Hartmann sensor by Kumar et al. [39] and the limitations of digital defocus correction have been studied by Ginner et al. [6]. It has been shown that due to the fact that LFOCT has only half of the confocal gating, still light with information from sample depths outside the confocal range is collected. Thus efficient correction across the full retina can be achieved.

Clearly, digital aberration correction will only correct aberrations based on the backscattered light. Hardware based adaptive optics on the other hand employs wavefront shaping devices, which ensure already in the illumination direction a diffraction limited spot size. This impacts on the SNR of the AO corrected system, which in theory could be higher, that that of the digital correction. Still, hardware based AO involves several additional components such as the wavefront sensor, a deformable mirror, or telescope systems that themselves introduce losses which need to be taken into account for a fair comparison. Combining both, wavefront sensor less hardware aberration correction to low orders with digital correction might however be an optimal solution for high SNR imaging performance.

With en-face line field DOCT we extract quantitative values for the axial blood velocity. For the calculation of the actual blood flow the Doppler angle of the imaged vessels needs to be known. Natural candidates of Doppler independent flow retrieval compatible with line field illumination is en-face flow calculation [44,45] or bidirectional DOCT [46–49]. Angle-independent en-face DOCT extracts the flow from cross sectional images in the en-face plane. Those are however best accessible in the region of the optic nerve head with larger FOV than currently realized. With respect to the axial bulk motion correction: the compensation becomes inaccurate in situations where only weak bulk structure signals are present across the thin en-face slice. This is less critical for standard Fourier domain OCT, where the full 3D volume information is available. Especially for micro capillaries present in the weakly scattering inner nuclear layer the exact velocity calculation becomes difficult as bulk motion can hardly be corrected for. Despite those challenges, the results are promising and are to the best of our knowledge the first demonstration of in-vivo en-face Doppler flow measurements within the human retina using an en-face OCT system. Especially the fast en-face rates could potentially overcome the timing problems related with the en-face DOCT quantification, where originally full volumes had to be recorded or gated reconstruction was needed [44,45].

Funding

Carl Zeiss Meditec AG; Exalos AG; Austrian Federal Ministry of Science, Research and Economy.

Disclosures

The authors declare that there are no conflicts of interest related to this article.