Optical property uncertainty estimates for spatial frequency domain imaging

Abstract

Spatial frequency domain imaging (SFDI) is a wide-field diffuse optical imaging modality that has attracted considerable interest in recent years. Typically, diffuse reflectance measurements of spatially modulated light are used to quantify the optical absorption and reduced scattering coefficients of tissue, and with these, chromophore concentrations are extracted. However, uncertainties in estimated absorption and reduced scattering coefficients are rarely reported, and we know of no method capable of providing these when look-up table (LUT) algorithms are used to recover the optical properties. We present a method to generate optical property uncertainty estimates from knowledge of diffuse reflectance measurement errors. By employing the Cramér-Rao bound, we can quickly and efficiently explore theoretical SFDI performance as a function of spatial frequencies and sample optical properties, allowing us to optimize spatial frequency selection for a given application. In practice, we can also obtain useful uncertainty estimates for optical properties recovered with a two-frequency LUT algorithm, as we demonstrate with tissue-simulating phantom and in vivo experiments. Finally, we illustrate how absorption coefficient uncertainties can be propagated forward to yield uncertainties for chromophore concentrations, which could significantly impact the interpretation of experimental results.

1. Introduction

Spatial frequency domain imaging (SFDI) is a wide-field, noncontact diffuse optical imaging technique that has attracted considerable interest for a variety of applications. In clinical settings, it has been used to evaluate skin and breast lesions, while in mouse models, it has been employed to monitor the response to chemotherapy regimens, drug delivery to the brain, and the progression of Alzheimer’s disease [1–8]. Typically, diffuse reflectance measurements of spatially modulated light are used to quantify the optical absorption and reduced scattering coefficients (µ_a and ${\mu }_s^{\prime }$) of tissue, and with these, chromophore concentrations of interest are extracted (e.g., hemoglobin). However, uncertainties in estimated absorption and reduced scattering coefficients (${\sigma }_{{\mu }_a}$ and ${\sigma }_{{\mu }_s^{\prime }}$) are rarely reported, and we know of no method capable of providing such uncertainties when look-up table (LUT) inversion algorithms are used to recover the optical properties. Quantifying these uncertainties would have several important benefits. For example, they could be propagated forward to yield uncertainties in estimated chromophore concentrations, which could significantly affect the interpretation of experimental results. They could also be employed to help guide the selection of spatial frequencies used for SFDI measurements, given the requirements of the specific application.

In the diffuse optics community, theoretical performance prediction for system design or optimization is usually accomplished with Monte Carlo simulation [6, 9, 10] or with singular value decomposition (SVD) [11–14]. The former can be very time- and resource-intensive, and the results are valid only for the particular inversion algorithm simulated. Methods that rely on SVD avoid these difficulties, as they require only the sensitivity matrix of the forward problem. While evaluating the singular value spectrum or condition number of the sensitivity matrix is conceptually straightforward, this has a number of limitations. It ignores the information contained in the singular vectors of the sensitivity matrix, which can lead to errors in performance predictions [15, 16]. It also cannot incorporate the noise of the input data into the analysis. Finally, it can only provide qualitative estimates of performance (i.e., this system configuration is better than the others), not quantitative ones. In recent years, other alternatives to SVD have been proposed [17, 18], but to our knowledge, none of these are capable of providing quantitative estimates of performance.

In this work, we make three novel contributions. First, we show how knowledge of the precision of diffuse reflectance measurements from an SFDI instrument (i.e., diffuse reflectance uncertainty estimates, ${\sigma }_{R_d}$) can be quickly and efficiently transformed to yield quantitative estimates of optical property uncertainties using the Cramér-Rao bound (CRB), a concept from the field of statistical signal processing. The CRB shares many of the advantages of SVD-based methods, but it can sometimes be difficult to compute. We leverage prior work in statistical signal processing for Gaussian data models and provide an expression for the CRB that applies to SFDI with an arbitrary number of spatial frequencies. We use this to evaluate trade-offs in theoretical system performance as a function of spatial frequency combinations and sample optical properties. Second, we demonstrate that a CRB-dervied metric can provide optical property uncertainty estimates when a two-frequency LUT inversion algorithm is used to recover µ_a and ${\mu }_s^{\prime }$. We validate this with both simulated and phantom (experimental) data. We make use of this metric and LUT algorithm for our third contribution: an end-to-end example using in vivo data that culminates in uncertainties for chromophore concentration estimates.

The remainder of this paper is organized as follows. In Sec. 2, we describe our procedure for generating a diffuse reflectance error model by characterizing the precision of our SFDI instrument and present those results therein. Sections 3–5 contain the methods and results for the three contributions described above. We discuss and summarize our results in Sec. 6, and we present conclusions and a description of future work in Sec. 7. Custom Matlab (The MathWorks, Inc., Natick, MA) code developed for Sec. 3 can be downloaded from OSA’s figshare repository [19].

2. Diffuse reflectance error model

2.1. Methods

In order to estimate uncertainties in recovered optical property estimates, we need to know the uncertainties associated with the diffuse reflectance measurements. We assumed that our diffuse reflectance measurements were unbiased (i.e., systematic errors had been eliminated) and could therefore be modeled as

$$m\left(\mathit{\theta },fx,\lambda \right)=R_d\left(\mathit{\theta },fx\right)+n\left(\mathit{\theta },fx,\lambda \right),$$ (1)

where $\mathit{\theta }=\left[{\mu }_a,{\mu }_s^{\prime }\right]$ represents the sample optical properties, fx denotes spatial frequency, λ is the spectral wavelength, m is the measured diffuse reflectance, R_d is the true value, and n is zero-mean Gaussian noise with standard deviation ${\sigma }_{R_d}\left(\mathit{\theta },fx,\lambda \right)$. (Our convention in this work will be to write scalar quantities in italics, and vector and matrix quantities in lower- and uppercase bold font, respectively.) With this data model, we allow for the possibility that ${\sigma }_{R_d}$ might depend on sample optical properties, spatial frequency, and/or spectral wavelength. The uncertainty in measured diffuse reflectance can be completely characterized by determining the precision of the diffuse reflectance measurements, which will depend, among other things, on the particular instrument employed and choice of data acquisition and processing parameters.

In Table 1 , we summarize the relevant properties of our SFDI instrument and data acquisition and processing parameters. A detailed description of spatial frequency domain instrumentation and image formation can be found in [20, 21]. Briefly, the instrument projects spatially modulated 1-D sinusoidal patterns of light, of varying spectral wavelengths and spatial frequencies, onto the sample, and the resulting diffuse reflectance at each location is measured by a CCD camera. The data is demodulated with a conventional communications algorithm and converted into calibrated reflectance using a calibration phantom with known optical properties. In our case, the measured reflectance of the calibration phantom was compared to that predicted by a Monte Carlo simulation [22]. This yields calibrated diffuse reflectance values over the surface of the sample (i.e., per pixel).

Table 1.

SFDI instrument, data acquisition, and data processing parameters.

	Instrument
Model	OxImager RS (Modulated Imaging, Irvine, CA)
Source	LEDs at 9 wavelengths (470–970 nm) + white light
Detector	CCD camera: 12-bit, 1.4 MP (1392 × 1040 pixels)
Field of view	20 × 15 cm2 (maximum)
Pixel size (at sample)	0.14 × 0.14 mm2
	Data Acquisition Parameters
Spectral wavelengths	659, 691, 731, 851 nm (4 total)
Spatial frequencies	0, 0.025, 0.05, 0.075, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5 mm−1 (13 total)
No. of measurements	10 (per wavelength per frequency)
	Data Processing Parameters
2 × 2 binning	Sum data over 2 × 2 groups of pixels

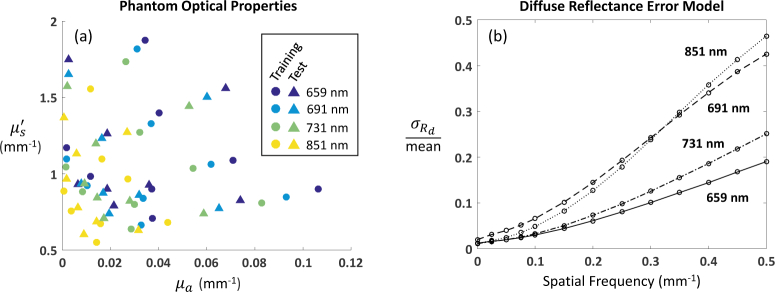
We characterized the precision of the instrument under these operating conditions by measuring 16 tissue-simulating phantoms with optical properties shown in Fig. 1(a). The optical properties are also listed in tabular form in Appendix A. The phantoms were homogeneous silicone blocks with Nigrosin and TiO₂ added to control µ_a and ${\mu }_s^{\prime }$, respectively, and they ranged in size from 13 × 20 × 3 cm³ to 7 × 11 × 3 cm³. Their optical properties spanned a range of values representative of typical applications in our lab, e.g., human breast and small animal (mouse) imaging. We made 10 measurements of each phantom at each wavelength and spatial frequency. The data was downsampled by a factor of two (2 × 2 binning) to increase the signal-to-noise ratio (SNR). After converting to calibrated diffuse reflectance, a circular region of interest (ROI) with a ~40 mm diameter was selected, and the mean and standard deviation $({\sigma }_{R_d})$ of pixel values in this region for all 10 repeat measurements was computed (∼2 × 10⁵ pixels per phantom). The phantoms were divided into two groups: 8 in the training set, and 8 in the test set, as shown in Fig. 1(a) , such that the training set spanned the range of optical properties of interest. The diffuse reflectance error model was constructed by averaging the ratio of the standard deviation to the mean value (at each wavelength and spatial frequency) of the phantoms in the training set. The data in the test set was used to validate the model (see Sec. 4 for results).

Fig. 1.

(a) Phantom optical properties for training (circles) and test (traingles) sets. (b) Diffuse reflectance error model. Data at 13 spatial frequencies and 4 spectral wavelengths.

2.2. Results

The diffuse reflectance error model is shown in Fig. 1(b). We note that the noise as a function of spatial frequency was rather flat, while the mean diffuse reflectance decreased with increasing spatial frequency, as expected. This results in the increasing trends of ${\sigma }_{R_d}/\mathit{\text{mean}}$ for all four spectral wavelengths, i.e., the SNR worsens with increasing spatial frequency. The differences due to spectral wavelengths are likely caused by the particular properties of the LEDs in our instrument.

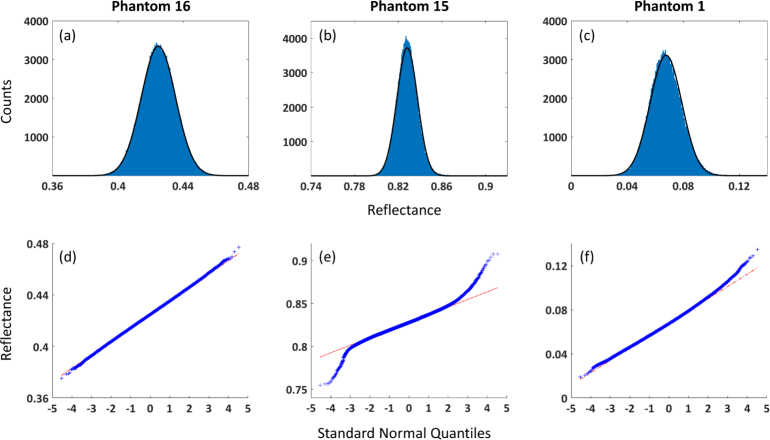
We conducted additional analyses to determine if the Gaussian noise assumption specified in Eq. (1) was appropriate for our diffuse reflectance measurements. In Fig. 2 , we display histograms and quantile-quantile plots of calibrated diffuse reflectance from the ROIs of three different phantoms. The data in Figs. 2(a) and 2(d) shows excellent agreement with the Gaussian noise assumption. However, some data does deviate from the Gaussian model, exhibiting some kurtosis (Figs. 2(b) and 2(e)) and skewness (Figs. 2(c) and 2(f)). Nevertheless, for the majority of the data, excess kurtosis and skewness are within ±0.5. (Both values are 0 for the normal distribution.) So overall it appears that our diffuse reflectance data is well described by the Gaussian noise model.

Fig. 2.

(a)–(c) Histogram and (d)–(f) quantile-quantile plots for ROIs of 3 phantoms (1 per column). See Appendix A for phantom optical properties. Data shown is for the following spectral wavelengths and spatial frequencies: Phantom 16: 851 nm, 0.05 mm⁻¹; Phantom 15: 659 nm, 0 mm⁻¹; Phantom 1: 691 nm, 0.2 mm⁻¹. Black trace on histograms represents Gaussian distribution with mean and standard deviation calculated from data. Red line on quantile-quantile plots represents response of data with Gaussian distribution.

3. Optical property uncertainty estimates using the Cramér-Rao bound

To transform diffuse reflectance precision estimates $({\sigma }_{R_d})$ into precision estimates for the absorption and reduced scattering coefficients (${\sigma }_{{\mu }_a}$ and ${\sigma }_{{\mu }_s^{\prime }}$), we employ the CRB [23]. The CRB considered here is a lower bound that defines the best theoretical precision (i.e., lowest variance) of any unbiased estimator for a given data model. We distinguish here between the concept of a “data model” (e.g., how optical properties determine measured R_d) and an “estimator” or “algorithm” (e.g., how measured R_d can be used to estimate optical properties). Loosely speaking, the data model defines the forward problem, while the estimator or algorithm solves the inverse problem. The CRB is often used in the statistical signal processing community, especially in the sonar and radar signal processing communities, to perform feasibility studies and system design. The basic idea is that the curvature of the log-likelihood function of the data model determines the precision with which an unknown (e.g., µ_a, ${\mu }_s^{\prime }$) may be estimated. The more sharply peaked the log-likelihood function is in the neighborhood of the unknown, the more precisely the value of the unknown may be determined. The CRB provides a measure of this curvature. For a vector of unknowns, it is computed by first calculating the Fisher information matrix, which requires second derivatives and first derivative cross products of the log-likelihood function with respect to each unknown, and then taking its inverse.

Because it uses information only about the data model, the CRB is independent of the particular algorithm employed to estimate the unknown(s). It is therefore ideally suited to explore trade-offs in performance as a function of the data, which, for our purposes, includes data with different spatial frequency combinations and sample optical properties. We note that the CRB has an additional advantage over SVD-based methods: it includes the impact of the input data noise.

3.1. Methods

3.1.1. Cramér-Rao bound for spatial frequency domain imaging

Let us organize our data, which consists of calibrated diffuse reflectance measurements for a given pixel (described by Eq. (1)) at K spatial frequencies, where K ≥ 2, into a column vector:

$$\mathbf{m}\left(\mathit{\theta },\lambda \right)=\left[\begin{array}{c}m\left(\mathit{\theta },f{x}_1,\lambda \right)\\ m\left(\mathit{\theta },f{x}_2,\lambda \right)\\ ⋮\\ m\left(\mathit{\theta },f{x}_K,\lambda \right)\end{array}\right],$$ (2)

where fx_k is the kth spatial frequency. We assume that measurements at different spatial frequencies are statistically independent, so the data follows a multivariate normal distribution, with mean

$$\mathbf{r}\left(\mathit{\theta }\right)=\left[\begin{array}{c}{R}_d\left(\mathit{\theta },f{x}_1\right)\\ R_d\left(\mathit{\theta },f{x}_2\right)\\ ⋮\\ R_d\left(\mathit{\theta },f{x}_K\right)\end{array}\right],$$ (3)

and diagonal covariance matrix

$$\begin{array}{l}{\mathbf{C}}_{R_d}\left(\mathit{\theta },\lambda \right)=\left[\begin{array}{cccc}{\sigma }_{R_d}^2\left(\mathit{\theta },f{x}_1,\lambda \right)& & & \\ & {\sigma }_{R_d}^2\left(\mathit{\theta },f{x}_2,\lambda \right)& & 0\\ 0& & \ddots & \\ & & & {\sigma }_{R_d}^2\left(\mathit{\theta },f{x}_K,\lambda \right)\end{array}\right]\\ =\left[\begin{array}{cccc}{c}^2\left(f{x}_1,\lambda \right)R_d^2\left(\mathit{\theta },f{x}_1\right)& & & \\ & c^2\left(f{x}_2,\lambda \right)R_d^2\left(\mathit{\theta },f{x}_2\right)& & 0\\ 0& & \ddots & \\ & & & c^2\left(f{x}_K,\lambda \right)R_d^2\left(\mathit{\theta },f{x}_K\right)\end{array}\right],\end{array}$$ (4)

where c(fx_k, λ) represents the ratio of ${\sigma }_{R_d}$ to R_d from the diffuse reflectance error model (Sec. 2) for the kth spatial frequency and spectral wavelength of measurement. For multivariate Gaussian data, the Fisher information matrix is given by

$${\left[\mathbf{F}\left(\mathit{\theta }\right)\right]}_{ij}=\frac{\partial {\mathbf{r}}^T\left(\mathit{\theta }\right)}{\partial {\theta }_i}{\mathbf{C}}_{R_d}^{-1}\left(\mathit{\theta }\right)\frac{\partial \mathbf{r}\left(\mathit{\theta }\right)}{\partial {\theta }_j}+\frac{1}{2}\text{tr}\left({\mathbf{C}}_{R_d}^{-1}\left(\mathit{\theta }\right)\frac{\partial {\mathbf{C}}_{R_d}\left(\mathit{\theta }\right)}{\partial {\theta }_i}{\mathbf{C}}_{R_d}^{-1}\left(\mathit{\theta }\right)\frac{\partial {\mathbf{C}}_{R_d}\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right),$$ (5)

where [F(θ)]_ij denotes the (i, j)th element of the Fisher information matrix, with i and j ranging over the number of elements in θ; (∗)^T signifies the transpose; and tr (∗) is the trace of the matrix (i.e., the sum of its diagonal elements) [23]. We have suppressed the dependency of ${\mathbf{C}}_{R_d}$ on λ in Eq. (5) for clarity. As we seek to estimate both µ_a and ${\mu }_s^{\prime }$, i and j will take on values of 1 and 2, so F(θ) will be a 2 × 2 matrix.

We computed the vectors and matrices of derivatives,

$$\frac{\partial \mathbf{r}\left(\mathit{\theta }\right)}{\partial {\theta }_1}=\frac{\partial \mathbf{r}\left(\mathit{\theta }\right)}{\partial {\mu }_a},$$ (6a)

$$\frac{\partial \mathbf{r}\left(\mathit{\theta }\right)}{\partial {\theta }_2}=\frac{\partial \mathbf{r}\left(\mathit{\theta }\right)}{\partial {\mu }_s^{\prime }},$$ (6b)

$$\frac{\partial {\mathbf{C}}_{R_d}\left(\mathit{\theta }\right)}{\partial {\theta }_1}=\frac{\partial {\mathbf{C}}_{R_d}\left(\mathit{\theta }\right)}{\partial {\mu }_a},$$ (6c)

$$\frac{\partial {\mathbf{C}}_{R_d}\left(\mathit{\theta }\right)}{\partial {\theta }_2}=\frac{\partial {\mathbf{C}}_{R_d}\left(\mathit{\theta }\right)}{\partial {\mu }_s^{\prime }},$$ (6d)

as follows. Consider a diffuse reflectance cube, where the x and y dimensions correspond to µ_a and ${\mu }_s^{\prime }$, respectively, and the z dimension corresponds to fx; i.e., each z “slice” represents R_d as a function of optical properties for a given spatial frequency. We discuss the generation of such a cube in Sec. 3.1.2. It follows that the quantities in Eqs. (6a)–(6d) can be computed by numerically differentiating each slice of the cube in the x and y directions, respectively, and evaluating the derivative at θ:

$${\left[\frac{\partial \mathbf{r}\left(\mathit{\theta }\right)}{\partial {\mu }_a}\right]}_k={\frac{\partial R_d\left({\mu }_a,{\mu }_s^{\prime },f{x}_k\right)}{\partial {\mu }_a}|}_{\mathit{\theta }},$$ (7a)

$${\left[\frac{\partial \mathbf{r}\left(\mathit{\theta }\right)}{\partial {\mu }_s^{\prime }}\right]}_k={\frac{\partial R_d\left({\mu }_a,{\mu }_s^{\prime },f{x}_k\right)}{\partial {\mu }_s^{\prime }}|}_{\mathit{\theta }},$$ (7b)

$${\left[\frac{\partial {\mathbf{C}}_{R_d}\left(\mathit{\theta }\right)}{\partial {\mu }_a}\right]}_{kk}={2c^2\left(f{x}_k,\lambda \right)R_d\left(\mathit{\theta },f{x}_k\right)\frac{\partial R_d\left({\mu }_a,{\mu }_s^{\prime },f{x}_k\right)}{\partial {\mu }_a}|}_{\mathit{\theta }},$$ (7c)

$${\left[\frac{\partial {\mathbf{C}}_{R_d}\left(\mathit{\theta }\right)}{\partial {\mu }_s^{\prime }}\right]}_{kk}={2c^2\left(f{x}_k,\lambda \right)R_d\left(\mathit{\theta },f{x}_k\right)\frac{\partial R_d\left({\mu }_a,{\mu }_s^{\prime },f{x}_k\right)}{\partial {\mu }_s^{\prime }}|}_{\mathit{\theta }},$$ (7d)

where the subscripts k and kk denote the kth and (k, k)th elements of the vectors and matrices, respectively. The degree of error due to numerical differentiation can be controlled by the algorithm employed and the resolution in µ_a and ${\mu }_s^{\prime }$. We used the central difference method implemented in Matlab’s “gradient” function and a resolution of Δµ_a = 1 × 10⁻⁴ mm⁻¹ and $\mathrm{\Delta }{\mu }_s^{\prime }=1\times {10}^{-3}{\text{mm}}^{-1}$.

The CRB for θ is obtained by taking the inverse of F(θ):

$$\mathbf{\text{CRB}}\left(\mathit{\theta }\right)=\left[\begin{array}{cc}{\sigma }_{{\mu }_a}^2& {\sigma }_{{\mu }_a,{\mu }_s^{\prime }}^2\\ {\sigma }_{{\mu }_a,{\mu }_s^{\prime }}^2& {\sigma }_{{\mu }_s^{\prime }}^2\end{array}\right]=\mathbf{F}{\left(\mathit{\theta }\right)}^{-1}.$$ (8)

In other words, CRB (θ) lower-bounds the covariance matrix of the joint estimate of the sample’s optical properties at a given pixel. We note that while this technique can provide uncertainties at each pixel of an SFDI image, as currently implemented it does not account for the likely image degradation that occurs near the edges of the field of view, since the same noise model is used for the entire image.

We can define a second quantity that employs only the first term of the Fisher information matrix:

$${\left[\tilde{\mathbf{F}}\left(\mathit{\theta }\right)\right]}_{ij}=\frac{\partial {\mathbf{r}}^T\left(\mathit{\theta }\right)}{\partial {\theta }_i}{\mathbf{C}}_{R_d}^{-1}\left(\mathit{\theta }\right)\frac{\partial \mathbf{r}\left(\mathit{\theta }\right)}{\partial {\theta }_j},$$ (9)

which leads to

$$\mathbf{r}\mathbf{\text{CRB}}\left(\mathit{\theta }\right)=\tilde{\mathbf{F}}{\left(\mathit{\theta }\right)}^{-1}.$$ (10)

We call this the “reduced CRB” (rCRB), and while this is not a bound per se for our problem, it is the CRB proper for the case where ${\mathbf{C}}_{R_d}$ is not a function of the sample optical properties. We can gain some insight into the relationship between the rCRB and CRB by rewriting Eq. (5) as

$${\left[\mathbf{F}\left(\mathit{\theta }\right)\right]}_{ij}={\displaystyle \sum _{k=1}^K\left(SN{R}_k^2\frac{1}{{\left[\mathbf{r}\left(\mathit{\theta }\right)\right]}_k^2}{\left[\frac{\partial \mathbf{r}\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right]}_k{\left[\frac{\partial \mathbf{r}\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right]}_k+2\frac{1}{{\left[\mathbf{r}\left(\mathit{\theta }\right)\right]}_k^2}{\left[\frac{\partial \mathbf{r}\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right]}_k{\left[\frac{\partial \mathbf{r}\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right]}_k\right)},$$ (11)

where $SN{R}_k^2=1/c^2\left(f{x}_k,\lambda \right)$. This expression was obtained by substituting Eqs. (4), Eq. (6), and (7) into Eq. (5). It reveals that when $SN{R}_k^2\gg 2$, the difference between the rCRB (computed with the first term) and CRB (computed with both terms) will be very small, and hence, for most cases of practical interest to us, the CRB is well approximated by the simpler expression of the rCRB. We make use of the rCRB in Secs. 4 and 5. Custom Matlab code that computes the CRB and rCRB is available in Code 1, [19].

3.1.2. Diffuse reflectance cube

We computed the diffuse reflectance cube in two different ways. Initially, we used a Monte Carlo simulation of diffuse reflectance for a semi-infinite homogeneous medium that was subsequently scaled for different values of µ_a and ${\mu }_s^{\prime }$, as described in [22]. We then took the Hankel transform to obtain results in the spatial frequency domain. However, we noticed some artifacts when computing the derivatives (Eqs. (7a)–(7d)) at spatial frequencies higher than 0.4 mm⁻¹. These are likely caused by the lower SNR at higher spatial frequencies coupled with the fact that differentiation amplifies noise. So we created a second cube employing the solution for the diffusion equation [21], and we used it for the results presented in Figs. 3 , 4 , and 6, which involved frequencies ≥ 0.4mm⁻¹.

Fig. 3.

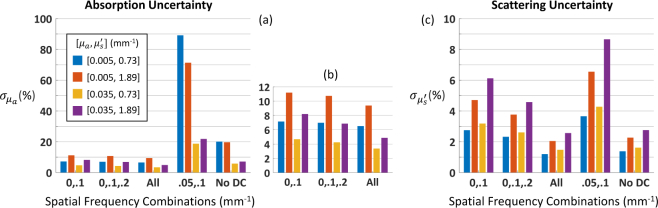
Cramér-Rao bounds for (a) absorption and (b) reduced scattering coefficient uncertainties for four sets of optical properties. Optical property recovery assumes data at DC (0 mm⁻¹) and one other spatial frequency. CRBs expressed as percentage of true optical properties.

Fig. 4.

Cramér-Rao bounds for (a) absorption and (c) reduced scattering coefficient uncertainties for four sets of optical properties; panel (b) zooms in on panel (a). “All” = 13 spatial frequencies (see Table 1); “No DC” = all spatial frequencies except DC (12 total). CRBs expressed as percentage of true optical properties.

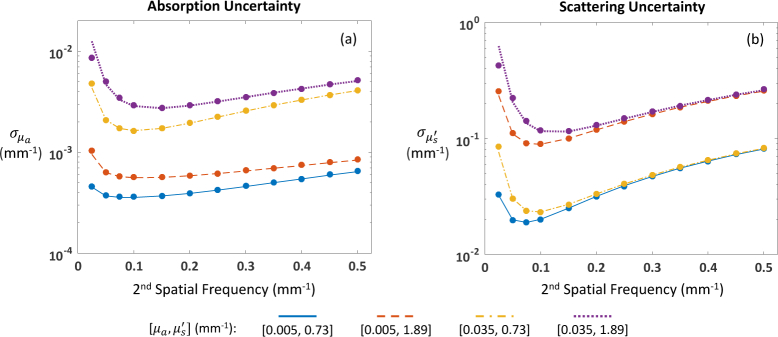
Fig. 6.

Reduced Cramér-Rao bounds (lines) and LUT algorithm uncertainties (symbols) for four sets of optical properties at 659 nm: (a) absorption and (b) reduced scattering coefficient. Optical property recovery assumes data at DC (0 mm⁻¹) and one other spatial frequency.

For SFDI, the diffusion equation approximation is considered valid when fx ≪ µ_tr, where ${\mu }_{tr}={\mu }_a+{\mu }_s^{\prime }$. For two of the four pairs of optical properties considered in these figures, this approximation should start to break down at fx ~ 0.2 mm⁻¹ [21]. However, the differences between CRB results generated with the diffusion-based cube and the Monte Carlo-based one were less than 3% for all spatial frequencies below 0.4 mm⁻¹. This led us to believe that the diffusion-based cube was capable of adequately capturing the trends as a function of spatial frequency that we were looking to explore.

In addition to providing us with a convenient way of evaluating Eqs. (7a)–(7d), diffuse reflectance cubes can serve as the core of an LUT algorithm that relates values of R_d at two or more spatial frequencies to unique pairs of µ_a and ${\mu }_s^{\prime }$. We implemented our LUT algorithm with Matlab’s “griddata” function, which accepts as input a cube and measured R_d values and returns the best fit optical properties, where “best fit” is determined by linear interpolation of the values in the cube. Although it may seem that we are linking the CRB computation—said to be algorithm-independent earlier—with our optical property recovery algorithm by using the same cube in both, notice that the CRB is agnostic as to how the information in the cube is used by the algorithm. For example, an LUT algorithm could employ linear, nearest neighbor, or cubic interpolation, or perform polynomial fitting [24]. The cube could also be used by a maximum likelihood estimator to create a chi-squared surface that could be minimized in a number of different ways. All of these particulars can significantly affect algorithm performance, but none of them appear in the CRB calculation. Indeed, the cube is just a numerical model that captures how µ_a, ${\mu }_s^{\prime }$, and fx determine R_d, and it is not surprising that optical property recovery algorithms would make use of that information somehow.

3.2. Results

We used the CRB (Eq. (8)) to explore performance as a function of spatial frequency combinations and sample optical properties. We show results using the diffuse reflectance error model for 659 nm, but the other three wavelengths yielded very similar patterns. In Fig. 3, we address the question of which spatial frequency to pair with DC (0 mm⁻¹) for the determination of four sets of optical properties relevant to our mouse studies [6]. We plot the uncertainties in recovered µ_a and ${\mu }_s^{\prime }$ as a function of the spatial frequency combination used. The sweet spot near fx = [0, 0.1] mm⁻¹ is likely caused by the confluence of two opposing trends: (1) performance improves as the gap between the two frequencies increases (as discussed in [6]); and (2) performance worsens as the SNR decreases with increasing spatial frequency (see Fig. 1(b)). An interesting pattern that emerged is that ${\sigma }_{{\mu }_a}$ and ${\sigma }_{{\mu }_s^{\prime }}$ are consistently lower for the lower value of ${\mu }_s^{\prime }$, irrespective of absorption.

In Fig. 4, we explore the potential advantage of using more than two frequencies to recover the sample optical properties, as well as the impact of not including DC. With respect to absorption uncertainty (Figs. 4(a) and 4(b)), we see that a well chosen spatial frequency pair (e.g., [0, 0.1] mm⁻¹) performs almost as well as 3 or even 13 spatial frequencies. The diminishing returns of adding more spatial frequencies was noted in [25], albeit under rather different circumstances. We also see that not including DC significantly degrades the precision of the µ_a estimate, an effect that is especially pronounced for the lower value of µ_a. Since a low spatial frequency like DC is known to propagate more deeply into tissue [21], it is perhaps not surprising that it is needed to adequately sample the rarer absorption events that correspond to very low absorption coefficients. The impact on scattering uncertainty, however, is much less severe, as none of the errors exceed 9% (Fig. 4(c)). We see the same pattern here as in Fig. 3(b): ${\sigma }_{{\mu }_s^{\prime }}$ is consistently lower for the lower value of ${\mu }_s^{\prime }$, irrespective of absorption.

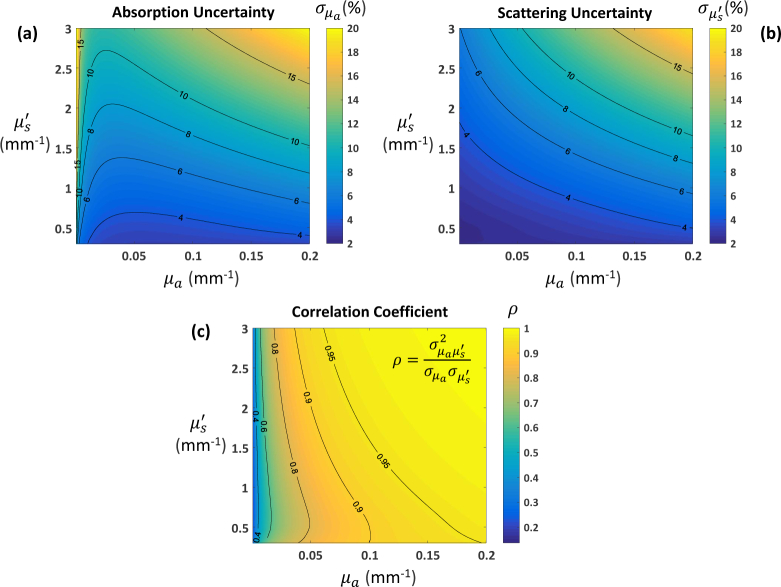
Finally, in Fig. 5 we consider the impact of sample optical properties on the precision of µ_a and ${\mu }_s^{\prime }$ estimates obtained using the spatial frequency pair [0, 0.1] mm⁻¹. Here we expand the range of optical properties considered well beyond that of Figs. 3 and 4. We see that while performance is reasonable for optical properties in the neighborhood of our previously considered set of four, higher variances are obtained for increasing values of µ_a and ${\mu }_s^{\prime }$ (Figs. 5(a) and 5(b)). The variances are not only larger in magnitude but also highly correlated (Fig. 5(c)). Thus the expected range of optical properties for a given application, along with desired precision, should inform the choice of spatial frequency combinations. These CRB “maps” are a quick and efficient way to explore this trade space. The maps in Fig. 5, which contain approximately 6 million combinations of µ_a and ${\mu }_s^{\prime }$, were generated in ~5 min on a desktop (Intel Core i7-6700 Processor, 16 GB RAM) using non-optimized Matlab code.

Fig. 5.

Cramér-Rao bounds as a function of optical properties for data at spatial frequencies [0, 0.1] mm⁻¹: (a) absorption and (b) reduced scattering coefficient uncertainties; (c) Pearson correlation coefficient. CRBs expressed as percentage of true optical properties.

4. Optical property uncertainty estimates for a two-frequency look-up table inversion algorithm

While the CRB has a number of advantages for feasibility studies and system design, there is no guarantee that the bound can be attained by a realizable estimator [23]. Under some circumstances, it is possible to prove that the CRB will be attained, at least asymptotically, as with maximum likelihood estimators [23]. But in general, there is no way to know if a particular algorithm’s performance can be described by this bound. In this section, we establish that the rCRB can be used to predict the performance of a two-frequency LUT inversion algorithm. This algorithm, which uses the Matlab function “griddata,” was described in Sec. 3.1.2. We characterized its performance with simulated diffuse reflectance data first, and then evaluated it with phantom data.

4.1. Methods

We created simulated diffuse reflectance data according to Eq. (1). The diffusion-based cube (Sec. 3.1.2) was used to define R_d, while the diffuse reflectance error model at 659 nm (Sec. 2) provided the components of ${\sigma }_{R_d}$. We generated 10⁴ samples for each of the optical property combinations shown in Fig. 3 at the 13 spatial frequencies listed in Table 1. These samples were fed to the LUT algorithm, using DC paired with one other spatial frequency at a time, and values for the mean and standard deviation of the recovered optical properties were computed. The diffusion-based cube was used to compute the CRB and rCRB (as described in Sec. 3.1).

We also tested the algorithm with calibrated diffuse reflectance data from the tissue-simulating phantoms described in Sec. 2. Since these are homogeneous phantoms, the optical properties should be the same over the surface of the sample, so estimates of optical property precision can be obtained by computing the standard deviation of recovered µ_a and ${\mu }_s^{\prime }$ values. We randomly selected 10⁴ samples from the ROI of each phantom and recovered the optical properties using two spatial frequency combinations: [0, 0.1] and [0.05, 0.1] mm⁻¹. We chose these two pairs based on earlier results that revealed them to be good ([0, 0.1]) and less ideal ([0.05, 0.1]) combinations for optical property recovery in the range spanned by our phantoms (e.g., see Fig. 4(a)). We used the Monte Carlo-based cube in the LUT algorithm and in the CRB and rCRB computations, as all frequencies considered are well below 4 mm⁻¹.

4.2. Results

While the CRB and rCRB computations yielded very similar values, we found that the rCRB was, on average, a better match for LUT algorithm performance than the CRB (results not shown). Hence, this became our method of choice when the task was to estimate LUT algorithm uncertainties, and we used this quantity in the performance comparisons described in this section. As the rCRB was derived from the CRB, which assumed an unbiased estimator, we first checked the LUT algorithm results for bias by comparing the means of the recovered optical properties to the true values used in the simulations. For the lowest spatial frequency pair ([0, 0.025] mm⁻¹), we found evidence of moderate bias, but for all other pairs, the average absolute deviation from the true values was quite small: 0.3% for µ_a and 0.2% for ${\mu }_s^{\prime }$. This pattern recurs in Figs. 6(a) and 6(b) , where we see excellent agreement between the rCRBs (lines) and the standard deviations of the recovered optical properties (symbols) for all but the lowest spatial frequency pair. Excluding this pair, the difference is ~0.1%, on average, for both ${\sigma }_{{\mu }_a}$ and ${\sigma }_{{\mu }_s^{\prime }}$.

We note that for spatial frequency combinations that are close together and have large CRB values (e.g., [0, 0.025] mm⁻¹), the LUT algorithm sometimes fails to produce a solution. This is because the inherent noise results in a value of diffuse reflectance that lies outside of the LUT. These cases bias the optical property estimates and produce values of ${\sigma }_{{\mu }_a}$ and ${\sigma }_{{\mu }_s^{\prime }}$ that do not match the rCRBs or CRBs.

In Table 2 , we summarize the results obtained with phantom data. We have excluded from our statistics 6 cases (out of 96 total) for which the LUT algorithm failed to work reliably. Recall that the phantom data was divided into two groups: the training set, which was used to create the diffuse reflectance error model, and the test set. We see no significant difference in performance between these two groups, which suggests that an error model can be successfully created by measuring a limited number of phantoms that span the optical properties of interest. In comparing the results at 659 nm for the spatial frequency pairs [0, 0.1] and [0.05, 0.1] mm⁻¹, we see that the mean absolute difference between LUT algorithm performance and the rCRB is slightly larger for the second pair, especially for ${\sigma }_{{\mu }_a}$. However, at roughly 2%, this value is still quite low and indicates good performance.

Table 2.

Optical property uncertainties for phantom data: mean absolute difference between predicted (rCRB) and measured (LUT algorithm), expressed as percentage of true optical properties. “All” refers to all four spectral wavelengths: 659, 691, 731, 851 nm.

λ (nm) / fx (mm−1)	Training Set		Test Set
	$\mathrm{\Delta }({\sigma }_{{\mu }_a})(\%)$	$\mathrm{\Delta }({\sigma }_{{\mu }_s^{\prime }})(\%)$	$\mathrm{\Delta }({\sigma }_{{\mu }_a})(\%)$	$\mathrm{\Delta }({\sigma }_{{\mu }_s^{\prime }})(\%)$
659 / [0, 0.1]	0.85	0.51	0.75	0.44
All / [0, 0.1]	1.01	0.78	1.11	0.74
659 / [0.05, 0.1]	2.14	0.81	2.16	0.57

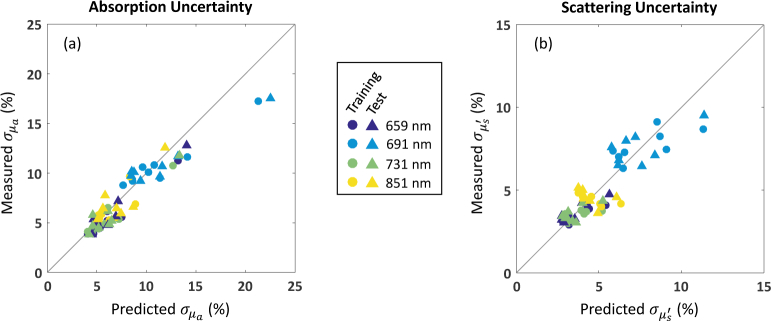
For a “good” spatial frequency pair like [0, 0.1] mm⁻¹, agreement between the rCRB and LUT algorithm performance is generally excellent. Averaged over all four spectral wavelengths, the mean absolute difference is ~ 1% for both ${\sigma }_{{\mu }_a}$ and ${\sigma }_{{\mu }_s^{\prime }}$. This is in spite of the fact that some phantom data does not satisfy the Gaussian noise assumption very well, as discussed in Sec. 2. In Fig. 7 , we display the individual data points summarized in the second line of the table. It appears that the rCRB is able to provide useful uncertainty estimates for our LUT algorithm.

Fig. 7.

Optical property uncertainties for phantom data: predicted (rCRB) versus measured (LUT algorithm), expressed as percentage of true optical properties. Recovery of optical properties is for data at [0, 0.1] mm⁻¹.

5. Uncertainties for chromophore concentration estimates

We have shown how optical property uncertainties can be obtained from diffuse reflectance uncertainties. Here we take it one step further and demonstrate, with an arterial cuff occlusion experiment, how uncertainties for chromophore concentration estimates can be obtained from absorption coefficient uncertainties.

5.1. Methods

5.1.1. Expression for chromophore concentration uncertainties

In near-infrared spectroscopy, absorption coefficients are usually related to chromophore concentrations via a linear model:

$${\mathit{\mu }}_{\mathbf{a}}=\mathbf{E}\mathit{\kappa }+\mathbf{n},$$ (12)

where µ_a = [µ_a(λ₁), µ_a(λ₂), … µ_a(λ_p)]^T is the vector of recovered absorption coefficients; E is the p × q matrix of extinction coefficients; κ = [O₂Hb, HHb, … κ_q]^T is the desired vector of chromophore concentrations; and n is a vector of independent noise with mean 0 and diagonal

$${\mathbf{C}}_{{\mu }_a}=\left[\begin{array}{cccc}{\sigma }_{{\mu }_a}^2\left({\lambda }_1\right)& & & \\ & {\sigma }_{{\mu }_a}^2\left({\lambda }_2\right)& & 0\\ 0& & \ddots & \\ & & & {\sigma }_{{\mu }_a}^2\left({\lambda }_p\right)\end{array}\right].$$ (13)

With knowledge of the elements of ${\mathbf{C}}_{{\mu }_a}$, which are given by CRB(θ) or rCRB(θ), we can compute the best linear unbiased estimate of the chromophore concentrations [23]:

$$\hat{\mathit{\kappa }}={\left({\mathbf{E}}^T{\mathbf{C}}_{{\mu }_a}^{-1}\mathbf{E}\right)}^{-1}{\mathbf{E}}^T{\mathbf{C}}_{{\mu }_a}^{-1}{\mathit{\mu }}_{\mathit{a}}.$$ (14)

This is equivalent to the weighted least squares solution, with the weights equal to ${\mathbf{C}}_{{\mu }_a}^{-1}$. The covariance matrix for the recovered chromophore concentrations estimates (i.e., the elements of $\hat{\mathit{\kappa }}$) is given by

$${\mathbf{C}}_{\hat{\mathit{\kappa }}}={\left({\mathbf{E}}^T{\mathbf{C}}_{{\mu }_a}^{-1}\mathbf{E}\right)}^{-1}.$$ (15)

We note that if n is Gaussian, then the best linear unbiased estimate (Eq. (14)) is optimal [23]. This means that ${\mathbf{C}}_{\hat{\mathit{\kappa }}}$ is equal to the CRB for this problem and could be used to optimize the choice of spectral wavelengths, as was done for spatial frequencies in Sec. 3.

5.1.2. Arterial cuff occlusion experiment

We performed an arterial cuff occlusion test on a 30-year-old healthy male. This experiment was designed to generate a well-known “signal” that could be used to help us evaluate the impact of chromophore concentration uncertainties along with some of the other claims made in this paper. The cuff was applied to the upper arm, and we measured the inner forearm with our SFDI instrument. We took measurements at three spatial frequencies (0, 0.05, 0.1 mm⁻¹) and four spectral wavelengths (659, 691, 731, 851 nm). Measurements were made every ~8.6 s for a total of 7 min. During the first 2 min, no pressure was applied to the cuff. At t = 2 min, the pressure was rapidly increased to ~ 200 mmHg. At t = 4 min, we released the pressure and continued measuring for another 3 min.

The data was converted to calibrated reflectance as described in Sec. 2. As with the phantom data, we performed 2 × 2 binning to increase the SNR. The optical properties were recovered with the two-frequency LUT algorithm (Sec. 4) using [0, 0.1] mm⁻¹ and [0.05, 0.1] mm⁻¹, and the corresponding uncertainties were estimated with the rCRB (Sec. 3). The Monte Carlo-based cube was used in the LUT algorithm and rCRB calculations. To further reduce the noise in our measurements, we averaged the recovered optical properties over a small ROI (diameter ~4 mm). We chose the ROI to be large enough to give us significant variance reduction but small enough that the optical properties within it could be considered uniform. This gave us one pair of µ_a and ${\mu }_s^{\prime }$ for each time point (50 total during the 7 min experiment).

The absorption coefficients at the four spectral wavelengths were converted into chromophore concentrations with Eq. (14), and the chromophore uncertainties were computed with Eq. (15). We focused on measuring changes (relative to the first measurement) in oxy- (O₂Hb) and deoxyhemoglobin (HHb) concentrations, so we solved only for these two chromophores. The chromophore extinction coefficients came from [26]. Because we took the average of µ_a over an ROI, ${\sigma }_{{\mu }_a}^2$ (assumed constant over the ROI) should be divided by the number of degrees of freedom to properly reflect the uncertainty in the averaged value. If the pixels were independent, the number of degrees of freedom would be equal to the number of pixels in the ROI. However, pixels in an SFDI image are typically not statistically independent, as the diffuse nature of light propagation results in spatial correlations. We can get an idea of the extent of the spatial correlations by taking the Fourier transform of the modulation transfer function in the spatial frequency domain (i.e., R_d as a function of spatial frequency), which gives us the point spread function (PSF) of the medium in space. We did this, assuming average values for µ_a and ${\mu }_s^{\prime }$ of 0.01 and 1.86 mm⁻¹, respectively, for all wavelengths over the course of the experiment, and arrived at a full-width half-maximum value of ~1 mm for the PSF. Given the long tails of the PSF, we decided to use 2 mm as our estimate of the PSF diameter. The ratio of the ROI to PSF area is therefore $r_{ROI}^2/r_{PSF}^2=2^2/1^2=4$, so we used 4 as the effective degrees of freedom in our computation of ${\mathbf{C}}_{{\mu }_a}$ for the chromophore concentration uncertainties. We note that this is only a rough estimate, and we are currently working to develop methods that can better quantify this value.

5.2. Results

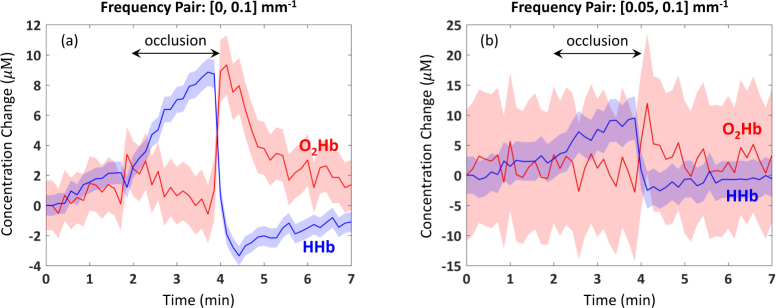
In Fig. 8 , we display the results of our cuff occlusion experiment with data at two pairs of spatial frequencies: [0, 0.1] mm⁻¹ and [0.05, 0.1] mm⁻¹. The data in Fig. 8(a) unambiguously shows the expected increase in HHb during the occlusion, coupled with the smaller rate of decrease in O₂Hb. The latter may be caused by an incomplete occlusion of the arterial blood supply. After releasing the cuff pressure, HHb decreases rapidly and O₂Hb increases. Both chromophore concentrations look like they are returning to baseline when the experiment ends 3 min later. On average, the uncertainty in O₂Hb concentration was ±1.8 µM, while the uncertainty in HHb concentration was ±0.73 µM. The behavior of O₂Hb and HHb concentrations during the experiment is consistent with previously reported results [14, 27]. Interestingly, the average uncertainty of the less noisy signal, HHb, is roughly a factor of two smaller than that of O₂Hb. Both uncertainties make it clear that we are seeing significant changes in chromophore concentrations as a result of the occlusion.

Fig. 8.

Cuff occlusion experiment: change in O₂Hb and HHb from data at spatial frequency combinations of (a) [0, 0.1] mm⁻¹ and (b) [0.05, 0.1] mm⁻¹. Shaded regions represent uncertainties in chromophore concentrations. Note the different y-axis scales.

This case is much harder to make with the data in Fig. 8(b), which is obviously a lot noisier. It is difficult to confirm the expected trend in HHb or to see any pattern at all in O₂Hb. And the much larger uncertainty of the latter suggests that one cannot make any meaningful claims about O₂Hb concentration with this data. This stark difference in performance with the two spatial frequency pairs is not very surprising, given the CRB results of Fig. 4. Here we saw that values of ${\sigma }_{{\mu }_a}$ for [0, 0.1] mm⁻¹ ranged from 5 to 11%, while for [0.05, 0.1] mm⁻¹, they ranged from 19 to 89%. This points to the importance of choosing the right spatial frequency combination for a given application and confirms the ability of the CRB to provide useful guidance for in vivo measurements.

6. Summary and discussion

In this work, we employed the CRB to estimate uncertainties in recovered optical properties using knowledge of diffuse reflectance measurement errors. The CRB is ideally suited to explore how theoretical SFDI performance varies as a function of sample optical properties and the spatial frequencies used to recover them, since it is algorithm-independent and can take into account data noise. We made two choices that allowed us to compute the CRB for our application: (1) diffuse reflectance data was modeled with a multivariate normal distribution; and (2) derivatives of R_d were computed by numerical differentiation. We validated the first choice, to the extent possible, with data from tissue-simulating phantoms. With respect to the second choice, evaluating the derivatives numerically proved not only convenient, but it gives one the flexibility to use Monte Carlo simulations of R_d, which may lead to more accurate results in some cases.

Although popular in other communities, the CRB has not received much attention in the diffuse optics community, in part likely due to the difficulty of applying it to ill-posed inverse problems (as discussed in [28]). But for many SFDI applications, where the goal is not tomography, the recovery of optical properties with data at two or more spatial frequencies is not an ill-posed problem. We can apply the same approach to other diffuse optics problems that are not ill-posed, e.g., the determination of optical properties from frequency domain measurements of amplitude and phase. If we can make the same two choices as above for the relevant data (e.g., amplitude and phase), computing the CRB for those applications could be accomplished with rather straightforward modifications of the code that we have made available.

We used the CRB to explore theoretical SFDI performance. One rather surprising result was that for optical properties typical of human breast or mouse imaging, there is not much benefit in using multiple spatial frequencies versus a well chosen pair. Selecting DC (0 mm⁻¹) as one member of that pair led to better µ_a estimation performance. We also saw that for a given set of spatial frequencies, ${\sigma }_{{\mu }_a}$ and ${\sigma }_{{\mu }_s^{\prime }}$ can vary significantly depending on the sample’s optical properties. We note that these results rely on the diffuse reflectance error model of Sec. 2. With a different error model (e.g., different instrument or operating conditions), these conclusions may not hold, so characterizing ${\sigma }_{R_d}$ is an indispensable prerequisite for this analysis.

From the CRB derivation, we arrived at a simpler quantity (the rCRB) capable of providing uncertainties when optical properties are recovered with a two-frequency LUT inversion algorithm. We characterized the performance of this algorithm with simulated diffuse reflectance data first, and then evaluated it with (experimental) phantom data, which at times deviated from the assumed data model. In both cases, the rCRB was able to successfully predict the uncertainties in estimated optical properties. With experimental data, the difference between predicted and measured ${\sigma }_{{\mu }_a}$ and ${\sigma }_{{\mu }_s^{\prime }}$ was ~1%, on average. This gives us a quick and efficient way to generate uncertainties for an LUT algorithm. It opens the door to the possibility of pre-computing an LUT of optical property uncertainties—in essence, the maps of Fig. 5—which could be a big asset for applications requiring near real-time performance. It also reveals that in the case of two spatial frequencies, a simple LUT algorithm is capable of achieving near-optimal performance.

Finally, we provided an end-to-end example, using in vivo data, that illustrated how absorption coefficient uncertainties could be propagated forward to yield uncertainties for chromophore concentration estimates. Since a linear model relates chromophore concentrations to absorption coefficients, obtaining uncertainties for the former is straightforward once the covariance matrix of the absorption coefficients is known. Our example reveals that chromophore concentration uncertainties can have an important impact on the interpretation of experimental results. While our method provides uncertainties at each pixel, it is not uncommon to average over an ROI when analyzing in vivo data, as we have done. To compute uncertainties when spatial averaging over an ROI is performed, we must develop a robust way to estimate the number of degrees of freedom, as pixels in an SFDI image are usually not statistically independent. This is an area of ongoing research in our group.

7. Conclusions and future work

We have developed a method to generate optical property uncertainty estimates from knowledge of diffuse reflectance measurement errors. By relying on the CRB, we are able to do this quickly and efficiently with non-optimized Matlab code that takes minutes to run on a desktop computer. Our method is ideally suited to characterize theoretical SFDI performance as a function of variables like spatial frequency combinations and sample optical properties. In practice, it can also provide useful uncertainty estimates for optical properties recovered with a two-frequency LUT inversion algorithm, as was demonstrated with phantom and in vivo data. We also showed how absorption coefficient uncertainty estimates could be propagated forward to yield uncertainties for chromophore concentration estimates. To fully realize this potential, however, a robust way of estimating the effective degrees of freedom when spatial averaging is performed over an ROI is needed. This work is currently in progress.

One important aspect of SFDI performance that we did not explore here is the impact of penetration depth. As mentioned in Sec. 3.2, it is known that penetration depth decreases with increasing spatial frequency. However, SFDI data processing assumes that the frequencies employed interrogate volumes with the same optical properties. This is true when measuring a homogeneous phantom, but it is likely not the case for heterogeneous biological tissue. To minimize the potential sampling mismatch, one might be tempted to choose spatial frequencies that are close together. But our CRB analysis shows that it is beneficial to have some separation between spatial frequencies, e.g., [0, 0.1] mm⁻¹ performs better than [0, 0.025] mm⁻¹. Developing a framework that can reconcile both of these concerns would be a valuable step forward.

Appendix A: Table of phantom optical properties

Table 3.

Phantom optical properties at four spectral wavelengths for training and test sets.

Phantom	µa (mm−1)				${\mu }_s^{\prime }({\text{mm}}^{-1})$
	659 nm	691 nm	731 nm	851 nm	659 nm	691 nm	731 nm	851 nm
Training Set
1	0.037	0.034	0.030	0.016	0.90	0.84	0.80	0.67
2	0.038	0.033	0.029	0.014	0.71	0.66	0.64	0.55
3	0.035	0.031	0.026	0.012	1.9	1.8	1.7	1.6
4	0.071	0.062	0.054	0.027	1.1	1.1	1.0	0.96
5	0.0018	0.0019	0.0016	0.00058	1.2	1.1	1.0	0.88
6	0.040	0.037	0.032	0.017	1.4	1.3	1.3	1.1
7	0.11	0.093	0.083	0.044	0.90	0.85	0.81	0.68
8	0.012	0.010	0.0083	0.0036	0.98	0.92	0.88	0.76
Test Set
9	0.074	0.065	0.059	0.032	0.82	0.77	0.74	0.63
10	0.019	0.017	0.014	0.0066	0.90	0.87	0.84	0.78
11	0.068	0.060	0.053	0.027	1.6	1.5	1.4	1.3
12	0.019	0.016	0.014	0.0060	1.3	1.2	1.2	1.1
13	0.036	0.032	0.028	0.014	0.93	0.86	0.82	0.69
14	0.021	0.020	0.017	0.0091	0.79	0.74	0.71	0.60
15	0.0025	0.0026	0.0021	0.00071	1.7	1.7	1.6	1.4
16	0.0064	0.0078	0.0092	0.0019	0.93	0.94	0.93	0.96

A typographical correction was made to Ref. 19.

Funding

This work was funded by a grant from the Dept. of Defense (Award No. W81XWH-15-1-0070).

Disclosures

The authors declare that there are no conflicts of interest related to this article.