Biomechanical assessment of myocardial infarction using optical coherence elastography

Abstract

Myocardial infarction (MI) leads to cardiomyocyte loss, impaired cardiac function, and heart failure. Molecular genetic analyses of myocardium in mouse models of ischemic heart disease have provided great insight into the mechanisms of heart regeneration, which is promising for novel therapies after MI. Although biomechanical factors are considered an important aspect in cardiomyocyte proliferation, there are limited methods for mechanical assessment of the heart in the mouse MI model. This prevents further understanding the role of tissue biomechanics in cardiac regeneration. Here we report optical coherence elastography (OCE) of the mouse heart after MI. Surgical ligation of the left anterior descending coronary artery was performed to induce an infarction in the heart. Two OCE methods with assessment of the direction-dependent elastic wave propagation and the spatially resolved displacement damping provide complementary analyses of the left ventricle. In comparison with sham, the infarcted heart features a fibrotic scar region with reduced elastic wave velocity, decreased natural frequency, and less mechanical anisotropy at the tissue level at the sixth week post-MI, suggesting lower and more isotropic stiffness. Our results indicate that OCE can be utilized for nondestructive biomechanical characterization of MI in the mouse model, which could serve as a useful tool in the study of heart repair.

1. Introduction

Myocardial infarction (MI) is the damage of cardiac muscle from ischemia caused by a decrease or block of blood supply to part of the heart. Due to cardiomyocyte loss and an extremely low cardiomyocyte turnover in adults, an MI once established often results in impaired cardiac function and eventually leads to heart failure [1,2]. Each year, MI affects nearly one million people in the United States [3], and is associated with substantial mortality despite a number of treatment options. Major research efforts are being made to explore new ways of regenerating cardiomyocytes for therapeutic applications [4–6]. Directly reactivating cardiomyocyte proliferation in the adult is an emerging and exciting direction to repair the injured heart [7]. Molecular genetic analyses on mice with induced MIs recently provided great insights into the regenerative capability of cardiomyocytes [8–13]. At the tissue level, mechanical factors such as elasticity are believed to serve as environmental cues regulating cardiomyocyte development and activity [14–16]. Recently, Yahalom-Ronen et al. showed that the substrate stiffness affects proliferation of mouse neonatal cardiomyocytes [17]. These studies suggest that the tissue biomechanics could play an important role in heart regeneration. To further understand the relation between molecular genetic activities of cardiomyocytes and tissue-level cardiac mechanical properties, biomechanical characterization of the heart in the mouse MI model is required.

Ultrasound elastography [18–21] and magnetic resonance elastography [22–24] are two clinically available nondestructive techniques for cardiac viscoelastic imaging and have been widely utilized for cardiac assessment after MI. These two approaches have an organ-level imaging scale and have been successfully deployed clinically and in large animal models for gross detection and evaluation of infarcted myocardium. In contrast, elastographic assessment with atomic force microscopy enables mechanical analysis of cardiomyocytes under different physiological and pathological conditions [25–28]. With nanoscale imaging, this technique has mostly been applied for characterization at the cellular and intracellular levels. Optical elastography [29], featuring a microscale resolution and a millimeter-level field of view, is well-suited for biomechanical imaging and assessment at the tissue level [30–32].

As an emerging optical elastography modality, optical coherence elastography (OCE) has recently undergone rapid development [33] and shows particular promise for novel applications in a number of biomedical areas [34]. Based on optical coherence tomography (OCT) [35] and combined with advanced tissue loading and displacement measurement techniques, a variety of mechanical contrasts were successfully employed by OCE for nondestructive assessment of tissue biomechanics [36, 37]. Among these, the velocity of elastic wave propagation [38–40] and the natural or resonant frequency [41–43] are two of the major contrasts that were widely used with dynamic OCE. Recent development of the OCE techniques based on these two parameters featured exciting advancements [33]. Specifically, assessing velocity of the directional elastic wave propagation provides the mechanical anisotropy of tissue [44, 45], and analyzing displacement damping characteristics allows for natural frequency measurement from a single localized pulsed stimulation [46, 47]. The major applications of such methods have been focused on ocular tissues [44–47]. Here we present the first application study of these OCE methods for two complementary biomechanical analyses of MI in the mouse model, demonstrating a noncontact elastography tool for mammalian cardiac regeneration research. Surgical ligation of the left anterior descending coronary artery was conducted to induce MI. Direction-dependent as well as spatially resolved tissue elastic parameters were obtained using OCE, which revealed distinct mechanical properties of the damaged heart region at the sixth week post-MI. Such tissue-level biomechanical information can be useful for investigating the role of environmental elasticity in the regenerative capability of adult cardiomyocytes.

2. Materials and methods

2.1 OCE system and displacement measurement

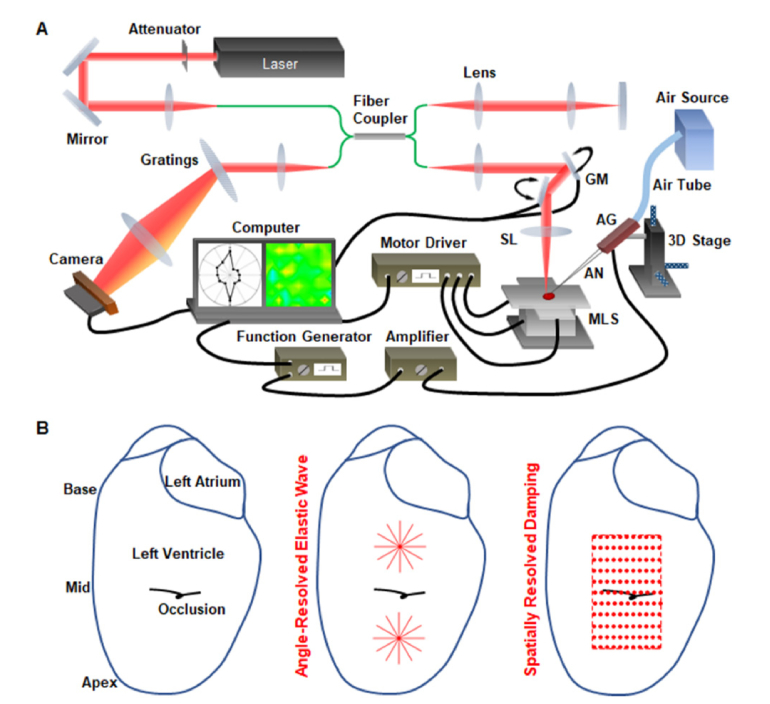
Our OCE system consists of an air-pulse loading unit and an OCT imaging unit (Fig. 1(A)). The focused air-pulse device [48] features an air gate with an electronically controlled solenoid valve, an air delivery port with a ~150 µm inner diameter, an air source, and a function generator with an amplifier to drive the system. A pulse signal with a 1 ms duration drove the air gate and was triggered by the computer. The air delivery port had an angle of around 58° with respect to the A-scan direction (axis of imaging beam) and a distance of less than 1 mm from the sample surface. Low pressure air (pascal level) was delivered to sample surface for noncontact low-magnitude stimulation with an induced tissue displacement at the micron level. This ensures minimal structural changes of tissues and cells, which helps to preserve the sample for further analysis and minimizes the effect of nonlinear mechanical properties of tissue. Although OCT has a spatial resolution on the order of microns, the phase of the low-coherence interferometry provides a nanoscale sensitivity to capture the sample deformation [33]. The spectral domain OCT system [49] utilized a Ti:Sapphire laser source with a ~810 nm central wavelength and a ~110 nm bandwidth. A fiber-based Michaelson interferometer was used for light interference. The OCT system had an axial resolution of ~5 µm in tissue, a transverse resolution of ~4 µm, and an A-scan rate of 62.5 kHz in this study. The phase stability of the system was measured to be ~0.1 rad from the surface of ex vivo cardiac muscle, corresponding to a displacement sensitivity of ~6 nm. This phase stability was measured as the standard deviation of a stationary temporal phase profile over 375 data points corresponding to 6 ms with an average OCT SNR of ~46 dB. A motorized 3D linear stage was utilized to provide easily controlled automatic movement of the tissue sample, which was synchronized with the air-pulse stimulation and OCT data acquisition. The temporal phase profiles were unwrapped. Since the phase profiles started at an arbitrary value between -π and + π, they were shifted so that the average of the phase values prior to the air-pulse stimulation was zero. The phase profiles were then transformed into displacements.

Fig. 1.

Mechanical assessment of MI using two OCE methods with a single imaging setup. (A) Schematic of the OCE system consisting of a focused air-pulse stimulation unit and an OCT imaging unit as well as a 3D motorized linear stage for automatic sample positioning. (B) Illustrations of the left ventricle with occlusion (left) as well as the locations for the angle-resolved elastic wave assessment (middle) and the spatially resolved damping analysis (right).

2.2 Mouse MI and heart preparation

Age-matched adult male CD-1 mice were used in this study. The MI was surgically induced by permanent occlusion of the left anterior descending coronary artery (LAD) [9]. An open-chest operation was performed on anesthetized and ventilated mice. A Nylon suture (8-0) was tied around the mid ventricle region of the LAD (Fig. 1(B), left). Blanching of myocardium was utilized as the sign for a proper occlusion. Due to ischemia, damage was expected at the left ventricle between the apex and the occlusion, which corresponds to the apex-mid region (Fig. 1(B), left). Sham surgeries with the same procedure but excluding the LAD occlusion were used as the control.

The OCE measurements were performed at the sixth week after the MI. Prior to the imaging experiment, the mouse was perfused with potassium chloride (30 mM) to ensure cardiac muscle relaxation as a controlled myocardial state across all samples for effective comparison. The whole heart was then dissected and placed in the potassium chloride (30 mM) solution with the left ventricle facing up and over the liquid surface. During the experiment, the same solution was periodically added to the sample surface to avoid dehydration. After the OCE measurements, the hearts were fixed in 4% paraformaldehyde and processed for embedding, sectioning, and trichrome staining for histological analysis.

All animal manipulation procedures were approved by the Institutional Animal Care and Use Committee of the Baylor College of Medicine and all experiments followed the approved protocols and guidelines.

2.3 Direction-dependent elastic wave assessment with OCE

To reveal the stiffness and mechanical anisotropy of the infarcted cardiac tissue, imaging of the air-pulse induced elastic wave propagation was performed in six directions with a 30° interval (Fig. 1(B), middle). For hearts in both the MI and the sham groups, such directional assessments were conducted in the apex-mid region as well as the mid-base region (Fig. 1(B), middle). To capture the elastic wave propagation in each direction, we performed a B-M-mode imaging that was synchronized with the air-pulse stimulation at the center of the scanning line [50]. The sample deformation process was obtained within each M-mode image, and cross-correlation of the displacement profiles from different locations provided the time delay of wave propagation [51]. The elastic wave velocity was then quantified as the reciprocal of the slope from a linear regression of the time delay versus the wave propagation distance [51]. Within each scan (or meridian), the velocity measurement was performed for both sides of the stimulation and are both shown in the resulting polar anisotropy plots. In this study, the sample was mounted on a manual rotation stage, and special care was taken to ensure that all meridional measurements were taken within the same target region of the heart. To quantify the mechanical anisotropy, the fractional anisotropy, FA, was calculated based on the meridional velocities through [52]

$$FA\text{}=\sqrt{\frac{{\left(C_{\text{max}}-C_{mean}\right)}^2+{\left(C_{\text{min}}-C_{mean}\right)}^2}{C_{\text{max}}^2-C_{\text{min}}^2}},$$ (1)

where C_max, C_min, and C_mean are the maximal, minimal, and mean velocity values among all meridional angles, respectively. The value of FA is between 0 and 1 with a greater degree of anisotropy when FA is closer to 1.

2.4 Localized damping analysis with OCE

To spatially resolve tissue biomechanical properties in the MI and sham hearts, localized analysis of the tissue surface displacement damping was performed, and the natural frequency was obtained for assessing tissue stiffness. Here, the OCT imaging beam was co-focused with the air-pulse stimulation. The air-pulse and OCT imaging beam were co-focused when we observed the maximal surface displacement during alignment in real-time. Spatial mapping was performed by rapidly moving the sample with the 3D motorized linear stage. For each heart, a total of 11 × 11 positions were assessed with a maximal spatial interval of 0.5 mm (Fig. 1(B), right). New air-pulse stimulations were applied for each new position, and M-mode data acquisition was performed, taking ~0.2-0.3 seconds. The whole experimental process, including the data recording from 121 positions, moving and positioning the sample between measurements, as well as periodically adding the potassium chloride solution, took around 60 minutes. In the MI hearts, efforts were made to ensure this measurement region covered both normal and infarcted myocardium with the occlusion location close to the center of the measurement region (Fig. 1(B), right). In the sham hearts, a similar area was assessed.

Measuring the natural frequency through damping analysis was previously established with both acoustic radiation force [46] and air-pulse stimulations [47]. A simple spring-mass-damper system was used to model the tissue surface recovery process, where the displacement, x, over time, t, was described with a differential equation:

$$\frac{m}{k}\frac{d^{2}x}{d{t}^2}+\frac{\lambda }{k}\frac{dx}{dt}+x=0.$$ (2)

Here, k is the spring constant representing the sample stiffness, m is the equivalent mass, and λ is the damping coefficient that characterizes the energy dissipation. For simplification, the damping ratio, ζ, and the natural frequency, ω, were introduced to the equation as

$$\frac{1}{{\omega }^2}\frac{d^{2}x}{d{t}^2}+\frac{2\zeta }{\omega }\frac{dx}{dt}+x=0.$$ (3)

where

$$\zeta =\frac{\lambda }{2\sqrt{km}},$$ (4)

and

$$\omega =\sqrt{\frac{k}{m}}.$$ (5)

Based on the value of ζ, there are three solutions to Eq. (3), which represent three damping cases [47]. We conducted pilot analyses where all three solutions of damping, including under damping, critical damping, and over damping, were used to fit the cardiac tissue surface recovery profile in response to the air-pulse stimulation. The R² value was utilized to evaluate the fitting process and the critical damping solution was found to have the highest R² value. Thus, we determined that the recovery profile of the cardiac tissue surface was best described as a critical damping process (ζ = 1), where the displacement, x, can be expressed as

$$x=[x_0+(v_0+\omega x_0)t]e^{-\omega t}.$$ (6)

Here, x₀ and v₀ are the initial values of displacement and velocity, respectively. Thus, Eq. (6) was utilized to fit the measured surface displacement profile to obtain ω. The natural frequency was presented as f which was calculated by f = ω/2π.

After the end of the air-pulse stimulation, the recovery of the tissue surface featured an initial slow reduction of displacement [46], which was compounded by various factors such as tissue inertia. This short process was not modeled by the damping solution, and, thus was not included in the damping analysis. The initial time point for the analysis region was when the peak recovery velocity occurred, which ensured elimination of the inertia process, improved the fitting results, and increased consistency. The end of the selected recovery profile was at the ending point of the M-mode imaging when the tissue surface recovered. As a result, the selected recovery profiles for the fitting analysis had an average length of 670 data points, corresponding to 10.72 ms. For quality control, only fitting results with an R² greater than 0.9 were utilized. Interpolation was used to cover missing values at any spatial measurement locations, which was solely for generation of 2D contour plots. The interpolated values were not used for curve plotting or statistical analysis.

3. Results

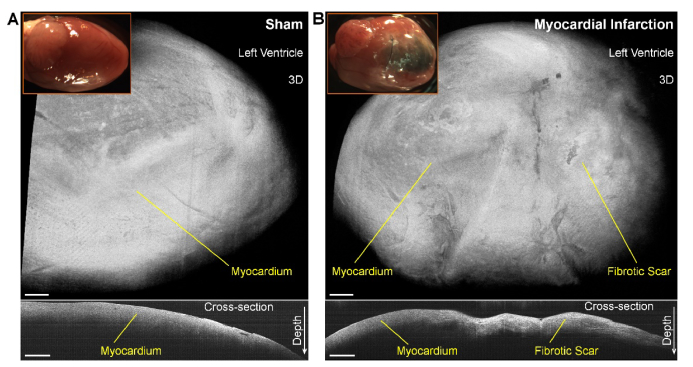
At the sixth week post-MI, compared with the normal heart (Fig. 2(A), top, inserted picture), clear damage of the myocardium can be directly visualized (Fig. 2(B), top, inserted picture). In the MI heart, fibrotic scar formed from the apex to the occlusion. The OCT 3D visualizations do not provide obvious differences between the scar and the muscle (Fig. 2, top), while the depth-resolved OCT cross-sectional images reveal a reduced attenuation of intensity over depth from the fibrotic scar (Fig. 2, bottom).

Fig. 2.

OCT and photo images of sham and MI hearts showing the myocardium damage in the mouse MI model. Photo images and OCT 3D and 2D cross-sectional visualizations of (A) sham and (B) MI hearts at the sixth week post-surgery. Scale bars are 500 µm.

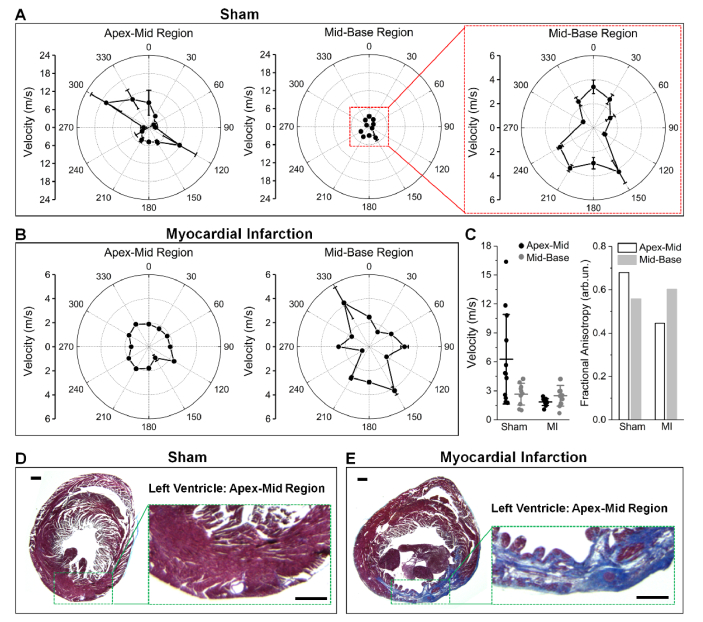
The wave velocities obtained from the OCE angle-resolved elastic wave assessment are plotted as a function of meridional angle in Figs. 3(A) and 3(B) for representative sham and MI hearts, respectively. For easy comparison, the velocity values from all directions were grouped together and the FA values were calculated, both shown in Fig. 3(C). It can be directly seen that the myocardium has a generally high degree of directional elastic anisotropy, which is caused by a similar orientation of the muscle fiber groups [53]. The polar plots clearly show that in the healthy heart, the wave velocity is overall higher in the apex-mid region than in the mid-base region, whereas in the MI heart, the difference is reversed. We also observed a relatively lower value of fractional anisotropy in the apex-mid region as compared to the mid-base region in the MI heart. The elastic wave velocities from the mid-base regions of both the sham and MI samples fall in the same range with a similar degree of anisotropy; however, the overall velocity in the apex-mid region is clearly reduced in the MI heart. More specifically, this reduction is mainly caused by the absence of high-velocity meridional angles, since the lower meridional velocities remain similar. This change in mechanical properties is a result of the alteration in tissue composition. As shown in Figs. 3(D) and 3(E), the myocardium in the apex-mid region of the MI heart has been largely replaced by a thin layer of fibrotic scar tissue, which has a significantly reduced functionality [13].

Fig. 3.

Mechanical anisotropy of sham and MI hearts revealed by angle-resolved OCE assessment of elastic wave propagation. Polar plots of the elastic wave velocities from both apex-mid region and mid-base region of (A) sham and (B) MI hearts. (C) Comparisons of the velocity and FA values from the hearts in (A) and (B). Corresponding histology of the (D) sham and (E) MI hearts in (A) and (B). Sections are from the apex-mid region with zoomed-in views of the left ventricular wall. Scale bars are 500 µm.

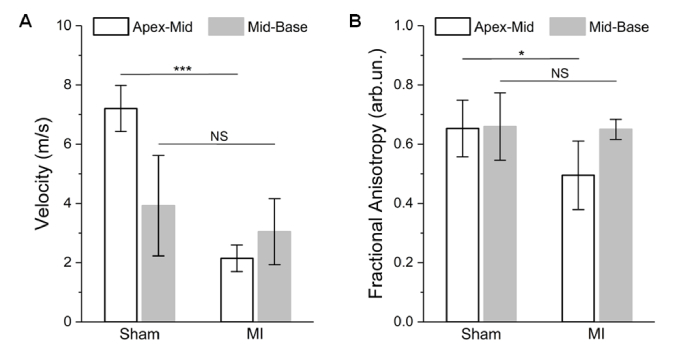
From statistical analysis across animals (N = 4 for sham and N = 3 for MI), the mid-base regions of the MI hearts show no significant difference from the same regions of sham hearts in terms of both wave velocity (Fig. 4(A)) and mechanical anisotropy (Fig. 4B). This suggests that, six weeks after MI, the biomechanical properties of the cardiac region remote to the infarcted site is largely not affected by the pathological remodeling of cardiomyocyte loss and fibrosis. In the apex-mid region, as shown in Fig. 4, statistically significant reductions in elastic wave velocity (p = 0.0002, t test) and mechanical anisotropy (p = 0.0475, t test) indicate the remodeled fibrotic scar tissue has relatively lower and more isotropic stiffness. Only focusing on the sham hearts, the data in Fig. 4 show that, although the apex-mid region has a relatively higher tissue stiffness, the ways that muscle fiber groups orient do not possess an apparent difference between the apex-mid and mid-base regions.

Fig. 4.

Statistics of elastic wave velocity and mechanical anisotropy from sham and MI hearts. Statistical comparisons (t test) of (A) the averaged wave velocity over meridional angles and (B) the FA from the apex-mid and mid-base regions between sham and MI hearts. The number of mice N = 4 for sham and N = 3 for MI. Data are mean ± s.d., p>0.05 for NS (non-significant), ***p<0.001, *p<0.05.

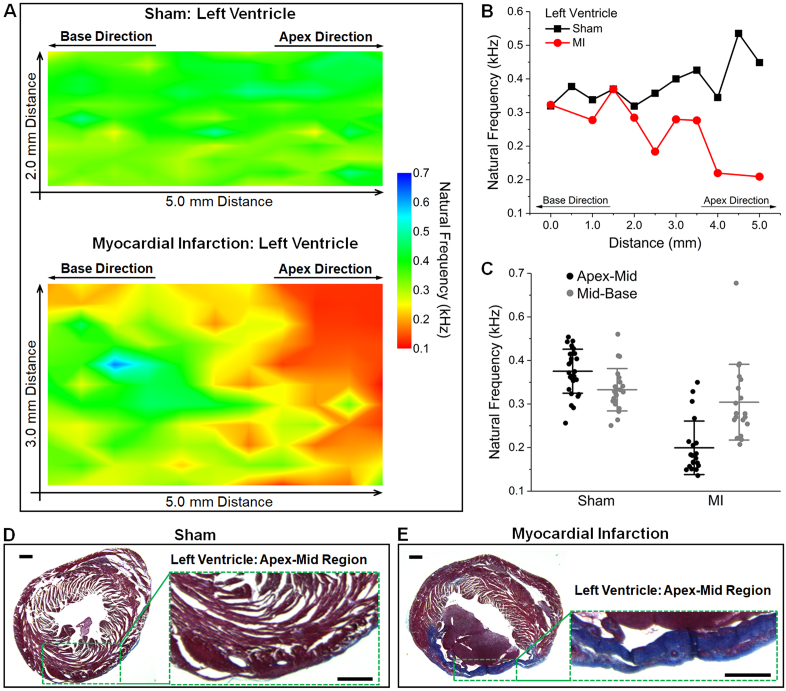
Sample elastograms based on 2D mapping of the natural frequency are shown in Fig. 5(A) for both sham and MI hearts. It is clear that towards the base, the natural frequencies in the MI heart are similar to the sham heart. In contrast, towards the apex, the infarcted tissue has reduced natural frequencies compared to the sham tissue. This spatial change is also well presented with the selected plots over distance (Fig. 5(B)). The natural frequency values from regions within 1.5 mm to the apex and base are grouped to represent the mechanical properties of the apex-mid and mid-base regions, respectively. Comparisons of such grouped data (Fig. 5(C)) show a similar trend as provided by the elastic wave velocity (Fig. 3(C)). The corresponding histology images from the two hearts (Figs. 5(D) and 5(E)) reveal the changes in tissue composition and thickness that are responsible for the observed reduction in stiffness. The averaged values of the natural frequencies from the apex-mid and mid-base regions were utilized for statistical analysis across animals (N = 3 for sham and N = 3 for MI), as shown in Fig. 6. The mid-base regions from the sham and MI hearts do not have a significant difference in the natural frequency, while the natural frequency of the apex-mid region in the MI hearts shows a statistically significant decrease (p = 0.0083, t test). This agrees with results from the elastic wave assessment.

Fig. 5.

Mapping of natural frequency from OCE localized displacement damping analysis provides spatially resolved mechanical properties of MI. (A) Elastograms of the natural frequency cover the mid-ventricular region of representative sham and MI hearts. (B) Plots of selected natural frequency profiles from (A) shows the spatial dependent mechanical change in MI. (C) Comparison of natural frequency values from the hearts in (A). Corresponding histology of the (D) sham and (E) MI hearts in (A). Sections are from the apex-mid region with zoomed-in views of the left ventricular wall. Scale bars are 500 µm.

Fig. 6.

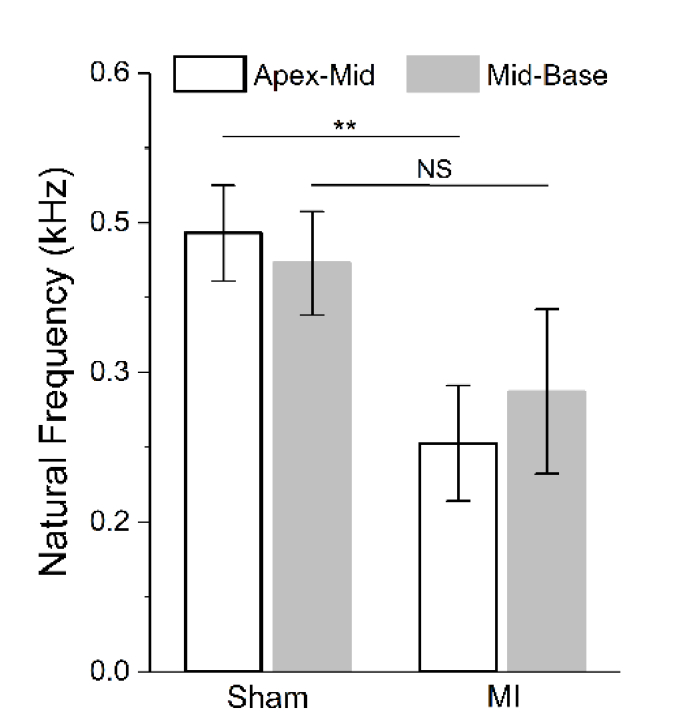
Natural frequency statistics from sham and MI hearts. Statistical comparisons (t test) of the averaged natural frequency from the apex-mid and mid-base regions between sham and MI hearts. The number of mice N = 3 for sham and N = 3 for MI. Data are mean ± s.d., p>0.05 for NS (non-significant), **p<0.01.

Even though direction-dependent stiffness was resolved with the elastic wave assessment, the relatively high wave velocity in the cardiac tissue is not suitable for spatial mapping of tissue biomechanical properties. In this case, the localized damping analysis, as performed with the same OCE system, complements the wave-based mechanical assessment well and further confirms the results of elastic wave imaging. Thus, the combination of these two OCE methods provides complementary analysis of MI in the mouse model and allows for a relatively more complete understanding of the spatial distribution of mechanical properties (Figs. 3(A), 3(B), and Fig. 5(A)) in the heart muscle tissue.

4. Discussion and conclusion

The mechanical contrasts utilized in this study were previously established and demonstrated to effectively represent tissue stiffness [34]. For elastic wave velocity, experiments with tissue-mimicking phantoms revealed that several elastic wave models (e.g. surface wave and shear wave) can be employed to estimate the shear or Young’s modulus based on the wave velocity [54–56], where a higher velocity corresponds to a stiffer sample. Recently, thickness was found to have an effect on reconstructing sample elasticity from elastic wave velocity [57]. Given that MI caused significant changes in the heart wall thickness (Fig. 3(D) and 3(E)), a more advanced and sophisticated model incorporating tissue thickness is needed to accurately obtain elastic modulus from the wave assessment. For natural frequency, previous phantom experiments have demonstrated its relationship with Young’s modulus [43, 47], showing that stiffer samples possess a higher natural frequency. This is also revealed from Eq. (5) which can be rewritten as k = mω². However, tissue remodeling at the infarcted region and the resulting fibrotic scar could alter the equivalent mass being loaded by the air-pulse. Thus, we note that the natural frequency obtained in this study is not a quantitative measure of tissue stiffness. Transforming natural frequency into quantitative material parameters would require further development of an approach able to exclude the influence from the sample mass, which may be possible based on normalization or direct measurements. Nevertheless, these two mechanical parameters produced sufficient contrast between healthy and damaged cardiac tissues and provided two complementary assessments of the spatially dependent tissue biomechanical properties.

The mouse has been a superior model for the heart repair and regeneration research, due to the well-established genetic tools allowing mutagenesis strategies [8–13]. The OCE methods described in this study were particularly developed for the mouse MI model, aiming to understand biomechanical factors in the process of heart regeneration [15]. Several existing elastography approaches, such as ultrasound/magnetic resonance elastography and atomic force microscopy, could also be used for assessment and detection of MI. However, unlike atomic force microscopy that measures the stiffness from individual cardiomyocytes [26], the presented OCE methods focus on a larger scale and characterizes the mechanical properties of groups of cardiomyocytes and extracellular matrix together as a tissue, which provides the biomechanical environment of cardiomyocytes and better represents how the cardiac muscle functions. At this tissue level, ultrasound elastography and magnetic resonance elastography are widely used approaches for in vivo analyses of MI in human and large animal models [18, 19, 22, 23]; however, to the best of our knowledge, their reported applications in the mouse MI model have been limited, primarily due to the small size of the mouse heart. Luo et al. reported the use of high-frequency ultrasonic imaging for in vivo elastography of the mouse MI [21]. Although a spatial resolution of 115 µm (lateral) and 55 µm (axial) was achieved, only displacement and strain images in response to heart beating were generated [21]. Given that the cardiac function is impaired with MI, the contractile force (or pressure) could be significantly altered during heart dynamics. As a result, the parameters of displacement and strain, although sufficient for the purpose of MI detection, are largely not suitable to measure the change of tissue elastic properties. In contrast, with the presented OCE methods, mechanical parameters, including elastic wave velocity, mechanical anisotropy and natural frequency, were obtained as measures of the intrinsic property (stiffness) of tissue, which can be studied as the candidate biomechanical cues potentially playing a role in cardiomyocyte proliferation [17]. In terms of the spatial resolution, imaging speed, and in vivo capability of the OCE methods, improvements are possible for more robust and efficient assessment, which are specifically discussed with details in the following paragraph. Therefore, for the myocardial regeneration research with the mouse MI model, we believe the presented OCE methods serve as a complementing approach in the context of the existing elastography techniques and could be useful to investigate tissue-stiffness-related factors in the repair and regeneration of the adult cardiac muscle.

In addition to the direction-dependent measurement, the elastic wave OCE method has the potential for spatially mapping tissue stiffness heterogeneity, as shown in a number of previous studies [44, 45, 55, 58]. Such capability largely relies on the wavelength of the induced elastic wave as well as windowed cross-correlation analysis of temporal displacement profiles from different locations. In this work, the elastic wave wavelength is on the order of millimeters, restricting spatial elasticity resolution. However, alternative excitation sources, such as acoustic radiation force [58] or Lorentz force [59], frequency-resolved analysis of the elastic waves, and OCE systems with higher temporal resolutions can improve the spatial elasticity resolution in heterogeneous tissue. The time required for OCE data acquisition is currently limited by the system A-scan rate and the scanning speed of the OCE system. A higher A-scan rate will enable elastic wave imaging with only repeated B-scans, which can be achieved with ultrafast [60] or line-field [61] OCE system. The presented direction-dependent elastography measurements relied on the rotation of the sample stage. Future work will incorporate a rotation scheme based on the computer-controlled galvanometer mirrors, which will reduce the subjectivity of the meridian selection while manually rotating the sample and will decrease the overall imaging time. For displacement damping analysis, the sample scanning was achieved by controlled automatic movement of 3D linear stages, resulting in a limited spatial sampling rate that could not preserve the high transverse resolution from OCT. To improve the speed and to achieve micrometer scale elasticity resolution, pulsed laser stimulation with photothermal effect [62] can be incorporated, and the pulsed laser beam can be coupled into the imaging optical path that is scanned by galvanometer mirrors. This will eliminate the need for moving the sample and will decrease the spatial sampling interval to be within the OCT resolution. In vivo OCE assessment with the presented method is potentially possible through minimally invasive thoracic window approaches, which will allow for longitudinal analyses of MI and cardiomyocyte regeneration; however, advanced algorithms will need to be developed for synchronization and material property reconstruction.

Some previous studies characterizing MI in animal models revealed a higher stiffness of the infarcted region compared with the remote region [19, 21–23]. Such results were obtained a relatively short time after MI, ranging from several hours to 21 days [19, 21–23]. With serial stiffness measurements of the infarcted left ventricle in rats at different time points, Raya et al. found that stiffness initially increased hours after infarction, then returned to normal by five days, and finally decreased at more than 22 days post-MI [63]. This indicates that the elasticity of the infarcted myocardium features a dynamic change over time and corroborates our experimental results of a reduced tissue stiffness at the sixth week post-infarction. In fact, recent studies have shown a highly dynamic tissue remodeling process at the infarcted region over 6-8 weeks after ischemia [64]. The process of tissue rebuilding and restoring could result in large time-dependent variations of mechanical properties [64]. Future work will assess the temporal dynamics of tissue biomechanical properties after MI to understand the biomechanics of the remodeling infarct scar.

In summary, we report the first application of OCE in biomechanical characterization of the effects of MI on cardiac tissue. Two complementary OCE methods, angle-resolved elastic wave assessment and localized displacement damping analysis, were utilized to assess the spatial distribution of stiffness of the infarcted left ventricle. Our results show that at the sixth week post-MI, the remodeled fibrotic scar tissue featured reduced and more isotropic stiffness in comparison with the sham. This nondestructive OCE approach is promising as a useful tool for studying the biomechanics of mammalian heart regeneration.

Funding

National Institute of Health grants R01HL130804 (J.F.M. and K.V.L.), DE023177, HL127717, HL118761 (J.F.M.), R01HL120140 (I.V.L.), and U54HG006348, Vivian L. Smith Foundation (J.F.M.), LeDucq Foundation Transatlantic Networks of Excellence in Cardiovascular Research (14CVD01) “Defining the genomic topology of atrial fibrillation.” (J.F.M.), U.S. Department of Defense (DOD) Congressionally Directed Medical Research Programs (CDMRP) grant PR150338 (K.V.L.), American Heart Association grant 16POST30990070 (S.W.).

Disclosures

The authors declare that there are no conflicts of interest related to this article.