Investigation of albumin-derived perfluorocarbon-based capsules by holographic optical trapping

Abstract

Albumin-derived perfluorocarbon-based capsules are promising as artificial oxygen carriers with high solubility. However, these capsules have to be studied further to allow initial human clinical tests. The aim of this paper is to provide and characterize a holographic optical tweezer to enable contactless trapping and moving of individual capsules in an environment that mimics physiological (in vivo) conditions most effectively in order to learn more about the artificial oxygen carrier behavior in blood plasma without recourse to animal experiments. Therefore, the motion behavior of capsules in a ring shaped or vortex beam is analyzed and optimized on account of determination of the optical forces in radial and axial direction. In addition, due to the customization and generation of dynamic phase holograms, the optical tweezer is used for first investigations on the aggregation behavior of the capsules and a statistical evaluation of the bonding in dependency of different capsule sizes is performed. The results show that the optical tweezer is sufficient for studying individual perfluorocarbon-based capsules and provide information about the interaction of these capsules for future use as artificial oxygen carriers.

1. Introduction

Artificial oxygen carriers (AOCs) display a further therapeutic alternative when red blood cell (RBC) concentrates are unavailable or cannot be applied (because of antibodies against blood compounds or religious reasons). Unlimited disposability of RBCs is still problematic because of multiple surgeries involving high blood loss and cannot fully be covered by patient blood management programs realized in many hospitals [1–3]. Furthermore, treatment with allogeneic RBC can be associated with underestimated side-effects, evolving in short-, medium- or long-term effects after transfusion [4,5]. AOCs are intended to preserve organ function until new endogenous RBCs are ready to take over [6]. However, until now, no artificial oxygen carriers are approved for human clinical use, both in Europe and USA [7].

There are two main classes of AOCs: hemoglobin-based and perfluorocarbon-based AOCs. While hemoglobin-based AOCs are extracted from animal or outdated human blood, perfluorocarbon-based AOCs are fully synthetic products and thus not susceptible for transmitting diseases or dependent on blood availability. Additionally, in contrast to hemoglobin-based AOCs, perfluorocarbon-based AOCs remain functional in the presence of flue gases, e.g. carbon monoxide, and thus can be used for treatment of smoke poisonings [8, 9].

Perfluorocarbons are synthetically manufactured fully perfluorinated compounds. Because of cavities formed between perfluorocarbon molecules, solubility of respiratory gases (oxygen and carbon dioxide) is, dependent on their partial pressure, very high compared to water. More than 90% of the dissolved oxygen can be released to the tissue; this is 3-fold higher than the oxygen extraction rate of a RBC [10]. This is why perfluorocarbons are suitable for transport of respiratory gases in blood. Due to the strong carbon-fluorine bonds, perfluorocarbons are physiologically inert and do not degrade to toxic metabolites [11]. Figure 1 shows the chemical structure of perfluorodecalin (PFD). However, to use perfluorocarbons as AOCs they have to be engineered as they are not mixable with the aqueous medium blood. While perfluorocarbon-based emulsions are associated with a lot of side-effects, perfluorocarbon-based capsules display an interesting alternative [11, 12]; especially, when the biopolymer albumin is used as wall material and biological emulsifier: Albumin-derived perfluorocarbon-based capsules (PBCs) performed very well in an animal top-load-model and kept alive an isolated heart under ischemic conditions [13, 14].

Fig. 1.

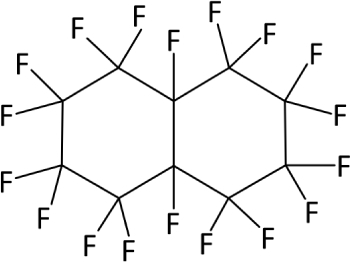
Chemical structure of PFD (C₁₀F₁₈).

A remaining task is the investigation of the interaction between individual PBCs, which has not yet been studied due to technical challenges. These investigations could provide important evidence of the overall behavior of the system such as agglomeration and are important to further improve the quality of the PBCs. Therefore, a technique has to be developed and applied that enables the handling and analysis of single capsules or the interaction between the specimens in the physiological environment of the capsules, thus in electrolyte- and colloid-containing aqueous medium mimicking blood plasma. This is a mandatory prerequisite to exclude any artifacts of in vitro investigations as it is already known that the PBCs do not remain functional under non-aqueous conditions. Furthermore, the capsules have to be studied without or minor mechanical, chemical, and thermal influences and treatment.

Optical tweezers (OTs) are widely used in biology, biomedicine or microfluidics and allow the handling and investigation of individual cells or organisms [15, 16]. The optical forces, caused by reflection and refraction at the interface, can be utilized to trap, move, and manipulate biological materials contactless and with high precision. For instance, automated sorting of cells or bacteria [17, 18] and the treatment, e.g., optical transfection, injection, or lysis, have successfully been demonstrated on microfluidic-based devices [19]. In addition, OTs are used for the measuring and sensing of minor forces in the femto- and piconewton range. In this way, the mechanical properties of RBCs have been analyzed and conclusions on blood-associated diseases could be drawn [20–22].

Typically, single or multiple Gaussian beams are used to trap microobjects which are transparent for the applied wavelength [23, 24]. However, if the refractive index of the object is lower than of the surrounding medium, they are pushed out of the beam. In addition, this problem occurs when using reflective or absorbing materials [25]. To still enable stable trapping, “donut”-shaped or annular beams are required. Therefore, a single beam can be scanned very fast on a circular path around the microparticle [26, 27]. A further developed and more flexible method to generate complex beam shapes like optical vortices is to use a spatial light modulator (SLM) [24]. An OT with integrated SLM is commonly referred to as holographic optical tweezer (HOT). With computer-generated holograms, trapping and moving of multiple low- and high-index particles simultaneously have been demonstrated [28, 29]. In addition, PBCs behave like low-index particles and, therefore, specific beam shapes are required for the optical handling.

The main aim of this paper is the characterization and provision of the HOT to investigate individual PBCs in a physiological environment (aqueous medium containing electrolytes and colloids) for future use as artificial blood. Thus, these investigations represent an experimental in vitro setting mimicking physiological (in vivo) conditions most effectively. The motion behavior of these capsules in an annular shaped beam by computer-generated holograms is studied. Therefore, the axial and radial optical forces are determined in dependency of the beam and capsule diameter. The focus is on stable trapping as well as precise moving of the capsules in all three dimensions. The results are utilized for first investigations on the aggregation behavior of individual PBCs and a statistical evaluation of the bonding in dependency of different capsule sizes is performed. Therefore, a novel method to join capsules by modified dynamic phase holograms is presented.

2. Materials and methods

2.1. Synthesis of PBCs

PBCs in the low micrometer range were synthesized similar to those described by Wrobeln et al. [13]. In this work, 10 ml aqueous 5% (w/v) solution of bovine serum albumin (BSA; Carl Roth, Germany) in purified water (purified with a Milli-Q® Integral System from Merck Millipore, USA) and 5 ml PFD (Fluorochem Chemicals, UK) were filled in a 50 ml reaction tube at ambient temperature and pressure. A sonotrode (H3, Hielscher Ultrasonics, Germany) was used for ultrasonic irradiation at an intensity of 80 W applied for 30 seconds without cooling. Under these conditions, PBCs with mean diameters from 1 µm–10 µm originated. The size distribution was determined by using the principle of dynamic light scattering (NANO-flex, Particle Metrix, Germany). After preparation, the capsules were separated from the surrounding fluid using a centrifuge (226 × g at ambient temperature) and dispersed in 5% BSA solution. Due to impurities of BSA powder, cations were present in the final preparation in low concentration (14 mM sodium, 0.2 mM potassium and 0.05 mM calcium).

Typically, the diameter of PBCs used as artificial oxygen carriers are slightly smaller (mean diameter <1 µm). Nevertheless, it is assumed that the structural composition of the capsule shell is independent of the capsule diameter and, therefore, the capsules used for this study display a suitable model system from which relevant properties can be transfered to the nanocapsules used as artificial oxygen carriers.

2.2. Holographic optical tweezer

The absorption of PFD in the visible range is negligible [30], which promotes the use of a green laser for optical trapping. Therefore, the HOT (Fig. 2 ) is based on a continuous wave laser emitting at a wavelength of 532 nm (Verdi G6, Coherent, USA). The choice of the laser was based only on those physically relevant parameters to maximize outcome; importantly, the experimental set-up will not be transferred to a physiological environment (to investigate tissue or living animals) but was developed to mimic physiological conditions of blood plasma in vitro most effectively in order to save animal experiments. Because of this fact, the laser emission was not restricted to biocompatible wavelengths but could be chosen to maximize the outcome of the in vitro experiment. After expansion, the laser beam is modulated and reflected at the SLM (Pluto-VIS, Holoeye, Germany). Next, the beam diameter is reduced by two lenses and the beam is directed into an inverse microscope. The zero-order beam is blocked by an aperture. The microscope objective (PlanApochromat, Zeiss, Germany) with an numerical aperture of 1.4 and a ion of approx. 73% focuses the beam into the sample chamber, which contains the PBCs and is sealed with two cover glasses. The used light source is linearly polarized and there are no polarizers or polarizing elements after the SLM. A high-speed camera is used to monitor the process of trapping and to analyze the diameter of the capsules with an accuracy down to a few tens of nanometers [31]. A more detailed explanation of the setup is described by Köhler et al. [32]. To reduce adhesion effects of the cover glasses, initially, the glasses are treated with a BSA solution. After 30 minutes, the dispersed capsules are added. The stated laser powers in the experiments were measured at the laser output. Due to losses on the optical components, in particular the SLM, the aperture and the microscope objective, the effective laser power is approx. 5% of the output power.

Fig. 2.

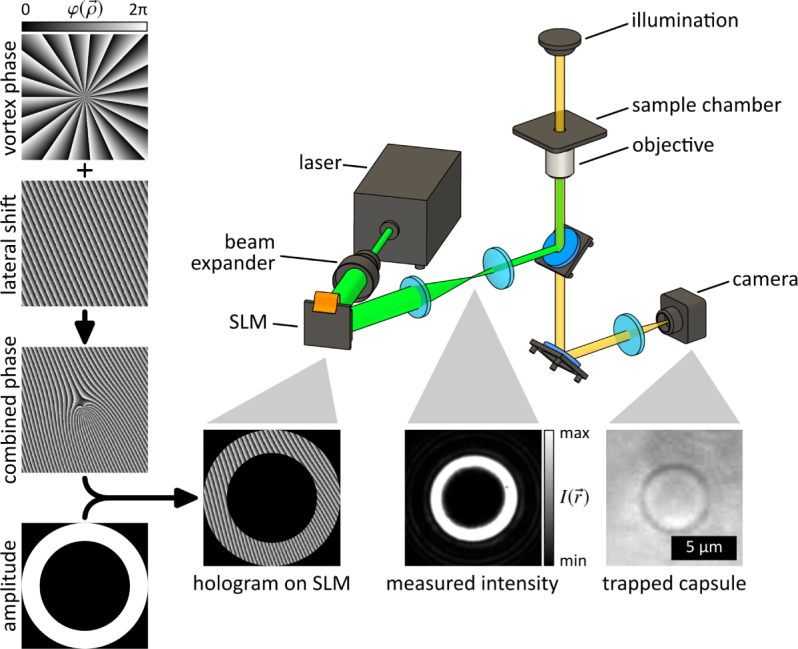
The used hologram on the SLM is a combination of the phase and amplitude patterns, which leads to a ring shaped intensity profile and enables trapping of the PBCs.

The refractive index of PFD is slightly lower than of the surrounding BSA solution [33, 34]. Therefore, the capsules behave like low-index particles and can not be trapped by a simple Gaussian beam. As a consequence, the HOT is used to generate helical modes of light which provide ring shaped intensity profiles $(I(\overrightarrow{r}))$ due to destructive interference along the beam axis. Therefore, a vortex phase pattern is generated which has the profile

$$\phi \left(\overrightarrow{\rho }\right)=\ell \theta \text{mod}2\pi ,$$ (1)

with the position vector $\overrightarrow{\rho }$, the polar coordinate θ and the topological charge ℓ [24]. This ℓ denotes the integral winding number of the helical mode and is directly proportional to the size of the annulus beam. Due to the combination of multiple phase patterns, shifting of the beam in axial and radial direction as well as the generation of multiple intensity profiles is feasible. In Fig. 2, the vortex is shifted by the addition of a blazed grating. Furthermore, an optimization by adding an amplitude with a certain diameter was performed according to Guo et al. [35] to generate a vortex beam with high contrast. The control of the SLM and the generation of the holograms were developed using MATLAB. This vortex beam is suitable to trap a PBC by laterally exert optical forces to the capsule from every side which lead to an equilibrium position at the center of zero intensity. In addition, the advantage of this beam shape is the low heat effect and no photodamage of the trapped specimen.

To analyze the aggregation behavior of the PBCs and to enable bonding, the vortex beam must be opened. Lorenz et al. [36] presented a technique to join aqueous droplets by using a microfabricated diffractive optical element (DOE) in combination with a pinhole and a dove prism which allows the generation of two vortex beams. Due to a relative motion between the optical elements, the intensity distribution of the trap changes and opening of the annulus beam can be achieved. In this study, no additional optical or mechanical elements are needed due to the utilization of the SLM. Therefore, a dynamic generation of multiple vortex beams with different sizes and positions is feasible by simply applying certain holographic patterns. This allows very flexible handling and real-time control. The process of opening a vortex beam is illustrated in Fig. 3 . The vortex phase pattern is combined with a changing amplitude which leads to a gradually opening of the vortex beam.

Fig. 3.

A combination of the vortex phase pattern and a changing amplitude leads to presented intensity distributions and opening of the vortex beam. The topological charge of the vortex is ℓ = 19 and the diameter is d_v = 5 µm, respectively. The MATLAB code is available in the supplementary information, see Code 1 [40].

This technique not only allows joining of low-index particles, but also paves the way for other applications. For instance, it enables the assembling of various types of materials (reflective or absorbing) with different properties, e.g., optical, mechanical, electrical, magnetical and thermal properties, to generate functionalized complex microstructures [37–39].

3. Characterization of the trapping system

3.1. Radial forces

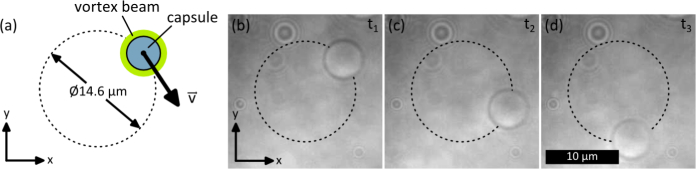
To quantify the optical forces in radial direction, the frictional or drag force induced by a relative motion between the capsule and the surrounding medium was used. Therefore, a capsule was moved through the medium with a dynamic vortex beam generated by the SLM (Fig. 4(a) ). This vortex beam was guided along a circular path with a diameter of 14.6 µm while the velocity was gradually increased by 0.5 µm/s after each rotation. The rotation of a capsule with a diameter of 5.2 µm and a velocity of 3.5 µm/s is shown in Fig. 4(b)–(d). Right before the critical velocity v_c was reached and the capsule fell out of the trap, the drag force was equal to the applied optical force. Here, the centripetal force can be neglected due to the low velocities and the dimensions of the capsules. According to Stokes’ law, the radial optical force can than be calculated by

$$F_{\text{rad}}=3\pi {\eta }_m{\nu }_c{d}_c{c}_F,$$ (2)

with the viscosity η_m of the surrounding BSA solution (values are calculated referring to Monkos et al. [41]), the diameter d_c of the capsule and the correction coefficient c_F due to boundary effects of the cover glass [15].

Fig. 4.

(a) The critical velocity v_c is determined by moving a capsule on a circular path while gradually increasing the velocity. (b)–(d) A capsule with a diameter of 5.2 µm is moved with a velocity of 3.5 µm/s.

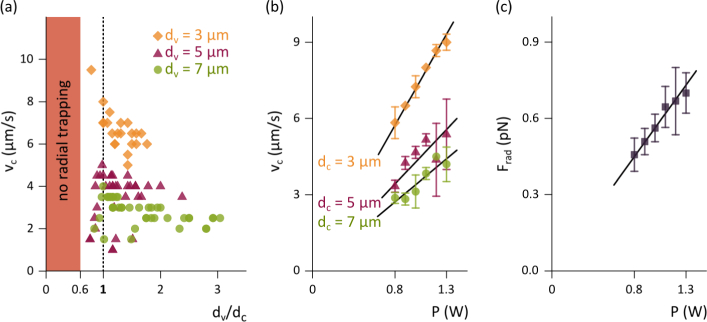
To ensure stable and efficient trapping, initially, the optimal ratio of the vortex-to-capsule diameter was determined. Therefore, capsules with three different diameters were moved at a constant laser power of 1 W and various vortex diameters. Figure 5(a) reveals, that there is an optimal ratio of d_v/d_c = 1 where the critical velocity can be maximized and the capsules are stably trapped. This is in good agreement with the results of Fury et al. [42]. To the right of this optimum operating point the critical velocity slowly decreases. To the left side where the ratio becomes smaller, instable trapping is prevalent and the capsules tend to fall out of the trap. From a ratio of approx. 0.6 radial trapping is no longer possible. Subsequent experiments are performed using the optimal value of ratio.

Fig. 5.

(a) The optimal ratio of the vortex-to-capsule diameter where the critical velocity can be maximized is d_v/d_c = 1. (b) Using this value, a linear correlation between velocity and laser power can be determined. (c) The radial optical force F_rad can be calculated by Equation 2.

The critical velocities of capsules with three different diameters as a function of the laser power are shown in Fig. 5(b). Each measurement was performed three times and averaged. As predicted by the theory, the velocity increases proportional to the laser power. Furthermore, smaller capsules reach higher velocities due to less flow resistance. However, the radial forces which were determined by Equation 2 are independent of the capsules size (Fig. 5(c)). Additionally, the radial forces increase proportionally with the laser power.

3.2. Axial forces

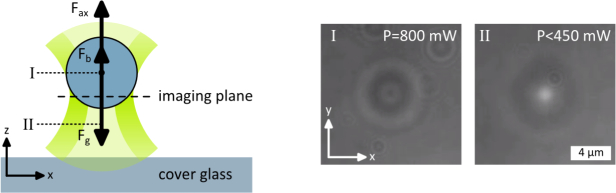
The density of the capsules is approx. twice as high as the density of the surrounding medium, which leads to sedimentation. Thus, the optical force in axial direction F_ax must be in balance to the buoyancy force F_b and the force due to gravity F_g to lift up a capsule from the cover glass (Fig. 6(a) ). Therefore, the following Equation must be satisfied to stably trap a capsule in direction of beam propagation:

$$F_{\text{ax}}=\frac{\pi g{d}_c^3}{6}({\rho }_c-{\rho }_m),$$ (3)

with the standard acceleration due to gravity g, the density of the capsule ρ_c and the surrounding medium ρ_m. The values of densities are calculated referring to Marsh et al. [43] and Monkos et al. [41]. Note, that the albumin shell is not taken into consideration due to a negligible thickness of 25 nm–35 nm [44].

Fig. 6.

The acting forces on a capsule must be balanced for stably trapping in axial direction. The equilibrium position is slightly above the imaging plane (I). The laser power is reduced until the capsule falls out of the trap onto the cover glass (II).

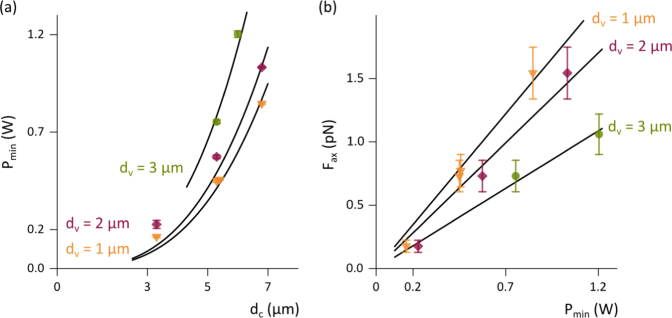
To experimentally determine the axial force, the minimal laser power P_min at which the capsule is just about to be trapped was measured. Therefore, a capsule was trapped, lifted up to a distance of approx. 8 µm above the cover glass, and the laser power was gradually reduced. Latter process is shown in Fig. 6. A capsule of 5.3 µm in diameter is trapped in equilibrium position. Because the capsule lies on the annulus beam, this position is slightly above the imaging plane and the capsule appears blurred. The smaller the vortex diameter, the higher is the position of the capsule above the imaging plane. In Fig. 6, the vortex diameter is 1 µm. If the laser power is reduced to a critical value (450 mW), the optical force is insufficient to hold the capsule and it falls out of the trap in direction of the cover glass. The minimal laser powers to stably trap different capsules with three altered vortex diameters are illustrated in Fig. 7(a) . Here, the data points represent the average values of three measurements. It can be noted that the required laser power increases with increasing vortex diameter. The plotted black lines correspond to fits by Equation 3 $\left(P_{\text{min}}\propto d_c^3\right)$. The calculated axial forces are proportional to the laser power (Fig. 7(b)). Due to the angle of incidence of the laser beam and the circular shape of the capsules, the axial force is larger for small vortex diameters. However, the condition d_v < d_c has to be satisfied to lift up a capsule in axial direction.

Fig. 7.

(a) The minimal laser power to stably trap different capsules augments with increasing diameter. The black lines correspond to fits by Equation 3 $\left(P_{\text{min}}\propto d_c^3\right)$. (b) The axial force F_ax can be calculated by Equation 3 (black lines are linear fits through the origin).

The axial forces are two to three times larger than the radial forces. This can be explained by the difference of the effective area of laser light: The whole beam interacts with the capsule by axial trapping, whereas for radial trapping only half of the annulus beam affects a capsule. In contrast, it is well known that the axial forces on a high-index particle optically trapped by a single Gaussian beam are smaller than the radial forces [45].

4. Intercapsular interactions

After system characterization and determination of the optimum vortex diameters and laser powers, the HOT was ready-to-use for analyzing the aggregation behavior of the PBCs. Therefore, bonding measurements of capsules in a medium similar to their natural environment (blood plasma) were performed by trapping and bringing them into contact. Bonding of PBC pairs of different size ranges was statistically examined.

To trap two PBCs at the same time and move them towards each other a dynamic phase pattern must be generated. Furthermore, the vortices must gradually be opened to enable contact of the capsules, as it is technically described before (see Fig. 3). This process is illustrated in Fig. 8 for two PBCs with a diameter of 5 µm. First, two capsules were trapped with annular shaped beams. Next, the capsules were brought closer together by moving the right vortex. Then, the vortices were opened by modifying the amplitude of the phase pattern and, finally, the half vortices were moved closer to push the capsules together. This state was maintained for a few seconds. If a pair of capsules adhered, the zeroth-order of the laser beam was applied in-between the capsules with a laser power of 0.4 W to confirm a stable bonding.

Fig. 8.

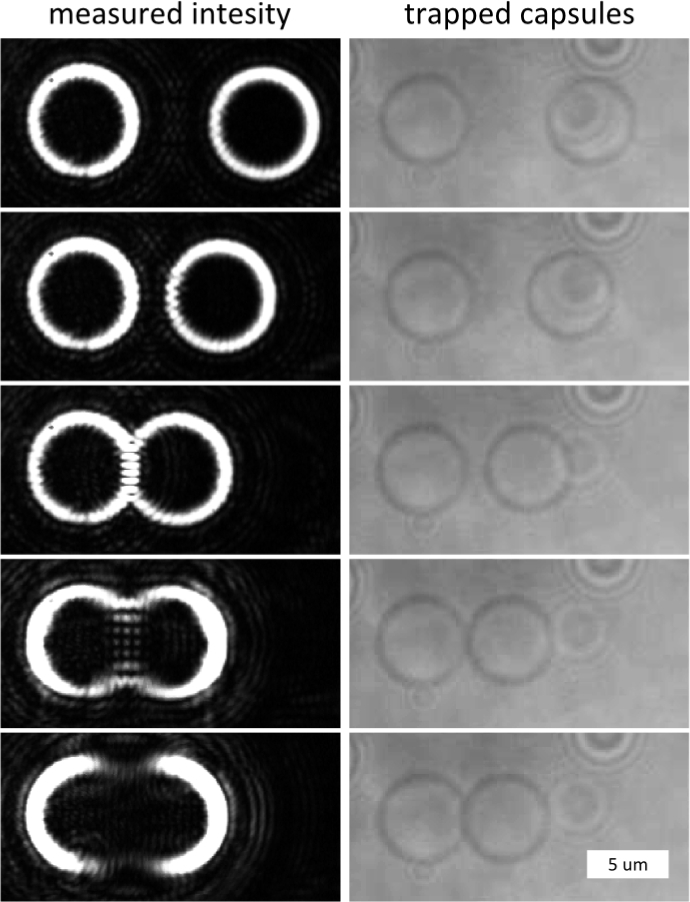
Two vortex beams are generated to simultaneously trap two PBCs. By moving and opening the vortices, the capsules were joined.

In this study, a total number of 168 PBCs in the range of 2 µm–7 µm were used and brought into contact. The probability of bonding is illustrated in Fig. 9 . It can be noted, that along with the expanding diameter of the PBCs (2 µm–6 µm), the probability of bonding increases. This is in good agreement to the results of Shchukin et al. [46] and Hodges et al. [47], who analyzed the adhesion forces between polymer and glass microparticles in liquid media. With increasing diameter of these microparticles, the contact area increases. Thus, the interparticle interaction increases and facilitates agglomeration of larger particles. Several models, e.g., Johnson-Kendall-Roberts (JKR), Derjaguin-Muller-Toporov (DMT), or Maugis-Dugdale (MD), can be used to describe the contact mechanics. A comparison of various contact theories is given by Shi et al. [48] and Johnson et al. [49]. Further information about forces and interactions between particles can be found in Cappella et al. [50].

Fig. 9.

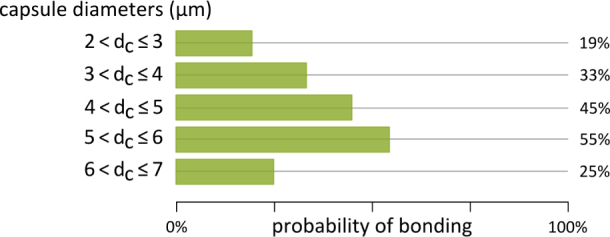
A number of 168 capsules were optically joined and the presented probability of bonding was determined.

In addition, different models are used to describe the aggregation process of RBCs as natural oxygen carriers and the mechanisms of interaction between RBCs. It is assumed that “depletion-mediated” mechanisms due to osmotic pressure as well as “cross-bridge” migration are responsible for cell interactions [51]. Investigations of the forces that occur during disaggregation are promising to further understand these processes [52, 53].

In order to decide which model of contact mechanics is suitable for the PBCs, the mechanical parameters, e.g., elasticity, of the capsules must be investigated and further work is required to analyze the separation forces of adhered PBCs. Furthermore, the roughness of the surfaces and the surrounding medium play an important role for the interaction between microspheres and must be analyzed [54–56]. However, we can presume that PBCs smaller than 2 µm adhere even less (< 19%), which is an important prerequisite for the use as artificial oxygen carriers.

In presented experiments, the probability of bonding of larger capsules (> 6 µm) significantly decreases. This could be related to the relatively low number of capsules examined. A number of 16 larger capsules (> 6 µm) were joined. For all other sizes ranges almost equal numbers were investigated. However, this observation may not necessarily be an artifact. Bonding is a result of the combination of various acting forces, that could have different influences at different scales. Thus, repulsive forces could become relevant at larger capsule diameters, e.g., due to albumin absorption on the capsules surfaces [57]. Further work is required to establish statistically significant results and to further elucidate the role of BSA on the surface of the PBCs. Nevertheless, the OT in combination with dynamic holograms has proven to be very suitable for the investigation of low-index particles. The HOT operates with defined and adjustable forces and is non-invasive. Therefore, the capsules can be studied in physiological environment without mechanical, chemical, and thermal influences and treatment. Additionally, fusion of the capsules was not observed in all experiments. It is assumed, that Oswald-ripening of the capsules failed, which is a very important finding regarding the use of the PBCs as artificial blood.

5. Conclusion

In this study, the HOT was successfully tested and established as a tool for the contactless examination of PBCs as artificial oxygen carriers, although basic conditions (only minor differences in refractive index between capsules and surrounding medium) were not encouraging at first sight. Trapping and moving in all three dimensions by using a vortex beam was demonstrated. Furthermore, procedures to quantify the optical forces in axial and radial direction were described and realized. Based on these findings, the HOT was successfully applied for initial investigations of surface interactions between PBCs in an experimental in vitro setting mimicking the (in vivo) physiological conditions of blood plasma very effectively. To get a deeper insight on the intercapsular interaction behavior, a suitable method to join two capsules by opening two vortices with a dynamic computer generated hologram was developed. This method represents a very flexible, fast, and simple technique for studying the agglomeration behavior of low-index particles. This analysis shows that agglomeration of capsules increases with increasing diameter of the capsules. This gives us reason to expect that nanocapsules do interact even less than the microcapsules studied in these experiments. However, more detailed studies are needed to make a more accurate statement and further experimental investigations have to be implemented to quantify the bonding forces. Furthermore, it is now possible to investigate other more physiologically relevant questions such as the interactions between PFD-capsules and erythrocytes; data that will really be helpful to further improve the PFD-capsules for in vivo applications.

Funding

The current project did not receive any third-party funds.

Disclosures

The authors declare that there are no conflicts of interest related to this article.