Automatic interstitial photodynamic therapy planning via convex optimization

Abstract

Finding a high-quality treatment plan is an essential, yet difficult, stage of Photodynamic therapy (PDT) as it will determine the therapeutic efficacy in eradicating malignant tumors. A high-quality plan is patient-specific, and provides clinicians with the number of fiber-based spherical diffusers, their powers, and their interstitial locations to deliver the required light dose to destroy the tumor while minimizing the damage to surrounding healthy tissues. In this work, we propose a general convex light source power allocation algorithm that, given light source locations, guarantees optimality of the resulting solution in minimizing the over/under-dosage of volumes of interest. Furthermore, we provide an efficient framework for source selection with concomitant power reallocation to achieve treatment plans with a clinically feasible number of sources and comparable quality. We demonstrate our algorithms on virtual test cases that model glioblastoma multiforme tumors, and evaluate the performance of four different photosensitizers with different activation wavelengths and specific tissue uptake ratios. Results show an average reduction of the damage to organs-at-risk (OAR) by 29% to 31% with comparable runtime to existing power allocation techniques.

1. Introduction and prior work

Photodynamic therapy (PDT) is the light activation of photosensitizers, inducing the production of oxygen radicals with the aim to destroy particular tissues in situ. The process starts by administering a photosensitizer to the patient, which will preferentially accumulate in the target tissue, followed after a photosensitizer-specific time delay with the irradiation of the treatment region with photosensitizer-specific visible or near-infrared light. The photosensitizer absorbs the light and initiates a series of photochemical reactions that generate cytotoxic products which lead to the desired treatment effects [1]. PDT has shown high efficacy in treating several superficial tumors such as skin cancer [2] and esophagus tumors [3] through surface illumination techniques. A more efficient illumination scheme that can target deep tissues is interstitial light delivery, in which fiber-based spherical light diffusers are placed directly into the target tissues [4]. However, several pre-clinical studies have shown that the treatment response with interstitial delivery is strongly dependent on the light dose distribution, which is itself dependent on the optical properties of the patient’s tissues and the placement of the light sources [5–7]. Therefore, the success and efficacy of interstitial photodynamic therapy (iPDT) strongly depends on planning the photon source placement based on a patient’s particular anatomy of the target and the surrounding tissues.

An iPDT treatment plan represents the proposed flow of the upcoming therapy. It specifies in particular the photosensitizer drug to use, its activation wavelength, the treatment time, and the number of light sources to use, their positions and the power for each light source. The success of PDT is contingent on attaining a sufficiently high cytotoxic dose in the target where the effective dose can be given by any of the existing PDT dose descriptions such as the photodynamic threshold model [8]. A perfect plan would result in a photon source distribution that leads to the complete destruction of the tissue in the target volume without affecting any surrounding healthy tissues, particularly organs at risk (OAR), i.e. healthy tissues that can tolerate only a limited amount of PDT dose without being harmed. Such a perfect plan usually does not exist, and clinicians face several challenges that hinder the establishment of a high-quality plan to destroy the target volume with minimal damage to the OAR.

To create an optimized treatment plan, we first need to accurately evaluate the plan by modeling the light distribution inside the tissues, the forward problem. For a given photon source, the light distribution, or fluence rate [mW/cm²], will vary among patients as it is dependent on the patient’s tissue optical properties and anatomy. The radiative transfer equation (RTE) which governs this process is generally not solvable for most realistic media of interest [1] and thus approximation methods are needed. Previous approaches to PDT treatment planning primarily used two methods. The simplest approach assumed an empirically determined radius around each source, in which cells are destroyed, and added sources with this kill-radius to cover the target tissue, while leaving other tissues unharmed [9, 10]. A more sophisticated method is to use a diffusion approximation of light transmission in combination with either homogeneous [4] or heterogeneous optical properties [11–13], while applying a fluence [Jcm⁻²] threshold above which a tissue is destroyed. The main weakness of both approaches is the failure to accurately model the reflection and refraction of light at tissue boundaries with different optical properties, which often occur in biological systems [14]. They also do not take into account direction-dependent scattering and assume isotropic scattering events, which is not the case within a few mean-free paths from the photon sources, boundaries or photon sinks. Other discrete and continuous analytical solutions have been studied recently [15], and were found to be accurate only within homogeneous tissues. To accurately model tissue inhomogeneities and scattering events, we have used the Monte Carlo photon simulator FullMonte [16], one of the fastest accurate simulators of dose distribution published to date. By combining the light distribution computed by FullMonte with the relative photosensitizer concentration and the various tissues uptake, we can compute the PDT response throughout the volume of interest.

The second component of treatment planning is determining the minimal number of light sources required, their locations, and their power allocation – the inverse problem – which remains a major challenge in iPDT planning. This step is of utmost importance as it affects the treatment efficacy and is known to be highly correlated to the damage caused to the OAR [1]. Finding a high-quality treatment plan generally involves a sub-problem of finding a good power allocation among the light sources. Several attempts on this problem have been investigated in the literature, and the best allocation algorithm to date is the Cimmino linear feasibility algorithm [4, 12, 17]. A more general problem to achieve better-quality plans is to optimize the sources’ locations along with their power allocation. This problem is highly non-linear, and there is no technique to our knowledge that finds the optimal solution in a reasonable time for clinical praxis. Several attempts at treatment planning varied the possible source positions with a variety of sub-optimal perturbation algorithms [4, 11, 18]. Another approach used for source position optimization is Powell’s method for nonlinear optimization, which finds a local minimum of an optimization cost function, at the risk of potentially missing the global minimum [9, 10]. The implementation of Powell’s method relies on a simplified dichotomous PDT dose model which assumes uniform fluence and complete tissue destruction within a certain radius, while tissues outside are unaffected. Another significant downside of most of the proposed source placement optimization techniques is to assume homogeneous tissues, such as the prostate, where the vascular perfusion tree supports the confinement of the light in the gland limiting its exposure to the surrounding OAR. Additionally, over-treatment within the prostatic gland is not necessarily considered a major drawback [4, 11, 19, 20]. Applying those approaches to tumors inside optically heterogeneous tissues, such as the brain, can yield low-quality plans that can not achieve the desired effect without potentially affecting eloquent areas of the brain.

In this work, we propose a fast and effective iPDT planning optimization work flow for most tissues, here evaluated on synthetic brain tumors. The proposed implementation operates on 3D meshes of segmented MRI or CT scan images of the target volume. Moreover, it assumes that the photosensitizer drug to use, its tissue uptake, and the tissue optical properties are all known to the clinician. The fluence dose threshold for each tissue can be determined based on that tissue’s response to the cytotoxic reactions due to the photosensitizer being used. Finally, the proposed approach requires a light propagation simulator to determine the fluence rate distribution for each source placement. As mentioned earlier, we use FullMonte [16] for this purpose. Given the aforementioned inputs, we propose a cost function that can be efficiently minimized to create a power allocation for a set of fixed light sources. The proposed power optimization approach generalizes the implicit least-squares cost function of the Cimmino algorithm [21] to the broader space of convex optimization problems, in this case to a linear program (LP, an optimization model with requirements expressed by linear relationships [22]). It has the benefit of allowing the use of a wide class of fast algorithms that are guaranteed to converge to a global optimum, along with the flexibility in adding constraints (such as total or per-source power limits). The latter can allow clinically relevant factors to be taken into account, such as minimizing treatment duration, which for fixed target dose, would imply higher irradiation power, potentially at the cost of slightly more damage to healthy tissues. We then leverage the robustness, speed and guaranteed optimality of this power allocation program to select and iteratively refine the light source locations to further optimize the treatment plan.

2. Cost-based optimization of power allocation with fixed source distribution

2.1. Problem formulation

To support automatic optimization, treatment plans must be ranked in terms of preference. This requires a cost function, which assigns a scalar value to a treatment plan to facilitate its comparison with any other plan. Plans with lower cost function values are more desirable. For a given set of source positions, dose optimization should be based on a cost function that attributes a cost value to each power allocation, such that the contribution to the cost value is zero for regions in which all target light dose criteria are fulfilled (e.g. exact match or upper/lower thresholds are obeyed), whereas the contribution to the cost value gradually increases for over/under-dosed regions. Ideally, we want all tumor elements to receive at least their minimum dose that would guarantee destruction of the tumor, while not affecting any healthy element. We formulate such a cost function as follows.

Let m be the number of available light sources, and x an m × 1 vector of all the light sources’ powers. Let also f(x) be a scalar cost function that measures the over/under-dose for a given plan (according to some metric) across all volume elements, where a smaller f(x) translates to a better-quality plan. Then the best power allocation of the m sources is a vector x^* that minimizes f(x) as shown in Eq. (1).

$$\begin{array}{ll}\underset{\mathbf{x}}{\text{minimize}}\hfill & f(\mathbf{x})\hfill \\ \text{Subject to}\hfill & \mathbf{\text{Ax}}\le {\mathbf{p}}_{\mathbf{\text{max}}}\hfill \end{array}$$ (1)

where the matrix A is used to set the power constraints on certain combinations of sources, i.e. it can be used to supply per-source power constraints and/or a total power limit for some (or all) sources. p_max is a column vector of size similar to the number of constraints (rows) in the matrix A, each element of which is the maximum power limit to the corresponding constraint. For example, assume that we have m = 5 sources, indexed from 1 to 5, and k constraints (A would be of size k × 5). Assume also that constraint i ≤ k requires that the total power limit on sources number 2 and 4 should not exceed 1W, then the i^th row of the matrix A would be as follows:

$${\mathbf{A}}_i=\left[\begin{array}{ccccc}0& 1& 0& 1& 0\end{array}\right]$$

and the i_th entry of p_max would be 1. Note that if treatment time is a variable in the optimization, then x and p_max will represent energies and not powers.

Depending on the definition of f(x), the speed of the optimization and the quality of the solution may change. While f(x) could be any function that models the treatment plan quality well, functions with convex forms are particularly amenable to optimization. A convex function is a function in which the line segment that connects any two points in the domain of the function is always above or on the graph of the function. In optimization problems, convex functions are distinguished by the fact that a local minimum is always a global minimum [22], which makes minimizing such functions across their domains easier and faster to converge with guaranteed optimality. The simplest form of convex optimization problems are those of a linear form [22], and several fast academic and commercial tools are available for the minimization of these problems. For the above reasons, we define our cost function f(x) in this work to be convex and linear in the optimization variable x as follows.

Let n be the number of discretized volume elements in the treatment planning volume. Let also d_min,i and d_max,i be the minimum and maximum light target doses, respectively, for each volume element i, where d_min,i < d_max,i∀i. In this work, we set d_max,i to be +∞ for all tumor elements, and d_min,i to be 0 for all healthy tissue elements. Moreover, let g_i be a 1 × m vector, each entry of which is the light fluence dose obtained at volume element i due to one of the m sources with unit power. Due to linearity, superposition applies, and therefore, the dot product (g_i · x) would give the total fluence dose obtained at element i due to m sources with their respective powers. Then the cost at element i, f_i(x), is

$$f_i(\mathbf{x})=\{\begin{array}{ll}{w}_i{v}_i\left(d_{\mathit{\text{min}},i}-{\mathbf{g}}_i\cdot \mathbf{x}\right)\hfill & {\mathbf{g}}_i\cdot \mathbf{x}<d_{\mathit{\text{min}},i}\hfill \\ w_i{v}_i\left({\mathbf{g}}_i\cdot \mathbf{x}-d_{\mathit{\text{max}},i}\right)\hfill & {\mathbf{g}}_i\cdot \mathbf{x}>d_{\mathit{\text{max}},i}\hfill \\ 0\hfill & \text{Otherwise}\hfill \end{array}$$ (2)

where w_i is an importance weight per volume element i that is set by the clinician to reflect the importance/priority of each tissue type, and v_i is the element i’s volume so that a larger element contributes more to the overall cost.

Summing f_i(x) over all volume elements yields the total plan cost

$$f(\mathbf{x})=\sum _{i=1}^n{f}_i(\mathbf{x})$$ (3)

By minimizing Eq. (3) over all possible source powers, we penalize under/over dosage on all elements, and the solution is the optimal source power allocation that minimizes this cost. Note that f(x) in this case is the sum of convex and piecewise continuous affine functions in the source power vector x, which means that f(x) is a convex function [22].

2.2. Overall program flow

In order to optimize the power allocation across a given set of sources, we need to simulate the light transport in the biological tissue under treatment. To this end, we use FullMonte [16], one of the fastest software packages (to date) for Monte-Carlo-based simulation of light propagation in turbid media. FullMonte’s modeling supports anisotropic scattering and refractive index changes. It also expresses its problem geometry in 3D tetrahedral meshes, giving accurate surface normals and avoiding artifacts introduced by voxel-based representations. FullMonte allows multiple types of light sources, making it flexible for various clinical applications.

After determining the number, m, of sources, and their positions, we run FullMonte with each of the m light sources with unit power, and find the fluence [Jmm⁻²] distribution obtained in every mesh element. From those distributions, we build a Fluence Matrix G of size n × m, where n is the number of tetrahedra in the mesh. Each element G_ij, 1 ≤ i ≤ n and 1 ≤ j ≤ m, of the matrix G is the resulting fluence [Jmm⁻²] at tetrahedron i due to the light source of index j with unit power.

After finding G, we introduce power constraints as in Eq. (1) that allow us to reduce the size of the fluence matrix by removing rows that correspond to unnecessary elements. This matrix reduction speeds up the optimization without affecting the results. An unnecessary element is a healthy tissue element that receives a total fluence that can never exceed its dose threshold and therefore its cost contribution is always zero and does not affect the minimization. In this work we set a constraint on the total power summed over all sources to be able to prune unnecessary elements. Due to the fact that the matrix was built by giving every source a unit power, then the maximum value in that element’s row would correspond to the worst-case fluence value that can be received after the optimizer is run (i.e., total power allowed is given to one source). Therefore, if the dose threshold at that element is not violated by that maximum value, it will not affect the results of the optimizer, and it can be pruned. With this pruning, the size of the matrix is significantly reduced (by around 90% in the test cases studied), and this speeds the optimizer up. We call the new number of tetrahedra n′.

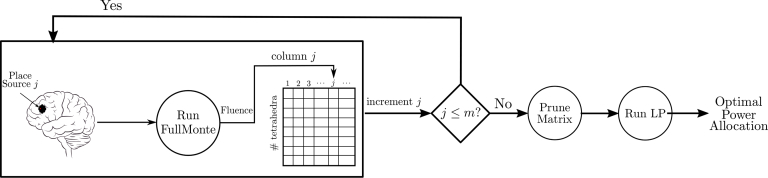
Finally, we run the linear program in Eq. (1) with f(x) as shown in Eq. (3) to determine the best power allocation given the m sources. Figure 1 displays the overall power allocation program flow.

Fig. 1.

Flow diagram of the proposed approach

3. Test scenario and evaluation metrics

In this section, we introduce our testing methodology and discuss how we evaluate the dose thresholds at which tissue death occurs. We also define the metrics that we use to evaluate our results.

3.1. Test cases

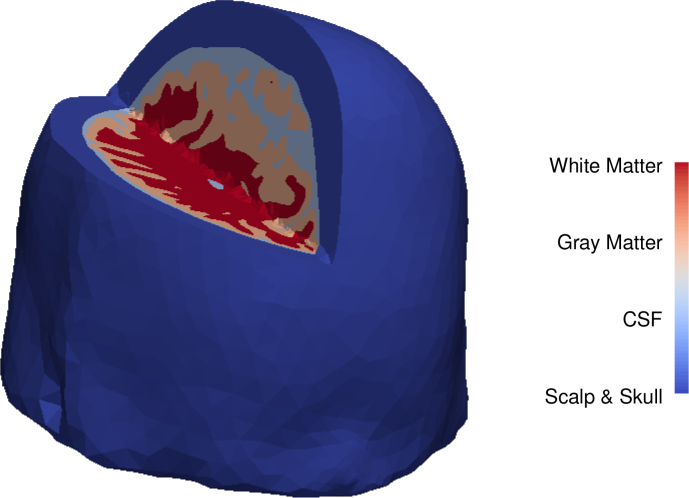
All our tests use a 3D tetrahedral mesh of a human brain comprising 423376 tetrahedra taken from [23]. The mesh is generated from a segmented human brain atlas [24, 25] and comprises four different materials: skull, cerebrospinal fluid (CSF), grey matter, and white matter. Figure 2 shows the human brain mesh under test, with a 3D cut that shows the four different materials. The lateral and third ventricles, which are filled with CSF, are not considered in this work. However, results should not be affected, since any tumor would compress the ventricles and displace the cerebrospinal fluid. We already consider tissue volumes containing CSF between the skull and the brain in our simulations.

Fig. 2.

Human brain mesh used in our simulations with a 3D cut showing the different materials

Nine different virtual brain tumors were modeled to approximate clinical glioblastoma multiforme images obtained from the cancer imaging archive [26]. The virtual tumors comprise operable as well as inoperable tumors. Locations were proximal to the brain stem, the cerebellum, and the motor and speech centers of the frontal lobes. The tumor shapes are either of elongated ovoid forms or of several connected spherical forms. Deformation of the brain and in particular the ventricles was not considered in these virtual cases. The tumor models consist of 3543 to 14974 tetrahedra representing 17.55 to 109.93cm³ volumes. The maximum long axis of the tetrahedra in the tumors is around 11.5mm with an average across the nine tumors modeled of 5.54mm which is approximately 4 – 6 times the penetration depth (reciprocal of the effective attenuation coefficient, μ_eff) of the tumor’s tissue optical properties at 630nm to 675nm used in these simulations (refer to Table 4). While the long axis of individual tetrahedra may exceed the penetration depth of the light and hence could undersample the light distribution, our simulations show that light attenuation within the tumor is sampled well and the ensemble of tetrahedra represents the theoretical fluence gradient well.

Table 4.

Optical properties of the different tissues at different wavelengths. The values are taken from [29–35].

Wavelength ( nm )	Optical Property	Tissue Type
		Tumor	Skull	CSF	White Matter	Grey Matter
630	μa(mm−1)	0.2	0.75	0.004	0.08	0.02
	μs(mm−1)	10	12.9	0.009	40.9	9
	g	0.8	0.8	0.89	0.84	0.89
	n	1.39	1.56	1.36	1.467	1.36
635	μa(mm−1)	0.18	0.55	0.0038	0.08	0.01
	μs(mm−1)	10	10.8	0.005	40.7	8.8
	g	0.8	0.8	0.87	0.84	0.89
	n	1.39	1.56	1.3891	1.467	1.36
662	μa(mm−1)	0.12	0.12	0.003	0.075	0.015
	μs(mm−1)	9.5	7.5	0.02	40.4	8.6
	g	0.8	0.8	0.83	0.85	0.9
	n	1.39	1.56	1.3891	1.467	1.36
675	μa(mm−1)	0.08	0.021	0.0025	0.07	0.02
	μs(mm−1)	9	5.95	0.05	40	8.4
	g	0.8	0.8	0.8	0.85	0.9
	n	1.39	1.56	1.3891	1.467	1.36

3.2. Light source locations

The approach discussed in Section 2.2 requires the light source locations as an input. We considered a placement of point sources inside the tumor with a spacing of 1cm between them and from the tumor’s boundary. This technique was adapted from the approach of Johansson et al. [27], which placed cylindrical diffusers at a maximum of 1cm distances in the brain for malignant glioblastoma treatment, and the approach taken in [28], which used cut end fibers in the prostate with a similar spacing, albeit at a longer wavelength. The number of resulting light sources used varied according to the tumor’s size and shape. The light sources are arranged in a hexagonal close-packed structure and are assumed to emit the light isotropically.

3.3. Dose thresholds and optical properties

It is well established that within the brain the PDT responsivity of the different tissues depends, among many factors, on the photosensitizers and their concentration in the tissue. Therefore, the minimum and maximum dose thresholds need to be tissue-specific [8]. Each tetrahedron is assigned a minimum dose threshold, d_min, if it is a cancerous element, or a maximum threshold, d_max, if it is a healthy element. Let TPV_k be the death threshold of tissue k in terms of the number of photons absorbed by the photosensitizer per unit volume to induce tissue necrosis. Then the dose threshold values are calculated based on the relative photosensitizer uptake ratios of the tumor with respect to the healthy tissue k and that tissue’s TPV_k. We considered four different photosensitizers with different activation wavelengths. Table 1 summarizes the photosensitizers considered, along with their corresponding activation wavelengths, and the relative uptake ratios of the brain tumor to the white and grey matters, respectively. Note that only the mean uptake ratios are considered in this work. Section 6 discusses the impact of the uptake ratios’ standard deviations. Table 2 shows the TPV_k of each material k in terms of the number of photons absorbed by each photosensitizer per cubic millimeter to induce necrosis [8].

Table 1.

PDT photosensitizers, their activation wavelengths and their relative uptake ratios. The uptake ratios data were taken from Table 3 in [8] for (a) 5mg.kg⁻¹ administered dose and 24hrs delay, (b) 100mg.kg⁻¹ administered dose and 6hrs delay, (c) 1mg.kg⁻¹ administered dose and 24hrs delay, and (d) 0.5mg.kg⁻¹ administered dose and 24hrs delay. Those ratios were calculated based on the tissue specific uptake ratios (SUR) as quantified tissue concentrations over administered concentrations in one (SnET as photosensitizer) to three animals.

Photosensitizer		Photofrin (a)	ALA (b)	SnET (c)	ALCIPc (d)
Activation Wavelength ( nm )		630	635	662	675
Relative Uptake Ratio	Tumor/Grey matter	10.6 ± 1.4	22 ± 3.4	1.5	12.7 ± 2.4
	Tumor/White matter	8.2 ± 0.9	72 ± 14	3.4	24.9 ± 4.3

Table 2.

Tissue death threshold values (TPV_k) given in number of photons absorbed by each photosensitizer per mm³ (×10¹⁸). The data were taken from Table 3 in [8] for (a) 5mg.kg⁻¹ administered dose and 24hrs delay, (b) 100mg.kg⁻¹ administered dose and 6hrs delay, (c) 1mg.kg⁻¹ administered dose and 24hrs delay, and (d) 0.5mg.kg⁻¹ administered dose and 24hrs delay.

Tissue Type	Photosensitizer
	Photofrin (a)	ALA (b)	SnET (c)	ALCIPc (d)
Tumor	18	1.3	0.6	28
Grey Matter	2.7	0.39	0.5	29
White Matter	2.8	14.2	0.01	42

From Tables 1 and 2, the relative tissue death dose threshold values of the healthy materials with respect to a tumor’s minimum threshold are calculated as shown in Eq. (4).

$$\text{Relative Tissue Death Dose Threshold of material}k=\frac{{\mathit{\text{TPV}}}_k}{{\mathit{\text{TPV}}}_{\mathit{\text{tumor}}}}\times \text{uptake ratio of tumor to material}k$$ (4)

By normalizing the minimum dose threshold of the tumor to 1J/mm², we can use Eq. (4) to calculate the relative death threshold for the two sensitive tissues to PDT in our test cases: the white and grey matters. To account for variability in tissue response and maximize therapeutic safety, we introduce a certain guardband on those death thresholds and provide the optimizer with lower relative dose targets. In this work, we aim to stay one order of magnitude below the death thresholds for the white and grey matters. As for the skull and CSF, they are considered rather resistant to PDT. The bone has little photosensitizer, and the scalp and skull are typically far from the light sources in any case (as they are spatially separated from the tumors), so PDT is highly unlikely to damage those tissues. However, the dura and the other meninges are adjacent to the skull and no threshold data for these structures are available. Therefore, we conservatively set the maximum relative dose threshold of the skull, d_max,skull, to be d_min of the tumor. As for the CSF, Table 4 shows that its absorption coefficient is very low compared to the other tissues involved. Additionally, the CSF is acellular liquid, and potentially damaged proteins within the CSF will be diluted as the CSF flows through the brain and spinal column. Therefore, we set the d_max of the CSF to be 10 times the maximum threshold of the other tissues. Table 3 summarizes the relative tissue dose threshold for each tissue type. In the rest of this paper, we refer to these values as evaluation thresholds, as we evaluate all our results based on those values.

Table 3.

Relative tissue dose threshold values with respect to the tumor’s minimum threshold value for each tissue and each photosensitizer. The white and grey matters’ maximum thresholds were scaled down by 10 to increase PDT safety.

Tissue Type	Photosensitizer
	Photofrin		ALA		SnET		ALCIPc
	dmin	dmax	dmin	dmax	dmin	dmax	dmin	dmax
Tumor	1	∞	1	∞	1	∞	1	∞
Grey Matter	0	0.16	0	0.67	0	0.13	0	1.32
White Matter	0	0.13	0	72	0	0.01	0	4.15
Scalp & Skull	0	1	0	1	0	1	0	1
CSF	0	10	0	720	0	10	0	41.5

The optical properties for each tissue type at the aforementioned wavelengths were extracted from the literature [29–35]. Table 4 shows the optical properties at the different wavelengths considered, where μ_a, μ_s, g and n are the absorption coefficient, scattering coefficient, anisotropy factor and the refractive index, respectively. Unless otherwise specified, the results shown in this work all assume the ALCIPc photosensitizer activated at 675nm wavelength, because Table 3 shows it has good tumor selectivity.

3.4. Evaluation metrics

In this section, we introduce the quality metrics that we use to evaluate our treatment plans and compare to previous approaches.

3.4.1. Dose volume histogram (DVH)

A Dose Volume Histogram (DVH) is a histogram that relates the dose irradiation to a tissue volume in treatment planning. It is most commonly used as a plan evaluation tool in the literature to compare the doses from different treatment plans. DVHs reduce 3D dose distributions within a defined volume of interest to simple 2D curves, which makes them easier to quantify visually.

It is worth noting that our proposed cost function in Eq. (2) is closely linked to the DVH, since the cost is weighted by the volume of each element and depends only on the dose received at each element and the target dose parameters (d_min and d_max) set for that element. Therefore, minimizing the volume-weighted positive difference between the actual received dose and the maximum threshold dose effectively translates to minimizing the area below the DVH curve for an OAR, and maximizing the negative difference between the actual received dose and the minimum threshold dose effectively maximizes the area under the DVH curve for the tumor. This means that a plan with a lower cost function value has a better-quality DVH.

3.4.2. Tissue v_α

A tissue v_α is the tissue volume (or percentage of the volume) that receives at least α% of its relative threshold dose. A tissue v_α can be extracted from its DVH curve by taking the point at α% of the dose threshold. An ideal plan has a v₁₀₀ of 100% for the target, and 0% for an OAR. In this work, we quantify our results and comparisons using tissue v₉₀, as it reflects the safety of the treatment on the OAR. In addition, v₉₀ reflects how close the plan is to fully destroying the tumor. One could alternatively evaluate treatment success with v₁₀₀, but we have found that a higher v₉₀ on the tumor effectively translates to a higher v₁₀₀, and our experimental results show that the average difference between the tumor v₉₀ presented here and its v₁₀₀ is less than 0.5%. It is also worth noting that v₁₀₀ is not widely used in ionizing therapy as a treatment plan evaluation parameter [36].

3.4.3. Integral overdose

Summing the excess dose (above the evaluation threshold) over all healthy tissue tetrahedra yields the integral overdose as defined in Eq. (5). This metric indicates not just how much healthy tissue volume is overdosed, but also the magnitude of the overdose.

$$\mathit{\text{integral overdose}}=\sum _{\forall \text{healthy elements}k}\text{max}\left\{0,v_k({\mathbf{g}}_k\cdot {\mathbf{x}}^{*}-d_{\mathit{\text{max}},k}^{\mathit{\text{eval}}})\right\}$$ (5)

where $d_{\mathit{\text{max}},k}^{\mathit{\text{eval}}}$ is the evaluation threshold of healthy element k.

3.5. Platform

C++ and Matlab codes were written for the proposed program flow, and run on a Linux machine with a 3.5GHz Xeon E5-1620 CPU and 64GB of RAM. For the C++ code, the MOSEK library [37] was used to solve convex optimization problems, while Matlab’s internal solver was used for the Matlab one. The interior point method for convex optimization was used in C++, while dual-simplex was used in the Matlab solver. The Cimmino algorithm was only written in Matlab, so its results use the Matlab solver.

4. Power allocation with fixed source distribution results

In this section, we present results to validate the power allocation algorithm of Section 2. We first show how our LP cost function shown in Section 2.1 correlates with v₉₀. Next we study how changing the importance weight, w_i,tumor, on the tumor elements in the LP affects the v₉₀. We then tune the maximum dose targets of the healthy tissues to see the effect on the tumor dose coverage of the optimal power allocation. Finally, we compare the results of our proposed approach to the Cimmino algorithm presented in [4].

4.1. Correlation to v₉₀

To test the correlation between the cost function value and v₉₀, we evaluated v₉₀ changes with the change in the final cost f(x) according to Eq. (1). To do this, we added one light source at a time sequentially (based on the placement discussed in Section 3.2) to the proposed work flow, prior to executing the LP, and computed the attained v₉₀. With increasing number of light sources, the final cost should be reduced, as the LP has more free parameters with the same number of constraints, which means a bigger search space to achieve a better solution.

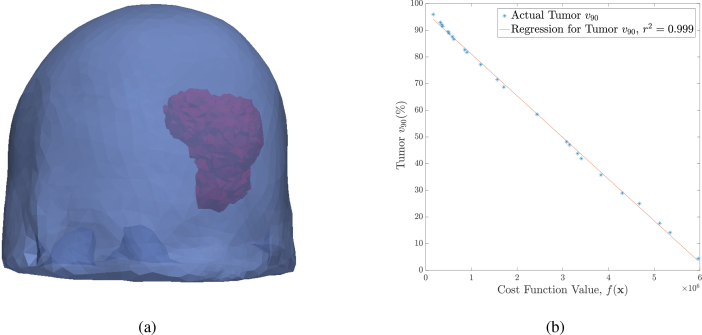
For this test, we used an 11079 tetrahedra tumor (see Fig. 3(a) ). Figure 3(b) shows the tumor v₉₀ versus the cost function value. We can see that the v₉₀ is strongly correlated to the cost (coefficient of determination, r² = 0.99), indicating that our proposed cost function directly reflects the overall coverage of the tissue. A zero cost entails a full destruction of the tumor with a tumor v₉₀ of 100% (from the figure), while no damage is caused on the healthy cells.

Fig. 3.

(a) The brain mesh (blue) used with one of the modeled tumors (red). (b) The tumor v₉₀ versus the cost function value when using ALCIPc as the photosensitizer drug (activated at 675nm), along with a fitted line of the data showing the strong correlation.

4.2. Trade-off of varying importance weight on tumor

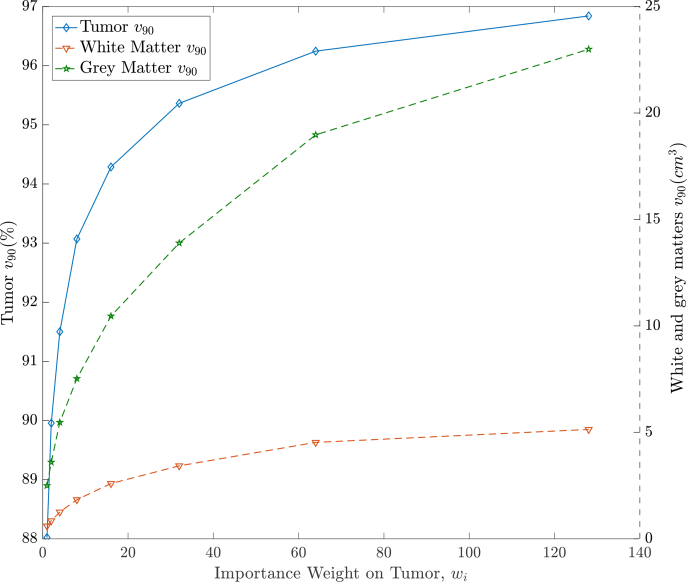
In the proposed cost function of Eq. (2), a certain weight, w_i, is given for every volume element to reflect its importance. In this section we examine the trade-off of increasing the weight on all tumor elements, but not on healthy tissues, by calculating the resulting v₉₀ of the tumor and the healthy tissues. We fixed the weight on all healthy tissues to be inversely proportional to their evaluation dose threshold, i.e., a lower evaluation threshold means a higher priority given to the corresponding tissue. We then varied the tumor weight by multiples of 2, and repeated the LP. Figure 4 shows the v₉₀ of the tumor (for the same model shown in Fig. 3(a)) on the left y – axis (blue curve), and that of the white and grey matters (red and green curves, respectively) on the right y – axis against the tumor’s weight. As expected, increasing the weight on the tumor increases the degree of tumor coverage in the optimized treatment plan, as the penalty associated with under-treated tumor tetrahedra and thus their influence on the optimization, is increased by the weighting. As a result, more damage is caused in healthy tissues. The figure indicates that more damage is caused in grey matter, which is expected since its sensitivity towards ALCIPc-mediated PDT is higher than that of white matter (relative death dose threshold is lower according to Table 3). However, the rate of increase in tumor coverage diminishes for large weights as can be seen in the figure. Since source placement is a fixed input and not optimized, tumor locations far from the sources may not reach the target dose, regardless of how large their importance weight is. From Fig. 4, we see that the saturation starts at an importance weight, w_i, of around 60. Table 5 shows the resulting v₉₀ of the tumor and the healthy tissues for all the tumor models with a tumor weight of 60. We see that, on average, 95% of the tumor is receiving 90% of the dose threshold, which reflects how effective our cost function is.

Fig. 4.

Increasing the importance weight on tumor dose drives the optimizer to increase the tumor v₉₀ (blue), at the expense of increased damage to the OAR (green and red). This test is made on a tumor volume of 103cm³ with 24 light sources at 675nm.

Table 5.

v₉₀ results with a tumor importance weight w_i,tumor = 60, using 675nm for ALCIPc activation.

Tumor Model	Volume ( cm 3 )	# Sources	Tumor v90(%)	Grey Matter v90(cm3)	White Matter v90(cm3)
Tumor 1	103.81	24	95.97	17.82	4.40
Tumor 2	109.93	23	96.42	16.81	3.09
Tumor 3	32.89	10	95.67	9.87	3.73
Tumor 4	31.77	10	94.89	11.45	3.42
Tumor 5	22.39	9	94.79	8.50	3.24
Tumor 6	59.74	14	95.62	14.49	5.11
Tumor 7	38.51	12	93.91	11.85	4.93
Tumor 8	39.27	7	92.06	7.10	4.62
Tumor 9	17.55	6	97.55	3.41	1.47
Geometric Average	42.19	12	95.20	10.20	3.58

4.3. Dose threshold guardband tuning

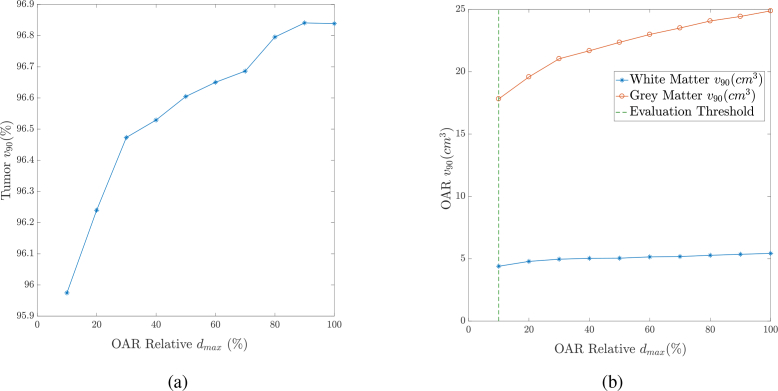
When planning PDT treatment, we must account for uncertainty in optical properties, drug concentration, and tissue response. Where uncertainty is large and/or OAR tissue structures are particularly critical, we may need to introduce some conservatism in protecting against overdose. One way to do this is increasing the importance weight of an organ to drive the optimizer to reduce the volume that is overdosed; however that may result in large volumes receiving a near-threshold dose. Alternatively, we can incentivize lower doses throughout a region by reducing the turn-on point of the cost function (the relative dose threshold) for a given region. In Section 3.3, we mentioned that the relative tissue dose thresholds of the white and grey matters were set to a factor of 10 (90% guardband) below the relative tissue death threshold to maximize safety (evaluation thresholds in Table 3). Here, we vary d_max,i of the healthy tissues in the cost function in Eq. (2). We start with d_max,i equal to the actual relative tissue death threshold computed in Eq. (4). Then, we start gradually adding a guardband of 10% at a time to those thresholds and quantify the effect on the tumor’s coverage and OAR’s damage. Specifically, we varied the guardband on the healthy tissue dose threshold from 0% (at 100% relative dose threshold) to 90% (at 10% relative dose threshold). Figures 5(a) and 5(b) show the tumor coverage and the OAR damage, respectively, against d_max,i of the healthy tissues (as a percentage of their relative tissue death thresholds). An x% means that d_max,i is equal to $\frac{x}{100}$ multiplied by the relative death threshold to destroy the tissue. The OAR curves in Fig. 5(b) correspond to white matter (in blue) and grey matter (in red). Note that those curves were calculated based on the evaluation thresholds of Table 3.

Fig. 5.

Tissue v₉₀ against the ratio of the OAR d_max to the relative tissue death threshold at 675nm for ALCIPc activation. (a) The tumor v₉₀. (b) The OAR v₉₀.

We see that the tumor coverage increases with the increase in the maximum permissible dose for the healthy tissues, but more healthy tissue is given a dose above the safe evaluation threshold as shown in Fig. 5(b). This demonstrates that the LP formulation can be guided via changes to the cost function d_max,i parameter to favor more complete tumor destruction or less damage to healthy tissues in the common case where no perfect treatment plan exists.

4.4. Comparison to Cimmino

Most of the existing work in iPDT planning uses the Cimmino linear feasibility algorithm to optimize the power allocation, since it converges quickly, and resorts to a least-square solution if the dose constraints cannot all be satisfied [4]. Here, we compare the quality of treatment plans resulting from the proposed LP to those obtained using the Cimmino algorithm for our brain tumor cases. The Cimmino algorithm was implemented in Matlab 2016a on the CPU mentioned in Section 3.5. We experimented with different stopping criteria for the Cimmino algorithm and found it was best to stop when the relative error between consecutive iterative solutions was less than 10⁻²⁵, or if the algorithm exceeded three times the runtime of the LP. The LP formulation is run with the cost function in Eq. (2) with d_min,i for the tumor elements set to the minimum dose threshold value of 1J/mm² as specified in Table 3, and their d_max,i set to +∞; tumor volume elements will then contribute to the cost value if they are undestroyed. For each healthy tissue, d_max,i is set to 90% of the value in Table 3, as the v₉₀ metric seeks to dose the tissue at 90% or less of the evaluation threshold of acceptable dose, and d_min,i is set to 0.

By changing the weighting parameters, both the Cimmino algorithm and our LP algorithm can trade-off a reduction in tumor destruction for a reduction in healthy tissue damage. To make a fair comparison, we adjusted the importance weight parameters for each algorithm and each tumor to achieve a v₉₀ of 98% of the tumor (previously shown to provide a survival benefit to glioblastoma patients [38]), and then compared the damage to the healthy tissues at this comparable point. Table 6 summarizes the results of the LP and the Cimmino algorithm on all nine tumors when achieving the same v₉₀ on the tumor (±0.2%). The table shows the v₉₀ of both the white and grey matters resulting from both algorithms, the Matlab runtime for both algorithms, and the C++ runtime for the LP. It also shows the number of tetrahedra n′ considered in the optimization after pruning (see Section 2.2). Finally, we show the integral overdose for both algorithms.

Table 6.

Proposed linear program versus Cimmino algorithm for power allocation, for ALCIPc mediated PDT at 675nm.

Tumor Model	n′	Cimmino				Our LP
		Integral Overdose	White Matter v90 (cm3)	Grey Matter v90 (cm3)	Matlab RT (sec)	Integral Overdose	White Matter v90 (cm3)	Grey Matter v90 (cm3)	Matlab RT (sec)	C++ RT (sec)
Tumor 1	110800	40949	10.56	34.08	113	6701	5.32 (−50%)	18.28 (−46%)	38	20
Tumor 2	77600	57086	7.78	29.12	56	5923	3.97 (−49%)	16.93 (−42%)	19	17
Tumor 3	62100	172379	6.74	16.79	3	113775	5.71 (−15%)	14.66 (−13%)	9	13
Tumor 4	62800	506118	7.21	13.97	2	222015	5.04 (−30%)	14.93 (+7%)	18	13
Tumor 5	45300	193998	4.37	11.62	1	147343	4.13 (−5%)	11.59 (−0.2%)	7	8
Tumor 6	63200	214163	11.56	33.03	40	93633	8.14 (−30%)	20.36 (−38%)	13	11
Tumor 7	51100	980304	9.24	28.06	6	488299	7.27 (−21%)	17.71 (−37%)	10	9
Tumor 8	43600	158054	8.50	15.89	3	116340	7.77 (−9%)	12.22 (−23%)	4	6
Tumor 9	39900	166656	2.23	9.15	3	40880	1.47 (−34%)	3.71 (−59%)	2	6
Geometric Average	58902	181970	6.90	19.26	8	68247	4.92 (−29%)	13.28 (−31%)	10	11
Arithmetic Average	61822	276633	7.58	21.30	25	137209	5.42 (−28%)	14.49 (−32%)	13	11

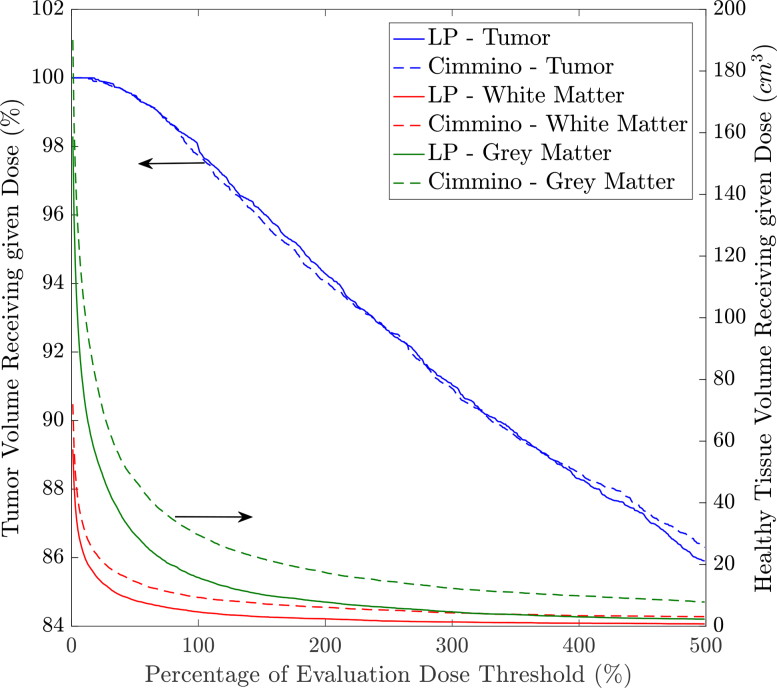
Figure 6 shows a dose volume histogram (DVH) for the tumor (blue curves), white matter (red curves), and grey matter (green curves) using both algorithms on Tumor 1. The solid curves correspond to the LP treatment plans, while the dashed curves correspond to the Cimmino treatment plans. We can see that the damage on the tumor is similar (as expected) but healthy tissues are less damaged with the LP suggested treatment plans. Depending on the tumor shape, number of sources (refer to Table 5), and their locations, we can see from Table 6 that treatment plan quality differs in terms of damage to the healthy tissues. However, our LP consistently causes less damage to the healthy tissues. The white matter damage is reduced on every tumor, with an average v₉₀ reduction of 29%, and the grey matter damage is reduced on 8 out of 9 tumors, with an average v₉₀ reduction of 31%. The integral overdose to healthy tissues is reduced even more dramatically, by an average factor of 2.02×. The runtime of both solvers is reasonable, usually in the tens of seconds, with the LP formulation being somewhat faster than Cimmino for the largest tumors with higher number of sources, indicating the LP formulation has good scalability.

Fig. 6.

DVH comparison between the proposed LP for power allocation and Cimmino algorithm for Tumor 1, treated with 675nm for ALCIPc mediated PDT.

4.5. Different photosensitizers

Table 7 shows the geometric average of the damage to healthy tissues across the nine tumor cases using both algorithms when using different photosensitizers with their respective specific uptake ratios, activation wavelength and tissue sensitivities and optical properties according to Tables 1–4. The weighting parameters were changed in both solvers to achieve a tumor v₉₀ of 98% in all cases. The table also reports the geometric average of the runtime across all tumor cases with the different photosensitizers. The table shows that our LP formulation is robust over different optical properties and dose thresholds in the sense that it always achieves a reduction in the OAR damage compared to Cimmino. The LP achieves 14% – 54% reduction in white matter damage and 12% – 35% reduction in grey matter damage with almost the same runtime of the Cimmino algorithm. Note that the average reduction ratio in OAR damage when using the ALA photosensitizer is better than when using ALCIPc with a 2.3× speedup in runtime. However, the amount of damage to the grey matter is 3.3 times higher in the ALA case (43cm³ compared to 13cm³). On the other hand, Photofrin-mediated PDT achieves comparable OAR damage reduction to ALCIPc-mediated PDT but the total OAR volume damage is around 6 times larger. Finally, SnET-mediated PDT results in the largest total OAR volume damage and the least damage reduction, and takes the longest runtime of all photosensitizers. This is expected as the tumor selectivity is very poor with this photosensitizer as can be inferred from Table 3. Nevertheless, this highlights how this flexible treatment planning system allows rapid evaluation of different photosensitizers in order to choose the most promising photosensitizer for the tumor case under treatment.

Table 7.

Proposed linear program versus Cimmino algorithm for power allocation using different photosensitizers. All values shown in the table are a geometric average across the nine tumor cases.

Photosensitizer	Activation Wavelength (nm)	Cimmino				Our LP
		Tumor v90(%)	White Matter v90(cm3)	Grey Matter v90(cm3)	Runtime (sec)	Tumor v90(%)	White Matter v90(cm3)	Grey Matter v90(cm3)	Runtime (sec)
Photofrin	630	98.10	60.35	94.00	3	98.12	41.18 (−32%)	69.60 (−26%)	3 (1.0×)
ALA	635	98.07	6.43	66.33	9	98.09	2.97 (−54%)	43.19 (−35%)	4 (2.3×)
SnET	662	98.07	87.52	82.99	12	98.02	75.65 (−14%)	73.20 (−12%)	19 (0.7×)
ALCIPc	675	98.05	6.90	19.26	8	98.10	4.92 (−29%)	13.28 (−31%)	10 (0.8×)

5. Optimization of source selection with power re-allocation

5.1. Optimization algorithm

Source position optimization introduces different challenges compared to power allocation optimization, since it is a non-convex problem, and thus finding an optimal solution is computationally expensive. Therefore, such problems generally need to be solved with heuristic techniques (methods for finding sub-optimal solutions to very hard problems in a reasonable time [39]). Previous work has optimized source position with algorithms that perturb positions to a local minimum from a random starting point, such as simulated annealing [11], Powell’s method [9, 10], or other perturbation algorithms [4, 18]. These approaches are inherently weakened by their random starting point and tendency to get trapped in local minima that may be far from the global minimum. We propose a method that takes advantage of the convex nature of the power allocation problem. We first create an evenly spaced grid of many virtual sources; in this work we use a grid spacing of 5mm comparable to 1/μ_eff for most tissues at the wavelengths considered (630 – 675nm), leading to 138 to 884 virtual sources in the nine test cases. Subsequently, we apply the methods described in Section 2 to optimize the power allocation among these sources. Since this power allocation is guaranteed to be the global optimum for a given set of sources, these source powers can be thought of as a heat map that indicates the locations at which it is most beneficial to place sources. With this large heatmap, source position optimization effectively translates to selecting a feasible number of sources from this heatmap that minimizes the OAR damage. However, conversion from the spatial distribution of virtual sources to a feasible, high-quality set of physical sources remains an open problem. We propose one solution for point sources below.

The most obvious way to reduce the large number of virtual sources to a clinically-feasible number of physical sources is to select the q virtual sources that were allocated the highest powers. However, such an immediate source reduction has the drawback of possibly eliminating a collection of closely grouped sources of relatively low power, that would be better replaced by one or two high power sources. To avoid this, we instead first reduce the number of virtual sources to some multiple of the clinically-allowable number of physical sources (e.g. 2× as many) by selecting the m₀ highest power virtual sources. We optimize the power allocation over these m₀ sources, and then create a new solution with m₀ − 1 sources by eliminating the lowest power source. We repeat this re-optimize/eliminate one source procedure until only one source is left. In this manner, we have sets of source combinations that differ in quality and number of sources, and the decision on which combination to take remains with the clinician. The process is summarized in the Light Source Reduction (LSR) Algorithm shown in Algorithm 1

Algorithm 1.

Light Source Reduction (LSR) Algorithm

Inputs: mvs, umvs, m0	// Number of virtual sources and their positions,
	// and maximum number of sources to consider, m0
Outputs: $\mathcal{S}$	// Set of plans with 1 to m0 sources
1: Run the LP in Eq. (3) on the mvs sources, and get the output power vector xvs.
2: Pick the m0 sources with the highest powers from xvs, and their coordinates um0.
3: $\mathcal{S}$ := {(m0, xm0, um0)}
4: m := m0 − 1
5: while m ≥ 1 do
6:   Pick the m sources with the highest powers from xm+1, and their coordinates um.
7:   Run the LP in Eq. (3) on the m sources.
8:   Get the output vector of the LP, xm.
9:   $\mathcal{S}$ := $\mathcal{S}$ ∪ {(m, xm, um)}
10:   m := m − 1
11: end while
12: return $\mathcal{S}$

, whose output is a set $\mathcal{S}$, each element of which is a combination of l sources, their respective power vector x_l, and their position vector u_l.

This approach has multiple advantages: it does not depend on any random initial starting point, making it robust; it uses the convex form of the power allocation problem to make informed decisions of where to place sources; and it allows the medical team to evaluate optimized plans with various numbers of sources and choose the best trade-off between light source count and achieved PDT dose. Note that in all this process, we only need to run FullMonte and extract the Fluence matrix once for all the virtual sources, so there is little computational overhead in re-optimizing over the different number of sources.

5.2. Optimization results

The testing methodology is identical to Section 3, except we now automatically compute source locations rather than taking them as input (starting from the initial grid of virtual sources). For all the tests in this section, we choose m₀ = 50, i.e., the LSR algorithm returns a set of plans with 1 to 50 sources. All results reported in this section are averaged across all nine tumor models under study and use the ALCIPc photosensitizer.

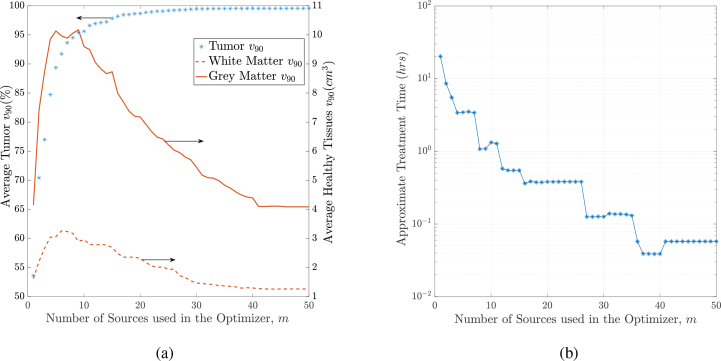
5.2.1. Treatment plan quality versus number of sources chosen

Figure 7(a) shows how the tissue v₉₀ on average changes across the different plans returned. The blue asterisks represent tumor v₉₀, the solid red curve corresponds to the grey matter v₉₀ and the dashed red curve corresponds to the white matter v₉₀. We can see that with more sources, the tumor coverage increases (≈ 99.5% with 50 sources). At the same time, we see that the resulting healthy tissues v₉₀ increases at low number of sources, and then decreases significantly (≈ 1cm³ damage of white matter). This is due to the fact that with a small number of sources, although power is implicitly limited by the cost of OAR, the power allocation optimization problem results in high-power sources (closer to their limit) to cover the tumor, at the cost of causing more damage on the healthy tissues. On the other hand, the power allocation with high number of sources results in a solution with low-power sources that can maximize the destruction of the tumor, and minimize the damage on the healthy tissues.

Fig. 7.

(a) Average tissue v₉₀ against the different plans generated in the LSR algorithm. (b) Average treatment time against the number of sources used in different plans. This treatment assumes the ALCIPc photosensitizer, which is activated at 675nm.

Figure 7(b) shows the approximate treatment time (in log scale) across the different plans. The treatment time was approximated by dividing the total required energy (from the optimizer) by the maximum power that a practical light emitter can output without tissue heating at the emitter tip, which is around 200mW [40, 41]. Note that while the actual light emitter or applicator type used is of interest as well as the tissue irradiated (predominantly due to its effective attenuation coefficient), the actual emitter type and its emission characteristics are outside the scope of the this manuscript, which presents an improved optimization algorithm for treatment planning. The figure shows that very high number of physical light sources (27 – 50 sources) results in good-quality plans that can treat the patient in 6 – 10 minutes (0.1 – 0.17hrs) with the ALCIPc photosensitizer. However, having too many sources is not desirable in PDT plans, as it increases the number of insertions into the malignancy. In our future work, we plan to target this problem by investigating line sources that can illuminate larger parts of the tumor with fewer number of light sources; the algorithms in this section should naturally generalize to this case.

5.2.2. Treatment plan quality with and without source selection

Table 8 compares the quality of the plan resulting from the fixed source placement technique discussed in the previous sections with that resulting from the LSR algorithm with the same number of sources (number of physical sources). We fix all the parameters in both approaches and compare the v₉₀ on all the tissues. We can see from the table that the number of virtual (initial) sources on each tumor in the LSR algorithm is fairly large. This is due to the fact that the virtual sources are placed 5mm apart and each tumor dimension is approximately 5 – 10 times that (see the tumors’ volumes in Table 5). This means that the total number of sources should be around 125 – 1000 sources. By covering the tumors initially with these large numbers of virtual sources, we allow the refinement technique to get closer to the global optimum of source locations. Table 8 shows that on average the LSR algorithm provides plans with better coverage of the tumor and less damage to the healthy tissues at the same number of physical sources.

Table 8.

Comparison of quality of plans between the LP with fixed sources technique and with the LSR technique at the same number of physical sources

Tumor Model	Number of Physical (Final) Sources	LP with Fixed Sources			LP with LSR algorithm
		Tumor v90(%)	White Matter v90(cm3)	Grey Matter v90(cm3)	Num Virtual (Initial) Sources	Tumor v90 (%)	White Matter v90(cm3)	Grey Matter v90(cm3)
Tumor 1	24	98.57	5.22	19.11	833	97.21	6.22	23.11
Tumor 2	23	98.92	5.56	20.81	884	97.98	3.99	20.54
Tumor 3	10	95.78	3.73	10.03	263	99.13	1.16	6.67
Tumor 4	10	95.41	3.48	11.99	261	94.24	3.91	11.97
Tumor 5	9	95.22	3.3	8.81	180	97.77	1.49	9.54
Tumor 6	14	95.73	5.17	14.79	472	97.4	3.96	12.59
Tumor 7	12	94.33	4.89	12.65	308	95.25	5.23	13.17
Tumor 8	7	94.08	4.84	7.63	314	97.49	4.46	6.2
Tumor 9	6	98.28	1.24	4.09	138	95.40	1.51	5.29
Geometric Average	–	96.24	3.86	11.05	–	96.86	3.06	10.78
Arithmetic Average	–	96.26	4.16	12.21	–	96.88	3.55	12.12

5.2.3. Breakdown of runtime

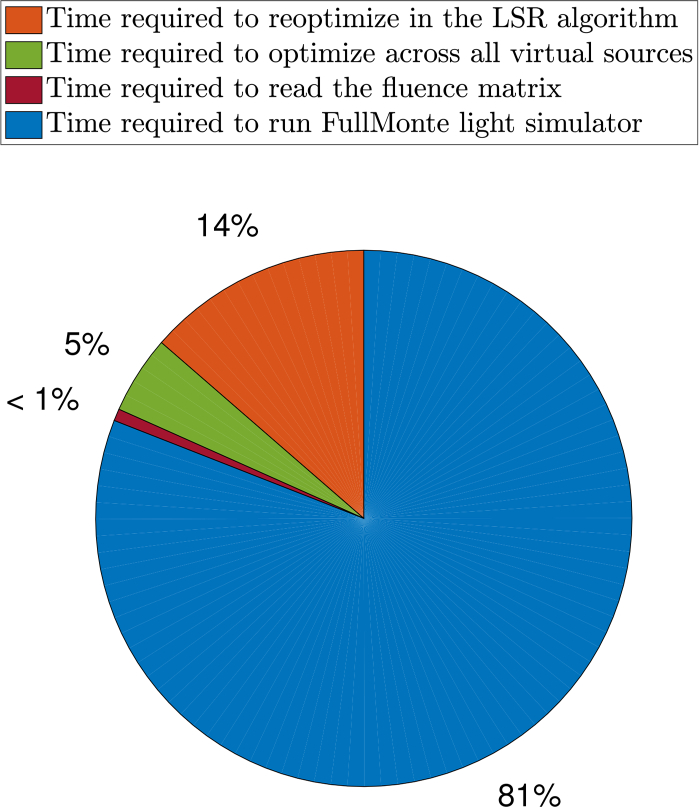
Figure 8 shows a breakdown of the average runtime for the whole implementation across the nine tumor models. The orange slice (14%) shows the average total time taken to reoptimize and generate the 50 different treatment plans in the LSR algorithm. The green slice (5%) represents the average time taken to optimize across the first big space of virtual sources. The burgundy slice (< 1%) is the average time taken by the optimizer to read the fluence matrix from the computer memory, and the blue slice (81%) is the average time taken by FullMonte to generate this matrix. The average total runtime is approximately two hours. The figure shows that the light simulator is the bottleneck in this work flow, and the proposed source location optimization technique does not add much to the planning time. Hence, there is little computational cost to both improving plan quality and quantifying the quality versus light source count trade-off using the LSR algorithm.

Fig. 8.

Breakdown of the average total runtime of the proposed implementation.

6. Discussion

In the first part of this study, we have introduced a convex and linear power allocation program for interstitial PDT planning. The program returns an optimal power allocation solution across a certain number of light sources that minimizes the damage to the OAR. We have tested our program on synthetic brain tumors modeling real GBM images, and have quantified the quality of our plans using different photosensitizers activated at different wavelengths with different tissues’ responses (uptake ratios, optical properties and photosensitizer concentration). We have validated how the program can be controlled to increase the coverage of the tumor by tuning the importance weight of that tissue, or how the resulting plan can be driven to increase PDT safety by introducing conservative guardbands on the necrosis thresholds of the OAR. Comparing our linear program to the most used algorithm in iPDT planning research, the Cimmino feasibility algorithm, we have shown that our program achieves a damage reduction at the same tumor coverage rate with all photosensitizers considered, which shows how robust the LP is. The reduction ratios varied from 12% – 35% on grey matter and 14% – 54% on white matter (Table 7).

In the second part of this manuscript, we have leveraged from the robustness of this LP and built on top of it an iterative optimization framework that searches and selects from a big space of possible source positions in order to further minimize the damage with possibly less number of sources. The framework introduced returns a set of plans with different qualities and number of sources that a clinician can choose from based on, among other factors, the treatment feasibility and the clinical equipment available. Finally, we have investigated the trade-off between the number of sources and the quality of the plan in terms of tumor coverage and damage to OAR.

However, there are some limitations to the results presented that are worth mentioning.

6.1. Variability of uptake ratios and optical properties

The results presented in this work are all based on the mean uptake ratios at the different wavelengths shown in Table 1. Taking the inter- and intra-patient variation of these ratios would definitely impact the quality of the resulting plans. A larger tumor to OAR uptake ratio would basically increase the tumor selectivity in the optimizer and result in better protection of the OAR, while a lower ratio would result in more OAR damage.

On the other hand, it is known that accurately calculating the different tissues’ optical properties is a major challenge, due to the variation among and within patients. Ongoing research is being conducted to facilitate accurate determination of optical properties in different biological tissues [42, 43]. For example, Giacalone et al. recently reported in [44] that the cortex’s (grey matter) mean absorption coefficient, μ_a is 0.144cm⁻¹ = 0.0144mm⁻¹ at 690nm wavelength, which is close to our reported value at 675nm of 0.02mm⁻¹ (see Table 4). Additionally, the same work reported that the mean reduced scattering coefficient at 690nm is ${\mu }_s^{\prime }$ = 8.3cm⁻¹ = 0.83mm⁻¹. Calculating ${\mu }_s^{\prime }$ for the grey matter at 675nm from Table 4, we find that

$${\mu }_s^{\prime }={\mu }_s(1-g)=8.4(1-0.9)=0.84m{m}^{-1}$$

which is almost the same as the value in [44]. On the other hand, Spinelli et al. reported in [45] different mean optical properties for neonate brains at 690nm, μ_a = 0.028mm⁻¹ and ${\mu }_s^{\prime }$ = 0.58mm⁻¹.

Similar to the uptake ratios, optical property variation highly impact iPDT treatment plans qualities as the actual dose received by the different tissues during treatment may be different from what was calculated during planning, and thus treatment efficacy would be hampered. Although we have tested our framework with four different optical properties at different wavelengths with different relative uptake ratios and reached the same conclusion, which is reduced damage to OAR, our future work will leverage this optimization work-flow to quantify the impact of variation and robustness of our plans as we optimize over realistic ranges for the possible tissue optical properties.

6.2. Runtime of the LSR algorithm

In section 5.2.3, we have seen that the LSR algorithm takes on average around two hours to return the different sets of plans. This may seem a long time for planning, however, the algorithm provides the clinician with several plans with different qualities and number of light sources to decide which one gives the best quality-source count trade-off. Therefore, spending this time in planning is justified. Additionally, by looking at the breakdown in Fig. 8, we see that most of the time is consumed by the Monte Carlo light simulator (80% = 1.6hrs). This time requirement stems from the fact that we are simulating a large search space (138 – 884 virtual sources) in order to get closer to the optimal and clinically feasible light source placement. Additionally, with every light source, we are simulating a large number of photons (10⁶) in order to accurately model the light propagation in the brain tissues. We have tried simulating with less number of photons (10³), and the simulator took on average less than 3 minutes to finish. However, tumor v₉₀ dropped significantly in some cases (sometimes below 50% of the tumor) with the given light sources due to the loss in accuracy and poor light propagation modeling. One way to speed-up the process is to run FullMonte with different virtual sources in parallel on different computers, as the computations for different virtual sources are independent. Additionally, we have previously shown in [46] that the FullMonte simulator can be accelerated with a programmable chip called Field Programmable Gate Array (FPGA) with an estimated speedup of 15-20× at the same accuracy. Incorporating this accelerated version would bring the runtime of the LSR algorithm down to around 30 minutes.

6.3. Source perturbation algorithms

In section 5, we have discussed how the source position optimization problem is non-convex and highly non-linear, which makes finding an optimal solution computationally expensive. We have suggested dividing the mesh into a fine-grained grid of virtual sources, that we can search and select from the sources to optimize the solution. However, eliminating the least power source and reoptimizing, though intuitively beneficial, is a greedy approach and can drive the solution away from the global optimum. Therefore, our future work will investigate this problem further by looking into other optimization algorithms such as simulated-annealing or genetic algorithms in order to perturb the source positions of the solutions of the LSR algorithm so that we arrive at potentially better-quality plans.

7. Conclusion

In this work, we have proposed a fast and effective linear program to be used in iPDT planning for source power allocation. Results on virtual brain tumor models have shown a significant reduction in healthy tissue damage for all photosensitizers and wavelengths tested versus existing power allocation techniques. With the ALCIPc photosensitizer that usually resulted in the best treatment plans due to its high tumor selectivity, our linear program method outperforms the prior Cimmino algorithm by reducing the damage to the white and grey matters by 29% and 31% respectively, while requiring comparable runtime. We have also shown that intuitive changes to the cost function thresholds and importance weights provide an effective way to trade-off between leaving some tumor volume under-treated versus damaging more healthy tissue, which is a useful feature for plan exploration. Additionally, we have proposed an optimization loop that would provide clinicians with a set of high-quality treatment plans with refined source locations. With these plans, a tumor could be fully destroyed with minimal damage to the healthy tissues by ALCIPc mediated PDT with theoretically less than 10 minutes of optical irradiation.

Funding

Ontario Centres of Excellence (OCE) (OCE-24491), Natural Sciences and Engineering Research Council (NSERC) (CRDPJ 490784-15), IBM (OCE-24491), Theralase Technologies Inc. (OCE-24491), and Southern Ontario Smart Computing Innovation Platform (SOSCIP) (OCE-24491).

Disclosures

The authors declare that there are no conflicts of interest related to this article.