Computationally Efficient Composite Likelihood Statistics for Demographic Inference

Abstract

Many population genetics tools employ composite likelihoods, because fully modeling genomic linkage is challenging. But traditional approaches to estimating parameter uncertainties and performing model selection require full likelihoods, so these tools have relied on computationally expensive maximum-likelihood estimation (MLE) on bootstrapped data. Here, we demonstrate that statistical theory can be applied to adjust composite likelihoods and perform robust computationally efficient statistical inference in two demographic inference tools: ∂a∂i and TRACTS. On both simulated and real data, the adjustments perform comparably to MLE bootstrapping while using orders of magnitude less computational time.

Many population genetic inference tools use composite likelihoods to estimate model parameters and choose between models (e.g., Gutenkunst et al. 2009; Gravel 2012; Excoffier et al. 2013; Harris and Nielsen 2013; Robinson et al. 2014; Fearnhead et al. 2015). Composite likelihoods approximate the full likelihood by a product of simpler likelihoods that are treated as if they were independent (Lindsay 1988; Varin et al. 2011). With full likelihoods, confidence intervals can be estimated from the Fisher Information Matrix (FIM), and model selection can be done using the likelihood ratio test (LRT), Akaike’s information criterion, or the Bayesian information criterion. But when applied to composite likelihoods these approaches underestimate parameter uncertainties and erroneously favor more complex models (Gao and Song 2010). These biases can be avoided by performing maximum-likelihood estimation (MLE) on many bootstrap data sets (Horowitz 2001), but at substantial computational cost. Statistical theory shows that one can compensate for the model misspecification inherent to composite likelihoods (Pace et al. 2011), and this theory has found some previous application in population genetics (RoyChoudhury 2011; Fearnhead et al. 2015). The FIM can be replaced with the Godambe Information Matrix (GIM; supplementary eq. S1, Supplementary Material online; Godambe 1960), and the LRT can be adjusted by normalizing the difference in log-likelihoods (supplementary eq. S2, Supplementary Material online; Rotnitzky and Jewell 1990). Here we apply composite likelihood statistical approaches to two popular demographic history inference tools, ∂a∂i (Gutenkunst et al. 2009) and TRACTS (Gravel 2012). We show that these approaches yield accurate uncertainty quantification and model selection, using orders of magnitude less computation than MLE on bootstrapped data.

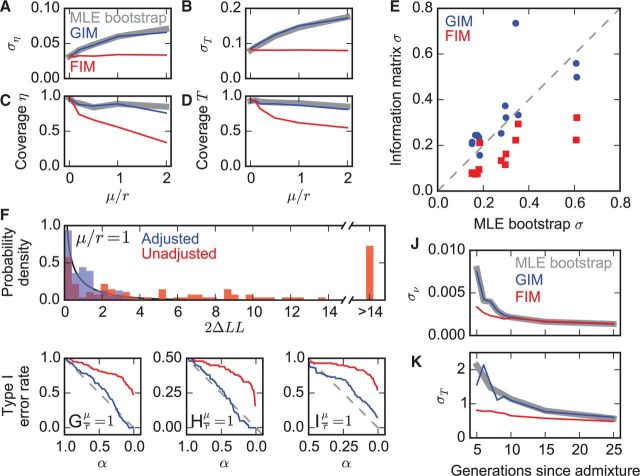
∂a∂i uses a diffusion approach to fit models of demographic history to the allele frequency spectrum (Gutenkunst et al. 2009). It calculates a composite likelihood, because it assumes that entries in the spectrum are independent Poisson variables (Sawyer and Hartl 1992), but this assumption is violated by linkage between the single-nucleotide polymorphisms (SNPs) from which the spectrum was built. In simulated data from a population growth model (supplementary fig. S1A, Supplementary Material online), reducing the recombination rate to increase linkage between SNPs increased parameter uncertainties, but this was not captured by the FIM (fig. 1A and B). The GIM, however, yielded confidence intervals that closely match MLE on bootstraps (fig. 1A and B), with similar coverage (fig. 1C and D). Results for a more complex isolation-with-migration model (supplementary fig. S1B, Supplementary Material online) were similar (supplementary fig. S2, Supplementary Material online). We also tested the GIM on a complex human Out-of-Africa model that was previously fit to gene resequencing data (Gutenkunst et al. 2009). The FIM consistently underestimated parameter uncertainties, but the GIM matched results from MLE on bootstrap data well (fig. 1E). Tests varying the number of sampled individuals and SNPs showed that the GIM performed well whenever the original data yielded a physically plausible set of maximum-likelihood parameter values (supplementary fig. S3, Supplementary Material online). In ∂a∂i analyses, it is common to project the allele frequency spectrum down to a smaller effective sample size, to incorporate SNPs that were not successfully called in all individuals (Marth et al. 2004). Such projection yields a composite likelihood even when SNPs are unlinked. In this case, the FIM overestimates parameter uncertainties, but the GIM agrees with MLE bootstrapping (supplementary fig. S4, Supplementary Material online).

Fig. 1.

Adjusted composite-likelihood statistics compared with MLE on bootstrapped data and assuming full likelihood. Throughout, results in gray are from MLE on bootstrapped data, in blue are from composite likelihood (GIM), and in red are from assuming full likelihood (FIM). The full likelihood assumption is incorrect when data are linked (μ/r ≠ 0). (A, B) Inferred ∂a∂i parameter standard deviations for data simulated with an instantaneous population size change η at a time T in the past. To vary the strength of linkage, the mutation rate μ was held constant while the recombination rate r was varied. Plotted are averages over 100 data sets per value of μ/r. (C, D) Coverage of 95% confidence intervals for model and simulations in (A) and (B). (E) Parameter standard deviations from Godambe and Fisher Information Matrices compared with conventional bootstrapping for the data and 13-parameter ∂a∂i model of Gutenkunst et al. (2009). (F) For 100 symmetric migration data sets simulated with linkage, log-likelihood differences (ΔLL) between asymmetric and symmetric migration ∂a∂i models, before (red) and after adjustment (blue) compared with expected ${\chi }_1^2$ null distribution (black line). (G) Type I error rate versus significance level α for LRT on simulations and models in F, using adjusted (blue) and nonadjusted (red) ΔLLs. (H) Type I error rate versus significance level α for LRT between ∂a∂i models of isolation with and without migration. (I) Type I error rate versus significance level α for LRT between instantaneous growth and standard neutral ∂a∂i models. (J, K) Standard deviations for parameters inferred by TRACTS for a model in which Europeans and African-Americans admixed T generations ago with admixture proportion ν and 1 − ν.

In the LRT, the difference in log-likelihoods between a more complex full model and a simpler nested model is compared with a null χ² distribution. For two-population data simulated with symmetric population sizes and fit with an asymmetric size model, the distribution of log-likelihood differences was broader than expected (fig. 1F), leading the traditional test to erroneously favor the model with asymmetric sizes (fig. 1G). Using first-order moment matching, however, restored the expected distribution of log-likelihood differences (fig. 1F and supplementary text, Supplementary Material online), resulting in a well-controlled Type 1 error rate (fig. 1G). If the simpler model lies on the boundary of parameter space, such as comparing models with and without migration, the null distribution is more complex (supplementary materials and Supplementary Data, Supplementary Material online), yet moment-matching still yielded a well-controlled error rate (fig. 1H). In many population genetics contexts, there is a degeneracy in the parameter space mapping the more complex to the simpler model. For example, a model of instantaneous growth can be reduced to the standard neutral model by setting either the magnitude or the time of the growth to zero. In this case, to achieve proper Type I error rates we calculated derivatives for moment-matching with time equal to zero and size change equal to 1 (fig. 1I). The Wald and score tests are alternatives to the LRT that can be also be adjusted for composite likelihood (Pace et al. 2011; RoyChoudhury 2011), although we find in our applications that they perform less well (supplementary fig. S5, Supplementary Material online).

To demonstrate the broad applicability of these statistical approaches, we also considered TRACTS (Gravel 2012), which models the distribution of ancestry tract lengths to infer recent gene flow. TRACTS calculates a composite likelihood, because it assumes a Poisson number of tracts in each length interval. As with ∂a∂i, on simulated data the FIM underestimated parameter uncertainties, but the GIM agreed well with MLE on bootstrap data sets (fig. 1J and K).

The GIM and LRT adjustment depend on the expectations of derivatives of the composite likelihood function with respect to parameters, where the expectations are over realizations of the stochastic process that generates the data (supplementary eqs. S1 and Supplementary Data, Supplementary Material online). Expectations of second derivatives can be approximated by the observed values (Efron and Hinkley 1978). The observed first derivatives, however, are zero at the MLE. We approximated their expectations over the stochastic process using a conventional bootstrap (supplementary eq. S3, Supplementary Material online; Catelan and Sartori 2015). In ∂a∂i and TRACTS, this bootstrapping of first-derivative calculations can be done extremely efficiently, because calculation of the likelihood decomposes into an expensive calculation of the expected spectrum of allele frequencies or tract lengths, which is only dependent on the parameter values, and an inexpensive Poisson calculation of the likelihood, which is dependent on the data. Reusing evaluations of the expected spectra thus enables fast computation. For example, MLE for all the bootstrap data for figure 1E took hundreds of CPU hours, but evaluating the GIM took only 1 CPU hour. Similar decompositions of the likelihood calculation occur in other population-genetic inference applications (e.g., Harris and Nielsen 2013; Kamm et al. 2015). Moreover, because likelihood calculation is deterministic in ∂a∂i and TRACTS, derivatives can be accurately approximated by finite differences. For analytical methods, automatic differentiation may more efficient and accurate (e.g., Bhaskar et al. 2015), but accurate derivative calculation may be challenging in methods that rely on stochastic simulation to estimate likelihoods (e.g., Excoffier et al. 2013; Mathew et al. 2013).

The methods described are implemented in ∂a∂i version 1.7.0, available at https://bitbucket.org/GutenkunstLab/dadi (last accessed November 23, 2015).