A new methodological approach to adjust alcohol exposure distributions to improve the estimation of alcohol-attributable fractions

Abstract

Background and Aims

To assess the burden of excessive alcohol use, researchers estimate alcohol-attributable fractions (AAFs) routinely. However, under-reporting in survey data can bias these estimates. We present an approach that adjusts for under-reporting in the estimation of AAFs, particularly within subgroups. This framework is a refinement of a previous method conducted by Rehm et al.

Methods

We use a measurement error model to derive the ‘true’ alcohol distribution from a ‘reported’ alcohol distribution. The ‘true’ distribution leverages per-capita sales data to identify the distribution average and then identifies the shape of the distribution with self-reported survey data. Data are from the National Alcohol Survey (NAS), the National Household Survey on Drug Abuse (NHSDA) and the National Epidemiologic Survey on Alcohol and Related Conditions (NESARC). We compared our approach with previous approaches by estimating the AAF of female breast cancer cases.

Results

Compared with Rehm et al.’s approach, our refinement performs similarly under a gamma assumption. For example, among females aged 18–25 years, the two approaches produce estimates from NHSDA that are within a percentage point. However, relaxing the gamma assumption generally produces more conservative evidence. For example, among females aged 18–25 years, estimates from NHSDA based on the best-fitting distribution are only 19.33% of breast cancer cases, which is a much smaller proportion than the gamma-based estimates of approximately 28%.

Conclusions

A refinement of Rehm et al.’s approach to adjusting for underreporting in the estimation of alcohol-attributable fractions provides more flexibility. This flexibility can avoid biases associated with failing to account for the underlying differences in alcohol consumption patterns across different study populations. Comparisons of our refinement with Rehm et al.’s approach show that results are similar when a gamma distribution is assumed. However, results are appreciably lower when the best-fitting distribution is chosen versus gamma-based results.

INTRODUCTION

Several health conditions have been associated with alcohol use, including many cancers [1–5]. Some conditions, such as female breast cancer, may be affected by even moderate consumption levels [4,6,7]. Alcohol-attributable fractions (AAFs) represent the number of cases that could have been avoided if no one had consumed alcohol as a proportion of all cases holding all other risk factors constant [8]. Accordingly, AAFs can be used to assess the public health impact of alcohol use and subsequent social costs [9]. AAFs are calculated by combining relative risk (RR) estimates with an estimated probability distribution over consumption levels. RR estimates can be obtained from meta-analyses or systematic reviews on alcohol consumption and disease risk, while the probability distribution over consumption levels is estimated typically with survey data. However, survey respondents may under-report consumption, because alcohol use is perceived to be a socially undesirable behavior [10] or because of recall error. Additionally, some underestimation may occur because of inaccurate assessments of the ethanol content of alcoholic beverages [11]. If the probability distribution is underestimated (i.e. more weight is placed on zero consumption and less weight is placed on higher levels of consumption), then AAFs will be underestimated. The quantity of alcohol reported in nationally representative surveys frequently falls short of the quantity of alcohol reported in records of per-capita sales [10–13]. Among the three nationally representative surveys we use in this paper, coverage rates range between 34 and 56%. Some of this discrepancy may reflect factors beyond under-reporting, such as undersampling dependent drinkers [11].

Recently, approaches have been developed that may mitigate the effect of under-reporting [10,11,13–18]. These approaches use per-capita sales data to adjust the distribution of alcohol consumption. For example, Rey et al. [18] shifted all observations by a common multiplier. Rehm et al. [10] proposed a more refined approach that involves adjusting the mean and standard deviation (SD) of alcohol consumption and then deriving the parameters of a standard gamma distribution. Although the approach proposed by Rehm et al. [10] is sophisticated, it has at least three limitations. First, Rehm et al. [10] assume that alcohol use follows a gamma distribution. Secondly, their approach to adjusting the standard deviation has little statistical or theoretical basis. Thirdly, they assume that a constant multiplier applies unilaterally to all demographic subpopulations, which can introduce bias if demographic characteristics are related to the extent of under-reporting.

We refine Rehm et al.’s [10] approach by relaxing the gamma assumption and eliminating the standard deviation adjustment. We show that when one adjusts the scale parameter of a gamma distribution, the resultant probability distribution is nearly identical to the distribution obtained using Rehm et al.’s [10] approach. However, one can easily adjust the scale parameter of a variety of statistical distributions. Therefore, our approach can be extended to many different probability distributions. Although previous research supported the use of the gamma distribution to model alcohol consumption [19], we have found that the gamma distribution frequently provides a poor fit. We have also found that AAF results are sensitive to the choice of statistical distribution. Accordingly, the additional flexibility of our approach is not trivial. Although the methodology described in this paper could be applied to other diseases or estimation objectives, we illustrate our method by calculating the AAF of breast cancer cases.

DESCRIPTION OF THE REHM APPROACH AND NEW METHOD

AAFs can be calculated as follows [20]:

$$\text{AAF}=\frac{{\int }_0^{\infty }RR(x)f(x)dx-1}{{\int }_0^{\infty }RR(x)f(x)dx}$$ (1)

where RR(x) denotes an RR mapping that indicates the risk of disease associated with consuming x grams of alcohol per day and normalized such that RR(0) = 1. The probability density function (PDF) of alcohol consumption is denoted by f(x). Typically, RR(x) is estimated by combining evidence meta-analytically on the relationship between alcohol consumption and disease risk. The PDF of alcohol consumption is estimated typically using nationally representative survey data, such as the Behavioral Risk Factor Surveillance System. Supporting information, Appendix S1 provides additional details regarding the estimation of AAFs, including details regarding integral approximation and confidence interval estimation.

The generalized gamma, standard gamma, Weibull and log-normal distributions all reflect many of the characteristics typically observed in alcohol consumption data (e.g. non-negative, right-skewed, large probability mass at zero). The generalized gamma distribution is particularly useful, as it nests the gamma, Weibull and log-normal distributions as special cases [21–23]. Accordingly, the generalized gamma distribution can be used to test whether any of the nested distributions are appropriate. Furthermore, if all other distributions are rejected, the generalized gamma is minimally restrictive and less susceptible to misspecification bias.

Rehm et al. [10] developed a method to shift an alcohol consumption distribution that accounts for under-reporting. Their approach proceeds as follows. First, they calculate a multiplier that relates per-capita sales to the average amount of alcohol reported:

$$\mathrm{m}=\frac{P}{C}$$ (2)

where P denotes the amount of alcohol sold per capita and C denotes the average amount of alcohol reported by all survey respondents (including drinkers and non-drinkers). Secondly, for each subpopulation of interest, the subpopulation-specific mean is shifted as follows:

$${\mu }_{j,\mathit{shifted}}=C_j·\mathrm{m},$$ (3)

where μ_{j, shifted} denotes the shifted mean for the j^th subpopulation, and C_j denotes the sample average for the j^th subpopulation. Thirdly, they shift subpopulation-specific standard deviations. For men, the shifted standard deviation is obtained by applying the following equation:

$${\sigma }_{j,\mathit{shifted}}=1.174·{\mu }_{j,\mathit{shifted}}.$$ (4)

An analogous equation is used for women:

$${\sigma }_{j,\mathit{shifted}}=1.258·{\mu }_{j,\mathit{shifted}}.$$ (5)

Rehm et al. [10] obtained the coefficients in equations 4 and 5 by regressing the standard deviation of alcohol consumption from several different surveys onto each survey’s mean alcohol consumption and adjusting for gender. Finally, Rehm et al. [10] transformed the shifted mean and SD into shape and scale parameters of a standard gamma. This approach has been used by other researchers. For example, Jones et al. [24] used this approach to update England-specific estimates of AAFs for a variety of diseases.

Rehm et al.’s [10] approach has at least two drawbacks. First, one must assume that alcohol consumption follows a standard gamma distribution. Secondly, equations 4 and 5 represent ad-hoc adjustments with little statistical or theoretical basis and may lead to meaningful and indeterminate biases in AAFs. The gamma is not, a priori, an inappropriate distribution. In previous work the unique mapping from mean and standard deviation to gamma distribution-specific parameters was probably perceived as a convenient feature to be exploited. Furthermore, Rehm et al. did compare the gamma with alternative distributions, and showed that the gamma provided a relatively good fit. However, it rarely provided the best fit. Our approach allows researchers to discover and use the best-fitting distribution. This generalizability is particularly important, as researchers continue to model consumption from a variety of surveys on distinct populations and moving into future generations.

Our approach is based on a measurement error model that relates the actual volume of alcohol consumed to the observed volume of alcohol consumed. We then derive an adjusted probability distribution from basic statistical principles. Thus, our approach can be extended to several statistical distributions. Let X denote actual alcohol consumption, and let X^* denote self-reported alcohol consumption. Our measurement error model is

$$X=\mathrm{m}·X^{\ast }.$$ (6)

Equation 6 assumes that all respondents under-report their alcohol consumption by a fixed proportion (i.e. m). Although restrictive, this assumption was also made in Rehm et al. [10] and elsewhere [13–18].

If one combines equation 6 with an assumed probability distribution for X^*, then one can derive the probability distribution of X. For example, assume that X^* is gamma-distributed with scale denoted by θ and shape denoted by α. Then X is also gamma-distributed with scale equal to m · θ and shape equal to α [25]. Thus, the probability distribution over actual alcohol consumption can be estimated in two steps:

1. Estimate gamma scale and shape parameters using the observed survey data, which gives the distribution of X^*.

2. Shift the estimated gamma scale with the multiplier defined in equation 2 to obtain the distribution of X.

With minor modifications, this approach can be generalized to other distributions by substituting the distribution used in step 1 and the scale parameter that is shifted in step 2. We provide additional detail on the use of this approach with the gamma and other statistical distributions in Supporting information, Appendix S2.

The intuition underlying our approach (and Rehm et al.’s [10]) is that per-capita sales data provide an accurate measure of average alcohol consumption, but do not inform how alcohol consumption is distributed around that average. Thus, survey data are used to estimate the shape of alcohol consumption distributions. Accordingly, the statistical distribution used should capture the ‘shape’ of the alcohol consumption distribution well. Standard goodness-of-fit tests, such as Kolmogorov–Smirnov testing, could be used to evaluate this. Additionally, the generalized gamma can be used to test whether one can reject gamma, Weibull or log-normal distributions [23].

Considerable heterogeneity in alcohol consumption is observed frequently throughout demographic populations. For example, in the National Survey on Drug Use and Health, the percentage of respondents aged 21 years or older who reported past-month heavy alcohol use was substantially different when comparing across gender, age and race/ethnicity categories [26]. Thus, it is unlikely that a single probability distribution will provide the best fit for all demographic subpopulations (e.g. females aged 21–25, females aged 26–34). Our methodology allows researchers to use demographic-specific distributions. Essentially, one can construct a probability distribution over alcohol consumption at the population level that is a mixture of subpopulation-specific distributions. Although we apply a common multiplier to each subpopulation-specific distribution, this allows the adjusted mixture distribution to reflect the degree to which alcohol consumption distributions are heterogeneous in the unadjusted data. To ensure that the resultant mixture distribution is centered on per-capita sales, we calculate the overall survey average (i.e. C in equation [2]) by taking the weighted sum of each subpopulation- and distribution-specific average.

METHODS

To illustrate our approach, we estimated the AAF of female breast cancer cases using three distinct survey sources. Specifically, we used data on adults aged 18 or older from (i) the 1999–2002 National Household Survey on Drug Abuse (NHSDA) (n = 140 417) [27], (ii) the 1999–2000 National Alcohol Survey (NAS) (n = 7562) [28] and (iii) the 2001–2002 National Epidemiologic Survey on Alcohol and Related Conditions (NESARC) (n = 42 802) [29]. We chose these three data sources because they collect alcohol consumption data for the US population during a comparable period, but with different survey instruments. This allows us to assess the extent to which our method and Rehm et al.’s [10] method produce similar findings across disparate surveys.

NHSDA records the number of days in the past 30 in which alcohol was consumed, the typical number of drinks consumed per drinking day and the number of days in the past 30 in which five or more drinks were consumed. We derived a measure of average alcohol consumption per day in standard drinking units as described in Stahre et al. [30]. We converted standard drinking units into g/day by assuming that a standard drink contains 14 g of ethanol. The NAS instrument uses a graduated frequency approach to record alcohol consumption. The graduated frequency approach asks respondents to report the frequency of occasions when they consume increasing quantities of alcohol. We used beverage-specific responses to derive the number of drinks per day, and we assumed 14 g of ethanol per drink to calculate the average grams per day of ethanol. The NESARC instrument asks about beverage-specific past-year alcohol consumption, and differentiates within beverage types higher versus lower ethanol content beverages. For example, respondents are asked to differentiate between 80- and 100-proof liquor. The public use NESARC file contains a pre-calculated measure of ounces of ethanol per day based on applying beverage-specific ethanol conversion factors, which we converted into grams.

Table 1 presents descriptive statistics from each data source. The demographic characteristics of each of the survey samples are broadly similar. However, reported alcohol consumption varies extensively across survey sources. For example, 34% of respondents in the NAS reported any alcohol use, while 65% of respondents in the NESARC reported any alcohol use. Despite this high variation in drinker proportions, average daily consumption levels vary only between 6.15 and 9.04 g/day.

Table 1.

Descriptive characteristics of the national survey data used to estimate the alcohol exposure distributions among various subpopulations.

Characteristic	NHSDA (1999–2002)	NAS(1999–2000)	NESARC (2001–2002)
Female (%)	52.54	52.32	52.19
Age 18–25 (%)	14.34	14.47	14.80
Age 26–34 (%)	16.56	16.78	16.70
Age 35–49 (%)	31.82	31.84	31.17
Age 50+ (%)	37.28	36.90	37.33
Drinker (%)	49.73	34.35	65.20
ADC	7.92	6.15	9.04
Observations	140 417	7562	42 802

ADC = average daily alcohol consumption in grams per day; NAS = National Alcohol Survey; NESARC = National Epidemiologic Survey on Alcohol and Related Conditions; NHSDA = National Household Survey on Drug Abuse. Drinkers represent those who reported any alcohol consumption; non-drinkers reported total abstention from alcohol. All estimates are weighted to make them nationally representative.

To calculate the multiplier defined in equation 2, we used figures reported by the National Institute on Alcohol Abuse and Alcoholism [31]. These estimates were derived from alcohol beverage sales records collected by the Alcohol Epidemiologic Data System and from industry sources. We calculated average annual per capita sales throughout 1999–2002. After dividing by 365, average per capita sales for 1999–2002 were 17.95 g/day.

To estimate the RR of breast cancer associated with consuming alcohol, we replicated an analysis conducted by Bagnardi et al. [6]. Specifically, we used a generalized least-squares meta-regression model to estimate the dose–response relationship. Our results indicate the following dose–response relationship:

$$ln\text{RR}(x)=0.009774x(\text{standard}\text{error}:0.00427)$$ (7)

RESULTS

Table 2 demonstrates the calculation of survey-specific multipliers. First, for each survey and substratum, we tested the fit of a generalized gamma, gamma, Weibull and log-normal distribution. We used three tests to determine the best-parametric model: (1) Kolmogorov–Smirnov testing, (2) χ² testing and (3) generalized gamma-based testing. All testing results are reported in Supporting information, Appendix S3. Ultimately, we determined the best-fitting distribution based on Kolmogorov–Smirnov testing, which generally agreed with other testing criteria. Secondly, we predicted mean average daily alcohol consumption (ADC) using parameter estimates associated with each substrata-specific parametric model. For example, if the best-fitting model is the log-normal distribution, then we used the log-normal mean function: E[X] = exp(μ + 0.5 · σ²) to predict mean ADC. Thirdly, we calculated an overall mean ADC by taking the weighted sum of each substratum-specific mean, where weights represent the proportion of the sample within each substratum. Fourthly, we calculated the multiplier in equation 2 by dividing per-capita sales by the overall survey average.

Table 2.

Calculating survey-specific multipliers to adjust alcohol consumption distributions.

Substrata	NHSDA			NAS			NESARC
	Percentage of sample	Sample mean ADC	Model predicted mean ADC	Percentage of sample	Sample mean ADC	Model predicted mean ADC	Percentage of sample	Sample mean ADC	Model predicted mean ADC
Non-drinkers	50.3	NA	NA	65.6	NA	NA	34.8	NA	NA
Drinkers
Females, 18–25	3.7	13.8	13.3a	3.1	16.6	16.3a	5.0	11.2	15.6a
Females, 26–34	4.2	9.1	8.1a	3.0	5.5	5.0b	5.8	6.5	7.9a
Females, 35–49	7.7	9.6	8.4a	4.9	8.2	9.1a	10.5	7.9	10.2a
Females, 50+	6.8	8.0	7.6a	2.0	5.9	6.9c	9.6	6.4	9.9a
Males, 18–25	4.4	28.0	27.9c	4.5	35.8	38.2c	5.6	28.0	29.9c
Males, 26–34	5.3	22.0	21.3a	4.9	21.4	22.2c	6.6	16.4	16.7c
Males, 35–49	9.5	20.2	19.6a	7.3	19.1	17.1b	11.3	21.0	21.3c
Males, 50+	8.2	17.7	18.8c	4.6	19.4	17.8b	10.7	15.2	15.1b
Overall	100.0	7.9	7.7	100.0	6.1	6.1	100.0	9.0	10.1
Per-capita sales		17.9	17.9		17.9	17.9		17.9	17.9
Survey coverage		44%	43%		34%	34%		50%	56%
Multiplier		2.3	2.3		2.9	2.9		2.0	1.8

ADC = average daily alcohol consumption in grams per day; NA = not applicable; NAS = National Alcohol Survey; NESARC = National Epidemiologic Survey of Alcohol and Related Conditions; NHSDA = National Household Survey of Drug Abuse The best-fitting distribution represents the distribution with the smallest calculated Kolmogorov–Smirnov statistic. Kolmogorov–Smirnov statistics indicate the absolute value of the maximum deviation across the assumed cumulative distribution function and the empirical distribution function. Thus, smaller Kolmogorov–Smirnov statistics indicate a closer fit to the underlying data. The overall predicted ADC represents the average amount of alcohol consumed across all survey respondents. The overall figure is calculated by taking the weighted average of strata-specific predicted ADC, where the weights are provided by the percentage of the sample represented by each substratum. Survey coverage indicates the proportion of per-capita sales that are captured in the overall predicted ADC figure. All estimates are weighted to make them nationally representative.

^aBest-fitting distribution for this substratum was the lognormal distribution.

^bBest-fitting distribution for this substratum was the Weibull distribution.

^cBest-fitting distribution for this substratum was the generalized gamma distribution.

Table 2 indicates that there is substantial heterogeneity throughout survey sources with respect to survey coverage. Specifically, survey coverage rates range from 34% (NAS) to 56% (NESARC). Calculated multipliers reflect this heterogeneity by assigning larger multipliers to surveys with lower coverage rates. There are some minor differences in predicted mean ADC levels and simple sample means, which are probably driven by the fact that best-fitting models capture more effectively the tails of alcohol consumption distributions.

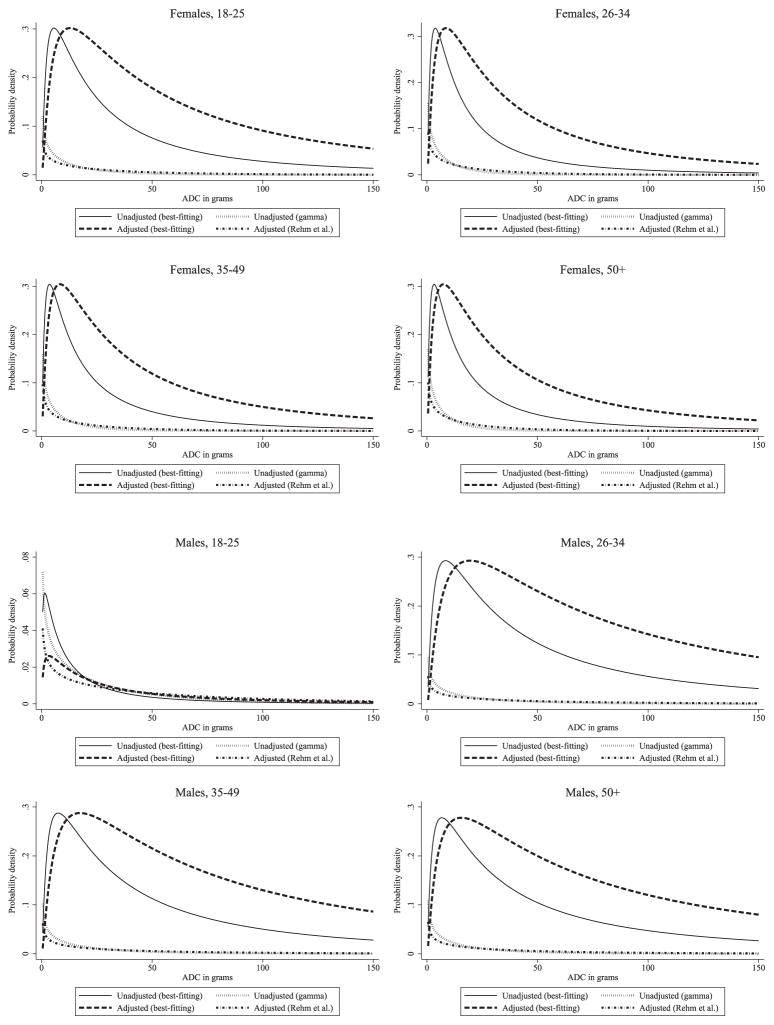
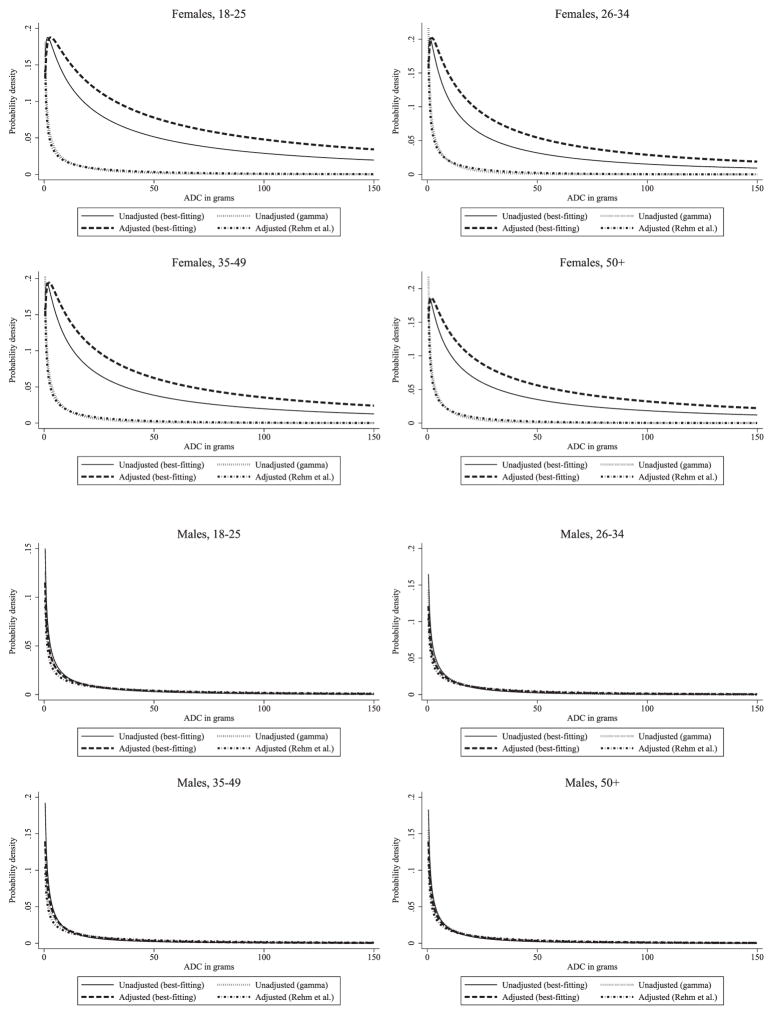
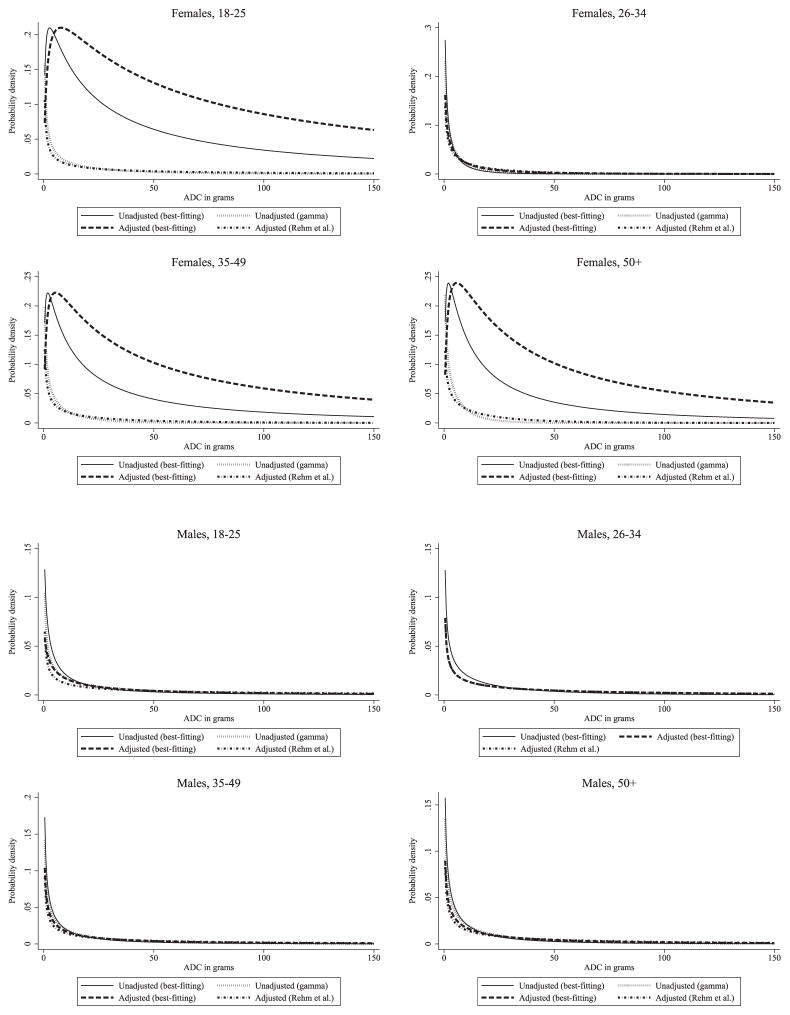
Figures 1–3 present estimated PDFs for each substratum and survey source used. Specifically, we present the (i) unadjusted best-fitting density, (ii) unadjusted gamma density, (iii) adjusted best-fitting density using our method and (iv) adjusted gamma density using Rehm et al.’s [10] method. In many cases, gamma densities assign nearly uniform probabilities to a substantial portion of the right tail of the alcohol consumption distribution. In contrast, best-fitting densities frequently assign higher probabilities to lower consumption levels and diminishing probabilities throughout the right tail of the distribution. Capturing these features of the underlying data is not possible with Rehm et al.’s [10] approach and is likely to have important implications in resulting estimates of AAFs. Specifically, if disease risks increase rapidly as consumption levels increase, then the relatively lower emphasis that best-fitting densities place on higher levels of alcohol consumption could result in lower estimated AAFs. In some cases, best-fitting densities are more similar in shape to the gamma density, and in these cases we might expect there to be less discrepancy between the two adjustment methodologies.

Figure 1.

Age- and gender-specific probability density functions for National Household Survey on Drug Abuse respondents before and after adjustment for under-reporting

Figure 3.

Age- and gender-specific probability density functions for National Epidemiological Survey of Alcohol and Related Conditions respondents before and after adjustment for under-reporting

Table 3 presents estimates of the AAF of breast cancer cases among females using non-adjusted alcohol exposure distributions as well as both adjustment methodologies. We make three observations. First, the AAF estimates based on adjusted alcohol exposure distributions are larger than estimates based on non-adjusted alcohol exposure distributions. Secondly, the estimates obtained using the approach detailed in Rehm et al. [10] are similar to those obtained using our new approach when the gamma assumption is imposed, suggesting that the main contribution of our approach is in providing flexibility over the choice of distribution. Thirdly, choosing the parametric distribution with which to model alcohol exposures flexibly makes a difference in the AAF estimates. In fact, AAF estimates using our method and choosing the parametric distribution flexibly tend to be more conservative than estimates using a gamma-based approach.

Table 3.

Age-specific estimates of the AAF of breast cancer cases, United States 1999–2002.

Method/substrata	NHSDA		NAS		NESARC
	AAF (%)	95% CI	AAF (%)	95% CI	AAF (%)	95% CI
Unadjusted (gamma)
Females, 18–25	7.84	(6.73–8.94)	13.51	(2.49–17.63)	9.90	(5.81–13.36)
Females, 26–34	2.78	(2.63–3.30)	1.10	(0.61–1.48)	1.26	(0.58–2.50)
Females, 35–49	3.12	(2.52–4.08)	1.64	(0.77–4.01)	3.17	(0.95–6.03)
Females, 50+	1.73	(1.70–1.96)	0.42	(0.29–0.51)	0.57	(0.19–1.05)
Unadjusted (best-fitting)
Females, 18–25	9.07a	(8.79–9.37)	7.76a	(6.06–9.68)	9.35a	(8.60–10.01)
Females, 26–34	5.00a	(4.68–5.35)	1.77b	(1.27–2.31)	6.37a	(5.86–6.89)
Females, 35–49	5.15a	(4.83–5.46)	3.47a	(2.79–4.20)	7.13a	(6.74–7.54)
Females, 50+	3.25a	(3.01–3.56)	1.04c	(0.75–1.42)	4.85a	(4.63–5.14)
Adjusted (Rehm et al.)
Females, 18–25	28.36	(27.99–28.70)	31.13	(27.68–31.84)	25.82	(19.26–30.39)
Females, 26–34	18.27	(17.80–18.62)	8.31	(6.04–10.16)	9.48	(5.96–13.61)
Females, 35–49	19.16	(18.48–19.60)	14.67	(10.40–16.61)	14.32	(7.81–20.87)
Females, 50+	10.49	(9.82–10.91)	3.03	(2.44–3.70)	6.22	(4.85–7.69)
Adjusted (gamma)
Females, 18–25	28.66	(28.37–28.94)	23.32	(20.18–25.61)	24.17	(23.15–24.96)
Females, 26–34	17.88	(17.12–18.33)	9.60	(8.18–10.92)	13.47	(11.67–14.62)
Females, 35–49	19.22	(18.68–19.61)	14.14	(12.36–15.09)	17.26	(15.43–18.13)
Females, 50+	10.12	(9.28–10.69)	3.26	(2.65–3.86)	9.20	(8.53–9.79)
Adjusted (best-fitting)
Female, 18–25	19.33a	(18.98–19.68)	14.51a	(12.62–16.23)	13.18a	(12.41–13.95)
Females, 26–34	12.72a	(12.11–13.32)	7.66b	(5.51–10.70)	9.93a	(9.29–10.59)
Females, 35–49	12.63a	(12.08–13.17)	8.05a	(6.92–9.15)	10.67a	(10.18–11.14)
Females, 50+	8.31a	(7.69–8.89)	2.77c	(2.12–3.47)	7.24a	(6.87–7.59)

AAF = alcohol-attributable fraction; CI = confidence interval; NAS = National Alcohol Survey; NESARC = National Epidemiologic Survey of Alcohol and Related Conditions; NHSDA = National Household Survey of Drug Abuse; CI = confidence interval. The best-fitting distribution represents the distribution with the smallest calculated Kolmogorov–Smirnov statistic. Kolmogorov–Smirnov statistics indicate the absolute value of the maximum deviation across the assumed cumulative distribution function and the empirical distribution function. Thus, smaller Kolmogorov–Smirnov statistics indicate a closer fit to the underlying data. All estimates are weighted to make them nationally representative.

^aBest-fitting distribution for this substratum was the lognormal distribution.

^bBest-fitting distribution for this substratum was the Weibull distribution.

^cBest-fitting distribution for this substratum was the generalized gamma distribution.

DISCUSSION

We have presented a refinement of Rehm et al.’s [10] adjustment approach. This refinement allows flexibility when choosing an alcohol distribution model and eliminates the need to adjust the standard deviation. We achieve this by defining a measurement error model for alcohol consumption, which assumes that the measurement error is generated by a constant proportionality factor. Future research should focus on allowing the error to vary across subpopulations, or even across individuals. This is important, as recent studies have shown that under-reporting can vary across the level of alcohol consumed [32,33].

We also presented a comparison of our approach across three nationally representative surveys. Regardless of the shifting approach taken, we found that AAFs are substantively higher when shifting the underlying alcohol consumption distribution. However, we caution that these AAF results may have limited current relevance, as the alcohol consumption data are more than a decade old. Despite this limitation, our analyses served their primary purpose well. Specifically, they allowed us to illustrate the use of our new method and compare methods across disparate survey sources. In theory, adjusting for under-reporting could remove some of the disparities in AAF findings across survey sources. However, we did not find strong evidence that this is the case with our approach or Rehm et al.’s [10] approach.

Even though our new approach improves existing methods used to estimate AAFs, there are some limitations with our and previous methods. First, the estimation of RRs also relies upon self-reported consumption data. Accordingly, RR estimates may also be inaccurate, and this may impact separately the accuracy of AAFs. Thus, AAF estimates may remain biased even after adjusting the PDF for under-reporting. However, in the absence of more knowledge concerning the direction and magnitude of the bias in RR estimates, it is not clear how much bias may remain. Secondly, the impact of alcohol on disease risks probably depends upon the average level of alcohol consumed and patterns of consumption, such as frequency of bingeing and life-time trends in alcohol use. In this paper, we focused upon adjusting the alcohol distribution of average daily consumption, which ignores some of these nuances. Nonetheless, the general principles used to adjust our basic consumption distributions could be refined and applied to probability distributions that capture some of these elements (e.g. probability of being a life-time versus current abstainer). Thirdly, to illustrate our approach, we assumed implicitly that all discrepancies between survey data and per capita sales data can be explained by under-reporting. However, we know that some discrepancy may be attributed to factors such as spillage/wastage, or because some high use consumers are not captured in national surveys [11]. This suggests that adjusting consumption distributions to line up with per capita sales may result in an overcorrection. Researchers may want to consider simple adjustments to our approach, such as calibrating survey data to only account for 80% of per capita sales, as did as World Health Organization researchers [34].

Attributable fractions are an important methodological tool. However, researchers should be aware of two important considerations when estimating and reporting attributable fractions. First, to aggregate attributable fractions across a population, researchers must be careful how they sum over strata-specific attributable fractions [35,36]. In this paper, we presented only strata-specific attributable fractions. Secondly, attributable fractions should be interpreted with caution when comparing attributable fractions across multiple risk factors. The AAF for diseases such as breast cancer represent the proportion of cases that could be avoided if alcohol consumption were eliminated completely holding all other risk factors constant. In studies such as the World Health Organization’s Comparative Quantification of Health Risks [34], attributable fractions are used to assess the public health burden of each risk factor individually. However, if a researcher wants to aggregate across risk factors to assess the impact of simultaneously eliminating all or multiple risk factors, then one must proceed in a way that avoids double-counting [37]. Trogdon et al. [38] present two approaches to aggregate condition-specific attributable fractions that avoid double-counting.

The method presented in this paper assumes that per-capita sales records provide an unbiased measure of the average amount of alcohol consumed. We then use survey data to fit a distribution around that overall average. Our approach provides an improvement over Rehm et al.’s [10] method because we allow more flexibility over the choice of statistical distribution one uses. Therefore, researchers can choose distributions that fit most closely the underlying data present in survey data sources. This is important, as we show that AAF results are sensitive to the choice of statistical distribution.

Supplementary Material

Appendix

Appendix S1 Details regarding the calculation of alcohol-attributable fractions.

Appendix S2 Details regarding the use of other statistical distributions in our new approach.

Appendix S3 Additional results.

Figure 2.

Age- and gender-specific probability density functions for National Alcohol Survey respondents before and after adjustment for under-reporting