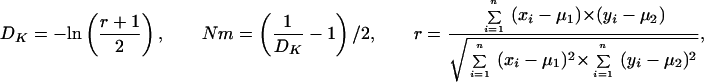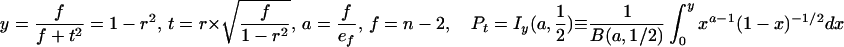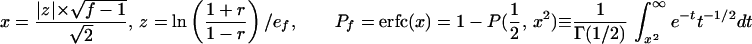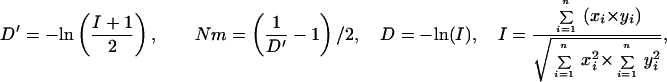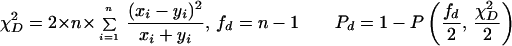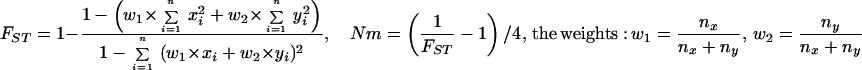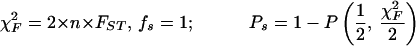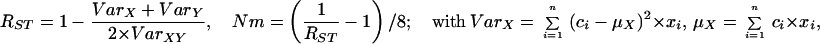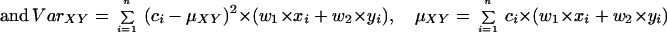When genetic distance matters: Measuring genetic differentiation at microsatellite loci in whole-genome scans of recent and incipient mosquito species

Abstract

Genetic distance measurements are an important tool to differentiate field populations of disease vectors such as the mosquito vectors of malaria. Here, we have measured the genetic differentiation between Anopheles arabiensis and Anopheles gambiae, as well as between proposed emerging species of the latter taxon, in whole genome scans by using 23–25 microsatellite loci. In doing so, we have reviewed and evaluated the advantages and disadvantages of standard parameters of genetic distance, F_ST, R_ST, (δμ)², and D. Further, we have introduced new parameters, D′ and D_K, which have well defined statistical significance tests and complement the standard parameters to advantage. D′ is a modification of D, whereas D_K is a measure of covariance based on Pearson's correlation coefficient. We find that A. gambiae and A. arabiensis are closely related at most autosomal loci but appear to be distantly related on the basis of X-linked chromosomal loci within the chromosomal Xag inversion. The M and S molecular forms of A. gambiae are practically indistinguishable but differ significantly at two microsatellite loci from the proximal region of the X, outside the Xag inversion. At one of these loci, both M and S molecular forms differ significantly from A. arabiensis, but remarkably, at the other locus, A. arabiensis is indistinguishable from the M molecular form of A. gambiae. These data support the recent proposal of genetically differentiated M and S molecular forms of A. gambiae.

Many major infectious diseases, such as malaria, leishmaniasis, and sleeping sickness, are transmitted by insect vectors. Molecular genetic markers have become powerful tools for elucidating the population biology and evolution of such vectors, topics that are highly relevant to disease transmission in the field (1–4). Genetic variation in vector populations contributes to their susceptibility to infection by the pathogen, their degree of anthropophily, their daily survival and reproductive rates, and the epidemiology of the disease in the human host (5). A case in point is the African mosquito of the Anopheles gambiae (sensu latu) complex (5). These include the most important vector of human malaria, A. gambiae (sensu strictu), as well as closely related species that are significant vectors in specific areas (e.g., Anopheles arabiensis) or are altogether unable to serve as vectors (Anopheles quadriannulatus). Furthermore, even within A. gambiae s.s., cytologically defined chromosomal forms (e.g., Mopti, Savanna, and Bamako) are reproductively isolated in the northern dry areas of West Africa, including Mali and Burkina Faso, and may represent emerging species with different disease transmission characteristics (5, 6). Although many DNA regions have been recently analyzed to examine genetic differentiation within A. gambiae s.s, the only fixed molecular differences found so far that consistently discriminate chromosomal forms are in the X-linked ribosomal (r)DNA region (1–4, 7). In Mali and Burkina Faso, these markers distinguish Mopti from Savanna and Bamako chromosomal forms; however, when the analysis is extended to additional populations in West Africa, two nonpanmictic units are identified even in the absence of chromosomal differentiation. This observation recently led to the definition of “molecular forms M and S” (1) or “molecular types I and II” (2), on the basis of fixed differences in the intergenic spacer or internal transcribed spacer rDNA regions, respectively. Because the repetitive nature of rDNA raises doubt as to its reliability as a marker of incipient speciation processes, much interest is now focused on possible new evidence of genetic distinctness between the forms/types.

Among molecular genetic markers, highly polymorphic microsatellites have been used extensively for population studies in humans (8), mammals (9), fruit flies (10), and anopheline mosquitoes (11–13). Various statistical models have been proposed for evaluating genetic differentiation (14–17), but additional theoretical and empirical comparisons regarding their efficacy would be helpful. For microsatellites, F_ST and D (14) are closely tied to the infinite allele model of mutation (IAM), where each mutation can produce an allele of any size (18). R_ST (16) and (δμ)² (15) are related to the stepwise-mutation model (SMM), which assumes that each allele mutates to either one of the immediately neighboring alleles with equal probability (19).

The standard genetic distance D (14) is an often used and popular parameter for classification and evolutionary studies. It was originally defined as an average value over all loci examined, but it can also be defined at each locus separately. Several variations of D have been used, for example, D_C (20), D_A, D_m (14), D_SW (17), and D_LR (9). In a bear study (9), D and D_LR were comparably satisfactory but failed to resolve the most distantly related pairs of species: when loci have no alleles shared between two populations, D and D_LR are not defined or, as has been proposed by Nei (14), take an infinite value that is problematical for any quantitative comparison. As part of our ongoing studies of A. gambiae taxa and populations, here we compare the performance of presently used parameters of genetic distance [e.g., D, F_ST, R_ST, and (δμ)²], and we introduce and compare new parameters, D′ and D_K. By using a battery of four parameters (F_ST, R_ST, D′, and D_K), we identify intriguing differences in genetic distance between A. arabiensis and the M and S molecular forms of A. gambiae, at loci representing different chromosomal regions.

Materials and Methods

Origin of Mosquitoes.

Field-collected female mosquitoes were species-identified with molecular markers (21). A total of 268 A. gambiae were collected in July 1996 in Mali, West Africa: 95 from Selenkenyi (Sel) and 92 and 81 from Soulouba (Soul) and Kokouna (Kn). Twenty of the 81 A. arabiensis were collected from the same villages in Mali at the same time as A. gambiae (1, 4, and 15 from Sel, Soul, and Kn, respectively). The remaining 61 A. arabiensis mosquitoes were collected from Kilifi, Kenya, in June 1998. A. gambiae mosquitoes from the villages Sel and Soul were also subjected to karyotyping on the basis of polytene chromosome inversions, but because of technical limitations, only 28, 24, and 11 mosquitoes were identified definitively as Mopti, Savanna, and Bamako (6). Use of a PCR restriction fragment length polymorphism marker (7) unambiguously classified the A. gambiae specimens as M or S molecular forms, with an efficiency of 91%. All mosquitoes were genotyped at microsatellite loci by previously described high-throughput methods (22). All 81 available A. arabiensis were used for Figs. 1–3. Because some parameters are sensitive to differences in sample size, we introduced sample weights for F_ST and partly for R_ST (Table 1) and also used a number of A. gambiae comparable to that of A. arabiensis. The percentages of M and S molecular form A. gambiae were 73/27 in Sel, 7/93 in Soul, and 17/83 in Kn, respectively. Figs. 1A and 2A are based on all A. gambiae from Sel; Figs. 1B, 2B, and 3 are based on all M- and S-form mosquitoes from Sel and Soul and an additional individuals 36 from Kn to make the sample sizes comparable.

Figure 1.

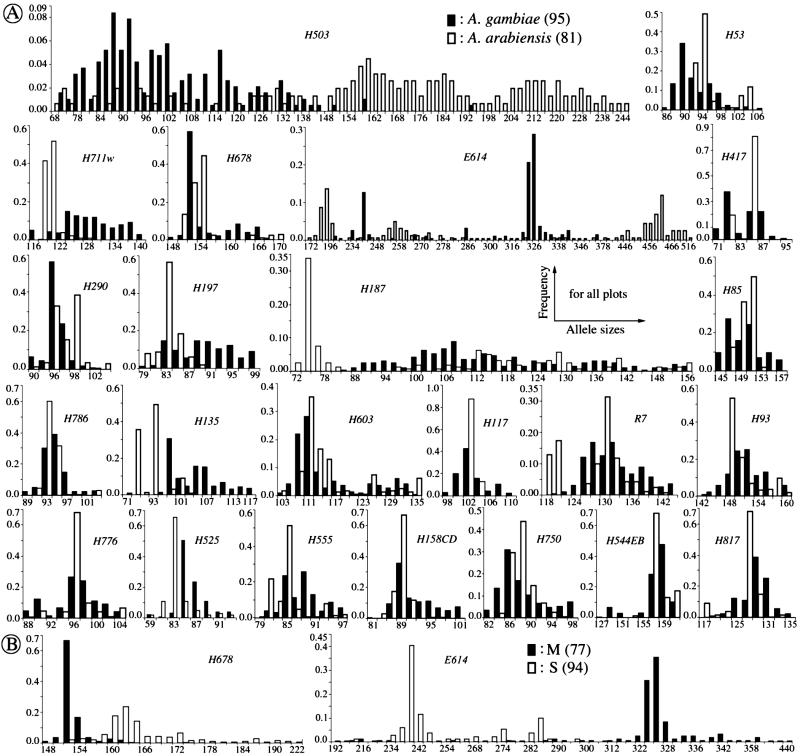
Comparison of frequencies of allele sizes at 23 microsatellite loci, in 95 A. gambiae and 81 A. arabiensis mosquitoes (A), as well as at two loci in 77 M- and 94 S-form A. gambiae (B). Because of space limitations, allele spacing has been shortened, and alleles at tails have been combined. The data are presented in full with helpful color views on our web site (http://www.embl-heidelberg.de/ExternalInfo/kafatos/publications/PROG/).

Figure 3.

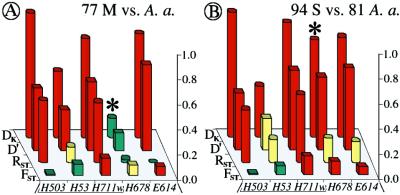
Comparison of 77 M and 94 S molecular form A. gambiae with 81 A. arabiensis (A and B, respectively) at five X-linked loci, both within and proximal to the Xag inversion. Compare to Fig. 2B.

Table 1.

Measures of genetic differentiation

DK: Covariance of the deviation of allele frequency (IAM): direct statistical significance tests (Pt, Pf)

D′: Covariance of allele frequency (IAM): indirect statistical significance tests (Pd)

FST: Variance of allele frequency (IAM): direct statistical significance tests (Ps)

RST: Variance of allele size (SMM): indirect statistical significance test (Nm)

Statistical concepts, emphasis, and significance tests for four parameters of genetic differentiation. Consider two populations X and Y with n_X and n_Y individuals, and let x_i and y_i denote the frequencies of the ith (i = 1, … , n) allele in populations X and Y, respectively, μ₁ and μ₂ are the mean allele frequencies, μ_X, μ_Y are the mean allele sizes, and Var_X and Var_Y are the variance of allele sizes in populations X and Y, respectively. The total number of alleles existing at a locus in both populations conbined is n, and alleles are numbered consistently in both populations. D_K:r is Pearson's correlation coefficient that varies from −1 to 1. Fisher's z-transformation value is z, and erfc(x) is the complementary error function. The degree of freedom is f, and e_f is the integer rounded upwards when f is divided by 10. The probabilities P_tand P_f are based on I_Y(a, 1/2) and P(1/2, x²), the specific incomplete β and Γ functions, respectively, whereas B(a,1/2) and Γ(1/2) are the actual β and Γ functions, respectively: D′. The same linear transformation as for (r + 1)/2 connects the genetic identity I to (I + 1)/2); correspondingly, Nei's D (14) is transformed to D′. p_dis the probability of a χ² test with the degree of freedom f_d. F_ST, R_ST: Parameters are as previously defined (see Material and Methods). With both populations combined, μ_XY and Var_XY are the mean and variance of allele sizes, respectively, and w₁ and w₂ represent the fraction of individuals in the two populations. For F_ST, P_S is the probability of a χ² test with the degree of freedom f_S. Nm is the effective migration rate estimated from the values of D_K, D′, F_ST, and R_ST. N is the effective population size and m the migration rate. Note that the statistical tests are direct for D_K and F_ST(they include r and F_ST values) but only indirect for D′ and R_ST. The potential range of values for D_K is 0 to +∞, for D′, 0 to 0.693, for F_ST, 0 to 1, and for R_ST, −∞ to +∞. 

Figure 2.

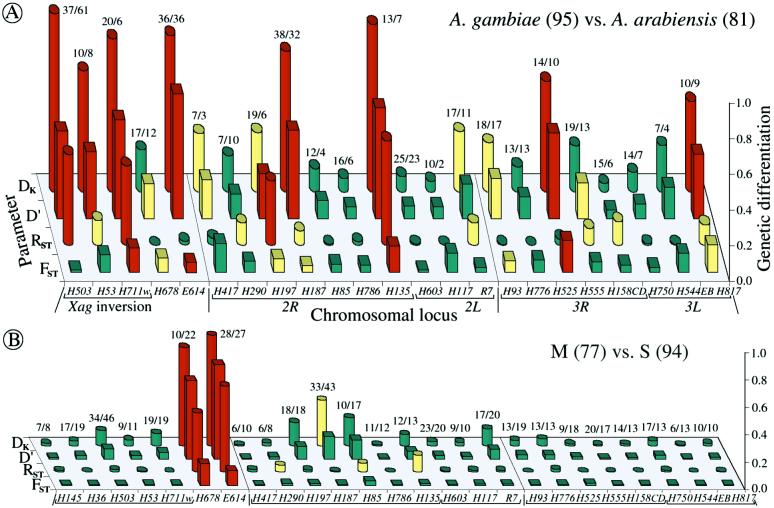
Genetic differentiation at 23 microsatellite loci across the genome on the basis of F_ST, R_ST, D′, and D_K. A compares A. gambiae and A. arabiensis, whereas B compares the M and S molecular forms of A. gambiae at 25 loci, the first two of which cannot be amplified for A. arabiensis. Note that the two A. gambiae forms are practically indistinguishable except at loci H678 and E614, where they are clearly distinct (see Fig. 1B). The numbers of sampled alleles are shown at each locus. Bars represent genetic distance values in red (“clearly different”), yellow (“marginal”), or green (“indistinguishable”), according to the following criteria. For D_K, P_t and P_f are at >10%, between 2.5 and 10% or at <2.5% probability, respectively; for D′ and F_ST, P_d and P_s are at <2.5%, between 2.5 and 10% or at >10% probability, respectively; for R_ST, the value of Nm is <0.5, between 0.5 and 3 or >3, respectively.

Statistical Parameters and Significance Tests.

We have introduced D_K as a normalized measure of differentiation on the basis of Pearson's correlation coefficient, r, which considers the distribution of alleles in two populations around their respective mean allele frequency (Table 1). Depending on the degree of freedom f, two direct statistical significance tests, P_t and P_f, can be applied. P_t is a modified version of Student's t test, which was originally introduced by Gosset in 1908 (23) to evaluate the difference between two means. However, it can also be used to evaluate the covariance of allele frequencies in two populations around their mean frequencies, which are assumed to be identical. The null hypothesis r = 0 supposes, with regard to population comparisons, that two analyzed populations are independent (23–25). In fact, Student's t test is related to the β function, and t serves only as an intermediate parameter; the parameter actually tested is y = 1 − r² in the specific incomplete β function I_y (a, 1/2). A condition imposed originally on the t test is that the degree of freedom f is not large, ≈30–60 (23). However, the polymorphism of microsatellites is large and variable between loci; the degree of freedom f varied from 5 to 79 when comparing A. gambiae and A. arabiensis (see below). We have introduced a necessary modification, defining a not as f/2 but as f/e_f, where e_f is the integer corresponding to f/10 rounded upwards. For example, e_f is 2 for 10 < f ≤ 20. P_t is the probability that the null hypothesis holds: two compared populations are certainly independent if P_t = 1 and indistinguishable if P_t < 0.05.

A different approach and significance estimate of r was proposed by Fisher, in particular to analyze statistical correlation in data with small degrees of freedom (23). The two populations are treated as measures of the same entity, and a complementary error function erfc(x) is used to quantify the deviation (or error) of the two data sets. erfc(x) is based on Fisher's z-transformation, which associates each measured r with a corresponding z. Similar to the t test, we have introduced a modified coefficient e_f to extend the range of f even below 10. The significance level P_f, at which the null hypothesis (r = 0) holds, is given by erfc(x) (23), which is related to the specific incomplete Γ function P(1/2, x²). It should be noted that the significance tests address the null hypothesis of complete independence in the case of D_K (r = 0) and the null hypothesis of identity in the case of D′, F_ST, and R_ST.

The standard genetic distance D was defined by Nei (14) as the negative logarithm of the genetic identity I, which also reflects allele frequencies; I ranges from 1 when the two populations have identical allelic frequencies to zero when they share no alleles. In this paper, we introduce a modified D′ based on the same linear transformation we have used for D_K, (I + 1)/2 (Table 1). Several indirect statistical significance tests have been proposed for D, and we adopt the χ² test for allele frequency differences at each locus (14, 26). P_d is the probability that the null hypothesis (D′ = 0) holds: if P_d = 1, the observed and expected (e.g., the two compared) populations are certainly the same.

On the basis of IAM and the statistical significance tests, the effective migration rate Nm can be estimated from the values of D′ and D_K (Table 1). When these values are high, Nm becomes much smaller than 1, indicating that no gene flow is occurring between the populations.

The well-known parameter F_ST defined by Wright (14) and elaborated by Nei (14) measures the degree of genetic differentiation between two populations by using allele frequencies; Goldstein's (δμ)² (15) is the square of the difference between mean allele sizes, and Slatkin's R_ST (16) focuses on the variance of allele sizes rather than frequencies (Table 1). A direct statistical significance test for F_ST is the contingency χ² test (27, 28), which includes the value of F_ST and n (which for microsatellites is the number of total alleles in both populations). P_s is the probability that the null hypothesis (F_ST = 0) holds: if P_s = 1, the two populations are certainly the same. A statistical significance test of (δμ)² is not available. For R_ST, the estimated value of Nm is used as an indirect test (16); in this study, Nm ≤ 0.5 is taken to indicate that no statistically significant gene flow occurs between the two populations, whereas Nm ≥ 3 indicates that the two compared populations are indistinguishable.

Results and Discussions

Statistical Parameters.

Genetic differentiation of populations on the basis of microsatellites is often measured by using one of four standard parameters, D, F_ST, R_ST, and (δμ)². It is difficult to select a single adequate measure of differentiation (8, 9) because of uncertainly concerning the underlying mutation processes (IAM and SMM). Furthermore, it can be argued a priori as well as empirically from the literature that different parameters have different drawbacks. In a human evolution study, two parameters based on SMM, R_ST, and (δμ)², gave results very different from those recognized from other genetic evidence (8). Although the SMM is often considered more appropriate for microsatellite loci, it appears that their mutational patterns can be often irregular (29); in a honeybee study, IAM produced a better overall fit than SMM (30). As recommended (11, 16), it is prudent to measure differentiation with parameters based on both models. A priori, the least satisfactory parameter is (δμ)², because it is based on the differences between means, ignoring the allele distribution in the data sets, and has no defined statistical significance test. R_ST focuses on the variance of allele sizes and, if the distribution is not normal, R_ST can minimize inappropriately the differences between quite disparate populations that happen to approach the same mean size; the value of R_ST will then approach zero.

F_ST is based on the analysis of variance of allele frequencies. An advantage of F_ST is that it can be weighed to take sample size differences into account. We have introduced a similar partial weighing for R_ST to accommodate data from samples of different size (Table 1). A human evolution study (8) concluded that F_ST is the best parameter when compared with R_ST, (δμ)², and D_SW. A disadvantage of F_ST might be uncertainty concerning the statistical significance tests, of which four have been used over several decades (27, 28, 31–33). In mosquito studies, the contingency χ² test is commonly used with the degree of freedom fixed to 1 when comparing two populations.

The standard genetic distance D is based on the analysis of covariance of allele frequencies. It and several proposed variants can fail to resolve distant relationships if loci have no shared alleles. To address this problem and further limitations of these measures (see Materials and Methods), we have introduced a linear transformation of D, D′ (Table 1), which has a defined value (−ln 0.5 = 0.693) when no alleles are shared. A χ² test of allele frequencies can evaluate the similarity of two populations and serve as an indirect test for D′. It uses the actual degree of freedom to define the statistical significance levels (Table 1) and, in this respect, represents an improvement over the contingency χ² test used for F_ST.

We have introduced a new parameter D_K (Table 1 and Materials and Methods) that uses Pearson's correlation coefficient r, a well-established measure of correlation in statistics. D_K is based on the analysis of covariance of the deviations of allele frequencies around the mean frequency. Importantly, its statistical significance can be tested directly in a robust manner by two mathematically distinct tests of significance. As is true for F_ST and R_ST, D′ and D_K can also be used to determine the effective migration rate Nm between populations, permitting the detection of gene flow.

Analysis of Mosquito Microsatellite Data with Four Parameters.

We have studied genetic differentiation between A. gambiae and A. arabiensis field populations on the basis of a systematic whole-genome scan. Microsatellite data were collected from 23 different chromosomal loci (25 for A. gambiae alone) across the genome (Figs. 1 and 2). This and a larger analysis, to be reported elsewhere, extending to the more distantly related species Anopheles merus and Anopheles melas (34), showed that the two most commonly used parameters for mosquito studies (11–13), F_ST and R_ST, can lead to significantly different results at several loci. After extensive trials of multiple parameters, we came to recommend the use of a panel of four parameters, also including D′ and D_K, for the analysis of population biology and evolution by using microsatellites. Additional parameters gave no significant advantage. For example, (δμ)² failed in our study by showing an unreasonably wide range of values (across 8 orders of magnitude). Software was developed to calculate all of the parameters mentioned in this paper, as well as to support additional useful calculations, for example, observed and expected heterozygosity, Wright's F_IS and F_IT (14), etc. This software is available on our web site (http://www.embl-heidelberg.de/ExternalInfo/kafatos/publications/PROG/).

The allele distributions in these collections of A. gambiae and A. arabiensis are plotted in Fig. 1A, and the genetic differentiation values at each locus are shown in the bar graph of Fig. 2A. For a visual display of statistical significance, the bars are colored: red, yellow and green indicate loci where the two compared populations are significantly different, marginal in terms of similarity or clearly similar (indistinguishable), respectively.

It is worth noting from Fig. 1 that, at many loci, the allele frequencies follow decidedly not normal distributions, which in some cases are bimodal; this is especially true for A. arabiensis, even for mosquito collections from the same region (data not shown). In many cases, visual comparison of the allele distributions can serve as a common-sense test for the efficacy of the four parameters in detecting obvious differences in allele distribution in the two species. Thus, four of the five sex-linked loci, H503, H53, H711w, and E614, have clearly disparate allele distributions (Fig. 1A), and all are scored as statistically different in the two species by both D_K and D′ (Fig. 2A). In contrast, only one of these loci, H711w, is scored as significantly different by both R_ST and F_ST. At two other loci with very high polymorphism, H503 and E614, R_ST and F_ST give exactly opposite results. Evidently, at these four loci of the X-chromosome, the use of multiple parameters, and D_K and D′ in particular, is highly advantageous for detecting clear differences.

Interspecies differences are less prominent among the 18 autosomal loci (Fig. 2A). Only five of these show differences that are validated as statistically significant by two or more parameters. In one of these loci (H135), all four parameters indicate a statistically significant difference; in three loci (H197, H187, and H817), two parameters indicate a significant and two a marginal difference, and in the fifth locus (H525), three parameters detect a clear difference, but R_ST indicates identity. It may be relevant that in H525, 29 of 81 A. arabiensis gave null alleles; these alleles were evidently mutated in a primer sequence and suggest that this locus may indeed be differentiated in the two species.

It is interesting to see how concordant are the three parameters that are based on the same mutation model, IAM (Fig. 2A). D_K and D′ are nonconcordant at only four loci (three marginal/indistinguishable, and one marginal/different). In contrast, D′ and D_K are each nonconcordant with F_ST at seven loci, at two of which F_ST gives opposite results (significantly different/indistinguishable). Failure of F_ST to detect clear differences often occurs when allele numbers are either very large (H503, H187) or quite small (H53). However, at E614, despite the large number of alleles, F_ST is able to detect a clear disparity between the species. The availability of two independent statistical tests for D_K proved valuable: both P_t and P_f show the same results for 10 < f < 40. Fisher's P_f should be used for f ≤ 10 and also appears more suitable for f ≥ 40.

Two biologically important conclusions emerge from this analysis: that the X chromosome shows substantially greater disparities between A. gambiae and A. arabiensis than do the autosomes and, in particular, that all three microsatellite loci that map to the Xag inversion of the X chromosome show large differences in allele frequency distribution. In fact, two additional A. gambiae microsatellite loci within this inversion, H145 and H36, could not be amplified in any of the 81 A. arabiensis (data not shown), reinforcing the conclusion of substantial molecular differences between the two species in this larger inversion. The inversion is present in A. gambiae but absent in A. arabiensis. These data are consistent with the observation that the effective migration rate (and estimated gene flow) Nm between A. gambiae and A. arabiensis is lower on the X as compared with the autosomes (12); they lend support to the notion of Coluzzi and coworkers that fixed inversion polymorphisms that discriminate between species of the A. gambiae complex are ancient and associated with local genetic divergence (5, 35).

It is thought that A. gambiae s.s. actually encompasses two or more emerging species, and we examined whether these taxa show different microsatellite profiles. The Mopti, Savanna, and Bamako chromosomal forms can be distinguished by their patterns of chromosomal inversions in the northern drier areas of West Africa (5, 6), but in the more humid southern coastal areas, the Forest chromosomal form is prevalent, and fixed differentiation at the rDNA locus, outside the Xag inversion, is a more robust indicator of two nonpanmictic molecular forms, M and S (1). Molecular typing of our samples yielded 77 M and 94 S individuals of A. gambiae, which were compared directly (Figs. 1B and 2B).

Interestingly, the M and S molecular forms were largely indistinguishable by microsatellites across the genome, except at the base of the X, outside the Xag inversion, where the two forms were unambiguously different according to all four parameters, at both H678 and E614 (cytogenetic divisions 5D and 6, respectively). At H678, most M mosquitoes have short alleles, and S have long alleles, whereas the opposite is true at E614 (Fig. 1B). The rDNA molecular marker distinguishing the M and S forms lies in the same region around cytogenetic division 6 (F. H. Collins, personal communication). Differentiation of the M and S forms on the basis of the tandemly repetitive rDNA locus alone could be ascribed to concerted evolution (1, 2), but the additional observation of clear differences at two nearby microsatellite loci provides strong evidence that the M and S forms are indeed genetically differentiated. Thus, our results to date lend strong support to the concept of emergent M and S taxa of A. gambiae s.s., which are of major taxonomic significance for studying the hypothesized incipient speciation process for which A. gambiae is a uniquely favorable model. Our results provide microsatellite tools to distinguish these forms, at least in Mali. In a preliminary analysis, we have obtained and genotyped 28 and 24 mosquitoes that were karyotyped as Mopti and Savanna, respectively. The results revealed that Mopti differs from Savanna at these two loci in the same way that M differs from S (data not shown); this is not surprising, as all Mopti are M and all Savanna are S in Mali (1).

A remarkable observation came from separate comparisons of M and S forms of A. gambiae with A. arabiensis (Fig. 3). Like the original pooled sample of A. gambiae (Fig. 2A), M-form mosquitoes are clearly different from A. arabiensis within the Xag inversion and at locus E614 but resemble A. arabiensis at locus H678. In sharp contrast, S-form mosquitoes are very clearly different from A. arabiensis in locus H678 as well. This observation raises the interesting possibility of introgression between A. gambiae (M) and A. arabiensis in cytogenetic division 5, where H678 maps. More extensive studies will be necessary to follow up this possibility, as well as to explore further the apparent mosaicism of the autosomes with respect to localized A. gambiae/A. arabiensis differences (36).

Field studies of genetic differentiation within vector populations can yield important information relating to evolution and population biology. Such studies are fundamentally important for understanding the epidemiology of malaria in Africa, where A. gambiae is, overall, the most important vector of the disease. Our work points out the advantages of a systematic whole-genome scan with a larger number of microsatellite loci for detecting chromosomally localized genetic differentiation in field populations. It is notable that this systematic study has detected two genetic differences at microsatellite loci, despite the failure of several previous attempts to find molecular markers specific for the M and S molecular forms in regions different from the rDNA locus (1–4, 7). Systematic genotyping is greatly facilitated by high-throughput methods (22). We have found it is important to subject the data to analysis with multiple parameters of genetic differentiation, including those that correspond to different mutational models. We have offered the modified D′ parameter and the new normalized parameter D_K to complement the parameters F_ST and R_ST, which are most commonly used in this field. The diversity of allele profiles at different loci, including nonnormal allele distributions with very high and low levels of polymorphism, have highlighted some problems encountered with individual parameters. We strongly suggest that all four parameters be used, together with appropriate statistical tests, at least until an extensive body of studies further clarifies the relative merits and limitations of the different parameters.

Abbreviations

IAM

infinite allele model of mutation

SMM

stepwise mutation model

rDNA

ribosomal DNA