Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2018 Jan 30;45(2):578–584. doi: 10.1002/2017GL076260

Electron Crescent Distributions as a Manifestation of Diamagnetic Drift in an Electron‐Scale Current Sheet: Magnetospheric Multiscale Observations Using New 7.5 ms Fast Plasma Investigation Moments

A C Rager 1,2,✉, J C Dorelli 2, D J Gershman 2, V Uritsky 1,2, L A Avanov 2,3, R B Torbert 4,5, J L Burch 5, R E Ergun 6, J Egedal 7, C Schiff 2, J R Shuster 2,3, B L Giles 2, W R Paterson 2, C J Pollock 8, R J Strangeway 9, C T Russell 9, B Lavraud 10, V N Coffey 11, Y Saito 12
PMCID: PMC5856066  PMID: 29576666

Abstract

We report Magnetospheric Multiscale observations of electron pressure gradient electric fields near a magnetic reconnection diffusion region using a new technique for extracting 7.5 ms electron moments from the Fast Plasma Investigation. We find that the deviation of the perpendicular electron bulk velocity from E × B drift in the interval where the out‐of‐plane current density is increasing can be explained by the diamagnetic drift. In the interval where the out‐of‐plane current is transitioning to in‐plane current, the electron momentum equation is not satisfied at 7.5 ms resolution.

Keywords: diamagnetic drift, reconnection

Key Points

  • Diamagnetic drift explains out‐of‐plane current in regions of deviation from frozen‐in flux

  • Perpendicular crescents exist in regions where electrons are diamagnetically drifting

  • New technique for extracting 7.5 ms electron moments produces reliable data

1. Introduction

Magnetic reconnection is often invoked to explain the rapid conversion of magnetic energy into plasma energy in astrophysical and laboratory plasmas. In our solar system, magnetic reconnection is the primary mode by which the solar wind couples electrodynamically to magnetized bodies, producing open magnetic topologies and enabling the transport of mass, momentum, and energy from the solar wind into planetary magnetospheres. While computer simulations have produced a wealth of predictions about the electron‐scale properties of reconnection (Bessho et al., 2016; Chen et al., 2016; Hesse et al., 2014, 2011; Jain & Sharma, 2009; Shay et al., 2007), there have been few direct measurements to test these predictions.

The Magnetospheric Multiscale (MMS) mission was designed to study the basic physics of magnetic reconnection in Earth's magnetosphere, resolving both the fields and plasma on electron scales for the first time (Burch, Moore, et al., 2016; Pollock et al., 2016). MMS consists of four spacecraft flying in a close tetrahedral formation (nominal spacecraft separations are ∼10 km). The close formation and high quality of the MMS tetrahedron permits the accurate calculation of sub‐ion‐scale spatial gradients, allowing for the first time a direct test of exact plasma fluid equations.

The MMS Fast Plasma Investigation (FPI) uses a suite of 64 top‐hat spectrometers to sample the three‐dimensional velocity space every 30 (150) ms for electrons (ions) (Pollock et al., 2016). The 30 ms resolution electron measurements from the FPI Dual Electron Spectrometer have resulted in the first electron‐scale measurements of a dayside magnetopause current sheet associated with magnetic reconnection (Burch, Torbert, et al., 2016). Burch, Torbert, et al. (2016) reported crescent‐shaped electron velocity distributions consistent with those observed in two‐dimensional particle‐in‐cell (PIC) simulations near the electron diffusion region (EDR) (e.g., Hesse et al., 2014), suggesting that the EDR was contained within the MMS tetrahedron.

Several explanations of the electron crescent distributions have since appeared in the literature. Bessho et al. (2016) modeled electron Speiser orbits (Speiser, 1965) in a one‐dimensional current sheet with a normal electric field, using Liouville's theorem to show how crescents can be produced from an assumed isotropic velocity distribution at the magnetic neutral sheet. Shay et al. (2016) used a similar model to explain the crescents as a consequence of cusp‐like electron orbits resulting from acceleration by the normal electric field.

Both Bessho et al. (2016) and Shay et al. (2016) invoke meandering electron orbits to explain the crescents, suggesting that the observation of crescents can, by comparison with two‐dimensional PIC simulations, be used to infer proximity to the EDR. In contrast, Egedal et al. (2016) argue that the electron crescents can be understood by a simple drift‐kinetic model in which the nongyrotropic electron distributions observed by MMS can be expressed in terms of an equivalent guiding center distribution:

f(x,v,t)=Fg(Xg,v‐vg,v∥,v⊥,t) (1)

where x and v are the electron position and velocity, v g is the guiding center drift (including the E × B, magnetic gradient, and curvature drifts), X g≡x − ρ(x,v,t) is the electron guiding center location, ρ ≡ v × b/Ωe is the electron gyroradius vector, b is the unit vector in the direction of the magnetic field B, Ωe=q B/(m e c) is the electron gyrofrequency, and v∥ and v⊥ are the electron velocity components parallel and perpendicular to the magnetic field.

Note that equation (1) makes no assumption about the size of the electron gyroradius relative to the scale over which F g(X g,v‐v g,v ∥,v ⊥,t) varies; one only assumes that in the frame of the guiding center drift, all of the gyrophase dependence of f(x,v,t) can be explained by spatial structure of the gyrotropic guiding center distribution. In particular, equation (1) allows large deviations from gyrotropy in the electron velocity phase space density measured at a given point and associated perpendicular currents despite the fact that the electrons are strongly magnetized.

To understand how strongly magnetized electrons can produce a significant perpendicular current in the E × B frame, we consider the electron momentum equation, neglecting the inertia terms:

neE+neVe×Bc+∇·Pe=0 (2)

where n is the plasma density (quasineutrality assumed), V e is the electron bulk velocity, and P e is the electron pressure tensor (defined in the electron bulk flow frame). Separating the electron pressure tensor into its gyrotropic and nongyrotropic components, P e=P eg+Π e (where P eg=P e∥ b b + P e⊥(I − b b), P e⊥=[T r(P e) − P e∥]/2, and Π e is the nongyrotropic component), the perpendicular component of (2) can be written as follows:

neE⊥=−neVe×Bc−∇⊥Pe⊥−(Pe∥−Pe⊥)κ−(∇·Πe)⊥ (3)

where κ = b·∇ b is the magnetic curvature. Equation (3) shows that the electron perpendicular bulk velocity can differ significantly from c E × B/B 2 (where B is the magnetic field magnitude) even when the divergence of the nongyrotropic component of the pressure tensor vanishes. The essential point is that sub‐ion‐scale electron pressure gradients and associated electron diamagnetic drift, represented by the second term on the right‐hand side of (3), may produce significant electron current density in the E × B frame even when the electrons are strongly magnetized (Hoffman & Bracken, 1965). We emphasize, however, that such diamagnetic drift should also be present at an asymmetric current sheet in which electrons exhibit meandering orbits from the high‐density magnetosheath to the low‐density magnetosphere.

Torbert et al. (2016) examined the terms in the generalized Ohm's law for the Burch, Torbert, et al. (2016) EDR event and found significant deviations of the perpendicular electron bulk velocity from c E × B/B 2 that were associated with the divergence of the full electron pressure tensor; however, they did not further separate the electron pressure tensor into its gyrotropic and nongyrotropic components, so that an important question remains unanswered: Are the nongyrotropic electron crescent distributions observed by Burch, Torbert, et al. (2016) a manifestation of the electron diamagnetic drift of strongly magnetized electrons in a thin sub‐ion‐scale current sheet? In what follows, we address this question using a new method we have developed to extract 7.5 ms plasma moments from the MMS FPI data. The details of the technique for generating 7.5 ms electron and 37.5 ms ion moments from the raw data are outside the scientific scope of this paper and are available in the supporting information.

2. Data and Results

In Figures 1a–1d we show the four 7.5 ms separated electron velocity distributions that constitute the 30 ms FPI product (Figure 1e). The complex crescent structure of the 30 ms distribution, with alternating sections of high‐ and low‐energy plasma, have been referred to colloquially as fingers of the crescent distribution. We observe that the energy and flux of the plasma increases from distributions in Figures 1a to 1d, over a time interval less than 30 ms. The intensity of flux in the crescent builds up over the four distributions leading to the 30 ms FPI composite distribution with distinctive flux variations, as highlighted by the arrows in Figures 1a–1d. These four intermediate distributions provide the first opportunity to observe that the variation in the 30 ms FPI distribution is the result of time aliasing in energy and flux intensity rather than a measured variation in the spatial quantities. The composite image shows that a simple image stacking of the four distributions roughly recovers the 30 ms distribution, validating our intermediate distributions. Comparing Figure 1e, the 30 ms FPI product, with Figure 1f, the intermediate distributions (Figures 1a–1d), allows us to conclude that the complex energy structure of the crescent fingers is a result of time aliasing the four evolving crescent distributions.

Figure 1.

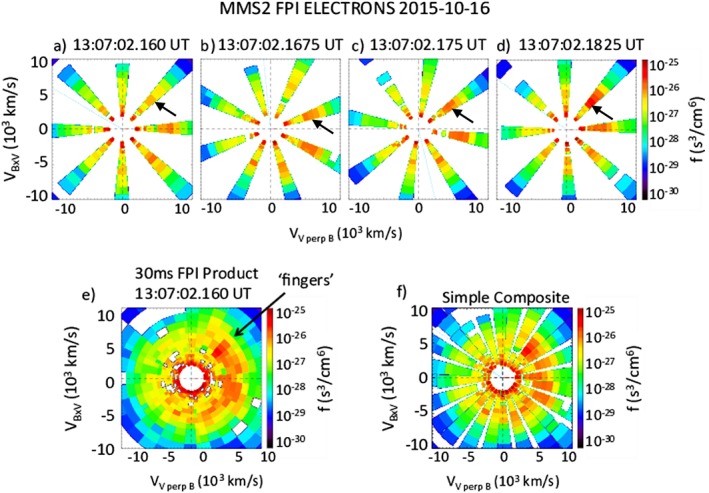
grl56872-fig-0001

Open in a new tab

(a–d) Four intermediate electron velocity distributions that are used to generate the 30 ms FPI electron velocity distribution. The sub‐30 ms changes in energy and intensity are highlighted by black arrows. (e) The FPI 30 ms electron velocity distribution highlighting the “fingers” structure in question. (f) The simple image composite of distributions (Figures 1a–1d) for comparison to the 30 ms distribution.

Burch, Torbert, et al. (2016) demonstrated that MMS encountered an electron diffusion region (EDR) on 16 October 2015. They identified the EDR based on several criteria: (1) a bipolar exhaust signature in the L component (in boundary normal coordinates) of the ion bulk velocity, (2) a strong perpendicular current in which the electron perpendicular bulk velocity differs significantly from E × B drift, (3) a strong depression in the magnetic field magnitude (suggesting a magnetic null in the reconnection plane), (4) strong parallel electron heating, (5) a strong electric field pointing outward along the current sheet normal, (6) crescent‐shaped electron velocity distributions, and (7) a strong J ⊥·E ⊥ signature in the electron rest frame. Figure 2 shows an overview of the FPI MMS2 burst data for the studied event at the FPI native 30 ms and 150 ms cadences for the 5 s around the diffusion region. We observe the parallel (0–30°) (Figure 2a) and antiparallel (150–180°) Figure 2b) electron energy‐time spectrograms, omnidirection ion energy‐time spectrogram (Figure 2c), magnetic field (Figure 2d), current density as calculated by FPI (Figure 2e), electric field (Figure 2f), and parallel and perpendicular electron temperatures (Figure 2g).

Figure 2.

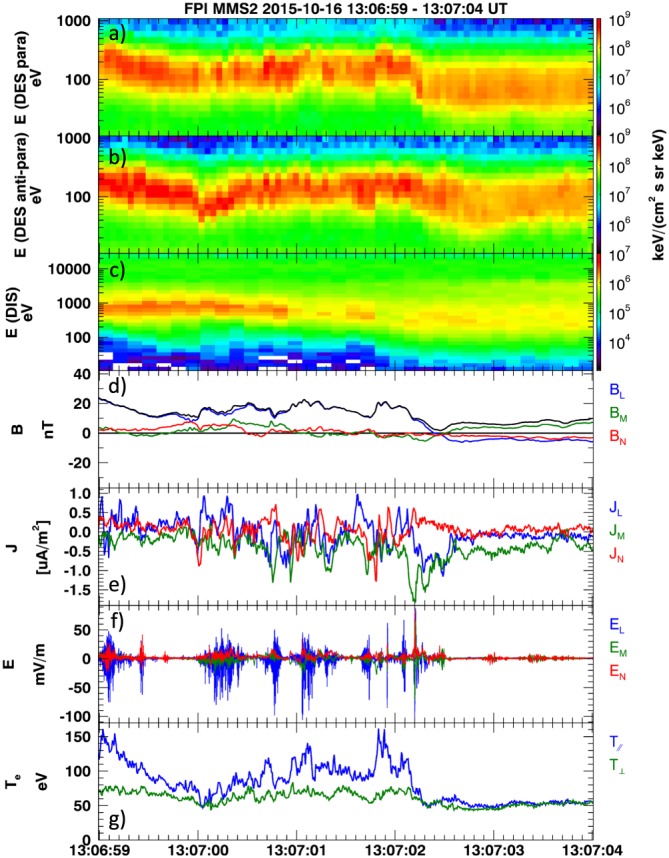
grl56872-fig-0002

Open in a new tab

MMS2 overview of the 5 s surrounding the EDR event on 16 October 2015. (a) Parallel (0–30°) electron energy‐time spectrogram, (b) antiparallel (150–180°) electron energy‐time spectrogram, (c) omnidirectional ion energy‐time spectrogram, (d) magnetic field, (e) current from FPI, (f) electric field, and (g) parallel and perpendicular electron temperature.

The presence of the electron crescent velocity distributions supporting J ⊥·E ⊥>0 is the most compelling evidence for proximity of MMS to the EDR, having been predicted by PIC simulations (e.g., Hesse et al., 2014) as a feature of the flow stagnation region. However, it is interesting to note that the onset of perpendicular crescents observed by MMS2 (at about 13:07:02.16 UT section II of Figure 4) is during the rising edge of J M and earlier than the onset of large‐amplitude electric field fluctuations (at about 13:07:02.2 UT and visible in Figure 2f). Recently, Burch et al. (2017) interpreted the large‐amplitude electric field fluctuations as nonlinear electrostatic whistler structures that can produce intense localized magnetic dissipation that drives magnetic reconnection at the boundary between closed and open magnetic field lines, where the perpendicular crescents are just beginning to transition to parallel crescents.

Figure 4.

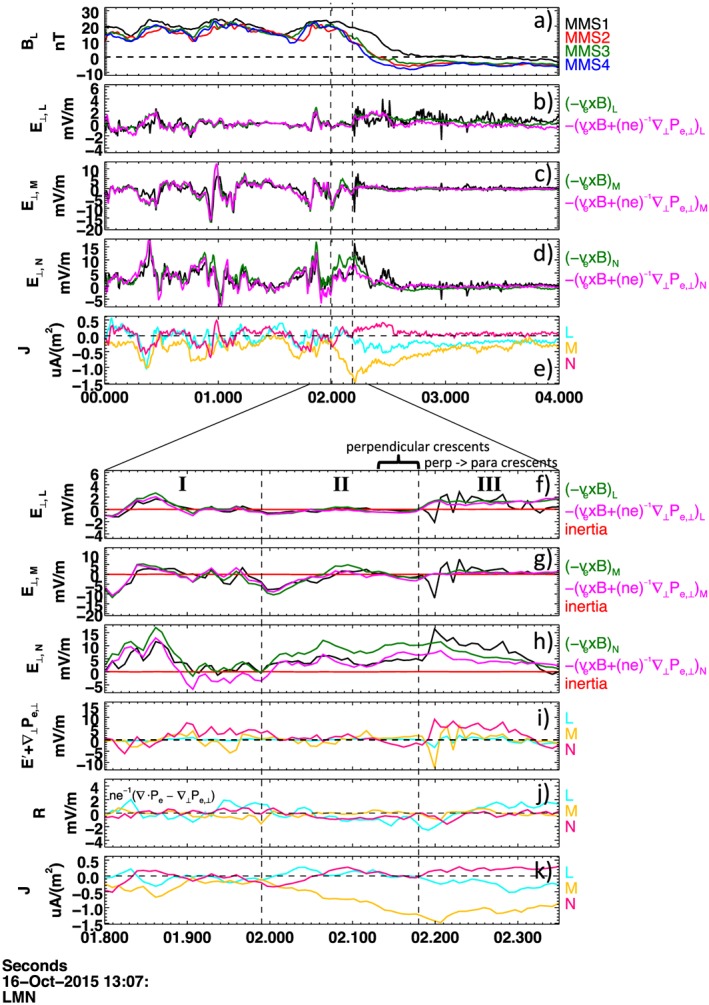
grl56872-fig-0004

Open in a new tab

Inclusion of the perpendicular electron pressure gradient, −(ne)−1∇⊥Pe⊥, results in reduced deviation from the perpendicular electric field (Figures 4b–4d and 4f–4h). The left and right vertical dashed lines indicate the onset of J M and J L, respectively. Excepting the magnetic field, for each measurement we use the four observatory average value. This is an approximation to the barycenter measurement, and for consistency in comparison to the four observatory average of electric field we use the 7.5 ms FPI calculation of the current density rather than the curlometer calculated value. Top panels include, in boundary normal coordinates, the (a) magnetic field, (b–d) observatory average perpendicular electric field compared with the components of the first two terms on the right‐hand side of equation (3), and (e) current via FPI. Bottom panels include a closer view of EDR region for the (f–h) observatory average perpendicular electric field comparison, (i) E ⊥+v e×B/c + (n e)−1∇⊥ P e,⊥, (j) residue defined as n e −1(∇·P e−∇⊥ P e,⊥), and (k) current via FPI. Boundary normal coordinates were calculated using the conversion matrix provided in Burch, Torbert, et al. (2016).

Figure 3 shows the electric field and electron pressure at 30 ms and 7.5 ms in an interval prior to entering the EDR where we expect the electrons to be E × B drifting (frozen‐in). The perpendicular components of the electric field are shown in red (FPI at 30 ms resolution), green (FPI at 7.5 ms resolution), and black (Electric field Double Probe (EDP) 8 kHz data averaged to 7.5 ms). It is clear that the FPI 7.5 ms perpendicular bulk velocity recovers additional structure that can be explained by E × B drift. This improved agreement between E ⊥ and −V e×B/c serves as the first step in validation of our 7.5 ms moments algorithm. On the other hand, the electron parallel and perpendicular pressures (Figures 3d and 3e) appear to have converged already at 30 ms resolution—not much additional structure is recovered at 7.5 ms. The full propagation of errors, as described for plasma moment calculations by Gershman et al. (2015), will require a more detailed study given the complex nature of the technique.

Figure 3.

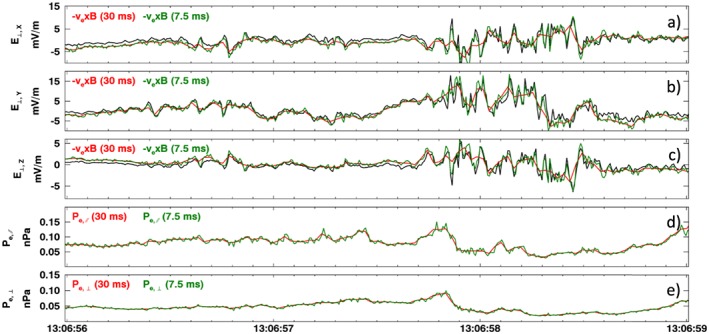
grl56872-fig-0003

Open in a new tab

The 7.5 ms electron bulk velocity shows much improved agreement with E × B drift in the interval from 13:06:57 to 13:06:59 where we expect the electrons to be frozen in and strongly magnetized. (a–c) The 8 kHz EDP electric field at MMS2 averaged to 7.5 ms (black) and the FPI −V e×B/c at 30 ms (red) and 7.5 ms (green) resolutions. (d and e) The MMS2 FPI parallel and perpendicular electron pressure at 30 ms (red) and 7.5 ms (green).

Figure 4, section II, shows that the deviation of the electron perpendicular bulk velocity from E × B drift coincides with the onset of electron diamagnetic drift. That is, in the region of nongyrotropic perpendicular electron crescents prior to region of large electric field fluctuations, the perpendicular gradient of the perpendicular electron pressure is making the dominant contribution to E ⊥+V e×B/c, as shown in Figures 4b–4d and 4f–4h. This result suggests that the strong nongyrotropy of the electron velocity distributions in this interval is a manifestation of the energy‐dependent magnetic gradient drifts that—when integrated over velocity space—produce an electron pressure gradient contribution in equation (3).

In section I, prior to the onset of J M shown in section I, there is an electron pressure gradient signal but no corresponding current density. This displacement in time between the pressure gradient signal and the J M signal is a result of averaging the J M measurements from the four observatories as they cross into the current sheet. The finite difference pressure gradient signal does not produce such a delay. It is for this reason that the inclusion of the perpendicular electron pressure gradient in section I results in worse agreement while the electrons are frozen in. We focus this study on the current sheet of section II where the electrons at first appear to be demagnetized when comparing only E ⊥ with −V e×B/c.

In Figures 4f–4h, section III, we observe a large deviation from the frozen‐in condition. From Figures 4b–4d we can see that this deviation is both large and persistent. For this reason we suggest that during the interval of large electric field fluctuations beginning at 13:07:02.2 UT (section III), the electron momentum equation does not appear to be satisfied at FPI 7.5 ms resolution. The residue calculation n e −1(∇·P e−∇⊥ P e,⊥) in Figure 4j shows that in section III the nongyrotropic component of the electron pressure tensor is negligible in comparison to the electric field shown in Figure 4h. Based on this calculation, the nongyrotropic contribution to the electron momentum equation is minimal and does not explain the discrepancy. Possible explanations include time variability on the scale of the FPI energy sweep and smoothing of spatial structures by the four spacecraft gradient operator.

3. Discussion and Conclusions

In summary, we have shown that the deviation of the electron bulk velocity from E × B drift observed in section II between 13:07:01.199 UT and 13:07:02.180 UT can be explained by electron diamagnetic drift in an electron‐scale current sheet. In section III, the region where the out‐of‐plane current is transitioning to in‐plane current, the electron momentum equation is not satisfied at 7.5 ms FPI resolution. Since electron diamagnetic drift does not itself produce any magnetic energy dissipation, our result is consistent with the observation of J·E′≈0 between 13:07:01.990 UT and 13:07:02.180 UT by Burch, Torbert, et al. (2016). The observation of perpendicular crescents preceding the region of J·E′>0 suggests that the presence of perpendicular crescents alone does not imply magnetic energy dissipation. However, we emphasize that our results do not rule out the existence of meandering electron orbits and associated magnetic energy dissipation (as argued by Burch, Torbert, et al., 2016) or anomalous resistivity (as suggested by Torbert et al., 2016) since the associated features in the electron velocity distribution may be very difficult to measure.

Our results raise important questions about the nature of magnetic energy dissipation at the magnetopause. In steady laminar reconnection, with a reconnection rate of about 0.1V A B/c (where V A is the Alfvén speed), the corresponding reconnection electric field is on the order of 0.1–1 mV/m. The observed electric field fluctuations in the interval where the electron momentum equation is not satisfied, however, are much larger than that, approaching 50–100 mV/m and varying over the 7.5 ms time scale of the FPI energy sweep. What role do these fluctuations play in changing the magnetic field topology and dissipating magnetic energy? What is their contribution to the global integrated reconnection rate?

Burch et al. (2017) has recently suggested that large‐amplitude electric field fluctuations over a region much more localized than that of the out‐of‐plane current density directly drive reconnection by producing localized J·E′ at the boundary between open and closed magnetic field lines. Our results, demonstrating that the electrons are diamagnetically drifting in the region of perpendicular crescents prior to the onset of large‐amplitude electric field fluctuations, are consistent with this suggestion.

However, it is also possible that the global reconnection rate is supported by electron meandering orbits interacting with a much smaller electric field on the order of 0.1V A B/c (the global integral of which gives the reconnection rate), as shown in two‐dimensional PIC simulations (e.g., Hesse et al., 2014). Although the observation of crescents by themselves does not imply meandering orbits, crescent distributions observed in such close proximity to an electron‐scale magnetic field reversal supports the idea of meandering orbits (Burch, Torbert, et al., 2016; Egedal et al., 2016).

A third possibility is that turbulent fluctuations facilitate anomalous transport at the magnetopause. For example, there is evidence from three‐dimensional PIC simulations of the Burch, Torbert, et al. (2016) event that lower hybrid turbulence (driven by the diamagnetic drift) can lead to anomalous heating and transport of plasma from the sheath onto closed magnetic field lines (Le et al., 2017). Torbert et al. (2016) has suggested that violation of the Generalized Ohm's law at 30 ms resolution might be evidence of such anomalous resistivity, and our 7.5 ms results have not eliminated this possibility.

Further progress will require the development of new techniques that move beyond the calculation of velocity moments and extract information about phase space density and its velocity space gradients on time scales shorter than the FPI 7.5 ms energy sweep.

Supporting information

Supporting Information S1

Click here for additional data file. (649.7KB, pdf)

Acknowledgments

This research was supported by the National Aeronautics and Space Administration (NASA) Magnetospheric Multiscale (MMS) Mission in association with NASA contract NNG04EB99C. Institut de Recherche en Astrophysique et Planétologie (IRAP) contributions to MMS FPI were supported by Centre National d'Etudes Spatiales (CNES) and Centre National de la Recherche Scientifique (CNRS). We thank the entire MMS team and instrument leads for data access and support. The L2 data of MMS can be accessed from MMS Science Data Center (https://lasp.colorado.edu/mms/sdc/public/).

Rager, A. C. , Dorelli, J. C. , Gershman, D. J. , Uritsky, V. , Avanov, L. A. , Torbert, R. B. , … Saito, Y. (2018). Electron crescent distributions as a manifestation of diamagnetic drift in an electron‐scale current sheet: Magnetospheric Multiscale observations using new 7.5 ms Fast Plasma Investigation moments. Geophysical Research Letters, 45, 578–584. https://doi.org/10.1002/2017GL076260

References

  1. Bessho, N. , Chen, L.‐J. , & Hesse, M. (2016). Electron distribution functions in the diffusion region of asymmetric magnetic reconnection. Geophysical Research Letters, 43, 1828–1836. https://doi.org/10.1002/2016GL067886 [Google Scholar]
  2. Burch, J. L. , Ergun, R. E. , Cassak, P. A. , Webster, J. M. , Torbert, R. B. , Giles, B. L. , … Newman, D. L. (2017). Localized oscillatory dissipation in magnetopause reconnection. ArXiv e‐prints. http://arxiv.org/abs/1712.05697 [Google Scholar]
  3. Burch, J. L. , Moore, T. E. , Torbert, R. B. , & Giles, B. L. (2016). Magnetospheric multiscale overview and science objectives. Space Science Reviews, 199(1), 5–21. https://doi.org/10.1007/ s11214-015-0164-9 [Google Scholar]
  4. Burch, J. L. , Torbert, R. B. , Phan, T. D. , Chen, L.‐J. , Moore, T. E. , Ergun, R. E. , … Chandler, M. (2016). Electron‐scale measurements of magnetic reconnection in space. Science, 352(6290), aaf2939 https://doi.org/10.1126/science.aaf2939 [DOI] [PubMed] [Google Scholar]
  5. Chen, L.‐J. , Hesse, M. , Wang, S. , Gershman, D. , Ergun, R. , Pollock, C. , … Avanov, L. (2016). Electron energization and mixing observed by MMS in the vicinity of an electron diffusion region during magnetopause reconnection. Geophysical Research Letters, 43, 6036–6043. https://doi.org/10.1002/2016GL069215 [Google Scholar]
  6. Egedal, J. , Le, A. , Daughton, W. , Wetherton, B. , Cassak, P. A. , Chen, L.‐J. , … Avanov, L. A. (2016). Spacecraft observations and analytic theory of crescent‐shaped electron distributions in asymmetric magnetic reconnection. Physical Review Letters, 117, 185101 https://doi.org/10.1103/PhysRevLett.117.185101 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Gershman, D. J. , Dorelli, J. C. , Viñas, A. F. , & Pollock, C. J. (2015). The calculation of moment uncertainties from velocity distribution functions with random errors. Journal of Geophysical Research: Space Physics, 120, 6633–6645. https://doi.org/10.1002/2014JA020775 [Google Scholar]
  8. Hesse, M. , Aunai, N. , Sibeck, D. , & Birn, J. (2014). On the electron diffusion region in planar, asymmetric, systems. Geophysical Research Letters, 41, 8673–8680. https://doi.org/10.1002/2014GL061586 [Google Scholar]
  9. Hesse, M. , Neukirch, T. , Schindler, K. , Kuznetsova, M. , & Zenitani, S. (2011). The diffusion region in collisionless magnetic reconnection. Space Science Reviews, 160, 3–23. [Google Scholar]
  10. Hoffman, R. A. , & Bracken, P. A. (1965). Magnetic effects of the quiet‐time proton belt. Journal of Geophysical Research, 70(15), 3541–3556. https://doi.org/10.1029/JZ070i015p03541 [Google Scholar]
  11. Jain, N. , & Sharma, A. S. (2009). Electron scale structures in collisionless magnetic reconnection. Physics of Plasmas, 16(5), 050704 https://doi.org/10.1063/1.3134045 [Google Scholar]
  12. Le, A. , Daughton, W. , Chen, L.‐J. , & Egedal, J. (2017). Enhanced electron mixing and heating in 3‐D asymmetric reconnection at the Earth's magnetopause. Geophysical Research Letters, 44, 2096–2104. https://doi.org/10.1002/2017GL072522 [Google Scholar]
  13. Pollock, C. , Moore, T. , Jacques, A. , Burch, J. , Gliese, U. , Saito, Y. , … Zeuch, M. (2016). Fast Plasma Investigation for Magnetospheric Multiscale. Space Science Reviews, 199(1), 331–406. https://doi.org/10.1007/s11214-016-0245-4 [Google Scholar]
  14. Shay, M. A. , Drake, J. , Swisdak, M. , Phan, T. , & Eastwood, J. (2007). Two‐scale structure of the electron dissipation region during collisionless magnetic reconnection. Physical Review Letters, 99, 155002 https://doi.org/10.1103/PhysRevLett.99.155002 [DOI] [PubMed] [Google Scholar]
  15. Shay, M. A. , Phan, T. D. , Haggerty, C. C. , Fujimoto, M. , Drake, J. F. , & Malakit, K. (2016). Kinetic signatures of the region surrounding the X line in asymmetric (magnetopause) reconnection. Geophysical Research Letters, 43, 4145–4154. https://doi.org/10.1002/2016GL069034 [Google Scholar]
  16. Speiser, T. W. (1965). Particle trajectories in model current sheets: 1. Analytical solutions. Journal of Geophysical Research, 70(17), 4219–4226. https://doi.org/10.1029/JZ070i017p04219 [Google Scholar]
  17. Torbert, R. B. , Burch, J. L. , Giles, B. L. , Gershman, D. , Pollock, C. J. , Dorelli, J. , … Bounds, S. (2016). Estimates of terms in Ohm's law during an encounter with an electron diffusion region. Geophysical Research Letters, 43, 5918–5925. https://doi.org/10.1002/2016GL069553 [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information S1

Click here for additional data file. (649.7KB, pdf)

Articles from Geophysical Research Letters are provided here courtesy of Wiley

RESOURCES