Multimodel Evidence for an Atmospheric Circulation Response to Arctic Sea Ice Loss in the CMIP5 Future Projections

Abstract

Previous single‐model experiments have found that Arctic sea ice loss can influence the atmospheric circulation. To evaluate this process in a multimodel ensemble, a novel methodology is here presented and applied to infer the influence of Arctic sea ice loss in the CMIP5 future projections. Sea ice influence is estimated by comparing the circulation response in the RCP8.5 scenario against the circulation response to sea surface warming and CO₂ increase inferred from the AMIPFuture and AMIP4xCO2 experiments, where sea ice is unperturbed. Multimodel evidence of the impact of sea ice loss on midlatitude atmospheric circulation is identified in late winter (January–March), when the sea ice‐related surface heat flux perturbation is largest. Sea ice loss acts to suppress the projected poleward shift of the North Atlantic jet, to increase surface pressure in northern Siberia, and to lower it in North America. These features are consistent with previous single‐model studies, and the present results indicate that they are robust to model formulation.

Key Points

• Multimodel evidence shows that future projections of atmospheric circulation change are influenced by Arctic sea ice loss

• The impact of Arctic sea ice loss on large‐scale atmospheric circulation is mainly confined to late winter

• The poleward shift of the North Atlantic jet with global warming is suppressed in late winter by Arctic sea ice loss

1. Introduction

Understanding the response of atmospheric circulation to increasing greenhouse gases is essential to have more confidence in the regional impacts of climate change (Shepherd, 2014). A common feature of the future projections is a poleward shift of midlatitude jets and Hadley cell edge (e.g., Ceppi et al., 2018), but at the regional scale the circulation response remains highly uncertain, thus making it important to identify the physical processes driving the response.

The warming of sea surface temperatures (SSTs) and the direct radiative impact of CO₂ have been shown to favor the poleward shift of midlatitude circulation (Grise & Polvani, 2014). However, in the Northern Hemisphere (NH), this process might be opposed by the loss of Arctic sea ice and the associated polar amplification of global warming (e.g., Blackport & Kushner, 2017; Harvey et al., 2015; Shaw et al., 2016). By analyzing the intermodel spread in the future projections from the Fifth Phase of the Coupled Model Intercomparison Project (CMIP5), evidence of this “tug‐of‐war” between tropical and polar forcing has been identified for the future response in the latitude of the North Atlantic jet (Barnes & Polvani, 2015), the strength of midlatitude storm tracks (Harvey et al., 2014), and the speed of midlatitude westerlies (Manzini et al., 2014; Zappa & Shepherd, 2017).

Additional evidence on the specific role of sea ice loss has been gathered by numerical experiments in which sea ice extent is perturbed while global SSTs are kept fixed (see reviews from Budikova, 2009, and Vihma, 2014). While the role of past sea ice decline and variability for the atmospheric circulation changes in the last decades remains debated (Overland et al., 2016; Perlwitz et al., 2015; Shepherd, 2016), a more consistent picture is emerging among the studies that employ larger sea ice perturbations, such as those expected by the end of the 21st century (Blackport & Kushner, 2016; Deser et al., 2010, 2015, McCusker et al., 2017; Oudar et al., 2017; Peings & Magnusdottir, 2014; Royer et al., 1990; Seierstad & Bader, 2009). The circulation response is typically characterized by either a weakening or southward shift of the midlatitude westerly jets, similar to the negative phase of the Arctic Oscillation (AO).

If sea ice loss exerts a substantial impact on midlatitude circulation, then a signature of its influence should be identifiable not just in the intermodel spread but also in the mean of the CMIP5 models' future projections. This will be investigated here by comparing the multimodel mean circulation response in the RCP8.5 scenario to the circulation response induced by SST warming and CO₂ increase alone. These responses are available thanks to the AMIPFuture and AMIP4xCO2 CMIP5 experiments, in which SSTs and CO₂ concentrations have been respectively increased while sea ice is kept at present day values. Sea ice loss‐related signals should thus be detectable as features of the RCP8.5 response that cannot be explained by the AMIPFuture and AMIP4xCO2 experiments. Although the approach requires assumptions on the linearity and state independence of the circulation response to forcing, it represents the first attempt to identify the impact of sea ice loss on atmospheric circulation in a large ensemble of climate models.

2. Data and Methods

2.1. CMIP5 Models

We analyze climate simulations from 37 models in the CMIP5 archive (see Table S1). The projected climate change response is evaluated as the difference between 31 year averages in the RCP8.5 scenario (2069–2099) and in the historical simulations (1975–2005) (Taylor et al., 2012). Historical simulations are forced by present‐day greenhouse gas and aerosol concentrations, while RCP8.5 describes a business‐as‐usual emission scenario in which CO₂ concentrations approximately double (from 354 to 799 ppm) between the above time periods. In order to test the robustness of the findings, the analyses have also been performed using the abrupt4xCO2 and 1%yr⁻¹CO₂ experiments, whose results are reported in the supporting information.

For a subset of 10 models (see Table S1), the RCP8.5 response is compared to the climate response obtained from the corresponding atmosphere‐only AMIP, AMIPFuture, and AMIP4xCO2 simulations. AMIP simulations are transient runs forced by observed variability in SSTs, sea ice extent, and atmospheric composition for the period 1979–2008. AMIP4xCO2 is an AMIP run where the CO₂ concentration is quadrupled. AMIPFuture is also an AMIP run, but a plausible SST warming pattern is added to the AMIP SSTs. The SST warming pattern is derived from the multimodel mean CMIP3 response in the 1%yr⁻¹CO₂ experiment and scaled to have a global average of 4° (K). Sea ice extent is kept unchanged at present‐day values in both AMIP4xCO2 and AMIPFuture. Climatologies are computed as time averages for 1979–2008.

2.2. Extracting the Sea Ice Loss Signal

In order to infer the impact of sea ice loss, the climate response in the RCP8.5 scenario will be compared to the climate response obtained by scaling and combining the AMIPFuture and AMIP4xCO2 responses, hereafter AMIPsst+co2,

$${\text{AMIP}}_{\text{sst+co2}}={\text{AMIP+k}}_{\text{sst}}·({\text{AMIP}}_{\text{Future}}-\text{AMIP})+k_{\text{co2}}·({\text{AMIP}}_{\text{4xCO2}}-\text{AMIP}),$$ (1)

so that the implied SST warming averaged in the tropics (30°S–30°N) and the CO₂ radiative forcing are equivalent to the climate response in RCP8.5. For the same subset of 10 CMIP5 models, we obtain k _sst=0.594 and $k_{\text{co2}}=\log (799/354)/\log \left(4\right)=0.587$ (The formula follows from the logarithmic scaling of radiative forcing on the concentration of CO₂). The impacts of sea ice changes on circulation are thus inferred by comparing the RCP8.5 and AMIPsst+co2 responses, where sea ice is unperturbed.

Three assumptions are implied in this approach: (1) linear scaling and additivity of the circulation response to the SST and CO₂ forcing, (2) linearity of the circulation response to the different SST patterns found in the CMIP5 future responses, and (3) independence of the circulation response to the differences in the circulation basic states between the AMIP and coupled runs. Additivity is often implied when separating the impact of sea ice and SST changes (Blackport & Kushner, 2017; Deser et al., 2015) and found to be reasonably well satisfied (McCusker et al., 2017; Staten et al., 2012). The proportional scaling of the circulation response between different emission scenarios suggests that the linearity in the magnitude of the forcing is also approximately satisfied (Ceppi et al., 2018; Tebaldi & Arblaster, 2014). However, deviations from linearity can exist in the response to SST anomalies (e.g., Robinson et al., 2003). Finally, a strong sensitivity in the climate response to circulation biases induced by SST biases has been found in Smith et al. (2017), while other studies have found weaker (Osborne et al., 2017; Screen & Francis, 2016) or no (McCusker et al., 2017) state dependencies. Deviations from these assumptions can lead to confounding effects, but these effects would have to be large and consistent across the CMIP5 models to overcome the signal from sea ice loss. Comparison of our findings with results from previous single‐model experiments will enable us to test our approach a posteriori.

2.3. Diagnostics

We define a monthly jet latitude index similar to that of Ceppi et al. (2018). We first take the zonal average of the monthly climatological zonal wind ( $ū$) at 850 hPa (U850) in the North Pacific (140°E–240°E) and North Atlantic (300°E–360°E) basins. The jet latitude (ϕ _jet) in each basin is then defined as the mean latitude (ϕ) of the westerlies weighted by the square of the westerly wind speed:

$${\varphi }_{\text{jet}}=\underset{20^{\circ }}{\overset{70^{\circ }}{\int }}\varphi {\overline{u_0}}^2\mathrm{d}\varphi /\underset{20^{\circ }}{\overset{70^{\circ }}{\int }}{\overline{u_0}}^2\mathrm{d}\varphi$$ (2)

$$\overline{u_0}\left(\varphi \right)=\max (0,ū(\varphi \left)\right)$$ (3)

To quantify the surface energy forcing associated with sea ice loss, we compute the area weighted surface integral of the change (RCP8.5‐historical) in the surface turbulent heat fluxes over all the NH grid points, where

1. The historical mean sea ice concentration is greater than 50%.

2. Sea ice concentration decreases from the present to the future climate.

3. Results

3.1. Seasonality in the Arctic Forcing and Jet Shift Responses

As a measure of the potential of Arctic sea ice loss to influence atmospheric circulation, Figure 1a shows the seasonality in the surface heat flux response associated with sea ice loss in the RCP8.5 scenario. In all the CMIP5 models, the largest heat flux response is found in the cold season, which implies a transfer of heat from the ocean to the atmosphere as also shown in previous single‐model experiments (e.g., Deser et al., 2010). The heat transfer change is found in all models from October to April and peaks in January at about 450 TW.

Figure 1.

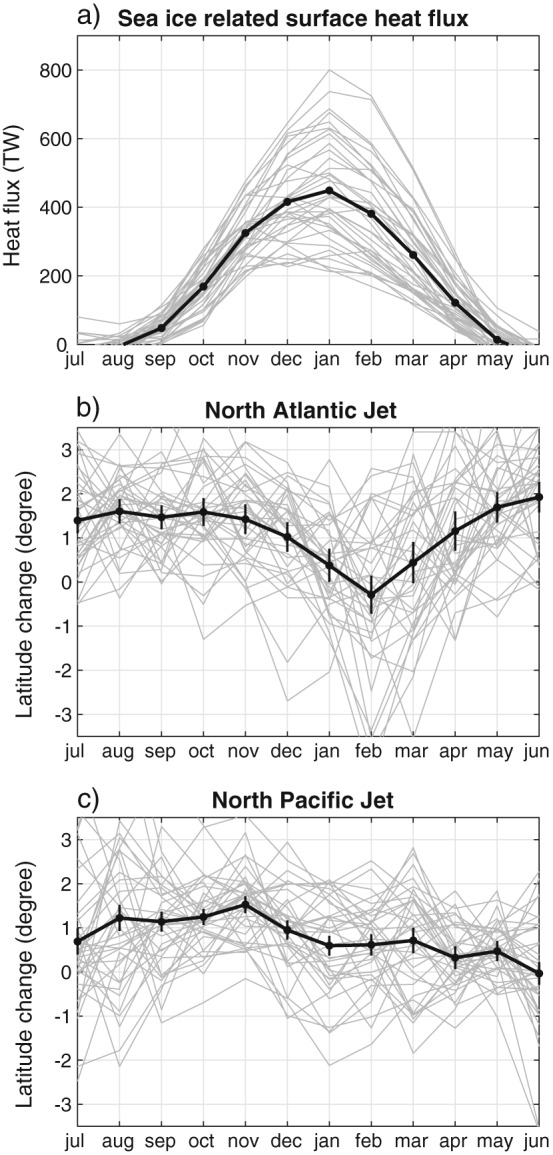
(a) Seasonality in surface heat flux forcing associated with sea ice loss in the CMIP5 multimodel mean response (black line) and in the individual models (gray lines). (b) As in Figure 1a but for the response in the North Atlantic jet latitude and (c) in the North Pacific jet latitude. In Figures 1b and 1c the vertical bars are 95% confidence intervals on the multimodel mean response due to internal variability (see supporting information).

Given the strong seasonality in the Arctic surface forcing, it could be expected that its influence on atmospheric circulation should be most detectable in the cold season. Consistent with previous studies on the seasonality of jet responses (Barnes & Polvani, 2013; Grise & Polvani, 2016; Simpson et al., 2014), Figure 1b shows that the North Atlantic jet tends to shift poleward with climate change, but the shift is largely suppressed between January and March. The multimodel mean even shows a southward shift of the jet in February. Such a seasonal southward anomaly in the jet response is consistent with the expected impact from sea ice loss on atmospheric circulation. This connection would imply that the circulation response lags the Arctic surface heat flux forcing by about 1 month, which is a reasonable time lag for atmospheric stationary perturbations to grow in response to anomalies in the SST and sea ice (Deser et al., 2007).

The North Pacific jet also tends to shift poleward with climate change (Figure 1c). However, in contrast to the Atlantic region, the poleward shift of the Pacific jet is abated by only about half a degree in the multimodel mean from autumn to winter, while the minimum in the poleward shift of the jet occurs in June. This suggests that the seasonality in the North Pacific jet response to climate change is not primarily influenced by the surface fluxes associated with Arctic sea ice loss but is rather conditioned by tropical processes (Shaw & Voigt, 2015).

Further insight is obtained by inspecting the spatial distribution in the multimodel mean response. In early winter (October‐November‐December, OND) Arctic sea ice loss mostly affects the central Arctic ocean, where sea ice concentration is reduced by up to 90% (Figure 2a). In all these areas additional heat fluxes up to 40 W m⁻² are transferred from the ocean to the atmosphere (Figure 2b). A different spatial distribution is found in late winter (January‐February‐March, JFM), when central Arctic sea ice has largely re‐formed and sea ice loss is confined to the Arctic marginal seas, particularly Hudson Bay, Barents and Kara Seas, the Bering Strait, and the Sea of Okhotsk (Figure 2d). In these areas the surface heat flux is locally increased by up to 75 W m⁻², which reflects the increased contrast between cold air masses forming over sea ice in the central Arctic and the exposed ocean in the Arctic marginal seas (Figure 2e).

Figure 2.

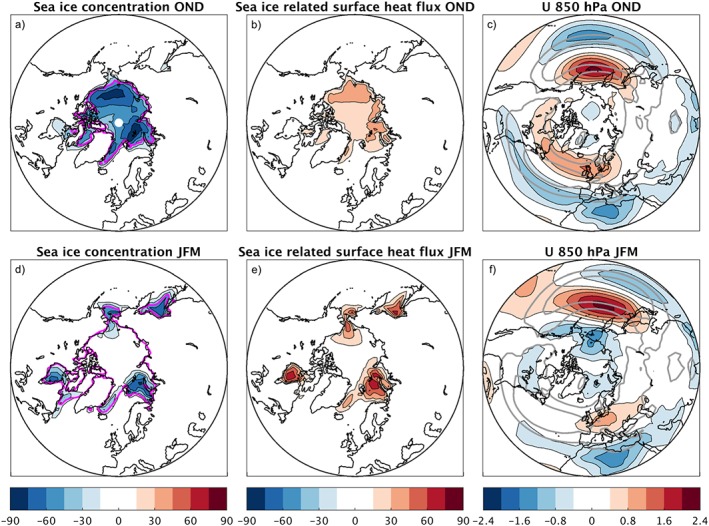
CMIP5 response in the RCP8.5 scenario in early winter (OND) for (a) the sea ice concentration (%), (b) the surface heat flux response associated with sea ice loss (W m⁻²), and (c) the zonal wind at 850 hPa (m s⁻¹). (d–f) As in Figures 2a–2c but for the late winter (JFM) response. The multimodel median, rather than mean, is used for the sea ice and the heat flux responses due to the large spatial biases of the models in these fields. In Figures 2a and 2d magenta lines give the 50% SIC in the median of the historical simulations. In Figures 2c and 2f the gray contours show the 4 m s⁻¹ (outer) and 8 m s⁻¹ (inner) mean zonal winds in the historical simulations.

Together with these surface Arctic seasonal changes, substantial variations between early and late winter are found in the atmospheric circulation response (Figures 2c and 2f). In the North Atlantic, a dipole in the zonal wind at 850 hPa reflecting the poleward shift of the jet is found in OND but not in JFM. A predominantly easterly wind response develops around the Arctic circle in JFM. The pattern in the North Pacific wind response shifts slightly southward from early to late winter, but the character of the response is not qualitatively affected.

These results suggest that the CMIP5 multimodel mean future projections feature seasonal variations in the circulation response that are potentially consistent with the surface forcing from Arctic sea ice loss, particularly in the North Atlantic sector and at high latitudes. This will now be tested by comparing the circulation response in RCP8.5 to that found under the AMIPFuture and AMIP4xCO2 experiments, where sea ice is unperturbed.

3.2. Estimating the Impact of Sea Ice Loss

The multimodel mean jet latitude response in the AMIPFuture and AMIP4xCO2 experiments are presented in Figure 3a, together with the mean response in the RCP8.5 scenario evaluated for the 10 coupled models corresponding to the AMIP experiments. While both the SST forcing (AMIPFuture) and CO₂ forcing (AMIP4xCO2) are individually sufficient to generate a poleward shift of the North Atlantic jet, neither of them is able to reproduce the significant suppression of the jet shift found in JFM in the RCP8.5 scenario (Figure 3a). In particular, in AMIP4xCO2 the poleward shift of the jet is largest in the cold season, and almost all models show a poleward shift of the jet in JFM (Figure 3b). A slight suppression of the poleward shift of the jet is found in late winter in AMIPFuture, but the multimodel mean still shows a 1° poleward shift. Therefore, these results support the hypothesis that SST and CO₂ forcing, in the absence of sea ice changes, are unable to generate the late winter suppression of the North Atlantic poleward jet shift found in the RCP8.5 projections.

Figure 3.

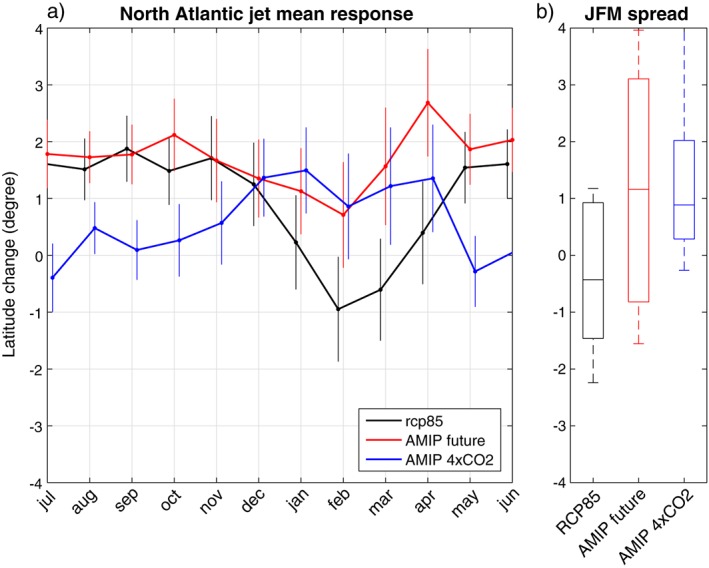
(a) CMIP5 multimodel mean response (10‐model subset) in the North Atlantic jet latitude: RCP8.5‐historical (black), AMIPFuture‐AMIP (red), and AMIP4xCO2‐AMIP (blue). The vertical bars give 95% confidence intervals on the multimodel mean response due to internal variability. (b) Distribution of the mean JFM jet latitude response across the CMIP5 models. The horizontal bar gives the median, the boxes delimit the interquartile range, and the whiskers delimit the maximum range.

To quantitatively explore the role of sea ice loss in JFM, we now compare in Figure 4 the RCP8.5 response to the combined AMIPsst+co2 mean response (see section 2.2). To estimate robustness (indicated as stippling), the scaling from equation (1) has been applied to the individual models, so as to pairwise compare the RCP8.5 and AMIPsst+co2 responses. These robustness estimates are conservative as the patterns in the SST response of an individual model in RCP8.5 will in general be different from that in AMIPFuture, and these SST variations can mask the coherence in the signal from sea ice loss.

Figure 4.

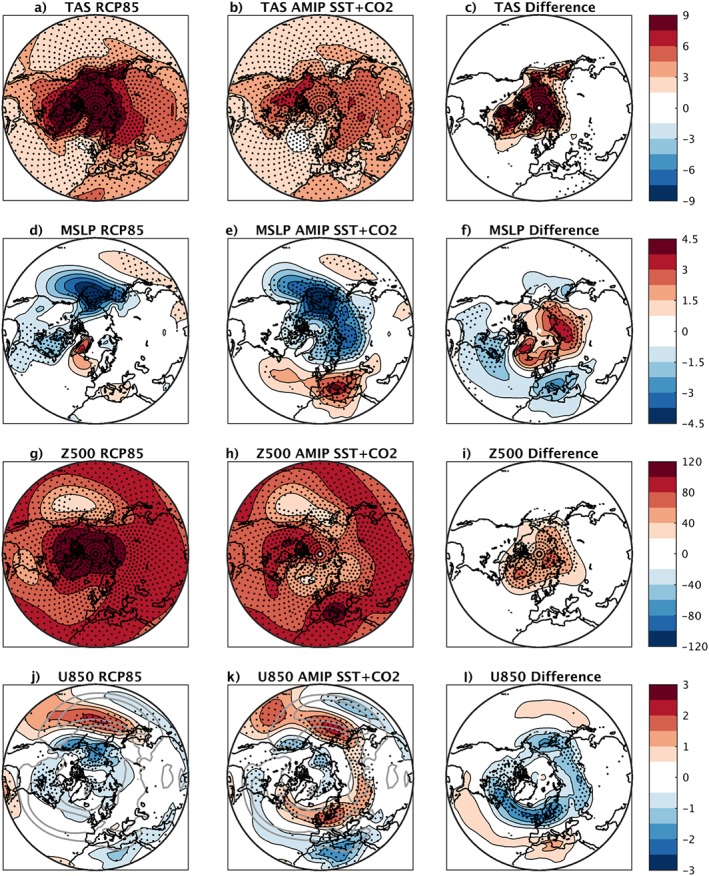
Late winter (JFM) CMIP5 mean response (10‐model subset) in near‐surface temperature (K) in (a) the RCP8.5 scenario and (b) AMIPsst+co2. (c) Figure 4a minus Figure 4b. The other panels are the same as Figures 4a–4c but (d–f) for the mean sea level pressure (hPa), (g–i) for the geopotential height at 500 hPa (m), and (j–l) for the zonal wind at 850 hPa (m s⁻¹). In Figures 4j and 4k the gray lines show the 4 m s⁻¹ (outer) and 8 m s⁻¹ (inner) mean zonal wind in the historical and AMIP simulations, respectively. Stippling indicates areas where the response has the same sign in at least 90% of the models.

Figures 4a–4c show that RCP8.5 is characterized by substantially larger near‐surface atmospheric warming in the Arctic region compared to AMIPsst+co2, which reflects the lack of sea ice changes in AMIPsst+co2. The oceanic surface warming is instead comparable (see Figure S1), so we can be confident that the differences in the circulation response between RCP8.5 and AMIPsst+co2 are most strongly influenced by the forcing due to sea ice loss rather than by SST differences.

The mean sea level pressure (MSLP) responses in RCP8.5 and AMIPsst+co2 are similar in the Pacific but are substantially different over North America, Europe, and Asia (Figures 4d–4f). Compared to AMIPsst+co2, the RCP8.5 response features higher surface pressure in northern Siberia and lower pressure in both North America and, with less model agreement, in the Mediterranean. At 500 hPa, the geopotential height increases in both experiments as a result of tropospheric warming, but in the Arctic the height increase in RCP8.5 is approximately twice that in AMIPsst+co2 (Figures 4g and 4h). Therefore, the difference between the RCP8.5 and AMIPsst+co2 response is characterized by an equivalent barotropic pressure increase extending through the depth of the Arctic troposphere. Consistently, the difference in the zonal wind at 850 hPa between RCP8.5 and AMIPsst+co2 (Figures 4j–4i) is dominated by a weakening of the westerly flow at 60°N, which is strongest in the North Atlantic sector, together with a slight, and less robust, strengthening further south in the oceanic basins. The same analyses have also been repeated using the abrupt4xCO2 (Figure S2) and 1%yr⁻¹CO₂ (Figure S3) CMIP5 experiments in place of RCP8.5, with all the experiments leading to consistent results.

The differences between the RCP8.5 and AMIPsst+co2 responses in JFM resemble the circulation response to sea ice loss found in previous single‐model experiments (Blackport & Kushner, 2017; Cvijanovic & Caldeira, 2015; Deser et al., 2010, 2016; Harvey et al., 2015; Oudar et al., 2017; Peings & Magnusdottir, 2014; Sun et al., 2015). In particular, the increase in surface pressure in the northern North Atlantic and northern Siberia, the pressure reduction over North America, the increase in Arctic geopotential height, and the weakening of the high‐latitude westerly flow, including the North Atlantic sector, are common features of these studies. This gives us high confidence in interpreting the difference between RCP8.5 and AMIPsst+co2 as evidence for robust impacts of sea ice loss on the atmospheric circulation response in the CMIP5 models. Interestingly, other aspects of the identified response are present in some, but not all, of the single‐model experiments. In particular, a large pressure reduction in the Mediterranean area in response to sea ice loss is only present in Blackport and Kushner (2017). Many studies have found a stronger Aleutian pressure deepening in response to sea ice loss, although this might result from the indirect effects of sea ice loss on global SST changes (Deser et al., 2016), which cannot be separated using this approach.

In contrast to these atmospheric circulation differences found in late winter, the early winter (OND) response is similar in RCP8.5 and AMIPsst+co2 (see Figure S4). This is consistent with Barnes and Polvani (2015), who showed that only between January and April were the CMIP5 models with higher polar amplification associated with a less poleward shifted North Atlantic jet. Furthermore, the difference in the Arctic response is baroclinic in OND, with an increase in Z500 but a lowering of the surface pressure. Such a shift from a baroclinic to a barotropic response during the cold season is also a feature of sea ice perturbation experiments (Barnes & Polvani, 2015; Deser et al., 2010; Smith et al., 2017), giving further confidence in the interpretation of the present results.

An open research question is the extent to which the late winter circulation response is mediated by a change in the strength of the stratospheric vortex (Wu & Smith, 2016). Although beyond the scope of this paper, we find that the seasonal evolution in the response of the vortex matches that in the North Atlantic jet latitude, as the vortex strengthens in autumn (until November) and then weakens until March (Figure S5). Furthermore, the weakening of the stratospheric vortex is absent in the AMIPsst+co2 response, where the North Atlantic jet shows a year‐round poleward shift (Figure S5). This supports the view that the stratospheric vortex strength and North Atlantic jet latitude responses are related, as also found across the CMIP5 intermodel spread (Zappa & Shepherd, 2017).

4. Conclusions

The impact of Arctic sea ice loss on the atmospheric circulation has been analyzed using a novel approach in the CMIP5 future projections. Several of the identified impacts of sea ice loss on atmospheric circulation are consistent with the published literature based on single‐model experiments. This gives credence to the interpretation of these results and suggests that aspects of the circulation response to projected sea ice loss are robust to model formulation. In particular,

1. The circulation response to Arctic sea ice loss is largest in late winter (JFM), which suggests a 1 month lag between the sea ice‐related surface heat flux forcing and the midlatitude circulation response.

2. The circulation response to sea ice loss tends to oppose the poleward shift of midlatitude circulation forced by the warming of SST and the direct radiative effect of CO₂.

3. This compensation is largest in the North Atlantic sector, where the poleward shift of the North Atlantic jet is entirely suppressed by Arctic sea ice loss in late winter, while no clear signal is found for the North Pacific jet.

4. The Arctic atmospheric response evolves from being primarily baroclinic in early winter (OND) to barotropic in late winter (JFM), when the westerly wind weakens at about 60°N.

5. In late winter, Arctic sea ice loss also tends to increase the surface pressure in northern Siberia and to lower it in North America and in the Mediterranean area, although the latter response is less robust across CMIP5 models.

While the comparison with previous single‐model studies supports the above conclusions, our methodology relies on assumptions that need to be further tested by future research (see section 2.2). Nonetheless, very similar results are also found using the Abrupt4xCO2 and 1%yr⁻¹CO₂ CMIP5 experiments in place of RCP8.5, which not only confirms the robustness of our findings but also shows that potential confounding factors such as aerosol and tropospheric ozone are negligible in this context.

In conclusion, this study has shown for the first time that there is evidence that Arctic sea ice loss contributes to the seasonal evolution of the circulation response to climate change in the CMIP5 ensemble. New experiments planned for the CFMIP‐CMIP6 project (Webb et al., 2017) will enable to more directly evaluate the role of sea ice loss in a multimodel ensemble and thus to test these findings.

Supporting information

Supporting Information S1

Zappa, G. , Pithan, F. , & Shepherd, T. G. (2018). Multimodel evidence for an atmospheric circulation response to Arctic sea ice loss in the CMIP5 future projections. Geophysical Research Letters, 45, 1011–1019. https://doi.org/10.1002/2017GL076096