Deep Reinforcement Learning for Dynamic Treatment Regimes on Medical Registry Data

Abstract

In this paper, we propose the first deep reinforcement learning framework to estimate the optimal Dynamic Treatment Regimes from observational medical data. This framework is more flexible and adaptive for high dimensional action and state spaces than existing reinforcement learning methods to model real life complexity in heterogeneous disease progression and treatment choices, with the goal to provide doctor and patients the data-driven personalized decision recommendations. The proposed deep reinforcement learning framework contains a supervised learning step to predict the most possible expert actions; and a deep reinforcement learning step to estimate the long term value function of Dynamic Treatment Regimes. We motivated and implemented the proposed framework on a data set from the Center for International Bone Marrow Transplant Research (CIBMTR) registry database, focusing on the sequence of prevention and treatments for acute and chronic graft versus host disease. We showed results of the initial implementation that demonstrates promising accuracy in predicting human expert decisions and initial implementation for the reinforcement learning step.

I. Introduction

Data-driven decision support systems for health care to facilitate medical doctors in delivering personalized medical decisions has been a future that artificial intelligence is aiming to create. Deep learning and deep reinforcement learning have demonstrated human level or even superior performance in the tasks of medical image processing [1], playing games such as Go and Atari [2], [3], etc. However, to the best of our knowledge, deep learning and deep reinforcement learning techniques have not been used for the task of making sequential treatment decisions. In this work, we aim at developing the first deep reinforcement learning framework to provide data-driven sequential decision making support based on the medical registry data.

The natural process of doctors making a sequence of intervention decisions adapted to the time-varying clinical status and features of a patient is coined as Dynamic treatment regimes (DTRs, [4]). The most common data source for these multiple decision making problems is through sequential multiple assignment randomized trial (SMART) [5], [6], which have been proposed to optimally construct DTRs that offer causal interpretation through randomization at each critical decision point. Methods to identify the optimal DTRs have recently received attentions in the statistical community [7], [8], [9], [10], [11], [12], [13], [14], and most of exsiting methods focused on data from randomized clinical trials. For multiple stage decision making, the existing methods implement dynamic programming, i.e., they estimate the optimal decision rules through backward induction across decision stages. In each step, a parametric prediction model is fitted for the value function (Q-learning [15]); or a classification model is constructed for modeling the decision policies directly (Outcome Weighted Learning (OWL) [16]). Our previous work [17] proposed augmenting the OWL with Q-learning to achieve better statistical efficiency. In both Q-learning and OWL, the action space is small, and in most cases only two actions are considered, where Q-learning fits a linear regression in each step and OWL is solving a classification problem weighted by outcome using classical methods such as SVM, logistic regression, random forest, etc.

These existing methods are proposed for applications in randomized controlled trials and are limited to clearly defined homogeneous decision stages and low-dimensional action spaces. They are difficult to implement using observational data (such as electronic medical records, registry data), which exhibits much more heterogeneity in decision stages among patients, and the treatment options (i.e., the action space) are often high-dimensional. The existing methods can only analyze certain simplification of stage and action spaces among the enormous ways. Simplification by human experts might not lead to the optimal DTRs and in many cases there is no clear way of simplification. In addition, the simplification process needs substantial domain knowledge and labor-intensive data mining and feature engineering. To make reinforcement learning accessible to more DTR problems in observational data, we want to develop a framework to automatically and adaptively deal with the heterogeneous high dimensional states and actions in real life.

Deep learning, or more specifically, deep reinforcement learning, is a promising new technique to model the real-life complexity, high dimensionality, and adaptivity. Reference [18] presented the pioneering work of the first deep reinforcement learning model, which successfully learns control policies directly from high-dimensional sensory inputs. Reference [2] developed an end-to-end deep reinforcement learning model to learn policies directly from high-dimensional sensory inputs and actions to excel in Atari game. Reference [19] presented an actor-critic, model-free algorithm based on the deterministic policy gradient that can operate over continuous action spaces. Reference [3] proposed a new approach for the Go game, in which ’value networks’ are used to evaluate board position and ’policy networks’ are used to select moves. A novel combination of supervised learning from human experts games and reinforcement learning from games of a self-play is adopted for training these deep neural networks. This new advancement in deep learning has led to human-level or superhuman performances in various tasks.

Existing literature on application of deep learning on medical diagnosis and treatment prediction and recommendations are limited. Some pioneering works [20], [21] are using recurrent neural networks (RNNs) to model the sequence of hospital admission, diagnosis and treatments for broad disease categories with large electronic health record (EHR) datasets. However, these works do not step forward to make decision recommendation based on the clinical outcomes, possibly due to the limitation of EHR data where the sample size with the same disease is limited, and long time follow-up might be largely missing since health providers typically do not share or merge their EHR data. Another type of observational medical data, the registry data, has shown the potential to overcome this limitation and enables DTR inferences with reinforcement learning. Reference [22] adopted Q-learning [15], [23] to study a two-stage decision making problem in GVHD prevention and treatment, it simplified the problem of our motivating example to consider only two treatment options and two stages. This simplification is needed due to the limited scalability of traditional Q-learning technique, and is based on clinician’s knowledge and dataset explorations. In this work we are studying a similar (and more complete) clinical problem, but we aim to utilize deep learning to model the actual state and action spaces directly with more decision points, as the emerging deep reinforcement learning technique could accommodate higher dimensionality in state and action spaces in a data-driven, model-free framework.

To sum up, the significance of the paper includes:

• This is the first paper to propose a systemetic deep reinforcement learning framework to provide data-driven sequential decision making support based on medical registry data.

• We generalize the emerging reinforcement learning framework in statistical literature to model a larger action and state space and build a discrete-time model based on the collection scheme of registry data.

II. Clinical Problem and Data Cohort Description

The motivating data example is from the Center for International Blood and Marrow Transplant Research (CIBMTR) registry database, which has focused on collecting outcome data for patients receiving hematopoietic cell transplantation (HCT) since 1972. The registry dataset enables multiple-stage decision comparisons by combining datasets across institutions both nation-wide and internationally, and it also tracks the long term follow-up of the patients. The multiple-stage decision problem we are targeting on the prevention and treatment of the Graft Versus Host Disease (GVHD), a common complication after HCT. GVHD is a manifestation of immunologic injury driven by donor immune cells. Especially the donor’s immune cells mistakenly attacking the patient’s normal cells leads to complications ranging from mild to severe or life threatening. There are two forms: acute GVHD typically occurs within the first 6 months after the transplant and lasts for a short term if successfully treated; chronic GVHD may occur from shortly after the transplant to a few years later, and often requires long-term treatment that can lead to long-term complications/morbidity.

The motivating dataset includes 6021 patients diagnosed with Acute Myeloid Leukemia (AML) who underwent HCT between 1995 and 2007. Data have been submitted by partners of the registry using standard follow-up forms at 100 days, 6 months, 12 months, 2 years, 4 years, etc., after the date of transplant. Due to the discrete data collection scheme, we have better quality data on the onsets of GVHD conditions and the subsequent treatment decisions in a discrete-time frame indicating the occurrence between two follow-up times. The exact date and sequence of treatment decisions between two periods of time are missing or not recorded to a greater extent. In this work, the state and action are considered to be the state and action taken at the time each form was recorded. We consider relapse and death as terminal states and occurrences of acute or chronic GVHD as transient states. The specific action sequence we are modeling consists of initial conditioning regimen (chemotherapy treatment) and GVHD prophylaxis (immune suppression for donor cells to prevent GVHD) applied at the time of transplant, along with the drug options to treat acute or chronic GVHD if it occurs.

III. Background on Deep Reinforcement Learning

In this section, we present a general deep reinforcement learning framework, which can be utilized to solve complicated problems with large state and action spaces. The deep reinforcement learning technique consists of two phases: an offline deep neural network (DNN) construction phase and an online deep Q-learning phase [18], [2], [3]. In the offline phase, a DNN is adopted to derive the correlation between each state-action pair (s, a) of the system under control and its value function Q(s, a). Q(s, a) represents the expected cumulative reward with discount when the system starts at state s and follows action a and certain policy thereafter. Q(s, a) for a discrete-time system is given as:

$$Q(s,a)=\mathbf{E}\left[{\displaystyle \sum _{k=0}^{\mathrm{\infty }}{\gamma }^{k}r(k)|s_0,a_0}\right]$$ (1)

where r(t) is the reward rate and γ is the discount rate in a discrete-time system.

In order to construct a DNN with desirable accuracy, the offline phase needs to accumulate sufficient samples of Q(s, a) value estimates and the corresponding (s, a). It can be a model-based procedure or obtained from actual measurement data [3]. This procedure includes simulating the control process, and obtaining the state transition profile and the estimations for Q(s, a) value, using an arbitrary but gradually refined policy. The state transition profile is stored in an experience memory D with capacity N_D. The use of experience memory can smooth out learning and avoid oscillations or divergence in the parameters [2]. Based on the stored state transition profile and Q(s, a) value estimates, the DNN is constructed with weight set θ trained using standard training algorithms (such as backpropagation and stochastic gradient descent).

For the online phase, the deep Q-learning technique can be utilized based on the offline-trained DNN to select actions and update Q-value estimates. To be more specific, at each decision epoch t_k of an execution sequence, suppose the system under control is in the state s_k. The deep reinforcement learning agent performs inference using the DNN to obtain the Q(s_k, a) value estimate for each state-action pair (s_k, a). Then according to the ε-greedy policy, the action with the maximum Q(s_k, a) value estimate is selected with probability 1 - ε and a random action is selected with probability ε. After choosing an action, which is denoted by a_k, before the next decision epoch t_k+1, the observed total reward r_k(s_k, a_k) during [t_k, t_k+1) leads to Q-value updates. The reference work [19] proposed to utilize a duplicate DNN $\widehat{Q}$ for Q-value estimate updating, in order to mitigate the potential oscillation of the inference results of the DNN. At the end of the execution sequence, the DNN is updated by the deep reinforcement learning agent using the lately observed Q-value estimates in a mini-batch manner, and will be employed in the next execution sequence.

It can be observed from above procedure that the deep reinforcement learning framework is highly scalable for large state space, which is distinctive from traditional reinforcement learning techniques. On the other hand, the deep reinforcement learning framework requires a relatively low-dimensional action space due to the fact that at each decision epoch the deep reinforcement learning agent needs to enumerate all possible actions under current state and perform inference using DNN to derive the optimal Q(s, a) value estimate, which implies that the action space in the general deep reinforcement learning framework needs to be reduced.

IV. Deep Reinforcement Learning Framework for Dynamic Treatment Regimes

Throughout the paper, we denote time index t = 0 for the time of transplant, t = 1 for 100 days, t = 2 for 6 months, t = 3 for 1 year, t = 4 for 2 years, and t = 5 for 4 years. We consider the DTR within 4 years after the transplant because a large portion of patients’ data will be missing after that time (and live patients without relapse can be considered to be cured from the disease). In this paper, we adopt the deep reinforcement learning technique for three tasks of DTR: initial treatment after the transplant including initial conditioning (chemotherapy to prevent relapse) and GVHD prophylaxis (to prevent GVHD), treatment of acute GVHD, and treatment of chronic GVHD. The initial preventive treatments takes place at the time of transplant t = 0; the treatment of acute GVHD takes place at times t = 1 (100days) and t = 2 (6 months); the treatment of chronic GVHD takes place at times t = 2 (6 months) through t = 5 (4 years).

A. Supervised Learning Framework to Determine Human Experts’ Actions

The first step is to build a supervised learning network to predict the distribution of human experts’ decisions on treatment actions. The proposed framework is applied for predicting the distribution of initial conditioning regime and GVHD prophylaxis at the time of transplant from baseline features, distributions of treatments for acute GVHD at 100 days and 6 months, and treatments for chronic GVHD at all time period after transplant up to 2 years using time varying features. These prediction networks are illustrated in Figure 1.

Fig. 1.

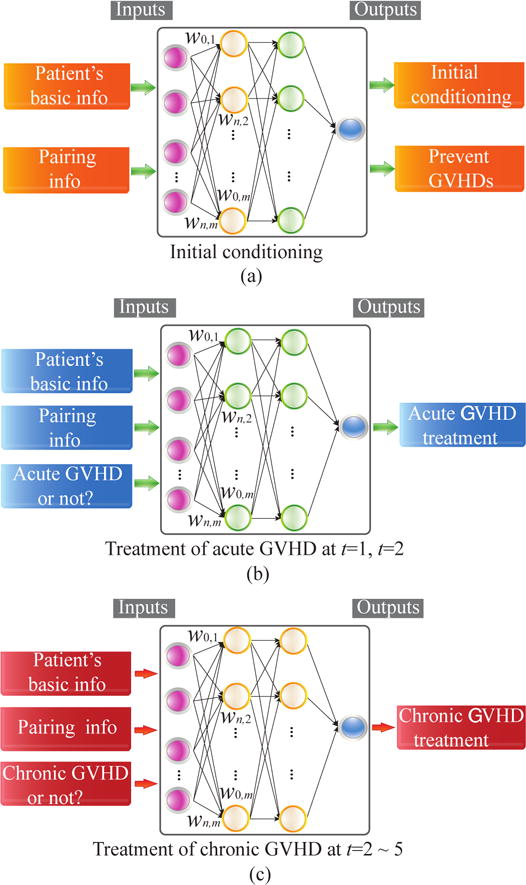
Illustration of the proposed supervised learning framework for (a) initial treatments, (b) acute GVHD treatment, and (c) chronic GVHD treatment.

For the initial treatment (conditioning) immediately after the transplant, the input features (state space) include the union of the basic information of patients (e.g., age, gender, and cormorbilities, etc.) and the genetic matching information between the patient and donor. The output label (action) is the combination of medicines to be utilized for the initial treatment which include conditioning to avoid disease relapse and GVHD prophylaxis to prevent GVHD.

For the treatment of acute GVHD at time stamps t = 1 and t = 2, the input features (the state space) include both the basic information of patients and the pairing conditions, as well as whether the patient has acute GVHD at that specific time stamp. The output label (action) is the combination of medicines to be utilized for the treatment of acute GVHD. Similar input features and actions also apply for the treatment of chronic GVHDs from t = 2 through t = 5.

To reduce the high dimensionality in the action space, we encode the actions using all the medicine combinations that have been already utilized by doctors. In this way the number of possible actions can be reduced to around 270. We adopt an auto-encoder [24] to automatically construct a combination of states and reduce the state space to a large extent, thereby accelerating the convergence speed and mitigating potential overfitting issues. For enhancing accuracy, separate multilayer deep neural networks are trained off-line for initial conditioning, prevention of GVHDs, treatment of acute and chronic GVHDs. The network training procedure at each time stamp t will only use patients with available data.

B. Deep Reinforcement Learning for Value Estimations and DTRs

The second step is to estimate the value function for expert actions with highest probabilities and make recommendations among treatment options. Our recommender only evaluates value function for actions with highest probabilities, since actions with small probability have too small number of samples in the observational medical datasets to arrive at a general conclusion. This restriction also reduces the computational complexity. The reward/outcome of major interests is the relapse-free survival time after transplant, which can be denoted as T_i. Let $\overrightarrow{a}$ denote the vector of actions at all stages, $\overrightarrow{\pi }$ denote the sequence decision rules (policies), mapping from the current observed history to action at each stage. The value function of a policy $\overrightarrow{\pi }$ is $V(\overrightarrow{\pi })=E(T_i|\overrightarrow{a}\in \overrightarrow{\pi }(s))$. The objective is to maximize $V(\overrightarrow{\pi })$ and the so-called Q-function is the expected reward if a subject is assigned to the optimal treatment in all the future stages, and can be estimated through Dynamic Programming following the ideas from Q-learning [15].

In this paper, we presented the preliminary implementation of the proposed deep reinforcement learning step with a simplified heuristic reward defined in the following. The more strict implementation of optimizing the relapse free survival time need incoorperating statistical methods to take care of biases introduced by censoring and lack of randomization, we differ more details to the discussion section about these future directions. For each patient i, let t_i denote the time when he/she enters the terminal state (death, relapse, or relapse-free survival after 4 years) or when his/hers data get lost. The delayed reward of patient i at time t_i can be classified into the following categories:

• Relapse-free and GVHD-free survival.

• Survival with acute or chronic GVHD.

• Relapse of the leukemia disease.

• Death.

• Data loss.

We assign different delayed rewards for the five cases. For relapse-free and GVHD-free survival in 4 years, the highest reward (1) is achieved. Survival with acute or chronic GVHD receives a slightly degraded reward (0.8). Relapsed patients receive a significantly degraded reward (0.2). Death receives zero. This reward can be viewed as a heuristic 4-year-survival probability adjusted for quality of life. There are also missing data problem caused by lost of follow-up, for which we impute their reward with average value of patients with the close starting state and the latest state at time t_i − 1.

Three separate deep neural networks are developed for DTRs of initial conditioning (chemotherapy and prevention of GVHDs), treatment of acute and chronic GVHDs. For the inputs of deep neural networks at time stamp t, the corresponding input states described in the previous section serve as states, and the predicted human experts’ decisions serve as actions. Auto-encoder is utilized to reduce the input state space. The output prediction will be the expected value/return starting at this state and taking the corresponding action. Multi-layer deep neural networks are constructed to achieve this goal, and only those patients whose data are available at each time t are utilized to train the deep neural networks.

V. Experimental Results

In this section, we provide experimental results on the accuracy in predicting human expert actions and effectiveness of deep reinforcement learning based DTR framework in terms of maximizing value functions. The training data is from the Center of International Blood and Marrow Transplant Research registry database and the preliminary results for accuracy is provided on the training sample, in the future we will retrieve and clean more data to estimate out-training-sample accuracy. We perform data preprocessing, supervised learning network construction, and deep reinforcement learning based DTR written in R and C++.

A. Accuracy in Predicting Human Expert Actions

First, we provide preliminary experimental results on predicting human expert actions for the chronic GVHD. Figure 2 illustrates the overall top-5 prediction accuracy as well as individual prediction accuracies at times t = 2 through t = 5. It can be observed that the prediction accuracies are in general high enough and increase with time elapses. This shows a first step towards the ultimate goal of DTR using machine learning techniques.

Fig. 2.

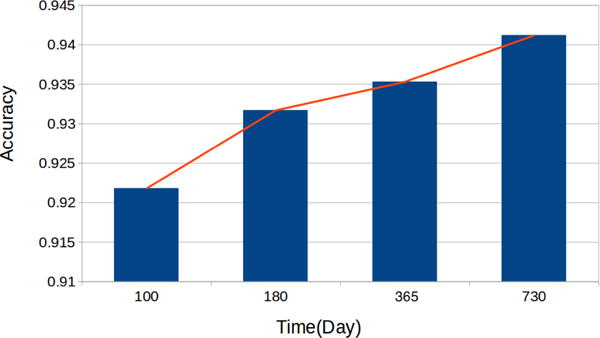
Top-5 prediction accuracies of human expert actions at different time stamps.

Also, it is worth noting that the state and action spaces can be significantly reduced using auto-encoders and action clustering technique. For example, the dimensionality of the state space is reduced from tens to six, whereas the action space is reduced from 17 dimensional binary vector to 270 distinct medicine combinations. The effective techniques for reducing state and action spaces are the key factor of success in predicting human expert actions.

B. Deep Reinforcement Learning Based DTR Framework

Second, we provide preliminary experimental results on the effectiveness of deep reinforcement learning based DTR framework for chronic GVHD treatments. In our preliminary study, we compare between the proposed deep reinforcement learning based approach with random action selection in terms of the value function. Figure 3 demonstrates the comparison results. It can be observed that the proposed deep reinforcement learning framework consistently outperforms the baseline at different time steps, with a maximum value enhancement of 21.4%.

Fig. 3.

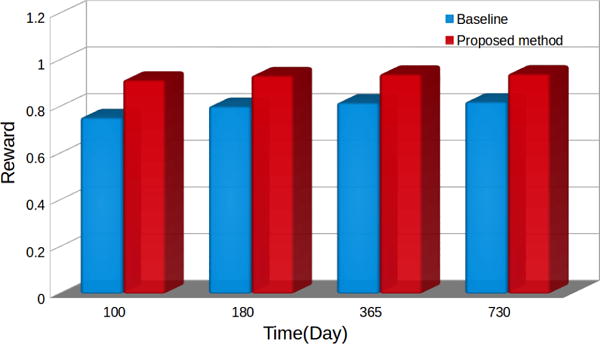
Comparison on the values in chronic GVHD treatments between the proposed deep reinforcement learning approach and baseline.

These preliminary results demonstrate the potential of the proposed deep reinforcement learning based DTR framework. In the future we will implement more comprehensive evaluation and comparison of the value function, which will borrow ideas from existing statistical literature on estimating value function of DTRs [15], [16], [17], we include more details about future work in the discussion section.

VI. Discussion

We propose a systematic framework for deep reinforcement learning on medical observational data with long time follow-up for enough patients from a focused disease group. The framework have the potential to achieve high accuracy in predicting human expert treatment decisions, and conceptually through reinforcement learning, it also has the potential to improve from observed human expert actions through optimizing the long term outcome of patients. This framework extended the existing DTR learning methods in its flexibility and adaptivity for high dimensional action and heterogeneous decision stages to model real life complexity.

We presented results from a preliminary implementation of the proposed deep reinforcement learning framework on the motivating Bone Marrow Transplant data example. In this initial implementation we considered the reward as a heuristic 4-year survival probability adjusted for quality of life. For future works, we will consider the disease free survival time as the main outcome. The reinforcement learning algorithm will be tailored for the specific censoring scheme of the data, denote M_i as the indicator of whether patient i is censored (M_i = 1 if death or relapse is observed), and C_i as the last observation time of patient i. Denote D_t,i as the indicator that death or relapse is observed within time period t − 1 to t. For time t and patient i, denote the indicator for observed terminal events at time t as $M_{t,i}=\mathbb{I}(D_{1,i}=0,\dots ,D_{t-1,i}=0,D_{t,i}=1)$, where $\mathbb{I}(\cdot )$ is the indicator function. The general Q-learning uses a backward induction procedure across time stamps (corresponding to stages). At stage t, each valid training sample (patient) i needs to satisfy C_i > t, and requires that action a_t to be observed. For patients with M_t+1,i = 1, we use their observed T_i as the outcome. For patients with C_i > t+1, or C_i = t + 1, M_i = 0, we use the estimated Q-function for future stage as the outcome. In other words, we are imputing patients who have survived beyond time stamp t + 1 using their optimal future value estimation, regardless of censoring.

For survival outcome in observational studies, reference [25] provided a linear regression method weighted by censoring probability and adjusted for propensity scores. This method can be generalized to multiple stages and deal with the discretized time model, where the decision rule is estimated by weighted linear regression, adjusted for censoring and non-randomization of treatment assignment. Furthermore, the recent DRL literature [2] implemented Q-learning with deep neural networks to approximate the Q-function, which is named as Deep Q-network. It is an open question for future researches that how to adjust for censoring and non-randomization within the Deep Q-network. With more resources we can improve the quality of data by checking the data integrity with the CIBMTR, retrieving more patients and minimizing the number of missing entries. There are eligible 43319 patients from the CIBMTR database that can be separated into training and testing dataset for validating our proposed framework in prediction of expert action and improving long term outcome through reinforcement learning.

There are other sequential decision making questions in the leukemia field. One other example is to decide whether transplant is a beneficial strategy compared to no-transplant, when is the personalized best time for transplant to take place. These questions can also be addressed by similar method. Although clinical trials have been the golden standard in addressing causal effect of interventions to establish sound scientific evidence of any proposed DTRs, SMART has not been conducted for treatments of leukemia partly due to the practical difficulties to get patients make commitment to participate in multiple-stage randomization with the such a high death rate, and the other reason might include the high cost of treatments and difficulty to recruiting enough samples for the power of the study. So we think reinforcement learning with observational data will be the most promising method to gain insights about multiple stage decision making in this field.

Our initial work are off-line learning with observational dataset. From the machine learning standpoint, reinforcement learning often update the policy based on on-line collecting new data. These reinforcement learning exploration policy can be borrowed into our recommendation system to add some randomness for exploring more treatment strategies, in other word, we can change from randomize the treatment to randomize the ’computer-based-recommendation’ from a set of treatment options with value function close to the optimal, taking account the clinical ethnics. The system only provide informations and predictions while leaving the actual decision to patients and their doctors.