Lamellipodium is a myosin-independent mechanosensor

Significance

Cell physiology can be regulated by the mechanics of the extracellular environment. Here, we demonstrate that cell spreading is a mechanosensitive process regulated by weak forces generated at the cell periphery and independent of motor activity. We show that stiffness sensing depends on the kinetics of the initial adhesion bonds that are subjected to forces driven by protein polymerization. This work demonstrates how the binding kinetics of adhesion molecules are sensitively tuned to a range of forces that enable mechanosensation.

Abstract

The ability of adherent cells to sense changes in the mechanical properties of their extracellular environments is critical to numerous aspects of their physiology. It has been well documented that cell attachment and spreading are sensitive to substrate stiffness. Here, we demonstrate that this behavior is actually biphasic, with a transition that occurs around a Young’s modulus of ∼7 kPa. Furthermore, we demonstrate that, contrary to established assumptions, this property is independent of myosin II activity. Rather, we find that cell spreading on soft substrates is inhibited due to reduced myosin-II independent nascent adhesion formation within the lamellipodium. Cells on soft substrates display normal leading-edge protrusion activity, but these protrusions are not stabilized due to impaired adhesion assembly. Enhancing integrin–ECM affinity through addition of Mn²⁺ recovers nascent adhesion assembly and cell spreading on soft substrates. Using a computational model to simulate nascent adhesion assembly, we find that biophysical properties of the integrin–ECM bond are optimized to stabilize interactions above a threshold matrix stiffness that is consistent with the experimental observations. Together, these results suggest that myosin II-independent forces in the lamellipodium are responsible for mechanosensation by regulating new adhesion assembly, which, in turn, directly controls cell spreading. This myosin II-independent mechanism of substrate stiffness sensing could potentially regulate a number of other stiffness-sensitive processes.

The ability of cells to sense mechanical forces and convert them into biochemical responses regulates a plethora of physiological functions (1–3). In particular, cells respond to changes in the stiffness of the extracellular matrix (ECM) by altering a number of adhesion-dependent behaviors, including spreading (4–12), migration (4, 13, 14), proliferation (15), differentiation (16, 17), and metastasis (18, 19). Matrix mechanosensing is thought to be mediated by focal adhesions, hierarchical organelles comprising ∼150 proteins that facilitate dynamic and force-sensitive interactions between the ECM and the actin cytoskeleton (20–22). How these dynamic organelles mediate environmental sensing in a variety of physiological contexts, however, is still largely unknown.

Previous efforts have focused primarily on myosin II-mediated mechanisms for substrate stiffness sensing (23–28). Stresses generated by myosin motors on the actin cytoskeleton are transmitted to the ECM via focal adhesions. These stresses, coupled with the matrix rigidity, impact the deformation and binding affinity of proteins within the focal adhesion (29–32). Changes in the composition and kinetics of proteins within focal adhesions are thought to variably regulate force transmission from the actin cytoskeleton and the matrix (33–35), leading many to describe focal adhesions as molecular clutches. Initial adhesion formation, however, occurs in the leading edge of the lamellipodium and is a myosin-independent process (36, 37). These structures, known as nascent adhesions, are instead subject to forces that primarily originate from polymerization of actin filaments. The contribution of nascent adhesions to mechanisms of substrate stiffness sensing has not been thoroughly explored.

One of the best-characterized metrics of environmental sensing by adherent cells is their ability to attach and spread on ligand-coated substrates. The extent of cell spreading is controlled by the density and spatial organization of matrix ligands (38–40), as well as the rigidity of the substrate to which these ligands are attached (4–12). It has also been suggested that the stress-relaxing properties of the matrix can contribute to cell spreading (41, 42). In the limit of soft substrates with a Young’s modulus <500 Pa, cell spreading is inhibited. As the substrate stiffness increases, the spread area increases and ultimately plateaus (8–12). While previous reports have differed on the exact range of relevant stiffness which regulates this behavior, likely due to variances in experimental approaches (43), cell spreading remains a robust metric to study substrate stiffness sensing.

Here, we study the mechanism regulating substrate stiffness-dependent cell spreading. We found that NIH 3T3 cell spreading is acutely impacted as the Young’s modulus of the substrate increases from 5 to 8 kPa. On substrates with a stiffness <5 kPa, cells spread poorly. Average cell spread area increased on substrates stiffer than 5 kPa, plateauing on substrates stiffer than 8 kPa. Above this threshold, cell spread area remained constant. Surprisingly, we found this stiffness-dependent change in cell spreading was independent of myosin II motor activity. Instead, we found that spreading on soft substrates is impaired by reduced assembly of nascent, myosin-independent adhesions at the cell periphery. Enhancing integrin–ligand affinity through the addition of Mn²⁺ was sufficient both to stabilize nascent adhesions and increase cell spread area on soft substrates. We then implemented a computational model to determine how changes in integrin–substrate catch-bond kinetics affected integrin binding on substrates of different stiffness. We found that the biophysical properties of integrin–matrix catch-bonds were optimized to sense changes in substrate stiffness at ∼6 kPa, consistent with our experimental results. Together, these results illustrate that nascent adhesion formation in the lamellipodium functions as a myosin II-independent mechanosensor to control cell adhesion and spreading.

Results

Spread Area Is a Biphasic Response of Substrate Stiffness, Independent of Myosin Activity.

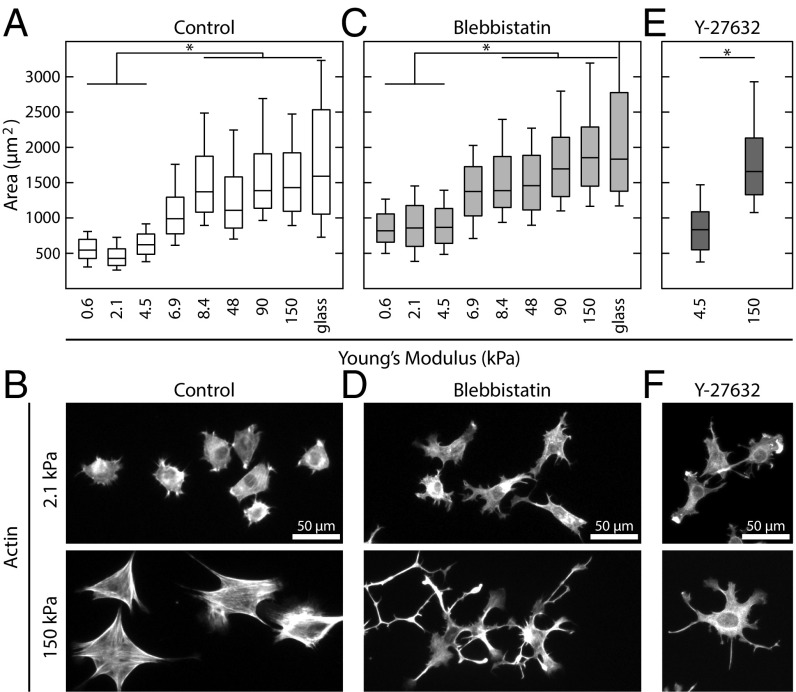
To investigate the mechanisms that drive substrate stiffness sensing, we chose to measure the spread area of adherent cells. We first plated NIH 3T3 fibroblasts on a series of polyacrylamide gels covalently coupled with fibronectin and with Young’s moduli ranging from 0.6 to 150 kPa (Fig. 1A). Cells were also plated on glass absorbed with fibronectin as a control. Consistent with previous reports (4, 6, 8–11), we found that cells’ spread area was sensitive to substrate stiffness (Fig. 1A). In contrast, however, we found that this response could be broken down into two regimes: There was poor spreading on soft (less than ∼5 kPa) substrates and high spreading on stiff (more than ∼8 kPa) substrates, with a transition region between these values and no statistical difference in spread area between populations within each regime (Fig. 1A). Furthermore, the morphology of cells on soft and stiff substrates was noticeably different (5). Cells on soft substrates were more rounded with a disorganized actin cytoskeleton (Fig. 1B). In contrast, cells on stiff substrates exhibited more polarized shapes and tended to have prominent stress fibers (Fig. 1B).

Fig. 1.

Spread area is a biphasic response of substrate stiffness, independent of myosin activity. (A) Boxplots of the spread area of NIH 3T3 fibroblasts plated on fibronectin-coated polyacrylamide gels of varying stiffness. Cells can be grouped into soft (≤4.5 kPa) and stiff (≥8.4 kPa) regimes. From left to right, n = 182, 674, 205, 155, 254, 400, 205, 487, and 170. (B) Representative images of control cells on soft and stiff substrates. (C) Boxplots of the spread area of cells treated with 50 µM blebbistatin to inhibit myosin activity. While blebbistatin-treated cells spread more than control cells, they exhibited the same biphasic response as a function of substrate stiffness. From left to right, n = 169, 228, 329, 67, 159, 125, 119, 183, and 56. (D) Representative images of blebbistatin-treated cells on soft and stiff substrates. (E) Boxplots of the spread area of cells treated with 20 µM Y-27632, which inhibits ROCK activity. Cells treated with Y-27632 still exhibited a difference in spread area on soft (n = 148) and stiff (n = 203) substrates. (F) Representative images of Y-27632–treated cells on soft and stiff substrates. Boxplots represent 25th, 50th, and 75th percentiles, while whiskers extend to the 10th and 90th percentiles. *P < 0.01.

Because myosin II activity has been widely implicated in mechanosensing (28), we next hypothesized that its inhibition would eliminate any change in spread area as a function of substrate stiffness. Surprisingly, cells incubated with 50 µM blebbistatin, a myosin II ATPase inhibitor, continued to exhibit a biphasic response to substrate stiffness (Fig. 1C). Cells treated with blebbistatin had an increased spread area compared with control cells across all stiffnesses, but exhibited the same soft and stiff regimes. Morphologically, myosin-inhibited cells on all substrates showed more protrusions, but on stiff substrates, the cells exhibited more spindle-like projections (Fig. 1D). Similar phenotypes were seen when cells were incubated with Rho-Kinase inhibitor (Y-27632; Fig. 1 E and F) and when cells were plated on other ECM proteins (Fig. S1). Thus, the change in cell spread area that occurred between the soft and stiff regimes did not require myosin II activity.

Substrate Stiffness Does Not Inhibit Lamellipodia Protrusion Dynamics.

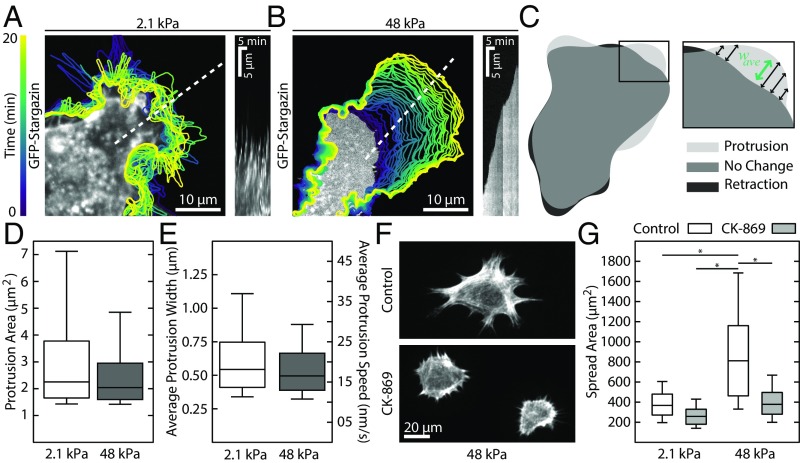
To understand how substrate stiffness impacts cell spread area, we investigated the effects of substrate stiffness on protrusion dynamics. We tracked lamellipodia formation by taking time-lapse images of cells transiently transfected with a fluorescent membrane marker (GFP-stargazin) and treated with 20 µM Y-27632 on representative soft (2.1 kPA) and stiff (48 kPa) substrates 30 min after plating (Fig. 2 A and B and Movies S1 and S2). Cells on soft substrates exhibited repeated cycles of protrusion and retraction, as seen in the kymograph (Fig. 2A), reducing their ability to spread. Cells on stiff substrates, however, exhibited continuous and steady protrusions that resulted in leading-edge advance (Fig. 2B). Using cell contours derived from the fluorescence images, we identified protrusive regions and measured their morphology and characteristics (Fig. 2C). We found no statistically significant difference between soft and stiff substrates for measurements of the average protrusion area (Fig. 2D) or the average protrusion width (Fig. 2E). These data indicate that substrate stiffness affects the stability of leading-edge protrusions, but not the protrusion dynamics themselves. Arp2/3-mediated lamellipodium formation is still required for spreading, as cells on both soft and stiff substrates that were treated with CK-869, an Arp2/3 inhibitor, were indistinguishable from control cells on soft substrates (Fig. 2 F and G). Together, these results illustrate that it is the stabilization, not the formation, of Arp2/3-dependent lamellipodial protrusions that is hindered on soft substrates.

Fig. 2.

Soft substrates do not inhibit lamellipodia protrusion dynamics. (A and B) Contours of a cell expressing a GFP membrane marker plated on soft and stiff substrates. On soft substrates, protrusions are followed by rapid retractions, resulting in no advancement of the leading edge. In contrast, on stiff substrates, the leading-edge advances continuously at each time step. The kymographs, taken along the dotted white lines, illustrate the different protrusion dynamics. (C) Protrusive regions were identified by overlaying successive contours and identifying new areas. Inset shows how the average width of the contour was calculated. (D) Boxplot showing the area of individual protrusions on soft (n = 1,722) and stiff (n = 1,800) substrates. No difference was seen between the two distributions. (E) The average protrusion width and speed were also indistinguishable between soft (n = 1,722) and stiff (n = 1,800) substrates. (F) Representative images of cells on stiff substrates treated with the arp2/3 inhibitor CK-869. Cells treated with CK-869 take on the morphology of control cells plated on soft substrates. (G) Boxplots of the spread area of cells treated with 50 µM CK-869. From left to right, n = 83, 212, 183, and 175. Boxplots represent 25th, 50th, and 75th percentiles, while whiskers extend to the 10th and 90th percentiles. *P < 0.01.

Soft Substrates Impair Nascent Adhesion Formation.

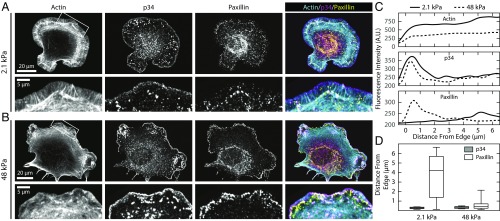
To explore the mechanism of substrate stiffness-dependent changes in stabilization of myosin II-independent protrusions, we examined the assembly of myosin II-independent, nascent adhesions that form at the base of the lamellipodium. Two hours after plating, cells were treated with 20 µM Y-27632 for 30 min and then fixed and stained for actin, p34 (a subunit of Arp 2/3), and the focal adhesion protein paxillin (Fig. 3 A and B). On both soft and stiff substrates, p34 localized to the cell periphery, indicative of the Arp2/3-dependent lamellipodium (Fig. 3 A and B). On stiff substrates, paxillin formed small punctate nascent adhesions near the leading edge, which is characteristic of nascent adhesion formation on glass substrates (44). By contrast, on soft substrates, paxillin-rich nascent adhesions were seen at a lower density and formed further away from the leading edge. To quantify these differences in protein localization, we measured the average actin, p34, and paxillin intensity in ∼0.5-µm bands measured radially from the edge of the cell (Fig. 3C). We found that the peak of p34 intensity was localized right at the edge of the cell on all substrates. On stiff substrates, paxillin was located within ∼0.5 μm of the p34 peak (Fig. 3D). On soft substrates, there was a significantly reduced accumulation of paxillin, and its peak was found ∼5 µm behind the leading edge (Fig. 3D). These data suggest that cells have reduced nascent adhesion formation on soft substrates.

Fig. 3.

Soft substrates impair nascent adhesion formation. (A and B) Representative immunofluorescence images of cells on soft and stiff substrates showing actin, p34 (a subunit of arp2/3), and paxillin (focal adhesion protein). Cells on soft substrates exhibit large lamellipodia and reduced paxillin staining. No noticeable difference can be seen in the p34 localization. (C) Average linescans for each of the three channels for the regions shown in A and B, Insets. While p34 shows a peak at the same position on both soft and stiff substrates, the peak for paxillin is much further behind the leading edge, and much less intense. (D) Boxplots showing the distance from the leading edge for both the p34 (gray) and paxillin (white) signal on soft (n = 46) and stiff (n = 42) substrates. Boxplots represent 25th, 50th, and 75th percentiles, while whiskers extend to the 10th and 90th percentiles.

Activation of Integrins via Mn²⁺ Is Sufficient to Promote Spreading on Soft Substrates.

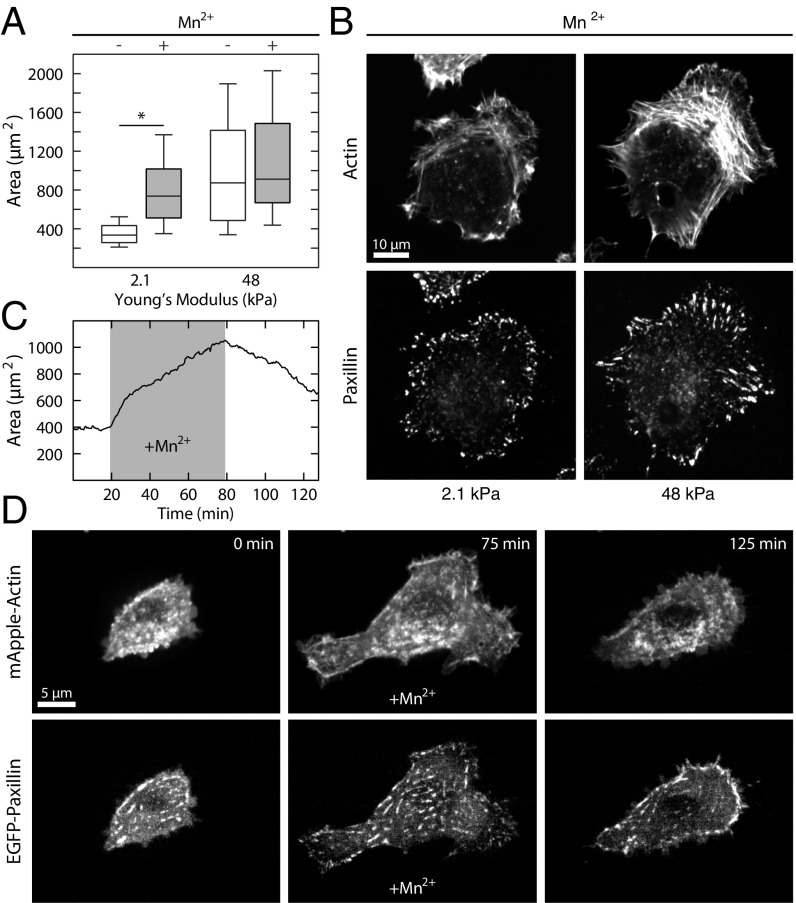
Given the reduced density of nascent adhesions on soft substrates, we sought to explore the extent to which changes in integrin–ligand affinity could stimulate their formation. The presence of 3 µM Mn²⁺ increased the lifetime of integrin–fibronectin bonds (45), but did not affect the contractility of the cell (Fig. S2). When cells were plated on soft substrates in the presence of 3 µM Mn²⁺, they exhibited a greater than twofold increase in spread area on soft substrates, similar to their spread area on stiff substrates either in the presence or absence of Mn²⁺ (Fig. 4A). To directly compare the effect of Mn²⁺ on adhesion assembly on soft substrates, we performed immunofluorescence of paxillin and actin. Addition of Mn²⁺ to cells on soft substrates stimulated the formation of paxillin-rich adhesions near the cell periphery and even the formation of lamellar actin bundles (Fig. 4B).

Fig. 4.

Activation of integrins via Mn²⁺ is sufficient to promote spreading on soft substrates. (A) Boxplots of spread area for control cells and cells treated with 3 µM Mn²⁺ on soft and stiff substrates. Cells treated with Mn²⁺ on soft substrates were not significantly different from control cells on stiff substrates. From left to right, n = 512, 634, 300, and 216. (B) Representative immunofluorescence images of cells treated with Mn²⁺ on soft substrates and control cells on stiff substrates. The cells treated with Mn²⁺ on soft substrates take on the morphology of control cells on stiff substrates. (C) Plot of area vs. time for a cell on soft substrate. A concentration of 3 µM Mn²⁺ was flowed into the imaging chamber at ∼20 min and then washed out again at ∼80 min. As soon as the Mn²⁺ is added to the solution, the cell begins to spread. When the Mn²⁺ is washed out, the cell begins to retract. (D) Representative images from the Mn²⁺ wash-in time course shown in C. After addition of Mn²⁺, both focal adhesions and actin stress fibers can be seen to form. Boxplots represent 25th, 50th, and 75th percentiles, while whiskers extend to the 10th and 90th percentiles. *P < 0.01.

To determine how rapidly Mn²⁺ could induce changes in adhesion formation and cell spread area, we performed live cell imaging of EGFP–paxillin and mApple–actin in cells plated on a soft substrate during addition of Mn²⁺ to the medium. (Fig. 4 C and D and Movie S3). Before addition of Mn2+, there was significant protrusive activity on soft substrates, but no change in area or cell shape. Upon addition of 3 µM Mn²⁺, protrusions stabilized, new focal adhesions formed, and the cell increased in spread area (Fig. 4 C and D and Movie S3). After an hour of incubation, the medium was again replaced with medium lacking Mn²⁺, and the cell immediately began to retract back toward its initial spread area (Fig. 4 C and D and Movie S3). Thus, the presence of Mn²⁺ was sufficient to promote spreading on soft substrates. This strongly suggests that integrin–fibronectin bond affinity plays an important role in substrate stiffness sensing to mediate cell spreading.

Integrin Catch-Bond Kinetics Mediate Substrate Stiffness Sensing.

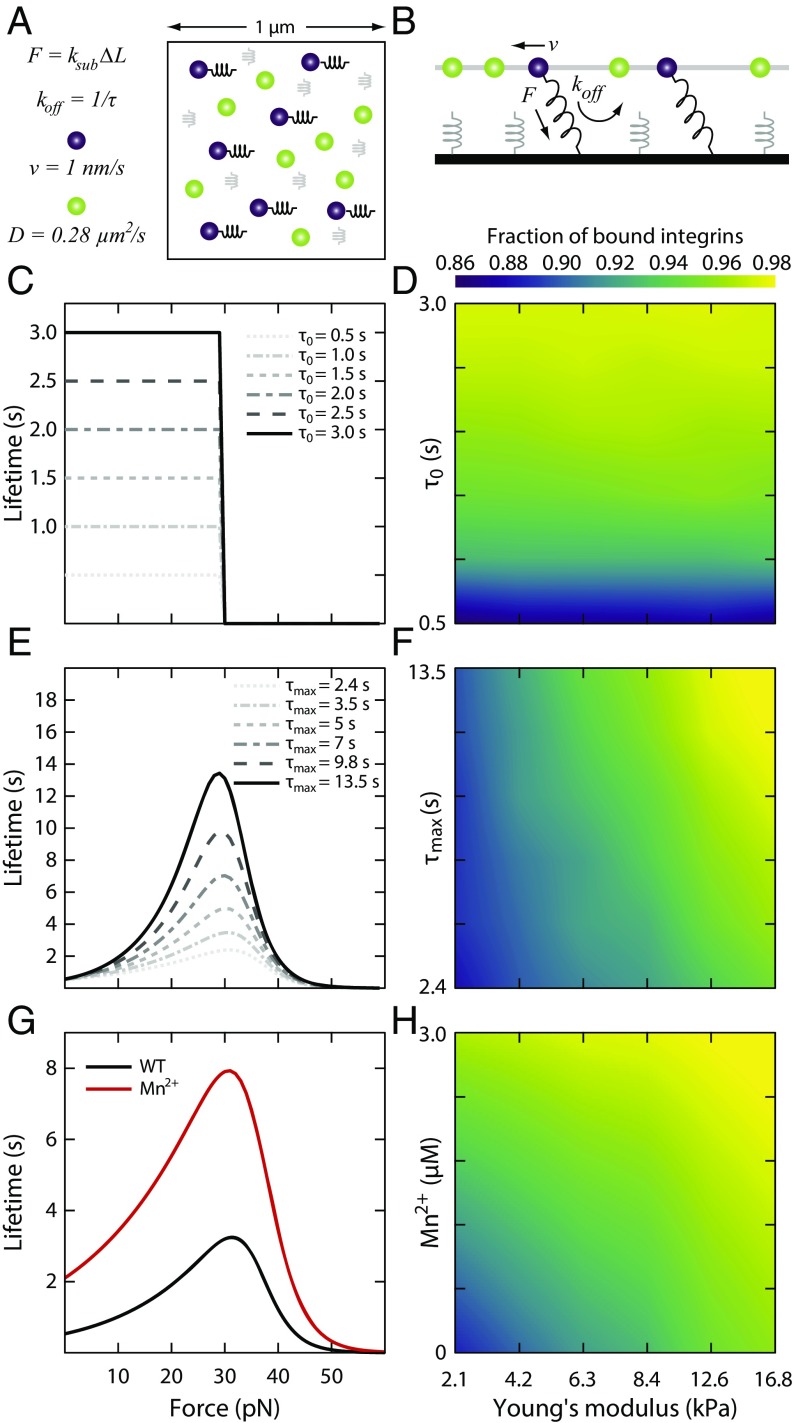
To explore how integrin–fibronectin binding kinetics could enable substrate stiffness sensing, we built a computational model of nascent adhesion assembly at the leading cell edge. The model, similar to previous approaches (23–27), incorporated biophysical properties of cell-matrix adhesions, actin retrograde flow, and substrate rigidity. Individual integrins in the model acted as molecular clutches, intermittently transmitting force produced by actin retrograde flow to the substrate. It has been shown that integrin–fibronectin bonds are catch-bonds, meaning that their lifetime increases as a function of load (45). We used our model to explore which features of these bond kinetics are important in mediating substrate stiffness sensing in nascent adhesions.

In the model, both integrins and ligands were represented as single point particles. Initially, a given number of fibronectin molecules were randomly attached to a substrate, to which integrins could bind. The integrins underwent cycles of diffusion, binding, and unbinding along a quasi-2D surface mimicking the ventral membrane of cells above the substrate (Fig. 5 A and B). Integrins bound to actin undergo retrograde flow, as was seen in the lamellipodium (46), while unbound integrins were free to diffuse on the surface (47). When an integrin came in close proximity of a free fibronectin, it established a harmonic potential interaction, which mimicked binding, with the stiffness determined by substrate rigidity. The assumption of simultaneous binding of the integrin to both the substrate ligand and the actin was motivated by the need to build tension on the integrin–fibronectin bond, and this tension regulated the bond lifetime. By keeping a constant actin flow, forces on the bonds were directly proportional to the substrate stiffness. All parameters in the model were based upon available experimental data (37, 47–49) (Materials and Methods). In particular, we directly incorporated the lifetime vs. force relationships of integrin–fibronectin bonds from atomic force microscopy single-molecule experiments (45). To quantify the amount of integrin binding, we measured the average fraction of bound integrins over the course of the simulations (between 10 and 300 s) for each condition.

Fig. 5.

Computational model of integrin-based adhesion dynamics. (A and B) Schematics of the computational model from the top (A) and side (B) perspectives. Two quasi-2D surfaces are placed 20 nm apart. The bottom surface represents the substrate and consists of a random distribution of ideal springs with stiffness, k_sub, proportional to the substrate Young’s modulus. The top surface mimics a representative unit of the ventral surface of a fibroblast, with integrins diffusing (green particles) with diffusion coefficient, D, and establishing interactions with the substrate springs (purple particles). Upon binding the substrate, a force is exerted on the integrin particle parallel to the substrate, building tension on the bond. This tension determines the integrin unbinding rate, k_off. (C and D) Role of unloaded lifetime on the fraction of bound integrin on different substrate stiffnesses. In C, graphs of lifetime vs. force with unloaded lifetimes equal to the maximum lifetime, τ₀ = τ_max, at tensions ≤30 pN and zero otherwise, used to calculate the average fraction of ligand-bound integrins as a function of the substrate’s Young’s modulus for the curves shown in D. The average fraction of bound integrins is insensitive to substrate stiffness. (E and F) Role of τ_max on the fraction of bound integrins at different substrate stiffnesses. In E, graphs indicating the bond lifetime vs. tension with fixed τ₀ and increasing τ_max used to calculate the fraction of bound integrin as a function of substrate stiffness in F. In this case, the average fraction of bound integrins is weakly sensitive to substrate stiffness. (G) Lifetime vs. tension relationship for WT and Mn²⁺-treated integrins, which amounts to both a shift in τ₀ and in τ_max. (H) The average fraction of bound integrins for the curves shown in G. The number of bound integrins on soft substrates in the presence of Mn²⁺ is identical to the number of bound integrins for WT integrins on stiff substrates.

We first tested whether catch-bond behavior was required for substrate stiffness sensing by simulating the lifetime vs. force relationship of the integrin-fibronectin bond as a step function. The bond lifetime was held constant below a peak force of 30 pN and 0 for higher forces (Fig. 5C). Varying the magnitude of the integrin–fibronectin lifetime had no effect on the fraction of bound integrins as a function of substrate stiffness (Fig. 5D). Therefore, in the absence of a force-dependent catch-bond mechanism, integrin binding kinetics were independent of substrate rigidity. We next explored how changes in catch-bond biophysical properties engendered stiffness sensing. We simulated the lifetime vs. force relationship as a typical catch-bond and varied the maximum lifetime for the 30-pN peak force, keeping the unloaded lifetime constant (Fig. 5E). In these conditions, because the integrin–fibronectin bond lifetime increased with increasing force, and force was modulated by substrate stiffness, actin flow enhanced the amount of bound integrins on stiff substrates (Fig. 5F). Changes in the maximum lifetime of the bond, however, had little impact on the fraction of bound integrins for a given substrate stiffness (Fig. 5F). Surprisingly, the transition between different regimes of integrin binding using known biophysical parameters of integrin catch-bonds occurred in the model naturally around a Young’s modulus of ∼7 kPa, as was seen in our experiments (Fig. 1).

In the presence of Mn²⁺, integrin–fibronectin bonds have both an increased affinity and enhanced bond lifetime in response to increased tension with respect to wild-type conditions (45, 50–52). To mimic these effects in the model, we combined our two previous results, increasing both the unloaded lifetime and the lifetime at the peak force (Fig. 5G). By increasing the integrin–fibronectin bond lifetime for forces <30 pN, actin flow enhanced the amount of bound integrins on soft substrates (Fig. 5H). Under these conditions, the fraction of bound integrins on soft substrates in the presence of Mn²⁺ was quantitatively similar to the fraction of bound integrins on stiff substrates in control conditions. Thus, while neither an increase in unloaded lifetime nor lifetime at peak force was sufficient on its own to recapitulate the effects of Mn²⁺, their combined effect was enough to abrogate the effects of substrate stiffness on cell spreading. This effect was not dependent on the number of ligands present in the model (Fig. S3).

Collectively, these results illustrate that rigidity sensing in the lamellipodium is determined by catch-bond kinetics of integrin–fibronectin bonds and that the fraction of bound integrins is sensitive to both the unloaded lifetime and the maximum lifetime of the catch-bond curve. Addition of Mn²⁺ resulted in longer integrin lifetimes on soft substrates, thereby increasing the average fraction of bound integrins. This change in integrin binding kinetics allows cells to spread on soft substrates.

Discussion

The ability to sense the stiffness of their extracellular environment is critical to cells’ ability to regulate growth, viability, migration, and differentiation (1–3). Here, we show that fibroblasts exhibit a biphasic response in spreading on matrices of variable stiffness (Fig. 1). For matrices with a Young’s modulus less than ∼5 kPa, cells were poorly spread with minimal adhesion assembly and few organized actin structures. Above ∼8 kPa, fibroblasts achieved a maximal spread area with typical adhesion assembly and highly organized actin cytoskeletons. This transition stiffness was comparable to physiological tissue stiffness (16) and was of the same order of magnitude as reported values (8–12). While it has been suggested that cell spread area as a function of substrate stiffness follows a power-law behavior (9, 12), using a larger number of substrates, we find that it is better described as biphasic.

Due to its overwhelming role in cellular force generation, myosin II has been presumed to be the predominant mechanism of substrate stiffness sensing by adherent cells (23–28). Here, however, we demonstrate a myosin-independent stiffness sensing mechanism that controls spread area and arises from forces generated by actin polymerization within the lamellipodium. Integrins, which connect and transmit stress between the cytoskeleton and the ECM, behave as catch-bonds whose lifetime is determined as a function of the applied load (45, 53). As the load on the integrin increases, the lifetime of the bond also increases (45). On stiff substrates, this increase in lifetime is sufficient to promote clustering and adhesion formation (Fig. 4). Conversely, on soft substrates, the reduction in stiffness leads to shorter bond lifetimes which inhibit the required clustering for adhesion formation (Fig. 5). Both our experimental and simulation data suggest that integrin force-dependent binding kinetics are most sensitive to substrates with a stiffness between ∼5 and 8 kPa. Addition of Mn²⁺, which alters the kinetics of integrin–ECM bonds by increasing the unloaded and peak force lifetimes (45, 50–52), both increased the number of bound integrins and decreased the average spacing between bound integrins. Together, these effects promoted adhesion formation and enabled cells on soft substrates to spread and take on the morphology characteristics of cells on stiff substrates (Fig. 4).

Conceptually, this framework is similar to the general motor-clutch model (54) that has been suggested as a mechanism for understanding mechanosensitivity (23, 24, 26, 27). Instead of forces being generated by myosin motors, the force applied across the integrin bonds is generated by actin polymerization in the lamellipodium. These polymerization forces modulate the integrin–ECM bond kinetics and offer a surprisingly simple and elegant mechanism to understand substrate stiffness sensing. Previous work has established that there is a minimum spacing required between integrins for adhesion formation (38). Binding of integrins to their ligands also limits their diffusion in the membrane (47) and drives clustering at the nanoscale (36). Once a nanoscale cluster of integrins has formed, the force required to rupture the adhesion (i.e., the adhesion strength) is more than an order of magnitude greater than typical tensions generated in the cytoskeleton (55). Thus, by increasing the density of bound integrins, adhesion stabilization is increased, and the cell is able to spread.

Together, these results suggest that the lamellipodium acts as a myosin-independent mechanosensor, applying force to bound integrins via actin polymerization-driven retrograde flow. On soft substrates, the increased pliability of the matrix leads to a reduced load on the integrin–ECM bond, resulting in a shorter lifetime. This shorter lifetime prevents integrin clustering and thereby inhibits adhesion stabilization, leading to a poor ability to spread. On stiff substrates, integrin–ECM bonds experience greater loads and thus increased lifetimes, which promote adhesion stabilization and enable cells to spread. While these results do not exclude the possibility that myosin-generated forces may be one mechanism to probe substrate stiffness, they suggest that stiffness sensing emerges passively from the properties of the integrin binding kinetics. Given that simply shifting these kinetics can induce spreading on soft substrates, it will be interesting in the future to explore whether this approach is sufficient to recover other functions found to be impaired by soft substrates, as in development, differentiation, and disease.

Materials and Methods

Polyacrylamide gels of different stiffnesses were fabricated on glass substrates by altering the ratio of acrylamide to bisacrylamide as reported (5, 56). Images were obtained on an inverted Nikon Ti-E microscope by using either a Yokogawa CSU-X1 confocal scanhead or a Lumen 200Pro metal halide light source. Detailed information about image analysis and the computational model can be found in SI Materials and Methods.