Significance
The discovery of “place cells,” “grid cells,” and other spatial cells in the rodent’s forebrain has strengthened the idea that animals navigate their home range environments thanks to a “cognitive map.” Tiny-brained insects, like bees, are also thought to use such a centralized metric mental representation. However, downstream optimal combination of two decentralized guidance routines suffices to explain multiple experimental results obtained in bees and ants. We show that these insect navigators behave analogously to particles oriented by a global elastic force and local magnetic forces directed to the goal. As if equipped with both Ariadne’s thread and Hansel-and-Gretel’s pebbles, insects seem to know where to go rather than where they are on a map.
Keywords: multisensory, vector field, path integration, compass, cue-conflict
Abstract
In the last decades, desert ants have become model organisms for the study of insect navigation. In finding their way, they use two major navigational routines: path integration using a celestial compass and landmark guidance based on sets of panoramic views of the terrestrial environment. It has been claimed that this information would enable the insect to acquire and use a centralized cognitive map of its foraging terrain. Here, we present a decentralized architecture, in which the concurrently operating path integration and landmark guidance routines contribute optimally to the directions to be steered, with “optimal” meaning maximizing the certainty (reliability) of the combined information. At any one time during its journey, the animal computes a path integration (global) vector and landmark guidance (local) vector, in which the length of each vector is proportional to the certainty of the individual estimates. Hence, these vectors represent the limited knowledge that the navigator has at any one place about the direction of the goal. The sum of the global and local vectors indicates the navigator’s optimal directional estimate. Wherever applied, this decentralized model architecture is sufficient to simulate the results of quite a number of diverse cue-conflict experiments, which have recently been performed in various behavioral contexts by different authors in both desert ants and honeybees. They include even those experiments that have deliberately been designed by former authors to strengthen the evidence for a metric cognitive map in bees.
When bees and ants perform their far-ranging foraging journeys, multiple sensory channels are at work and provide two major navigational systems (guidance routines) with the necessary input information. On the one hand, path integration guidance (PI) (1, 2) continually updates a home vector by combining compass information derived, for example, from celestial cues (3) and the direction of the prevailing winds (4) with odometric information provided by proprioceptive and optic flow cues (5, 6). On the other hand, landmark guidance (LG) relies primarily on terrestrial cues, which the animals acquire during well-structured learning walks or flights (7, 8) as well as during travels along habitual routes (9, 10). These landmark views are stored in long-term memory, from where they can be retrieved in flexible and context-dependent ways, compared with the currently experienced views and thus, used by view-based image matching for computing the courses to particular goal locations (11–16).
Extensive studies performed especially in the last two decades in desert ants have shown that these two major routines can operate quite independently of each other (9, 10, 17). In particular, the path integrator does not attach metric coordinates to landmark memories acquired at particular locations (18, 19). How then do the two navigational routines interact in steering the animal’s courses? For instance, Cruse and coworkers (20, 21) simulated a number of behavioral results obtained in studies on ant and honey bee navigation by implementing a decentralized model based on dominance hierarchy, in which LG, when available, suppressed PI. However, several recent cue-conflict experiments indicate that the two guidance systems may continually cooperate in steering the animal along particularly biased intermediate courses (22–26). Here, we ask whether a decentralized architecture with a downstream combination of the guidance routine outputs (26) suffices for explaining the experimental data presently available or whether it is necessary to assume that all spatial information is centralized in a metric “cognitive map” as claimed from studies in honey bee navigation (27).
Moreover, the compromise directions observed in cue-conflict situations suggest that insect foragers, just as humans and monkeys (28, 29), might optimally integrate the noisy multimodal information available to them (23). Optimality as defined here in statistical terms means maximizing the certainty (i.e., reliability) of the combined information (28–30). Accordingly, the animal would need to know the uncertainty inherent in each guidance routine and use this knowledge to estimate the optimal direction to steer. As yet, this theoretical aspect has received only partial attention (23, 24). In this paper, we show that a decentralized architecture composed of independent guidance routines can propagate uncertain directional information and combine it optimally at a downstream processing stage. By using simulations, we further show that this navigation model accounts for the results of various cue-conflict experiments performed in ants and bees.
Results
In contrast to classical Bayesian fusion of linear quantities (28, 29), the optimal combination of conflicting noisy directions is not a weighted average of individual circular estimates. Rather, it can be most conveniently modeled by planar vector summation if the individual estimates are represented as vectors instead of angles (30), where the length of each vector is proportional to the certainty of the individual estimates. We call a “belief vector” any vector of this type, as it represents the limited knowledge—the belief (31)—that an observer has about an uncertain direction (a formal definition is in Methods). Provided that two belief vectors are properly calibrated (Methods), their sum is a belief vector representing the optimal direction estimate and its relative certainty (30).
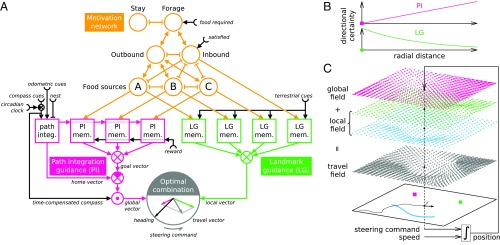
As a working hypothesis, we assume that, when insects are on their foraging journeys, the two main navigational routines—PI and LG—work concurrently and contribute optimally to the directions to be steered. This hypothesis is formalized in the model depicted in Fig. 1A. Following a decentralized approach, the model comprises two independent navigational routines modulated by a motivation network (Fig. 1A, yellow), which indicates whether the animal is on its outbound (foodward) or inbound (homeward) trip, etc. The PI, fed by odometric and compass cues, computes a global vector (Fig. 1A, red). In parallel, LG relies on terrestrial visual cues for computing a local vector (Fig. 1A, green). Considering plausible models of PI and LG, we show that each routine can itself estimate the certainty of the direction that it computes (Methods). In other words, both global and local vectors are belief vectors. Thus, the sum of the two appropriately calibrated vectors—the travel vector (Fig. 1A, gray)—defines the optimal direction to steer.
Fig. 1.
(A) Optimal multiguidance model. Organized as two banks of procedural memories, PI and LG (red and green boxes, respectively) operate concurrently and independently but are orchestrated by a network of motivation units (yellow circles). This network of coupled winner-take-all layers (e.g., A–B–C) exhibits multiple and stable activity patterns encoding various motivational states (e.g., forage outbound to food source B) in response to current context (e.g., food required). Each memory, when activated by its motivation unit, issues a belief vector representing a direction estimate and its certainty. Being always active, the path integrator, fed by time-compensated compass and odometric cues, maintains a geocentric home vector compared first with the goal vector (i.e., a past home vector) and then with the current compass direction to produce the egocentric global vector. The active LG memory compares current and learned panoramic terrestrial cues to estimate the visually most familiar direction. The resulting local vector is summed with the global vector (gray circle) to give the optimal travel vector that steers the agent. (B) PI certainty increases in proportion to the distance to the fictive home (red square). LG certainty decays exponentially with increasing distance to a familiar panorama (green dot). (C) Simulation of a fictional cue-conflict experiment. A random walk (black trajectory) is directed by the optimal travel field (gray) obtained by superposing (i.e., optimally combining) the global field (red) with the local field, itself built arbitrarily from superposing a place field (green) and a route field (in blue for clarity), as different landmarks can also be set in conflict. The red square indicates the fictive home. The green dot indicates the visually familiar place. The blue curve indicates the visually familiar route. Fig. S2 shows more precise 2D views of each type of vector field. integ., integrator; mem., memory.
Both guidance routines can be idealized by static fields of belief vectors—the global and local fields (Methods). The global field derived from our PI model points to the PI-based goal location (e.g., the fictive home). We propose to design the local field as a superposition (optimal combination) of elementary fields among two types—place and route fields—as needed to reflect the forager’s visual experience of the environment. The magnitudes of the global and elementary local fields, which describe PI and LG certainties, are idealized by simple radial functions (Fig. 1B) (Methods). In this context, optimal courses are simulated by random walks oriented by the optimal field (i.e., the superposition of the global and local fields by means of belief vector summation) (Fig. 1C).
We now test whether this abstraction suffices to simulate a number of paradigmatic cue-conflict experiments, which have recently been performed by various researchers in ants and bees. We start with two experiments in which desert ants displaced to cue-conflict locations exhibit compromised homing directions. The two experiments are complementary in so far as the impact of either only PI or only LG was manipulated. In the first experiment (constant LG impact), Wystrach et al. (24) trained Cataglyphis velox ants in a scrub desert landscape along a straight 7-m path to a habitual feeder. During the tests, these ants were captured on their way to the feeder at different distances (1, 3, and 7 m) and released for homing at a point nearby the nest, such that their visually familiar LG direction was in 110° conflict with the PI direction to the fictive nest. Thus, only the home vector length varied across the test conditions. In the second experiment (constant PI impact), Legge et al. (25) trained Melophorus bagoti ants along an 11-m straight path to a feeder, where they were later captured for testing. These “full-vector ants” were then released at one of three release points located at various distances (4, 32, and 64 m) and directions from the nest. This procedure resulted in cue-conflicts of about 132°, 117°, and 65° between the constant PI direction and varying LG directions. In both experiments, other ants were captured right before they reached the nest (“zero-vector ants”) and tested at the previous release points so as to control that they headed directly to the nest when initially deprived of PI information (and thereby, showing LG’s sufficiency and efficacy).
In our theoretical framework, both experiments can be modeled by superposing the global field centered on the fictive nest location to a place type local field centered on the actual nest location. Thus, each condition is characterized by a different superposition (i.e., optimal travel vector field). By regression analysis (Methods), we find the parameter values of the model (Table S1) for which the travel vector at the release point fits the experimental data best (Fig. S3). For each cue-conflict (Fig. 2) and control (Fig. S4) condition of either experiment, we then simulate a series of short random walks directed by the best-fit optimal field. The resulting simulated mean headings do not differ significantly from the experimental ones (Watson–Williams tests on pairwise comparisons: , ), except in the 7-m condition of Wystrach et al. (24) (, ). As in the experiment by Legge et al. (25), the simulated distribution for the most distant release point (64 m) is not significantly oriented (Rayleigh test: , ).
Fig. 2.
Ants’ optimal initial headings in the cue-conflict experiments of (A) Wystrach et al. (24) and (B) Legge et al. (25). Thick red and green lines indicate PI and LG directions, respectively. Histograms indicate heading distributions. Thin lines indicate mean headings. Arcs indicate 95% CIs. Black, simulation data; yellow, experimental data from ref. 24, figure 2C and ref. 25, figure 4 D–F. Asterisks indicate a significant difference (Watson–Williams test; P 0.001) between experimental and simulated mean headings in the 7-m condition of Wystrach et al. (24).
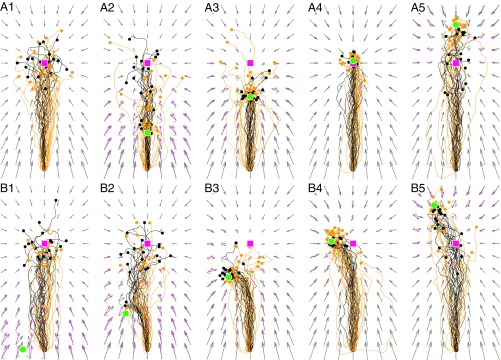
Having shown that ants presumably take optimal bearings when released at discrete cue-conflict locations, we next examine whether they do so continually along their entire journeys. The drifting homeward runs observed in Cataglyphis fortis under continuous cue-conflict situations provide a telling example. Bregy et al. (22) trained ants to visit a feeder 15 m apart from the nest. The latter was marked by an artificial beacon (black cylinder) located directly behind its entrance in an otherwise featureless salt-pan environment. Trained foragers were then captured at the feeder and released as full-vector ants in a distant test area, in which a beacon identical to the training one was placed at different positions on (Fig. 3A) or alongside (Fig. 3B) the ideal PI homing path. In terms of vector fields, this means that each condition features a different optimal field due to the (mis-)alignment of the unchanged global field pointing at the fictive nest and the local place field linked to the displaced beacon. As Fig. 3 shows, the model replicates well the animals’ trajectories. Similar to what happens in the experiments, the virtual ants’ lateral drifts increase as the beacon is placed closer and closer to the fictive position of the nest (Fig. 3 B2–B5). Moreover, in nearly all conditions, the starts of search behavior (Fig. 3, black dots) scatter in the same way as in the experiments, and the search densities of simulated and real ants qualitatively match (Fig. S5).
Fig. 3.
Ants’ continually optimal steering in the cue-conflict experiment of Bregy et al. (22). The red squares indicate PI-based fictive nest. The green dots indicate nest-marking beacon placed along (A1–A5) or to the left (B1–B5) of the ideal home vector course. Red, green, and gray arrows indicate global, local, and optimal fields, respectively. The small dots indicate start of search [i.e., first turn 90° (measured between 2-m spaced trajectory points)]. Controls are no beacon (A1) and training-like (A4). Black, simulated trajectories; yellow, experimental trajectories from ref. 22, figure 2.
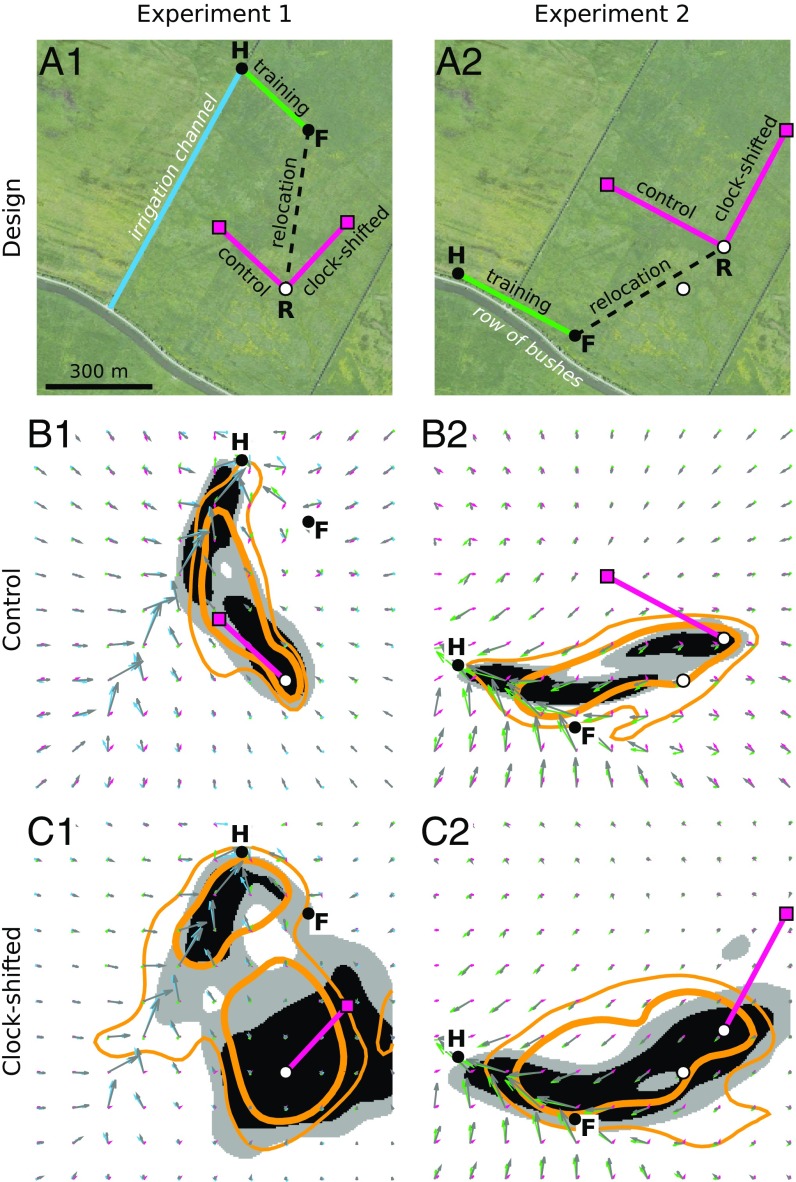
In the last account, we assess whether our navigation model can also describe how flying foragers resolve conflicting guidance information. Cheeseman et al. (27) reported successful and robust homing performance in honeybees across a variety of cue-conflict situations. In a couple of displacement experiments conducted in a large, flat, and open pasture (Fig. 4A), full-vector bees were captured at a feeder (Fig. 4A, F) to which they had been trained and released at sites (Fig. 4A, white dots) more than 600 m from their hive (Fig. 4A, H). The two experiments essentially differed in so far as, at the release sites, the panorama was either largely featureless (experiment 1) or a salient familiar cue was present (a row of bushes running along the bees’ training path; experiment 2). Two groups of bees were tested in each experiment: (i) control bees were simply displaced to the release site, and (ii) clock-shifted bees underwent a 6-h anesthesia treatment beforehand to shift their time-compensated celestial compass (32). From both sets of experiments, the authors conclude that the displaced bees first follow more or less their global vector, be it clock-shifted or not, but after having “discovered their error,” they are “equally accurately directed toward the hive” (27).
Fig. 4.
Bees’ robust homing in the experiments of Cheeseman et al. (27). (A) Experimental designs of experiments 1 (A1) and 2 (A2). The red squares indicate the fictive hives. Red lines indicate predicted ideal PI courses. Aerial imagery of the experimental site in 2008 reproduced from Google Earth and provided by GeoBasis-DE/BKG. (B and C) For control (B1 and B2) and clock-shifted (C1 and C2) conditions, 50%/75% probability mass contours of homing trajectories in bees (thick/thin yellow lines, respectively) (ref. 27, figures S4–S7) and simulations (black/gray area outlines, respectively) are shown. Red, green, blue, and gray arrows indicate global field, feeder-to-hive route field, irrigation channel route field, and optimal field, respectively. In experiment 2, bees departed from either of two sites (white dots), whereas only point R was used in simulations. F, feeder; H, hive; R, release point.
In our simulations, we proceed as previously described by matching the expected visual experience and PI state of each group of foragers by global and local fields superposed according to the different experimental conditions. This task is somewhat complicated by the fact that, for LG, the bees might have used, in addition or arguably as part of the panoramic cues, the local structures and patterns that were available on the ground (27). However, except for an irrigation channel passing nearby the hive in experiment 1, clearly used by some control and clock-shifted bees (Fig. 4 B1 and C1), these cues were unspecified. As a minimal assumption, for each experiment, we placed a route field from the feeder to the hive on the straight homing path along which the bees have been trained (Fig. 4 B and C, green arrows). Moreover, to simulate experiment 1, another route field (Fig. 4 B1 and C1, blue arrows) is added to account for the bees’ familiarity with the irrigation channel and any nearby salient ground patterns.
Fig. 4B shows that, in control conditions, the simulated optimally directed random walks exhibit similar distributions to those of the bees’ trajectories. As in experiment 1, PI initially dominates due to the relatively weak local field at the release point, leading the virtual bees toward the irrigation channel’s route field, where LG then takes over. For experiment 2, the global and local field strengths at the release point roughly equate and induce the simulated foragers to take average bearings until they have come close enough to the feeder-to-hive training route, so that from then on, LG dominates the behavior. Interestingly, our model is able to replicate the data of the clock-shifted bees sufficiently well (rates of successful returns: 17 of 20 for experiment 1 and 18 of 20 for experiment 2) when we apply two assumptions. The first and obvious one concerns the clock shift-induced rotation of the global field (by 90° as estimated in ref. 27 and also used here). The second implies a reduction of its magnitude (i.e., PI certainty) to 30% of its value in the controls, thus increasing the scatter, especially around the release point (Fig. 4C). This is in line with the lower precision of the initial bearings observed in clock-shifted bees and may reflect various effects of the anesthesia treatment (32). In contrast to the conclusion of Cheeseman et al. (27) that the displaced bees proceed in a stepwise way—first, PI and second, error discovery followed by landmark-based map reading—in our model, the guidance systems involved in the bees’ navigational performances are continually active and cooperate optimally.
Discussion
While finding their ways in their far-ranging foraging territories, ants and bees take advantage of a plethora of sensory cues, be they visual (celestial or terrestrial), olfactory, geomagnetic, wind-borne, or haptic cues (33, 34). Recent neuroethological work has mainly focused on how these cues are perceived and used, but how their use is embedded in the insect’s overall navigational toolset has remained a much debated issue. Some researchers hold that all spatial information is finally channeled into a central processing unit akin to “an integrated, metric cognitive map” suited for informing the animal about where it is (27, 35). Others have devised decentralized network architectures, in which navigational routines cooperate in flexible, context-dependent ways and at any one time, inform the animal about where to go (20, 21). By simulating the results of a number of paradigmatic behavioral experiments, we support the latter view and show that optimal navigation is possible without invoking a cognitive map.
Our analyses and simulations are based on the well-supported conclusion from a large body of experimental work that insect foragers use spatial information in the context of two major guidance routines: PI and LG (10, 14, 15, 36). While the former provides the animal with a global vector pointing from the central place, the nest, to habitual foraging sites and back to the nest, the latter relies on visual memories of panoramic views (i.e., memories of how the world looks from particular locations). The power of this LG routine is in the fact that the panoramic view at one location will have much in common with the views taken from locations nearby. Although broadly similar to the linear Bayesian theory used by Wystrach et al. (24), the circular theory that we used here differs in significant ways (30) relevant to the large PI–LG discrepancies typically presented to insects in cue-conflict experiments. In particular, either routine contributes to the course to be steered depending nonlinearly on its reliability and how much it conflicts with the other. For example, Fig. S3B1 shows that the circular model is robust to large guidance conflicts in switching its output toward the most reliable routine (Fig. S3B1, shaded blue sigmoid) rather than smoothly mitigating both directions as the linear model does (Fig. S3B1, shaded gray curve).
Our model is best understood when the guidance routines are idealized by what we have called belief vector fields. It is important to note that, although such a field may look like a map when sampled systematically as in Figs. 3 and 4, it is anything but a map. At any one time and location, the animal has access only to information stored in memory that is relevant to its current motivational state (i.e., its goal) and compares it with ongoing sensory information. It is “blind” to the rest of the fields and thus, cannot plan ahead its path. Moreover, rather than computing metric positions, both routines estimate directions and their certainties. Directional statistics theory applied to the model of Mittelstaedt (37) shows (SI Text) that PI directional certainty scales in proportion to the direct distance from the goal (i.e., global vector length), although the positional error grows with the path length. This counterintuitive prediction fully fits the experimental observations of Wystrach et al. (24) (“pot” vs. control conditions) but disagrees with the dependence on path length found using their directed walk model (ref. 24, equation 2.2) and their subsequent interpretation that ants steer heuristically rather than optimally. Additional experiments, which systematically combine the experimental paradigms of Wystrach et al. (24) and Legge et al. (25), would allow us to (i) assess if, as predicted from the compass’ inherent precision limit, PI certainty saturates and (ii) accurately characterize LG certainty, which here has been assumed to decay exponentially with distance. Then, it is an open question as to how the independently estimated certainties are properly calibrated so as to meaningfully and optimally fuse the two guidance outputs.
In principle, our network structure is compatible with recent neurophysiological analyses of the computational role that two major neuropils in the insect’s forebrain play. On the one hand, the convergence of sky-based compass information and optic flow-based odometric information occurs at the central complex (a set of midline neuropils), which is highly conserved across insect species and which may provide the insect with a common internal representation of azimuthal space (38–40). In particular, the Cartesian vector representation that we used here is functionally equivalent to more plausible ring-like neuron representations (41, 42). On the other hand, the mushroom bodies—higher-order integration and association centers in the insect brain—have all of the computational capabilities to encode large numbers of panoramic views (43, 44). Although direct neural pathways between these two forebrain systems have not been found yet, it is plausible that the mushroom bodies finally provide the central complex with view-based directional outputs.
In conclusion, while previously it has often been assumed that various guidance routines contribute to the insect’s final navigational decision in a hierarchical order or in temporal succession (a review is in ref. 26), we now provide a body of evidence supporting that all systems operate simultaneously and that, depending on the certainty and conflict of the cues involved as well as the motivational state of the animal, their outputs are optimally integrated. At any one time, the animal knows where to go rather than where it is on some kind of cognitive map.
Methods
Coordinates.
We model each forager as an oriented particle on the complex plane with position and absolute heading defined in geocentric coordinates arbitrarily attached to the environment. Any geocentric vector may be expressed relative to the forager frame (the positive real axis pointing forward) using egocentric coordinates, denoted by primes, such that , where is Euler’s formula.
Belief Vectors.
To model uncertain directions, we use random variables distributed as (denoted ) the von Mises distribution (a circular analogue of the normal distribution) (45) denoted with mean direction and concentration (a circular analogue to the reciprocal of the variance). We call a belief vector for a direction any vector satisfying . According to Murray and Morgenstern (30), if and only if two belief vectors for independent directions are calibrated (i.e., ), then the sum
| [1] |
is a belief vector for the optimally combined (maximum likelihood) direction approximatively distributed as (denoted ) with and , such that .
Global Field.
Assuming relatively low and constant compass noise, we show (SI Text) that the biologically plausible (41, 42) PI model of Mittelstaedt (37) computes a belief vector—the (egocentric) global vector . Moreover, in a forager possibly displaced from to and clock-shifted by an angle , PI can be idealized (SI Text) by a geocentric belief vector field—the global field
| [2] |
where the fictive goal location is . Thus, PI certainty can be approximated by a linear radial function.
Local Field.
We argue (SI Text) that the Graham–Philippides–Baddeley (46) model, a plausible LG model requiring minimal interaction with PI only during learning (16, 47), can be used to estimate a belief vector—the (egocentric) local vector . We then propose to idealize LG by a geocentric belief vector field—the local field —obtained by superposing (i.e., combined optimally using Eq. 1) a number of place and route belief vector fields as needed to account for the visual experience of foragers. Assuming that LG certainty decays exponentially with increasing distance to familiar panoramas, we model place and route fields using the respective formulas (SI Text):
| [3] |
| [4] |
where is the panorama-based goal location, is the point on a route to the goal closest to the forager location , is the route’s unit tangent vector at , the decay constant characterizes the catchment area (12) around the place or route, and the complex conjugate of is denoted .
Optimal Multiguidance.
Assuming that both and are calibrated belief vectors, from Eq. 1, it follows that the travel vector is a belief vector for the optimal multiguidance travel direction relative to the forager’s absolute heading . Thus, optimal multiguidance can be idealized by the superposition of the global and local fields—the optimal field
| [5] |
Steering of the forager is performed by a stochastic adaptation of the homing model given in ref. 42:
| [6] |
where is the steering coefficient, is the imaginary part of , and is white Gaussian noise with variance . Thus, using geocentric coordinates, we have
| [7] |
where is the optimal multiguidance absolute travel direction. Hence, according to ref. 45, is a von Mises process with stationary distribution with concentration . That is, the shorter the travel vector, the noisier the forager’s heading. Considering the shape of the global field, this explains why searching behavior emerges and remains concentrated around the PI-based goal location in absence of familiar landmarks.
The position of the forager moving at constant speed is updated according to
| [8] |
Supplementary Material
Acknowledgments
We thank Holk Cruse for support throughout this study and Loes C. J. van Dam for hinting at ref. 30. This research was supported by the European Research Council’s Seventh Framework Programme; Information and Communication Technologies (FP7-ICT) Grant 270182; Embodied Motion Intelligence for Cognitive, Autonomous Robots (EMICAB); and CITEC (EXC 277) at Bielefeld University, which is funded by the German Research Foundation (DFG).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1721668115/-/DCSupplemental.
References
- 1.Collett M, Collett TS. How do insects use path integration for their navigation? Biol Cybern. 2000;83:245–259. doi: 10.1007/s004220000168. [DOI] [PubMed] [Google Scholar]
- 2.Wehner R, Srinivasan MV. In: The Neurobiology of Spatial Behaviour. Jeffery KJ, editor. Oxford Univ Press; Oxford: 2003. pp. 9–30. [Google Scholar]
- 3.Wehner R, Müller M. The significance of direct sunlight and polarized skylight in the ant’s celestial system of navigation. Proc Natl Acad Sci USA. 2006;103:12575–12579. doi: 10.1073/pnas.0604430103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Müller M, Wehner R. Wind and sky as compass cues in desert ant navigation. Naturwissenschaften. 2007;94:589–594. doi: 10.1007/s00114-007-0232-4. [DOI] [PubMed] [Google Scholar]
- 5.Wittlinger M, Wehner R, Wolf H. The ant odometer: Stepping on stilts and stumps. Science. 2006;312:1965–1967. doi: 10.1126/science.1126912. [DOI] [PubMed] [Google Scholar]
- 6.Pfeffer SE, Wittlinger M. Optic flow odometry operates independently of stride integration in carried ants. Science. 2016;353:1155–1157. doi: 10.1126/science.aaf9754. [DOI] [PubMed] [Google Scholar]
- 7.Fleischmann PN, Christian M, Müller VL, Rössler W, Wehner R. Ontogeny of learning walks and the acquisition of landmark information in desert ants, Cataglyphis fortis. J Exp Biol. 2016;219:3137–3145. doi: 10.1242/jeb.140459. [DOI] [PubMed] [Google Scholar]
- 8.Stürzl W, Zeil J, Boeddeker N, Hemmi JM. How wasps acquire and use views for homing. Curr Biol. 2016;26:470–482. doi: 10.1016/j.cub.2015.12.052. [DOI] [PubMed] [Google Scholar]
- 9.Kohler M, Wehner R. Idiosyncratic route-based memories in desert ants, melophorus bagoti: How do they interact with path-integration vectors? Neurobiol Learn Mem. 2005;83:1–12. doi: 10.1016/j.nlm.2004.05.011. [DOI] [PubMed] [Google Scholar]
- 10.Collett M, Chittka L, Collett TS. Spatial memory in insect navigation. Curr Biol. 2013;23:R789–R800. doi: 10.1016/j.cub.2013.07.020. [DOI] [PubMed] [Google Scholar]
- 11.Cartwright BA, Collett TS. Landmark learning in bees. J Comp Physiol. 1983;151:521–543. doi: 10.1007/BF01324825. [DOI] [PubMed] [Google Scholar]
- 12.Zeil J, Hofmann MI, Chahl JS. Catchment areas of panoramic snapshots in outdoor scenes. J Opt Soc Am A. 2003;20:450–469. doi: 10.1364/josaa.20.000450. [DOI] [PubMed] [Google Scholar]
- 13.Stürzl W, Zeil J. Depth, contrast and view-based homing in outdoor scenes. Biol Cybern. 2007;96:519–531. doi: 10.1007/s00422-007-0147-3. [DOI] [PubMed] [Google Scholar]
- 14.Graham P. Insect navigation. Encyclopedia Anim Behav. 2010;2:167–175. [Google Scholar]
- 15.Zeil J. Visual homing: An insect perspective. Curr Opin Neurobiol. 2012;22:285–293. doi: 10.1016/j.conb.2011.12.008. [DOI] [PubMed] [Google Scholar]
- 16.Stürzl W, Grixa I, Mair E, Narendra A, Zeil J. Three-dimensional models of natural environments and the mapping of navigational information. J Comp Physiol A. 2015;201:563–584. doi: 10.1007/s00359-015-1002-y. [DOI] [PubMed] [Google Scholar]
- 17.Andel D, Wehner R. Path integration in desert ants, Cataglyphis: How to make a homing ant run away from home. Proc R Soc Lond B Biol Sci. 2004;271:1485–1489. doi: 10.1098/rspb.2004.2749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bisch S, Wehner R. Visual navigation in ants: Evidence for site-based vectors. In: Elsner N, Wehner R, editors. Proceedings of the 26th Göttingen Neurobiology Conference 1998. Thieme; Stuttgart: 1998. p. 417. [Google Scholar]
- 19.Collett M, Collett T, Chameron S, Wehner R. Do familiar landmarks reset the global path integration system of desert ants? J Exp Biol. 2003;206:877–882. doi: 10.1242/jeb.00176. [DOI] [PubMed] [Google Scholar]
- 20.Cruse H, Wehner R. No need for a cognitive map: Decentralized memory for insect navigation. PLoS Comput Biol. 2011;7:1–10. doi: 10.1371/journal.pcbi.1002009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hoinville T, Wehner R, Cruse H. 2012. Learning and retrieval of memory elements in a navigation task. Biomimetic and Biohybrid Systems. Living Machines 2012, eds Prescott TJ, Lepora NF, Mura A, Verschure PFMJ. Lecture Notes in Computer Science (Springer, Berlin), Vol 7375, pp 120–131.
- 22.Bregy P, Sommer S, Wehner R. Nest-mark orientation versus vector navigation in desert ants. J Exp Biol. 2008;211:1868–1873. doi: 10.1242/jeb.018036. [DOI] [PubMed] [Google Scholar]
- 23.Collett M. How navigational guidance systems are combined in a desert ant. Curr Biol. 2012;22:927–932. doi: 10.1016/j.cub.2012.03.049. [DOI] [PubMed] [Google Scholar]
- 24.Wystrach A, Mangan M, Webb B. Optimal cue integration in ants. Proc R Soc Lond B Biol Sci. 2015;282:20151484. doi: 10.1098/rspb.2015.1484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Legge ELG, Wystrach A, Spetch ML, Cheng K. Combining sky and earth: Desert ants (melophorus bagoti) show weighted integration of celestial and terrestrial cues. J Exp Biol. 2014;217:4159–4166. doi: 10.1242/jeb.107862. [DOI] [PubMed] [Google Scholar]
- 26.Wehner R, Hoinville T, Cruse H, Cheng K. Steering intermediate courses: Desert ants combine information from various navigational routines. J Comp Physiol A. 2016;202:459–472. doi: 10.1007/s00359-016-1094-z. [DOI] [PubMed] [Google Scholar]
- 27.Cheeseman JF, et al. Way-finding in displaced clock-shifted bees proves bees use a cognitive map. Proc Natl Acad Sci USA. 2014;111:8949–8954. doi: 10.1073/pnas.1408039111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ernst MO, Banks M. Humans integrate visual and haptic information in a statistically optimal fashion. Nature. 2002;415:429–433. doi: 10.1038/415429a. [DOI] [PubMed] [Google Scholar]
- 29.Knill DC, Pouget A. The bayesian brain: The role of uncertainty in neural coding and computation. Trends Neurosci. 2004;27:712–719. doi: 10.1016/j.tins.2004.10.007. [DOI] [PubMed] [Google Scholar]
- 30.Murray RF, Morgenstern Y. Cue combination on the circle and the sphere. J Vis. 2010;10:15. doi: 10.1167/10.11.15. [DOI] [PubMed] [Google Scholar]
- 31.de Finetti B. Theory of Probability: A Critical Introductory Treatment. Wiley & Sons; London: 1974. [Google Scholar]
- 32.Cheeseman JF, et al. General anesthesia alters time perception by phase shifting the circadian clock. Proc Natl Acad Sci USA. 2012;109:7061–7066. doi: 10.1073/pnas.1201734109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.von Frisch K. The Dance Language and Orientation of Bees. Harvard Univ Press; Cambridge, MA: 1967. [Google Scholar]
- 34.Knaden M, Graham P. The sensory ecology of ant navigation: From natural environments to neural mechanisms. Ann Rev Entomol. 2016;61:63–76. doi: 10.1146/annurev-ento-010715-023703. [DOI] [PubMed] [Google Scholar]
- 35.Menzel R, et al. Honey bees navigate according to a map-like spatial memory. Proc Natl Acad Sci USA. 2005;102:3040–3045. doi: 10.1073/pnas.0408550102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wehner R. The desert ant’s navigational toolkit: Procedural rather than positional knowledge. Navigation. 2008;55:101–114. [Google Scholar]
- 37.Mittelstaedt H. The role of multimodal convergence in homing by path integration. Fortschr Zool. 1983;28:197–212. [Google Scholar]
- 38.Seelig JD, Jayaraman V. Neural dynamics for landmark orientation and angular path integration. Nature. 2015;521:186–191. doi: 10.1038/nature14446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Heinze S. Neuroethology: Unweaving the senses of direction. Curr Biol. 2015;25:R1034–R1037. doi: 10.1016/j.cub.2015.09.003. [DOI] [PubMed] [Google Scholar]
- 40.Stone T, et al. An anatomically constrained model for path integration in the bee brain. Curr Biol. 2017;27:3069–3085. doi: 10.1016/j.cub.2017.08.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Cheung A, Vickerstaff R. Finding the way with a noisy brain. PLoS Comput Biol. 2010;6:1–15. doi: 10.1371/journal.pcbi.1000992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Vickerstaff RJ, Cheung A. Which coordinate system for modelling path integration? J Theor Biol. 2010;263:242–261. doi: 10.1016/j.jtbi.2009.11.021. [DOI] [PubMed] [Google Scholar]
- 43.Heisenberg M. Mushroom body memoir: From maps to models. Nat Rev Neurosci. 2003;4:266–275. doi: 10.1038/nrn1074. [DOI] [PubMed] [Google Scholar]
- 44.Ardin P, Peng F, Mangan M, Lagogiannis K, Webb B. Using an insect mushroom body circuit to encode route memory in complex natural environments. PLoS Comput Biol. 2016;12:e1004683. doi: 10.1371/journal.pcbi.1004683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mardia KV, Jupp PE. Directional Statistics. Wiley & Sons; Chichester, England: 2000. [Google Scholar]
- 46.Graham P, Philippides A, Baddeley B. Animal cognition: Multi-modal interactions in ant learning. Curr Biol. 2010;20:R639–R640. doi: 10.1016/j.cub.2010.06.018. [DOI] [PubMed] [Google Scholar]
- 47.Dewar AD, Philippides A, Graham P. What is the relationship between visual environment and the form of ant learning-walks? An in silico investigation of insect navigation. Adapt Behav. 2014;22:163–179. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.