3D Spatially-Adaptive Canonical Correlation Analysis: Local and Global Methods

Abstract

Local spatially-adaptive canonical correlation analysis (local CCA) with spatial constraints has been introduced to fMRI multivariate analysis for improved modeling of activation patterns. However, current algorithms require complicated spatial constraints that have only been applied to 2D local neighborhoods because the computational time would be exponentially increased if the same method is applied to 3D spatial neighborhoods.

In this study, an efficient and accurate line search sequential quadratic programming (SQP) algorithm has been developed to efficiently solve the 3D local CCA problem with spatial constraints. In addition, a spatially-adaptive kernel CCA (KCCA) method is proposed to increase accuracy of fMRI activation maps. With oriented 3D spatial filters anisotropic shapes can be estimated during the KCCA analysis of fMRI time courses. These filters are orientation-adaptive leading to rotational invariance to better match arbitrary oriented fMRI activation patterns, resulting in improved sensitivity of activation detection while significantly reducing spatial blurring artifacts. The kernel method in its basic form does not require any spatial constraints and analyzes the whole-brain fMRI time series to construct an activation map. Finally, we have developed a penalized kernel CCA model that involves spatial low-pass filter constraints to increase the specificity of the method.

The kernel CCA methods are compared with the standard univariate method and with two different local CCA methods that were solved by the SQP algorithm. Results show that SQP is the most efficient algorithm to solve the local constrained CCA problem, and the proposed kernel CCA methods outperformed univariate and local CCA methods in detecting activations for both simulated and real fMRI episodic memory data.

1. INTRODUCTION

Spatially-adaptive multivariate methods have been used for fMRI data analysis as an alternative to the most commonly used single voxel analysis with isotropic Gaussian smoothing (SV) (Almodóvar-Rivera and Maitra, 2017; Borga and Rydell, 2007; Cordes et al., 2012; Friman et al., 2001; Harrison et al., 2008; Luessi et al., 2011; Tabelow et al., 2006; Weeda et al., 2009; Yue et al., 2010; Zhuang et al., 2017). While Gaussian smoothing can improve the signal-to-noise ratio (SNR) of fMRI data (Kriegeskorte and Bandettini, 2007), it also introduces spatial blurring of activation patterns leading to poor specificity.

One such spatially adaptive method is local canonical correlation analysis (local CCA), where fMRI time series are convolved with spatially anisotropic basis functions with unknown weight coefficients (Cordes et al., 2012; Friman et al., 2003; Friman et al., 2001). These basis functions act as low-pass spatial filters to better match arbitrary activation patterns. CCA (Hotelling, 1936) is then applied to determine the optimal weight coefficients of the spatial basis functions contingent on the design matrix that specifies the temporal regressors. Because CCA has more degrees of freedom than a univariate analysis that contains only one filter function (i.e. a spatial Gaussian function), spatial constraints on the weight coefficients are required to improve specificity of activation detection.

Friman et al. (2003) used 2D spatially oriented steerable filters (Kass and Witkin, 1988; Knutsson et al., 1983) as spatial basis functions for local CCA and restricted the weights of the basis functions to be nonnegative, so that the spatial filter acts as an adaptive spatial low-pass filter on the data. Cordes et al. (2012) showed how different spatial constraints impact the sensitivity and specificity of local CCA using time series convolved with 9 spatial 2D Dirac delta functions (2D- δ functions) on 3 × 3 in-plane neighboring voxels. Three different spatial constraints were investigated, namely a nonnegative constraint (the weights of all spatial basis functions are nonnegative), a so-called dominant constraint (the weight of the spatial basis functions acting on the center voxel is greater than the weights of all other spatial basis functions acting on neighboring voxels) and a so-called sum constraint (the weight of the spatial basis functions acting on the center voxel is greater than the sum of weights of all other spatial basis functions acting on neighboring voxels). The technique used to solve the constrained CCA problem is called restricted CCA (Das and Sen, 1994) and works by repeatedly excluding one or more unknown coefficients from the CCA equation until a solution satisfying all spatial constraints is found. Consequently, the computational time exponentially increases with the number of unknown variables. Recently, Zhuang et al. (2017) generalized these three spatial constrained models and implemented a family of constraints model controlled by two parameters, which includes previous constrained models as specific cases. Local CCA with the family of constraints was solved by nonlinear optimization algorithms such as the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm, the Generalized Reduced Gradient method (GRG) and the Augmented Lagrangian (AL) method. It was shown that GRG is the most time-efficient method and BFGS is the most accurate method among these three algorithms.

The first unsolved problem in local CCA of fMRI data is how to analyze data when 3D spatial filter functions (such as 3D-δ functions) are specified for local neighborhoods in 3D (such as cubic neighborhoods containing 3×3×3 voxels). Current local CCA methods are exclusively focused on analyzing 2D in-plane (same slice) neighborhoods which create activation maps that may depend on the direction of the slice acquisition. A justification for only analyzing 2D neighborhoods is that the in-plane (within a slice) resolution of fMRI data is usually higher than the out-of-plane (between slices) resolution to limit the number of slices required for full brain coverage at an acceptable scanning time. For data with isotropic voxel sizes, 3D local CCA methods are more appropriate because neighbors from all directions of a given center voxel are equally relevant to the center voxel and accurate brain maps can be produced independently of the direction of slice acquisition. However, existing algorithms, e.g. BFGS, for local constrained CCA with 2D spatial constraints cannot be extended to the 3D case because the number of variable partitionings is exponentially increased going from 2D to 3D and the 3D CCA problems become intractable. To solve local CCA with 3D spatial constraints, a fundamentally-different optimization algorithm is required.

The second unsolved problem in local CCA (whether with 2D or 3D spatial constraints) is how to correctly specify the functional form of the spatial constraints. A spatial constraint that is too strict will lower sensitivity of activation detection and leads to less correctly identified active voxels whereas a constraint that is too loose (as in conventional unconstrained CCA) will lower the specificity of detection and give a smaller proportion of correctly identified inactive voxels. In principle, the spatial constraint together with the spatial filter functions should better fit fMRI activation patterns.

The kernel variant of the CCA method is an attractive method in terms of computational efficiency, since this method analyzes whole-brain fMRI data simultaneously. This global method has been introduced in fMRI data analysis (Blaschko et al., 2011; Hardoon et al., 2007; Murayama et al., 2010; Bießmann et al., 2009). Hardoon et al. (2007) applied KCCA as an unsupervised machine learning algorithm on task fMRI data with pleasant and unpleasant visual stimuli. Blaschko et al. (2011) implemented supervised and semi-supervised KCCA on video-task fMRI data and obtained brain spatial weight maps corresponding to different types of visual processing. Murayama et al. (2010) and Bießmann et al. (2009) associated neural signals with time-delayed fMRI signals.

However, current methods involving KCCA are limited in their application to fMRI data. The first deficiency is that KCCA is restricted to a simple contrast design and can obtain only activation maps equivalent to a one-sample t-test. KCCA has not been formulated for a more general contrast design specified by a contrast matrix. Unlike KCCA, any local CCA and standard general linear model analysis of fMRI data can be carried out for any arbitrary contrast matrix of interest to determine contrast-specific statistical activation maps. A second deficiency is that the data in current KCCA methods are spatially smoothed by an isotropic Gaussian filter with a fixed full-width at-half-maximum (FWHM) in a preprocessing step. Thus KCCA, in its current form, does not adaptively fit activation patterns.

In this study, our main goal is twofold: First, we developed a 3D local constrained CCA method and solved it with a sequential quadratic programming method (SQP) (Nocedal and Wright, 2006). Second, we proposed a global spatially-adaptive KCCA method, called steerable filter KCCA (sf-KCCA), and developed a penalized sf-KCCA model (sf-pKCCA). These two KCCA methods can handle any general linear contrast of interests defined by an arbitrary contrast matrix to compute t- and F-statistical maps of the task design.

To test the time efficiency and accuracy of the SQP algorithm, we compared SQP with BFGS and the GRG algorithms for local CCA with 2D and 3D constraints. To evaluate the performance of the sf-KCCA method, we used nonnegative constrained CCA with the same steerable filters (sf-nonnegCCA). Along with the standard SV method, the best constrained CCA model in Cordes et al. (2012), namely the sum constraint CCA (sumCCA) with spatial δ functions as filters was used in addition. As sf-KCCA uses 3D neighboring information for analysis, the sf-nonnegCCA and sumCCA methods were also applied with 3D local neighboring information and solved using the SQP algorithm. We evaluated the performance of these methods with simulated data using receiver operating characteristic (ROC) curves. The same analysis methods were applied on real fMRI episodic memory data where single-domain amnestic mild cognitive impairment (aMCI) subjects and normal controls (NCs) performed a visual memory task. We also estimated ROC curves for real fMRI data (Nandy and Cordes, 2003; Nandy and Cordes, 2004) to evaluate the performance of the different methods. We computed activation maps and applied a radial basis function network (RBFN) technique and support vector machine (SVM) method to classify the population of subjects. The computed prediction accuracies provide a realistic assessment of the performance for the different analysis methods in classification and prediction of a neurodegenerative disorder.

2. METHOD

2.1. Spatial modeling and CCA

Classical univariate methods for analyzing fMRI data rely on isotropic data smoothing using a fixed Gaussian spatial low-pass filter. This type of smoothing is optimal for detecting activation patterns only if the spatial filter function matches the size and shape of the activated voxels. This is, however, not the case for fMRI data because shapes of active brain regions vary considerably depending on the task performed (Friman et al., 2003). Furthermore, a fixed spatial filter will lead to blurring of gray matter activation patterns into white matter regions.

For episodic memory tasks, it is known that important activation patterns of the medial temporal lobes covering the hippocampus and adjacent regions have a small contrast-to-noise ratio. If the spatial filter is non-adaptive it is less likely to obtain optimal activation detection using classical univariate methods (Nandy and Cordes, 2003). It was shown that the use of adaptive spatial basis functions in the framework of multivariate CCA can lead to an increased sensitivity for a given specificity to detect episodic memory activations (Cordes et al, 2012). In general, using adaptive spatial basis functions in a multivariate analysis may improve not only episodic memory task data but may also improve activation detection for arbitrary fMRI data as well.

The conventional general linear model (GLM) uses a single spatial basis function F(ξ) to model the shape of activation patterns, formulated as:

$$F(\mathit{\xi })\otimes Y_{un}(\mathit{\xi },t)={\sum }_{n=1}^N{\beta }_n(\mathit{\xi })x_n(t),t=1,\dots ,T$$ (1)

In this equation, the variable Y_un represents the raw fMRI data, ξ = (x, y, z) the spatial coordinate vector of a voxel, β_n the n-th linear regression coefficient corresponding to the n-th temporal response function x_n(t), and t the time point. The symbol ⊗ indicates spatial convolution with respect to ξ, namely, F(ξ) ⊗ Y_un(ξ, t) = Σ_ξ′ F(ξ − ξ′)Y_un(ξ′, t), where the summation is over all voxels ξ′. The design matrix X = (x₁, … x_n, …, x_N) ∈ ℝ^T×N represents N functions at T time points modeling the blood oxygenation level-dependent (BOLD) response. Once β = (β₁, …, β_N)^T ∈ ℝ^N×1 is calculated by linear regression, the t-statistic or F-statistic can be used to construct an activation map for a contrast of interest.

To account for spatial variations of active brain areas, a set of oriented filters (e.g. steerable filters) are introduced for adaptive spatial modeling. Adaptive spatial modeling estimates the shapes of activation regions, leading to improved activation detection. When a single spatial filter is replaced by a set of spatial filters, the data analysis becomes multivariate. We solve the corresponding multivariate problem by CCA.

2.2. Steerable filters

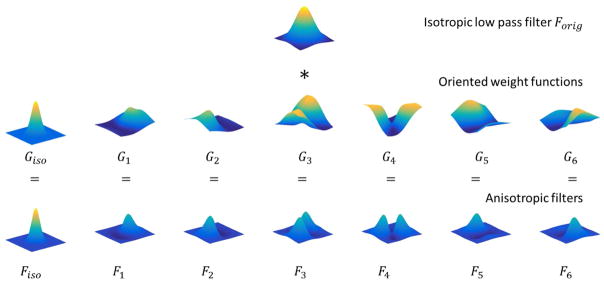
Steerable filtering is an efficient orientation-adaptive method for improving the SNR without significant blurring of the oriented spatial patterns in the images (Kass and Witkin, 1988; Knutsson et al., 1983; Martens, 1989). The 3D steerable filters consist of one isotropic function G_iso(x) and six oriented functions G_i(x). The six oriented functions are defined according to Granlund and Knutsson (2013) by:

$$\begin{gathered} G_i(\mathit{x})=\left(1-G_{\mathit{iso}}(\mathit{x})\right)\left({({\widehat{\mathit{n}}}_i^T\widehat{\mathit{x}})}^2-\frac{1}{6}\right) \\ {\widehat{\mathit{n}}}_1=\left(\begin{array}{c}a\\ 0\\ b\end{array}\right),{\widehat{\mathit{n}}}_2=\left(\begin{array}{c}-a\\ 0\\ b\end{array}\right),{\widehat{\mathit{n}}}_3=\left(\begin{array}{c}b\\ a\\ 0\end{array}\right) \\ {\widehat{\mathit{n}}}_4=\left(\begin{array}{c}b\\ -a\\ 0\end{array}\right),{\widehat{\mathit{n}}}_5=\left(\begin{array}{c}0\\ b\\ a\end{array}\right),{\widehat{\mathit{n}}}_6=\left(\begin{array}{c}0\\ b\\ -a\end{array}\right) \\ a=\frac{2}{\sqrt{10+2\sqrt{5}}},b=\frac{1+\sqrt{5}}{\sqrt{10+2\sqrt{5}}}. \end{gathered}$$ (2)

In Eq.(2) the variable x̂ is the unit vector along x and represents an arbitrary direction in 3D voxel space. G_iso(x) is chosen as a Gaussian function with FWHM equal to half of the Gaussian filter F_orig(x) used in single voxel analysis (Friman et al., 2003). The 3D anisotropic filters are computed by weighting the original filter F_orig(x)according to

$$F_{\mathit{iso}}(\mathit{x})=G_{\mathit{iso}}(\mathit{x})F_{\mathit{orig}}(\mathit{x}),F_i(\mathit{x})=G_i(\mathit{x})F_{\mathit{orig}}(\mathit{x})\text{for}i=1,\dots ,6.$$ (3)

Fig. 1 shows the construction of the set of oriented spatial filters from the Gaussian filter F_orig(x) and the oriented functions F_i. The sum of these seven spatial oriented filters with unit coefficients is equal to the original Gaussian filter F_orig(x), i.e. $F_{\mathit{iso}}(\mathit{x})+{\sum }_{i=1}^6{F}_i(\mathit{x})=F_{\mathit{orig}}(\mathit{x})$. When steerable filters are employed for spatial modeling, seven filtered time series are computed at voxel ξ and time point t by spatially convolving the raw time series Y_un(ξ, t) with F_iso(ξ) and F_i(ξ), i = 1, …, 6,

Figure 1.

Construction of 3D anisotropic spatial filters. A single slice with a fixed z-coordinate (z=0) is shown for the purpose of visualization. The isotropic low pass filter (first row) is the isotropic Gaussian filter. The figures on the second row show the oriented spatial weight functions. The last row shows the constructed steerable filters after element-by-element multiplication of the isotropic low pass filter and the oriented weight functions. The sum of the steerable filters with uniform coefficients is equal to the original isotropic Gaussian filter.

$$[Y_{un}\otimes F_{\mathit{iso}},Y_{un}\otimes F_1,\dots ,Y_{un}\otimes F_6](\mathit{\xi },t),t=1,\dots ,T.$$ (4)

An important feature of steerable filtering is that a filter along any direction can be determined as a linear combination of these basis filters. With these filtered data it is possible to adaptively smooth fMRI volumes and estimate weight coefficients during the CCA analysis.

2.3. 3D local constrained CCA: sf-nonnegCCA and sumCCA

CCA maximizes the correlation between two groups of multivariate random variables. Local CCA methods for fMRI data analysis are a generalization of SV by allowing the incorporation of multiple spatial filters,

$${\sum }_{i=1}^M{\alpha }_i(\mathit{\xi })[F_i(\mathit{\xi })\otimes Y_{un}(\mathit{\xi },t)]={\sum }_{n=1}^N{\beta }_n(\mathit{\xi })x_n(t).$$ (5a)

The functions F_i, i = {1, …, M}, represent the spatial filters modeling the spatial activation pattern in a neighborhood. In the case of SV with Gaussian smoothing, there is only one filter (M = 1) In this case, F₁ is the isotropic Gaussian filter and α₁(ξ) = 1 for all voxels. Once α = (α₁, …, α_M)^T ∈ ℝ^M×1 and β = (β₁, …, β_N)^T ∈ ℝ^N×1 are determined, the F-statistic can be used to construct the activation map. If the combined filter at voxel ξ is defined as $F_{\mathit{comb}}({\mathit{\xi }}^{\prime }\mid \mathit{\xi })={\sum }_{i=1}^M{\alpha }_i(\mathit{\xi })F_i(\mathit{\xi }-{\mathit{\xi }}^{\prime })$, Eq.(5a) can be expressed in the form

$${\sum }_{{\mathit{\xi }}^{\prime }}{F}_{\mathit{comb}}({\mathit{\xi }}^{\prime }\mid \mathit{\xi })Y_{un}({\mathit{\xi }}^{\prime },t)={\sum }_{n=1}^N{\beta }_n(\mathit{\xi })x_n(t).$$ (5b)

Let Y = (y₁, …, y_M) ∈ ℝ^T×M with y_i(ξ, t) = F_i(ξ) ⊗ Y_un(ξ, t) represent the M filtered time series. CCA determines the linear combination vectors α and β for Y and X, respectively, by maximizing the canonical correlation

$$\rho (\mathit{\alpha },\mathit{\beta })=\text{corr}(\mathit{Y}\mathit{\alpha },\mathit{X}\mathit{\beta })=\frac{{\mathit{\alpha }}^{\mathit{T}}{\mathit{Y}}^{\mathit{T}}\mathit{X}\mathit{\beta }}{\sqrt{({\mathit{\alpha }}^{\mathit{T}}{\mathit{Y}}^{\mathit{T}}\mathit{Y}\mathit{\alpha })({\mathit{\beta }}^{\mathit{T}}{\mathit{X}}^{\mathit{T}}\mathit{X}\mathit{\beta })}}$$ (6)

for each local neighborhood. If we define C_XX and C_YY as the sample covariance matrix for X and Y, respectively, and C_YX as the covariance matrix between Y and X, the above equation can be rewritten as

$$\rho (\mathit{\alpha },\mathit{\beta })=\text{corr}(\mathit{Y}\mathit{\alpha },\mathit{X}\mathit{\beta })=\frac{{\mathit{\alpha }}^{\mathit{T}}{\mathit{C}}_{\mathit{YX}}\mathit{\beta }}{\sqrt{({\mathit{\alpha }}^{\mathit{T}}{\mathit{C}}_{\mathit{YY}}\mathit{\alpha })({\mathit{\beta }}^{\mathit{T}}{\mathit{C}}_{\mathit{XX}}\mathit{\beta })}}.$$ (7)

In conventional unconstrained CCA, maximal canonical correlation can be found by setting the partial derivatives with respect to α and β to be zero. The resulting equations can be converted to two standard eigenvalue problems given by

$$\begin{gathered} {\mathit{C}}_{\mathit{YY}}^{-1}{\mathit{C}}_{\mathit{YX}}{\mathit{C}}_{\mathit{XX}}^{-1}{\mathit{C}}_{\mathit{XY}}\mathit{\alpha }={\rho }^2\mathit{\alpha }, \\ {\mathit{C}}_{\mathit{XX}}^{-1}{\mathit{C}}_{\mathit{XY}}{\mathit{C}}_{\mathit{YY}}^{-1}{\mathit{C}}_{\mathit{YX}}\mathit{\beta }={\rho }^2\mathit{\beta }. \end{gathered}$$ (8)

The optimal weights α and β are the eigenvectors corresponding to the largest eigenvalues (ρ²) of above equations.

To improve the specificity of conventional CCA, constraints on the weights of spatial filters are required. For a general case, constrained CCA no longer can be solved as an eigenvalue problem. Iterative algorithms such as BFGS, GRG and AL have been implemented recently to solve the 2D local CCA problem with a general spatial constraint (Zhuang et al., 2017) defined by

$$\{\begin{array}{cc}\text{Objective}\text{function}f(\mathit{\alpha })\text{to}\text{be}\text{minimized}:& -\rho (\mathit{\alpha })=-\frac{{\mathit{\alpha }}^{\mathit{T}}{\mathit{C}}_{\mathit{YX}}\mathit{\beta }}{\sqrt{({\mathit{\alpha }}^{\mathit{T}}{\mathit{C}}_{\mathit{YY}}\mathit{\alpha }){\mathit{\beta }}^{\mathit{T}}{\mathit{C}}_{\mathit{XX}}\mathit{\beta }}}\\ \text{Subject}\text{to}\mathit{c}(\mathit{\alpha }):& {\alpha }_1^p\ge \psi {\sum }_{m=2}^M{\alpha }_m^p,{\alpha }_1\ge 0,\dots ,{\alpha }_M\ge 0.\end{array}$$ (9)

The vector β is a function of α and is given by β(α) = (X^TX)⁻¹X^TYα.

The constraints in Eq. (9) are controlled by two nonnegative parameters p and ψ, which allow the incorporation of the non-negative constraint and the sum constraint as special cases. In 3D sumCCA, the spatial constraint requires that the weight of the center voxel, denoted as α₁, is not less than the sum of the weights of 3 × 3 × 3 neighboring voxels α_m (m ∈ 2, …, M = 27), namely ${\alpha }_1\ge {\sum }_{m=2}^{27}{\alpha }_m$. This condition arises for parameters (p, ψ) = (1, 1). In 3D sf-nonnegCCA, the nonnegative constraint requires that the weights of F_iso and F_i, i = 1, …, 6 as in Eq.(3) are nonnegative, α_iso ≥ 0 and α_i ≥ 0, i = 1, …, 6 (M = 27 in this case). This condition arises for parameters (p, ψ) = (1, 0). However, current algorithms for 2D constrained CCA are computationally too intensive to be applied for the 3D case because α has many more variables in a 3D neighborhood. To solve this problem, we implemented a SQP algorithm (Nocedal and Wright, 2006) for 3D local constrained CCA.

2.4. Sequential Quadratic Programming (SQP) for 3D local CCA

SQP is an iterative nonlinear constrained optimization method, which outperforms many other methods with respect to efficiency, accuracy and percentage of successful solutions (Schittkowski, 1986). In each iteration, SQP optimizes a quadratic approximation of the objective function subject to constraints that have been linearized. There are three main steps in SQP: (a) quadratic programming step to determine the search direction d, (b) a line search and merit function to optimize the step size u, and (c) update of the Hessian matrix H for the next iteration.

To convert the constrained CCA problem in Eq.(9) to a quadratic problem, the gradient g_init and Hessian matrix H_init of the objective function f(α) and the Jacobian matrix A_init of the constraints c(α) are calculated by a finite difference method (Hoffman and Frankel, 2001) at the initialization point α₀. If H_init is indefinite, a modified Cholesky decomposition algorithm (Gill et al., 1981) is applied to transform it to a positive-definite matrix. The search direction d_k and corresponding Lagrangian multiplier λ_new at iteration k are found by active-set quadratic programming (Nocedal and Wright, 2006).

The widely used exact non-smooth merit function, the ℓ−1 merit function ϕ(α_k; μ_k) = f_k + μ_k||c(α_k)||₁, is implemented in the line search process (Pietrzykowski, 1969; Powell, 1978a, b), where the second term is a penalty term and μ_k is a penalty parameter. Since ϕ(α_k; μ_k) is not differentiable at every point due to the use of the ℓ−1 norm function, we compute the directional derivative along the direction d_k (which exists everywhere) instead of the derivative. The directional derivative along d_k is well defined for all α_k and is given by

$$D(\varphi ({\mathit{\alpha }}_k;{\mu }_k);{\mathit{d}}_k)=\nabla f_k^T{\mathit{d}}_k-{\mu }_k{\Vert \mathit{c}({\mathit{\alpha }}_k)\Vert }_1.$$ (10)

Then, in the back-tracking line search process, a step u_kd_k is accepted if the following sufficient decrease condition holds at u_k:

$$\varphi ({\mathit{\alpha }}_k+u_k{\mathit{d}}_k;{\mu }_k)\le \varphi ({\mathit{\alpha }}_k;{\mu }_k)+\eta u_{k}D(\varphi ({\mathit{\alpha }}_k;\mu );{\mathit{d}}_k),$$ (11)

for a given constant η = 0.1. The Hessian matrix H_k+1 is updated by a damped BFGS formula (Powell, 1978b), which keeps the Hessian matrix to be positive-definite. The property of positive definiteness is desired for two reasons: to accelerate convergence and to make the quadratic programming subproblem easier to solve.

A good search direction d_k found by quadratic programming might be rejected during the line search, which is called the Maratos effect. This effect may occur due to an inaccurate linear approximation of the constraints (Maratos, 1978). The Maratos effect can be avoided by using a second-order correction of the linearized constraints, which replaces the linear terms c_i(x_k) + ∇c_i(x_k)^T d with a quadratic approximations by $c_i(x_k)+\nabla c_i{(x_k)}^T\mathit{d}+\frac{1}{2}{\mathit{d}}^T{\nabla }^2{c}_i(x_k)\mathit{d}$. A flow diagram of the line search SQP algorithm is shown in Table 1 and a pseudocode is provided in Appendix A.

Table 1.

Iterative algorithm of the line search sequential quadratic programming (SQP) method.

Initialize α0, λ0, H0, A0, g0. Solve a quadratic objective function with linearized constraints to find search direction dk: Apply simplex method in linear programming to find a feasible starting point dinit for second phase. A second order correction is applied if the Maratos effect occurs. Apply active-set quadratic programming method with initialization dinit to form search direction dk and Lagrangian multiplier λk. Define l-1 merit function and use back-tracking line search to find step length ukdk. Update Hessian matrix by BFGS updating formula. Repeat step 2–4 until convergence

2.5. Steerable filter KCCA (sf-KCCA)

Unlike local CCA methods, sf-KCCA is a global method, which considers whole brain fMRI data simultaneously in the analysis. There are two main challenges to directly apply CCA to whole brain data. The first challenge is limited computer memory. With a voxel size of 2 mm × 2 mm × 2 mm there are about 200,000 voxels in fMRI data. Then, the covariance matrix C_YY within dataset Y has the dimension of 200,000 × 200,000, which requires 160 GB RAM for storage as single-precision numbers. A more severe challenge is that C_YY is a highly singular matrix. Since the temporal dimension of the data is usually much smaller than the spatial dimension, CCA can always perfectly correlate dataset X with Y regardless of the association between them (Song et al., 2015). KCCA, however, is a promising method to avoid these problems. The matrix in KCCA is a kernel matrix instead of the usual covariance matrix and has a size of only T × T.

If Q is defined as the total number of voxels in fMRI data, sf-KCCA projects Q raw time series into a higher dimensional feature space as in Eq.(4) by spatially convolving the voxel time series with F_iso(ξ) and F_i(ξ), i = {1, …, 6}, giving 7Q filtered time series. This step is crucial since it transforms the raw data into new data (filtered voxel time series) that contains the orientation-adaptive property. Then KCCA is applied on the filtered time series Y ∈ ℝ^T×7Q and on the design matrix X to determine the weight coefficient of each time point. The kernel matrices are constructed by K_XX = XX^T and K_YY = YY^T. Since K_YY are linear kernels in the high-dimensional feature space, the solutions vector ω_Y of the KCCA problem can be mapped onto the weight coefficients α in the conventional CCA problem by a linear transformation given by α = Y^Tω_Y and β = X^Tω_X. With the computed weight vectors α we can generate voxel-specific spatial activation maps for any contrast of interest.

KCCA maximizes the correlation function ρ(ω_X, ω_Y) defined as

$$\rho ({\mathit{\omega }}_X,{\mathit{\omega }}_Y)=\frac{{\mathit{\omega }}_X^{\mathit{T}}{\mathit{K}}_{XX}{\mathit{K}}_{YY}{\mathit{\omega }}_Y}{\sqrt{{\mathit{\omega }}_X^{\mathit{T}}{\mathit{K}}_{XX}^2{\mathit{\omega }}_X{\mathit{\omega }}_Y^T{\mathit{K}}_{YY}^2{\mathit{\omega }}_Y}}$$ (12)

(Hardoon et al., 2004). All the relevant signals are now contained in the kernel matrices K_XX and K_YY. As shown in Appendix B, due to the high-dimensional feature space, regularization is required to avoid overfitting. Regularization is imposed by limiting the sum of the squares of the weight vector norms (Shawe-Taylor and Cristianini, 2004). The correlation function ρ(ω_X, ω_Y; γ) for regularized KCCA then becomes

$$\rho ({\mathit{\omega }}_X,{\mathit{\omega }}_Y;\gamma )=\frac{{\mathit{\omega }}_X^{\mathit{T}}{\mathit{K}}_{XX}{\mathit{K}}_{YY}{\mathit{\omega }}_Y}{\sqrt{({\mathit{\omega }}_X^{\mathit{T}}{\mathit{K}}_{XX}^2{\mathit{\omega }}_X+\gamma {\mathit{\omega }}_X^{\mathit{T}}{\mathit{K}}_{XX}{\mathit{\omega }}_X)({\mathit{\omega }}_Y^T{\mathit{K}}_{YY}^2{\mathit{\omega }}_Y+\gamma {\mathit{\omega }}_Y^T{\mathit{K}}_{YY}{\mathit{\omega }}_Y)}},$$ (13)

where γ ∈ (0, ∞) is the regularization parameter. Like conventional CCA, ω_X and ω_Y are the eigenvectors corresponding to the largest eigenvalue ρ² in the following two eigenvalue equations

$$\begin{gathered} {({\mathit{K}}_{XX}+\gamma \mathit{I})}^{-1}{\mathit{K}}_{YY}{({\mathit{K}}_{YY}+\gamma \mathit{I})}^{-1}{\mathit{K}}_{XX}{\mathit{\omega }}_X={\rho }^2{\mathit{\omega }}_X \\ {({\mathit{K}}_{YY}+\gamma \mathit{I})}^{-1}{K}_{XX}{({\mathit{K}}_{XX}+\gamma \mathit{I})}^{-1}{\mathit{K}}_{YY}{\mathit{\omega }}_Y={\rho }^2{\mathit{\omega }}_Y. \end{gathered}$$ (14)

The regularization parameter γ is selected to maximize the correlation difference between active-state data and null data. For null data we chose resting-state data that were collected with the same acquisition parameters for each subject and then wavelet-resampled to destroy intrinsic patterns of correlations (Breakspear et al., 2004; Bullmore et al., 2001). Since γ varies in an infinite interval, we define it as a monotonically increasing function of ε by $\gamma (\epsilon )=\frac{\epsilon }{1-\epsilon }$ and employ a grid search on ε in the unit interval (0, 1) to find the optimal ε_opt and corresponding γ_opt.

Each element in ω_Y provides the weight of each time point. Denote Y_ξ ∈ ℝ^T×7 as the seven filtered time series at voxel ξ, then ${\mathit{\alpha }}_{\xi }={\mathit{Y}}_{\xi }^T{\mathit{\omega }}_Y$ is the corresponding weight vector of the steerable filters, which determines the smoothing direction at voxel ξ. However, in the previous published KCCA methods for fMRI data analysis, fMRI time series are filtered by a fixed (non-adaptive) Gaussian function so that the computed weight vector α has the dimension Q × 1, and α or its z-score value is directly used as a statistic to represent the spatial activation map. In contrast, our method estimates the β_ξ vector and allows the creation of statistical activation maps for any arbitrary contrast matrix C of interest. The β = X^Tω_X ∈ ℝ^N×1 cannot be used since it is not voxel-specific. Instead, the least square algorithm is then used to determine β_ξ by

$$\mathit{arg}{\mathit{min}}_{{\mathit{\beta }}_{\xi }}{\Vert \mathit{X}{\mathit{\beta }}_{\xi }-{\mathit{Y}}_{\xi }{\mathit{\alpha }}_{\xi }\Vert }_2.$$ (15)

The Wilk’s Λ statistic and the F statistic given by Cordes et al. (2012), Friston et al.(1994), and Worsley and Friston (1995) can be computed using

$$\begin{gathered} \mathrm{\Lambda }=\frac{{\mathit{E}}_{\alpha }}{{\mathit{E}}_{\alpha }+{\mathit{H}}_{\alpha }},F=(\frac{1-\mathrm{\Lambda }}{\mathrm{\Lambda }})\frac{v_{{\mathit{E}}_{\alpha }}}{v_{{\mathit{H}}_{\alpha }}}, \\ {E}_{\alpha }={(\mathit{Y}{\mathit{\alpha }}_{\xi }-\mathit{X}{\mathit{\beta }}_{\xi })}^T(\mathit{Y}{\mathit{\alpha }}_{\xi }-\mathit{X}{\mathit{\beta }}_{\xi }), \\ {H}_{\alpha }={(\mathit{C}{\mathit{\beta }}_{\xi })}^T{[\mathit{C}{({\mathit{X}}^T\mathit{X})}^{-1}{\mathit{C}}^T]}^{-1}(\mathit{C}{\mathit{\beta }}_{\xi }), \end{gathered}$$ (16)

where v_Eα and v_Hα are the degrees of freedom of the error matrix E_α and the hypothesis matrix H_α, respectively. The F statistic is used to construct activation maps for all the methods used in this study. Nonparametric methods using wavelet-resampled resting-state data are used to compute the p values of the statistical maps for a given contrast (Breakspear et al., 2004; Bullmore et al., 2001). If the previous KCCA method follows Eq.(15) and Eq.(16) to construct contrast-specific activation map, the map is still the same as in SV with Gaussian smoothing. In addition, KCCA with δ functions is not spatially adaptive and suffers from low SNR. A detailed explanation of this fact is provided in Appendix C.

2.6. Penalized sf-KCCA method (sf-pKCCA)

Regardless of the analysis methods, the combined filter F_comb(ξ′|ξ) in Eq.(5b) should ideally be a spatial low-pass filter to act as a smoothing function of the data, so that the noise in the data is reduced and SNR is increased. Low-pass filters, for example the spatial Gaussian filter, have the property that all elements in the filtering matrix are nonnegative. Steerable filters relax this nonnegativity property to gain spatial adaptability. The combined steerable filter in sf-KCCA is F_comb(ξ′|ξ) = α_iso(ξ)F_iso(ξ − ξ′) + α₁(ξ)F₁(ξ − ξ′) + ··· + α₆(ξ)F₆(ξ − ξ′), which has the same formula as in sf-nonnegCCA. Unlike sf-nonnegCCA requiring α_iso, α₁, …, α₆ ≥ 0, we penalize negative elements of the filters so that the values in combined filters become overall nonnegative. Let us denote the penalty function F̄ = Σ_ξΣ_ξ′F_comb(ξ′|ξ)/Q, where the summations are over all voxel combinations ξ and ξ′. The model can be formulated as

$${max}_{{\mathit{\omega }}_X,{\mathit{\omega }}_Y}{f}_{\mathit{obj}}({\mathit{\omega }}_X,{\mathit{\omega }}_Y;\gamma ,\lambda )=\rho ({\mathit{\omega }}_X,{\mathit{\omega }}_Y;\gamma )+\lambda \overline{F}({\mathit{\omega }}_Y),\lambda \ge 0,$$ (17)

where λ is a fixed penalty parameter, and maximum area under the ROC curve (AUC) is used to determine the optimal λ. For increasing λ the solution of Eq.(17) leads to a penalty function F̄ that is more positive. Note that sf-pKCCA is no longer an eigenvalue problem, nevertheless the Karush-Kuhn-Tucker conditions (see Appendix D) lead to the solution vector ω_X = (K_XX + γI)⁻¹K_YYω_Y up to a scaling factor. Since ω_X is a linear function of ω_Y, the unknown independent variables in f_obj are reduced by a factor of 2 and f_obj = f_obj(ω_Y; γ, λ). Eq.(17) is solved by BFGS, and ∇f_obj is analytically calculated rather than by numerical differentiation to speed up computation.

2.7. SV, SumCCA, sf-nonnegCCA, sf-KCCA and sf-pKCCA

When the spatial Gaussian filter in SV is replaced by a set of oriented filters, for example the spatial δ functions in sumCCA or the steerable filters in sf-nonnegCCA, the analysis becomes multivariate because multiple filtered times series are considered at each voxel location. To show the difference between local CCA and kernel CCA, we used the same spatial steerable filter functions in sf-nonnegCCA, sf-KCCA and sf-pKCCA. The sf-nonnegCCA is solved with nonnegative constraint parameters (p, ψ) = (1, 0) and sumCCA is solved with constraint parameters (p, ψ) = (1, 1), as described previously. Both kernel CCA methods (sf-KCCA, sf-pKCCA) are global approaches and the solution for all voxel is obtained in one step. Table 2 shows a comparison of these different method in terms of spatial filters used, constraints involved, dimensions of dataset Y and number of times the analysis is performed to determine activation maps for the entire brain.

Table 2.

Comparison of SV, sumCCA, sf-nonnegCCA, sf-KCCA and sf-pKCCA.

Methods	Spatial filters	Spatial Constraint	Size of Y matrix	# of Times
SV	A single Gaussian filter	No constraint	t × 1	Q
SumCCA	27 δ -function filters	(p, ψ) = (1, 1)	t × 27	Q
sf-nonnegCCA	7 3D steerable filters	(p, ψ) = (1, 0)	t × 7	Q
sf-KCCA	7 3D steerable filters	No constraint	t × 7Q	1
sf-pKCCA	7 3D steerable filters	Low-pass constraint	t × 7Q	1

Note: The symbol Q represents the total number of voxels in the fMRI data set. # of Times refers to how often the algorithm needs to be performed to obtain a whole brain activation map.

3. DATA APPLICATION

3.1. Software

A MATLAB toolbox implementation of our algorithms (2D and 3D local constrained CCA, sf-KCCA and sf-pKCCA) is available at https://github.com/pipiyang/CCA_GUI.

3.2. Toy example

Spatial activation patterns were generated on a 100 × 100 × 24 voxel grid with voxel size 2mm × 2mm × 2mm. The activation patterns were simulated with varying shapes, sizes and orientations. Gaussian noise was added to the simulated data with an SNR of 0.4, which was close to the SNR of our real fMRI data.

3.3. Realistic simulated data

More realistic simulated data were generated to evaluate the sensitivity and specificity of the different analysis methods (3D sumCCA, sf-nonnegCCA, sf-KCCA, and sf-pKCCA). The simulated data were generated by the following procedure:

1. Determine activation status using real fMRI data: SV was applied on real fMRI data to get a correlation map (Corr_sv) between fMRI data and the design matrix. The voxels with the highest 0.5% correlation values in Corr_sv were labeled as active voxels ξ_act and all other voxels were labeled as inactive voxels ξ_in. Subsets ξ̂_act and ξ̂_in, containing 1000 voxels each, were randomly chosen from ξ_act and ξ_in, respectively.

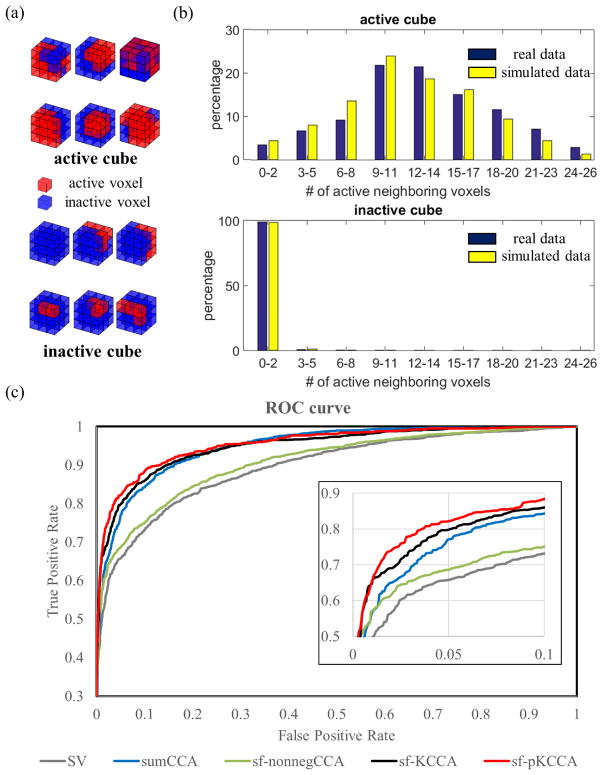
2. Obtain activation patterns from real data: Since local CCA methods require time series from neighboring voxels to determine activation status of the center voxels, the activation patterns of cubes centered at ξ̂_act and ξ̂_in were recorded. The cube size was limited to 3 × 3 × 3 voxels due to high computational cost of 3D sumCCA. The filtering for all the other methods was also confined to the 3 × 3 × 3 cubes to have an equal comparison, and only center voxels were analyzed in the simulation. The distribution of the number of active voxels in the 3×3×3 voxel neighborhood of the 1000 active and 1000 inactive central voxels was similar to the distribution of active voxels in real data.

3. Generate time courses for simulated data: The simulated time courses at active voxels were generated by adding the noise y_noise to the activation signal y_sig with a noise fraction f according to y_act(t) = (1 − f)y_sig(t) + fy_noise(t), and at inactive voxels the simulated time courses are given by y_in = y_noise. The time series for the activation signal (y_sig) was chosen from the real data where the activation status of Corr_sv had a significance of p < 10⁻⁴. For each active voxel in the simulation, y_sig is the randomly assigned real fMRI time course of one of those voxel time series with p < 10⁻⁴. Wavelet resampled resting-state time series were used as the noise signal y_noise and randomly assigned to all voxels.

   Determine the noise ratio f: The noise fraction f was determined by following the steps in Zhuang et al. (2017). We applied SV to simulated data for f from 0 to 1 with a step size of 0.05. The average correlation value with a significance level of p<0.05 (uncorrected), was compared with the average correlation value of the same significance level acquired from real fMRI time series. The noise fraction, f, at which the mean correlation value for simulated data was equal to the correlation value of the real data was chosen as the noise fraction for our simulation, yielding a corresponding $\mathit{SNR}=\frac{1-f}{f}$.

3.4. Data acquisition

FMRI data of 14 subjects (7 aMCI subjects and 7 normal controls) were acquired with Institutional Review Board approval on a 3T GE HDx MRI scanner equipped with an 8-channel head coil. The subjects in the two groups were matched by age, education and right-handedness. Acquisition parameters for the EPI sequence were: TR/TE=2000 ms/30 ms, parallel imaging factor=2, slices=25 (coronal oblique, perpendicular to the long axis of hippocampus), slice thickness/gap = 4.0 mm/1.0 mm, 288 time frames (total scan duration 9.6 min), in plane matrix 96 × 96 voxels, FOV=220 mm. The fMRI volumes were interpolated to have an isotropic voxel size of 2 mm × 2 mm × 2 mm. A conventional structural T1-weighted image (0.43 mm × 0.43 mm × 1 mm) and a standard T2-weighted image (coplanar to the EPI) but with higher resolution (0.43 mm × 0.43 mm × 2.5 mm) were also acquired.

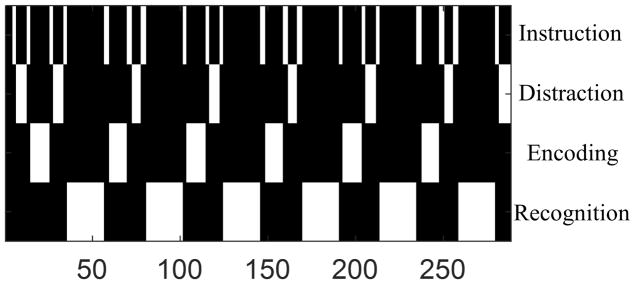
An episodic memory task was performed to obtain fMRI data for each subject. Resting-state data with eyes closed were collected with the same acquisition parameters. The episodic memory task contained visual stimuli which show a novel face paired with an occupation. The entire task consisted of six periods of encoding, distraction, recognition and brief instructions to remind subjects of the task ahead. Specifically, during the encoding task, the subject was asked to memorize 7 faces paired with occupations, displayed in sequential order for a duration of 3s each and 21s in total. A distraction task (duration 11s) then followed each encoding task, where the subject was instructed to press the right or left button as fast as possible when the letter “Y” or “N” randomly appeared on the screen (right button for “Y” and left button for “N”). The recognition task consisted of fourteen stimuli, half novel and half identical to the stimuli seen in the previous encoding task. The subject was instructed to press the right button when the stimulus was previously shown and the left button when the stimulus was new. Scan duration was 9 min 36 s, and 288 time frames were collected. The design matrix X was constructed by convolving the task design consisting of 4 regressors for Instruction, Encoding, Distraction and Recognition (see Fig. 2) with the canonical hemodynamic response function.

Figure 2.

Episodic memory task design. The horizontal axis indicates the time frame.

3.5. Preprocessing

All fMRI data were preprocessed in SPM12 (http://www.fil.ion.ucl.ac.uk/spm/). The first five volumes were discarded to avoid data with unsaturated T1 signal. Each volume was slice-timing corrected and realigned to the first volume. All voxel time series were high-pass filtered by using a discrete cosine basis function regression with cut-off frequency 1/120 Hz (Frackowiak et al., 2004). The spatial filters applied in SV were the Gaussian function G_iso(x) (FWHM = 4 mm), in sumCCA the 27 spatial 3D δ functions, and in sf-nonnegCCA, sf-KCCA and sf-pKCCA the 7 steerable filter functions. The filter function F_iso(x) for the steerable filter set was also a Gaussian filter with half the FWHM as in SV. The same parameters were also used in the analysis of simulated data.

3.6. Data analysis

To validate the SQP algorithm, we compare results with SQP, BFGS and GRG for the local CCA methods using spatial constraints applied to 2D 3 × 3 and 3D 3 × 3 × 3 neighborhoods. The AL method was not used for this comparison because it was slower than GRG and less accurate than BFGS for solving the local CCA problem on 2D 3 × 3 neighborhoods. Computations were run with in-house MATLAB (The Mathworks, Inc., version R2015a) programs on a Dell workstation with 2 Intel Xeon E5-2643 processors. About 200,000 voxels having intensity larger than 10% of the mean intensity for the entire brain data were analyzed and 12 cores were used for parallel computation. First we ran BFGS, GRG and SQP algorithms over the time series for 2D 3 × 3 neighborhoods with family constraint parameters p ∈ {1, 2} and ψ = 1. The parameter ψ was fixed since changing ψ did not influence the complexity of the problem and thus the computational time remained the same. Since the BFGS algorithm needs to solve 2²⁶ unconstrained subproblems for each 3D 3 × 3 × 3 neighborhood, it is not a practical algorithm for 3D local CCA. Only the GRG and the SQP algorithms were used for 3D local CCA with the same constraint models applied to in-plane neighborhoods.

We tested the accuracy of these algorithms and compared the computational time with sf-KCCA. The accuracy of these three algorithms was evaluated in the following way: Treat the maximal correlations at each voxel by all these algorithms as the “true” maximal correlation vector ρ_max. We introduced a parameter r_p that measures the inaccuracy of a method by

$$r_p=\frac{\#of\mathit{voxels}\{{\rho }_{\mathit{max}}-\mathit{tol}\ge \rho \ge {\rho }_p\}}{\#of\mathit{voxels}\{\rho \ge {\rho }_p\}}\text{for}{\rho }_p\le {\rho }_{\mathit{max}}.$$ (18)

In the above equation, ρ is the voxel-wise correlation coefficient, tol is a small tolerance value (for example 0.001 or 0.01) and ρ_p is a correlation-coefficient threshold according to the desired p-value. The null distribution of the correlation coefficient, p-value, and the correlation-coefficient threshold were computed using wavelet-resampled resting-state data.

SV, sumCCA, sf-nonnegCCA, sf-KCCA and sf-pKCCA were applied on the toy example, simulated data, and real fMRI data. Two local CCA methods including sumCCA and sf-nonnegCCA were solved by the SQP algorithm. In the simulation, since both sf-KCCA and sf-pKCCA are global methods, the 7 anisotropically filtered time series of all 2,000 center voxels of dimension T × (2,000 × 7) were the input for KCCA. Then, ROC curves were used to evaluate the performance of the different methods.

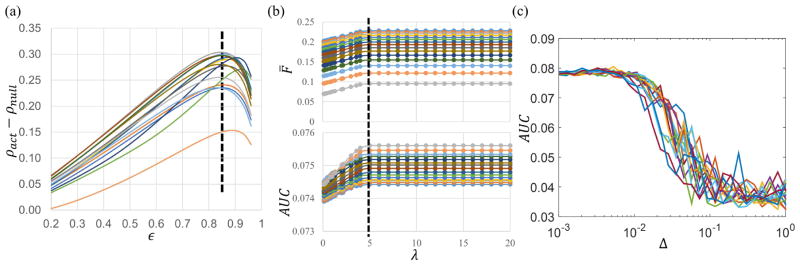
To find the best regularization parameter ε_opt for sf-KCCA, we maximized the difference of ρ(ω_X, ω_Y;γ(ε)) between episodic memory task data and wavelet-resampled resting-state data by a grid-search algorithm. In Fig. 3a we show the correlation difference with ε ranging from 0.2 to 0.96 for all subjects. Since most subjects have maximal differences around ε_opt = 0.85, this value was chosen for the analysis. In sf-pKCCA, both ε and λ need to be optimized. The vector ω_Y was initialized with the value from sf-KCCA with the assumption that the optimal ω_Y, denoted as ${\mathit{\omega }}_Y^{\mathit{opt}}$, should be close to the one without penalty. We applied sf-pKCCA on simulated data with various ε and λ. Fig. 3b shows the curves of the penalty term F̄ and area under the ROC curve (AUC) with a false positive rate (FPR) thresholded at 0.1 versus different values of λ. Only a small portion of the ROC curve with FPR≤0.1 was used because methods in fMRI neuroscience research are most often applied to limit the type I error and identify brain activations with very few false positives (Skudlarski et al., 1999). Each curve in Fig. 3b belongs to a fixed ε value. Since AUC(λ; ε) reaches its maximum at the same λ value (λ = 5) regardless of ε value, the parameter λ can be selected independently from ε and the ε_opt in sf-KCCA can also be used in sf-pKCCA. We found that the curves for AUC and F̄ have similar shape and reach a saturation point at the same value of λ. For larger values of λ there is no further improvement in AUC or F̄. For real data we use the λ having the largest value for F̄ at fixed ε in the analysis. Since BFGS can only find a local extremum depending on the initial point, we also used a perturbation process to determine different initial points that are more distant from the solution computed by sf-KCCA. In detail, the solution vector computed by BFGS, ${\mathit{\omega }}_Y^{\mathit{opt}}$, was perturbed to find a new initial point by

Figure 3.

Parameter selection in sf-KCCA and sf-pKCCA. (a) The figure shows correlation difference between episodic memory task data and wavelet-resampled resting-state data acquired from 7 aMCI subjects and 7 normal controls in sf-KCCA with regularization parameter ε ranging from 0.2 to 0.96. The optimal value for ε is ε_opt = 0.85 (see vertical black dashed line). (b) The penalty term F̄ and area under the ROC curve (AUC) versus penalty parameter λ for the simulated data. Each curve is for a different regularization parameter ε. The vertical dashed line indicates when the maximum plateau is reached for increasing λ. (c) Calculated AUC as a function of the perturbation strength Δ at fixed ε value, as calculated by the perturbation method.

$${\mathit{\omega }}_Y^{\mathit{int}}\leftarrow {\mathit{\omega }}_Y^{\mathit{opt}}+\mathrm{\Delta }\ast ℛ(\mathbf{0},\mathit{I})$$ (19)

where Δ is a perturbation factor and ℛ(0, I) is a random vector from the multivariate normal distribution with mean zero and unit covariance matrix. Then ${\mathit{\omega }}_Y^{\mathit{int}}$ was used as the initial input in BFGS to search for another extremum. The perturbation process was performed 10 times for each given pair of (λ, ε), and the largest AUC value was recorded. A plot of the recorded AUC vs Δ for different ε values is shown in Fig. 3c. This figure shows that the AUC is in general unaffected for small Δ, and as Δ is increased the AUC decreases significantly (not accounting for some convergence randomness of the BFGS algorithm). Thus, optimum AUC can be obtained without perturbation. Once ${\mathit{\omega }}_Y^{\mathit{opt}}$ is found, the activation map can be constructed using the method outlined in section 2.4.

The toy example and the simulated data were used to compute correlation maps for SV, sumCCA, sf-nonnegCCA, sf-KCCA and sf-pKCCA. ROC curves were then used to quantify the performance of these methods. For the real fMRI data, F statistic maps were computed for contrast “encoding – distraction”. To compute the F value at a given p value, the same preprocessing and analysis steps were used on wavelet-resampled resting-state fMRI data. Resampled null data sets from resting-state data were created until the null distribution of the activation maps stabilized. Calculating ROC curves for real data is not straightforward because the ground truth in real data is unknown. However, approximate ROC curves can be determined even for real data (Nandy and Cordes, 2003; Nandy and Cordes, 2004). In the ROC estimation method for real data, the upper bound of the fraction of true positive (FTP) voxels and the fraction of false positive (FFP) voxels are computed as approximated true positive rate and false positive rate, respectively. We also used machine-learning algorithms to determine the group classification accuracy and evaluated the performance of the different described analysis methods. The activation maps for all subjects were co-registered to the corresponding T1 structural brain images using Advanced Normalization Tools (ANTs) software (http://stnava.github.io/ANTs/). Each subject’s high resolution T1 image was input into Freesurfer (Fischl, 2012; Iglesias et al., 2015) to obtain six subject-specific hippocampal subregion masks, including Cornu Ammonis area 1 (CA1), Cornu Ammonis areas 2 to 4 combined with Dentate Gyrus (CA234&DG), Subiculum (SUB), Entorhinal Cortex (ERC), Parahippocampal Cortex (PHC) and Fusiform Gyrus (FUS). We classified subjects as aMCI subjects or NCs using an RBFN classifier (Broomhead and Lowe, 1988; Haykin et al., 2009) and also an SVM method. The hippocampus is known to be involved with episodic memory tasks, and its subregions have different functions in memory formation (Zeineh et al., 2001). For the input feature vector of the classification, we calculated the percentage of activated voxels for all hippocampal subregions at a certain significance level. To calculate the prediction accuracy, the leave-2-out cross-validation method was used. In each leave-2-out validation loop, one subject from each group was left out for testing to balance the size of the two groups. The leave-2-out method resulted in $\left(\begin{array}{c}7\\ 1\end{array}\right)\times \left(\begin{array}{c}7\\ 1\end{array}\right)=49$ different combinations of subjects. Cross-validation was repeated for every combination. The machine learning process was carried out for activation maps thresholded at p values 10⁻³, 10⁻⁴, 10⁻⁵. To test the statistical significance of the prediction accuracy, we used the permutation test to compute the p-value at the 0.05 level non-parametrically. The group indices (aMCI subjects or NCs) were randomly permuted. The exact same analysis was run on every possible random permutation to acquire the null-distribution of the prediction accuracy.

4. RESULTS

Table 3 lists the computational time cost and optimization accuracy of local CCA with a family of constraints on 2D and 3D neighborhoods by employing the BFGS, GRG and SQP optimization algorithms. The computational time of local constrained CCA varies with the algorithms employed and the number of neighboring voxels considered. BFGS is the slowest among these three algorithms. With 2D local CCA, BFGS takes 17.11 hours to analyze one subject (around 200,000 voxels) if the family constraint is (1, 1), and 20.22 hours if a nonlinear constraint (2, 1) is specified. BFGS solves 3D constrained CCA by transforming it into 2²⁶ unconstrained optimization subproblems, instead of 2⁸ as in the 2D neighborhood case. The accumulated time to solve those enormous subproblems makes BFGS infeasible for 3D neighborhoods. GRG is as fast as SQP for 2D local CCA methods with linear constraint, and to analyze one subject takes less than half an hour. However, when nonlinear constraints are considered and the problem is taken to 3D, SQP shows its advantage over GRG. For constraints in 3D neighborhoods, SQP needs 0.45 hours/subject but GRG requires 1.14 hours/subject. It appears that SQP is the most efficient and probably the best method to solve local constrained CCA regardless of the neighborhood involved. However, sf-KCCA and its penalized model are even more efficient and need less than five minutes to analyze one subject.

Table 3.

CPU Time and accuracy of sf-(p)KCCA and local CCA methods with family constraints for 2D and 3D neighborhoods.

	Time (hours)			Accuracy (ρmax − ρ<0.01) (%)
	BFGS	GRG	SQP	BFGS	GRG	SQP
2D (1, 1)	17.11	0.45	0.44	100.00	98.13	98.03
2D (2, 1)	20.22	1.05	0.84	100.00	98.28	98.25
3D (1, 1)	∞	1.14	0.45	NA	99.77*	99.75*
3D (2, 1)	∞	1.89	0.99	NA	99.70*	99.70*
sf-KCCA	<5 min			NA
sf-pKCCA	<5 min			NA

Note: The symbol * means that accuracy is calculated based on the apparent maximal correlation. FMRI data resolution is 110 × 110 × 63 and about 200,000 voxels are analyzed. The estimated time required for BFGS would be more than 1000 years on our computer for a basis set with 27 functions. Thus, BFGS is impractical to solve the 3D local CCA problem.

The most accurate algorithm is the BFGS method and with this method it is always possible to find the maximal canonical correlation value. Thus, BFGS has 100% accuracy as shown in Table 3 and which was also shown by Zhuang et al. (2017). GRG and SQP are slightly less accurate than BFGS but their accuracy is still more than 98.0% for 2D local CCA. Since BFGS is not applicable for 3D local constrained CCA, the accuracy for 3D local CCA was calculated without BFGS and labeled with an asterisk in Table 3. In this case the best solution by running GRG and SQP 100 times with different random initialization points is used as an estimated maximum correlation coefficient to calculate the accuracy of each method. With this definition, GRG and SQP have more than 99.7% accuracy for 3D local CCA.

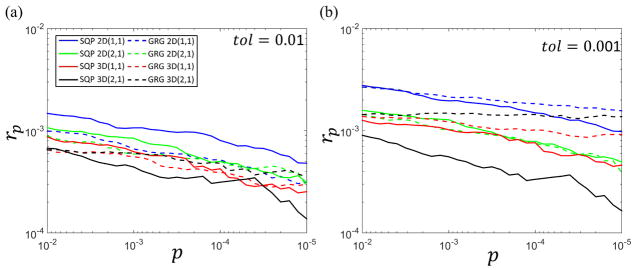
Fig. 4 shows a log-log scatter plot of the inaccuracy r_p as defined in Eq.(18) versus p value for GRG (dash line) and SQP (solid line) with tol set at 0.01 and 0.001. The constraint model 2D (1, 1), 2D (2, 1), 3D (1, 1) and 3D (2, 1) are labelled blue, green, red and black, respectively. The performance of BFGS is not shown because it has 100% accuracy for 2D neighborhoods and could not be carried out for 3D neighborhoods due to heavy computational time requirements. At different p values, the inaccuracy r_p is approximately 0.1%

Figure 4.

Log-log scatter plot of inaccuracy r_p for different methods as a function of the p value. Each color corresponds to a particular local CCA method with family constraints (p, ψ) = (1, 1) and (2, 1) on 2D 3 × 3 and 3D 3 × 3 × 3 neighborhoods: Blue: 2D (1, 1), green: 2D (2, 1), red: 3D (1, 1), and black: 3D (2, 1). The GRG method is indicated by a dashed line and the SQP method by a solid line. The values of tol used in Eq.(17) are (a) 0.01, and (b) 0.001. Data shown are for one representative normal subject. The small value of r_p for all methods indicates that both SQP and GRG are accurate for 2D and 3D constrained CCA.

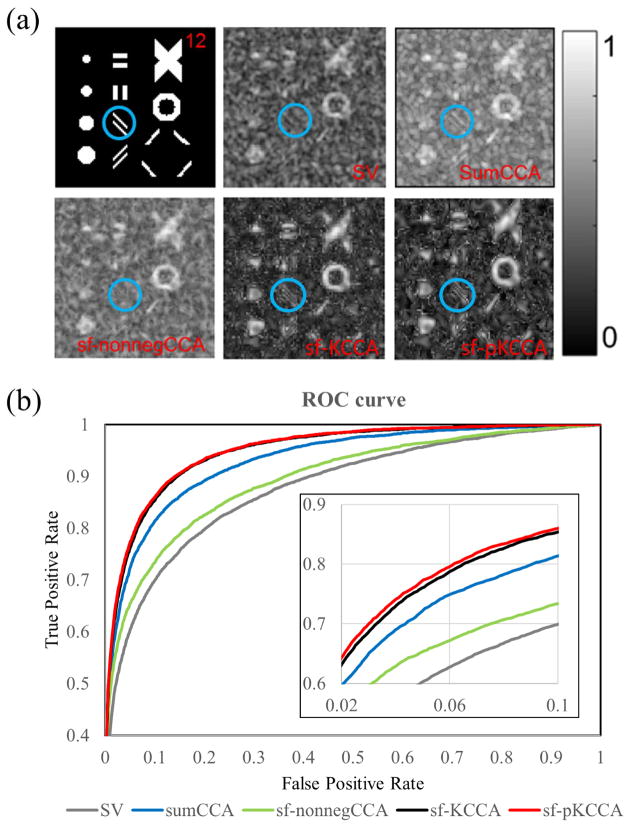
Fig. 5 presents the activation patterns and performance of these four methods on a toy example. Fig. 5a shows the activation patterns with various orientations, sizes and shapes and the correlation maps produced from SV, sum-CCA, nonneg-stCCA, sf-KCCA and sf-pKCCA at slice 12. As can be seen, isotropic Gaussian smoothing blurred the edges of the activated regions in the SV analysis. The activation pattern inside the blue circle is completely eliminated in SV and sf-nonnegCCA. The mean correlation differences between active regions and inactive regions ρ̄_act − ρ̄_inact from SV, sum-CCA, nonneg-stCCA, sf-KCCA and sf-pKCCA are 0.083 ± 0.0017, 0.090 ± 0.0013, 0.087 ± 0.0014, 0.119 ± 0.0015 and 0.119 ± 0.0007, respectively. Since sf-KCCA and sf-pKCCA have largest difference, they have sharper contrast between active regions and inactive regions than all other methods. In Fig. 5b, ROC curves are calculated to evaluate the performance of these analysis methods. The AUC values with a false positive rate (FPR) <0.1 for SV, sumCCA, sf-nonnegCCA, sf-KCCA and sf-pKCCA were 0.0571, 0.0681, 0.0623, 0.0720 and 0.0729, respectively. The smaller standard deviation of ρ̄_act − ρ̄_inact in the sf-pKCCA method may explain why it performs better than sf-KCCA.

Figure 5.

Activation patterns and performance of different methods for a toy example. (a) Artificial activation patterns of toy example at slice 12 and correlation map produced by SV, sumCCA, sf-nonnegCCA, sf-KCCA and sf-pKCCA. Note that blue encircled parallel lines are only recovered by sumCCA, sf-pKCCA and sf-pKCCA. (b) ROC curves for all analysis methods. Note that the AUC curve for sf-pKCCA is always larger than sf-KCCA at any given False Positive Rate.

Six active blocks and six inactive blocks obtained from real fMRI data, which were typical to construct spatial patterns in the simulation, are shown in Fig. 6a. The distribution of the number of active voxels around active and inactive center voxels in the simulated and real data are shown as histogram plots in Fig. 6b. Note that the distributions of active and inactive voxels in the simulation is consistent with the distributions in real data. For simulated data, sf-pKCCA has the best performance among all methods considered in this project. Please see the corresponding ROC curves in Fig. 6c. The calculated AUC values for FPR<0.1 for SV, sumCCA, sf-nonnegCCA, sf-KCCA and sf-pKCCA were 0.0646, 0.0729, 0.0682, 0.0768 and 0.0789, respectively. While the AUC difference between sf-KCCA and sf-pKCCA is small, sf-pKCCA consistently improves AUC by 1%~3% when performing simulations multiple times.

Figure 6.

Performance of different analysis methods for simulated data. (a) Examples of 3 × 3 × 3 voxel cubes obtained from real fMRI data; (b) the distribution of number of active neighboring voxels around active and inactive center voxels; (c) ROC curves for different analysis methods.

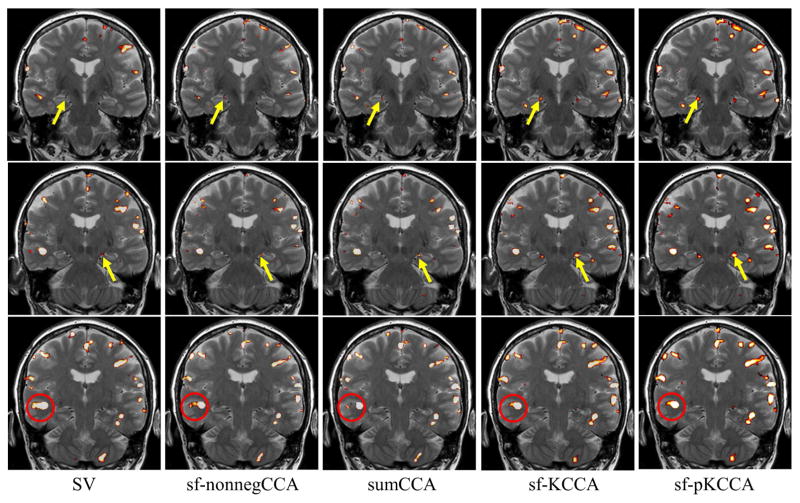
The same analysis methods were also applied to the episodic memory task fMRI data. We computed F statistic maps for the contrast “encoding – distraction” for each method. Fig. 7 presents the F statistic maps at p < 10⁻⁴ from left to right for SV, sumCCA, sf-nonnegCCA sf-KCCA and sf-pKCCA. The sf-KCCA method and its penalized version produce similar activation maps. Our main interest is the detection of memory activation in the medial temporal lobes (MTL) (see area pointed by yellow arrow in Fig. 7), particularly at the hippocampus. Due to the small size, the hippocampal activations are relatively weak. The activation in MTL is barely recognized in the activation map by SV. Local CCA methods and sf-(p)KCCA methods can clearly show activation in MTL. The sf-(p)KCCA methods detected the strongest activation pattern. As shown in the area encircled in red in Fig. 7, both sf-nonnegCCA and sf-(p)KCCA activation pattern are following the spatial contour of gray matter without significant blurring, which is not the case for the SV method where a strong smoothing artifact is observed. Among these CCA methods (sumCCA, sf-nonnegCCA and sf-(p)KCCA), the sf-nonnegCCA method shows a stronger smoothing artifact than the other two methods.

Figure 7.

Activation maps for contrast “encoding - distraction” at p value 10⁻⁴. Results are shown at three different slices (top to bottom) for different methods (left to right). Activation maps are shown as F statistical maps for SV, sf-nonnegCCA, sumCCA, sf-KCCA and sf-pKCCA. Yellow arrows point to the hippocampal region. The activation map for SV shows some blurring of activation patterns into white matter or CSF regions, whereas for the other methods spatial blurring is reduced (compare activations in red circle).

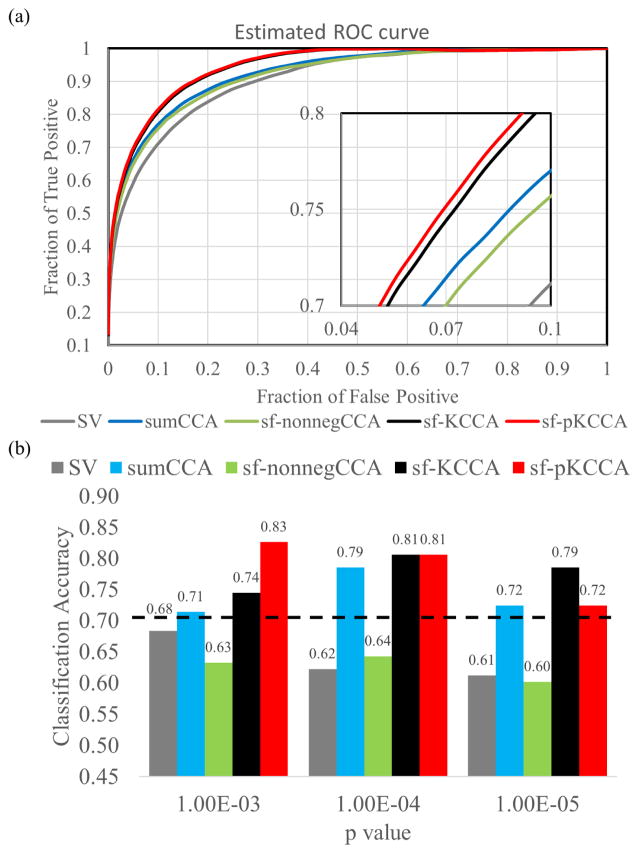
By applying the ROC estimation method to real fMRI data, ROC curves for different analysis methods were computed (see Fig. 8a). The performance for the different methods was consistent with results obtained from the toy example and the simulated data. Fig. 8b shows the classification accuracy of the RBFN classifier at p value 10⁻³, 10⁻⁴ and 10⁻⁵. The maximum prediction accuracies computed for SV (gray bars), sumCCA (blue bars), sf-nonnegCCA (green bars), sf-KCCA (black bars) and sf-pKCCA (red bars) were 68.37%, 78.57%, 64.29%, 80.61% and 82.65%, respectively. The sf-pKCCA and sf-pKCCA methods outperform SV and local CCA methods in terms of prediction accuracy. The black dashed line indicates the 95^th percentile of the prediction accuracy for the null distribution by performing a permutation test. We obtained a similar plot for the SVM classifier which is not shown explicitly in Fig. 8b to avoid redundancy. The sf-pKCCA and sf-KCCA methods also outperformed all the other methods using SVM with prediction accuracy 79.59% and 78.57%, respectively.

Figure 8.

Estimated ROC curves and prediction accuracy using RBFN machine learning classifier for real fMRI data.

(a) Estimated ROC curves for real fMRI data. (b) Classification accuracy between aMCI subjects and NCs based on activation maps from 5 analysis methods (SV: gray bar; sf-nonnegCCA: green bar; sumCCA: blue bar; sf-KCCA: black bar; sf-pKCCA: red bar) at different p values. By using the leave-2-out cross validation method, a radial basis function network (RBFN) machine-learning technique was used to determine the prediction accuracy using activation maps thresholded at p values of {10⁻³, 10⁻⁴ and 10⁻⁵}. The black dashed line is the prediction accuracy corresponding to the 95^th percentile of the null distribution.

5. DISCUSSION

In this study, we have extended 2D local constrained CCA (e.g. (sf-nonnegCCA and sumCCA) to 3D by solving it with the SQP algorithm, and proposed a global kernel variant of CCA method (sf-KCCA and sf-pKCCA) for adaptive analysis of fMRI data. SQP is shown to be more efficient than BFGS and GRG algorithms in solving the local CCA problem with linear or nonlinear constraints for 2D or 3D neighborhoods, especially when more neighbors are considered or nonlinear constraints are applied. Also, SQP has comparable accuracy with GRG. Compared to SV and local CCA methods, the global methods have the best performance in terms of AUC in the toy example and the simulation. From the F statistic maps produced from real fMRI data with contrast “encoding – distraction”, sf-KCCA and sf-pKCCA are superior in detecting small-region activations than local CCA methods. The detected activation patterns did not blur into white matter regions and followed the shape of gray matter cortex. Since there is no ground truth to construct conventional ROC curves for real fMRI data, we estimated ROC curves from real data, and also used machine-learning algorithms to perform group classification based on the activation maps. Both simulated and real fMRI data consistently showed that the sf-KCCA and sf-pKCCA methods are superior to local CCA methods and that sf-pKCCA is slightly better than sf-KCCA.

5.1. SQP validation

We have validated the SQP algorithm in solving the local CCA problem by comparing it with previous proposed algorithms including BFGS and GRG. Unlike BFGS which converts constrained CCA to many convex unconstrained subproblems, both SQP and GRG tackle the constrained optimization problem directly. However, SQP is more efficient when more spatial basis functions are considered or nonlinear constraints are used. In each iteration, SQP only deals with active constraints while GRG updates the gradient of all constraints in each iteration, which involves expensive inverse matrix operations. While GRG and SQP appear to be less accurate than BFGS, Fig. 4 shows that the proportion of voxels having inaccurate correlation value as defined by Eq.(18) is about 0.1%. This small value indicates that the inaccuracy of GRG and SQP have negligible influence on the precision to detect activation. Thus, SQP is a reliable and efficient algorithm to solve the local constrained CCA problem.

5.2. Performance comparison for a toy example and for simulated data

The activation map using the SV method showed a strong smoothing artifact that eliminated small-size activation patterns. Because fMRI volumes are usually smoothed by isotropic Gaussian filtering in a preprocessing step, a small active region may be falsely declared as inactive. Though the sf-nonnegCCA method can adaptively filter fMRI volumes and recover the activation patterns better than the SV method, small oriented active patterns in the blue circle in Fig. 5a still cannot be detected. Compared with SV and sf-nonnegCCA, the sumCCA method detects activation patterns more precisely, even for small patterns in the blue circle. However, since the data Y contain the time series of 27 voxels, sumCCA still has many degrees of freedom in finding spatial filter weights which may lead to low specificity. Of all methods considered in this study, sf-KCCA and sf-pKCCA show best performance in obtaining accurate activation maps.

5.3. Performance comparison for real fMRI data

Since BOLD fMRI signal is associated with increased capillary flow near neural firing events, activated voxels should be detected only in gray matter (Logothetis and Wandell, 2004). Using adaptive spatial basis functions, spatial blurring artifacts are reduced in multivariate methods and activations are mostly found in gray matter regions. In sumCCA, the spatial filters are δ functions where each function has an effective width of 1 voxel, which makes it possible that a single isolated voxel may be detected as active. Previous studies have shown that the MTL plays a critical role in episodic memory tasks and different subregions of the hippocampus are involved in encoding and retrieving memory information (Eichenbaum et al., 2007; Squire et al., 2004; Zeineh et al., 2001). For example, using a task consisting of a sequence of pictures shows more activation in parahippocampal gyrus and fusiform gyrus when the pictures are novel and were presented for the first time. With each repetition of the same picture, activation reduces substantially (repetition suppression). During name retrieval, only the subiculum is active and the fusiform is active regardless of encoding or retrieval. In our study, we are interested in detecting memory activation in subjects with amnestic MCI. It is known that the memory circuit involving the hippocampus and nearby region in the MTL are mostly affected in amnestic MCI (Petersen et al., 2001). Using memory activation maps for MTL subregions could potentially be used to classify a subject as aMCI or NC solely based on the fMRI activation. The sf-KCCA and sf-pKCCA methods have the highest prediction accuracy to distinguish the 2 groups using MTL activation maps.

5.4. Local and global methods

Both the kernel analysis method and the type of spatial basis functions implemented contribute to the superior performance of sf-KCCA. While the same spatial filtering basis functions were used in sf-nonnegCCA and sf-KCCA, the improved performance of sf-KCCA compared to sf-nonnegCCA indicates that the kernel method is important. The use of steerable filter functions leads to further improvement of the kernel method because it allows orientation-adaptive spatial modeling of activation patterns. As explained in Appendix C, if the steerable filters are replaced by a fixed Gaussian kernel with equivalent FWHM, KCCA will show spatial blurring artifacts in activation maps like the SV method. If the steerable filters in KCCA are replaced by spatial δ functions as in sumCCA, it leads to the same activation map as in SV without spatial filtering. To the best of our knowledge, this is the first study to implement spatial adaptability in KCCA for fMRI analysis.

Both local and global CCA methods have shown improved performance compared to SV, primarily because spatially adaptive filters are used in KCCA and local CCA methods (Borga and Rydell, 2007). However, sf-(p)KCCA differentiate itself from local CCA methods in several aspects:

1. Intrinsic difference: Local CCA methods only use local neighboring information and are performed over each voxel while the proposed KCCA method considers the whole brain time series simultaneously, and the filtering orientations for all voxels are estimated in a single run.

2. Computational complexity: Local CCA methods are computationally intensive since the iteration algorithm (e.g. SQP) is performed many times. The sf-KCCA method does not have spatial constraints and can be solved as a single eigenvalue problem. Although sf-pKCCA has added a penalty term to emphasize the spatial low-pass property and is no longer a standard eigenvalue problem, it still can be solved without considerable time cost as we have shown.

3. Parameter optimization: The optimal regularization parameter in sf-KCCA can be computed by maximizing the difference in activation maps using null data and activation data using a grid search algorithm. Since the optimal penalty parameter in sf-pKCCA is independent of the regularization parameter, a 2D grid search algorithm is not required to optimize these two parameters. Instead, the penalty parameter can be determined by a separate 1D grid search algorithm with a fixed regularization parameter. This process does not increase the time cost significantly. While local CCA methods gain their power by using spatial constraints, it is still unclear which spatial constraints are optimal for each neighborhood.

4. Rotational invariance: The sf-nonnegCCA does not provide rotationally invariant detection of activated regions because of the nonnegativity constraint (Rydell et al., 2006). The sf-KCCA method, however, is rotationally invariant because the coefficients of filtered time series are free of any constraint.

5.6. Other non-fMRI applications of CCA and KCCA

In other applications, CCA and KCCA were implemented to preserve local information content. For example, Noh and de Sa (2013) applied CCA with local temporal common spatial patterns to take temporally local variances into consideration. Sun and Chen (2007) incorporated local neighboring information into CCA and applied it to data visualization and pose estimation. Samarov et al. (2011) used indefinite KCCA with “local kernel” function having varying bandwidth to exploit group structure for virtual drug screening.

5.7. Limitations and further study

While an efficient and accurate SQP algorithm is proposed to solve the local constrained CCA problem, how to optimally specify constraints for each local neighborhood remains unknown. A fixed sum constraint is applied in sumCCA and a nonnegative constraint is applied in sf-nonnegCCA for all neighborhoods. Similar to adaptive spatial modeling, an adaptive constraint model may further improve the precision of fMRI activation detection. In our study, sf-KCCA was applied on the whole brain time series simultaneously to construct activation maps. Certainly, it can also be applied region by region. For example, sf-KCCA can be applied on parcellated functionally distinct regions based on the AAL atlas (Tzourio-Mazoyer et al., 2002). Applying sf-KCCA over each region instead of the entire brain is desired when a region-specific hemodynamic response function of the BOLD signal is critical in a study. When analyzing each region independently, a region-specific regularization parameter is required because all regions have the same degrees of freedom as the number of time points while the dimension of feature space is proportional to the number of voxels. In such a case, the computational time increases linearly with the number of regions specified.

In previous KCCA fMRI studies (Bießmann et al., 2009; Blaschko et al., 2011; Hardoon et al., 2007), a linear kernel was used. For sf-KCCA, we also use a linear kernel because nonlinear kernels generally cannot be used to compute voxel-specific activation maps as we argue in the following: Let us denote Y_t(q), q = {1, … Q}, as the fMRI signal at time point t and voxel q. The Gaussian kernel $k_{\sigma }\left({\mathit{Y}}_{t_1},{\mathit{Y}}_{t_2}\right)=exp(-\frac{{\Vert {\mathit{Y}}_{t_1}-{\mathit{Y}}_{t_2}\Vert }^2}{2{\sigma }^2})$, exponential kernel $k_{\sigma }\left({\mathit{Y}}_{t_1},{\mathit{Y}}_{t_2}\right)=exp(-\frac{\Vert {\mathit{Y}}_{t_1}-{\mathit{Y}}_{t_2}\Vert }{2{\sigma }^2})$ and hyperbolic tangent kernel $k\left({\mathit{Y}}_{t_1},{\mathit{Y}}_{t_2}\right)=tanh(a{\mathit{Y}}_{t_1}^T{\mathit{Y}}_{t_2}+b)$ have an infinite-dimensional feature space. Hence, the weight vector α is also infinite-dimensional. The polynomial kernel $k_d\left({\mathit{Y}}_{t_1},{\mathit{Y}}_{t_2}\right)={\left(a{\mathit{Y}}_{t_1}^T{\mathit{Y}}_{t_2}+b\right)}^d$ and the power kernel k(Y_t1, Y_t2) = −〈Y_t1, Y_t2 〉^d have embedded features that arise as combinations from multiple voxels when d ≥ 2. For example, the power kernel for d = 2 has the feature mapping $\mathit{\varphi }({\mathit{Y}}_t)=(\dots ,{\mathit{Y}}_t^2(q_1),\dots ,{\mathit{Y}}_t^2(q_2),\dots ,{\mathit{Y}}_t(q_1){\mathit{Y}}_t(q_2),\dots ,{\mathit{Y}}_t(q_2){\mathit{Y}}_t(q_1),\dots )$ and has contribution Y_t(q₁)Y_t(q₂) from the two voxels q₁, q₂ and thus cannot be assigned to a single voxel. This is not the case for the linear kernel because each feature in the mapping ϕ(Y_t) = (…, Y_t(q), …) can be assigned to a unique voxel. To compute an activation map by KCCA, the kernel must have a finite-dimensional feature space and each feature must be uniquely associated to a single voxel. However, it is still an open question which nonlinear kernel may be used to compute activation maps in fMRI data analysis.

6. CONCLUSION

In this study, the 2D local constrained CCA problem was extended to 3D for fMRI data analysis and solved with an efficient SQP algorithm. Different algorithms for local constrained CCA were evaluated and the line search SQP algorithm was found to be the most efficient for a general family of local constraints. In addition, a 3D global spatially-adaptive KCCA method (sf-KCCA) and its penalized model (sf-pKCCA) were proposed, which can produce contrast-specific activation maps. All analysis methods were applied to both simulated and real fMRI data. The global kernel methods (sf-KCCA and sf-pKCCA) outperformed local CCA methods and univariate methods in detecting brain activation, especially in small regions such as the hippocampus and its subfields. Among the two global kernel methods, the penalized kernel method (sf-pKCCA) showed slightly improved performance over sf-KCCA in detecting brain activations at a given specificity in simulated and real data. Furthermore, prediction accuracy to classify the two subject groups was also slightly improved by introducing penalty using sf-pKCCA.

APPENDIX A

The pseudo code of the line search sequential quadratic programming (SQP) method is shown below. The SQP method can be applied to solve the nonlinear constrained optimization problem in CCA with family constraints for 2D and 3D neighborhoods or by using spatially oriented filter functions. A second order correction is omitted for simplicity. Parameter θ_k ∈ (0,1] produces a matrix that interpolates the current approximation of the Hessian matrix H_k and the one computed by the unmodified BFGS formula. The choice of θ_k ensures positive definiteness of the updated Hessian matrix.

Initialization

Set η, α0, λ0, k ← 1

Use finite difference method to calculate the gradient ginit, Hessian matrix Hinit of objective function and Jacobian matrix of all constraints Ainit

If Hinit is indefinite, modified Cholesky algorithm is applied to transform Hinit to be positive-definite, Hinit = mchol(Hinit).

αk ← α0, λk ← λ0, Hk ← Hinit, Ak ← Ainit, gk ← ginit

Repeat until convergence

$\mathbf{Quadratic}\mathbf{Programming}\{\begin{array}{c}{min}_{\mathit{d}}{\mathit{d}}^T{\mathit{H}}_k\mathit{d}+{\mathit{g}}_k^T\mathit{d}\\ {\mathit{A}}_k^{(i)}\mathit{d}=b_i,i\in \text{equality}\text{constraints}E\\ {\mathit{A}}_k^{(i)}\mathit{d}\le b_i,i\in \text{inequality}\text{constraints}I\end{array}$

First phase: Convert inequality constraints I to equality constraints by adding slack variables z on the left side of constraints and revise the Jacobian matrix Ak correspondingly as $A_k^{\mathit{ext}}$ to include z as extra independent variables besides d. Solve a linear programming problem $\{\begin{array}{c}{min}_{(\mathit{d},\mathit{z})}{\sum }_i{z}_i\\ {\mathit{A}}_k^{\mathit{ext}}\left(\begin{array}{c}\mathit{d}\\ \mathit{z}\end{array}\right)=\mathit{b},\mathit{z}\ge 0\end{array}$ by the simplex method to find a feasible starting point dinit for the second phase.

Second phase: Active-set quadratic programming method is applied to form search direction dk and corresponding multiplier λk with initialization dinit.

Line search and merit function

Define the l-1 merit function (αk; μk) = f(αk) + μk||c(αk)||1. Then, the directional derivative of ϕ(αk; μk) is D(ϕ(αk; μk);d) = gTd − μk||c(αk)||1

Set α ← 1, newpoint ← false, ${\mu }_k\leftarrow max(\frac{1.05\times \left({\mathit{g}}_k^T{\mathit{d}}_k+\frac{{\mathit{d}}_k^T{\mathit{H}}_k{\mathit{d}}_k}{2}\right)}{(1-\rho ){\mid \mathit{c}({\mathit{x}}_k)\mid }_1},0)$

while ϕ(xk + ukdk;μk) > ϕ(xk;μk) + ηukD(ϕ(xk;μk);dk)

Reset uk ← τuk

end (while)

Set αk+1 ← αk + ukdk and λk+1 ← λk + uk(λnew − λk)

Evaluate fk+1, gk+1, ck+1, Ak+1

Updating the Hessian matrix

Update Hk+1 by using damped BFGS given by $\{\begin{array}{c}{\mathit{H}}_{k+1}={\mathit{H}}_k-\frac{{\mathit{H}}_k{\mathit{s}}_k{\mathit{s}}_k^T{\mathit{H}}_k}{{\mathit{s}}_k^T{\mathit{H}}_k{\mathit{s}}_k}+\frac{{\mathit{r}}_k{\mathit{r}}_k^T}{{\mathit{s}}_k^T{\mathit{r}}_k}\\ {\mathit{r}}_k={\theta }_k{\mathit{y}}_k+(1-{\theta }_k){\mathit{H}}_k{\mathit{s}}_k\\ {\theta }_k=\{\begin{array}{cc}1& \text{if}{\mathit{s}}_k^T\ge 0.2{\mathit{s}}_k^T{\mathit{H}}_k{\mathit{s}}_k\\ 0.8{\mathit{s}}_k^T{\mathit{H}}_k{\mathit{s}}_k/({\mathit{s}}_k^T{\mathit{H}}_k{\mathit{s}}_k-{\mathit{s}}_k^T{\mathit{y}}_k)& \text{if}{\mathit{s}}_k^T<0.25{\mathit{s}}_k^T{\mathit{H}}_k{\mathit{s}}_k\end{array}\\ {\mathit{s}}_k={\mathit{\alpha }}_{k+1}-{\mathit{\alpha }}_k\\ {\mathit{y}}_k=({\mathit{g}}_{k+1}+{\mathit{A}}_{k+1}^T{\mathit{\lambda }}_{k+1})-({\mathit{g}}_k+{\mathit{A}}_k^T{\mathit{\lambda }}_{k+1})\end{array}$

end (repeat)

APPENDIX B

The correlation function ρ(ω_X, ω_Y) in kernel CCA without regularization is

$$\rho ({\mathit{\omega }}_X,{\mathit{\omega }}_Y)=\frac{{\mathit{\omega }}_X^{\mathit{T}}{\mathit{K}}_{XX}{\mathit{K}}_{YY}{\mathit{\omega }}_Y}{\sqrt{{\mathit{\omega }}_X^T{\mathit{K}}_{XX}^2{\mathit{\omega }}_X{\mathit{\omega }}_Y^T{\mathit{K}}_{YY}^2{\mathit{\omega }}_Y}}.$$ (B1)

By setting the partial derivatives of Eq.(B1) with respect to ω_X and ω_Y to zero, we obtain two equations

$$\begin{gathered} {\mathit{K}}_{XX}{\mathit{K}}_{YY}{\mathit{\omega }}_Y-\frac{{\mathit{\omega }}_X^{\mathit{T}}{\mathit{K}}_{XX}{\mathit{K}}_{YY}{\mathit{\omega }}_Y{\mathit{K}}_{XX}^2{\mathit{\omega }}_X}{{\mathit{\omega }}_X^{\mathit{T}}{K}_{XX}^2{\mathit{\omega }}_X}=0, \\ {\mathit{K}}_{YY}{\mathit{K}}_{XX}{\mathit{\omega }}_X-\frac{{\mathit{\omega }}_X^{\mathit{T}}{\mathit{K}}_{XX}{\mathit{K}}_{YY}{\mathit{\omega }}_Y{\mathit{K}}_{YY}^2{\mathit{\omega }}_Y}{{\mathit{\omega }}_Y^T{\mathit{K}}_{YY}^2{\mathit{\omega }}_Y}=0. \end{gathered}$$ (B2)

If the kernel matrix K_YY is invertible, from the second equation in Eq.(B2) we can derive

$${\mathit{\omega }}_Y=\frac{{\mathit{\omega }}_X^{\mathit{T}}{\mathit{K}}_{XX}{\mathit{K}}_{YY}{\mathit{\omega }}_Y}{{\rho }^2{\mathit{\omega }}_X^{\mathit{T}}{\mathit{K}}_{XX}^2{\mathit{\omega }}_X}{\mathit{K}}_{YY}^{-1}{\mathit{K}}_{XX}{\mathit{\omega }}_X.$$ (B3)

Then by substituting ω_Y in the first equation of Eq.(B2), we can obtain a simple equation

$${\mathit{K}}_{XX}^2{\mathit{\omega }}_X-{\rho }^2{\mathit{K}}_{XX}^2{\mathit{\omega }}_X=0.$$ (B4)

For any ω_X this equation holds with ρ = 1, which means we can find perfect correlation between arbitrary projection in the feature space of X and the projection as Eq.(B3) in feature space of Y. Therefore, perfect correlation can be found even though these two representations are not correlated.

APPENDIX C

KCCA with fixed spatial Gaussian smoothing

The weight vector α = Y^Tω_Y computed from previous published KCCA methods, where the data were spatially smoothed by a fixed Gaussian filter in a preprocessing step, has the dimension Q × 1. For each voxel ξ, α_ξ is a scalar. Following the steps in Eq.(14) and Eq.(15) to construct voxel-specific Λ or F maps, the β_ξ is the same as in SV with Gaussian smoothing up to a scaling factor (in SV, α_ξ = 1 in Eq.(14)). Since the scaling factor does not affect the significance of the determined statistical map, the resulting activation map is identical to SV with Gaussian smoothing.

KCCA with spatial δ functions

While both steerable filters and δ functions were used to obtain spatial adaptability in local CCA methods, KCCA with spatial δ functions does not lead to adaptive filtering as we will point out in the following: If one δ function is used for each voxel for filtering, the input dataset Y in KCCA constitutes the whole-brain raw time series and has dimension T × Q Following the same logic in KCCA with Gaussian spatial smoothing, the Λ or F activation map would be identical to the map for SV analysis with one single δ filter function. Therefore, KCCA with one spatial δ filter function is not adaptive and suffers from low SNR. In 3D sumCCA, 27 spatial δ functions are used for each center voxel and each δ function has nonzero value at only one voxel within the 3 × 3 × 3 neighborhood. Then the input time series for each voxel are the 27 raw time series from the 3 × 3 × 3 cube. If this filtering scheme is applied in KCCA, the input dataset Y is expanded to dimension T × 27Q by simply repeating the original time series 27 times. This process does not produce any useful or additional information because each time series is only repeated multiple times while remaining unchanged by the filter functions.

APPENDIX D

The penalized sf-KCCA can be written in a Lagrangian form by

$$L({\mathit{\omega }}_X,{\mathit{\omega }}_Y;{\lambda }_X,{\lambda }_Y,\lambda ,\gamma )={\mathit{\omega }}_X^T{\mathit{K}}_{XX}^T{\mathit{K}}_{YY}{\mathit{\omega }}_Y+\frac{{\lambda }_X}{2}({\mathit{\omega }}_X^T({\mathit{K}}_{XX}^2+\gamma {\mathit{K}}_{XX}){\mathit{\omega }}_X-1)+\frac{{\lambda }_Y}{2}({\mathit{\omega }}_Y^T({\mathit{K}}_{YY}^2+\gamma {\mathit{K}}_{YY}){\mathit{\omega }}_Y-1)+\lambda \overline{F}({\mathit{\omega }}_Y).$$ (C1)

Since F̄ only depends on ω_Y, $\frac{\partial \overline{F}}{\partial {\mathit{\omega }}_X}=0$. The Karush-Kuhn-Tucker conditions of L over ω_X, ω_Y, λ_X, λ_Y are

$$\begin{gathered} \frac{\partial L}{\partial {\mathit{\omega }}_X}={\mathit{K}}_{XX}^T{\mathit{K}}_{YY}{\mathit{\omega }}_Y+{\lambda }_X({\mathit{K}}_{XX}^2+\gamma {\mathit{K}}_{XX}){\mathit{\omega }}_X=0, \\ \frac{\partial L}{\partial {\mathit{\omega }}_Y}={\mathit{K}}_{YY}^T{\mathit{K}}_{XX}{\mathit{\omega }}_X+{\lambda }_Y({\mathit{K}}_{YY}^2+\gamma {\mathit{K}}_{YY}){\mathit{\omega }}_Y+\lambda \frac{\partial \overline{F}}{\partial {\mathit{\omega }}_Y}=0, \\ \frac{\partial L}{\partial {\lambda }_X}=\frac{{\mathit{\omega }}_X^T({\mathit{K}}_{XX}^2+\gamma {\mathit{K}}_{XX}){\mathit{\omega }}_X-1}{2}=0, \\ \frac{\partial L}{\partial {\lambda }_Y}=\frac{{\mathit{\omega }}_Y^T({\mathit{K}}_{YY}^2+\gamma {\mathit{K}}_{YY}){\mathit{\omega }}_Y-1}{2}=0. \end{gathered}$$ (C2)

Using the first equation of Eq.(C2), we solve for ω_X and obtain

$${\mathit{\omega }}_X={({\mathit{K}}_{XX}+\gamma \mathit{I})}^{-1}{\mathit{K}}_{YY}{\mathit{\omega }}_Y,$$ (C3)

where I is an unit matrix of the same size as K_XX. If ${\mathit{\omega }}_X^T\frac{\partial L}{\partial {\mathit{\omega }}_X}-{\mathit{\omega }}_Y^T\frac{\partial L}{\partial {\mathit{\omega }}_Y}$ is substituted with the expression of $\frac{\partial L}{\partial {\mathit{\omega }}_X}$ and $\frac{\partial L}{\partial {\mathit{\omega }}_Y}$ in Eq.(C2), we obtain

$${\lambda }_X-{\lambda }_Y-\lambda {\mathit{\omega }}_Y^T\frac{\partial \overline{F}}{\partial {\mathit{\omega }}_Y}=0.$$ (C4)

As long as the last term in Eq.(C4) is nonzero, we obtain λ_X ≠ λ_Y in general, and the penalized KCCA model is not an eigenvalue problem anymore.